Буквенные выражения
Буквенное выражение (или выражение с переменными) — это математическое выражение, которое состоит из чисел, букв и знаков математических операций. Например, следующее выражение является буквенным:
a + b + 4
С помощью буквенных выражений можно записывать законы, формулы, уравнения и функции. Умение манипулировать буквенными выражениями — залог хорошего знания алгебры и высшей математики.
Любая серьёзная задача в математике свóдится к решению уравнений. А чтобы уметь решать уравнения, нужно уметь работать с буквенными выражениями.
Чтобы работать с буквенными выражениями, нужно хорошо изучить базовую арифметику: сложение, вычитание, умножение, деление, основные законы математики, дроби, действия с дробями, пропорции. И не просто изучить, а понять досконально.
Переменные
Буквы, которые содержатся в буквенных выражениях, называются переменными.
Например, в выражении a + b + 4 переменными являются буквы  Если вместо этих переменных подставить любые числа, то буквенное выражение a + b + 4 обратится в числовое выражение, значение которого можно будет найти.
Если вместо этих переменных подставить любые числа, то буквенное выражение a + b + 4 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных a и b. Для изменения значений используется знак равенства
a = 2, b = 3
Мы изменили значения переменных a и b. Переменной a присвоили значение 2, переменной b присвоили значение 3. В результате буквенное выражение
2 + 3 + 4 = 9
Когда происходит умножение переменных, то они записываются вместе. Например, запись ab означает то же самое, что и запись a × b. Если подставить вместо переменных a и b числа 2 и 3, то мы получим 6
2 × 3 = 6
Слитно также можно записать умножение числа на выражение в скобках. Например, вместо a × (b + c) можно записать a(b + c). Применив распределительный закон умножения, получим a(b + c) = ab + ac
Например, вместо a × (b + c) можно записать a(b + c). Применив распределительный закон умножения, получим a(b + c) = ab + ac
Коэффициенты
В буквенных выражениях часто можно встретить запись, в которой число и переменная записаны вместе, например 3a. На самом деле это короткая запись умножения числа 3 на переменную a и эта запись выглядит как 3 × a.
Другими словами, выражение 3a является произведением числа 3 и переменной a. Число 3 в этом произведении называют коэффициентом. Этот коэффициент показывает во сколько раз будет увеличена переменная a. Данное выражение можно прочитать как «a три раза» или «трижды а«, или «увеличить значение переменной a в три раза», но наиболее часто читается как «три
К примеру, если переменная a равна 5, то значение выражения 3a будет равно 15.
3 × 5 = 15
Говоря простым языком, коэффициент это число, которое стоит перед буквой (перед переменной).
Букв может быть несколько, например 5abc. Здесь коэффициентом является число 5. Данный коэффициент показывает, что произведение переменных abc увеличивается в пять раз. Это выражение можно прочитать как «abc пять раз» либо «увеличить значение выражения abc в пять раз», либо «пять abc«.
Если вместо переменных abc подставить числа 2, 3 и 4, то значение выражения 5abc будет равно 120
5 × 2 × 3 × 4 = 120
Можно мысленно представить, как сначала перемнóжились числа 2, 3 и 4, и полученное значение увеличилось в пять раз:
Знак коэффициента отнóсится только к коэффициенту, и не отнóсится к переменным!
Рассмотрим выражение −6b. Минус, стоящий перед коэффициентом 6, отнóсится только к коэффициенту 6, и не отнóсится к переменной b. Понимание этого факта позвóлит не ошибаться в будущем со знаками.
Найдем значение выражения −6b при b = 3.
−6b это короткая форма записи от −6 × b. Для наглядности запишем выражение −6b в развёрнутом виде и подставим значение переменной b
−6b = −6 × b = −6 × 3 = −18
Пример 2. Найти значение выражения −6b при b = −5
Запишем выражение −6b в развёрнутом виде
−6b = −6 × b
и далее подставим значение переменной b
−6b = −6 × b = −6 × (−5) = 30
Пример 3. Найти значение выражения −5a + b при a =
−5a + b это короткая форма записи от −5 × a + b, поэтому для наглядности запишем выражение −5 × a + b в развёрнутом виде и подстáвим значения переменных a и b
−5a + b = −5 × a + b = −5 × 3 + 2 = −15 + 2 = −13
Иногда буквы записаны без коэффициента, например a или ab. В этом случае коэффициентом является единица:
В этом случае коэффициентом является единица:
1a, 1ab
но единицу по традиции не записывают, поэтому просто пишут a или ab
Если перед буквой стоит минус, то коэффициентом является число
−1 × a = −1a
Здесь крóется небольшой подвох. В выражении −a минус, стоящий перед переменной a на самом деле относится к невидимой единице, а не к переменной a. Поэтому при решении задач следует быть внимательным.
К примеру, если дано выражение −a и нас прóсят найти его значение при a = 2, то в школе мы подставляли двойку вместо переменной a и получали ответ
−a = −1 × a
−1 × a = −1 × 2 = −2
Если дано выражение −a и требуется найти его значение при a = −2, то мы подставляем −2 вместо переменной a
−a = −1 × a
−1 × a = −1 × (−2) = 2
Чтобы не допускать ошибок, первое время невидимые единицы можно записывать явно.
Пример 4. Найти значение выражения abc при a=2, b=3
Выражение abc это короткая форма записи от 1×a×b×c. Для наглядности запишем выражение abc в развёрнутом виде и подставим значения переменных a, b и c
1 × a × b × c = 1 × 2 × 3 × 4 = 24
Пример 5. Найти значение выражения abc при a=−2, b=−3 и c=−4
Запишем выражение abc в развёрнутом виде и подставим значения переменных a, b и c
1 × a × b × c = 1 × (−2) × (−3) × (−4) = −24
Пример 6. Найти значение выражения −abc при a=3, b=5 и c=7
Выражение −abc это короткая форма записи от
−abc = −1 × a × b × c = −1 × 3 × 5 × 7 = −105
Пример 7. Найти значение выражения −abc при a=−2, b=−4 и c=−3
Найти значение выражения −abc при a=−2, b=−4 и c=−3
Запишем выражение −abc в развёрнутом виде:
−abc = −1 × a × b × c
Подставим значение переменных a, b и c
−abc = −1 × a × b × c = −1 × (−2) × (−4) × (−3) = 24
Как определить коэффициент
Иногда требуется решить задачу, в которой требуется определить коэффициент выражения. В принципе, данная задача очень простá. Достаточно уметь правильно умножать числа.
Чтобы определить коэффициент в выражении, нужно отдельно перемножить числа, входящие в это выражение, и отдельно перемножить буквы. Получившийся числовой сомножитель и будет коэффициентом.
Пример 1. Определить коэффициент в выражении: 7m×5a×(−3)×n
Выражение состоит из нескольких сомножителей. Это можно отчетливо увидеть, если записать выражение в развёрнутом виде. То есть произведения 7m и 5a записать в виде 7×m и 5×a
7 × m × 5 × a × (−3) × n
Применим сочетательный закон умножения, который позволяет перемножать сомножители в любом порядке.
−3 × 7 × 5 × m × a × n = −105man
Коэффициент равен −105. После завершения буквенную часть желательно расположить в алфавитном порядке:
−105amn
Пример 2. Определить коэффициент в выражении: −a×(−3)×2
Перемножим отдельно числа и буквы:
−a × (−3 ) × 2 = −3 × 2 × (−a) = −6 × (−a) = 6a
Коэффициент равен 6.
Пример 3. Определить коэффициент в выражении:
Перемножим отдельно числа и буквы:
Коэффициент равен −1. Обратите внимание, что единица не записана, поскольку коэффициент 1 принято не записывать.
Эти казалось бы простейшие задачи могут сыграть с нами очень злую шутку. Часто выясняется, что знак коэффициента поставлен не верно: либо пропущен минус либо наоборот он поставлен зря. Чтобы избежать этих досадных ошибок, тема умножения целых чисел должна быть изучена на хорошем уровне.
Слагаемые в буквенных выражениях
При сложении нескольких чисел получается сумма этих чисел. Числа, которые складывают называют слагаемыми. Слагаемых может быть несколько, например:
1 + 2 + 3 + 4 + 5
Когда выражение состоит из слагаемых, вычислять его намного проще, поскольку складывать легче, чем вычитать. Но в выражении может присутствовать не только сложение, но и вычитание, например:
1 + 2 − 3 + 4 − 5
В этом выражении числа 3 и 5 являются вычитаемыми, а не слагаемыми. Но нам ничего не мешает, заменить вычитание сложением. Тогда мы снова получим выражение, состоящее из слагаемых:
1 + 2 + (−3) + 4 + (−5)
Не суть, что числа −3 и −5 теперь со знаком минус. Главное, что все числа в данном выражении соединены знаком сложения, то есть выражение является суммой.
Оба выражения 1 + 2 − 3 + 4 − 5 и 1 + 2 + (−3) + 4 + (−5) равны одному и тому значению — минус единице:
1 + 2 − 3 + 4 − 5 = −1
1 + 2 + (−3) + 4 + (−5) = −1
Таким образом, значение выражения не пострадает от того, что мы где-то заменим вычитание сложением.
Заменять вычитание сложением можно и в буквенных выражениях. Например, рассмотрим следующее выражение:
7a + 6b − 3c + 2d − 4s
Заменим вычитание сложением там, где это можно:
7a + 6b + (−3c) + 2d + (−4s)
При любых значениях переменных a, b, c, d и s выражения 7a + 6b − 3c + 2d − 4s и 7a + 6b + (−3c) + 2d + (−4s) будут равны одному и тому же значению.
Вы должны быть готовы к тому, что учитель в школе или преподаватель в институте может называть слагаемыми даже те числа (или переменные), которые ими не являются.
Например, если на доске будет записана разность a − b, то учитель не будет говорить, что a — это уменьшаемое, а b — вычитаемое. Обе переменные он назовет одним общим словом — слагаемые. А всё потому, что выражение вида a − b математик видит, как сумму a + (−b). В таком случае выражение становится суммой, а переменные a и (−b) станóвятся слагаемыми.
Подобные слагаемые
Подобные слагаемые — это слагаемые, которые имеют одинаковую буквенную часть.
Например, рассмотрим выражение 7a + 6b + 2a. Слагаемые 7a и 2a имеют одинаковую буквенную часть — переменную a. Значит слагаемые 7a и 2a являются подобными.
Обычно подобные слагаемые складывают, чтобы упростить выражение или решить какое-нибудь уравнение. Это действие называют приведéнием подобных слагаемых.
Чтобы привести подобные слагаемые, нужно сложить коэффициенты этих слагаемых, и полученный результат умножить на общую буквенную часть.
Например, приведём подобные слагаемые в выражении 3a + 4a + 5a. В данном случае подобными являются все слагаемые. Слóжим их коэффициенты и результат умножим на общую буквенную часть — на переменную a
3a + 4a + 5a = (3 + 4 + 5)×a = 12a
Подобные слагаемые обычно привóдят в уме и результат записывают сразу:
3a + 4a + 5a = 12a
Также, можно рассуждать следующим образом:
Было 3 переменные a, к ним прибавили еще 4 переменные a и ещё 5 переменных a. В итоге получили 12 переменных a
В итоге получили 12 переменных a
Если подсчитать на рисунке количество переменных a, то насчитается 12.
Рассмотрим несколько примеров на приведение подобных слагаемых. Учитывая, что данная тема очень важна, на первых порах будем записывать подробно каждую мелочь. Несмотря на то, что здесь всё очень просто, большинство людей допускают множество ошибок. В основном по невнимательности, а не по незнанию.
Пример 1. Привести подобные слагаемые в выражении 3a + 2a + 6a + 8a
Сложим коэффициенты в данном выражении и полученный результат умножим на общую буквенную часть:
3a + 2a + 6a + 8a= (3 + 2 + 6 + 8) × a = 19a
Конструкцию (3 + 2 + 6 + 8) × a можно не записывать, поэтому сразу запишем ответ
3a + 2a + 6a + 8a = 19a
Пример 2. Привести подобные слагаемые в выражении 2a + a
Второе слагаемое a записано без коэффициента, но на самом деле перед ним стоит коэффициент 1, который мы не видим по причине того, что его не записывают. Стало быть, выражение выглядит следующим образом:
Стало быть, выражение выглядит следующим образом:
2a + 1a
Теперь приведем подобные слагаемые. То есть сложим коэффициенты и результат умножим на общую буквенную часть:
2a + 1a = (2 + 1) × a = 3a
Запишем решение покороче:
2a + a = 3a
Приводя подобные слагаемые в выражении 2a+a, можно рассуждать и по-другому:
Было 2 переменные a, добавили ещё одну переменную a, в итоге получилось 3 переменные a.
Пример 3. Привести подобные слагаемые в выражении 2a − a
Заменим вычитание сложением:
2a + (−a)
Второе слагаемое (−a) записано без коэффициента, но на самом деле оно выглядит как (−1a). Коэффициент −1 опять же невидимый по причине того, что его не записывают. Стало быть, выражение выглядит следующим образом:
2a + (−1a)
Теперь приведем подобные слагаемые. Сложим коэффициенты и результат умножим на общую буквенную часть:
2a + (−1a) = (2 + (−1)) × a = 1a = a
Обычно записывают короче:
2a − a = a
Приводя подобные слагаемые в выражении 2a−a можно рассуждать и по-другому:
Было 2 переменные a, вычли одну переменную a, в итоге осталась одна единственная переменная a
Пример 4. Привести подобные слагаемые в выражении 6a − 3a + 4a − 8a
Привести подобные слагаемые в выражении 6a − 3a + 4a − 8a
Заменим вычитание сложение там, где это можно:
6a − 3a + 4a − 8a = 6a + (−3a) + 4a + (−8a)
Теперь приведем подобные слагаемые. Сложим коэффициенты и результат умножим на общую буквенную часть
(6 + (−3) + 4 + (−8)) × a = −1a = −a
Запишем решение покороче:
6a − 3a + 4a − 8a = −a
Встречаются выражения, которые содержат несколько различных групп подобных слагаемых. Например, 3a + 3b + 7a + 2b. Для таких выражений справедливы те же правила, что и для остальных, а именно складывание коэффициентов и умножение полученного результата на общую буквенную часть. Но чтобы не допустить ошибок, удобно разные группы слагаемых подчеркнуть разными линиями.
Например, в выражении 3a + 3b + 7a + 2b те слагаемые, которые содержат переменную a, можно подчеркнуть одной линией, а те слагаемые которые содержат переменную b, можно подчеркнуть двумя линиями:
Теперь можно привести подобные слагаемые. То есть сложить коэффициенты и полученный результат умножить на общую буквенную часть. Сделать это нужно для обеих групп слагаемых: для слагаемых, содержащих переменную a и для слагаемых содержащих переменную b.
То есть сложить коэффициенты и полученный результат умножить на общую буквенную часть. Сделать это нужно для обеих групп слагаемых: для слагаемых, содержащих переменную a и для слагаемых содержащих переменную b.
3a + 3b + 7a + 2b = (3+7)×a + (3 + 2)×b = 10a + 5b
Опять же повторимся, выражение несложное, и подобные слагаемые можно приводить в уме:
3a + 3b + 7a + 2b = 10a + 5b
Пример 5. Привести подобные слагаемые в выражении 5a − 6a −7b + b
Заменим вычитание сложение там, где это можно:
5a − 6a −7b + b = 5a + (−6a) + (−7b) + b
Подчеркнём подобные слагаемые разными линиями. Слагаемые, содержащие переменные a подчеркнем одной линией, а слагаемые содержащие переменные b, подчеркнем двумя линиями:
Теперь можно привести подобные слагаемые. То есть сложить коэффициенты и полученный результат умножить на общую буквенную часть:
5a + (−6a) + (−7b) + b = (5 + (−6))×a + ((−7) + 1)×b = −a + (−6b)
Если в выражении содержатся обычные числа без буквенных сомножителей, то они складываются отдельно.
Пример 6. Привести подобные слагаемые в выражении 4a + 3a − 5 + 2b + 7
Заменим вычитание сложением там, где это можно:
4a + 3a − 5 + 2b + 7 = 4a + 3a + (−5) + 2b + 7
Приведем подобные слагаемые. Числа −5 и 7 не имеют буквенных сомножителей, но они являются подобными слагаемыми — их необходимо просто сложить. А слагаемое 2b останется без изменений, поскольку оно единственное в данном выражении, имеющее буквенный сомножитель b, и его не с чем складывать:
4a + 3a + (−5) + 2b + 7 = (4 + 3)×a + 2b + (−5) + 7 = 7a + 2b + 2
Запишем решение покороче:
4a + 3a − 5 + 2b + 7 = 7a + 2b + 2
Слагаемые можно упорядочивать, чтобы те слагаемые, которые имеют одинаковую буквенную часть, располагались в одной части выражения.
Пример 7. Привести подобные слагаемые в выражении 5t+2x+3x+5t+x
Поскольку выражение является суммой из нескольких слагаемых, это позволяет нам вычислять его в любом порядке. Поэтому слагаемые, содержащие переменную t, можно записать в начале выражения, а слагаемые содержащие переменную x в конце выражения:
Поэтому слагаемые, содержащие переменную t, можно записать в начале выражения, а слагаемые содержащие переменную x в конце выражения:
5t + 5t + 2x + 3x + x
Теперь можно привести подобные слагаемые:
5t + 5t + 2x + 3x + x = (5+5)×t + (2+3+1)×x = 10t + 6x
Запишем решение покороче:
5t + 2x + 3x + 5t + x = 10t + 6x
Сумма противоположных чисел равна нулю. Это правило работает и для буквенных выражений. Если в выражении встретятся одинаковые слагаемые, но с противоположными знаками, то от них можно избавиться на этапе приведения подобных слагаемых. Иными словами, просто вычеркнуть их из выражения, поскольку их сумма равна нулю.
Пример 8. Привести подобные слагаемые в выражении 3t − 4t − 3t + 2t
Заменим вычитание сложением там, где это можно:
3t − 4t − 3t + 2t = 3t + (−4t) + (−3t) + 2t
Слагаемые 3t и (−3t) являются противоположными. Сумма противоположных слагаемых равна нулю. Если убрать этот ноль из выражения, то значение выражения не изменится, поэтому мы его и уберём. А уберём мы его обычным вычеркиванием слагаемых 3t и (−3t)
Сумма противоположных слагаемых равна нулю. Если убрать этот ноль из выражения, то значение выражения не изменится, поэтому мы его и уберём. А уберём мы его обычным вычеркиванием слагаемых 3t и (−3t)
В итоге у нас останется выражение (−4t) + 2t. В данном выражении можно привести подобные слагаемые и получить окончательный ответ:
(−4t) + 2t = ((−4) + 2)×t = −2t
Запишем решение покороче:
Упрощение выражений
Часто можно встретить задание, в котором сказано «упростите выражение» и далее приводится выражение, которое требуется упростить. Упростить выражение значит сделать его прóще и корóче.
На самом деле мы уже занимались упрощением выражений, когда сокращали дроби. После сокращения дробь становилась короче и проще для восприятия.
Рассмотрим следующий пример. Упростить выражение .
Это задание буквально можно понять так: «Примените к данному выражению любые допустимые действия, но сделайте его прóще».
В данном случае можно осуществить сокращение дроби, а именно разделить числитель и знаменатель дроби на 2:
Что ещё можно сделать? Можно вычислить полученную дробь . Тогда мы получим десятичную дробь 0,5
В итоге дробь упростилась до 0,5.
Первый вопрос, который нужно себе задавать при решении подобных задач, должен быть: «а что можно сделать?». Потому что есть действия, которые можно делать, и есть действия, которые делать нельзя.
Ещё один важный момент, о котором нужно помнить, заключается в том что значение выражение не должно измениться после упрощения выражения. Вернемся к выражению . Данное выражение представляет собой деление, которое можно выполнить. Выполнив это деление, мы получаем значение данного выражения, которое равно 0,5
Но мы упростили выражение и получили новое упрощённое выражение . Значение нового упрощённого выражения по-прежнему равно 0,5
Но выражение мы тоже попытались упростить, вычислив его. В итоге получили окончательный ответ 0,5.
В итоге получили окончательный ответ 0,5.
Таким образом, как бы мы не упрощали выражение, значение получаемых выражений по-прежнему равно 0,5. Значит упрощение выполнялось верно на каждом этапе. Именно к этому нужно стремиться при упрощении выражений — значение выражения не должно пострадать от наших действий.
Часто требуется упрощать буквенные выражения. Для них справедливы те же правила упрощения, что и для числовых выражений. Можно выполнять любые допустимые действия, лишь бы не изменилось значение выражения.
Рассмотрим несколько примеров.
Пример 1. Упростить выражение 5,21s × t × 2,5
Чтобы упростить данное выражение, можно отдельно перемножить числа и отдельно перемножить буквы. Это задание очень похоже на то, которое мы рассматривали, когда учились определять коэффициент:
5,21s × t × 2,5 = 5,21 × 2,5 × s × t = 13,025 × st = 13,025st
Таким образом, выражение 5,21s × t × 2,5 упростилось до 13,025st.
Пример 2. Упростить выражение −0,4 × (−6,3b) × 2
Второе произведение (−6,3b) можно перевести в понятный для нас вид, а именно записать в виде (−6,3)×b, затем отдельно перемножить числа и отдельно перемножить буквы:
−0,4 × (−6,3b) × 2 = −0,4 × (−6,3) × b × 2 = 5,04b
Таким образом, выражение −0,4 × (−6,3b) × 2 упростилось до 5,04b
Пример 3. Упростить выражение
Распишем данное выражение более подробно, чтобы хорошо увидеть, где числа, а где буквы:
Теперь отдельно перемножим числа и отдельно перемножим буквы:
Таким образом, выражение упростилось до −abc. Данное решение можно записать покороче:
При упрощении выражений, дроби можно сокращать в процессе решения, а не в самом конце, как мы это делали с обычными дробями. Например, если в ходе решения мы наткнёмся на выражение вида , то вовсе необязательно вычислять числитель и знаменатель и делать что-то вроде этого:
Дробь можно сократить, выбирая по множителю в числителе и в знаменателе и сокращать эти множители на их наибольший общий делитель. Другими словами, использовать короткую версию сокращения дроби, в которой мы не расписываем подробно на что был разделен числитель и знаменатель.
Другими словами, использовать короткую версию сокращения дроби, в которой мы не расписываем подробно на что был разделен числитель и знаменатель.
Например, в числителе множитель 12 и в знаменателе множитель 4 можно сократить на 4. Четвёрку храним в уме, а разделив 12 и 4 на эту четвёрку, ответы записываем рядом с этими числами, предварительно зачеркнув их
Далее в числителе множитель 9 и в знаменателе множитель 3 можно сократить на 3
Далее в числителе множитель 6 и в знаменателе множитель 2 можно сократить на 2
Теперь можно перемножить получившиеся маленькие множители. В данном случае их немного и можно перемножить в уме:
Со временем можно обнаружить, что решая ту или иную задачу, выражения начинают «толстеть», поэтому желательно приучиться к быстрым вычислениям. То, что можно вычислить в уме, нужно вычислять в уме. То, что можно быстро сократить, нужно быстро сокращать.
Пример 4. Упростить выражение
Перемножим отдельно числа и отдельно буквы:
Таким образом, выражение упростилось до
Пример 5. Упростить выражение
Упростить выражение
Перемножим отдельно числа и отдельно буквы:
Таким образом, выражение упростилось до mn.
Пример 6. Упростить выражение
Запишем данное выражение более подробно, чтобы хорошо увидеть, где числа, а где буквы:
Теперь отдельно перемножим числа и отдельно буквы. Для удобства вычислений десятичную дробь −6,4 и смешанное число можно перевести в обыкновенные дроби:
Таким образом, выражение упростилось до
Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:
Пример 7. Упростить выражение
Перемножим отдельно числа и отдельно буквы. Для удобства вычисления смешанное число и десятичные дроби 0,1 и 0,6 можно перевести в обыкновенные дроби:
Таким образом, выражение упростилось до abcd. Если пропустить подробности, то данное решение можно записать значительно короче:
Обратите внимание на то, как сократилась дробь. Новые множители, которые получаются в результате сокращения предыдущих множителей, тоже допускается сокращать.
Новые множители, которые получаются в результате сокращения предыдущих множителей, тоже допускается сокращать.
Теперь поговорим о том, чего делать нельзя. При упрощении выражений категорически нельзя перемножать числа и буквы, если выражение является суммой, а не произведением.
Например, если требуется упростить выражение 5a + 4b, то нельзя записывать следующим образом:
Это равносильно тому, что если бы нас попросили сложить два числа, а мы бы их перемножали вместо того, чтобы складывать.
При подстановке любых значений переменных a и b выражение 5a +4b обращается в обыкновенное числовое выражение. Предположим, что переменные a и b имеют следующие значения:
a = 2, b = 3
Тогда значение выражения будет равно 22
5a + 4b = 5 × 2 + 4 × 3 = 10 + 12 = 22
Сначала выполняется умножение, а затем полученные результаты складывают. А если бы мы попытались упростить данное выражение, перемножив числа и буквы, то получилось бы следующее:
5a + 4b = 5 × 4 × a × b = 20ab
20ab = 20 × 2 × 3 = 120
Получается совсем другое значение выражения. В первом случае получилось 22, во втором случае 120. Это означает, что упрощение выражения 5a + 4b было выполнено неверно.
В первом случае получилось 22, во втором случае 120. Это означает, что упрощение выражения 5a + 4b было выполнено неверно.
После упрощения выражения, его значение не должно изменяться при одних и тех же значениях переменных. Если при подстановке в изначальное выражение любых значений переменных получается одно значение, то после упрощения выражения должно получаться то же самое значение, что и до упрощения.
С выражением 5a + 4b на самом деле ничего делать нельзя. Оно не упрощается.
Если в выражении содержатся подобные слагаемые, то их можно сложить, если нашей целью является упрощение выражения.
Пример 8. Упростить выражение 0,3a−0,4a+a
Чтобы упростить данное выражение можно привести подобные слагаемые:
0,3a − 0,4a + a = 0,3a + (−0,4a) + a = (0,3 + (−0,4) + 1)×a = 0,9a
или покороче: 0,3a − 0,4a + a = 0,9a
Таким образом, выражение 0,3a−0,4a+a упростилось до 0,9a
Пример 9. Упростить выражение −7,5a − 2,5b + 4a
Упростить выражение −7,5a − 2,5b + 4a
Чтобы упростить данное выражение можно привести подобные слагаемые:
−7,5a − 2,5b + 4a = −7,5a + (−2,5b) + 4a = ((−7,5) + 4)×a + (−2,5b) = −3,5a + (−2,5b)
или покороче −7,5a − 2,5b + 4a = −3,5a + (−2,5b)
Слагаемое (−2,5b) осталось без изменений, поскольку его не с чем было складывать.
Пример 10. Упростить выражение
Чтобы упростить данное выражение можно привести подобные слагаемые:
Коэффициент был переведён в неправильную дробь для удобства вычисления.
Таким образом, выражение упростилось до
Пример 11. Упростить выражение
Чтобы упростить данное выражение можно привести подобные слагаемые:
Таким образом, выражение упростилось до .
В данном примере целесообразнее было бы сложить первый и последний коэффициент в первую очередь. В этом случае мы получили бы короткое решение. Выглядело бы оно следующим образом:
Выглядело бы оно следующим образом:
Пример 12. Упростить выражение
Чтобы упростить данное выражение можно привести подобные слагаемые:
Таким образом, выражение упростилось до.
Слагаемое осталось без изменения, поскольку его не с чем было складывать.
Данное решение можно записать значительно короче. Выглядеть оно будет следующим образом:
В коротком решении пропущены этапы замены вычитания сложением и подробная запись, как дроби приводились к общему знаменателю.
Ещё одно различие заключается в том, что в подробном решении ответ выглядит как , а в коротком как . На самом деле, это одно и то же выражение. Различие в том, что в первом случае вычитание заменено сложением, поскольку в начале когда мы записывали решение в подробном виде, мы везде где можно заменили вычитание сложением, и эта замена сохранилась и для ответа.
Тождества. Тождественно равные выражения
После того как мы упростили какое-нибудь выражение, оно станóвится проще и короче. Чтобы проверить верно ли упрощено выражение, достаточно подстáвить любые значения переменных сначала в предыдущее выражение, которое требовалось упростить, а затем в новое, которое упростили. Если значение в обоих выражениях будет одинаковым, то это означает, что выражение упрощено верно.
Чтобы проверить верно ли упрощено выражение, достаточно подстáвить любые значения переменных сначала в предыдущее выражение, которое требовалось упростить, а затем в новое, которое упростили. Если значение в обоих выражениях будет одинаковым, то это означает, что выражение упрощено верно.
Рассмотрим простейший пример. Пусть требуется упростить выражение 2a × 7b. Чтобы упростить данное выражение, можно по-отдельности перемнóжить числа и буквы:
2a × 7b = 2 × 7 × a × b = 14ab
Проверим верно ли мы упростили выражение. Для этого подставим любые значения переменных a и b сначала в первое выражение, которое требовалось упростить, а затем во второе, которое упростили.
Пусть значения переменных a, b будут следующими:
a = 4
b = 5
Подстáвим их в первое выражение 2a × 7b
2a × 7b = 2 × 4 × 7 × 5 = 280
Теперь подстáвим те же значения переменных в выражение, которое получилось в результате упрощения выражения 2a × 7b, а именно в выражение 14ab
14ab = 14 × 4 × 5 = 280
Видим, что при a = 4 и b = 5 значение первого выражения 2a × 7b и значение второго выражения 14ab равны
2a × 7b = 2 × 4 × 7 × 5 = 280
14ab = 14 × 4 × 5 = 280
То же самое произойдет и для любых других значений. Например, пусть a = 1 и b = 2
Например, пусть a = 1 и b = 2
2a × 7b = 2 × 1 × 7 × 2 = 28
14ab = 14 × 1 × 2 = 28
Таким образом, выражения 2a × 7b и 14ab при любых значениях переменных равны одному и тому же значению. Такие выражения называют тождественно равными.
Делаем вывод, что между выражениями 2a × 7b и 14ab можно поставить знак равенства, поскольку они равны одному и тому же значению:
2a × 7b = 14ab
Равенством называют любое выражение, которые соединено знаком равенства (=).
А равенство вида 2a × 7b = 14ab называют тождеством.
Тождеством называют равенство, которое верно при любых значениях переменных.
Другие примеры тождеств:
a + b = b + a
a(b + c) = ab + ac
a(bc) = (ab)c
Да, законы математики, которые мы изучали, являются тождествами.
Верные числовые равенства тоже являются тождествами. Например:
2 + 2 = 4
3 + 3 = 5 + 1
10 = 7 + 2 + 1
Решая сложную задачу, чтобы облегчить себе вычисление, сложное выражение заменяют на более простое выражение, тождественно равное предыдущему. Такую замену называют тождественным преобразованием выражения или просто преобразованием выражения.
Например, мы упростили выражение 2a × 7b, и получили более простое выражение 14ab. Это упрощение можно называть тождественным преобразованием.
Часто можно встретить задание, в котором сказано «докажите, что равенство является тождеством» и далее приводится равенство, которое требуется доказать. Обычно это равенство состоит из двух частей: левой и правой части равенства. Наша задача состоит в том, чтобы выполнить тождественные преобразования с одной из частей равенства и получить другую часть. Либо выполнить тождественные преобразования с обеими частями равенства и сделать так, чтобы в обеих частях равенства оказались одинаковые выражения.
Например, докажем, что равенство 0,5a × 5b = 2,5ab является тождеством.
Упростим левую часть этого равенства. Для этого перемножим числа и буквы по отдельности:
0,5 × 5 × a × b = 2,5ab
2,5ab = 2,5ab
В результате небольшого тождественного преобразования, левая часть равенства стала равна правой части равенства. Значит мы доказали, что равенство 0,5a × 5b = 2,5ab является тождеством.
Из тождественных преобразований мы научились складывать, вычитать, умножать и делить числа, сокращать дроби, приводить подобные слагаемые, а также упрощать некоторые выражения.
Но это далеко не все тождественные преобразования, которые существуют в математике. Тождественных преобразований намного больше. В будущем мы ещё не раз в этом убедимся.
Задания для самостоятельного решения: Задание 1. Найдите значение выражения при и Задание 2. Найдите значение выражения при Задание 4. Найдите значение выражения при и
Найдите значение выражения при иЗадание 5. Запишите в виде буквенного выражения следующую последовательность действий:
- Число a умножить на три, и из этого произведения вычесть пятнадцать
- Число t умножить на девять, и к полученному произведению прибавить тридцать пять
Задание 6. Приведите подобные слагаемые в следующем выражении:
Задание 7. Приведите подобные слагаемые в следующем выражении:
Задание 8. Приведите подобные слагаемые в следующем выражении:
Задание 9. Приведите подобные слагаемые в следующем выражении:
Задание 10. Приведите подобные слагаемые в следующем выражении:
Задание 11. Упростите выражение:
Задание 12. Упростите выражение:
Задание 13. Упростите выражение:
Задание 14. Упростите выражение:
Задание 15. Упростите выражение:
Задание 16. Упростите выражение:
Упростите выражение:
Задание 17. Упростите выражение:
Задание 18. Упростите выражение:
Задание 19. Упростите выражение:
Задание 20. Упростите выражение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Какие из следующих выражений имеют значение, равное 1:
представь котангенс как частное и приведи к общему знаменателю. тогда в числителе формула синуса суммы двух углов ,а в знаменателе синус Х
получается синус 4Х деленное на синус Х равен синус 4Х
перенгосим и преобразуем . получается
(синус 4Х умноженное на (1-синусХ))/синус Х =0
первое решение синус 4х=0 х=пк/4. от 0 до 2п к=0 ,1,2,3,4,5,6,7,8
от 0 до 2п к=0 ,1,2,3,4,5,6,7,8
второе решение синус х равен 1. х= п/2+пк второе включается в первое…значит число корней 8.
1)
3,26*(-10)=-32,6
3,26*(-100)=-326
2)
2/11*(-13+2)=2/11*(-11)=-22/11=-2
3)
-0,8*(-10)*(-0,5)=-4
4)
-3/4*(5-13)=-3/4*(-8)=24/4=6
4 580 м = 4 км 580 м
2 500 см = 250 дм = 25000 мм
25 км 500 м = 25 500 м = 255000 дм
25036 см = 250 м 3 дм 6 см
2007 м = 2 км 70 дм ( 700 см )
4 580 м = 458000
25036 см = 250360 мм
10 кв. см = 1000 кв. мм
1 кв. м = 1000 см кв. = 10000 мм кв.
1000000 кв. м = 100 кв. км
Определение. Параллельные прямые — это две непересекающиеся прямые, лежащие в одной плоскости. Параллельные прямые записываются через знак параллельности «||».На рисунках 6 и 7 показаны параллельные прямыеAD и BC. Запись параллельности прямых: AD || BC.Свойства параллельных прямых1. Если одна из Пары параллельных прямых параллельна третьей прямой, то и другая прямая параллельна третьей прямой (рис. 8). Если AB || CD и AB || MN, то и CD || MN.2. В одной плоскости с заданной прямой через точку, лежащую вне прямой, можно провести только одну прямую, параллельную заданной прямой (рис. 9). Через точку C можно провести только MN || AB.3. Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны друг другу (рис. 10). Если MN ⊥ AB и MN ⊥ CD, то AB || CD.
Параллельные прямые — это две непересекающиеся прямые, лежащие в одной плоскости. Параллельные прямые записываются через знак параллельности «||».На рисунках 6 и 7 показаны параллельные прямыеAD и BC. Запись параллельности прямых: AD || BC.Свойства параллельных прямых1. Если одна из Пары параллельных прямых параллельна третьей прямой, то и другая прямая параллельна третьей прямой (рис. 8). Если AB || CD и AB || MN, то и CD || MN.2. В одной плоскости с заданной прямой через точку, лежащую вне прямой, можно провести только одну прямую, параллельную заданной прямой (рис. 9). Через точку C можно провести только MN || AB.3. Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны друг другу (рис. 10). Если MN ⊥ AB и MN ⊥ CD, то AB || CD.
4a-4b, при a-b=45
=> 45×4=180, т. к. мы берём a-b 4 раза
к. мы берём a-b 4 раза
100 NumPy задач | Python 3 для начинающих и чайников
100 (на самом деле, пока меньше) задач для NumPy, перевод английского варианта https://github.com/rougier/numpy-100
Импортировать NumPy под именем np
Напечатать версию и конфигурацию
print(np.__version__) np.show_config()
Создать вектор (одномерный массив) размера 10, заполненный нулями
Z = np.zeros(10) print(Z)
Создать вектор размера 10, заполненный единицами
Создать вектор размера 10, заполненный числом 2.5
Z = np.full(10, 2.5) print(Z)
Как получить документацию о функции numpy.add из командной строки?
python3 -c "import numpy; numpy.info(numpy.add)"
Создать вектор размера 10, заполненный нулями, но пятый элемент равен 1
Z = np.zeros(10) Z[4] = 1 print(Z)
Создать вектор со значениями от 10 до 49
Z = np.arange(10,50) print(Z)
Развернуть вектор (первый становится последним)
Z = np.arange(50) Z = Z[::-1]
Создать матрицу (двумерный массив) 3×3 со значениями от 0 до 8
Z = np.arange(9).reshape(3,3) print(Z)
Найти индексы ненулевых элементов в [1,2,0,0,4,0]
nz = np.nonzero([1,2,0,0,4,0]) print(nz)
Создать 3×3 единичную матрицу
Создать массив 3x3x3 со случайными значениями
Z = np.random.random((3,3,3)) print(Z)
Создать массив 10×10 со случайными значениями, найти минимум и максимум
Z = np.random.random((10,10)) Zmin, Zmax = Z.min(), Z.max() print(Zmin, Zmax)
Создать случайный вектор размера 30 и найти среднее значение всех элементов
Z = np.random.random(30) m = Z.mean() print(m)
Создать матрицу с 0 внутри, и 1 на границах
Z = np.ones((10,10)) Z[1:-1,1:-1] = 0
Выяснить результат следующих выражений
0 * np.nan np.nan == np.nan np.inf > np.nan np.nan - np.nan 0.3 == 3 * 0.1
Создать 5×5 матрицу с 1,2,3,4 под диагональю
Z = np.diag(np.arange(1, 5), k=-1) print(Z)
Создать 8×8 матрицу и заполнить её в шахматном порядке
Z = np.zeros((8,8), dtype=int) Z[1::2,::2] = 1 Z[::2,1::2] = 1 print(Z)
Дан массив размерности (6,7,8). Каков индекс (x,y,z) сотого элемента?
print(np.unravel_index(100, (6,7,8)))
Создать 8×8 матрицу и заполнить её в шахматном порядке, используя функцию tile
Z = np.tile(np.array([[0,1],[1,0]]), (4,4)) print(Z)
Перемножить матрицы 5×3 и 3×2
Z = np.dot(np.ones((5,3)), np.ones((3,2))) print(Z)
Дан массив, поменять знак у элементов, значения которых между 3 и 8
Z = np.arange(11) Z[(3 < Z) & (Z <= 8)] *= -1
Создать 5×5 матрицу со значениями в строках от 0 до 4
Z = np.zeros((5,5)) Z += np.arange(5) print(Z)
Есть генератор, сделать с его помощью массив
def generate():
for x in xrange(10):
yield x
Z = np.fromiter(generate(),dtype=float,count=-1)
print(Z)Создать вектор размера 10 со значениями от 0 до 1, не включая ни то, ни другое
Z = np.linspace(0,1,12)[1:-1] print(Z)
Отсортировать вектор
Z = np.random.random(10) Z.sort() print(Z)
Проверить, одинаковы ли 2 numpy массива
A = np.random.randint(0,2,5) B = np.random.randint(0,2,5) equal = np.allclose(A,B) print(equal)
Сделать массив неизменяемым
Z = np.zeros(10) Z.flags.writeable = False Z[0] = 1
Дан массив 10×2 (точки в декартовой системе координат), преобразовать в полярную
Z = np.random.random((10,2)) X,Y = Z[:,0], Z[:,1] R = np.hypot(X, Y) T = np.arctan2(Y,X) print(R) print(T)
Заменить максимальный элемент на ноль
Z = np.random.random(10) Z[Z.argmax()] = 0 print(Z)
Создать структурированный массив с координатами x, y на сетке в квадрате [0,1]x[0,1]
Z = np.zeros((10,10), [('x',float),('y',float)])
Z['x'], Z['y'] = np.meshgrid(np.linspace(0,1,10),
np.linspace(0,1,10))
print(Z)Из двух массивов сделать матрицу Коши C (Cij = 1/(xi — yj))
X = np.arange(8) Y = X + 0.5 C = 1.0 / np.subtract.outer(X, Y) print(np.linalg.det(C))
Найти минимальное и максимальное значение, принимаемое каждым числовым типом numpy
for dtype in [np.int8, np.int32, np.int64]: print(np.iinfo(dtype).min) print(np.iinfo(dtype).max) for dtype in [np.float32, np.float64]: print(np.finfo(dtype).min) print(np.finfo(dtype).max) print(np.finfo(dtype).eps)
Напечатать все значения в массиве
np.set_printoptions(threshold=np.nan) Z = np.zeros((25,25)) print(Z)
Найти ближайшее к заданному значению число в заданном массиве
Z = np.arange(100) v = np.random.uniform(0,100) index = (np.abs(Z-v)).argmin() print(Z[index])
Создать структурированный массив, представляющий координату (x,y) и цвет (r,g,b)
Z = np.zeros(10, [ ('position', [ ('x', float, 1),
('y', float, 1)]),
('color', [ ('r', float, 1),
('g', float, 1),
('b', float, 1)])])
print(Z)Дан массив (100,2) координат, найти расстояние от каждой точки до каждой
import scipy.spatial Z = np.random.random((10,2)) D = scipy.spatial.distance.cdist(Z,Z) print(D)
Преобразовать массив из float в int
Z = np.arange(10, dtype=np.int32) Z = Z.astype(np.float32, copy=False)
Дан файл:
1,2,3,4,5 6,,,7,8 ,,9,10,11
Как прочитать его?
Z = np.genfromtxt("missing.dat", delimiter=",")Каков эквивалент функции enumerate для numpy массивов?
Z = np.arange(9).reshape(3,3) for index, value in np.ndenumerate(Z): print(index, value) for index in np.ndindex(Z.shape): print(index, Z[index])
Сформировать 2D массив с распределением Гаусса
X, Y = np.meshgrid(np.linspace(-1,1,10), np.linspace(-1,1,10)) D = np.hypot(X, Y) sigma, mu = 1.0, 0.0 G = np.exp(-((D - mu) ** 2 / (2.0 * sigma ** 2))) print(G)
Случайно расположить p элементов в 2D массив
n = 10 p = 3 Z = np.zeros((n,n)) np.put(Z, np.random.choice(range(n*n), p, replace=False), 1)
Отнять среднее из каждой строки в матрице
X = np.random.rand(5, 10) Y = X - X.mean(axis=1, keepdims=True)
Отсортировать матрицу по n-ому столбцу
Z = np.random.randint(0,10,(3,3)) n = 1 # Нумерация с нуля print(Z) print(Z[Z[:,n].argsort()])
Определить, есть ли в 2D массиве нулевые столбцы
Z = np.random.randint(0,3,(3,10)) print((~Z.any(axis=0)).any())
Дан массив, добавить 1 к каждому элементу с индексом, заданным в другом массиве (осторожно с повторами)
Z = np.ones(10) I = np.random.randint(0,len(Z),20) Z += np.bincount(I, minlength=len(Z)) print(Z)
Дан массив (w,h,3) (картинка) dtype=ubyte, посчитать количество различных цветов
w,h = 16,16 I = np.random.randint(0, 2, (h,w,3)).astype(np.ubyte) F = I[...,0] * 256 * 256 + I[...,1] * 256 + I[...,2] n = len(np.unique(F)) print(np.unique(I))
Дан четырехмерный массив, посчитать сумму по последним двум осям
A = np.random.randint(0,10, (3,4,3,4)) sum = A.reshape(A.shape[:-2] + (-1,)).sum(axis=-1) print(sum)
Найти диагональные элементы произведения матриц
# Slow version
np.diag(np.dot(A, B))
# Fast version
np.sum(A * B.T, axis=1)
# Faster version
np.einsum("ij,ji->i", A, B).Дан вектор [1, 2, 3, 4, 5], построить новый вектор с тремя нулями между каждым значением
Z = np.array([1,2,3,4,5]) nz = 3 Z0 = np.zeros(len(Z) + (len(Z)-1)*(nz)) Z0[::nz+1] = Z print(Z0)
Поменять 2 строки в матрице
A = np.arange(25).reshape(5,5) A[[0,1]] = A[[1,0]] print(A)
Рассмотрим набор из 10 троек, описывающих 10 треугольников (с общими вершинами), найти множество уникальных отрезков, составляющих все треугольники
faces = np.random.randint(0,100,(10,3))
F = np.roll(faces.repeat(2,axis=1),-1,axis=1)
F = F.reshape(len(F)*3,2)
F = np.sort(F,axis=1)
G = F.view( dtype=[('p0',F.dtype),('p1',F.dtype)] )
G = np.unique(G)
print(G)Дан массив C; создать массив A, что np.bincount(A) == C
C = np.bincount([1,1,2,3,4,4,6]) A = np.repeat(np.arange(len(C)), C) print(A)
Посчитать среднее, используя плавающее окно
def moving_average(a, n=3):
ret = np.cumsum(a, dtype=float)
ret[n:] = ret[n:] - ret[:-n]
return ret[n - 1:] / n
print(moving_average(np.arange(20), 3))Дан вектор Z, построить матрицу, первая строка которой (Z[0],Z[1],Z[2]), каждая последующая сдвинута на 1 (последняя (Z[-3],Z[-2],Z[-1]))
from numpy.lib import stride_tricks def rolling(a, window): shape = (a.size - window + 1, window) strides = (a.itemsize, a.itemsize) return stride_tricks.as_strided(a, shape=shape, strides=strides) Z = rolling(np.arange(10), 3) print(Z)
Инвертировать булево значение, или поменять знак у числового массива без создания нового
Z = np.random.randint(0,2,100) np.logical_not(arr, out=arr) Z = np.random.uniform(-1.0,1.0,100) np.negative(arr, out=arr)
Рассмотрим 2 набора точек P0, P1 описания линии (2D) и точку р, как вычислить расстояние от р до каждой линии i (P0[i],P1[i])
def distance(P0, P1, p):
T = P1 - P0
L = (T**2).sum(axis=1)
U = -((P0[:,0] - p[...,0]) * T[:,0] + (P0[:,1] - p[...,1]) * T[:,1]) / L
U = U.reshape(len(U),1)
D = P0 + U * T - p
return np.sqrt((D**2).sum(axis=1))
P0 = np.random.uniform(-10,10,(10,2))
P1 = np.random.uniform(-10,10,(10,2))
p = np.random.uniform(-10,10,( 1,2))
print(distance(P0, P1, p))Дан массив. Написать функцию, выделяющую часть массива фиксированного размера с центром в данном элементе (дополненное значением fill если необходимо)
Написать функцию, выделяющую часть массива фиксированного размера с центром в данном элементе (дополненное значением fill если необходимо)
Z = np.random.randint(0,10, (10,10)) shape = (5,5) fill = 0 position = (1,1) R = np.ones(shape, dtype=Z.dtype)*fill P = np.array(list(position)).astype(int) Rs = np.array(list(R.shape)).astype(int) Zs = np.array(list(Z.shape)).astype(int) R_start = np.zeros((len(shape),)).astype(int) R_stop = np.array(list(shape)).astype(int) Z_start = (P - Rs//2) Z_stop = (P + Rs//2)+Rs%2 R_start = (R_start - np.minimum(Z_start, 0)).tolist() Z_start = (np.maximum(Z_start, 0)).tolist() R_stop = np.maximum(R_start, (R_stop - np.maximum(Z_stop-Zs,0))).tolist() Z_stop = (np.minimum(Z_stop,Zs)).tolist() r = [slice(start,stop) for start,stop in zip(R_start,R_stop)] z = [slice(start,stop) for start,stop in zip(Z_start,Z_stop)] R[r] = Z[z] print(Z) print(R)
Посчитать ранг матрицы
Z = np.random.uniform(0,1,(10,10)) rank = np.linalg.matrix_rank(Z)
Найти наиболее частое значение в массиве
Z = np.random.randint(0,10,50) print(np.bincount(Z).argmax())
Извлечь все смежные 3×3 блоки из 10×10 матрицы
Z = np.random.randint(0,5,(10,10)) n = 3 i = 1 + (Z.shape[0] - n) j = 1 + (Z.shape[1] - n) C = stride_tricks.as_strided(Z, shape=(i, j, n, n), strides=Z.strides + Z.strides) print(C)
Создать подкласс симметричных 2D массивов (Z[i,j] == Z[j,i])
# Note: only works for 2d array and value setting using indices
class Symetric(np.ndarray):
def __setitem__(self, (i,j), value):
super(Symetric, self).__setitem__((i,j), value)
super(Symetric, self).__setitem__((j,i), value)
def symetric(Z):
return np.asarray(Z + Z.T - np.diag(Z.diagonal())).view(Symetric)
S = symetric(np.random.randint(0,10,(5,5)))
S[2,3] = 42
print(S)Рассмотрим множество матриц (n,n) и множество из p векторов (n,1). Посчитать сумму p произведений матриц (результат имеет размерность (n,1))
p, n = 10, 20 M = np.ones((p,n,n)) V = np.ones((p,n,1)) S = np.tensordot(M, V, axes=[[0, 2], [0, 1]]) print(S) # It works, because: # M is (p,n,n) # V is (p,n,1) # Thus, summing over the paired axes 0 and 0 (of M and V independently), # and 2 and 1, to remain with a (n,1) vector.
Дан массив 16×16, посчитать сумму по блокам 4×4
Z = np.ones((16,16))
k = 4
S = np.add.reduceat(np.add.reduceat(Z, np.arange(0, Z.shape[0], k), axis=0),
np.arange(0, Z.shape[1], k), axis=1)Написать игру «жизнь»
def iterate(Z):
# Count neighbours
N = (Z[0:-2,0:-2] + Z[0:-2,1:-1] + Z[0:-2,2:] +
Z[1:-1,0:-2] + Z[1:-1,2:] +
Z[2: ,0:-2] + Z[2: ,1:-1] + Z[2: ,2:])
# Apply rules
birth = (N == 3) & (Z[1:-1,1:-1]==0)
survive = ((N == 2) | (N == 3)) & (Z[1:-1,1:-1] == 1)
Z[...] = 0
Z[1:-1,1:-1][birth | survive] = 1
return Z
Z = np.random.randint(0,2,(50,50))
for i in range(100):
print(Z)
Z = iterate(Z)Найти n наибольших значений в массиве
Z = np.arange(10000) np.random.shuffle(Z) n = 5 print (Z[np.argpartition(-Z,n)[:n]])
Построить прямое произведение массивов (все комбинации с каждым элементом)
def cartesian(arrays):
arrays = [np.asarray(a) for a in arrays]
shape = map(len, arrays)
ix = np.indices(shape, dtype=int)
ix = ix.reshape(len(arrays), -1).T
for n, arr in enumerate(arrays):
ix[:, n] = arrays[n][ix[:, n]]
return ix
print(cartesian(([1, 2, 3], [4, 5], [6, 7])))Даны 2 массива A (8×3) и B (2×2). Найти строки в A, которые содержат элементы из каждой строки в B, независимо от порядка элементов в B
A = np.random.randint(0,5,(8,3)) B = np.random.randint(0,5,(2,2)) C = (A[..., np.newaxis, np.newaxis] == B) rows = (C.sum(axis=(1,2,3)) >= B.shape[1]).nonzero()[0] print(rows)
Дана 10×3 матрица, найти строки из неравных значений (например [2,2,3])
Z = np.random.randint(0,5,(10,3)) E = np.logical_and.reduce(Z[:,1:] == Z[:,:-1], axis=1) U = Z[~E] print(Z) print(U)
Преобразовать вектор чисел в матрицу бинарных представлений
I = np.array([0, 1, 2, 3, 15, 16, 32, 64, 128], dtype=np.uint8) print(np.unpackbits(I[:, np.newaxis], axis=1))
Дан двумерный массив. Найти все различные строки
Z = np.random.randint(0, 2, (6,3)) T = np.ascontiguousarray(Z).view(np.dtype((np.void, Z.dtype.itemsize * Z.shape[1]))) _, idx = np.unique(T, return_index=True) uZ = Z[idx] print(uZ)
Даны векторы A и B, написать einsum эквиваленты функций inner, outer, sum и mul
# Make sure to read: http://ajcr.net/Basic-guide-to-einsum/
np.einsum('i->', A) # np.sum(A)
np.einsum('i,i->i', A, B) # A * B
np.einsum('i,i', A, B) # np.inner(A, B)
np.einsum('i,j', A, B) # np.outer(A, B)Иллюстративная математика
Задача
Какие из следующих выражений эквивалентны? Почему? Если выражение не имеет соответствия, напишите 2 эквивалентных выражения, чтобы оно соответствовало.
- $ 2 (x + 4) $
- $ 8 + 2x $
- $ 2x + 4 $
- $ 3 (x + 4) — (4 + x) долларов США
- $ x + 4 $
Комментарий IM
В этой задаче мы должны преобразовать выражения, используя коммутативные, ассоциативные и распределительные свойства, чтобы решить, какие выражения эквивалентны. Исправлены распространенные ошибки, такие как неправильное распределение 2. Эта задача также касается 6.EE.3.
Исправлены распространенные ошибки, такие как неправильное распределение 2. Эта задача также касается 6.EE.3.
Решение
Во-первых, мы замечаем, что выражения в (a) и (d) можно переписать так, чтобы они не содержали круглых скобок.
Чтобы переписать (a), мы можем использовать свойство распределения: $ 2 (x + 4) = 2x + 8 $
Переписать (d):
$$ \ begin {alignat} {2} 3 (x + 4) — (4 + x) & = 3 (x + 4) — (x + 4) & \ qquad & \ text {с использованием коммутативного свойства сложения} \\ & = (3-1) (x + 4) & \ qquad & \ text {с использованием свойства распределения} \\ & = 2 (х + 4) & \ qquad & \\ & = 2x + 8 & \ qquad & \ text {снова используя свойство распределения} \ end {alignat} $$
Итак, пять выражений эквивалентны:
- $ 2x + 8 $
- $ 8 + 2x $
- $ 2x + 4 $
- $ 2x + 8 $
- $ x + 4 $
Сразу видно, что выражения (a), (b) и (d) эквивалентны, поскольку сложение коммутативно: $ 2x + 8 = 8 + 2x $. Теперь нам нужно только проверить (c) и (e). Если $ x = 0 $, (c) и (e) имеют значение 4, тогда как (a), (b) и (d) имеют значение 8. Итак, (c) и (e) не эквивалентны ( а), (б) и (г). Более того, если $ x = 1 $, то (c) имеет значение 6, а (e) имеет значение 5, поэтому эти два выражения также не эквивалентны.
Теперь нам нужно только проверить (c) и (e). Если $ x = 0 $, (c) и (e) имеют значение 4, тогда как (a), (b) и (d) имеют значение 8. Итак, (c) и (e) не эквивалентны ( а), (б) и (г). Более того, если $ x = 1 $, то (c) имеет значение 6, а (e) имеет значение 5, поэтому эти два выражения также не эквивалентны.
Для (c) мы можем использовать свойство распределения и разложить одно из чисел, чтобы записать два эквивалентных выражения:
$$ \ begin {align} & 2x + 4 \\ & 2 (х + 2) \\ & 2 (x + 1 + 1) \ end {align} $$
Возможны многие другие эквивалентные выражения.
Для (e) мы можем складывать и вычитать одно и то же число или один и тот же член, чтобы записать два эквивалентных выражения:
$$ \ begin {align} & х + 4 \\ & х + 4 + 7-7 \\ & 3x -3x + x +4 \ end {align} $$
Возможны многие другие эквивалентные выражения.
переменных и выражений | Безграничная алгебра
Введение в переменные
Переменные используются в математике для обозначения произвольных или неизвестных чисел.
Цели обучения
Опишите использование переменных в математике
Основные выводы
Ключевые моменты
- Переменные, как правило, представляют собой буквенные символы, которые представляют числа и используются в математике для нескольких целей.
- Параметры уравнений часто обозначаются переменными (такими как [латекс] a [/ латекс], [латекс] b [/ латекс] или [латекс] c [/ латекс]) и являются частью данной информации в уравнении. .
- Неизвестные переменные — это переменные, которые необходимо решить в уравнениях, и они часто обозначаются такими переменными, как [latex] x [/ latex] и [latex] y [/ latex].
Ключевые термины
- термин : значение или выражение, отделенное от других таких значений операцией.
- переменная : алфавитный символ, представляющий произвольное или неизвестное число.
- параметр : Число или переменная в уравнении, которое считается «известным».

- коэффициент : величина (обычно число), значение которой остается неизменным в пределах задачи.
- неизвестно : переменная в уравнении, для которого необходимо решить.
В элементарной математике переменная — это буквенный символ, представляющий число, называемое значением переменной, которое является произвольным, не полностью определенным или неизвестным.
Переменные полезны по нескольким причинам.
Неизвестные значения
Переменные могут представлять числа, значения которых еще не известны. Например, если температура текущего дня [латекс] C [/ латекс] на 20 градусов выше, чем температура предыдущего дня, [латекс] P [/ латекс], то проблема может быть описана алгебраически как [ латекс] \ displaystyle C = P + 20 [/ latex].
Общие формулы
Различные количества
Переменные могут описывать математические отношения между изменяющимися величинами.Например, соотношение между окружностью [латекс] C [/ latex] и диаметром [латекс] d [/ latex] круга описывается формулой [latex] \ displaystyle \ pi = C / d [/ latex ].
Переменные также могут описывать общие проблемы без указания значений задействованных величин. Например, можно конкретно указать, что 5 минут эквивалентны [latex] \ displaystyle 60 \ times 5 = 300 [/ latex] секундам. В более общем (алгебраическом) описании количество секунд может быть указано как [latex] \ displaystyle s = 60 \ times m [/ latex], где [latex] m [/ latex] — количество минут.
Математические свойства
Переменные могут описывать некоторые математические свойства. Например, основным свойством сложения является коммутативность, которая гласит, что порядок сложения чисел не имеет значения. Коммутативность алгебраически формулируется как [латекс] \ displaystyle (a + b) = (b + a) [/ latex].
Типы переменных
Переменные могут использоваться для представления различных типов чисел. Часто в одной математической формуле фигурирует множество переменных, и они могут играть разные роли.{2} + cx + d = 0 [/ latex], есть пять переменных. Четыре из них ([латекс] a [/ латекс], [латекс] b [/ латекс], [латекс] c [/ латекс], [латекс] d [/ латекс]) представляют собой заданные числа, которые называются параметров уравнения. Последний, [latex] x [/ latex], представляет собой решение уравнения, которое неизвестно и должно быть решено. Чтобы различать различные переменные, [латекс] x [/ latex] называется неизвестным , а переменные, умноженные на [latex] x [/ latex], называются коэффициентами .В этом уравнении коэффициентами являются [латекс] a [/ латекс], [латекс] b [/ латекс] и [латекс] c [/ латекс]. Само по себе число (без неизвестной переменной) называется константой ; в этом случае [латекс] d [/ латекс] представляет собой константу.
Последний, [latex] x [/ latex], представляет собой решение уравнения, которое неизвестно и должно быть решено. Чтобы различать различные переменные, [латекс] x [/ latex] называется неизвестным , а переменные, умноженные на [latex] x [/ latex], называются коэффициентами .В этом уравнении коэффициентами являются [латекс] a [/ латекс], [латекс] b [/ латекс] и [латекс] c [/ латекс]. Само по себе число (без неизвестной переменной) называется константой ; в этом случае [латекс] d [/ латекс] представляет собой константу.
Обратите внимание, что термин уравнения — это любое значение (переменная или число) или выражение, которое отделено от другого члена пробелом или символом (например, «[latex] + [/ latex]»). Следовательно, термин может быть просто константой или переменной, или он может включать как коэффициент, так и неизвестную переменную.2 [/ латекс], [латекс] сх [/ латекс] и [латекс] d [/ латекс].
Обратите внимание, что неизвестные переменные часто обозначаются [latex] x [/ latex], [latex] y [/ latex] или [latex] z [/ latex], а параметры уравнений — [latex] a [/ latex] , [латекс] b [/ латекс], [латекс] c [/ латекс] или [латекс] d [/ латекс]. Тем не менее, это не всегда так. Например, вас могут попросить решить следующее уравнение для [латекс] b [/ латекс]:
Тем не менее, это не всегда так. Например, вас могут попросить решить следующее уравнение для [латекс] b [/ латекс]:
[латекс] 12 — b = 3 [/ латекс]
В этом случае [латекс] b [/ латекс] является неизвестной переменной, а не параметром уравнения.Мы можем решить эту проблему и обнаружить, что [latex] b = 9 [/ latex].
Сложение и вычитание алгебраических выражений
Упрощение алгебраических выражений включает объединение одинаковых терминов, часто путем сложения и вычитания.
Цели обучения
Использование одинаковых терминов для сложения и вычитания выражений, содержащих переменные
Основные выводы
Ключевые моменты
- «Подобные термины» — это термины в алгебраических выражениях, которые являются константами или содержат одни и те же переменные, возведенные в один и тот же показатель степени (например,2 [/ latex] — это , а не , как термины, потому что они имеют разные переменные ([latex] x [/ latex] и [latex] y [/ latex]).

Объединение похожих терминов
Выражения с двумя членами
Мы можем упростить алгебраическое выражение, комбинируя одинаковые термины. Например, давайте попробуем упростить [латекс] 3x + 6x [/ latex].
Во-первых, давайте запишем оба термина как задачи сложения:
- [латекс] 3x = x + x + x [/ латекс]
- [латекс] 6x = x + x + x + x + x + x [/ латекс].
Суммируя эти термины, получаем:
[латекс] 3x + 6x = x + x + x + x + x + x + x + x + x [/ латекс]
Если вы посчитаете, то обнаружите, что в этом развернутом выражении 9 [latex] x [/ latex]. Следовательно:
[латекс] 3x + 6x = 9x [/ латекс]
Обратите внимание, что выражение, с которого мы начали, [latex] 3x + 6x [/ latex], содержало только два члена. Если выражение содержит более двух терминов, может быть полезно переупорядочить термины так, чтобы похожие термины были вместе.
Выражения с более чем двумя членами
Коммутативность сложения говорит о том, что мы можем изменить порядок членов, не меняя значения выражения (суммы).
 Итак, мы можем изменить порядок следующего выражения, прежде чем пытаться объединить похожие термины:
Итак, мы можем изменить порядок следующего выражения, прежде чем пытаться объединить похожие термины:[латекс] 4a + 6b + 2a + b [/ латекс]
Мы можем определить, что термины [латекс] 4a [/ латекс] и [латекс] 2a [/ латекс] похожи, как и [латекс] 6b [/ латекс] и [латекс] b [/ латекс]. Мы хотим переставить выражение, чтобы сгруппировать похожие термины вместе:
[латекс] 4a + 2a + 6b + b [/ латекс].
Теперь мы можем более легко сложить похожие термины, чтобы упростить выражение:
[латекс] (4a + 2a) + (6b + b) = 6a + 7b [/ латекс]
Те же правила применяются, когда выражение включает вычитание. Однако будьте осторожны: при изменении порядка терминов убедитесь, что знак минус следует за термином, к которому он применяется. Например, рассмотрим [латекс] 2x — 3 + 5x [/ латекс]. Это выражение правильно перефразировано и упрощено следующим образом:
[латекс] 2x-3 + 5x = 2x + 5x — 3 = 7x — 3 [/ латекс].2 + 3г [/ латекс]
Умножение алгебраических выражений
Процесс умножения алгебраических выражений для одночленов и многочленов различается.

Цели обучения
Вычислить произведение выражений, содержащих переменные
Основные выводы
Ключевые моменты
- Чтобы умножить два одночлена, умножьте целые коэффициенты вместе и сложите экспоненты всех одинаковых переменных.
- Чтобы умножить одночлен на многочлен, умножьте одночлен на каждый отдельный член многочлена.
- Чтобы умножить два бинома, следуйте методу FOIL: умножьте первый, внешний, внутренний и последний члены перед сложением всех полученных членов.
Ключевые термины
- бином : многочлен с двумя членами.
- полином : алгебраическое выражение с более чем одним членом.
- моном : один член, состоящий из произведения чисел и переменных.
- трехчлен : многочлен с тремя членами.2 [/ латекс]
- [латекс] (5x) (3y) = 15xy [/ латекс]
Умножение одночленов и многочленов
Моном можно умножить на многочлен любого размера (обратите внимание, что многочлен называется биномом, если он состоит из двух членов, и трехчленом, если он состоит из трех членов).
 Моном следует умножить на каждый член многочлена отдельно. Любой отрицательный знак термина должен быть включен при умножении этого термина. Полученный многочлен будет иметь то же количество членов, что и многочлен в задаче.2 + 6x [/ латекс]
Моном следует умножить на каждый член многочлена отдельно. Любой отрицательный знак термина должен быть включен при умножении этого термина. Полученный многочлен будет иметь то же количество членов, что и многочлен в задаче.2 + 6x [/ латекс]
Умножение двух биномов
Умножение двух биномов не так просто; однако есть метод, который делает процесс довольно удобным. «FOIL» — это мнемоника стандартного метода умножения двух биномов (поэтому этот метод часто называют методом FOIL). Слово FOIL является аббревиатурой от четырех терминов продукта:
- Сначала («первые» члены каждого бинома умножаются вместе)
- Внешний («внешние» члены умножаются — i.е., первый член первого двучлена со вторым членом второго)
- Внутренний («внутренние» члены умножаются, т. Е. Второй член первого бинома на первый член второго)
- Последний («последние» члены каждого бинома перемножаются)
По завершении этого процесса все полученные члены складываются в один полином.
Метод FOIL можно записать алгебраически:
[латекс] (a + b) (c + d) = ac + ad + bc + bd [/ латекс]
- Первые термины: [латекс] ас [/ латекс]
- Внешние условия: [латекс] объявление [/ латекс]
- Внутренние термины: [латекс] bc [/ латекс]
- Последние условия: [латекс] бд [/ латекс]
Помните, что любой отрицательный знак члена бинома также должен быть включен при умножении этого члена.2 — х — 2 [/ латекс]
Упрощение радикальных выражений
Радикальное выражение, содержащее переменные, часто можно упростить до более простого выражения, так же как и выражения, содержащие только целые числа.
Цели обучения
Упростить радикальные выражения, содержащие переменные
Основные выводы
Ключевые моменты
- Если радикал полностью упрощен, нет множителя подкоренного выражения, который можно было бы записать в степени, большей или равной индексу, под знаком радикала нет дробей и нет радикалов в знаменателе.

- Когда радикальные выражения содержат переменные, их упрощение происходит так же, как и для выражений, содержащих только целые числа.
- Точно так же правила умножения и деления радикальных выражений по-прежнему применяются, когда выражения содержат переменные.
Ключевые термины
- radicand : Число или выражение, квадратный корень или другой корень которого рассматривается; например, 3 дюйма [латекс] \ sqrt [n] {3} [/ latex]. Проще говоря, число под корневым символом.{n} = x [/ латекс]
где [латекс] n [/ латекс] — степень корня. Корень степени 2 называется квадратным корнем; корень степени 3 называется кубическим корнем. Корни более высоких степеней обозначаются порядковыми числами (например, корень четвертой степени, корень двадцатого и т. Д.).
Упрощенная форма
Радикальное выражение называется упрощенным, если:
- нет множителя корневого числа, который можно было бы записать как степень, большую или равную индексу,
- нет дроби под знаком корня, а
- , в знаменателе нет радикалов.
 2 \ cdot \ frac {2} {5}} = 4 \ sqrt {\ frac {2} {5}} [/ латекс]
2 \ cdot \ frac {2} {5}} = 4 \ sqrt {\ frac {2} {5}} [/ латекс]Далее отделите дробь под знаком корня:
[латекс] \ displaystyle 4 \ sqrt {\ frac {2} {5}} = \ frac {4 \ sqrt {2}} {\ sqrt {5}} [/ латекс]
Наконец, удалим радикал из знаменателя:
[латекс] \ displaystyle 4 \ sqrt {\ frac {2} {5}} = \ frac {4 \ sqrt {2}} {\ sqrt {5}} \ cdot \ frac {\ sqrt {5}} {\ sqrt {5}} = \ frac {4 \ sqrt {10}} {5} [/ латекс]
Радикальные выражения с переменными
В целях упрощения радикальные выражения, содержащие переменные, обрабатываются так же, как выражения, содержащие целые числа.3 [/ латекс]
Упрощение экспоненциальных выражений
Правила работы с числами с показателями степени могут применяться также к переменным с показателями степени.
Цели обучения
Упростить экспоненциальные выражения, содержащие переменные
Основные выводы
Ключевые моменты
- Правила работы с экспоненциальными выражениями такие же для выражений с переменными, как и для выражений с целыми числами.
 {n} [/ latex]
{n} [/ latex]
Ранее мы применяли эти правила только к выражениям, содержащим целые числа.6 [/ латекс]
Рациональные алгебраические выражения
Сложение и вычитание рациональных выражений подчиняется тем же правилам, что и сложение и вычитание дробей.
Цели обучения
Управление рациональными выражениями, содержащими переменные
Основные выводы
Ключевые моменты
- Всегда учитывайте рациональные выражения, прежде чем делать что-либо еще.
- Когда два рациональных выражения складываются или вычитаются друг из друга, каждое из них необходимо сначала умножить на некоторую константу, чтобы оба выражения имели одинаковый знаменатель.
- Если у двух рациональных выражений один и тот же знаменатель, их числители можно комбинировать. Тогда общее оставшееся выражение можно упростить.
Ключевые термины
- рациональное выражение : выражение в терминах частного двух многочленов.

- простой множитель : множитель заданного целого числа, которое также является простым числом.
- фактор : Любой из различных объектов, умноженных вместе, чтобы сформировать единое целое.
- Факторинг : процесс создания списка элементов, умножение которых дает желаемое количество или выражение.
Сложение и вычитание дробей должно быть привычным процессом, и мы будем полагаться на эту концепцию при обсуждении сложения и вычитания рациональных выражений.
[латекс] \ displaystyle \ frac 1 2 + \ frac 1 3 = \ frac 3 6 + \ frac 2 6 = \ frac 5 6 [/ latex]
Ключ в том, чтобы найти наименьший общий знаменатель для двух рациональных выражений: наименьшее кратное обоих знаменателей.Затем вы переписываете две дроби, используя этот знаменатель. Наконец, вы складываете (или вычитаете) дроби, комбинируя числители и оставляя знаменатель в покое.
Но как найти наименьший общий знаменатель?
Рассмотрим эту проблему:
[латекс] \ displaystyle \ frac 5 {12} + \ frac 7 {30} =? [/ Latex]
Вероятно, вы сможете найти наименьший общий знаменатель, если поиграете с числами достаточно долго.
 Здесь мы покажем вам систематический метод поиска наименьших общих знаменателей — метод, который работает с рациональными выражениями так же хорошо, как и с числами.
Здесь мы покажем вам систематический метод поиска наименьших общих знаменателей — метод, который работает с рациональными выражениями так же хорошо, как и с числами.Нахождение наименьшего общего знаменателя
Начнем, как обычно, с факторинга. Для каждого знаменателя мы находим все простые множители, т. Е. Простые числа, которые умножаются, чтобы получить это число.
[латекс] \ displaystyle \ frac 5 {2 \ cdot 2 \ cdot 3} + \ frac 7 {2 \ cdot 3 \ cdot 5} [/ латекс]
Если вы не знакомы с концепцией простых множителей, вам может потребоваться несколько минут, чтобы к ней привыкнуть. [latex] 2 \ cdot 2 \ cdot 3 [/ latex] — это [latex] 12 [/ latex], разбитый на простые множители: то есть это список простых чисел, которые при умножении дают 12.Точно так же простые множители 30 — 2, 3 и 5. Но почему это помогает?
Поскольку [latex] 12 = 2 \ cdot 2 \ cdot 3 [/ latex], любое число, простые множители которого включают две двойки и одну 3, будет кратно 12.
 Аналогично, любое число, простые множители которого включают 2 и 3 , а 5 будет кратно 30.
Аналогично, любое число, простые множители которого включают 2 и 3 , а 5 будет кратно 30.Основные множители дробей: Нахождение простых множителей знаменателей двух дробей позволяет нам найти общий знаменатель.
Наименьший общий знаменатель — это наименьшее число, которое содержит перекрытие обоих факторизованных знаменателей: в этом случае оно должно иметь две двойки, одну 3 и одну 5.Следовательно, наименьший общий знаменатель должен быть [латекс] 2 \ cdot 2 \ cdot 3 \ cdot 5 = 60 [/ latex].
Теперь мы можем закончить задачу:
[латекс] \ begin {align} \ frac {5} {2 \ cdot 2 \ cdot 3} + \ frac {7} {2 \ cdot 3 \ cdot 5} & = \ left (\ frac {5} {2 \ cdot 2 \ cdot 3} \ cdot \ frac {5} {5} \ right) + \ left (\ frac {7} {2 \ cdot 3 \ cdot 5} \ cdot \ frac {2} {2} \ right ) \\ & = \ frac {25} {60} + \ frac {14} {60} \\ & = \ frac {39} {60} \\ & = \ frac {13} {20} \ end {align } [/ латекс]
Это может показаться очень странным способом решения задач, которые вы умели решать с третьего класса.
 Однако вам следует внимательно изучить приведенное выше решение в течение нескольких минут. Как только вы поймете, почему [латекс] 2 \ cdot 2 \ cdot 3 \ cdot 5 = 60 [/ latex] гарантированно будет наименьшим общим знаменателем, у вас будет ключевая концепция, необходимая для сложения и вычитания рациональных выражений.
Однако вам следует внимательно изучить приведенное выше решение в течение нескольких минут. Как только вы поймете, почему [латекс] 2 \ cdot 2 \ cdot 3 \ cdot 5 = 60 [/ latex] гарантированно будет наименьшим общим знаменателем, у вас будет ключевая концепция, необходимая для сложения и вычитания рациональных выражений.Сложение и вычитание рациональных выражений
При применении этой стратегии к рациональным выражениям сначала посмотрите на знаменатели двух рациональных выражений и посмотрите, совпадают ли они. Если они одинаковы, то просто сложите или вычтите числители друг из друга, оставив знаменатель в покое.Однако, если два знаменателя различны, вам нужно будет использовать описанную выше стратегию поиска наименьшего общего знаменателя.
Когда мы складываем или вычитаем рациональные выражения, мы не будем просто рассматривать простые множители целых чисел при поиске наименьшего общего знаменателя. Скорее, мы будем искать мономиальные и биномиальные множители, общие для обоих рациональных выражений.
 2 + 4 [/ latex].2 + 2)} [/ латекс]
2 + 4 [/ latex].2 + 2)} [/ латекс]Выводы
Сначала , всегда учитывайте рациональные выражения, прежде чем делать что-либо еще.
Второй , следуйте обычной процедуре для дробей, которая в данном случае включает в себя поиск общего знаменателя.
Третье , вычтите числители, не трогая знаменатель.
Наконец, , упростите.
Алгебраическое выражение — объяснение и примеры
Алгебра — интересный и увлекательный раздел математики, в котором числа, формы и буквы используются для выражения задач.Независимо от того, изучаете ли вы алгебру в школе или сдаете какой-то тест, вы заметите, что почти все математические задачи представлены словами.
Следовательно, потребность в переводе задач с письменным словом в алгебраические выражения возникает тогда, когда нам нужно их решить.
Большинство алгебраических задач со словами состоят из рассказов или примеров из реальной жизни. Другие — простые фразы, такие как описание математической задачи.
 Что ж, в этой статье мы узнаем, как написать алгебраических выражений из простых задач со словами, а затем перейдем к слегка сложным задачам со словами.
Что ж, в этой статье мы узнаем, как написать алгебраических выражений из простых задач со словами, а затем перейдем к слегка сложным задачам со словами.Что такое алгебраическое выражение?
Многие люди попеременно используют алгебраические выражения и алгебраические уравнения, не подозревая, что это совершенно разные термины.
Алгебраическая фраза — это математическая фраза, в которой две стороны фразы соединены знаком равенства (=). Например, 3x + 5 = 20 — это алгебраическое уравнение, где 20 представляет собой правую часть (RHS), а 3x +5 представляет собой левую часть (LHS) уравнения.
С другой стороны, алгебраическое выражение — это математическая фраза, в которой переменные и константы объединяются с помощью операционных символов (+, -, × & ÷).В алгебраическом символе отсутствует знак равенства (=). Например, 10x + 63 и 5x — 3 являются примерами алгебраических выражений.
Давайте рассмотрим терминологию, используемую в алгебраическом выражении:
- Переменная — это буква, значение которой нам неизвестно.
 Например, x — это наша переменная в выражении: 10x + 63.
Например, x — это наша переменная в выражении: 10x + 63. - Коэффициент — это числовое значение, используемое вместе с переменной. Например, 10 — это переменная в выражении 10x + 63.
- Константа — это терм, который имеет определенное значение.В данном случае 63 — это константа в алгебраическом выражении, 10x + 63.
Существует несколько типов алгебраических выражений, но основной тип включает:
- Мономиальное алгебраическое выражение
Это тип выражения имеющий только один член, например, 2x, 5x 2 , 3xy и т. д.
Алгебраическое выражение, содержащее два разных члена, например 5y + 8, y + 5, 6y 3 + 4 и т. д.
Это алгебраическое выражение с более чем одним членом и ненулевыми показателями переменных.Пример полиномиального выражения: ab + b c + ca и т. Д.
Алгебраические выражения других типов:
Числовое выражение состоит только из чисел и операторов. В числовое выражение переменная не добавляется.
 Примеры числовых выражений: 2 + 4, 5-1, 400 + 600 и т. Д.
Примеры числовых выражений: 2 + 4, 5-1, 400 + 600 и т. Д.Это выражение, которое содержит переменные вместе с числами, например, 6x + y, 7xy + 6 и т. Д.
Как решить алгебраическое выражение?
Цель решения алгебраического выражения в уравнении — найти неизвестную переменную.Когда два выражения приравниваются, они образуют уравнение, и поэтому становится легче найти неизвестные члены.
Чтобы решить уравнение, поместите переменные с одной стороны, а константы — с другой. Переменные можно изолировать, применяя арифметические операции, такие как сложение, вычитание, умножение, деление, квадратный корень, кубический корень и т. Д.
Алгебраические выражения всегда взаимозаменяемы. Это означает, что вы можете переписать уравнение, поменяв местами LHS и RHS.
Пример 1
Вычислите значение x в следующем уравнении
5x + 10 = 50
Решение
Задано уравнение как 5x + 10 = 50
- Изолируйте переменные и константы;
- Правила работы с экспоненциальными выражениями такие же для выражений с переменными, как и для выражений с целыми числами.
- Вы можете сохранить переменную на левой стороне, а константы на правой.

5x = 50-10
5x = 40
Разделим обе части на коэффициент переменной;
x = 40/5 = 8
Следовательно, значение x равно 8.
Пример 2
Найдите значение y, когда 5y + 45 = 100
Решение
Изолировать переменные от констант;
5y = 100-45
5y = 55
Разделим обе части на коэффициент;
y = 55/5
y = 11
Пример 3
Определите значение переменной в следующем уравнении:
2x + 40 = 30
Решение
Разделите переменные из константы;
2x = 30-40
2x = -10
Разделите обе стороны на 2;
x = -5
Пример 4
Найдите t, когда 6t + 5 = 3
Решение
Отделите константы от переменной,
6t 3
6t = -2
Разделим обе части на коэффициент,
t = -2/6
Упростим дробь,
t = -1/3
Практические вопросы
1. Если x = 4 и y = 2, найдите следующие выражения:
Если x = 4 и y = 2, найдите следующие выражения:
a. 2г + 4
б. 10х + 40л;
г. 15лет — 5x
д. 5x + 7
e. 11y + 6
ф. 6x — 2
г. 8лет — 5
ч. 60 — 5x — 2y
2. Сэм кормит свою рыбу одинаковым количеством корма (пусть равным x ) трижды в день. Сколько еды он накормит рыбу в неделю?
3. Нина испекла по 3 кекса для сестры и по 2 кекса для каждой подруги (пусть равно x ).Сколько всего кексов она испекла?
4. У Джонса на ферме 12 коров. Большинство коров дают 30 литров молока в день (пусть равно х ). Сколько коров не дают 30 литров молока в день?
Предыдущий урок | Главная страница | Следующий урокРациональные выражения: поиск домена
Рациональный Выражения: поиск домена (стр. 1 из 3)
Секции: Поиск область, Упрощение рациональных выражений
«Рациональное выражение»
является полиномиальной дробью, и все, что вы могли бы сделать с обычными дробями
можно обойтись рациональными выражениями. Однако, поскольку есть переменные
в рациональных выражениях есть некоторые дополнительные соображения.
Однако, поскольку есть переменные
в рациональных выражениях есть некоторые дополнительные соображения.
Когда вы имели дело с дробями, вы знали, что в числителе дроби могут быть любые целые числа и знаменатель, если вы не пытались разделить на ноль. При работе с рациональными выражениями вам часто нужно будет вычислить выражение, и может быть полезно знать, какие значения вызовут деление на ноль, поэтому вы можете избежать этих значений x .Так вероятно, первое, что вы сделаете с рациональными выражениями, — это найдите их области.
- Найдите домен 3 / x .
Домен все значения
что x разрешено быть. Поскольку я не могу делить на ноль (деление на ноль не
разрешено), мне нужно найти все значения x , которые вызовут деление на ноль.Тогда в домене будут все других -значений x . Когда этот знаменатель равен нулю? Когда x = 0,
Когда этот знаменатель равен нулю? Когда x = 0,
Тогда домен «все x не равны нулю» .
- Определить домен из x / 3 . Авторские права © Элизабет Стапель 2003-2011 Все права защищены
Домену все равно что находится в числителе рационального выражения.Домен только под влиянием нулей знаменателя. Будет «3» когда-либо равняется нулю? Конечно, нет. Поскольку знаменатель никогда не будет равен ноль, независимо от того, какое значение x , то для этого рационального выражения нет запрещенных значений, а x может быть любым. Таким образом, домен «все x » .
- Отдать домен следующее выражение:
Чтобы найти домен, я
игнорировать « x + 2″ в
числитель (так как числитель не вызывает деления на ноль) и
вместо этого я посмотрю на знаменатель. Я установлю знаменатель равным
к нулю и решите. x -значения
в решении будут значения x что приведет к делению на ноль. Тогда домен будет иметь все остальные значения x .
Я установлю знаменатель равным
к нулю и решите. x -значения
в решении будут значения x что приведет к делению на ноль. Тогда домен будет иметь все остальные значения x .
x 2 + 2 x — 15 = 0
( x + 5) ( x — 3) = 0
x = –5, x = 3
По факторингу
квадратичный,
Я нашел нули знаменателя.Тогда домен будет иметь все остальные значения x :
- Найдите домен следующее выражение:
Чтобы найти домен, я найти нули знаменателя:
Это не имеет решения, так что знаменатель никогда не равен нулю.Тогда домен «все x » .
Вверх | 1 | 2 | 3 | Вернуться к оглавлению Далее >>
Цитируйте эту статью как: | Стапель, Елизавета. |
Синтаксис HOC — документация NEURON 7.7
HOC был исходным языком программирования, поддерживаемым NEURON. NEURON также можно запрограммировать на Python.
Аргументы
Аргументы функций и процедур извлекаются позиционно. $ 1, $ 2, $ 3 относятся к первому, второму и третьему скалярным аргументам.
соответственно.
Если « i » объявлено как локальная переменная, $ i ссылается на
к скалярному аргументу в позиции, заданной значением i .
Значение i должно быть в
диапазон {1… numarg ()}.
Обычная идиома —
для i = 1, numarg () {print $ i}
Скалярные аргументы используют вызов по значению, поэтому переменная в вызывающем
заявление не может быть изменено.
Если в операторе вызова есть «&»
добавляется к переменной, то она передается по ссылке и должна
быть восстановленным с
синтаксис $ & 1, $ & 2,..., $ & я . Если переменная передана по ссылке
является одномерным массивом, тогда $ & 1 относится к первому (0-му) элементу
а индекс i обозначен как $ & 1 [i] . Предупреждение, проверка границ массива НЕ
done, и массив считается одномерным. Скаляр или
ссылка на массив может быть передана другой процедуре с помощью & $ & 1 . Чтобы сохранить скалярную ссылку, используйте класс Pointer .
Для получения аргументов strdef используется синтаксис: $ s1, $ s2,..., $ si .
Для получения аргументов objref используется синтаксис: $ o1, $ o2, ..., $ oi .
Аргументы типа strdef и objref используют вызов по ссылке, поэтому вызывающий
значение может быть изменено.
Пример:
func mult () { возврат $ 1 * $ 2 }определяет функцию, которая умножает два аргумента.
Следовательно,
mult (4,5)вернет значение 20.proc pr () { распечатать $ s3 распечатать $ 1 * $ 2 распечатать $ o4 }определяет процедуру, которая сначала печатает строку, определенную в позиции 3, затем распечатывает произведение двух чисел в позиции 1 и 2, и, наконец, печатает ссылку указателя на объект в позиции 4.
Для строки «
s», которая определяется какs = "hello", и objref ‘r’,pr (3,5, s, r)вернетпри условии, что
rотносится к первому графику.
-
число() - Синтаксис:
-
n = numarg () - Описание:
- Число аргументов, переданных пользовательской функции hoc.
-
argtype() - Синтаксис:
-
itype = тип аргумента (iarg) - Описание:
- Тип i-го аргумента.
 Возвращаемое значение — 0 для чисел, 1 для objref,
2 для strdef, 3 для указателей на числа и -1, если arg не существует.
Возвращаемое значение — 0 для чисел, 1 для objref,
2 для strdef, 3 для указателей на числа и -1, если arg не существует.
Операторы и выражения в Python — Real Python
После завершения нашего предыдущего руководства по переменным Python в этой серии вы должны хорошо понимать, как создавать и присваивать имена объектам Python различных типов. Давай поработаем с ними!
Вот что вы узнаете в этом руководстве: Вы увидите, как вычисления могут выполняться с объектами в Python.К концу этого руководства вы сможете создавать сложные выражения , комбинируя объекты и операторы .
Пройдите тест: Проверьте свои знания с помощью нашей интерактивной викторины «Операторы и выражения Python». По завершении вы получите оценку, чтобы вы могли отслеживать свой прогресс в обучении с течением времени:
Пройти тест »
В Python операторы — это специальные символы, обозначающие, что необходимо выполнить какое-то вычисление. Значения, над которыми действует оператор, называются операндами .
Значения, над которыми действует оператор, называются операндами .
Вот пример:
>>> >>> a = 10
>>> b = 20
>>> а + б
30
В этом случае оператор + складывает операнды a и b вместе. Операндом может быть буквальное значение или переменная, которая ссылается на объект:
>>> a = 10
>>> b = 20
>>> а + б - 5
25
Последовательность операндов и операторов, например a + b - 5 , называется выражением.Python поддерживает множество операторов для объединения объектов данных в выражения. Они рассматриваются ниже.
Арифметические операторы
В следующей таблице перечислены арифметические операторы, поддерживаемые Python:
| Оператор | Пример | Значение | Результат |
|---|---|---|---|
+ (одинарный) | + а | Унарный положительный | a Другими словами, на самом деле он ничего не делает.  В основном он существует ради полноты, чтобы дополнить Унарное отрицание . В основном он существует ради полноты, чтобы дополнить Унарное отрицание . |
+ (двоичный) | а + б | Дополнение | Сумма a и b |
- (одинарный) | -а | Унарное отрицание | Значение равно a , но с противоположным знаком |
- (двоичный) | а - б | Вычитание | b вычитается из a |
* | а * б | Умножение | Изделие из a и b |
/ | а / б | Отдел | Частное, когда a делится на b . Результат всегда имеет тип float . |
% | a% b | По модулю | Остаток после деления a на b |
// | а // б | Подразделение этажа (также называется Целочисленное подразделение ) | Частное при делении a на b с округлением до следующего наименьшего целого числа |
** | а ** б | Возведение в степень | a возведен в степень b |
Вот несколько примеров использования этих операторов:
>>> >>> a = 4
>>> b = 3
>>> + а
4
>>> -b
-3
>>> а + б
7
>>> а - б
1
>>> а * б
12
>>> а / б
1.3333333333333333
>>> a% b
1
>>> а ** б
64
Результатом стандартного деления (/) всегда является с плавающей запятой , даже если дивиденд делится без остатка на делитель:
>>> 10/5
2. 0
>>> тип (10/5)
<класс 'float'>
0
>>> тип (10/5)
<класс 'float'>
Если результат деления по полу ( // ) положительный, дробная часть как бы обрезается, остается только целая часть.Если результат отрицательный, результат округляется до следующего наименьшего (большего отрицательного) целого числа:
>>> 10/4
2,5
>>> 10 // 4
2
>>> 10 // -4
-3
>>> -10 // 4
-3
>>> -10 // -4
2
Кстати, обратите внимание, что в сеансе REPL вы можете отобразить значение выражения, просто набрав его в приглашении >>> без print () , так же, как вы можете с буквальным значением или переменная:
>>> 25
25
>>> х = 4
>>> у = 6
>>> х
4
>>> у
6
>>> х * 25 + у
106
Операторы сравнения
| Оператор | Пример | Значение | Результат |
|---|---|---|---|
== | a == b | Равно | Истинно , если значение a равно значению b Ложно в противном случае |
! = | а! = Б | Не равно | Верно , если a не равно b Ложно в противном случае |
< | a | Менее | Верно , если a меньше b Ложно в противном случае |
<= | a <= b | Меньше или равно | Верно , если a меньше или равно b Ложно в противном случае |
> | a> b | Больше | Верно , если a больше b Ложно в противном случае |
> = | a> = b | Больше или равно | Верно , если a больше или равно b Ложно в противном случае |
Вот примеры используемых операторов сравнения:
>>> >>> a = 10
>>> b = 20
>>> а == б
Ложь
>>> а! = б
Истинный
>>> а <= б
Истинный
>>> а> = б
Ложь
>>> а = 30
>>> б = 30
>>> а == б
Истинный
>>> а <= б
Истинный
>>> а> = б
Истинный
Операторы сравнения обычно используются в логических контекстах, таких как условные операторы и операторы цикла, для направления выполнения программы, как вы увидите позже.
Сравнение равенства значений с плавающей запятой
Вспомните из предыдущего обсуждения чисел с плавающей запятой, что значение, хранимое внутри для объекта float , может быть не совсем таким, как вы думаете. По этой причине сравнивать значения с плавающей запятой на предмет точного равенства - плохая практика. Рассмотрим этот пример:
>>> х = 1,1 + 2,2
>>> х == 3.3
Ложь
Ура! Внутреннее представление операндов сложения не совсем равно 1.1 и 2.2 , поэтому вы не можете полагаться на x для точного сравнения с 3.3 .
Предпочтительный способ определить, равны ли два значения с плавающей запятой, - это вычислить, близки ли они друг к другу, с учетом некоторого допуска. Взгляните на этот пример:
>>> >>> допуск = 0,00001
>>> х = 1,1 + 2,2
>>> абс (x - 3,3) <допуск
Истинный
abs () возвращает абсолютное значение. Если абсолютное значение разницы между двумя числами меньше указанного допуска, они достаточно близки друг к другу, чтобы считаться равными.
Если абсолютное значение разницы между двумя числами меньше указанного допуска, они достаточно близки друг к другу, чтобы считаться равными.
Логические операторы
Логические операторы , а не , или , а также и изменяют и объединяют выражения, вычисленные в логическом контексте, для создания более сложных условий.
Логические выражения, включающие булевы операнды
Как вы видели, некоторые объекты и выражения в Python на самом деле имеют логический тип.То есть они равны одному из объектов Python True или False . Рассмотрим эти примеры:
>>> х = 5
>>> х <10
Истинный
>>> тип (x <10)
<класс 'bool'>
>>> т = х> 10
>>> т
Ложь
>>> type (t)
<класс 'bool'>
>>> вызываемый (x)
Ложь
>>> тип (вызываемый (x))
<класс 'bool'>
>>> t = вызываемый (лен)
>>> т
Истинный
>>> type (t)
<класс 'bool'>
В приведенных выше примерах x <10 , callable (x) и t - все это логические объекты или выражения.
Интерпретация логических выражений, включающих , а не , или , а также и , проста, если операнды являются логическими:
| Оператор | Пример | Значение |
|---|---|---|
не | не x | Верно , если x равно Ложно Ложно , если x равно Истинно (Логически меняет смысл x на противоположный) |
или | x или y | True , если x или y равно True False в противном случае |
и | x и y | Верно , если и x , и y равны Истина Ложь в противном случае |
Посмотрите, как они работают на практике, ниже.
«
, а не » и логические операнды х = 5
не x <10
Ложь
не вызывается (x)
Истинный
| Операнд | Значение | Логическое выражение | Значение |
|---|---|---|---|
x <10 | Правда | не x <10 | Ложь |
возможность вызова (x) | Ложь | не подлежит вызову (x) | Правда |
«
или » и логические операнды х = 5
x <10 или вызываемый (x)
Истинный
x <0 или вызываемый (x)
Ложь
| Операнд | Значение | Операнд | Значение | Логическое выражение | Значение |
|---|---|---|---|---|---|
x <10 | Правда | , по телефону (x) | Ложь | x <10 или по телефону (x) | Правда |
x <0 | Ложь | , по телефону (x) | Ложь | x <0 или вызываемый (x) | Ложь |
«
и » и логические операнды х = 5
x <10 и вызываемый (x)
Ложь
x <10 и вызываемый (len)
Истинный
| Операнд | Значение | Операнд | Значение | Логическое выражение | Значение |
|---|---|---|---|---|---|
x <10 | Правда | , по телефону (x) | Ложь | x <10 и вызываемый (x) | Ложь |
x <10 | Правда | по телефону (длина) | Правда | x <10 или по запросу (длина) | Правда |
Оценка небулевых значений в логическом контексте
Многие объекты и выражения не равны True или False . Тем не менее, они могут быть оценены в логическом контексте и определены как «правдивые» или «ложные».
Тем не менее, они могут быть оценены в логическом контексте и определены как «правдивые» или «ложные».
Итак, что правда, а что нет? Как философский вопрос, это выходит за рамки этого урока!
Но в Python это четко определено. Все следующие значения считаются ложными при оценке в логическом контексте:
- Логическое значение
Ложь - Любое числовое значение, равное нулю (
0,0,0,0,0 + 0.0j) - Пустая строка
- Пустой объект встроенного составного типа данных (см. Ниже)
- Специальное значение, обозначаемое ключевым словом Python
Нет
Практически любой другой объект, встроенный в Python, считается истинным.
Вы можете определить «истинность» объекта или выражения с помощью встроенной функции bool () . bool () возвращает True , если его аргумент истинный, и False , если он ложный.
Числовое значение
>>>Нулевое значение ложно.
Ненулевое значение верно.
>>> print (bool (0), bool (0.0), bool (0.0 + 0j))
Ложь Ложь Ложь
>>> print (bool (-3), bool (3.14159), bool (1.0 + 1j))
Правда правда правда
Строка
>>>Пустая строка неверна.
Верна непустая строка.
>>> print (bool (''), bool (""), bool ("" "" ""))
Ложь Ложь Ложь
>>> print (bool ('foo'), bool (""), bool ('' '' ''))
Правда правда правда
Встроенный объект составных данных
>>>Python предоставляет встроенные составные типы данных, которые называются
list,tuple,dictиset.Это «контейнерные» типы, содержащие другие объекты. Объект одного из этих типов считается ложным, если он пуст, и истинным, если он не пуст.Примеры ниже демонстрируют это для списка
типа.(Списки определены в Python в квадратных скобках.)
Для получения дополнительной информации о списке
, кортеже,dictизадайте типы, см. Следующие руководства.
>>> тип ([])
<список классов>
>>> bool ([])
Ложь
>>> тип ([1, 2, 3])
<список классов>
>>> bool ([1, 2, 3])
Истинный
Ключевое слово «
Нет » Нет всегда ложно:
Логические выражения, включающие небулевы операнды
Не-логические значения также могут быть изменены и объединены с помощью , а не , или и и .Результат зависит от «истинности» операндов.
«
, а не » и небулевы операнды Вот что происходит с не-логическим значением x :
Если x - это | не x равно |
|---|---|
| «правда» | Ложь |
| «ложь» | Правда |
Вот несколько конкретных примеров:
>>> >>> х = 3
>>> bool (x)
Истинный
>>> не х
Ложь
>>> х = 0. 0
>>> bool (x)
Ложь
>>> не х
Истинный
0
>>> bool (x)
Ложь
>>> не х
Истинный
«
или » и небулевы операнды Вот что происходит с двумя не-логическими значениями x и y :
Если x - это | x или y - это |
|---|---|
| правда | x |
| ложь | y |
Обратите внимание, что в этом случае выражение x или y не оценивается как Истина или Ложь , а вместо x или y :
>>> х = 3
>>> у = 4
>>> х или у
3
>>> х = 0.0
>>> у = 4,4
>>> х или у
4.4
Даже в этом случае выражение x или y будет истинным, если либо x , либо y истинно, и ложным, если и x , и y ложны.
«
и » и небулевы операнды Вот что вы получите для двух не-логических значений x и y :
Если x - это | x и y равно |
|---|---|
| «правда» | y |
| «ложь» | x |
>>> х = 3
>>> у = 4
>>> х и у
4
>>> х = 0. 0
>>> у = 4,4
>>> х и у
0,0
0
>>> у = 4,4
>>> х и у
0,0
Как и в случае с или , выражение x и y не оценивается как Истинно или Ложно , а вместо x или y . x и y будут истинными, если и x , и y истинны, и ложными в противном случае.
Составные логические выражения и оценка короткого замыкания
До сих пор вы видели выражения только с одним оператором или или и и двумя операндами:
Несколько логических операторов и операндов могут быть объединены в составные логические выражения.
Составное «
или » ВыраженияРассмотрим следующее выражение:
x 1
илиx 2илиx 3или… x n
Это выражение истинно, если любое из значений x i истинно.
В подобном выражении Python использует методологию, называемую оценкой короткого замыкания, также называемую оценкой Маккарти в честь компьютерного ученого Джона Маккарти.Операнды x i оцениваются в порядке слева направо. Как только одна из них оказывается верной, все выражение становится истинным. На этом этапе Python останавливается, и термины больше не оцениваются. Значение всего выражения - это значение x i , которое завершило вычисление.
Чтобы продемонстрировать оценку короткого замыкания, предположим, что у вас есть простая «идентификационная» функция f () , которая ведет себя следующим образом:
-
f ()принимает единственный аргумент. - Отображает аргумент в консоли.
- Он возвращает переданный ему аргумент в качестве возвращаемого значения.
(Вы увидите, как определить такую функцию в предстоящем руководстве по функциям. )
)
Несколько примеров звонков на номер f () показаны ниже:
>>> f (0)
-> f (0) = 0
0
>>> f (Ложь)
-> f (Ложь) = Ложь
Ложь
>>> f (1.5)
-> f (1,5) = 1,5
1.5
Поскольку f () просто возвращает переданный ему аргумент, мы можем сделать выражение f (arg) правдивым или ложным по мере необходимости, указав значение для arg , которое является соответственно правдивым или ложным.Кроме того, f () выводит на консоль свой аргумент, который визуально подтверждает, был ли он вызван.
Теперь рассмотрим следующее составное логическое выражение:
>>> >>> f (0) или f (ложь), или f (1), или f (2), или f (3)
-> f (0) = 0
-> f (Ложь) = Ложь
-> f (1) = 1
1
Интерпретатор сначала оценивает f (0) , что составляет 0 . Числовое значение 0 неверно. Выражение еще не соответствует действительности, поэтому оценка выполняется слева направо. Следующий операнд,
Следующий операнд, f (False) , возвращает False . Это тоже неверно, поэтому оценка продолжается.
Далее идет f (1) . Это составляет 1 , что верно. На этом этапе интерпретатор останавливается, потому что теперь он знает, что все выражение истинно. 1 возвращается как значение выражения, а остальные операнды, f (2) и f (3) , никогда не оцениваются. На дисплее видно, что вызовы f (2) и f (3) не выполняются.
Соединение «
и » Выражения Аналогичная ситуация существует в выражении с несколькими операторами и :
x 1
иx 2иx 3и… x n
Это выражение истинно, если истинны все значения x i .
В этом случае оценка короткого замыкания диктует, что интерпретатор прекращает оценку, как только какой-либо операнд оказывается ложным, потому что в этот момент известно, что все выражение ложно.В этом случае операнды больше не вычисляются, и ложный операнд, завершивший вычисление, возвращается как значение выражения:
>>> >>> f (1) и f (ложь) и f (2) и f (3)
-> f (1) = 1
-> f (Ложь) = Ложь
Ложь
>>> f (1) и f (0.0) и f (2) и f (3)
-> f (1) = 1
-> f (0,0) = 0,0
0,0
В обоих примерах выше оценка останавливается на первом ложном члене - f (False) в первом случае, f (0.0) во втором случае - и ни f (2) , ни f (3) не происходит. False и 0,0 , соответственно, возвращаются как значение выражения.
Если все операнды истинны, все они вычисляются, и последний (крайний правый) возвращается как значение выражения:
>>> >>> f (1) и f (2.2) и f ('bar')
-> f (1) = 1
-> f (2. 2) = 2.2
-> f (бар) = бар
'бар'
2) = 2.2
-> f (бар) = бар
'бар'
Идиомы, использующие оценку короткого замыкания
Есть несколько распространенных идиоматических паттернов, которые используют оценку короткого замыкания для краткости выражения.
Как избежать исключения
Предположим, вы определили две переменные a и b и хотите знать, действительно ли (b / a)> 0 :
>>> a = 3
>>> b = 1
>>> (б / а)> 0
Истинный
Но вы должны учитывать возможность того, что a может быть 0 , и в этом случае интерпретатор вызовет исключение:
>>> a = 0
>>> b = 1
>>> (б / а)> 0
Отслеживание (последний вызов последний):
Файл "", строка 1, в
(б / а)> 0
ZeroDivisionError: деление на ноль
Вы можете избежать ошибки с помощью такого выражения:
>>> >>> a = 0
>>> b = 1
>>> a! = 0 и (b / a)> 0
Ложь
Когда - это 0 , a! = 0 ложно. Оценка короткого замыкания гарантирует, что оценка остановится на этом этапе.
Оценка короткого замыкания гарантирует, что оценка остановится на этом этапе. (b / a) не оценивается, и ошибка не возникает.
На самом деле, вы можете быть еще более кратким. Когда a равно 0 , выражение a само по себе является ложным. В явном сравнении нет необходимости a! = 0 :
>>> a = 0
>>> b = 1
>>> а и (б / а)> 0
0
Выбор значения по умолчанию
Другая идиома предполагает выбор значения по умолчанию, когда заданное значение равно нулю или пусто.Например, предположим, что вы хотите присвоить переменной s значение, содержащееся в другой переменной, называемой строка . Но если строка пуста, вы хотите указать значение по умолчанию.
Вот краткий способ выразить это с помощью оценки короткого замыкания:
s = строка или '<значение по умолчанию>'
Если строка не пуста, это правда, и выражение строка или '<значение по умолчанию>' будет истинным в этой точке.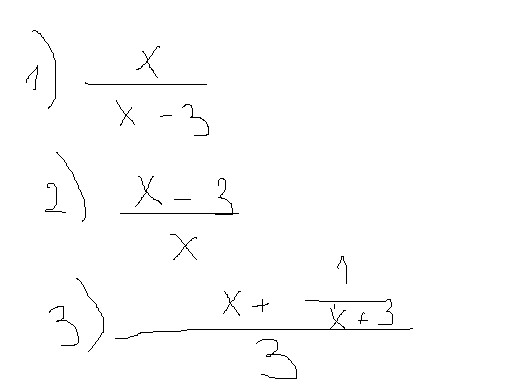 Оценка останавливается, и значение строки
Оценка останавливается, и значение строки возвращается и присваивается s :
>>> строка = 'foo bar'
>>> s = строка или '<значение по умолчанию>'
>>> с
'foo bar'
С другой стороны, если строка является пустой строкой, она ложна. Оценка строки или «<значение по умолчанию>» продолжается до следующего операнда, «<значение по умолчанию>» , который возвращается и присваивается s :
>>> строка = ''
>>> s = строка или '<значение по умолчанию>'
>>> с
'<значение по умолчанию>'
Цепные сравнения
Операторы сравнения могут быть объединены в цепочку произвольной длины.Например, следующие выражения почти эквивалентны:
х <у <= г
х <у и у <= г
Оба они вычисляют одно и то же логическое значение. Тонкое различие между ними заключается в том, что в цепном сравнении x y оценивается только один раз. Более длинное выражение
Более длинное выражение x y .
Примечание: В случаях, когда y является статическим значением, это не будет значительным различием.Но рассмотрим эти выражения:
х <е () <= г
x Если f () - это функция, которая вызывает изменение данных программы, разница между ее вызовом один раз в первом случае и дважды во втором случае может быть важной.
В более общем смысле, если op 1 , op 2 , …, op n являются операторами сравнения, то следующие значения имеют такое же логическое значение:
x 1 op 1 x 2 op 2 x 3 … x n-1 op n x n
x 1 op 1 x 2
x nиx 2 op 2 x 3и… x n-1 n
В первом случае каждый x i оценивается только один раз. В последнем случае каждый будет оцениваться дважды, кроме первого и последнего, если оценка короткого замыкания не вызывает преждевременного завершения.
В последнем случае каждый будет оцениваться дважды, кроме первого и последнего, если оценка короткого замыкания не вызывает преждевременного завершения.
Побитовые операторы
Побитовые операторы обрабатывают операнды как последовательности двоичных цифр и работают с ними побитно. Поддерживаются следующие операторы:

 zeros(10)
Z[4] = 1
print(Z)
zeros(10)
Z[4] = 1
print(Z) ones((10,10))
Z[1:-1,1:-1] = 0
ones((10,10))
Z[1:-1,1:-1] = 0 zeros((5,5))
Z += np.arange(5)
print(Z)
zeros((5,5))
Z += np.arange(5)
print(Z) random.random(10)
Z[Z.argmax()] = 0
print(Z)
random.random(10)
Z[Z.argmax()] = 0
print(Z) arange(100)
v = np.random.uniform(0,100)
index = (np.abs(Z-v)).argmin()
print(Z[index])
arange(100)
v = np.random.uniform(0,100)
index = (np.abs(Z-v)).argmin()
print(Z[index])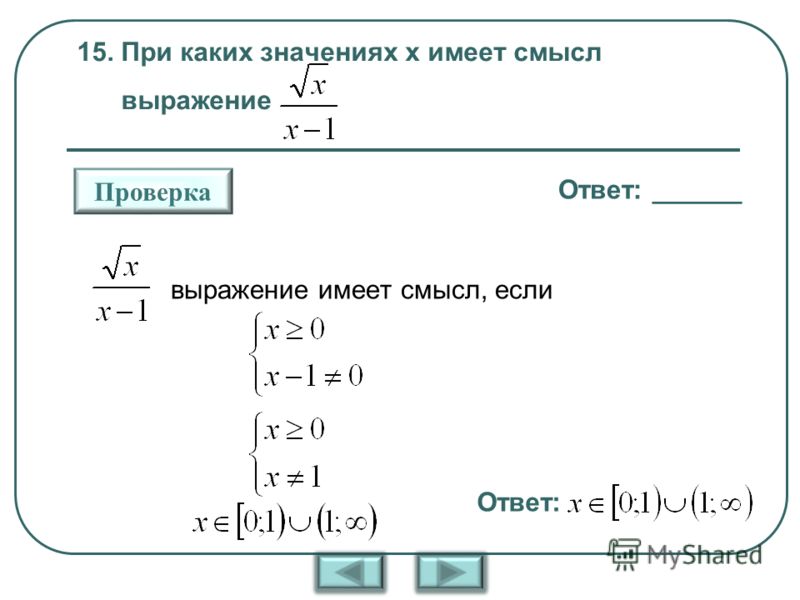 arange(9).reshape(3,3)
for index, value in np.ndenumerate(Z):
print(index, value)
for index in np.ndindex(Z.shape):
print(index, Z[index])
arange(9).reshape(3,3)
for index, value in np.ndenumerate(Z):
print(index, value)
for index in np.ndindex(Z.shape):
print(index, Z[index]) ones(10)
I = np.random.randint(0,len(Z),20)
Z += np.bincount(I, minlength=len(Z))
print(Z)
ones(10)
I = np.random.randint(0,len(Z),20)
Z += np.bincount(I, minlength=len(Z))
print(Z) arange(25).reshape(5,5)
A[[0,1]] = A[[1,0]]
print(A)
arange(25).reshape(5,5)
A[[0,1]] = A[[1,0]]
print(A) lib import stride_tricks
def rolling(a, window):
shape = (a.size - window + 1, window)
strides = (a.itemsize, a.itemsize)
return stride_tricks.as_strided(a, shape=shape, strides=strides)
Z = rolling(np.arange(10), 3)
print(Z)
lib import stride_tricks
def rolling(a, window):
shape = (a.size - window + 1, window)
strides = (a.itemsize, a.itemsize)
return stride_tricks.as_strided(a, shape=shape, strides=strides)
Z = rolling(np.arange(10), 3)
print(Z) random.randint(0,10,50)
print(np.bincount(Z).argmax())
random.randint(0,10,50)
print(np.bincount(Z).argmax()) ones((p,n,1))
S = np.tensordot(M, V, axes=[[0, 2], [0, 1]])
print(S)
# It works, because:
# M is (p,n,n)
# V is (p,n,1)
# Thus, summing over the paired axes 0 and 0 (of M and V independently),
# and 2 and 1, to remain with a (n,1) vector.
ones((p,n,1))
S = np.tensordot(M, V, axes=[[0, 2], [0, 1]])
print(S)
# It works, because:
# M is (p,n,n)
# V is (p,n,1)
# Thus, summing over the paired axes 0 and 0 (of M and V independently),
# and 2 and 1, to remain with a (n,1) vector. arange(10000)
np.random.shuffle(Z)
n = 5
print (Z[np.argpartition(-Z,n)[:n]])
arange(10000)
np.random.shuffle(Z)
n = 5
print (Z[np.argpartition(-Z,n)[:n]]) array([0, 1, 2, 3, 15, 16, 32, 64, 128], dtype=np.uint8)
print(np.unpackbits(I[:, np.newaxis], axis=1))
array([0, 1, 2, 3, 15, 16, 32, 64, 128], dtype=np.uint8)
print(np.unpackbits(I[:, np.newaxis], axis=1))

 Итак, мы можем изменить порядок следующего выражения, прежде чем пытаться объединить похожие термины:
Итак, мы можем изменить порядок следующего выражения, прежде чем пытаться объединить похожие термины:
 Моном следует умножить на каждый член многочлена отдельно. Любой отрицательный знак термина должен быть включен при умножении этого термина. Полученный многочлен будет иметь то же количество членов, что и многочлен в задаче.2 + 6x [/ латекс]
Моном следует умножить на каждый член многочлена отдельно. Любой отрицательный знак термина должен быть включен при умножении этого термина. Полученный многочлен будет иметь то же количество членов, что и многочлен в задаче.2 + 6x [/ латекс]
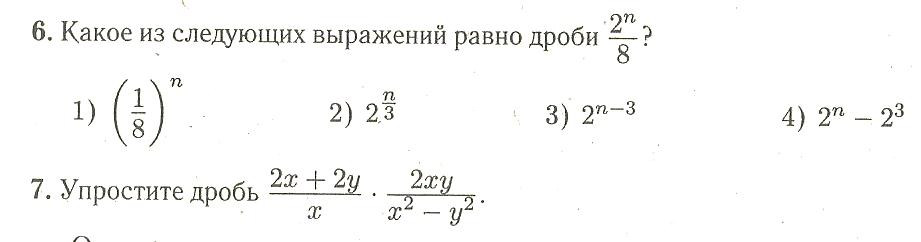 2 \ cdot \ frac {2} {5}} = 4 \ sqrt {\ frac {2} {5}} [/ латекс]
2 \ cdot \ frac {2} {5}} = 4 \ sqrt {\ frac {2} {5}} [/ латекс] {n} [/ latex]
{n} [/ latex]
 Здесь мы покажем вам систематический метод поиска наименьших общих знаменателей — метод, который работает с рациональными выражениями так же хорошо, как и с числами.
Здесь мы покажем вам систематический метод поиска наименьших общих знаменателей — метод, который работает с рациональными выражениями так же хорошо, как и с числами. Аналогично, любое число, простые множители которого включают 2 и 3 , а 5 будет кратно 30.
Аналогично, любое число, простые множители которого включают 2 и 3 , а 5 будет кратно 30. Однако вам следует внимательно изучить приведенное выше решение в течение нескольких минут. Как только вы поймете, почему [латекс] 2 \ cdot 2 \ cdot 3 \ cdot 5 = 60 [/ latex] гарантированно будет наименьшим общим знаменателем, у вас будет ключевая концепция, необходимая для сложения и вычитания рациональных выражений.
Однако вам следует внимательно изучить приведенное выше решение в течение нескольких минут. Как только вы поймете, почему [латекс] 2 \ cdot 2 \ cdot 3 \ cdot 5 = 60 [/ latex] гарантированно будет наименьшим общим знаменателем, у вас будет ключевая концепция, необходимая для сложения и вычитания рациональных выражений. 2 + 4 [/ latex].2 + 2)} [/ латекс]
2 + 4 [/ latex].2 + 2)} [/ латекс] Что ж, в этой статье мы узнаем, как написать алгебраических выражений из простых задач со словами, а затем перейдем к слегка сложным задачам со словами.
Что ж, в этой статье мы узнаем, как написать алгебраических выражений из простых задач со словами, а затем перейдем к слегка сложным задачам со словами. Например, x — это наша переменная в выражении: 10x + 63.
Например, x — это наша переменная в выражении: 10x + 63. Примеры числовых выражений: 2 + 4, 5-1, 400 + 600 и т. Д.
Примеры числовых выражений: 2 + 4, 5-1, 400 + 600 и т. Д.
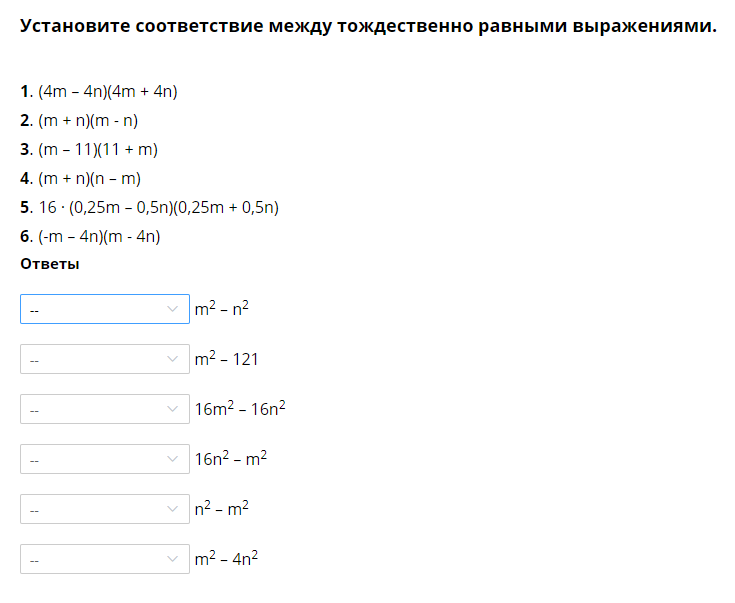 «Рациональные выражения: поиск предметной области». Пурпурная математика . Доступна с
«Рациональные выражения: поиск предметной области». Пурпурная математика . Доступна с  Следовательно,
Следовательно,  Возвращаемое значение — 0 для чисел, 1 для objref,
2 для strdef, 3 для указателей на числа и -1, если arg не существует.
Возвращаемое значение — 0 для чисел, 1 для objref,
2 для strdef, 3 для указателей на числа и -1, если arg не существует. 0
>>> тип (10/5)
<класс 'float'>
0
>>> тип (10/5)
<класс 'float'>
 (Списки определены в Python в квадратных скобках.)
(Списки определены в Python в квадратных скобках.) 0
>>> bool (x)
Ложь
>>> не х
Истинный
0
>>> bool (x)
Ложь
>>> не х
Истинный
 0
>>> у = 4,4
>>> х и у
0,0
0
>>> у = 4,4
>>> х и у
0,0
 2) = 2.2
-> f (бар) = бар
'бар'
2) = 2.2
-> f (бар) = бар
'бар'
 (
( Format ()
Format () 
 Это стандартная алгебраическая процедура, которая присутствует практически во всех языках программирования.
Это стандартная алгебраическая процедура, которая присутствует практически во всех языках программирования. Любые операторы в одной строке таблицы имеют одинаковый приоритет.
Любые операторы в одной строке таблицы имеют одинаковый приоритет.
 Конечно, вполне возможно, чтобы значение справа от присвоения было выражением, содержащим другие переменные:
Конечно, вполне возможно, чтобы значение справа от присвоения было выражением, содержащим другие переменные:
 Вы (и интерпретатор) можете идентифицировать строки, потому что они
заключен в кавычки.
Вы (и интерпретатор) можете идентифицировать строки, потому что они
заключен в кавычки. (”):
(”): Первый присваивает строку «Что
вверх, Doc? "в новую переменную с именем message. Вторая возвращает целое число
17 в n, а третий дает число с плавающей запятой 3.14159 в
число Пи.
Первый присваивает строку «Что
вверх, Doc? "в новую переменную с именем message. Вторая возвращает целое число
17 в n, а третий дает число с плавающей запятой 3.14159 в
число Пи. У переменных также есть
типы; опять же, мы можем спросить переводчика, что это такое.
У переменных также есть
типы; опять же, мы можем спросить переводчика, что это такое. больше $
является незаконным, поскольку содержит недопустимый символ - знак доллара. Но
что не так с классом?
больше $
является незаконным, поскольку содержит недопустимый символ - знак доллара. Но
что не так с классом? Если переводчик жалуется на одного
имен ваших переменных, и вы не знаете почему, посмотрите, есть ли она в этом списке.
Если переводчик жалуется на одного
имен ваших переменных, и вы не знаете почему, посмотрите, есть ли она в этом списке. Ценность все по
сам по себе является простым выражением, как и переменная.
Ценность все по
сам по себе является простым выражением, как и переменная. Значения, которые использует оператор, называются операндами .
Значения, которые использует оператор, называются операндами .

 Для строк оператор + представляет конкатенация , что означает соединение двух операндов путем их связывания
концы с концами. Например:
Для строк оператор + представляет конкатенация , что означает соединение двух операндов путем их связывания
концы с концами. Например: 9. Ввод .
9. Ввод . Дело в том, что любое выражение
с числами, строками и переменными можно использовать внутри оператора печати.
Вы уже видели пример:
Дело в том, что любое выражение
с числами, строками и переменными можно использовать внутри оператора печати.
Вы уже видели пример: Слева от
оператор присваивания = - это имя. Справа от
оператор присваивания - это выражение, которое вычисляется Python
переводчик, а затем присвоить имя. Разница между
левая и правая части оператора присваивания часто
сбивает с толку начинающих программистов. В присвоении:
Слева от
оператор присваивания = - это имя. Справа от
оператор присваивания - это выражение, которое вычисляется Python
переводчик, а затем присвоить имя. Разница между
левая и правая части оператора присваивания часто
сбивает с толку начинающих программистов. В присвоении:

 Имена переменных в Python состоят из
последовательность букв (a..z, A..Z и _) и цифр (0..9), которая начинается
с письмом. В лучшей практике программирования имена переменных должны быть
выбраны так, чтобы они описывали свое использование в программе, делая
программа самодокументирующая .
Имена переменных в Python состоят из
последовательность букв (a..z, A..Z и _) и цифр (0..9), которая начинается
с письмом. В лучшей практике программирования имена переменных должны быть
выбраны так, чтобы они описывали свое использование в программе, делая
программа самодокументирующая .

Leave A Comment