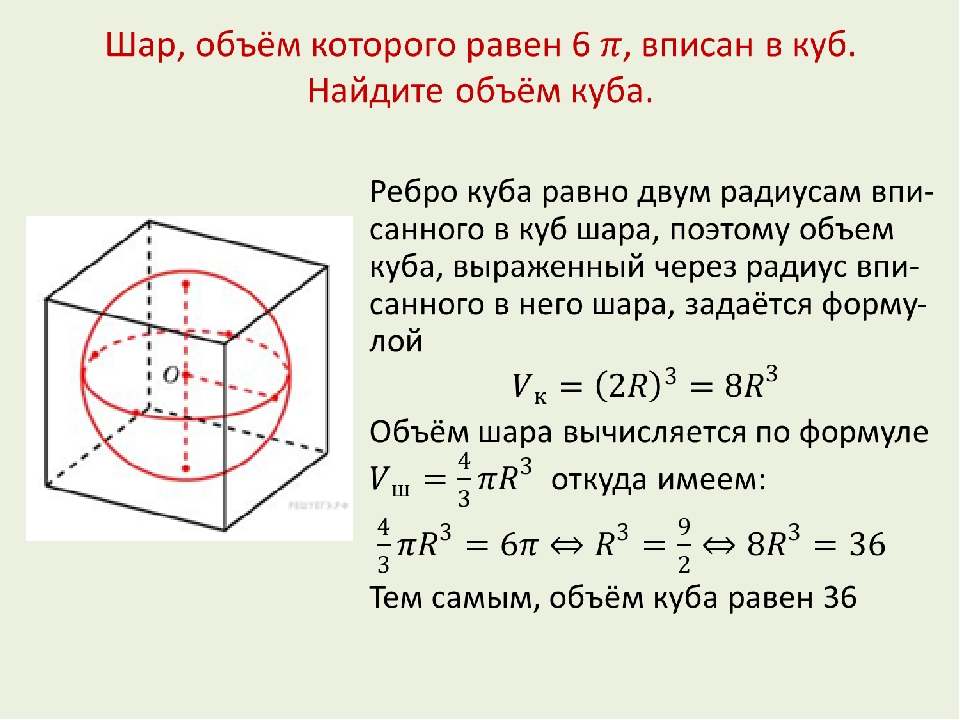
Объем куба равен Найдите площадь его поверхности
Задание B9 (5043)
(показов: 2452, ответов: 860)
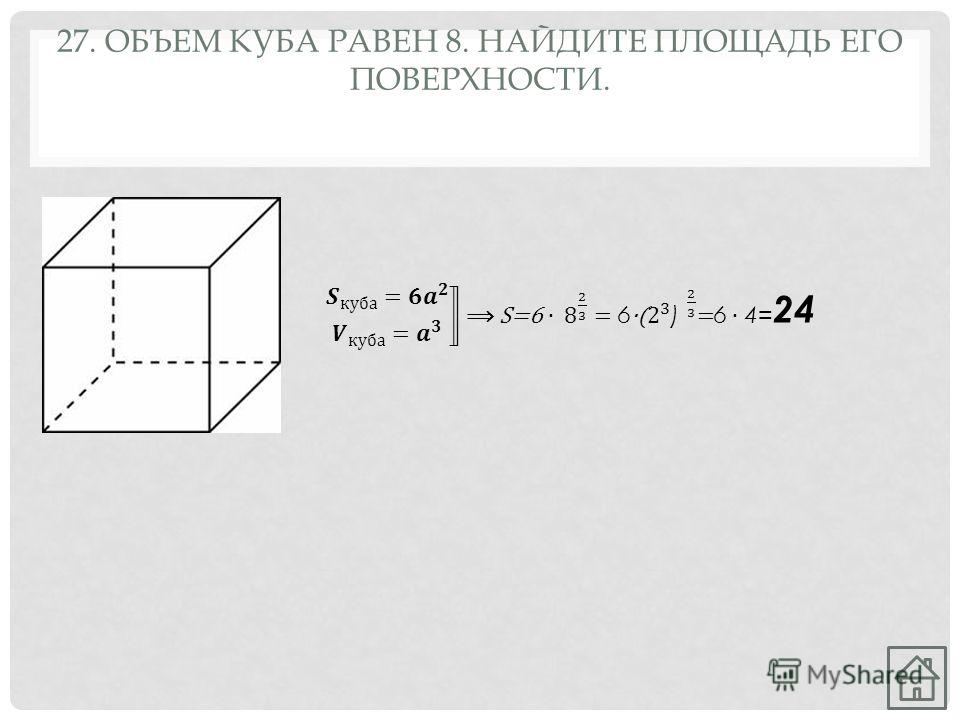
Объем куба равен 8. Найдите площадь его поверхности.
Ответ: 24
Задание B9 (5073)
(показов: 2272, ответов: 775)
Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Ответ: 14
Задание B9 (4895)
(показов: 2422, ответов: 692)
Найдите обьем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Ответ: 36
Задание
B9 (4897
(показов: 2280, ответов: 686)
Найдите
обьем многогранника, изображенного на
рисунке (все двугранные углы многогранника
прямые).
Ответ: 39
Задание B9 (5047)
(показов: 2347, ответов: 652)
Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .
Ответ: 12
Задание B9 (4903
(показов: 2193, ответов: 636)
Найдите обьем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Ответ: 39
Задание B9 (4899)
(показов: 2248, ответов: 630)
Найдите обьем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Ответ: 5
Задание B9 (5021)
(показов: 2397, ответов: 628
Объем конуса
равен 16. Через середину высоты параллельно
основанию конуса проведено сечение,
которое является основанием меньшего
конуса с той же вершиной. Найдите объем
меньшего конуса.
Через середину высоты параллельно
основанию конуса проведено сечение,
которое является основанием меньшего
конуса с той же вершиной. Найдите объем
меньшего конуса.
Ответ: 2
Задание B9 (4861)
(показов: 2320, ответов: 620)
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
Ответ:
Задание B9 (4901)
(показов: 2210, ответов: 618)
Найдите обьем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Ответ: 1
Стороны основания
правильной четырехугольной пирамиды
равны 10, боковые ребра равны 13. Найдите
площадь поверхности этой пирамиды.
Ответ: 340
Задание
B9 (4865
(показов: 2364, ответов: 600)
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 6. Найдите объем параллелепипеда.
Ответ: 864
Задание B9 (4999)
(показов: 2219, ответов: 598)
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 16.
Ответ: 48
Задание B9 (4997)
(показов: 2319
Цилиндр и конус
имеют общее основание и общую высоту.
Вычислите объем цилиндра, если объем
конуса равен 14.
Ответ: 42
Задание B9 (5027)
(показов: 2259, ответов: 595)
Объем конуса равен 120. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Ответ: 15
Задание B9 (5005)
(показов: 2353, ответов: 590)
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 87.
Ответ: 261
Задание B9 (5001)
(показов: 2253, ответов: 589)
Цилиндр и конус
имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем
конуса равен 11.
Вычислите объем цилиндра, если объем
конуса равен 11.
Ответ: 33
Задание B9 (5033)
(показов: 2286, ответов: 585)
Объем конуса равен 64. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Ответ: 8
Задание B9 (5009)
(показов: 2277, ответов: 582)
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 81.
Ответ: 243
Задание B9 (4951)
(показов: 2340, ответов: 572)
В сосуд, имеющий
форму правильной треугольной призмы,
налили воду.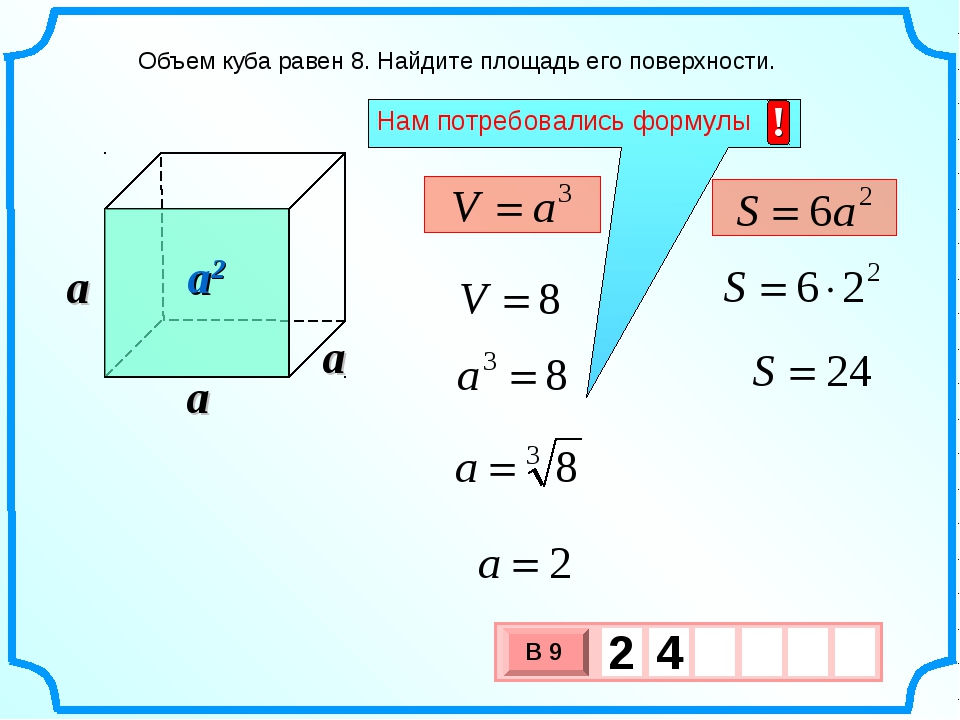 Уровень воды достигает 80
см. На какой высоте будет находиться
уровень воды, если ее перелить в другой
такой же сосуд, у которого сторона
основания в 4 раза больше, чем у первого?
Уровень воды достигает 80
см. На какой высоте будет находиться
уровень воды, если ее перелить в другой
такой же сосуд, у которого сторона
основания в 4 раза больше, чем у первого?
Ответ: 5
Задание
B9 (
(показов: 2351, ответов: 561)
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
Ответ: 0.25
Задание B9 (4959)
(показов: 2300, ответов: 556)
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 9 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 3 раза больше, чем у первого?
Ответ: 1
Задание B9 (4957)
(показов: 2272, ответов: 552)
В сосуд, имеющий
форму правильной треугольной призмы,
налили воду. Уровень воды достигает 27
см. На какой высоте будет находиться
уровень воды, если ее перелить в другой
такой же сосуд, у которого сторона
основания в 3 раза больше, чем у первого?
Уровень воды достигает 27
см. На какой высоте будет находиться
уровень воды, если ее перелить в другой
такой же сосуд, у которого сторона
основания в 3 раза больше, чем у первого?
Ответ: 3
Задание B9 (4963)
(показов:
В основании прямой призмы лежит прямоугольный треугольник с катетами 4 и 1. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
Ответ: 8.5
Задание B9 (4863)
(показов: 2351, ответов: 540)
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны . Найдите объем параллелепипеда.
Ответ: 13.5
Задание B9 (4881)
(показов:
Прямоугольный
параллелепипед описан около цилиндра,
радиус основания которого равен 6. Объем
параллелепипеда равен 36. Найдите высоту
цилиндра.
Объем
параллелепипеда равен 36. Найдите высоту
цилиндра.
Ответ: 0.25
Задание B9 (4869)
(показов: 2267, ответов: 523)
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны . Найдите объем параллелепипеда.
Ответ: 3429.5
Задание B9 (4955)
(показов: 2218, ответов: 522)
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 18 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 3 раза больше, чем у первого?
Ответ: 2
Задание B9 (4889)
(показов: 2333, ответов: 505)
Прямоугольный
параллелепипед описан около сферы
радиуса
. Найдите его объем.
Найдите его объем.
Ответ: 4913
Задание B9 (5039)
(показов: 2323, ответов: 500)
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Ответ: 5
Задание B9 (4991)
(показов: 1170, ответов: 292)
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 23.
Ответ: 69
Задание B9 (5017)
(показов: 1182, ответов: 292)
Цилиндр и конус
имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем
конуса равен 63.
Вычислите объем цилиндра, если объем
конуса равен 63.
Ответ: 189
Задание B9 (5015)
(показов: 1185, ответов: 286)
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 57.
Ответ: 171
Задание B9 (5007)
(показов: 1128, ответов: 285)
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 45.
Ответ: 135
Задание B9 (5025)
(показов: 1261, ответов: 285)
Объем конуса
равен 128. Через середину высоты параллельно
основанию конуса проведено сечение,
которое является основанием меньшего
конуса с той же вершиной. Найдите объем
меньшего конуса.
Найдите объем
меньшего конуса.
Ответ: 16
Задание B9 (5013)
(показов: 1199, ответов: 280)
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 75.
Ответ: 225
Задание B9 (5029)
(показов: 1142, ответов: 280)
Объем конуса равен 112. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Ответ: 14
Задание B9 (5003)
(показов: 1205, ответов: 278)
Цилиндр и конус
имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем
конуса равен 17.
Вычислите объем цилиндра, если объем
конуса равен 17.
Ответ: 51
Задание B9 (4989)
(показов: 1225, ответов: 276)
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 25.
Ответ: 75
Задание B9 (4883)
(показов: 1147, ответов: 275)
Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем.
Ответ: 8
Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза?
Ответ: 9
Задание B9 (4875)
(показов: 1173, ответов: 263)
Прямоугольный
параллелепипед описан около цилиндра,
радиус основания которого равен 1. Объем
параллелепипеда равен 5. Найдите высоту
цилиндра.
Объем
параллелепипеда равен 5. Найдите высоту
цилиндра.
Ответ: 1.25
Задание B9 (5059)
(показов: 1131, ответов: 262)
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Ответ: 8
Задание B9 (25713)
(показов: 915, ответов: 259)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 26
Задание B9 (5023)
(показов: 1192, ответов: 258)
Объем конуса
равен 168. Через середину высоты параллельно
основанию конуса проведено сечение,
которое является основанием меньшего
конуса с той же вершиной. Найдите объем
меньшего конуса.
Найдите объем
меньшего конуса.
Ответ: 21
Задание B9 (4891)
(показов: 1142, ответов: 257)
Прямоугольный параллелепипед описан около сферы радиуса . Найдите его объем.
Ответ: 6859
Задание B9 (4995)
(показов: 1138, ответов: 257)
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 18.
Ответ: 54
Задание B9 (5057)
(показов: 1134, ответов: 255)
Найдите боковое
ребро правильной четырехугольной
призмы, если сторона ее основания равна
20, а площадь поверхности равна 1760.
Ответ: 12
Задание B9 (25597)
(показов: 947, ответов: 253)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 56
Задание B9 (5035)
(показов: 1174, ответов: 250)
Объем конуса равен 144. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Ответ: 18
Задание B9 (25539)
(показов: 905, ответов: 237)
Найдите объем
многогранника, изображенного на рисунке
(все двугранные углы прямые).
Ответ: 25
Задание B9 (25569)
(показов: 896, ответов: 235)
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 58
Задание B9 (25671)
(показов: 928, ответов: 234)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 14
Задание B9 (4981)
(показов: 1211, ответов: 234)
В основании прямой призмы лежит квадрат со стороной 4. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
Ответ: 16
Задание B9 (25887)
(показов: 958, ответов: 232)
Найдите площадь
поверхности многогранника, изображенного
на рисунке (все двугранные углы прямые).
Ответ: 126
Задание B9 (4879)
(показов: 1148, ответов: 232)
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 3. Объем параллелепипеда равен 27. Найдите высоту цилиндра.
Ответ: 0.75
Задание B9 (25613)
(показов: 940, ответов: 231)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 62
Задание B9 (27043)
(показов: 731, ответов: 230)
Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем.
Ответ: 8
Задание B9 (25595)
(показов: 892, ответов: 226)
Найдите объем
многогранника, изображенного на рисунке
(все двугранные углы прямые).
Ответ: 47
Задание B9 (25715)
(показов: 897, ответов: 225)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 33
Задание B9 (25599)
(показов: 969, ответов: 209)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 46
Задание B9 (5077)
(показов: 1194, ответов: 206)
Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
Ответ: 12
Задание B9 (25873)
(показов: 934, ответов: 205)
Найдите объем
многогранника, изображенного на рисунке
(все двугранные углы прямые).
Ответ: 72
Задание B9 (25633)
(показов: 922, ответов: 204)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 52
Задание B9 (25575)
(показов: 828, ответов: 204)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 10
Задание B9 (25651)
(показов: 920, ответов: 201)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 90
Задание B9 (25857)
(показов: 823, ответов: 200)
Объем
параллелепипеда
равен
6. Найдите объем треугольной пирамиды
.
Найдите объем треугольной пирамиды
.
Ответ: 1
Задание B9 (25879)
(показов: 853, ответов: 200)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 78
Задание B9 (27216)
(показов: 686, ответов: 200)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 78
Задание B9 (25649)
(показов: 881, ответов: 197)
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 54
Задание B9 (27136)
(показов: 517, ответов: 167)
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?
Ответ: 3
Задание B9 (27052)
(показов: 593, ответов: 165)
Объем конуса
равен 16. Через середину высоты параллельно
основанию конуса проведено сечение,
которое является основанием меньшего
конуса с той же вершиной. Найдите объем
меньшего конуса.
Через середину высоты параллельно
основанию конуса проведено сечение,
которое является основанием меньшего
конуса с той же вершиной. Найдите объем
меньшего конуса.
Ответ: 2
Задание B9 (25753)
(показов: 831, ответов: 164)
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
Ответ: 13.5
Задание B9 (25819)
(показов: 853, ответов: 164)
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите .
Ответ: 168
Задание B9 (25693)
(показов: 723, ответов: 160)
Найдите объем
многогранника, изображенного на рисунке
(все двугранные углы прямые).
Ответ: 32
Задание B9 (27178)
(показов: 745, ответов: 158)
В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
Ответ: 13
Задание B9 (25553)
(показов: 700, ответов: 153)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 40
Задание B9 (5063)
(показов: 1151, ответов: 151)
Найдите
площадь боковой поверхности правильной
шестиугольной призмы, описанной около
цилиндра, радиус основания которого
равен
,
а высота равна 2.
Ответ: 24
Задание B9 (27079)
(показов: 483, ответов: 148)
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Ответ: 4
Задание B9 (25817)
(показов: 904, ответов: 146)
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите .
Ответ: 648
Задание B9 (27157)
(показов: 278, ответов: 60)
Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
Ответ: 9
Задание B9 (25805)
(показов: 561, ответов: 59)
Найдите
объем V части конуса, изображенной на рисунке. В ответе укажите
.
В ответе укажите
.
Ответ: 117
Задание B9 (25877)
(показов: 475, ответов: 59)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 76
Задание B9 (27068)
(показов: 413, ответов: 58)
Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Ответ: 12
Задание B9 (25863)
(показов: 500, ответов: 56)
Объем
параллелепипеда
равен
. Найдите объем треугольной пирамиды
.
Найдите объем треугольной пирамиды
.
Ответ: 0.6
Задание B9 (27058)
(показов: 284, ответов: 52)
Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .
Ответ: 12
Задание B9 (27077)
(показов: 350, ответов: 51)
Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Ответ: 8
Задание B9 (27200)
(показов: 275, ответов: 50)
Найдите
объем V части цилиндра, изображенной на рисунке.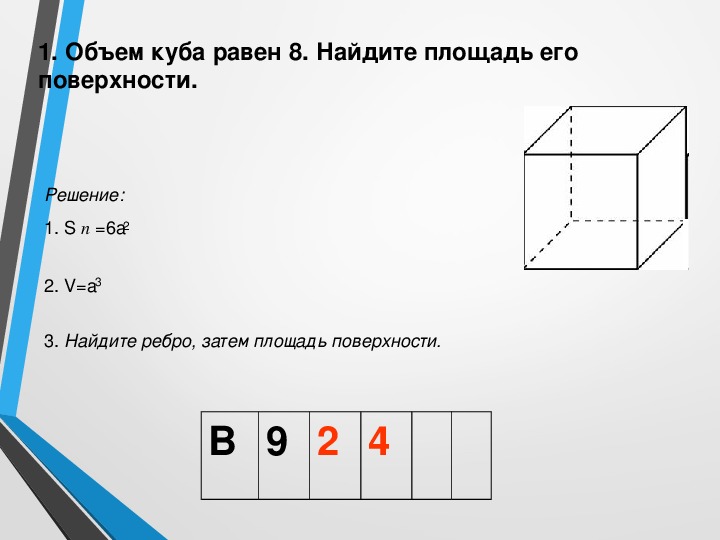 В ответе укажите
.
В ответе укажите
.
Ответ: 14
Задание B9 (25659)
(показов: 470, ответов: 49)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 54
Задание B9 (25733)
(показов: 561, ответов: 49)
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
Ответ: 2
Задание B9 (27137)
(показов: 358, ответов: 67)
Во сколько раз уменьшится площадь боковой поверхности конуса, если его радиус его основания уменьшить в 1,5 раза?
Ответ: 1. 5
5
Задание B9 (5055)
(показов: 644, ответов: 67)
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
Ответ: 248
Задание B9 (27047)
(показов: 377, ответов: 65)
Сосуд, имеющий форму правильной треугольной призмы, налили воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки см до отметки см. Найдите объем детали. Ответ выразите в .
Ответ: 184
Задание B9 (27093)
(показов: 407, ответов: 65)
Найдите
объем конуса, площадь основания которого
равна 2, а образующая равна 6 и наклонена
к плоскости основания под углом 30.
Ответ: 2
Задание B9 (27163)
(показов: 408, ответов: 65)
Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Ответ: 10
Задание B9 (25945)
(показов: 523, ответов: 65)
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 80
Задание B9 (27140)
(показов: 387, ответов: 64)
Площадь поверхности куба равна 8. Найдите его диагональ.
Ответ: 2
Задание B9 (25775)
(показов: 548, ответов: 62)
Найдите
объем V части цилиндра, изображенной на рисунке. В ответе укажите
.
В ответе укажите
.
Ответ: 64
Задание B9 (27190)
(показов: 366, ответов: 61)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 34
Задание B9 (25965)
(показов: 544, ответов: 61)
Площадь поверхности тетраэдра равна 1. Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра.
Ответ: 0.5
%PDF-1.4 % 34 0 obj >>>]/ON[38 0 R]/Order[]/RBGroups[]>>/OCGs[38 0 R]>>/OpenAction[1 0 R/XYZ null null 0]/Pages 16 0 R/Type/Catalog>> endobj 36 0 obj >/Font>>>/Fields 42 0 R>> endobj 37 0 obj >stream application/pdf
 2uuid:47c33a38-1f83-443e-81a7-de17e57adcc9uuid:5483d90a-7223-48a4-96e5-a8a8edfbf9f3
endstream
endobj
16 0 obj
>
endobj
33 0 obj
>
endobj
32 0 obj
>
endobj
26 0 obj
>
endobj
21 0 obj
>
endobj
31 0 obj
>
endobj
29 0 obj
>
endobj
30 0 obj
>stream
x]j0E
-E,’YCH xu4v$_=8;/v:k{Czt4V#,nEtXR
5KOX`蚆[ntwn=aGݯa(‘mK5γ/r]Nǰ !Z>6Td]QӰx
2uuid:47c33a38-1f83-443e-81a7-de17e57adcc9uuid:5483d90a-7223-48a4-96e5-a8a8edfbf9f3
endstream
endobj
16 0 obj
>
endobj
33 0 obj
>
endobj
32 0 obj
>
endobj
26 0 obj
>
endobj
21 0 obj
>
endobj
31 0 obj
>
endobj
29 0 obj
>
endobj
30 0 obj
>stream
x]j0E
-E,’YCH xu4v$_=8;/v:k{Czt4V#,nEtXR
5KOX`蚆[ntwn=aGݯa(‘mK5γ/r]Nǰ !Z>6Td]QӰx1.
 1. Объем куба равен 8. Найдите площадь его поверхности.
1. Объем куба равен 8. Найдите площадь его поверхности.B9
Ответ: 24 1.2. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Ответ: 5 1.3. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
Ответ:248
1.4. Площадь поверхности куба
равна 18. Найдите его диагональ.
Найдите его диагональ.
Ответ:3 1.5. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
Ответ: 12 1.6. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза?
Ответ: 9 1.7. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
Ответ: 3 1.8. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Ответ:4
2.1. Найдите объем многогранника,
изображенного на рисунке (все двугранные
углы многогранника прямые).
Ответ: 39 2.2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Ответ: 36 2.3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Ответ: 18 2.4. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 16 2.5. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 26 2.6. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 33 2.7. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 68 2.8. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 56
2.
 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).Ответ: 62 2.10. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 62 2.11. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 126 2.12. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 78 2.13. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 72 2.14. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ:
54
2. 15.
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные
углы прямые).
15.
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные
углы прямые).
Ответ:126 2.16. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 32 2.17. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 14 2.18. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 15 2.19. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 40 2.20. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 50
Презентация для отработки №8 ЕГЭ профиль
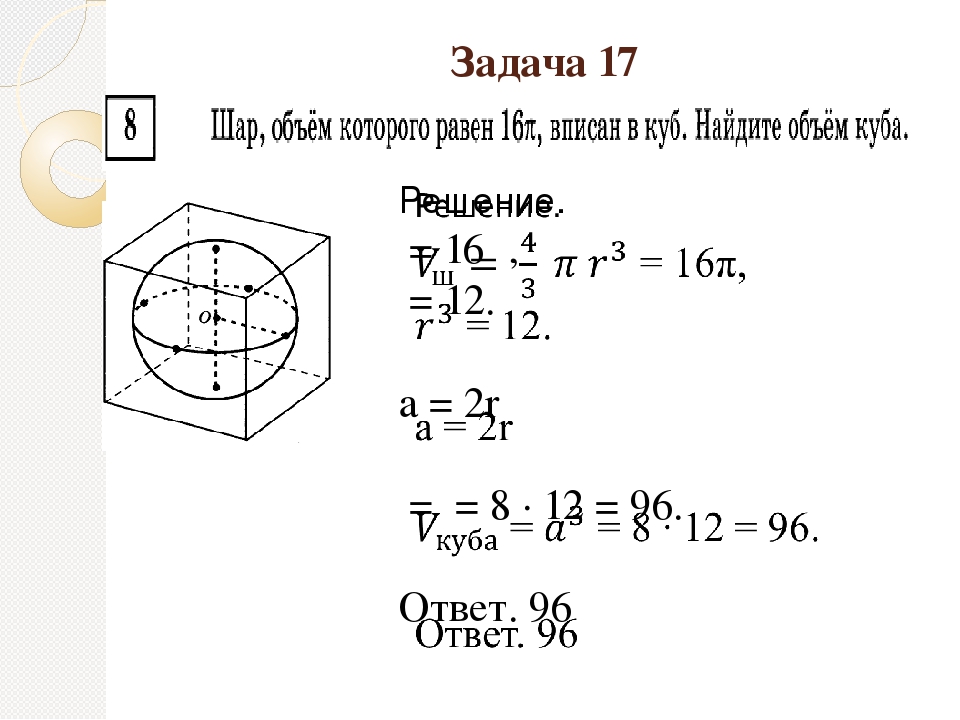
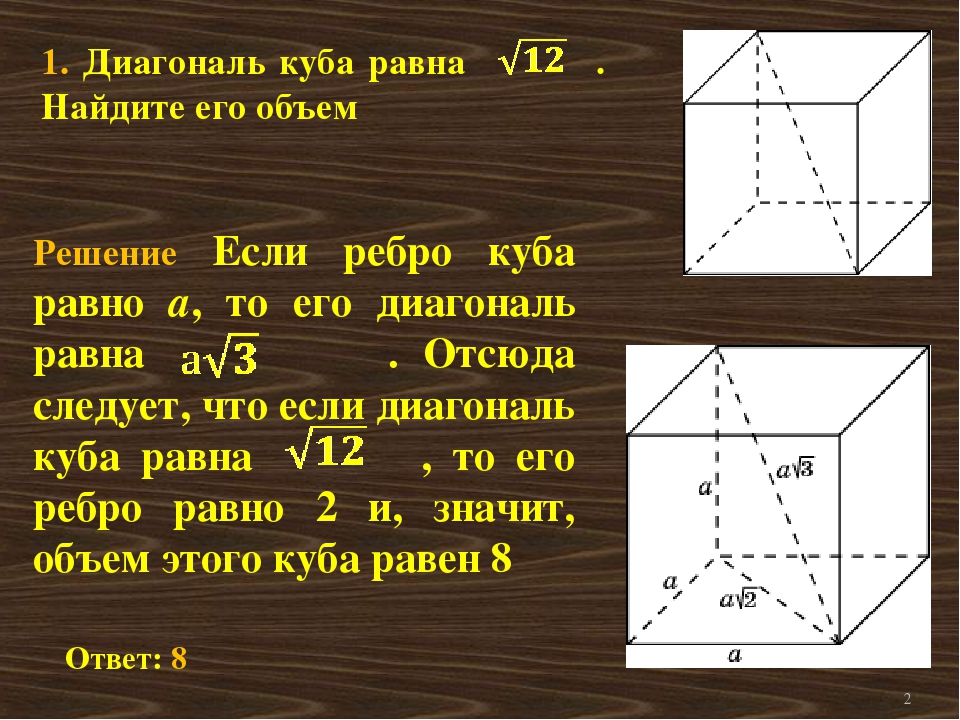
1. Диагональ куба равна . Найдите его объем.
Диагональ куба равна . Найдите его объем.
Решение. Если ребро куба равно a , то его диагональ равна . Отсюда следует, что если диагональ куба равна , то его ребро равно 2 и, значит, объем этого куба равен 8.
2 . Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 30. Найдите ребро куба.
Решение. Если ребро куба равно x , то площадь его поверхности равна 6 x 2 . Если ребро куба увеличить на 1, то его площадь поверхности будет равна 6( x + 1) 2 . Учитывая, что площадь поверхности куба при этом увеличивается на 30, получаем уравнение 6( x + 1) 2 = 6 x 2 + 30, решая которое, находим x = 2.
3 . Гранью параллелепипеда является ромб со стороной 1 и острым углом 60 о . Одно из ребер параллелепипеда составляет с этой гранью угол в 60 о и равно 2. Найдите объем параллелепипеда.
Решение. Площадь грани параллелепипеда, являющейся ромбом со стороной 1 и острым углом 60 о , равна . Высота, опущенная на эту грань, равна . Объем параллелепипеда равен 1,5.
Высота, опущенная на эту грань, равна . Объем параллелепипеда равен 1,5.
4 . Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Решение. Площадь основания отсеченной призмы равна четверти площади основания исходной призмы. Высота отсеченной призмы равна высоте исходной призмы. Следовательно, объем отсеченной призмы равен четверти объема исходной призмы, т.е. равен 8.
5 . Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
Решение. Воспользуемся тем, что если два тетраэдра подобны и коэффициент подобия равен k , то отношение объемов этих тетраэдров равно k 3 . Если ребра тетраэдра увеличить в два раза, то объем тетраэдра увеличится в 8 раз.
6 . Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности пирамиды.
Найдите площадь боковой поверхности пирамиды.
Решение. Высота боковой грани пирамиды равна 12. Площадь боковой грани равна 60. Площадь боковой поверхности этой пирамиды равна 360.
7 . Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение. Поверхность многогранника состоит из двух квадратов, площадь которых равна 4, четырех прямоугольников, площадь которых равна 2, и двух невыпуклых шестиугольников, площадь которых равна 3. Следовательно, площадь поверхности многогранника равна 22.
8 . Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.
Решение. Площадь основания пирамиды равна 27, высота равна 3. Следовательно, объем пирамиды равен 27.
9 . В цилиндрический сосуд, в котором находится 6 3 воды, опущена деталь.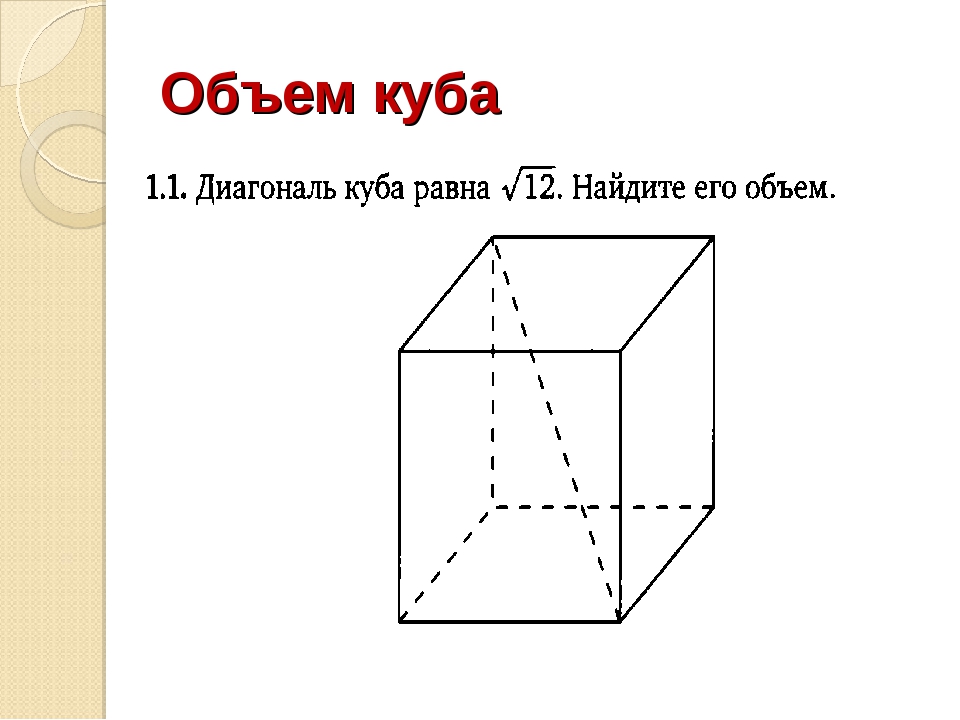 При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали?
При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали?
Решение. Так как уровень жидкости в сосуде поднялся в 1,5 раза, то и объем увеличился в 1,5 раза, т.е. стал равен 9 дм 3 . Следовательно, объем детали равен 3 дм 3 .
10 . Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Решение. Площади поверхностей данных шаров равны и . Их сумма равна . Следовательно, радиус шара, площадь поверхности которого равна этой сумме, равен 10.
11 . Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объем параллелепипеда.
Решение. Ребра параллелепипеда равны 4, 4, 2 и, следовательно, его объем равен 32.
12 . В куб с ребром 6 вписан шар. Найдите объем шара, деленный на .
Решение. Радиус шара равен 3. Объем шара равен , а объем, деленный на равен 36.
Задания №13 и №16 базового уровня с кубом
1. Практикум №1 по решению стереометрических задач (базовый уровень)
Задания №13 и №16базового уровня
с кубом
3. Содержание
• Задача №1• Задача №2
• Задача №3
• Задача №4
• Задача №5
• Задача №6
• Задача №7
• Задача №8
• Задача №9
• Задача №10
• Задача №11
• Задача №12
• Задача №13
• Задача №14
4. ВСПОМНИМ
• Куб – прямоугольный параллелепипед, все граникоторого – квадраты.
• Все грани куба равные квадраты.
• Sп.пов. = 6а²;
Sосн. = а²
• V = a³
• Все диагонали куба равны, пересекаются в одной точке
и делятся этой точкой пополам.
• Боковые рёбра перпендикулярны его основаниям
• d² = 3·a²
5. Задача №1
Площадь поверхности куба равна 18. Найдите егодиагональ.
Решение.
Пусть ребро куба равно а, тогда площадь
поверхности куба S=6a², а диагональ куба
d = a√3.
 Тогда
ТогдаОтвет: 3.
6. Задача №2
Объем куба равен 8. Найдите площадь егоповерхности.
Решение.
Площадь поверхности куба выражается через
его ребро а как S=6a², а объем — как V=a³.
Отсюда видно, что площадь поверхности куба
выражается через его объем как
.
Отсюда находим, что
7. Задача №3
Если каждое ребро куба увеличить на 1, то егоплощадь поверхности увеличится на 54. Найдите
ребро куба.
Решение.
Площадь поверхности куба выражается через его ребро a
как S=6a², поэтому при увеличении длины ребра на 1
площадь увеличится на
Отсюда находим, что ребро
8. Задача №4
Во сколько раз увеличится объем куба, если егоребра увеличить в три раза?
Решение.
Объем куба с ребром а равен V=a³. Если ребра
увеличить в 3 раза, то объем куба увеличится
в 3³=27 раз.
Ответ: 27
9. Задача №5
Объем куба равен 24√3 . Найдите его диагональ.Решение.
Пусть ребро куба равно а, тогда площадь
поверхности куба S=6a², а диагональ
куба d = a√3.
 Тогда
ТогдаЗначит d = 6.
Можно решить и через….
10. Задача №6
Если каждое ребро куба увеличить на 1, то его объемувеличится на 19. Найдите ребро куба.
Решение.
Объем куба с ребром а равен V=a³. Увеличение объема равно
19:
Решим уравнение: a² + a — 6 = 0 => a=2; a= -3(не подходит)
Ответ: 2.
11. Задача №7
Во сколько раз увеличится площадь поверхностикуба, если его ребро увеличить в три раза?
Решение.
Площади подобных тел относятся как квадрат
коэффициента подобия, поэтому при увеличении
ребра в 3 раза, площадь поверхности увеличится
в 9 раз.
12. Задача №8
Диагональ куба равна 1. Найдите площадь егоповерхности.
Решение.
Знаем, что d = a√3. => а = d:√3 = 1/√3 , тогда
13. Задача №9
Площадь поверхности куба равна 24. Найдите его объем.Решение.
Объем куба с ребром а равен V=a³, а S=6a². => а²=S/6
Т.е. а=√S/6, тогда
14. Задача №10
Объем одного куба в 8 раз больше объема другого куба.
Во сколько раз площадь поверхности первого куба
больше площади поверхности второго куба?
Решение.
Объемы подобных тел относятся как куб коэффициента
подобия, поэтому один из кубов в 2 раза больше
другого.
Площади поверхностей подобных тел относятся как
квадрат коэффициента подобия, поэтому их отношение
равно 4.
15. Задача №11
От деревянного кубика отпилили все его вершины (см.рис). Сколько граней у получившегося многогранника
(невидимые ребра на рисунке не обозначены)?
Решение.
У кубика 6 граней. В результате
отпиливания 8 вершин появились 8
граней. Всего 14 граней.
16. Задача №12
Плоскость, проходящая через три точки A, B и С,разбивает куб на два многогранника. Сколько граней у
многогранника, у которого больше рёбер?
Решение.
В
сечении
получается
четырёхугольник.
У одной отсечённой фигуры 15 рёбер
и 7 граней, у второй — 9 рёбер и 5
граней.

Ответ: 7 граней.
17. Задача №13
Ящик, имеющий форму куба с ребром 10 см без однойграни, нужно покрасить со всех сторон снаружи.
Найдите площадь поверхности, которую необходимо
покрасить. Ответ дайте в квадратных сантиметрах.
Решение.
Площадь одной грани равна 10 · 10 = 100 см². В кубе
шесть граней, но нам надо найти только площадь пяти
граней, следовательно 100 · 5 = 500 см².
Ответ: 500
18. Задача №14
Диагональ куба равна √12 . Найдите его объем.Решение.
Диагональ куба d = a√3 , т.е. в √3 раз
больше его ребра. Получим, что ребро равно
Тогда V=a³ = 2³ = 8
Задачи
для самостоятельного
решения
20. Задача №1 Решите самостоятельно
1) Площадь поверхности куба равна 2592. Найдитеего диагональ.
Ответ: 36
2) Площадь поверхности куба равна 1568. Найдите
его диагональ.
3) Площадь поверхности куба равна 18. Найдите
его диагональ.
21. Задача №2 Решите самостоятельно
1) Объем куба равен 8. Найдите площадь его
Найдите площадь егоповерхности.
2) Объем куба равен 343. Найдите площадь его
поверхности.
3) Объем куба равен 216. Найдите площадь его
поверхности.
4) Объем куба равен 125. Найдите площадь его
поверхности.
22. Задача №3 Решите самостоятельно
1) Если каждое ребро куба увеличить на 5, то егоплощадь поверхности увеличится на 390.
Найдите ребро куба.
Ответ: 4
2) Если каждое ребро куба увеличить на 2, то его
площадь поверхности увеличится на 144.
Найдите ребро куба.
3) Если каждое ребро куба увеличить на 4, то его
площадь поверхности увеличится на 240.
Найдите ребро куба.
23. Задача №4 Решите самостоятельно
1) Во сколько раз увеличится объем куба, если егоребра увеличить в пятнадцать раз?
2) Во сколько раз увеличится объем куба, если его
ребра увеличить в шесть раз?
3) Во сколько раз увеличится объем куба, если его
ребра увеличить в 12 раз?
4) Во сколько раз увеличится объем куба, если его
ребра увеличить в 10 раз?
24.
 Задача №5 Решите самостоятельно Задача №5
Задача №5 Решите самостоятельно Задача №51)
2)
3)
4)
5)
6)
Решите самостоятельно
Объем куба равен 0,003√3. Найдите его диагональ.
Объем куба равен 1536√3. Найдите его диагональ.
Объем куба равен 3000√3. Найдите его диагональ.
Объем куба равен 81√3. Найдите его диагональ.
Объем куба равен 192√3. Найдите его диагональ.
Объем куба равен 2187√3. Найдите его диагональ.
25. Задача №6 Решите самостоятельно
1) Если каждое ребро куба увеличить на 2, то его объемувеличится на 728. Найдите ребро куба.
2) Если каждое ребро куба увеличить на 3, то его объем
увеличится на 819. Найдите ребро куба.
3) Если каждое ребро куба увеличить на 3, то его объем
увеличится на 1413. Найдите ребро куба.
4) Если каждое ребро куба увеличить на 1, то его объем
увеличится на 721. Найдите ребро куба.
26. Задача №7 Решите самостоятельно
1) Во сколько раз увеличится площадьповерхности куба, если его ребро увеличить в 2
раза?
2) Во сколько раз увеличится площадь
поверхности куба, если его ребро увеличить в 24
раза?
3) Во сколько раз увеличится площадь
поверхности куба, если его ребро увеличить в 33
раза?
27.
 Задача №8 Решите самостоятельно 1) Диагональ куба равна 6. Найдите площадь его
Задача №8 Решите самостоятельно 1) Диагональ куба равна 6. Найдите площадь егоповерхности.
2) Диагональ куба равна 34. Найдите площадь его
поверхности.
3) Диагональ куба равна 41. Найдите площадь его
поверхности.
4) Диагональ куба равна 9. Найдите площадь его
поверхности.
28. Задача №9 Решите самостоятельно
1) Площадь поверхности куба равна 864. Найдите егообъем.
2) Площадь поверхности куба равна 54. Найдите его
объем.
3) Площадь поверхности куба равна 216. Найдите его
объем.
4) Площадь поверхности куба равна 96. Найдите его
объем.
29. Задача №10 Решите самостоятельно
1) Объем одного куба в 125 раз больше объема другогокуба. Во сколько раз площадь поверхности первого куба
больше площади поверхности второго куба?
2) Объем одного куба в 64 раз больше объема другого
куба. Во сколько раз площадь поверхности первого куба
больше площади поверхности второго куба?
3) Объем одного куба в 729 раз больше объема другого
куба.
 Во сколько раз площадь поверхности первого куба
Во сколько раз площадь поверхности первого кубабольше площади поверхности второго куба?
30. Задача №13 Решите самостоятельно
1) Ящик, имеющий форму куба с ребром 30 см безодной грани, нужно покрасить со всех сторон
снаружи. Найдите площадь поверхности,
которую необходимо покрасить. Ответ дайте в
квадратных сантиметрах. Ответ: 4500
31. Задача №14 Решите самостоятельно
1)2)
3)
4)
5)
6)
Диагональ куба равна √243 . Найдите его объем.
Диагональ куба равна √588 . Найдите его объем.
Диагональ куба равна √48 . Найдите его объем.
Диагональ куба равна √300 . Найдите его объем.
Диагональ куба равна √27 . Найдите его объем.
Диагональ куба равна √675 . Найдите его объем.
32. Интернет ресурсы
• Шаблон подготовила учитель русского языка и литературыТихонова Надежда Андреевна
• «Решу ЕГЭ» Образовательный портал для подготовки к ЕГЭ и ОГЭ. Режим доступа:
http://mathb.reshuege.
 ru
ruhttp://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg
http://a550.phobos.apple.com/us/r30/Purple/v4/0c/91/17/0c9117c4-c866-54fc68ce-0e5aa31f5929/mzl.dfcpkqki.png
Диагональ куба равна корню
Для вас следующая статья с кубами и прямоугольными параллелепипедами. Посмотрите предыдущую, там перечислены используемые формулы (вдруг позабылись). Задачи здесь представлены несложные, они очень похожи друг на друга. Думаю, будет полезно.
Рассмотрим задания:
Диагональ куба равна корню из трёхсот. Найдите его объем.
Обозначим ребро куба как a.
Объём куба вычисляется по формуле:
То есть для нахождения объёма куба необходимо найти его ребро.
Диагональ куба находится по формуле:
Значит
Таким образом:
Ответ: 1000
Объём куба равен 81√3. Найдите его диагональ.
Это задача обратная предыдущей.
Диагональ куба находится по формуле:
Выразим ребро куба из формулы объёма подставим:
*Если вы хотите вспомнить как работать со степенями и корнями, тогда вам сюда.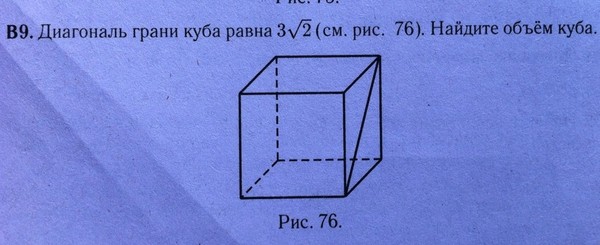
Ответ: 9
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 72 и 18. Диагональ параллелепипеда равна 78. Найдите объем параллелепипеда.
Пусть рёбра параллелепипеда равны a, b и с.
Для нахождения объёма нам необходимо знать его третье ребро. Как его найти?
Мы можем воспользоваться формулой диагонали параллелепипеда:
Получается:
Вычислим неизвестное ребро:
Таким образом, объём параллелепипеда равен:
*При разности квадратов используйте формулу, решение упрощается.
Ответ: 31104
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 12 и 6. Объем параллелепипеда равен 864. Найдите его диагональ.
Задача обратная предыдущей. Для того, чтобы найти диагональ, необходимо знать чему равно третье ребро. Мы можем вычислить его воспользовавшись формулой объёма:
Диагональ параллелепипеда равна:
Ответ: 18
Диагональ куба равна 41. Найдите площадь его поверхности.
Найдите площадь его поверхности.
Площадь поверхности куба равна:
Формула длины диагонали куба:
Выразим ребро и подставим полученное выражение в формулу площади поверхности:
Тогда площадь поверхности куба:
Ответ: 3362
Площадь поверхности куба равна 216. Найдите его объем.
Площадь поверхности куба со стороной равна S = 6 a2.
Найдём ребро куба:
Объем куба равен:
Ответ: 216
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.
Для того, чтобы вычислить площадь поверхности необходимо знать третье ребро:
Используем формулу длины диагонали:
Получается:
Таким образом:
Ответ: 64
27128. Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности. Ответ: 22.
Найдите его площадь поверхности. Ответ: 22.
27146. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 2 Объем параллелепипеда равен 6. Найдите площадь его поверхности. Ответ: 22
27098. Диагональ куба равна корню из двенадцати. Найдите его объем.
Посмотреть решение
27101. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.
Посмотреть решение
27139. Диагональ куба равна 1. Найдите площадь его поверхности.
Посмотреть решение
27141. Площадь поверхности куба равна 24. Найдите его объем.
Посмотреть решение
Вот ещё задачи с кубами и параллелепипедами, но они чуть посложнее, не пропустите!
На этом всё! Успеха вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
| Стереометрия1 Куб Ответ: 3 Ответ: 24 Ответ: 4 Ответ: 27 Ответ: 6 Ответ: 2 Ответ: 7 Ответ: 9 Ответ: 2 Ответ: 8 Ответ: 4 1. B 10 № 27079. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины. Ответ: 4 Ответ: 36 3. B 10 № 27209. Объем параллелепипеда равен 4,5. Найдите объем треугольной пирамиды . Ответ: 1,5 4.
Ответ: 30 5. B 10 № 245336. Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , , .
Ответ: 8 6. B 10 № 245337. Найдите объем многогранника, вершинами которого являются точки , , , , прямоугольного параллелепипеда , у которого , , .
Ответ: 16 7. B 10 № 245338. Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , , .
Ответ: 6 8. B 10 № 245339. Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , , .  Ответ: 10 Призма 1. B 10 № 916. В прямоугольном параллелепипеде известно, что Найдите длину ребра . Ответ: 3 Ответ: 2 Ответ: 4 Ответ: 5 Ответ: 184 6. B 10 № 27048. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.  Ответ: 5 Ответ: 300 8. B 10 № 27062. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10. Ответ: 248 9. B 10 № 27063. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760. Ответ: 12 10. B 10 № 27106. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы. Ответ: 8 Ответ: 20 Ответ: 4 Ответ: 288 Ответ: 10 15. B 10 № 27151. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы. Ответ: 10 16.  B 10 № 27153. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы. B 10 № 27153. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.Ответ: 16 17. B 10 № 27183. Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины. Ответ: 1,5 18. B 10 № 245340. Найдите объем многогранника, вершинами которого являются точки , , , правильной треугольной призмы , площадь основания которой равна 2, а боковое ребро равно 3.
Ответ: 2 19. B 10 № 245341. Найдите объем многогранника, вершинами которого являются точки , , , , правильной треугольной призмы , площадь основания которой равна 3, а боковое ребро равно 2. 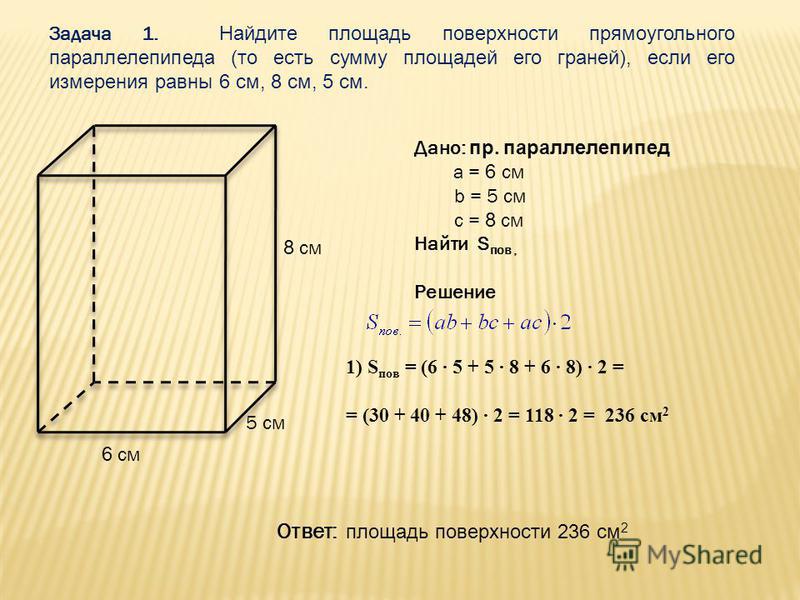 Ответ: 4 Ответ: 4 Ответ: 4 22. B 10 № 245344. Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 3. Ответ: 3
Ответ: 8 24.  B 10 № 245346. Найдите объем многогранника, вершинами которого являются точки , , , , , , , правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 2. B 10 № 245346. Найдите объем многогранника, вершинами которого являются точки , , , , , , , правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 2.
Ответ: 6 25. B 10 № 245347. Найдите объем многогранника, вершинами которого являются точки , , , правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 3. Ответ: 1 26. B 10 № 245356. Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все ее ребра увеличить в три раза? Ответ: 54 27. B 10 № 245359. Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1=3. Ответ: 50 28. B 10 № 245360. Найдите расстояние между вершинами А и D прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA = 3.  Ответ: 5 Достарыңызбен бөлісу: |
Объем 8-дюймового куба
Каков объем куба со стороной 8 дюймов?
Объем куба со сторонами 8 ″
| 512 | кубических дюймов |
| 0,29630 | кубических футов |
| 0,010974 | кубических ярдов |
| 0,0083902 | кубических метров | 000кубических сантиметров |
| 8,3902 | литров |
| 2,2165 | галлонов |
(результаты могут быть округлены)
Формула объема куба
Объем куба — это длина одной стороны куба.
Объем = Сторона 3
Объем по длине сторон
(результаты округлены)
| Сторона | дюйм 2 | футов 2 | см 2 |
|---|---|---|---|
8. 0 из 0 из | 512,0 | 0,2963 | 0,008390 |
| 8,1 дюйма | 531,4 | 0,3075 | 0,008709 |
| 8,2 дюйма | 551,4 | 0,3191 | 0,009035 |
| 8,3 дюйма | 571,8 | 0,3309 | 0,009370 |
| 8,4 дюйма | 592,7 | 0,3430 | 0,009713 |
| Сторона | дюйм 2 | футов 2 | см 2 |
|---|---|---|---|
| 8.5 из | 614,1 | 0,3554 | 0,01006 |
| 8,6 дюйма | 636,1 | 0,3681 | 0,01042 |
| 8,7 дюйма | 658,5 | 0,3811 | 0,01079 |
| 8,8 дюйма | 681,5 | 0,3944 | 0,01117 |
| 8,9 дюйма | 705,0 | 0,4080 | 0,01155 |
Объем куба с калькулятором
Объем куба с калькулятором — Math Open ReferenceОпределение: Количество кубических единиц, которое точно заполнит куб
Попробуй это
Перетащите оранжевую точку, чтобы изменить размер куба.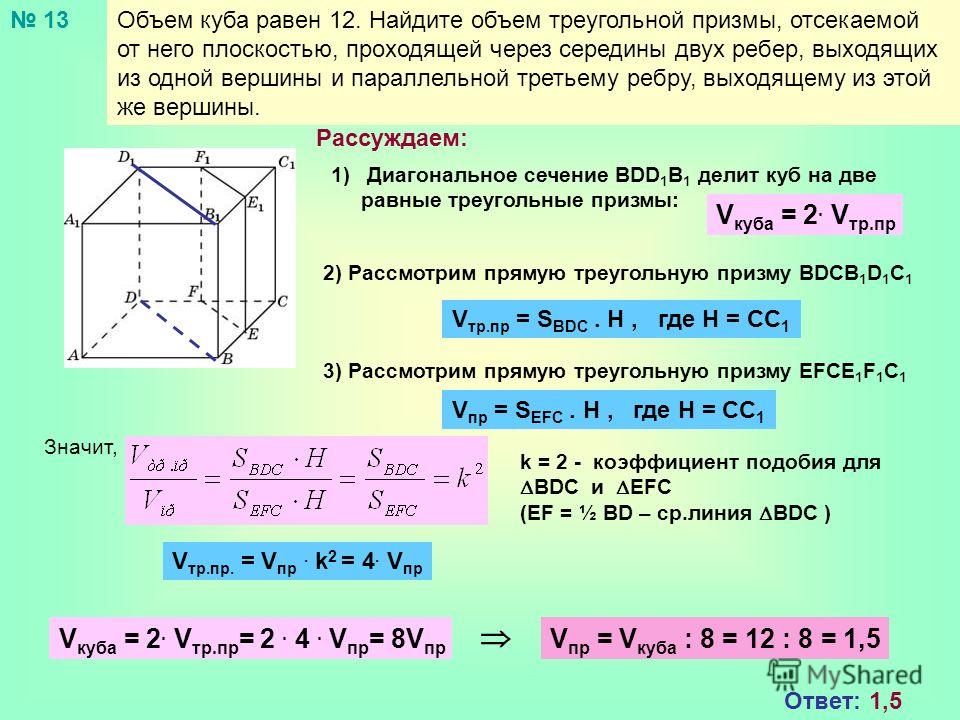 Объем рассчитывается при перетаскивании.
Объем рассчитывается при перетаскивании.
Как найти объем куба
Напомним, что все ребра куба имеют одинаковую длину (см. Определение куба). Объем куба определяется двойным умножением длины любого ребра на него самого. Так, если длина ребра равна 4, объем будет 4 x 4 x 4 = 64
.Или как формула:
| объем = с 3 | где: s — длина любого ребра куба. |
На рисунке выше перетащите оранжевую точку, чтобы изменить размер куба. По показанной длине ребра рассчитайте объем куба и убедитесь, что он соответствует расчету на рисунке.
Когда мы пишем volume = s 3 , строго говоря, это следует читать как «s в степени 3», но поскольку он используется для вычисления объема кубов, он обычно обозначается как «s cubed».
Калькулятор
Воспользуйтесь калькулятором выше, чтобы вычислить свойства куба.
Введите любое одно значение, и остальные будут рассчитаны. Например, введите длину стороны, и будет рассчитан объем.
Аналогичным образом, если вы введете площадь поверхности, будет рассчитана длина стороны, необходимая для получения этой площади.
Примечания к объему куба
Напомним, что куб похож на пустую коробку. Внутри ничего нет, а стенки ящика имеют нулевую толщину. Строго говоря, куб имеет нулевой объем. Когда мы говорим об объеме куба, на самом деле мы говорим о том, сколько жидкости он может удерживать, или сколько единичных кубов поместится внутри него.
Подумайте об этом так: если вы возьмете настоящую пустую металлическую коробку и расплавите ее, вы получите небольшой кусок металла. Если бы ящик был сделан из металла нулевой толщины, вы бы вообще не получили металла. Вот что мы имеем в виду, когда говорим, что куб не имеет объема.
Строго правильно сказать, что это «объем, заключенный в куб» — количество места внутри него. Но многие учебники просто говорят «объем куба» , что означает одно и то же.
Однако с математической точки зрения это не совсем правильно.Когда они говорят, что они обычно имеют в виду объем , заключенный в куб .
Но многие учебники просто говорят «объем куба» , что означает одно и то же.
Однако с математической точки зрения это не совсем правильно.Когда они говорят, что они обычно имеют в виду объем , заключенный в куб .
шт.
Помните, что длина края и объем будут в одинаковых единицах. Так, если длина кромки указана в милях, объем будет в кубических милях и так далее.Связанные темы
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Объем куба — основы и примеры
00:00:04.170
В этом уроке мы узнаем, как найти объем куба.
00: 00: 09.000
Сначала рассмотрим этот квадрат с каждой стороной и длиной L.
00: 00: 14.210
Теперь мы уже должны знать, что площадь A этого квадрата равна LxL.
00: 00: 21.110
Теперь давайте превратим этот квадрат в куб.
00: 00: 25.190
Обратите внимание, что все стороны куба имеют одинаковую длину L.
00: 00: 30.220
Чтобы найти объем куба, нам просто нужно умножить площадь A на Л.
00: 00: 37.200
Следовательно, умножая эти три буквы L вместе, мы получаем L куб.
00: 00: 43.010
Таким образом, формула для объема V = L куб.
00: 00: 52.190
Теперь важно, чтобы мы включили единицу измерения объема.
00: 00: 56.210
Так как единица измерения L не указана, мы можем записать единицу измерения этого объема как кубическую единицу.
00: 01: 03.040
Хорошо, давайте посмотрим на несколько примеров, как найти объем куба.
00: 01: 08.220
Найдите объем этого куба, если длина каждой стороны равна 5 см.
00: 01: 14.060
Чтобы решить эту проблему, нам нужно использовать формулу V = L куб.
00: 01: 19.120
Теперь, поскольку мы знаем, что длина каждой стороны этого куба равна 5 см, мы можем заменить L на 5.
00: 01: 28.230
Далее, 5 в степени 3 равно , 5 умножить на 5 умножить на 5. Получается 125. Давайте запишем это здесь.
Получается 125. Давайте запишем это здесь.
00: 01: 41.090
Теперь у нас объем 125.Обратите внимание: это число не имеет смысла, если мы не укажем для него единицу измерения.
00: 01: 51.030
Поскольку единицей измерения длины является сантиметр, единицей измерения объема будет кубический сантиметр.
00: 01: 57.070
Отсюда объем 125 куб.
00: 02: 04.010
В следующем примере, если объем куба составляет 8 кубических футов, найдите длину каждой стороны.
00: 02: 10.180
Теперь давайте начнем с формулы: V равно L кубу, где L — длина каждой стороны.
00: 02: 18.150
Поскольку объем куба равен 8, мы можем заменить V на 8.
00: 02: 23.210
Итак, теперь у нас есть 8 = L куб.
00: 02: 28.000
Чтобы найти «L», мы можем увидеть, что, поскольку 8 равно кубу «L», L можно найти, вычислив кубический корень из 8.
00: 02: 38.040
До того, как мы продолжим, давайте перепишем это уравнение как следует, поменяв местами эти члены.
00: 02: 45.080
Далее кубический корень из 8 равен 2. Итак, у нас L равно 2.
00:02:52.120
Это число не имеет смысла, если мы не включим для него единицу измерения.
00: 02: 57.210
Поскольку объем указан в кубических футах, длина сторон будет в футах.
00: 03: 03.000
Следовательно, длина сторон L = 2 фута.
00: 03: 08.130
Это все для этого урока. Попробуйте ответить на практический вопрос, чтобы проверить свое понимание.
Как найти объем куба
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Выполните следующие действия, чтобы отправить уведомление:
Вы должны указать следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или агентом такого владельца; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или агентом такого владельца; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как найти объем куба
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Выполните следующие действия, чтобы отправить уведомление:
Вы должны указать следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или агентом такого владельца; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или агентом такого владельца; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Объем кубов — объяснения и примеры
Объем куба определяется как количество кубических единиц, занимаемых кубом.
В геометрии куб — это 3-мерная форма с 6 равными сторонами, 6 гранями и 6 вершинами .Каждая грань куба представляет собой квадрат. В трехмерном измерении стороны куба равны; длина, ширина и высота.
На иллюстрации выше сторон куба равны, то есть Длина = Ширина = Высота =
Кубы повсюду! Общие примеры кубиков в реальном мире включают квадратные кубики льда, игральные кости, кубики сахара, запеканки, сплошные квадратные столы, ящики для молока и т. Д.
Объем твердого куба — это объем пространства, занимаемый твердым кубом .Для полого куба объем — это разница между пространством, занимаемым кубом, и объемом пространства внутри куба.
Как найти объем куба?
Чтобы найти объем куба, выполните следующие действия:
- Определите длину стороны или длину края.
- Умножьте длину на себя три раза.
- Запишите результат с указанием единиц объема.

Объем измеряется в кубических единицах, т.е. кубических метрах (м 3 ), кубических сантиметрах (см 3 ) и т. Д.Объем также можно измерять в литрах или миллилитрах. В таких случаях объем называется емкостью.
Формула объема куба
Формула объема куба определяется как;
Объем куба = длина * ширина * высота
V = a * a * a
= a 3 кубических единиц
Где, V = объем
a = длина края.
Давайте попробуем формулу на нескольких примерах задач.
Пример 1
Каков объем куба со сторонами по 10 см?
Решение
Учитывая, что длина стороны = 10 см.
По формуле объема куба
V = a 3
Подставим a = 10 в формулу.
V = 10 3
= (10 x 10 x 10) см 3
= 1000 см 3
Следовательно, объем куба равен 1000 см 3 .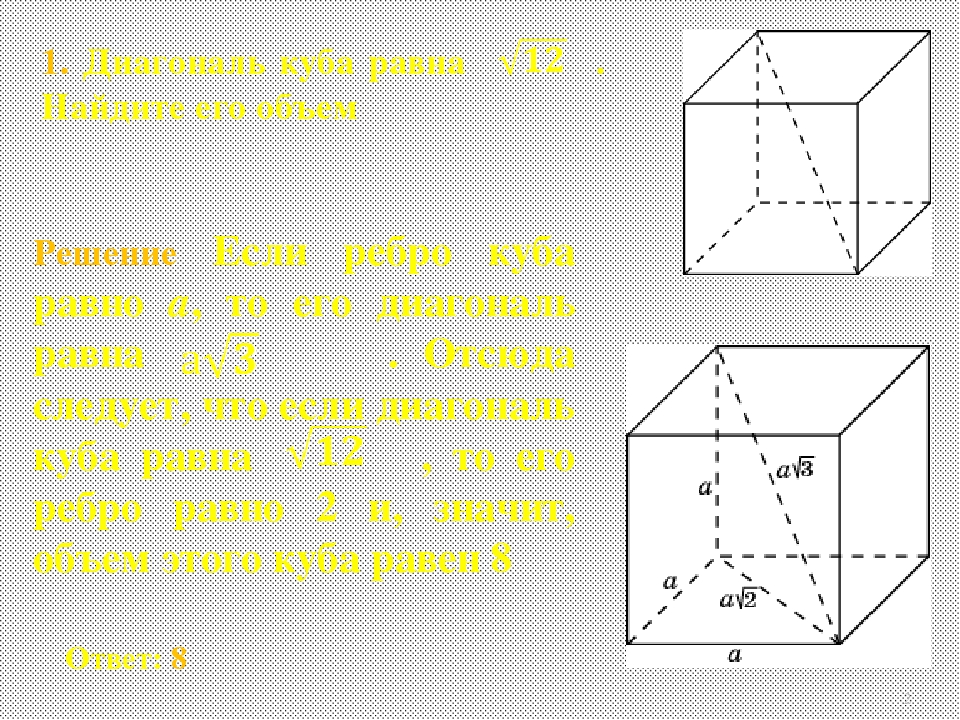
Пример 2
Объем куба 729 м 3 . Найдите длины сторон куба.
Раствор
Заданный объем, V = 729 м 3 .
а =?
Чтобы получить длины сторон куба, мы находим кубический корень из объема.
V = a 3
729 = a 3
3 √ 729 = 3 √ a 3
a = 9
Итак, длина куба равна 9 м.
Пример 3
Край кубика Рубика составляет 0,06 м. Найдите объем кубика Рубика?
Раствор
Объем = a 3
= (0,06 x 0,06 x 0,06) м 3
= 0,000216 м 3
= 2,16 x 10 — 4 м 3
Пример 4
Кубическая коробка с внешними размерами 100 мм на 100 мм на 100 мм открыта вверху.Если деревянный ящик сделан из дерева толщиной 4 мм. Найдите объем куба.
Решение
В этом случае вычтите толщину, чтобы получить размеры куба.
Учитывая, что куб открыт вверху, получаем
Длина = 100 — 4 x 2
= 100 — 8
= 92 мм.
Ширина = 100 — (4 x 2)
= 92 мм
Высота = (100 — 4) мм …………. (куб открыт вверху)
= 96 мм
Теперь посчитаем объем.
V = (92 x 92 x 96) мм 3
= 812544 мм 3
= 8.12544 x 10 5 мм 3
Пример 5
Кубики длиной Пачки по 5 см укладываются так, чтобы высота, ширина и длина стопки составляли по 20 см каждая. Найдите количество кирпичей в стопке.
Решение
Чтобы получить количество кирпичей в стопке, разделите объем стопки на объем кирпича.
Объем штабеля = 20 x 20 x 20
= 8000 см 3
Объем кирпича = 5 x 5 x 5
= 125 см 3
Количество кирпичей = 8000 см 3 /125 см 3
= 64 кирпича.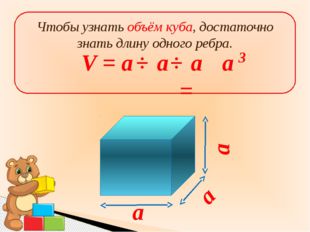
Пример 6
Сколько кубических коробок размером 3 см x 3 см x 3 см можно упаковать в большой кубический ящик длиной 15 см.
Solution
Чтобы определить количество коробок, которое можно упаковать в ящик, разделите объем коробки на объем коробки.
Объем каждой коробки = (3 x 3 x 3) см 3
= 27 см 3
Объем кубической коробки = (15 x 15 x 15) см 3
= 3375 см 3
Количество ящиков = 3375 см 3 /27 см 3 .
= 125 коробок.
Пример 7
Найдите объем металлического куба длиной 50 мм.
Раствор
Объем куба = a 3
= (50 x 50 x 50) мм 3
= 125000 мм 3
= 1.25 x 10 5 мм 3
Пример 8
Объем кубического сплошного диска 0,5 дюйма 3 . Найдите размеры диска?
Решение
Объем куба = a 3
0,5 = a 3
a = 3 √0,5
a = 0,794 дюйма
Практические вопросы Ответы Куб — это прямоугольное тело, длина, ширина и высота которого равны.{2} [/ латекс]. Для любого куба со сторонами длиной [латекс] с [/ латекс], Куб [латекс] 2,5 [/ латекс] дюйма с каждой стороны. Найдите его 1. объем и 2. площадь поверхности. Решение пометьте его данной информацией.{3} [/ латекс] [латекс] V = 15,625 [/ латекс] [латекс] S = 37,5 [/ латекс] Кубик блокнота размером [латекс] 2 [/ латекс] дюйма с каждой стороны. Найдите его 1. объем и 2. площадь поверхности. Решение пометьте его данной информацией. Напишите соответствующую формулу.{3} [/ латекс] [латекс] V = 8 [/ латекс] правильно. [латекс] S = 24 [/ латекс] 9000
Определение объема и площади поверхности куба
Результаты обучения
Объем и площадь куба
пример
Шаг 1 одинаков для 1. и 2., поэтому мы покажем его только один раз. Шаг 1. Прочтите проблему. Нарисуйте фигуру и Шаг 6. Проверка: Проверьте свою работу. Шаг 7. Ответьте на вопрос. Объем [латекс] 15,625 [/ латекс] кубических дюймов. 2. Шаг 2. Определите то, что вы ищете. площадь поверхности куба Шаг 3. Имя.{2} [/ латекс] Шаг 6. Чек: Чек предоставляется вам. Шаг 7. Ответьте на вопрос. Площадь поверхности [латекс] 37,5 [/ латекс] квадратных дюймов. пример
Шаг 1. Прочтите задачу. Нарисуйте фигуру и 1. Шаг 2. Определите то, что вы ищете. объем куба Шаг 3. Имя. Выберите переменную для ее представления. лет В = объем Шаг 4. Translate. Шаг 6. Проверка: Убедитесь, что вы выполнили расчеты Шаг 7. Ответьте на вопрос. Объем [латекс] 8 [/ латекс] кубических дюймов.
. 2. Шаг 2. Определите то, что вы ищете. площадь поверхности куба Шаг 3.{2} [/ латекс] Шаг 6. Чек: Чек предоставляется вам. Шаг 7. Ответьте на вопрос. Площадь поверхности [латекс] 24 [/ латекс] квадратных дюймов.

 Площадь поверхности куба равна 18. Найдите его диагональ.
Площадь поверхности куба равна 18. Найдите его диагональ. B 10 № 27139. Диагональ куба равна 1. Найдите площадь его поверхности.
B 10 № 27139. Диагональ куба равна 1. Найдите площадь его поверхности.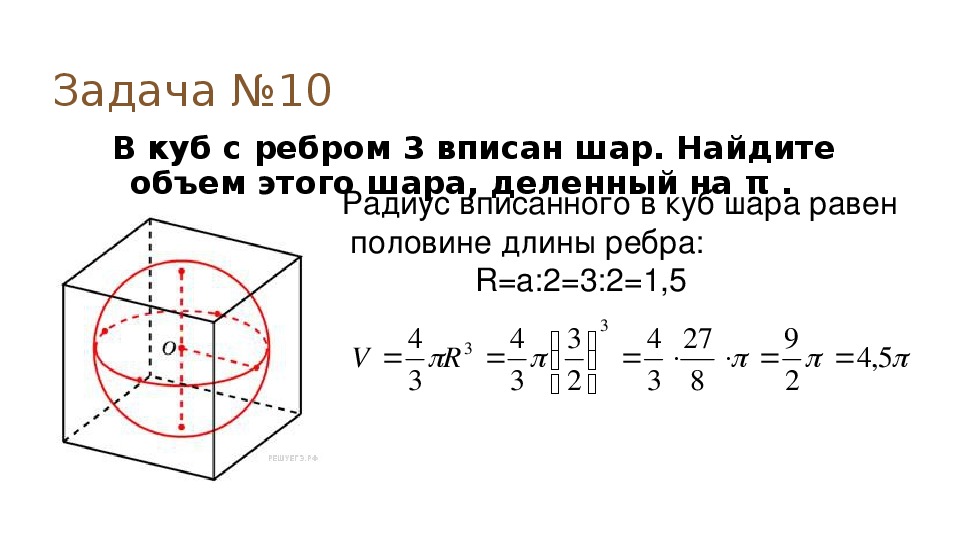 B 10 № 245335. Найдите объем многогранника, вершинами которого являются точки , , , , , прямоугольного параллелепипеда , у которого , , .
B 10 № 245335. Найдите объем многогранника, вершинами которого являются точки , , , , , прямоугольного параллелепипеда , у которого , , . Найдите объем исходной призмы.
Найдите объем исходной призмы.
Leave A Comment