Существует ромб диагонали которого различны: Attention Required! | Cloudflare

Материал для подготовки к ЕГЭ (ГИА) по геометрии (9 класс) по теме: Методическая разработка к уроку геометрии в 9 классе

5.Укажите в ответе номера
неверных
утверждений
.
1)В любом ромбе все стороны равны
.
2)Существует ромб, все стороны
которого-различны
.
3)В любом прямоугольнике все стороны равны
.
4)Существует прямоугольник, все стороны
которого-различны
.
5)В любой трапеции все стороны равны
.
6)Существует трапеция, все стороны
которой-различны
.

Тест
«Проверь себя»
ГИА
(Четырёхугольники)
4.Укажите в ответе номера
неверных
утверждений
.

1)В любом прямоугольнике диагонали равны
.
2)Существует прямоугольник, диагонали которого различны
.
3)В любом ромбе диагонали равны
.
4)Существует ромб, диагонали которого различны
.
5)В любой трапеции диагонали равны
.
6)Существует трапеция, диагонали которой различны
.
Методическая разработка к уроку математики в
9
классе
Мамаева Татьяна Евгеньевна
Учитель математики
МБОУ «СОШ № 11»
г.Бологое
Тверской области
3.Укажите в ответе номера
верных
утверждений
.

1)В любом ромбе диагонали равны
.
2)В любом ромбе диагонали перпендикуляры
.
3)В любом прямоугольнике диагонали равны
.
4)В любом прямоугольнике диагонали перпендикулярны
.
5)В любой трапеции диагонали равны
.
6)В любой трапеции диагонали перпендикулярны
.
2.Укажите в ответе номера
верных
утверждений
.

1)Есть один из углов параллелограмма — острый, то и остальные его углы — острые
.
2)Если один из углов трапеции — острый, то и остальные её углы — острые
.
3)Если один из углов параллелограмма-прямой, то и остальные его углы-прямые
.
4)Если один из углов трапеции прямой, то и остальные её углы-прямые
.
5)Если один из углов
параллелограмма-тупой,то
и остальные его
углы-тупые
.
6)Если один из углов
трапеции-тупой
, то и остальные её
углы-тупые
.
Правильные ответы
4
3
2,3
2,3,5
2,3,4,5
4,6
1.Укажите в ответе номера
верных
утверждений
.

1)В любом выпуклом четырёхугольнике все
углы-острые
.
2)
Существует выпуклый четырёхугольник, все углы
которого-острые
.
3)В любом выпуклом четырёхугольнике все углы-прямые
.
4)Существует выпуклый четырёхугольник,

все углы которого –прямые
.
5)
В любом выпуклом четырёхугольнике все
углы-тупые
.
6)Существует выпуклый четырёхугольник, все углы
которого-тупые
.
6.Укажите в ответе номера
верных
утверждений
.
1)В любом параллелограмме есть хотя бы один острый угол
.
2)В любом параллелограмме есть хотя бы один прямой угол
.
3) В любом параллелограмме есть хотя бы один тупой угол
.
4)В любой трапеции есть хотя бы один острый угол
.
5)В любой трапеции есть хотя бы один прямой угол
.
6)В любой трапеции есть хотя бы один тупой угол
.

Ромб и его свойства. Метод площадей.

По определению, ромб — это параллелограмм, все стороны которого равны.

Свойства ромба:

1. Диагонали ромба перпендикулярны.
2. Диагонали ромба делят его углы пополам.

Воспользуемся свойствами ромба для решения задач.

1. Найдите меньшую диагональ ромба, стороны которого равны , а острый угол равен .

Проведите меньшую диагональ ромба и рассмотрите треугольник . Поскольку , а угол равен , треугольник  — равносторонний. Следовательно, меньшая диагональ ромба равна .

1. Найдите высоту ромба, сторона которого равна , а острый угол равен ?.

Один из подходов к решению задач по геометрии — метод площадей. Он состоит в том, что площадь фигуры выражается двумя разными способами, а затем из полученного уравнения находится неизвестная величина.

Пусть  — сторона ромба. Тогда

Отсюда .

2. Диагонали ромба относятся как . Периметр ромба равен . Найдите высоту ромба.

Пусть диагонали ромба равны  и .
Диагонали ромба перпендикулярны, значит, треугольник  — прямоугольный.

По теореме Пифагора
,
,
Отсюда .
Поскольку периметр равен ,

, , а диагонали ромба равны  и .

Нам надо найти высоту ромба.
Давайте запишем, чему равна площадь ромба. С одной стороны, . С другой стороны, площадь ромба складывается из площадей двух равных треугольников и , то есть равна .
Отсюда .

Ответ: .

Укажите номера верных утверждений. — КиберПедия

1) В любой ромб можно вписать окружность.

2) В прямоугольном треугольнике косинус одного из углов равен 0.

3) Отношение площадей подобных треугольников равно коэффициенту подобия.

Укажите в порядке возрастания номера неверных утверждений.

1) Ромб, диагонали которого равны, является квадратом.

2) Противоположные углы параллелограмма равны между собой.

3) тангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету.

4) если в треугольнике все углы равны между собой, то это – равносторонний треугольник.

5) сумма углов треугольника равна 180 градусам.

Укажите в ответе номера неверных утверждений.

1) Около любого прямоугольника можно описать окружность.

2) В любой ромб можно вписать окружность.

3) Если в параллелограмм можно вписать окружность, то этот параллелограмм – ромб.

4) Если около параллелограмма можно описать окружность, то этот параллелограмм – прямоугольник.

5) Если в трапецию можно вписать окружность, то эта трапеция – равнобедренная.

Какие из следующих утверждений верны?

1) Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

2) Середина гипотенузы прямоугольного треугольника равноудалена от всех его сторон.

3) Сумма углов выпуклого четырехугольника не превышает 360⁰ .

4) Если две стороны и три угла одного треугольника равны соответственно двум сторонам и трем углам другого треугольника, то такие треугольники равны.

5) Существует треугольник, в котором точка пересечения серединных перпендикуляров, проведенных ко всем его сторонам, лежит на одной из этих сторон.

Укажите в ответе номера неверных утверждений.

1) В любом ромбе все стороны равны.

2) Существует ромб, все стороны которого – различны.

3) В любом прямоугольнике все стороны равны.

4) Существует прямоугольник, все стороны которого – различны.

5) В любой трапеции все стороны равны.

Итоговый тест по теме: Основные теоремы и факты. Вариант 2.

1. Какие из данных утверждений верны? Запишите их номера.

1) Любой параллелограмм можно вписать в окружность.

2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти прямые параллельны.

3) Точка пересечения двух окружностей равно удалена от центров этих окружностей.

2. Какие из данных утверждений верны?

1) Сумма углов любого выпуклого шестиугольника равна 940°

2) В любой параллелограмм можно вписать окружность.

3) Существует только одна точка, равноудаленная от всех вершин данного треугольника.

4) Одна из высот прямоугольного треугольника всегда делит его на два подобных треугольника.

3. Укажите в порядке возрастания номера неверных утверждений:

1) Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

2) Соседние углы параллелограмма равны между собой.

3) Сумма углов треугольника равна 90°.

4) Параллелограмм, диагонали которого равны, является прямоугольником

5) Если в треугольнике два угла равны между собой, то это – равнобедренный треугольник.

4. Укажите в ответе номера неверных утверждений.

1) В любом прямоугольнике диагонали равны.

2) Существует прямоугольник, диагонали которого различны.

3) В любом ромбе диагонали равны.

4) Существует ромб, диагонали которого различны.

5) В любой трапеции диагонали равны.

 

5. Какие из следующих суждений верны?

1) если в ромбе диагонали равны, то этот ромб – квадрат.

2) Середина гипотенузы прямоугольного треугольника равноудалена от всех его вершин.

3) Сумма углов треугольника не превышает 180°.

4) Если сторона и три угла одного треугольника равны стороне и трем углам другого треугольника, то такие треугольники равны.

5) Существует треугольник, все высоты которого пересекаются в одной из его вершин.

6. Укажите в ответе номера верных утверждений.

1) В любом параллелограмме есть хотя бы один острый угол.

2) В любом параллелограмме есть хотя бы один прямой угол.

3) В любом параллелограмме есть хотя бы один тупой угол.

4) В любой трапеции есть хотя бы один острый угол.

5) В любой трапеции есть хотя бы один тупой угол.

 

 

Углы

1. В равнобедренном треугольнике угол при вершине, противолежащей основанию, равен 58⁰.Найдите угол при основании. Ответ дайте в градусах.

2. В треугольнике АВС внешний угол при вершине А равен 125 ⁰, а внешний угол при вершине В равен 59⁰.Найдите угол С. . Ответ дайте в градусах.

3. В треугольнике АВС проведена высота СН, которая делит угол С на два угла, величины которых 47⁰ и 71⁰. Найдите наименьший из двух оставшихся углов. Ответ дайте в градусах.

4. В параллелограмме АВСМ прямая АС делит угол при вершине А пополам. Найдите угол, под которым пересекаются диагонали параллелограмма. Ответ дайте в градусах.

5. Угол А равнобедренной трапеции АВСD с основаниями ВС и AD равен 53⁰. Найдите сумму углов В и С.

6. Два угла ромба относятся как 4:6. Найдите меньший угол Ответ дайте в градусах.

7. Найдите острый вписанный угол, опирающийся на хорду, равную радиусу окружности.

8. Найдите центральный угол АОВ, если он на 67⁰ больше вписанного угла АСВ, опирающегося на ту же дугу.

 

Задачи повышенного уровня

9. Сумма углов А и В вписанного четырёхугольника АВСD равна 204

0, а сумма углов В и С равна 192⁰. Найдите угол D.

10. Докажите, что биссектрисы смежных углов перпендикулярны.

11. Докажите, что градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу.

12. Докажите, что если биссектриса пересекает основание трапеции, то от трапеции отсекается равнобедренный треугольник.

13. Биссектрисы всех внутренних углов параллелограмма попарно пересекаются. Докажите, что полученный четырёхугольник является прямоугольником.

14. Биссектриса угла В треугольника АВС делит медиану, проведённую из вершины С, в отношении 7:2, считая от вершины С. В каком отношении, считая от вершины А, эта биссектриса делит медиану, проведённую из вершины А?

 

 

Тема: Углы. Вариант 1

А

1.Какой угол (в градусах) образуют

минутная и часовая стрелки часов в 5 часов?

 

2. .На рисунке∠1=108°, ∠2=72°,∠5=83°. а в f

Найдите угол 4. 4

1 d

c

2 5

 

3. .Точка О – центр окружности ∠АОВ=84°

(см. рисунок). Найдите величину

угла AСB (в градусах) С О

 

А В

 

4. Найдите ∠ С, если ∠А=62°. В

 

А О С

 

 

5. Найдите величину угла АВС. Ответ дайте в градусах

 

В

 

 

А С

Тема: Углы. Вариант 2

1.Точка О – центр окружности∠ВОС=50° (см. рисунок). Найдите величину угла ВАС (в градусах) А В

О С

 

2.На плоскости даны четыре прямые (см. рисунок) 3

.Известно, что ∠1=130°, ∠2=50°,∠3=45°. 2

Найдите ∠5. Ответ дайте в градусах. 1 6 4

3. Точка О – центр окружности,

∠АСВ=25° (см. рисунок). Найдите С О

величину угла АОВ (в градусах). А В

4 Точка О – центр окружности∠ВАС=70°

(см. рисунок). Найдите величину В

угла ВОС (в градусах). А О

С

5. Найдите величину угла АВС. Ответ дайте в градусах

 

В В

 

А С

 

Тема: Углы Вариант 5

1. Величина центрального угла AOD равна 110⁰.

Найдите величину вписанного угла ACB. Ответ дайте в градусах.

2. В треугольнике ABC AD— биссектриса, угол С равен 30⁰,

∠ BAD =22⁰. Найдите угол ADB.

3. Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если ∠ВОС = 114⁰.

 

4. Отрезок АВ является диаметром окружности с центром О. Через точку В проведены касательная ВК и секущая ВМ. Докажите, что углы МВК и ВАМ равны.

Тема: Углы Вариант 6

1. Точки А, В, С и D лежат на одной окружности так, что хорды АВ и СD взаимно перпендикулярны, а ∠АСD = 55⁰. Найдите величину угла ВDС.

2 . Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если ∠ВОС =127⁰. Ответ дайте в градусах.

3. Диагональ прямоугольника образует с одной из его сторон угол, равный 34⁰. Найдите угол между прямыми, содержащими диагонали прямоугольника.

4. Отрезок АВ является диаметром окружности с центром О. Через точку В проведены касательная ВК и секущая ВМ. Докажите, что углы МВК и ВАМ равны.

 

Итоговый тест по теме: Углы

1.Хорда АВ стягивает дугу, равную 1600, а хорда АС – дугу в 600. Найдите угол ВАС.   1)700 , 2)1000, 3)1200, 4)1400

2.Найдите угол А, если угол С равен 320.

3.Один из углов параллелограмма на 20⁰ больше другого. Найдите наибольший угол параллелограмма (в градусах).

4. В окружности вписан равносторонний восьмиугольник. Найдите величину угла АВС .

5.В угол величиной 50⁰ вписана окружность, которая касается его

сторон в точках А и В. На одной из дуг этой окружности выбрали точку С так, как показано на рисунке. Найдите величину угла АCВ.

Вариант-1

6.В треугольнике АВС АВ=ВС, а внешний угол при вершине С равен 1230. Найдите величину угла В. Ответ дайте в градусах.

7.Сумма двух углов равнобедренной трапеции равна 96⁰. Найдите

больший угол трапеции. Ответ дайте в градусах.

8.Найдите величину угла DOB, если ОЕ – биссектриса угла АОС, OD – биссектриса угла СОВ.

9.Укажите номера неверных утверждений:

1) Если один из углов, прилежащих к стороне параллелограмма, равен 50⁰, то другой угол, прилежащий к той же стороне, равен 40⁰.

2) Если вписанный угол равен 24⁰, то дуга окружности, на которую опирается этот угол, равна 48⁰.

3) Внешний угол треугольника равен сумме двух его внутренних углов.

10. В треугольник АВС АС=18, АВ=12. Точки L и K отмечены на сторонах АС и АВ так, что АL= 6 и АК= 9. Докажите, что углы АВС и АLK равны.

Итоговый тест теме: Углы

1. Хорда АВ стягивает дугу, равную 140°, а хорда ВС – дугу 60°. Найдите угол АВС. А

В С

1. Найдите угол С, если АВ = ВС.

1. Один из углов параллелограмма на 40° больше другого.

Найдите наименьший угол параллелограмма (в градусах).

4.В окружность вписан равносторонний восьмиугольник. Найдите величину угла АВС (см. рисунок).

 

5.В угол величиной 70° вписана окружность, которая касается его сторон в точках А и В. На одной из дуг этой окружности выбрали точку С так, как показано на рисунке. Найдите величину угла АСВ.

Вариант 2

6.В треугольнике АВС АВ=ВС, а внешний угол при вершине С равен 132°. Найдите величину угла В. Ответ дайте в градусах.

7.Сумма трёх углов равнобедренной трапеции равна 234°. Найдите меньший угол трапеции. Ответ дайте в градусах.

 

8.Найдите величину угла АОЕ, если ОЕ – биссектриса угла АОС, ОD – биссектриса угла СОВ, угол DOВ равен 25⁰ .

 

9.Укажите номера верных утверждений:

1) Если один из углов вписанного в окружность четырехугольника равен 63°, то противоположный ему угол четырехугольника равен 117°.

2) Если дуга окружности составляет 73°, то вписанный угол, опирающийся на эту дугу, равен 73⁰ …

3) Противоположные углы параллелограмма равны…

 

10.В треугольнике АВС АС = 24, ВС = 12. Точки L и K отмечены на сторонах АС и ВС так, что LC = 4 и КС = 8. Докажите, что углы ВАС и LKC равны.

 

Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции. Примерно 7-9 класс (13-15 лет)

Виды четырехугольников:
Параллелограмм — это четырехугольник у которого противолежащие стороны параллельны
Ромб — это параллелограмм, у которого все стороны равны.
Прямоугольник — это параллелограмм, у которого все углы прямые.
Квадрат — это прямоугольник, у которого все стороны равны.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.
Свойства произвольных четырехугольников:
Сумма внутренних углов четырехугольника равна 360o

Плоские геометрические фигуры: свойства и основные формулы

В статье дается определение, основные свойства и формулы для следующих геометрических фигур:

Четырёхугольник

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

• Сумма углов четырёхугольника равна 360°
• Не существует четырёхугольников, у которых все углы острые или все углы тупые.
• Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
• Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Квадрат

Квадрат —  правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Основные формулы:

Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a²или S=d²/2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2

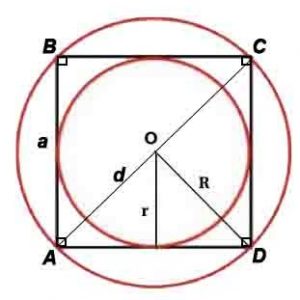где a-сторона, d-диагональ, P-периметр, S-площадь
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.

Свойства:

• Все стороны равны, все углы равны и составляют 90°;
• Диагонали квадрата равны и перпендикулярны;
• У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
• Квадрат является одновременно частным случаем ромба и прямоугольника.

Прямоугольник

Прямоугольник — четырехугольник, у которого все углы прямые.

Основные формулы:

Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S =  d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a²+b²)/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a²+b²)/2 (теорема Пифагора)

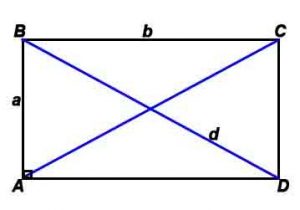где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a²+b²) – корень квадратный из (a²+b²).

Свойства:

• Диагонали прямоугольника равны и делятся точкой пересечения пополам.
• Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.

Параллелограмм

Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Определения:

Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.

Основные формулы:

Стороны и диагональ связаны соотношением: (d₁)²+(d₂)²=(a²+b²)*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте:  S = a*h
Площадь по двум сторонам и углу между ними: S=a*b*sin α
Площадь по двум диагоналям и углу между ними:  S=(d₁*d₂)/2*sin γ

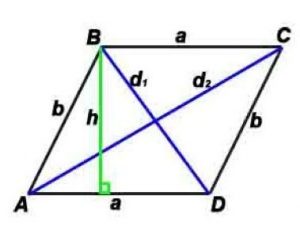где a, b — длины сторон, d₁, d₂ –диагонали, P-периметр, S-площадь,
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).

Свойства:

• У параллелограмма противоположные стороны равны и противоположные углы равны.
• Сумма любых двух соседних углов параллелограмма равна 180°.
• Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
• Каждая диагональ делит параллелограмм на два равных треугольника.
• Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
• Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
• Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Ромб

Ромб — это параллелограмм, у которого все стороны равны.

Основные формулы:

Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d₁*d₂)/2
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a² · sin α
Радиус окружности, вписанной в ромб: r=h/2 или  r =(d₁*d₂)/4a

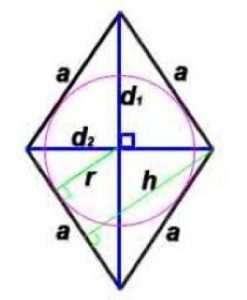где a — длина стороны, d₁, d₂ –диагонали, P-периметр, S-площадь,
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба

Свойства:

• Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
• В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d₁*d₂/4a.

Трапеция

Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.

Определения:

• Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
• Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.  
• Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
• Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
• Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
• Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.

Основные формулы:

Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2

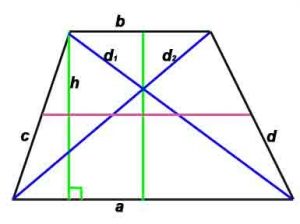где a,b — основания, c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d₁, d₂ –диагонали,
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне

Свойства:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

• Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
• Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
• Медиана треугольника — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
• Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
• Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
• Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
• Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
• Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Основные формулы:

Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь по сторонам и углу между ними:  S=(a*b)/2* sin γ
Площадь по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
Площадь по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c²=a²+b² (Теорема Пифагора)

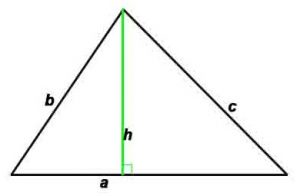где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
d₁, d₂ –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ  — угол между сторонами a и b
r — радиус вписанной окружности, R — радиус описанной окружности

Свойства:

• В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
• Сумма углов треугольника равна 180°:
• Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| <c<a+b
• Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
• Медиана делит треугольник на два равновеликих (с равными площадями) треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников
• Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник
• В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
• Все углы равностороннего треугольника равны 60°. Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c²=a²+b² (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Окружность

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

• Радиус — отрезок, который соединяет центр окружности с любой её точкой.
• Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
• Диаметр — хорда, проходящая через центр окружности(d).  Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует. 
• Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
• Секущая — прямая, которая пересекает окружность в двух различных точках.

Основные формулы:

Длина окружности: L = 2πR
Площадь круга: S = π*r² или S = π*d²/4

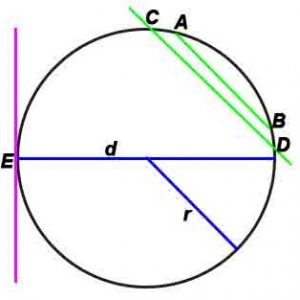где π = 3,14 (3,1415926535) – величина постоянная,
где r-радиус, d –диаметр, L – длина окружности, S-площадь.

 

Каков периметр ромба с диагоналями 16 и 30?

Геометрия

Наука

• Анатомия и физиология
• астрономия
• астрофизика
• Биология
• Химия
• наука о планете Земля
• Наука об окружающей среде
• Органическая химия
• физика

математический

• Алгебра
• Исчисление
• Геометрия
• Prealgebra
• тригонометрия и алгебра

.

Ромб — математическое определение слова

Ромб — определение слова в математике — открытый справочник по математике Попробуйте это Перетащите оранжевые точки на каждую вершину чтобы изменить форму ромба. Обратите внимание, как четыре стороны остаются одинаковой длины, а противоположные стороны остаются параллельными.

На самом деле ромб — это просто особый тип параллелограмма. Напомним, что в параллелограмме все пары противоположных сторон равны по длине. У ромба все четыре стороны имеют одинаковую длину.Следовательно, он обладает всеми свойствами параллелограмма. См. Определение параллелограмма

Это немного похоже на квадрат, который может « наклониться » и внутренние углы должны быть , а не 90 °. Иногда ее называют ромбовидной или ромбовидной формы.

Свойства ромба

База	Базой можно считать любую сторону. Выбирайте любой понравившийся. Если используется для расчета площади (см. Ниже), необходимо использовать соответствующую высоту. На рисунке выше была выбрана одна из четырех возможных баз.
Высота	Высота ромба — перпендикулярное расстояние от основания на противоположную сторону (которую, возможно, придется расширить). На рисунке выше показана высота, соответствующая базовому CD.
Площадь	Есть несколько способов найти площадь ромба. Чаще всего используется (база × высота). Каждый описан в Области ромба
Периметр	Расстояние вокруг ромба.Сумма длин его сторон. См. Периметр ромба
Диагонали	Каждая из двух диагоналей — это серединный перпендикуляр другого. См. Диагонали ромба

Другие полигоны

Общие

Типы многоугольника

Площадь различных типов полигонов

Периметр различных типов полигонов

Углы, связанные с многоугольниками

Именованные полигоны

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

,

Определение площади ромба

Ромб — это параллелограмм, стороны которого равны. Диагонали ромба перпендикулярны друг другу. Они также делят друг друга пополам. В этом посте мы собираемся найти общую формулу для определения площади ромба с использованием этих свойств. Мы собираемся изучить два метода.

Метод 1

Рассмотрим ромб ниже.

Мы можем разделить его на два равных треугольника, используя диагональ.Поскольку диагонали ромба перпендикулярны друг другу, мы можем использовать как основание и половину как высоту верхнего треугольника (Почему?). Если принять за площадь верхнего треугольника, то, вычислив его площадь, получим

.

Теперь мы рассчитали только площадь верхнего треугольника. Так как площадь ромба в два раза больше площади верхнего треугольника, умножаем на 2. То есть

.

Метод 2

Второй способ — заключить ромб в прямоугольник.Это можно сделать, проведя линии, параллельные диагоналям и проходящие через вершины (см. Рисунок ниже).

Две диагонали делят ромб на четыре треугольника. Обратите внимание, что если мы переместим два треугольника, как показано стрелкой на рисунке выше, то превратит параллелограмм в прямоугольник.

Теперь длина прямоугольника равна, а ширина равна. Площадь прямоугольника равна произведению его длины и ширины, поэтому

.

Используя два вышеупомянутых метода, мы показали, что площадь ромба равна половине произведения длины двух его диагоналей.

,