График пути от времени: Графическое представление движения - О'Пять пО физике!

Скорость и путь при равноускоренном движении — урок. Физика, 9 класс.

Рассмотрим некоторые особенности перемещения тела при прямолинейном равноускоренном движении без начальной скорости. Уравнение, которое описывает это движение, было выведено Галилеем в \(XVI\) веке. Необходимо помнить, что при прямолинейном равномерном или неравномерном движении модуль перемещения совпадает по своему значению с пройденным путём. Формула выглядит следующим образом:

s=v0t+at22, где \(а\) — это ускорение.

Сравним графики равномерного и равноускоренного движения.

Графики прямолинейного равномерного движения

Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость \(a(t)\) — прямая линия, которая лежит на оси времени.

Зависимость скорости от времени. Скорость со временем не изменяется, график \(v(t)\) — прямая линия, параллельная оси времени.

Правило определения пути по графику \(v(t)\): численное значение перемещения (пути) — это площадь прямоугольника под графиком скорости.

Зависимость пути от времени. График \(s(t)\) — наклонная линия.

Графики равноускоренного движения

Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график \(a(t)\) — прямая линия, параллельная оси времени.

Зависимость скорости от времени. Скорость изменяется согласно линейной зависимости.

Зависимость пути от времени. При равноускоренном движении путь изменяется согласно квадратной зависимости: s=v0t+at22. В координатах зависимость имеет вид: x=x0+v0xt+axt22.

Графиком является ветка параболы.

Источники:

http://fizmat.by/kursy/kinematika/ravnouskorennoe

2. Графики зависимости перемещения и координаты тела от времени при движении с постоянным ускорением

Зависимость проекции перемещения от времени при равноускоренном движении имеет вид:

Δrx=v0xt+axt22.

Учитывая, что проекция перемещения движущегося тела равна:

Δrx=x−x0 —

зависимость координаты движущегося тела от времени имеет вид:

x=x0+v0xt+axt22.

Последняя формула выражает кинематический закон равнопеременного движения.

Поскольку при равнопеременном движении зависимости перемещения и координаты тела от времени являются квадратичными функциями, то графиками зависимости данных величин от времени являются участки парабол.

На рисунке \(1\) представлены графики зависимости скорости движения тела при ax=a>0 (прямая \(1\)), при ax=a=0 (прямая \(2\)) и при ax=a<0 (прямая \(3\)).

Рис. \(1\)

На рисунке \(2\) представлены графики зависимости проекции перемещения движущегося тела от времени при ax=a>0 (кривая \(1\)), при ax=a=0 (прямая \(2\)) и при ax=a<0 (кривая \(3\)).

Рис. \(2\)

При ax=a>0 проекция перемещения всё время увеличивается (кривая \(1\)).

А при ax=a<0 проекция перемещения увеличивается до момента времени t=tп, а затем уменьшается. Это происходит потому, что в момент времени tn скорость тела становится равной нулю, а направление его движения меняется на противоположное, то есть происходит поворот.

Моменту времени tn на кривой \(3\) рисунка \(2\) соответствует вершина параболы.

График зависимости пути \(s\) от времени при движении, направление скорости при котором не изменяется, совпадает с графиком зависимости проекции перемещения от времени (рис. \(3\), кривые \(1\) (график проекции перемещения) и \(2\) (график пути)).

Рис. \(3\)

Если же направление скорости во время движения изменяется, то есть происходит поворот, то эти графики совпадают только при 0<t<tn (рис. \(3\), кривые \(3\) (график проекции перемещения) и \(4\) (график пути)).

После момента поворота tn проекция перемещения начинает уменьшаться, а путь продолжает увеличиваться. При этом путь увеличивается на столько, на сколько за то же время уменьшается проекция перемещения.

График зависимости координаты от времени (рис. \(4\), кривые \(1\) и \(3\)) получается из графика зависимости перемещения от времени (рис. \(4\), кривая \(2\)) смещением последнего на величину x0 вверх при x0>0 (рис. \(4\), кривая \(1\)) или вниз при x0<0 (рис. \(4\), кривая \(3\)), поскольку x=x0+Δrx (рис. \(4\)).

Рис. \(4\)

1. График зависимости скорости от времени при прямолинейном движении с постоянным ускорением

Самое простое из всех неравномерных движений — это прямолинейное движение с постоянным ускорением.

При движении с постоянным ускорением (a→=const→) скорость тела линейно зависит от времени:

v→=v→o+a→t.

В проекциях на ось \(Ox\) данные равенства имеют вид:

ax=const;

vx=vox+axt.

Построим графики зависимостей axt и vxt для случаев ax>0 и ax<0.

Примем vox>0.

Поскольку в обоих случаях ax=const, то графиком зависимости axt ускорения от времени в обоих случаях будет прямая, параллельная оси времени.

Только при ax>0 данная прямая будет лежать в верхней полуплоскости (рис. \(1\)), а при ax<0 — в нижней (рис. \(2\)).

Рис. \(1\)

Рис. \(2\)

Графиком зависимости скорости движения тела от времени vxt является прямая, пересекающая ось скорости в точке v0 и образующая с положительным направлением оси времени острый угол при ax>0 (рис. \(3\)) и тупой угол при ax<0 (рис. \(4\)).

Рис. \(3\)

Рис. \(4\)

График на рисунке \(3\) описывает возрастание проекции скорости vx. При этом модуль скорости тела также растёт. Данный график соответствует равноускоренному движению тела.

График на рисунке \(4\) показывает, что проекция vx скорости тела вначале положительна.

Она уменьшается и в момент времени t=tп становится равной нулю.

В этот момент тело достигает точки поворота, в которой направление скорости тела меняется на противоположное, и при t>tп проекция скорости становится отрицательной.

Из последнего графика также видно, что до момента поворота модуль скорости уменьшался — тело двигалось равнозамедленно.

При t>tп модуль скорости растёт — тело движется равноускоренно.

Для любого равнопеременного прямолинейного движения площадь фигуры между графиком vx и осью времени \(t\) численно равна проекции перемещения Δrx.

Рис. \(5\)

Согласно данному правилу, проекция перемещения Δrx при равнопеременном движении определяется площадью трапеции \(ABCD\) (рис. \(5\)). Эта площадь равна полусумме оснований трапеции, умноженной на её высоту:

S=AB+DC2⋅AD.

В результате:

Δrx=vox+vx2⋅Δt.

Из данной формулы получим формулу для среднего значения проекции скорости:

vxср=ΔrxΔt=vox+vx2.

При движении с постоянным ускорением данное отношение выполняется не только для проекций, но и для векторов скорости:

vcp→=vo→+v→2.

Средняя скорость движения с постоянным ускорением равна полусумме начальной и конечной скоростей.

Физика 7 класс → Графики пути и скорости при равномерном движении – eSchool.by

Чтобы наглядно представить движение, не прибегая к
расчётам, нужно использовать не формулу, а график
движения. Основных графиков два: график пути и
график скорости.
График пути (обозначается S(t)) – линия на
координатной плоскости, которая показывает
зависимость пути от времени. Значения пути
указываются по вертикальной оси, а значения
времени – по горизонтальной.

Давайте построим график пути автомобиля, который двигается равномерно со скоростью 20 м/с.
1) Записываем формулу пути:

2) Подставляем в формулу пути значение скорости движения тела:

3) Составляем и заполняем таблицу зависимости пути от времени.

4) По данным таблицы строим точки на координатной прямой. У нас получились точки с
координатами (0 c; 0 м), (1 c; 20 м), (2 c; 40 м).

5) Соединяем точки линией (эта линия и есть график пути).

По графику пути можно узнать много важной информации. Давайте по графику пути S(t) найдём
скорость тела:
1) Выбираем любую точку на графике (точка М).
2) Проводим от точки перпендикуляры к оси времени и оси пути.
3) Значения на пересечениях перпендикуляров с осями и есть значения пути S_М и времени Δt_Мдля этой точки графика.
4) Подставляем Δt_М и S_М в формулу и производим расчёты:

По углу наклона графика пути можно судить о величине скорости тела. Чем больше угол наклона графика (угол между графиком и осью времени), тем больше скорость тела.

Кроме графика пути, есть график скорости.

График скорости (обозначается υ(t)) – линия на координатной плоскости, которая
показывает зависимость скорости от времени.

На нём по вертикальной оси указывается
скорость, а по горизонтальной – промежутки
времени.

Давайте попробуем построить график зависимости скорости тела υ от времени Δt. Принцип
построения такого графика практически полностью повторяет построение графика пути S(t), с
той лишь разницей, что скорость при таком движении всегда остаётся постоянной и в данном
случае равна 20 м/с. Запишем координаты наших будущих точек в виде таблицы:

Графиком будет горизонтальная прямая, так как скорость не изменяется со временем при равномерном движении.
По графику скорости υ(t) можно определить путь, пройденный телом за определённое время. Давайте попробуем узнать, какое расстояние тело прошло за 2 секунды. Для этого проводим вертикальную прямую от оси времени до графика.

У нас получился прямоугольник. Если мы
перемножим значения сторон этого
прямоугольника (найдём площадь), то получим
значение пройденного телом пути, так как путь
можно найти по формуле S = υ • Δt. Перемножая
значения сторон прямоугольника, мы по сути и
умножаем значение скорости (υ) на значение
времени (Δt).

S = 20 • 2 = 40 м

Вопросы и задания:

1. Что представляет из себя график пути для равномерно движущегося тела (прямую, кривую)?
2. Каким образом можно рассчитать скорость тела, используя график его пути?
3. Изучая графики пути двух тел, каким образом можно определить: какое из них движется
быстрее?
4. Как из графика скорости тела найти пройденный им путь за определённое время?
5. Постройте графики пути и скорости для велосипедиста, движущегося равномерно, который за 7 секунд преодолел расстояние в 42 м. По графику пути определите его скорость, а по графику скорости определите расстояние, которое он проедет за 15 секунд.

Равномерное прямолинейное движение

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:

v_cp = v

Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t:

= / t

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:

= • t

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

v_x = v,	то есть v > 0

Проекция перемещения на ось ОХ равна:

s = vt = x – x₀

где x₀ – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x₀ + vt

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v

х = x₀ - vt

Зависимость скорости, координат и пути от времени

Зависимость проекции скорости тела от времени показана на рис. 1.11. Так как скорость постоянна (v = const), то графиком скорости является прямая линия, параллельная оси времени Ot.

Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.

Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна

v = s₁ / t₁ = tg α

где α – угол наклона графика к оси времени. Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:

tg α = v

Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что

tg α₁ > tg α₂

следовательно, скорость тела 1 выше скорости тела 2 (v₁ > v₂).

tg α₃ = v₃ < 0

Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть

х = х₀

Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.

Как построить график зависимости пути от времени

☰

Построение графиков используют, чтобы показать зависимость одной величины от другой. При этом на одной оси откладывают изменение одной величины, а на другой оси — изменение другой величины. При прямолинейном равномерном движении скорость тела остается постоянной, меняются только время и зависимый от него пройденный путь. Поэтому наибольший интерес для такого движения представляет график, отражающий зависимость пути от времени.

При построении такого графика на одной из осей координатной плоскости отмечается изменение времени (t). Например, 1 с, 2 с, 3 с и т. д. Пусть это будет ось x. На другой оси (в данном случае y) отмечается изменение пройденного пути. Например, 10 м, 20 м, 30 м и т. д.

Начало системы координат принимается за начало движения. Это точка старта, в которой промежуток времени, потраченный на движение, равен нулю, и пройденный путь также равен нулю. Это первая точка графика зависимости пути от времени.

Далее на координатной плоскости находят вторую точку графика. Для этого для какого-либо времени пути находят пройденный за это время путь. Если скорость тела равна 30 м/с, то это может быть точка с координатами (1; 30) или (2; 60) и так далее.

После того, как вторая точка отмечена, проводят луч через две точки (первая — начало координат). Начало луча — это начало координат. Данный луч и является графиком зависимости пути от времени при прямолинейном равномерном движении. У луча нет конца, это говорит о том, что чем больше затраченное на путь время, тем больше будет пройденный путь.

Вообще говорят, что графиком зависимости пути от времени является прямая, проходящая через начало координат.

Чтобы доказать, что графиком является прямая, а, допустим, не ломаная линия, можно построить ряд точек на координатной плоскости. Например, если скорость равна 5 км/ч, то на координатной плоскости можно отметить точки (1; 5), (2; 10), (3; 15), (4; 20). Затем соединить их последовательно между собой. Вы увидите, что получится прямая.

Чем больше скорость тела, тем быстрее увеличивается пройденный путь. Если на одной и той же координатной плоскости начертить зависимости пути от времени для двух тел, движущихся с разными скоростями, то график тела, которое движется быстрее, будет иметь больший угол с положительным направлением оси времени.

Например, если одно тело движется со скоростью 10 км/ч, а второе — 20 км/ч, то на координатной плоскости можно отметить точки (1; 10) для одного тела и (1; 20) для другого. Понятно, что вторая точка находится дальше от оси времени, и прямая через нее образует больший угол, чем прямая через точку, отмеченную для первого тела.

Графики зависимости пути от времени при прямолинейном равномерном движении можно использовать для быстрого нахождения затраченного времени по известному значению пройденного пути или пути по известному времени. Для этого надо провести перпендикулярную линию из значения координатной оси, которое известно, до пересечения с графиком. Далее из полученной точки пересечения провести перпендикуляр к другой оси, получив тем самым искомое значение.

Кроме графиков зависимости пути от времени, можно построить графики зависимости пути от скорости и скорости от времени. Однако, так как при прямолинейном равномерном движении скорость постоянна, эти графики представляют собой прямые, параллельные осям пути или времени и проходящие на уровне заявленной скорости.

Равномерное прямолинейное движение – FIZI4KA

1. Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Слова «любые равные» означают, что за каждый час, за каждую минуту, за каждые 30 минут, за каждую секунду, за каждую долю секунды тело совершает одинаковые перемещения.

Равномерное движение — идеализация, поскольку практически невозможно создать такие условия, чтобы движение тела было равномерным в течение достаточно большого промежутка времени. Реальное движение может лишь приближаться к равномерному движению с той или иной степенью точности.

2. Изменение положения тела в пространстве при равномерном движении может происходить с разной быстротой. Это свойство движения — его «быстрота» характеризуется физической величиной, называемой скоростью.

Скоростью равномерного прямолинейного движения называют векторную физическую величину, равную отношению перемещения ко времени, за которое это перемещение произошло.

Если за время \( t \) тело совершило перемещение \( \vec{s} \), то скорость его движения \( \vec{v} \) равна \( \vec{v}=\frac{\vec{s}}{t} \).

Единица скорости: \( [\,v\,]=\frac{[\,s\,]}{[\,t\,]} \); \( [\,v\,]=\frac{1\,м}{1\,с}=1\frac{м}{с} \). За единицу скорости принимается 1 м/с — скорость такого равномерного движения, при котором тело за 1 с совершает перемещение 1 м.

Зная скорость равномерного движения, можно найти перемещение за любой промежуток времени: \( \vec{s}=\vec{v}t \). Вектор скорости и вектор перемещения направлены в одну сторону — в сторону движения тела.

3. Поскольку основной задачей механики является определение в любой момент времени положения тела, т.е. его координаты, необходимо записать уравнение зависимости координаты тела от времени при равномерном движении.

Пусть \( \vec{s} \) — перемещение тела (рис. 11). Направим координатную ось ОХ по направлению перемещения. Найдем проекцию перемещения на координатную ось ОХ. На рисунке \( x_0 \) — координата начальной точки перемещения, \( x \) — координата конечной точки перемещения. Проекция перемещения равна разности координат конечной и начальной точек: \( \vec{s}_x=x-x_0 \). С другой стороны, проекция перемещения равна проекции скорости, умноженной на время, т.е. \( \vec{s}_x=\vec{v}_xt \). Откуда \( x-x_0=\vec{v}_xt \) или \( x=x_0+\vec{v}_xt \). Если начальная координата \( x_0 \) = 0, то \( x=\vec{v}_xt \).

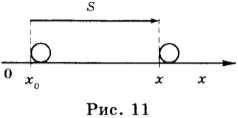
Полученная формула позволяет определить координату тела при равномерном движении в любой момент времени, если известны начальная координата и проекция скорости движения.

Проекция скорости может быть как положительной, так и отрицательной. Проекция скорости положительна, если направление движения совпадает с положительным направлением оси ОХ (рис. 12). В этом случае \( x>x_0 \). Проекция скорости отрицательна, если тело движется против положительного направления оси ОХ (рис. 12). В этом случае \( x<x_0 \).

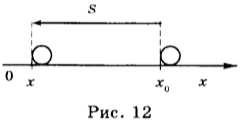
4. Зависимость координаты от времени можно представить графически.

Предположим, что тело движется из начала координат вдоль положительного направления оси ОХ с постоянной скоростью. Проекция скорости на ось ОХ равна 4 м/с. Уравнение движения в этом случае имеет вид: \( x \) = 4 м/с · \( t \). Зависимость координаты от времени — линейная. Графиком такой зависимости является прямая линия, проходящая через начало координат (рис. 13).

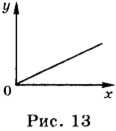
Для того чтобы её построить, необходимо иметь две точки: одна из них \( t \) = 0 и \( x \) = 0, а другая \( t \) = 1 с, \( x \) = 4 м. На рисунке приведён график зависимости координаты от времени, соответствующий данному уравнению движения.

Если в начальный момент времени координата тела \( x_0 \) = 2 м, а проекция его скорости \( v_x \) = 4 м/с, то уравнение движения имеет вид: \( x \) = 2 м + 4 м/с · \( t \). Это тоже линейная зависимость координаты от скорости, и её графиком является прямая линия, проходящая через точку, для которой \( t \) = 0, \( x \) = 2 м (рис. 14).

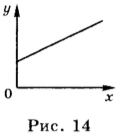
В том случае, если проекция скорости отрицательна, уравнение движения имеет вид: \( x \) = 2 м – 4 м/с · \( t \). График зависимости координаты такого движения от времени представлен на рисунке 15.

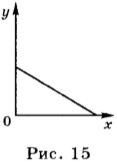
Таким образом, движение тела может быть описано аналитически, т.е. с помощью уравнения движения (уравнения зависимости координаты тела от времени), и графически, т.е. с помощью графика зависимости координаты тела от времени.

График зависимости проекции скорости равномерного прямолинейного движения от времени представлен на рисунке 16.

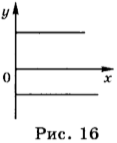
5. Ниже приведён пример решения основной задачи кинематики — определения положения тела в некоторый момент времени.

Задача. Два автомобиля движутся навстречу друг другу равномерно и прямолинейно: один со скоростью 15 м/с, другой — со скоростью 12 м/с. Определите время и место встречи автомобилей, если в начальный момент времени расстояние между ними равно 270 м.

При решении задачи целесообразно придерживаться следующей последовательности действий:

Кратко записать условие задачи.
Проанализировать ситуацию, описанную в условии задачи:
— выяснить, можно ли принять движущиеся тела за материальные точки;
— сделать рисунок, изобразив на нём векторы скорости;
— выбрать систему отсчёта — тело отсчёта, направления координатных осей, начало отсчёта координат, начало отсчёта времени; записать начальные условия (значения координат в начальный момент времени) для каждого тела.
Записать в общем виде уравнение движения в векторной форме и для проекций на координатные оси.
Записать уравнение движения для каждого тела с учётом начальных условий и знаков проекций скорости.
Решить задачу в общем виде.
Подставить в формулу значения величин и выполнить вычисления.
Проанализировать ответ.

Применим эту последовательность действий к приведённой выше задаче.

Дано: \( v_1 \) = 15 м/с \( v_2 \) = 12 м/с \( l \) = 270 м. Найти: \( t \) – ? \( x\) – ?

Автомобили можно считать материальными точками, поскольку расстояние между ними много больше их размеров и размерами автомобилей можно пренебречь

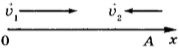
Система отсчёта связана с Землёй, ось \( Ox \) направлена в сторону движения первого тела, начало отсчёта координаты — т. \( O \) — положение первого тела в начальный момент времени.

Начальные условия: \( t \) = 0; \( x_{01} \) = 0; \( x_{02} \) = 270.

Уравнение в общем виде: \( \vec{s}=\vec{v}t \); \( x=x_0+v_xt \).

Уравнения для каждого тела с учётом начальных условий: \( x_1=v_1t \); \( x_2=l-v_2t \). В месте встречи тел \( x_1=x_2 \); следовательно: \( v_1t=l-v_2t \). Откуда \( t=\frac{l}{v_1+v_2}\cdot t \). Подставив значение времени в уравнение для координаты первого автомобиля, получим значение координаты места встречи автомобилей: \( x \) = 150 м.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Чему равна проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?

1) 320 м/с
2) 80 м/с
3) 20 м/с
4) 0,05 м/с

2. Чему равен модуль перемещения мухи за 0,5 мин., если она летит со скоростью 5 м/с?

1) 0,25 м
2) 6 м
3) 10 м
4) 150 м

3. Автомобиль «Рено» проезжает за 1 мин. путь 1,2 км. Автомобиль «Пежо» проезжает за 20 с путь 0,2 км. Сравните значения скорости «Рено» — \( v_1 \) и скорости «Пежо» — \( v_2 \).

1) \( v_1=v_2 \)
2) \( v_1=2v_2 \)
3) \( 2v_1=v_2 \)
4) \( 1,2v_1=10v_2 \)

4. На рисунке приведена столбчатая диаграмма. На ней представлены значения пути, которые при равномерном движении пролетают за одно и то же время муха (1) и воробей (2). Сравните их скорости \( v_1 \) и \( v_2 \).

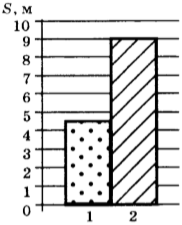
1) \( v_1=v_2 \)
2) \( v_1=2v_2 \)
3) \( 3v_1=v_2 \)
4) \( 2v_1=v_2 \)

5. На рисунке приведён график зависимости модуля скорости равномерного движения от времени. Модуль перемещения тела за 2 с равен

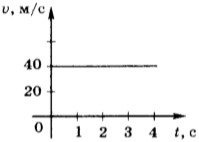
1) 20 м
2) 40 м
3) 80 м
4) 160 м

6. На рисунке приведён график зависимости пути, пройденного телом при равномерном движении от времени. Модуль скорости тела равен

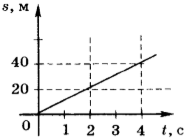
1) 0,1 м/с
2) 10 м/с
3) 20 м/с
4) 40 м/с

7. На рисунке приведены графики зависимости пути от времени для трёх тел. Сравните значения скорости \( v_1 \), \( v_2 \) и \( v_3 \) движения этих тел.

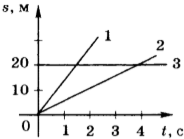
1) \( v_1=v_2=v_3 \)
2) \( v_1>v_2>v_3 \)
3) \( v_1<v_2<v_3 \)
4) \( v_1=v_2 \), \( v_3<v_1 \)

8. Какой из приведённых ниже графиков представляет собой график зависимости пути от времени при равномерном движении тела?

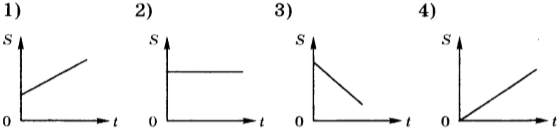
9. На рисунке приведён график зависимости координаты тела от времени. Чему равна координата тела в момент времени 6 с?

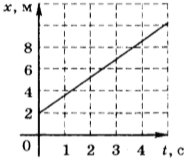
1) 9,8 м
2) 6 м
3) 4 м
4) 2 м

10. Уравнение движения тела, соответствующее приведённому в задаче 9 графику, имеет вид

1) \( x=1t \) (м)
2) \( x=2+3t \) (м)
3) \( x=2-1t \) (м)
4) \( x=4+2t \) (м)

11. Установите соответствие между величинами в левом столбце и зависимостью значения величины от выбора системы отсчёта в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ВЕЛИЧИНА
A) перемещение
Б) время
B) скорость

ЗАВИСИМОСТЬ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЁТА
1) зависит
2) не зависит

12. На рисунке приведён график зависимости координаты тела от времени. Какие выводы можно сделать из анализа графика? Укажите два правильных ответа.

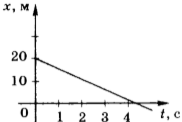
1) тело двигалось все время в одну сторону
2) в течение четырёх секунд модуль скорости тела уменьшался, а затем увеличивался
3) проекция скорости тела все время была положительной
4) проекция скорости тела в течение четырёх секунд была положительной, а затем — отрицательной
5) в момент времени 4 с тело остановилось

Часть 2

13. Два автомобиля движутся друг за другом равномерно и прямолинейно: один со скоростью 20 м/с, другой — со скоростью 15 м/с. Через какое время второй автомобиль догонит первый, если в начальный момент времени расстояние между ними равно 100 м?

Ответы

Равномерное прямолинейное движение

4.7 (93.33%) 3 votesАлгоритм

— Найти кратчайший путь на графике, посещающий все узлы Переполнение стека

Товары
Клиенты
Случаи использования

Переполнение стека Публичные вопросы и ответы
Команды Частные вопросы и ответы для вашей команды
предприятие Частные вопросы и ответы для вашего предприятия
работы Программирование и связанные с ним технические возможности карьерного роста
Талант Нанимать технический талант

Создать график онлайн и найти кратчайший путь или использовать другой алгоритм

Создать график и найти кратчайший путь. На странице справки вы найдете обучающее видео.

Настройка матрицы смежности. Используйте запятую «,» в качестве разделителя

Мультиграфная матрица содержит вес минимальных ребер между вершинами.

Матрица неверна. Используйте запятую «,» в качестве разделителя. Матрица должна быть квадратной

Настройка матрицы заболеваемости.Используйте запятую «,» в качестве разделителя.

Матрица неверна. Используйте запятую «,» в качестве разделителя.

Ваш алгоритм отправлен на проверку и в случае успеха будет добавлен на сайт.

Невозможно создать график. Матрица смежности имеет неправильный формат. Нажмите кнопку «исправить матрицу», чтобы исправить матрицу, или кнопку «справка», чтобы открыть справку о формате матрицы смежности

Невозможно создать график. Матрица заболеваемости имеет неправильный формат.Нажмите кнопку «исправить матрицу», чтобы исправить матрицу, или кнопку «Справка», чтобы открыть справку о формате Матрица инцидентности

Выбор и перемещение объектов мышью или перемещение рабочей области.

Перетащите курсор для перемещения объектов

Выбор и перемещение объектов мышью или перемещение рабочей области.

Перетащите курсор для перемещения объектов

Нажмите в рабочую область, чтобы добавить новую вершину. Перечисление вершин

Выберите первую вершину ребра

Выберите второй вершин ребра

Выберите начальную вершину кратчайшего пути

Выберите конечную вершину кратчайшего пути

Самая короткая длина пути составляет% d

Путь не существует

Нажмите на объект, чтобы удалить

Добавить ребро

Направление

Ненаправленный

Матрица смежности

Сохранить

Отмена

самое низкое расстояние

Матрица заболеваемости

Сохранение График

закрыть

Количество подключенных компонентов

Количество слабо связанных компонентов составляет

Что вы думаете о сайте?

Имя (электронная почта для обратной связи)

Обратная связь

Отправить

Чтобы задать нам вопрос или отправить нам комментарий, напишите нам на

исправить матрицу

помощь

Матрица имеет неправильный формат

Сохранить графическое изображение

Полный отчет

Краткий отчет

График не имеет эйлерова цикла

График имеет цикл Эйлера

Обработка…

Добавить вершину

Переименовать вершину

переименовать

Редактировать вес

не имеет веса

переименование группы

Голосовать

Рекомендовать алгоритмы

Граф не имеет эйлерова траектории

Граф имеет эйлерову траекторию

График минимальных расстояний

Проверить, чтобы сохранить

Показать матрицу расстояний

Матрица расстояний

Выберите источник максимального потока

Выберите мойку максимального потока

Максимальный поток от% 2 до% 3 равен% 1

Поток из% 1 в% 2 не существует

Источник

Мойка

График имеет не гамильтонов цикл

График имеет гамильтонов цикл

График не имеет гамильтонова пути

График

имеет гамильтонову траекторию

Выберите начальную вершину обхода

Заказ прохождения:

Кромочный изгиб

Отменить

Сохранить график

По умолчанию

Vertex Style

Edge Style

Цвет фона

Multigraph поддерживает не все алгоритмы

не имеет веса

Используйте Cmd⌘ для выбора нескольких объектов.

Используйте Ctrl для выбора нескольких объектов.

Перетащите группу.

Копировать группу

Удалить группу

Поиск в ширину

Граф раскраски

Найти подключенные компоненты

Поиск в глубину

Найти цикл Эйлера

Найти Эйлерова дорожка

Алгоритм Флойда – Варшалла

Организовать график

Найти гамильтонов цикл

Найти гамильтонову дорожку

Найти Максимальный поток

Поиск минимального остовного дерева

Визуализация на основе веса

Поиск по графику радиуса и диаметра

Найти кратчайший путь, используя алгоритм Дейкстры

Рассчитать степень вершин

Равномерное прямолинейное движение

Зависимость скорости, координат и пути от времени

Как построить график зависимости пути от времени

Равномерное прямолинейное движение – FIZI4KA

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

Часть 2

Ответы

Приставки рос рас роз рас рос: Ошибка 403 — доступ запрещён

2 х 5 9: решите уравнение 2(x-5)=9 — Школьные Знания.com

Какие свойства человека относят к биологическим: 1. Какие свойства человека относят к биологическим? 2. Что, по вашему мнению, произошло бы с

Высшим исполнительным органом рф является: Статья 32. Высший исполнительный орган субъекта Российской Федерации \ КонсультантПлюс

Leave A Comment Отменить ответ

График пути от времени: Графическое представление движения — О’Пять пО физике!

Равномерное прямолинейное движение

Зависимость скорости, координат и пути от времени

Как построить график зависимости пути от времени

Равномерное прямолинейное движение – FIZI4KA

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

Часть 2

Ответы

Share This Story, Choose Your Platform!

Related Posts

Приставки рос рас роз рас рос: Ошибка 403 — доступ запрещён

2 х 5 9: решите уравнение 2(x-5)=9 — Школьные Знания.com

Какие свойства человека относят к биологическим: 1. Какие свойства человека относят к биологическим? 2. Что, по вашему мнению, произошло бы с

Высшим исполнительным органом рф является: Статья 32. Высший исполнительный орган субъекта Российской Федерации \ КонсультантПлюс

Leave A Comment Отменить ответ