Как найти радиус описанной вокруг трапеции окружности: Радиус описанной окружности трапеции | Треугольники

Как найти радиус описанной окружности для трапеции?

В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.

I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции

Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.

В общем случае радиус описанной около треугольника окружности может быть найден по одной из формул

где a — сторона треугольника, α — противолежащий ей угол;

либо по формуле

где a, b, c — стороны, S — площадь треугольника.

Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:

или

где синус угла A можно найти из прямоугольного треугольника ABF:

III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров

Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).

Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.

Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить

и приравнять правые части

Решив это уравнения относительно x, можно найти R.

IV. Если диагональ трапеции перпендикулярна боковой стороне, центр описанной окружности лежит на середине большего основания и радиус равен половине большего основания.

точка O — середина AD

Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной окружности лежит вне трапеции, за большим основанием.

I вариант нахождения радиуса для этого случая не изменяется.

Во II случае OK=h+x, соответственно, изменяется уравнение для нахождения x и R.

Позже рассмотрим конкретные задачи нахождения радиуса описанной около трапеции окружности.

Найти радиус описанной около трапеции окружности

Рассмотрим задачи, в которых нужно найти радиус описанной около трапеции окружности.

1) Найти радиус окружности, описанной около трапеции, основания которой равны 11 см и 21 см, а диагональ — 20 см.

Дано: ABCD — трапеция, AD∥BC, AD=21 см, BC=11 см, BD=20 см, окружность (O; R) — описанная около ABCD.

Найти: R.

Анализ задачи.

Радиус описанной около трапеции окружности можно найти как радиус окружности, описанной около треугольника ABD:

Таким образом, задача сводится к нахождению синуса угла A.

Решение:

1) Описать окружность можно только около равнобедренной трапеции, следовательно, CD=AB.

2) Проведём высоту трапеции BF.

По свойству равнобедренной трапеции,

Тогда FD=AD-AF=21-5=16 (см).

3) Рассмотрим треугольник BDF. ∠BFD=90º (так как BF — высота трапеции).

По теореме Пифагора,

4) Рассмотрим прямоугольный треугольник ABF.

По теореме Пифагора

По определению синуса,

5) По формуле

Ответ: 10 5/6 см.

2) Найти радиус описанной около трапеции окружности, если известно, что её боковые сторона и меньшее основание равны 10 см, а один из углов 60º.

Дано: ABCD — трапеция, AD∥BC,

AB=BC=CD=10 см, ∠D=60º,

окружность (O;R) — описанная около ABCD.

Найти: R.

Решение:

Проведём диагональ BD.

Треугольник ABC — равнобедренный с основанием AC (AB=BC по условию).

Следовательно, ∠BAC=∠BCA (как углы при основании).

∠BCA=∠DAC (как внутренние накрест лежащие при AD∥BC и секущей AC).

Отсюда ∠BAC=∠DAC, то есть диагональ AC является биссектрисой угла BAD.

∠BAD=∠D=60º (как углы при основании равнобедренной трапеции). Поэтому 

Рассмотрим треугольник ACD.

Так как сумма углов треугольника равна 180º,

∠ACD=180º-(∠DAC+∠D)=180º-(30º+60º)=90º.

Значит, вписанный угол ACD опирается на диаметр.

Катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы. Поэтому AD=2∙CD=2∙10=20(см). Следовательно, радиус

Ответ: 10 см.

Все формулы для радиуса описанной окружности

 ,  ,     —  стороны треугольника

  — полупериметр

Формула радиуса описанной окружности треугольника ( R  ) :

— сторона треугольника

— высота

— радиус описанной окружности

Формула радиуса описанной окружности равностороннего треугольника через его сторону:

Формула радиуса описанной окружности равностороннего треугольника через высоту:

Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.

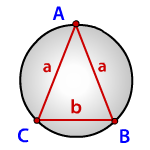
a, b — стороны треугольника

Формула радиуса описанной окружности равнобедренного треугольника(R):

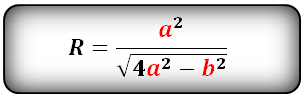
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.

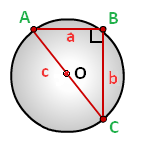
a, b — катеты прямоугольного треугольника

c — гипотенуза

Формула радиуса описанной окружности прямоугольного треугольника (R):

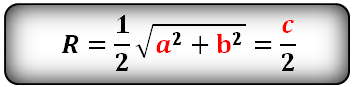
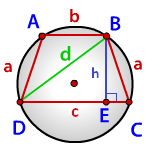
a — боковые стороны трапеции

c — нижнее основание

b — верхнее основание

d — диагональ

p — полупериметр треугольника DBC

p = (a+d+c)/2

Формула радиуса описанной окружности равнобокой трапеции, (R)

Радиус описанной окружности квадрата равен половине его диагонали

a — сторона квадрата

d — диагональ

Формула радиуса описанной окружности квадрата (R):

Радиус описанной окружности прямоугольника равен половине его диагонали

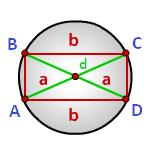
a, b — стороны прямоугольника

d — диагональ

Формула радиуса описанной окружности прямоугольника (R):

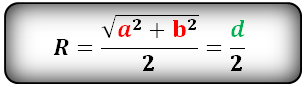
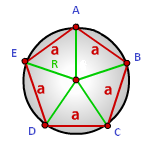
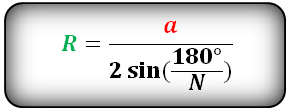
a — сторона многоугольника

N — количество сторон многоугольника

Формула радиуса описанной окружности правильного многоугольника, (R):

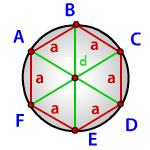
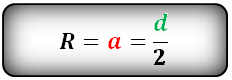
a — сторона шестиугольника

d — диагональ шестиугольника

Радиус описанной окружности правильного шестиугольника (R):

Радиус описанной окружности

© 2011-2020   Все права защищены.

При использовании материалов данного сайта обязательно указывать ссылку на источник.

Описанная окружность и трапеция

Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.

Какую теорию необходимо помнить? Это:

1. Свойство сторон четырёхугольника описанного около окружности.

2. Теорему Пифагора. *Куда мы без неё )

3. Понятие средней линии трапеции.

Задачи с трапециями, которые имеются на блоге можно посмотреть здесь.

27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.

Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:

Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания).  Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.

Ответ: 6

27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60⁰, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.

Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?

Посмотрите: равнобедренная трапеция с углом при основании равным 60⁰ и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:

В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее здесь п.6

То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.

*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 180⁰ и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.

Ответ: 6

27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:

Отрезок EF является высотой трапеции, его нам нужно найти.

В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности),  FC=3 (так как  DF=FC). По теореме Пифагора можем вычислить OF:

В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности),  EB=4 (так как  AE=EB). По теореме Пифагора можем вычислить OE:

Таким образом EF=FO+OE=4+3=7.

Ответ: 7

Теперь важный нюанс!

В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.

А если бы в условии не было дано эскиза?

Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:

*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.

И решение будет «второго варианта» будет следующим.

По теореме Пифагора вычисляем OF:

Также вычислим OE:

Таким образом EF=FO–OE=4–3=1.

Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.

27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.

Здесь сразу следует вспомнить свойство  четырёхугольника описанного около окружности:

Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.

Значит

А средняя линия равна половине суммы оснований, то есть 10.

Ответ: 10

27938. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.

Радиус окружности равен половине высоты. Используя свойство указанное в предыдущей задаче получим:

Большая сторона у нас это СВ, следовательно можем вычислить AD=11–CB=11–7=4. Таким образом, радиус будет равен 2.

Ответ: 2

27915. Найдите высоту трапеции, в которую вписана окружность радиуса 1.

Посмотреть решение

27936. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.

Посмотреть решение

На этом всё, успеха вам!

С уважением, Александр Крутицких.

*Расскажите о сайте в социальных сетях.

Свойства трапеции, описанной около окружности: формулы и теоремы

Трапеция — это геометрическая фигура с четырмя углами. При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как «трапедзион», что означало «столик», «обеденный столик».

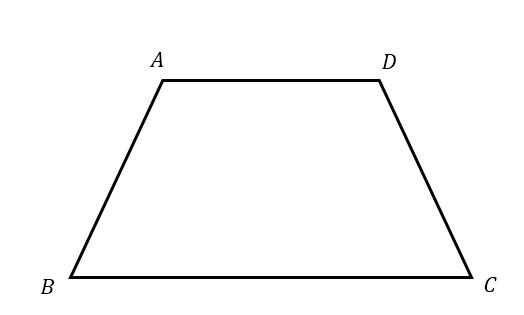
Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.

Элементы, виды и признаки геометрической фигуры трапеция

Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны — боковыми сторонами. При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.

У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:

1. Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.
2. При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
3. Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.
4. При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
5. При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
6. Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°. Отрезок, соединяющий основания, будет равен 1/2 их разности.

Свойства трапеции, описанной около окружности

Заключить окружность в трапецию возможно лишь при одном условии. Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.

Итак, подробнее о свойствах трапеции, описанной около окружности:

1. Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
2. При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
3. Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.

Еще немного о свойствах трапеции, заключенной в окружность

Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.

Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. Это значит, что при построении окружности, описанной около трапеции AFDM, применимо: AD × FM = AF × DM + FD × AM.

На школьных экзаменах довольно часто встречаются задачи, требующие решения задач с трапецией. Большое количество теорем необходимо запоминать, но если выучить сразу не получиться — не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.

формулы и теоремы. Главные принципы методики изучения свойств трапеции

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим н

Радиус описанной окружности | Треугольники

Удобно, когда все формулы, по которым можно найти радиус описанной окружности для треугольника, квадрата, многоугольника размещены на одной странице.

Радиус описанной окружности для произвольного треугольника

Формулы для нахождения радиуса описанной окружности треугольника (верны для треугольника любого вида):

   

   

где a, b, c — длины сторон треугольника, α, β, γ — противолежащие этим сторонам углы, S — площадь треугольника.

Центр описанной окружности лежит:

у остроугольного треугольника — внутри треугольника;

у прямоугольного — на середине гипотенузы;

у тупоугольного — вне треугольника, напротив тупого угла.

Радиус описанной окружности для прямоугольного треугольника

Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы:

   

 

 

Окружность, описанная около многоугольника

Если около многоугольника можно описать окружность, ее центр является точкой пересечения серединных перпендикуляров к сторонам многоугольника.

Радиус описанной около многоугольника окружности  находят как радиус окружности, описанной около треугольника. Для этого берут любые три вершины многоугольника.

Например, для пятиугольника ABCDE можно взять любой из треугольников ABC, ABD, ABE, BCD, BCE, CDE, ACD, ACE, ADE, BDE.

 

Радиус окружности, описанной около правильного многоугольника

Формула радиуса описанной окружности для правильного многоугольника

   

где a — длина стороны многоугольника, n — количество его сторон.

Частные случаи — правильный треугольник, правильный четырехугольник (то есть квадрат), правильный шестиугольник.

Радиус описанной окружности правильного треугольника

Формула радиуса описанной окружности для правильного треугольника

   

Если без иррациональности в знаменателе —

   

У правильного треугольника радиус описанной окружности в два раза больше радиуса вписанной окружности:

   

 

Радиус описанной окружности квадрата

Формула радиуса описанной окружности для квадрата

   

Если без иррациональности в знаменателе —

   

 

Радиус описанной окружности правильного шестиугольника

Формула радиуса описанной окружности для правильного шестиугольника

   

р — Нахождение радиуса окружности, которая описывает многоугольник Переполнение стека

1. Товары
2. Клиенты
3. Случаи использования

1. Переполнение стека Публичные вопросы и ответы
2. Команды Частные вопросы и ответы для вашей команды
3. предприятие Частные вопросы и ответы для вашего предприятия
4. работы Программирование и связанные с ним технические возможности карьерного роста
5. Талант Нанимать технический талант
6. реклама Связаться с разработчиками по всему миру

,

Радиус определения круга и калькулятор

Радиус определения круга и калькулятор — Math Open Reference

1. Линия от центра круга до точки на круге.
2. Расстояние от центра круга до точки на круге.

Попробуйте это Перетащите оранжевую точку. Синяя линия всегда будет оставаться радиусом круга.

Радиус круга — это длина линии от центра до любой точки на его краю.Форма множественного числа — радиусы (произносится «луч-ди-глаз»). На рисунке выше перетащите оранжевую точку вокруг и убедитесь, что радиус всегда постоянен в любой точке круга.

Иногда слово «радиус» используется для обозначения самой линии. В этом смысле вы можете увидеть «нарисовать радиус круга». В более позднем смысле это длина линии, и поэтому ее называют «радиус круга составляет 1,7 сантиметра»

Если вы знаете диаметр

Учитывая диаметр круга, радиус просто равен половине диаметра: где:
D — диаметр круга

Если вы знаете, окружность

Если вам известна окружность круга, радиус можно найти по формуле
, где:
C — длина окружности
π — это Pi, приблизительно 3.142

Если вы знаете область

Если вы знаете площадь круга, радиус можно найти по формуле
, где:
A — это площадь круга.
π — это Пи, примерно 3,142.

Калькулятор

Используйте калькулятор выше, чтобы рассчитать свойства круга.

Введите любое значение, а остальные три будут рассчитаны. Например: введите радиус и нажмите «Рассчитать». Площадь, диаметр и окружность будут рассчитаны.

Точно так же, если вы введете площадь, будет вычислен радиус, необходимый для ее получения, а также диаметр и окружность.

Похожие товары

Диаметр Какова ширина круга. Диаметр в два раза больше радиуса. См диаметр круга

Окружность Окружность — это расстояние вокруг края круга. Видеть Окружность круга больше.

Что попробовать

1. На рисунке выше нажмите «сброс» и перетащите оранжевую точку.Обратите внимание, что в любой точке круга радиус одинаковой длины.
2. Нажмите на «Показать диаметр». Перетащите любую оранжевую точку на концах линии диаметра. Обратите внимание, что радиус всегда равен половине диаметра.
3. Снимите флажок «фиксированный размер». Повторите вышеизложенное и обратите внимание, что радиус всегда равен половине диаметра, независимо от размера круга.

Другие темы круга

General

Уравнения окружности

Углы по кругу

дуг

(C) 2011 Copyright Math Открытая ссылка.
Все права защищены

,

Окружность треугольника — Математика Открытая ссылка Окружность треугольника — Math Open Reference Круг, который проходит через все три вершины треугольника
Также «Описанный круг». Попробуйте это Перетащите оранжевые точки на каждую вершину изменить форму треугольника. Обратите внимание, что окружность всегда проходит через все три точки.

Окружность всегда проходит через все три вершины треугольника. Его центр находится в точке, где все перпендикулярные биссектрисы стороны треугольника встречаются.Этот центр называется круговым центром. Видеть Обведите центр треугольника, чтобы узнать больше об этом.

Обратите внимание, что центр круга может быть внутри или снаружи треугольника. Отрегулируйте треугольник выше и попробуйте получить эти случаи.

Радиус окружности также называют круговым радиусом треугольника.

Для правильных треугольников

В случае прямоугольный треугольник, гипотенуза это диаметр окружности, и его центр находится точно на середина гипотенузы.Это та же ситуация, что и теорема Фалеса, где диаметр стягивает прямой угол к любой точке на окружности круга.

Если вы перетащите треугольник на рисунке выше, вы можете создать такую ​​же ситуацию.

Для равносторонних треугольников

В случае равностороннего треугольника, где все три стороны (a, b, c) имеют одинаковую длину, радиус окружности определяется по формуле: где s — длина стороны треугольника.

Если вы знаете все три стороны

Если вы знаете длину (a, b, c) трех сторон треугольника, радиус его окружности определяется по формуле:

Если вы знаете одну сторону и ее противоположный угол

Диаметр от окружности определяется по формуле: где и — это длина одной стороны, а A — это угол, противоположный этой стороне.

Это дает диаметр , так что радиус составляет половину этого

Это происходит от Закон Синусов.

Построение треугольника по окружности

Можно построить центр окружности и окружность треугольника только с помощью компаса и линейки. Построение Кругового Треугольника имеет анимационную демонстрацию техники и рабочий лист, чтобы попробовать его самостоятельно.

Другие темы треугольника

General

Периметр / Площадь

Типы треугольников

Треугольные центры

Конгруэнтность и Сходство

Решение треугольников

Тесты по треугольнику и упражнения

(C) 2011 Copyright Math Открытая ссылка.
Все права защищены

,

Радиус описанной окружности равнобедренной трапеции

Подробнее

Написано администратором

Опубликовано: 26 июня 2019 г.

Последнее обновление: 18 июля 2019 года

---

— равные стороны трапеции

, — базы

— диагональ

— центр окружности

Рассчитайте радиус окружности равнобедренной трапеции, если даны стороны и диагональ ( R ):

---

---

,

Share This Story, Choose Your Platform!

FacebookTwitterLinkedInRedditWhatsappGoogle+TumblrPinterestVkEmail

Related Posts

• Насморк при прорезывании зубов у детей: причины, симптомы и лечение

  Насморк при прорезывании зубов у детей: причины, симптомы и лечение

• Как развивать ребенка в 10 месяцев: игры и занятия для малыша

  Как развивать ребенка в 10 месяцев: игры и занятия для малыша

• Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования

  Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования

• УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов

  УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов

• Когда и как вводить прикорм грудному ребенку: рекомендации педиатров

  Когда и как вводить прикорм грудному ребенку: рекомендации педиатров

Leave A Comment Отменить ответ

Comment

Save my name, email, and website in this browser for the next time I comment.