|
|
Тесты по физике взяты из
сборника А.Е. Марон, Е.А. Марон Электрический ток. Сила тока. Источник тока |
|
| 1.
Проводник находится в электрическом поле. Как движутся в нем свободные
электрические заряды? A. Совершают колебательное движение. Б. Хаотично. B. Упорядоченно. 2. Что принято за направление электрического тока? A. Направление упорядоченного движения положительно заряженных частиц. Б. Направление упорядоченного движения отрицательно заряженных частиц. B. Определенного ответа дать нельзя. 3. Как изменилась сила тока в цепи, если увеличилась концентрация заряженных частиц в 4 раза, а скорость электронов и сечение проводника остались прежними? A.  Б. Уменьшилась в 4 раза. B. Увеличилась в 4 раза. 4. Какова роль источника тока в электрической цепи? A. Порождает заряженные частицы. Б. Создает и поддерживает разность потенциалов в электрической цепи. B. Разделяет положительные и отрицательные заряды. 5. Какой заряд пройдет через поперечное сечение проводника за 2 мин, если сила тока в проводнике равна 1 А? А. 60 Кл. Б. 120 Кл. В. 30 Кл. |
||
| 6. В
проводнике отсутствует электрическое поле. Как движутся в нем свободные
электрические заряды? A. Совершают колебательное движение. Б. Хаотично. 7. Направление электрического тока… A. совпадает с направлением напряженности электрического поля, вызывающего этот ток; Б. противоположно направлению напряженности электрического поля, вызывающего этот ток; B.  определенного ответа дать нельзя. определенного ответа дать нельзя.8. Сила тока в цепи возросла в 2 раза, концентрация зарядов и площадь сечения проводника не изменились. Как изменилась скорость движения электронов? A. Уменьшилась в 2 раза. Б. Увеличилась в 2 раза. 9. Какие силы вызывают разделение зарядов в источнике тока? A. Кулоновские силы отталкивания. Б. Сторонние (неэлектрические) силы. B. Кулоновские силы отталкивания и сторонние (неэлектрические) силы. 10. За какое время через поперечное сечение проводника пройдет заряд в 100 Кл при силе тока 2 А? А. 200 с. Б. 60 с. В. 50 с. |
||
| Закон Ома для участка цепи. Сопротивление проводника. 1. Напряжение на проводнике
увеличили в 5 раз. Как при этом изменится сопротивление проводника?  Б. Уменьшится в 5 раз. B. Не изменится. 2. Как изменится сила тока, протекающего по проводнику, если напряжение на его концах и площадь сечения проводника увеличить в 2 раза? A. Не изменится. Б. Уменьшится в 4 раза. B. Увеличится в 4 раза. |
||
| 3. По
вольт-амперной характеристике проводника, изображенной на рисунке 1,
определите, какой из проводников имеет наибольшее сопротивление. А.1. В. 2. В. 3. |
||
|
4. Каково сопротивление резистора, если при напряжении 8 В сила тока в
резисторе 4 мкА? А. 4 МОм. Б. 2 МОм. В. 8 МОм. |
||
| 5. На рисунке
2 показана вольт-амперная характеристика проводника. Определите
сопротивление проводника. А. 3000 Ом. Б. 4000 Ом. В. 2000 Ом.
|
||
6. По вольт-амперной характеристике проводника, изображенной на
рисунке 3, определите, какой из проводников имеет наименьшее
сопротивление. По вольт-амперной характеристике проводника, изображенной на
рисунке 3, определите, какой из проводников имеет наименьшее
сопротивление.А. 1. В. 2. В. 3. |
||
|
7. На рисунке 4
показана вольт-амперная характеристика проводника. Определите
сопротивление проводника. A. 2000 Ом. Б. 4000 Ом. B. 5000 Ом. |
||
|
8. Как
изменится сила тока в проводнике при уменьшении напряжения на его концах
в 2 раза? A. Увеличится в 2 раза. Б. Уменьшится в 2 раза. B. Не изменится. 9. Как изменится сила тока, протекающего по проводнику, если напряжение на его концах и длину проводника уменьшить в 3 раза? A. Не изменится. Б. Уменьшится в 9 раз. B. Увеличится в 9 раз. 10. Чему равна разность потенциалов на концах проводника сопротивлением 10 Ом, если сила тока в проводнике 2 А? А. 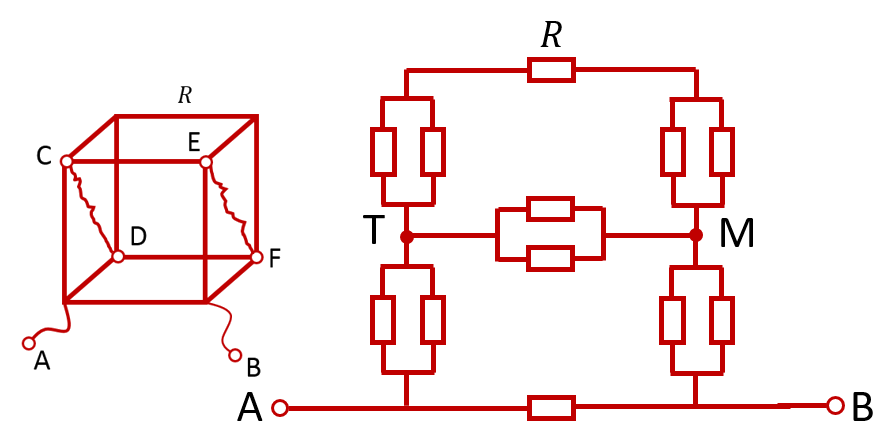 20 В. Б. 30 В. В. 10 В. 20 В. Б. 30 В. В. 10 В.
| ||
| Удельное сопротивление проводников. Зависимость удельного сопротивления проводников от температуры | ||
| 1.
Металлический проводник имеет сопротивление 1 Ом.
Каким сопротивлением будет обладать проводник, имеющий в 2 раза
большую длину и в 2 раза большую площадь
сечения, сделанный из того же материала? А. 0,25 Ом. Б. 2 Ом. В. 1 Ом. 2. Как изменится сопротивление проволоки, если ее сложить вдвое? A. Уменьшится в 4 раза. Б. Уменьшится в 2 раза. B. Увеличится в 2 раза. |
||
| 3. Какой график (рис. 5) соответствует зависимости удельного сопротивления металла от температуры? | ||
|
4. Каким сопротивлением обладает
нихромовый проводник длиной 5 м и площадью поперечного сечения 0,75мм А. 10,5 Ом. Б. 7,3 0м. В. 14,6 Ом. |
||
|
5. Сопротивление угольного стержня уменьшилось от 5 до 4,5 Ом при повышении температуры от 50 до 5450С. Каков температурный коэффициент сопротивления угля?
А. 0,0002 К-1. Б.
0,0004 К-1 В. 0,0008 К |
||
| 6. Какой график (рис. 5) соответствует зависимости удельного сопротивления полупроводника от температуры? | ||
|
7. Металлический проводник имеет сопротивление
4 Ом. Каким сопротивлением будет обладать
проводник, имеющий в 4 раза большую длину и в 4 раза меньшую площадь
сечения, сделанный из того же материала? А. 32 Ом. Б. 16 Ом. В.  8 Ом. 8 Ом.8. Как изменится сопротивление проволоки, если ее сложить втрое? A. Уменьшится в 3 раза. Б. Уменьшится в 9 раз. B. Увеличится в 3 раза. |
||
|
9. Чему равно сопротивление константановой проволоки длиной 8 м и площадью поперечного сечения 2 мм2? Удельное сопротивление константана равно 0,5 Ом * мм2/м. А. 2 Ом. Б. 20 Ом. В. 30 Ом. 10. Сопротивление медного проводника при 0 °С равно 4 Ом. Каково его сопротивление при 100 °С, если температурный коэффициент сопротивления меди равен 0,0043 К-1? А. 57,2 Ом. Б. 6,43 Ом. В. 5,72 Ом | ||
| Соединение проводников | ||
|
1. А. 11Ом. Б. 3 Ом. В. 5 0м. |
||
|
2. Определите общее сопротивление цепи, показанной на рисунке 8. А. 4R. Б. 3R. В. 2,5R. |
||
| 3. Рассчитайте
общее сопротивление между точками а и b (рис. 9), если сопротивление
каждого элемента цепи равно 3,3 Ом. А. 1,5 0м. Б. 2 0м. В. 5 0м. |
||
|
4. Чему равна сила тока, протекающего через общую часть электрической цепи (рис. 10), если R1 = R2 = 5 Ом, R3 = R4 = R5 = 10 Ом?
А. |
||
| 5. Каково общее
сопротивление цепи, представленной на рисунке 11, если сопротивление
каждого отрезка равно 10м? A. 4/5 Ом. Б. 1 Ом. В. 4/3Ом. |
||
|
6. Найдите общее сопротивление электрической цепи, показанной на рисунке 12, если R1=3Ом, R2=R3=R4=6 Ом. А. 5 Ом. Б. 2 Ом. В. 3 Ом. |
||
|
7. Определите общее сопротивление цепи, показанной на
рисунке 13. A. 2R. Б. 3R. В. 5R. |
||
8. Рассчитайте общее сопротивление между точками а и
b (рис. 14), если R1 = 4 Ом, R2 = 3 Ом, R3 = 2
Ом, R4 = 5 Ом, R5 = 1,5 0м, R6 = 4 0м. А. 1,5 0м. Б. 6 0м. В. 2,5 0м. |
||
|
9. Чему равна сила тока, протекающего через общую часть электрической цепи (рис.15), если R1 = R2= R3 = 3 Ом, R4 = R5 = 6 Ом? А. 2 А. Б. 0,5 А. В. 1 А. |
||
|
10.
Каково общее сопротивление цепи, представленной на
рисунке 16? A. 2R. Б. 3R. В. 1R. |
||
| В начало | ||
|
2009 год |
|
|
Найти сопротивление между соседними вершинами проволочного куба.
 Сопротивление куба
Сопротивление кубаРассмотрим классическую задачу. Дан куб, рёбра которого представляют собой проводники с каким-то одинаковым сопротивлением. Этот куб включается в электрическую цепь между всевозможными его точками. Вопрос: чему равно сопротивление куба в каждом из этих случаев? В данной статье репетитор по физике и математике рассказывает о том, как решается эта классическая задача. Присутствует также видеоурок, в котором вы найдёте не только подробное объяснение решения задачи, но и реальную физическую демонстрацию, подтверждающую все вычисления.
Итак, куб может быть включен в цепь тремя различными способами.
Сопротивление куба между противоположными вершинами
В этом случае ток, дойдя до точки A , распределяется между тремя рёбрами куба. При этом, поскольку все три ребра эквивалентны с точки зрения симметрии, ни одному из рёбер нельзя придать большую или меньшую «значимость». Поэтому ток между этими рёбрами должен распределиться обязательно поровну. То есть сила тока в каждом ребре равна :
То есть сила тока в каждом ребре равна :
В результате получается, что падение напряжения на каждом из этих трёх рёбер одинаково и равно , где — сопротивление каждого ребра. Но падение напряжение между двумя точками равно разности потенциалов между этими точками. То есть потенциалы точек C , D и E одинаковы и равены . Из соображений симметрии потенциалы точек F , G и K также одинаковы.
Точки с одинаковым потенциалом можно соединять проводниками. Это ничего не изменит, потому что по этим проводникам всё равно не потечёт никакой ток:
В результате получим, что рёбра AC , AD и AE T . Точно также рёбра FB , GB и KB соединятся в одной точке. Назовём её точкой M . Что касается оставшихся 6 рёбер, то все их «начала» окажутся соединены в точке T , а все концы — в точке M . В результате мы получим следующую эквивалентную схему:
Сопротивление куба между противолежащими углами одной грани
В данном случае эквивалентными являются рёбра AD и AC . По ним потечёт одинаковый ток . Кроме того, эквивалентными также являются KE и KF . По ним потечёт одинаковый ток . Ещё раз повторим, что ток между эквивалентными рёбрами должен распределиться поровну, в противном случае нарушится симметрия:
По ним потечёт одинаковый ток . Кроме того, эквивалентными также являются KE и KF . По ним потечёт одинаковый ток . Ещё раз повторим, что ток между эквивалентными рёбрами должен распределиться поровну, в противном случае нарушится симметрия:
Таким образом, в данном случае одинаковым потенциалом обладают точки C и D , а также точки E и F . Значит эти точки можно объединить. Пусть точки C и D объединятся в точке M , а точки E и F — в точке T . Тогда получится следующая эквивалентная схема:
На вертикальном участке (непосредственно между точками T и M ) ток не течёт. Действительно, ситуация аналогична уравновешенному измерительному мосту . Это означает, что данной звено можно исключить из цепи. После этого посчитать общее сопротивление не составит труда:
Сопротивление верхнего звена равно , нижнего — . Тогда общее сопротивление равно:
Сопротивление куба между прилежащими вершинами одной грани
Это последний возможный вариант подключения куба в электрическую цепь. В этом случае эквивалентными рёбрами, через которые будет течь одинаковый ток, являются рёбра AC и AD . И, соответственно, одинаковые потенциалы будут иметь точки C и D , а также симметричные им точки E и F :
В этом случае эквивалентными рёбрами, через которые будет течь одинаковый ток, являются рёбра AC и AD . И, соответственно, одинаковые потенциалы будут иметь точки C и D , а также симметричные им точки E и F :
Вновь соединяем попарно точки с одинаковыми потенциалами. Мы можем это сделать, потому что ток между этими точками не потечёт, даже если соединить их проводником. Пусть точки C и D объединятся в точку T , а точки E и F — в точку M . Тогда можно нарисовать следующую эквивалентную схему:
Общее сопротивление полученной схемы рассчитывается стандартными способами. Каждый сегмент из двух параллельно соединённых резисторов заменяем на резистор сопротивлением . Тогда сопротивление «верхнего» сегмента, состоящего из последовательно соединённых резисторов , и , равно .
Этот сегмент соединён со «средним» сегментом, состоящим из одного резистора сопротивлением , параллельно. Сопротивление цепи, состоящей из двух параллельно соединённых резисторов сопротивлением и , равно:
Сопротивление цепи, состоящей из двух параллельно соединённых резисторов сопротивлением и , равно:
То есть схема упрощается до ещё более простого вида:
Как видно, сопротивление «верхнего» П-образного сегмента равно:
Ну а общее сопротивление двух параллельно соединённых резисторов сопротивлением и равно:
Эксперимент на измерению сопротивления куба
Чтобы показать, что всё это не математический трюк и что за всеми этими вычислениями стоит реальная физика, я решил провести прямой физической эксперимент по измерению сопротивления куба. Вы можете посмотреть этот эксперимент в видео, которые находится в начале статьи. Здесь я размещу фотографии экспериментальной установки.
Специально для этого эксперимента я спаял куб, рёбрами которого являются одинаковые резисторы. Также у меня есть мультиметр, который я включил в режиме измерения сопротивления. Сопротивление одиночного резистора равно 38.3 кОм:
Электрическое сопротивление куба
Дан каркас в виде куба, изготовленный из металлической проволоки. Электрическое сопротивление каждого ребра куба равно одному Ому. Чему равно сопротивление куба при прохождении электрического тока от одной вершины к другое, если он подключен к источнику постоянного тока как это показано на рисунке?
Электрическое сопротивление каждого ребра куба равно одному Ому. Чему равно сопротивление куба при прохождении электрического тока от одной вершины к другое, если он подключен к источнику постоянного тока как это показано на рисунке?
Интересные факты про задачу про сопротивление куба резисторов
1. Решение задачки про сопротивление куба в общем виде можно прочитать на сайте журнала Квант или посмотреть здесь: «В конце сороковых годов в математических кружках Москвы появилась задача об электрическом сопротивлении проволочного куба. Кто ее придумал или нашел в старых учебниках мы не знаем. Задача была очень популярной, и о ней быстро узнали все. Очень скоро ее стали задавать на экзаменах и она стала…
0 0
Рассмотрим классическую задачу. Дан куб, рёбра которого представляют собой проводники с каким-то одинаковым сопротивлением. Этот куб включается в электрическую цепь между всевозможными его точками. Вопрос: чему равно сопротивление куба в каждом из этих случаев? В данной статье репетитор по физике и математике рассказывает о том, как решается эта классическая задача. Присутствует также видеоурок, в котором вы найдёте не только подробное объяснение решения задачи, но и реальную физическую демонстрацию, подтверждающую все вычисления.
Этот куб включается в электрическую цепь между всевозможными его точками. Вопрос: чему равно сопротивление куба в каждом из этих случаев? В данной статье репетитор по физике и математике рассказывает о том, как решается эта классическая задача. Присутствует также видеоурок, в котором вы найдёте не только подробное объяснение решения задачи, но и реальную физическую демонстрацию, подтверждающую все вычисления.
Итак, куб может быть включен в цепь тремя различными способами.
Сопротивление куба между противоположными вершинами
В этом случае ток, дойдя до точки A, распределяется между тремя рёбрами куба. При этом, поскольку все три ребра эквивалентны с точки зрения симметрии, ни одному из рёбер нельзя придать большую или меньшую «значимость». Поэтому ток между этими рёбрами должен распределиться обязательно поровну. То есть сила…
0 0
Странно..
Вы ведь сами ответили на свой вопрос..
— Спаять и «подключив щупы омметра к двум точкам, через которые проходит главная диагональ куба» «его измерять»
Прилагается рисунок: —
Достаточно простых рассуждений. Хватит школьных знаний по физике. Геометрия здесь не нужна, поэтому перенесём куб на плоскость и для начала отметим характерные точки.
Хватит школьных знаний по физике. Геометрия здесь не нужна, поэтому перенесём куб на плоскость и для начала отметим характерные точки.
Прилагается рисунок: —
Все же лучше приводить логику рассуждений, а не просто цифры наугад. Тем не менее не угадали!
Предлагаю поискать оригинальные способы решения.Угадали, но как решили? Ответ абсолютно верный и можно тему закрывать. Единственное что, решать так задачу можно не только для одинаковых R. Просто, если…
0 0
Позволю себе прокомментировать утверждение Учителя
Пусть к противоположным рёбрам куба A и C» приложено напряжение U, в результате чего на внешнем по отношению к кубу участку цепи течёт ток I.
На рисунке изображены токи, текущие по граням куба. Из соображений симметрии видно, что токи, текущие по гранямAB, AA» и AD, равны — обозначим этот ток I1; точно так же получаем, что токи по гранямDC, DD», BC, BB», A»B», A»D» равны (I2)l; токи по гранфм CC», B»C» и D»C» также равны (I3).
Записываем законы Кирхгофа (например, для узлов A, B, C, C»):
{ I = 3I1
{ I1 = 2I2
{ 2I2 = I3
{ 3I3 = I
Отсюда получаем I1= I3 = I/3; I2 = I/6
Пусть общее сопротивление куба равно r; тогда по закону Ома
(1) U = Ir.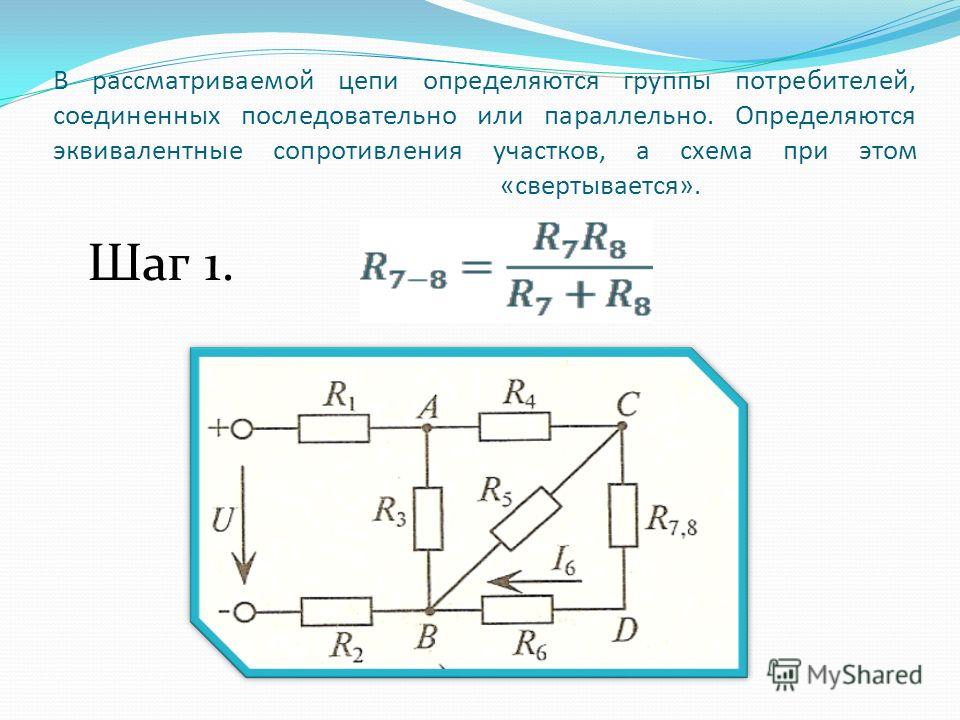
С другой стороны, при обходе контура ABCC» получаем, что
(2) U = (I1 + I2 + I3)R
Из сравнения (1) и (2) имеем:
r = R*(I1 + I2 + I3)/I = R*(1/3 + 1/6 + 1/3) =…
0 0
Студенты? Это школьные задачи. Закон Ома, последовательное и параллельное соединения сопротивлений, задача про три сопротивления и сразу эти.
Конечно, я не учел аудиторию сайта, где большая часть участников не только решает с удовольствием задачки, но и сама готовит задания. И, конечно, знает про классические задачки возрастом не менее 50 лет (я их решал из сборника более старого чем первое издание Иродова — 1979 год, как я понимаю).
Но все таки странно слышать, что «задачки не олимпиадные». ИМХО, «олимипиадность» задач определяется не столько и даже не столько сложностью, а во многом тем, что при решении надо (о чем то) догадаться, после чего задача из очень сложной становится очень простой.
Средний студент напишет систему из уравнений Киргофа и решит её. И никто ему не докажет, что решение неверное.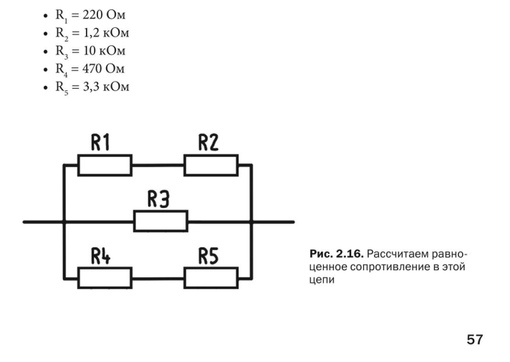
Сообразительный школьник догадается о симметрии и решит задачки быстрее среднего студента.
P.S. Впрочем, «средние студенты» тоже разные бывают.
P.P.S….
0 0
Использовать универсальные математические пакеты — неразумно при наличии программ анализа схем. Результаты можно получать и в численном виде и в аналитическом (для линейных схем).
Попробую привести алгоритм вывода формулы (R_екв=3/4 R)
Разрезаем куб на 2 части по диагоналям горизонтальных граней плоскостью, проходящей через заданные точки. Получаем 2 половины куба с сопротивлением, равным удвоенному искомому сопротивлению (проводимость половину куба равна половине искомой проводимости). Там, где секущая плоскость пересекает ребра, их проводимости делим пополам (сопротивления удваиваем). Разворачиваем половинку куба. Получаем затем схему с двумя внутреннеми узлами. Заменяем один треугольник на одну звезду, благо числа целые. Ну а дальше елементарная арифметика. Может быть возможно и еще проще решить, гложат смутные сомнения.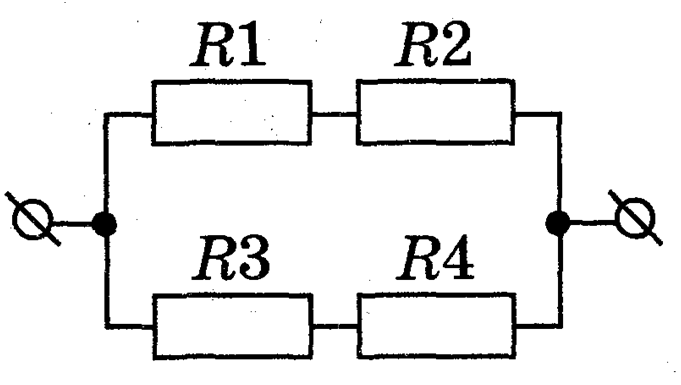 ..
..
PS. В Маппл и/или Сироп можно получить формулу для любых сопротивлений, но глядя на эту формулу вы поймете, что только компьютер захочет с ней…
0 0
Смешные цитаты
xxx: Да! ДА! Быстрее, ещё быстрее! Я хочу сразу два, нет, три! И этот тоже! О, да-а-а!
yyy: … мужик, ты чего это там?
xxx: Наконец-то безлимит, качаю торренты:D
type_2: интересно, а если ему туда литой чугунный кубик засунуть, раскрашенный в кубик–рубика? 🙂
Обсуждение робота из лего, собирающего кубик рубика за 6 секунд.
type_2: интересно а если ему туда литой чугунный кубик засунуть раскрашенный в кубик–рубика? 🙂
punky: угадайте страну по комментариям…
xxx: померил труселя новые?
yyy: Неа)
yyy: Завтра…
0 0
Решение задач на расчет электрического сопротивления с помощью моделей
Разделы: Физика
Цели: обучающая: систематизировать знания и умения учащихся решать задачи ан расчет эквивалентных сопротивлений с помощью моделей, каркасов и т. д.
д.
Развивающая: развитие навыков логического мышления абстрактного мышления, умений заменять схемы эквивалентности, упрощать расчет схем.
Воспитательная: воспитание чувства ответственности, самостоятельности, необходимости навыков приобретенных на уроке в будущем
Оборудование: проволочный каркас куба, тетраэдера, сетки бесконечной цепочки сопротивлений.
ХОД УРОКА
Актуализация:
1. Учитель: “Вспомним последовательное соединение сопротивлений”.
Учащиеся на доске зарисовывают схему.
и записывают
Учитель: вспомним параллельное соединение сопротивлений.
Учащийся на доске зарисовывает элементарную…
0 0
Для развития творческих способностей учащихся представляют интерес задачи на решение резисторных схем постоянного тока методом равнопотенциальных узлов. Решение этих задач сопровождается последовательным преобразованием исходной схемы. Причём наибольшее изменение она претерпевает после первого шага, когда используется данный метод. Дальнейшие преобразования связаны с эквивалентной заменой последовательных или параллельных резисторов.
Дальнейшие преобразования связаны с эквивалентной заменой последовательных или параллельных резисторов.
Для преобразования цепи пользуются тем свойством, что во всякой цепи точки с одинаковыми потенциалами можно соединять в узлы. И наоборот: узлы цепи можно разделить, если после этого потенциалы точек, входящих в узел, не изменятся.
В методической литературе часто пишут так: если схема содержит проводники с одинаковыми сопротивлениями, расположенными симметрично относительно какой-либо оси или плоскости симметрии, то точки этих проводников, симметричные относительно этой оси или плоскости, имеют одинаковый потенциал. Но вся сложность в том, что такую ось или плоскость никто на схеме не обозначает и отыскать её непросто.
Предлагаю другой, упрощённый способ решения подобных задач.
Задача 1 . Проволочный кубик (рис. 1) включён в цепь между точками А к В.
Найдите его общее сопротивление, если сопротивление каждого ребра равно R.
Поставим кубик на ребро АВ (рис. 2) и «распилим» его на две
параллельные половинки
плоскостью АА 1
B
1 В , проходящей через нижнее и верхнее ребро.
2) и «распилим» его на две
параллельные половинки
плоскостью АА 1
B
1 В , проходящей через нижнее и верхнее ребро.
Рассмотрим правую половинку куба. Учтём, что нижнее и верхнее ребро расщепились пополам и стали в 2 раза тоньше, а их сопротивления увеличились в 2 раза и стали по 2R (рис. 3).
1) Находим сопротивление R 1 трёх верхних проводников, соединённых последовательно:
4) Находим общее сопротивление этой половинки куба (рис. 6):
Находим общее сопротивление куба:
Получилось сравнительно просто, понятно и доступно для всех.
Задача 2 . Проволочный кубик подключён в цепь не ребром, а диагональю АС любой грани. Найдите его общее сопротивление, если сопротивление каждого ребра равно R (рис. 7).
Снова ставим кубик на ребро АВ. «Распиливаем» кубик на две параллельные половинки той же вертикальной плоскостью (см. рис. 2).
Опять рассматриваем правую половинку проволочного куба. Учитываем, что верхнее и нижнее ребро расщепились пополам и их сопротивления стали по 2R .
Учитываем, что верхнее и нижнее ребро расщепились пополам и их сопротивления стали по 2R .
С учётом условия задачи имеем следующее соединение (рис. 8).
Электроны влетают в плоский конденсатор длиной L под углом а к плоскости пластин, а вылетают под углом β. Определите начальную кинетическую энергию электронов, если напряженность поля конденсатора равна E.
Сопротивление любого ребра проволочного каркаса куба равно R. Найдите сопротивление между наиболее удаленными друг от друга вершинами куба.
При длительном пропускании тока 1,4 А через проволоку последняя нагрелась до 55°С, а при силе тока 2,8 А — до 160 °С. До какой температуры нагревается проволока при силе тока 5,6А? Сопротивление проволоки не зависит от температуры. Температура окружающего воздуха постоянна. Теплоотдача прямо пропорциональна разности температур проволоки и воздуха.
Свинцовая проволока диаметром d плавится при длительном пропускании тока I1, При каком токе расплавится проволока диаметром 2d? Потери теплоты проволокой в обоих случаях считать пропорциональными поверхности проволоки.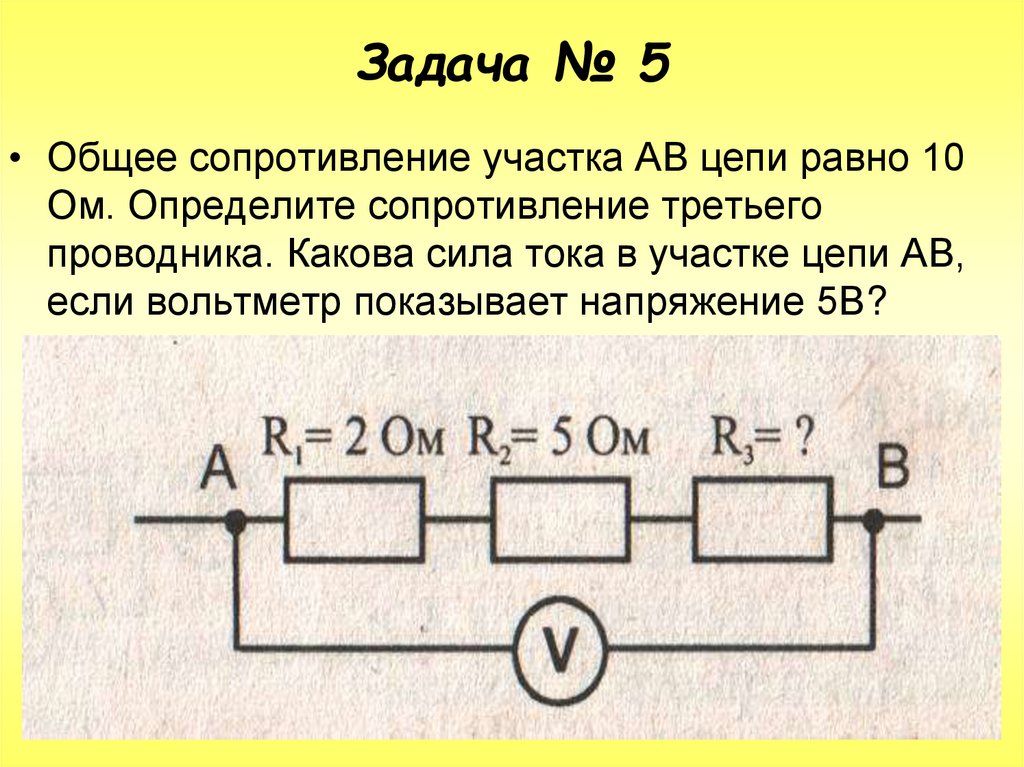
Какое количество теплоты выделится в схеме после размыкания ключа K? Параметры схемы показаны на рисунке.
Электрон влетает в однородное магнитное поле, направление которого перпендикулярно к направлению его движения. Скорость электрона v = 4·107 м/с. Индукция магнитного поля B = 1 мТл. Найти тангенциальное aτ и нормальное an ускорения электрона в магнитном поле.
В цепи, изображенной на рисунке тепловая мощность, выделяемая во внешней цепи, одинакова при замкнутом и разомкнутом ключе K. Определите внутреннее сопротивление батареи r, если R1 = 12 Ом, R2 = 4 Ом.
Две частицы, имеющие отношение зарядов q1/q2 = 2 и отношение масс m1/m2 = 4, влетели в однородное магнитное поле перпендикулярно его линиям индукции и движутся по окружностям с отношением радиусов R1/R2 = 2. Определите отношение кинетических энергий W1/W2 этих частиц.
Колебательный контур состоит из конденсатора емкостью С = 400 пФ и катушки индуктивностью L = 10 мГн. Найти амплитуду колебаний силы тока Im, если амплитуда колебаний напряжения Um = 500 В.
Через какое время (в долях периода t/T) на конденсаторе колебательного контура впервые будет заряд, равный половине амплитудного значения? (зависимость заряда на конденсаторе от времени задана уравнением q = qm cos ω0t)
Сколько электронов вылетает с поверхности катода за 1 с при токе насыщения 12 мА? q = 1,6·10-19 Кл.
Сила тока в цепи электрической плитки равна 1,4 А. Какой электрический заряд проходит через поперечное сечение ее спирали за 10 мин?
Определите площадь поперечного сечения и длину медного проводника, если его сопротивление 0,2 Ом, а масса 0,2 кг. Плотность меди 8900 кг/м3, удельное сопротивление 1,7*10-8 Ом*м.
На рисунке участка цепи АВ напряжение 12 В, сопротивления R1 и R2 равны соответственно 2 Ом и 23 Ом, сопротивление вольтметра 125 Ом. Определите показания вольтметра.
Определить величину сопротивления шунта амперметра для расширения пределов измерения тока с 10 миллиампер(I1) до 10 Ампер(I). Внутреннее сопротивление амперметра равно 100 Ом(R1).
Какая тепловая мощность выделяется в резисторе R1 в цепи, схема которой показана на рисунке, если амперметр показывает силу постоянного тока I = 0,4 А? Значения сопротивлений резисторов: R1 = 5 Ом, R2 = 30 Ом, R3 = 10 Ом, R4 = 20 Ом. Амперметр считать идеальным.
Два одинаковых металлических маленьких шарика заряжены так, что заряд одного из них в 5 раз больше заряда другого. Шарики привели в соприкосновение и раздвинули на прежнее расстояние. Во сколько раз изменилась по модулю сила их взаимодействия, если: а) шарики заряжены одноименно; б) шарики заряжены разноименно?
Длина цилиндрического медного провода в 10 раз больше, чем длина алюминиевого, а их массы одинаковы. Найдите отношение сопротивлений этих проводников.
Проволочное кольцо включено в цепь, по которой проходит ток 9 A. Контакты делят длину кольца в отношении 1:2. При этом в кольце выделяется мощность 108 Вт. Какая мощность при той же силе тока во внешней цепи будет выделяться в кольце, если контакты разместить по диаметру кольца?
Два шарика одинакового объёма, обладающие массой 0,6 ∙ 10 -3 г каждый, подвешены на шелковых нитях длиной 0,4 м так, что их поверхности соприкасаются. Угол, на который разошлись нити при сообщении шарикам одинаковых зарядов, равен 60°. Найти величину зарядов и силу электрического отталкивания.
Угол, на который разошлись нити при сообщении шарикам одинаковых зарядов, равен 60°. Найти величину зарядов и силу электрического отталкивания.
Два одинаковых шарика, заряженные один отрицательным зарядом—1,5 мкКл, другой положительным 25 мкКл, приводят в соприкосновение и вновь раздвигают на расстояние 5 см. Определите заряд каждого шарика после соприкосновения и силу их взаимодействия.
Разделы: Физика
Цели: обучающая : систематизировать знания и умения учащихся решать задачи ан расчет эквивалентных сопротивлений с помощью моделей, каркасов и т.д.
Развивающая: развитие навыков логического мышления абстрактного мышления, умений заменять схемы эквивалентности, упрощать расчет схем.
Воспитательная: воспитание чувства ответственности, самостоятельности, необходимости навыков приобретенных на уроке в будущем
Оборудование: проволочный каркас куба, тетраэдера, сетки бесконечной цепочки сопротивлений.
ХОД УРОКА
Актуализация:
1. Учитель: “Вспомним последовательное
соединение сопротивлений”.
Учитель: “Вспомним последовательное
соединение сопротивлений”.
Учащиеся на доске зарисовывают схему.
и записывают
U об =U 1 +U 2
Y об =Y 1 =Y 2
Учитель: вспомним параллельное соединение сопротивлений.
Учащийся на доске зарисовывает элементарную схему:
Y об =Y 1 =Y 2
; для для n равных
Учитель: А теперь будем решать задачи на расчет эквивалентного сопротивления участок цепи представлен в виде геометрической фигуры, либо металлической сетки.
Задача № 1
Проволочный каркас в виде куба, рёбра которого
представляют равные сопротивления R. Рассчитать
эквивалентное сопротивление между точками А и В.
Чтобы рассчитать эквивалентное сопротивление
данного каркаса необходимо заменить
эквивалентной схемой. Точки 1, 2, 3 имеют
одинаковый потенциал, их можно соединить в один
узел. А точки (вершины) куба 4, 5, 6 можно соединить в
другой узел по той же причине. Учащиеся имеют на
каждой парте такую модель. После выполнения
описанных действий зарисовывают эквивалентную
схему.
После выполнения
описанных действий зарисовывают эквивалентную
схему.
На участке АС эквивалентное сопротивление ; на СD ; на DB ; и окончательно для последовательного соединения сопротивлений имеем:
По тому же принципу потенциалы точек А и 6 равны, В и 3 равны. Учащиеся совмещают эти точки на своей модели и получают эквивалентную схему:
Расчёт эквивалентного сопротивления такой цепи прост
Задача № 3
Эта же модель куба, с включением в цепь между точками 2 и В. Учащиеся соединяют точки с равными потенциалами 1 и 3; 6 и 4. Тогда схема будет выглядеть так:
Точки 1,3 и 6,4 имеют равные потенциалы, и ток по сопротивлениям между этими точками не потечёт и схема упрощается до вида; эквивалентное сопротивление которой рассчитывается так:
Задача № 4
Равносторонняя треугольная пирамида, ребро которой имеет сопротивление R. Рассчитать эквивалентное сопротивление при включении в цепь.
Точки 3 и 4 имеют равный потенциал, поэтому по
ребру 3,4 ток не потечёт. Учащиеся убирают его.
Учащиеся убирают его.
Тогда схема будет выглядеть так:
Эквивалентное сопротивление рассчитывается так:
Задача № 5
Металлическая сетка с сопротивлением звена равном R. Рассчитать эквивалентное сопротивление между точками 1 и 2.
В точке 0 можно звенья отделить, тогда схема будет иметь вид:
— сопротивление одной половины симметричной по 1-2 точкам. Параллельно ей такая же ветвь, поэтому
Задача № 6
Звезда состоит из 5-и равносторонних треугольников, сопротивление каждого.
Между точками 1 и 2 один треугольник параллелен четырём, последовательно соединенным между собой
Имея опыт расчёта эквивалентного сопротивления проволочных каркасов можно приступить к расчету сопротивлений цепи, содержащий бесконечное число сопротивлений. Например:
Если отделить звено
от общей схемы, то схема не изменится, тогда можно представить ввиде
или ,
решаем данное уравнение относительно R экв.
Итог урока: мы научились абстрактно представлять схемы участков цепи, заменять их эквивалентными схемами, которые позволяют легко рассчитать эквивалентное сопротивление.
Указание: Эту модель представить в виде:
Учебник по физике: комбинированные цепи
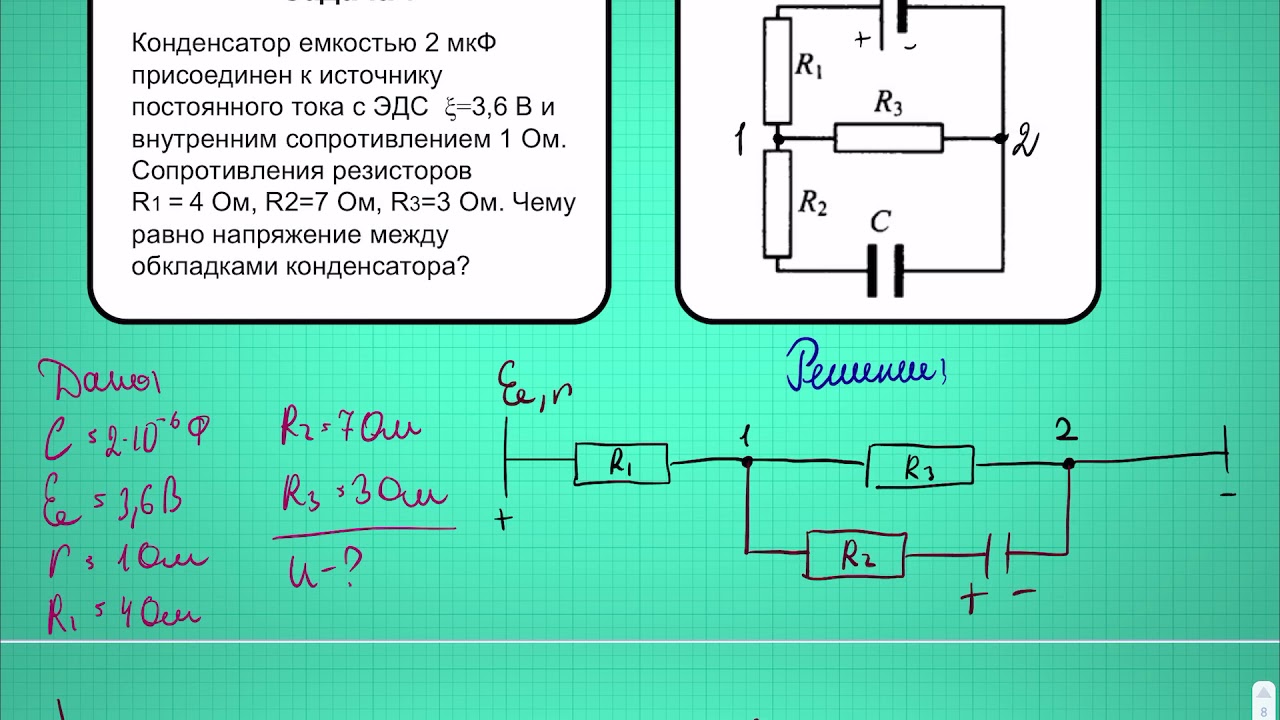
Ранее в уроке 4 упоминалось, что существует два различных способа соединения двух или более электрических устройств в цепь. Они могут быть соединены посредством последовательных соединений или посредством параллельных соединений. Когда все устройства в цепи соединены последовательным соединением, тогда цепь называется последовательной цепью. Когда все устройства в цепи соединены параллельными соединениями, тогда цепь называется параллельной цепью. Третий тип схемы предполагает двойное использование последовательных и параллельных соединений в цепи; такие схемы называются составными схемами или комбинированными схемами. Схема, изображенная справа, является примером использования как последовательных, так и параллельных соединений в одной и той же цепи. В этом случае лампочки А и В соединены параллельным соединением, а лампочки С и D — последовательно. это пример комбинированная схема .
В этом случае лампочки А и В соединены параллельным соединением, а лампочки С и D — последовательно. это пример комбинированная схема .
При анализе комбинированных цепей крайне важно хорошо понимать концепции, относящиеся как к последовательным, так и к параллельным цепям. Поскольку в комбинированных схемах используются оба типа соединений, понятия, связанные с обоими типами схем, применяются к соответствующим частям схемы. Основные понятия, связанные с последовательными и параллельными цепями, представлены в таблице ниже.
 .. .. |
|
Каждое из приведенных выше понятий имеет математическое выражение. Сочетание математических выражений вышеприведенных понятий с уравнением закона Ома (ΔV = I • R) позволяет провести полный анализ комбинированной цепи.
Анализ комбинированных цепей Основная стратегия анализа комбинированных цепей включает использование значения эквивалентного сопротивления для параллельных ветвей для преобразования комбинированной цепи в последовательную. После преобразования в последовательную цепь анализ можно проводить обычным образом.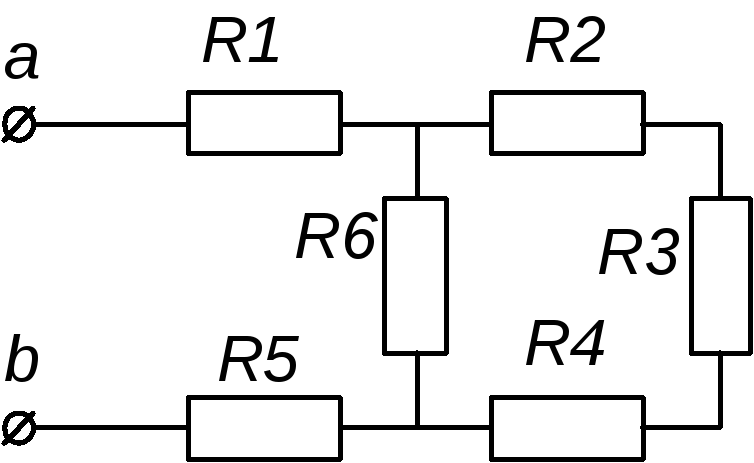 Ранее в Уроке 4 метод определения эквивалентного сопротивления параллельных ветвей равен, тогда общее или эквивалентное сопротивление этих ветвей равно сопротивлению одной ветви, деленному на количество ветвей.
Ранее в Уроке 4 метод определения эквивалентного сопротивления параллельных ветвей равен, тогда общее или эквивалентное сопротивление этих ветвей равно сопротивлению одной ветви, деленному на количество ветвей.
Этот метод согласуется с формулой
где R 1 , R 2 и R 3 — значения сопротивления отдельных резисторов, соединенных параллельно. Если два или более резистора, находящиеся в параллельных ветвях, не имеют одинакового сопротивления, то необходимо использовать приведенную выше формулу. Пример этого метода был представлен в предыдущем разделе урока 4.
Применяя понимание эквивалентного сопротивления параллельных ветвей к комбинированной цепи, комбинированную цепь можно преобразовать в последовательную цепь. Затем понимание эквивалентного сопротивления последовательной цепи можно использовать для определения полного сопротивления цепи. Рассмотрим следующие диаграммы ниже. На схеме А представлена комбинированная схема с резисторами R 2 и R 3 , размещенными в параллельных ветвях. Два резистора по 4 Ом, соединенные параллельно, эквивалентны сопротивлению 2 Ом. Таким образом, две ветви можно заменить одним резистором с сопротивлением 2 Ом. Это показано на диаграмме B. Теперь, когда все резисторы соединены последовательно, можно использовать формулу для полного сопротивления последовательных резисторов для определения общего сопротивления этой цепи: Формула для последовательного сопротивления равна
Рассмотрим следующие диаграммы ниже. На схеме А представлена комбинированная схема с резисторами R 2 и R 3 , размещенными в параллельных ветвях. Два резистора по 4 Ом, соединенные параллельно, эквивалентны сопротивлению 2 Ом. Таким образом, две ветви можно заменить одним резистором с сопротивлением 2 Ом. Это показано на диаграмме B. Теперь, когда все резисторы соединены последовательно, можно использовать формулу для полного сопротивления последовательных резисторов для определения общего сопротивления этой цепи: Формула для последовательного сопротивления равна
Таким образом, на диаграмме B полное сопротивление цепи равно 10 Ом.
После определения общего сопротивления цепи анализ продолжается с использованием закона Ома и значений напряжения и сопротивления для определения значений тока в различных местах. Весь метод проиллюстрирован ниже двумя примерами.
Весь метод проиллюстрирован ниже двумя примерами.
Первый пример — самый простой случай — параллельно расположенные резисторы имеют одинаковое сопротивление. Целью анализа является определение тока и падения напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Два последовательных резистора на 8 Ом эквивалентны одному резистору на 4 Ом. Таким образом, два ответвленных резистора (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 4 Ом. Этот резистор на 4 Ом включен последовательно с R 1 и R 4 . Таким образом, общее сопротивление равно
Ом.0012 R to = R 1 + 4 Ом + R 4 = 5 Ом + 4 Ом + 6 ОмR to = 15 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи.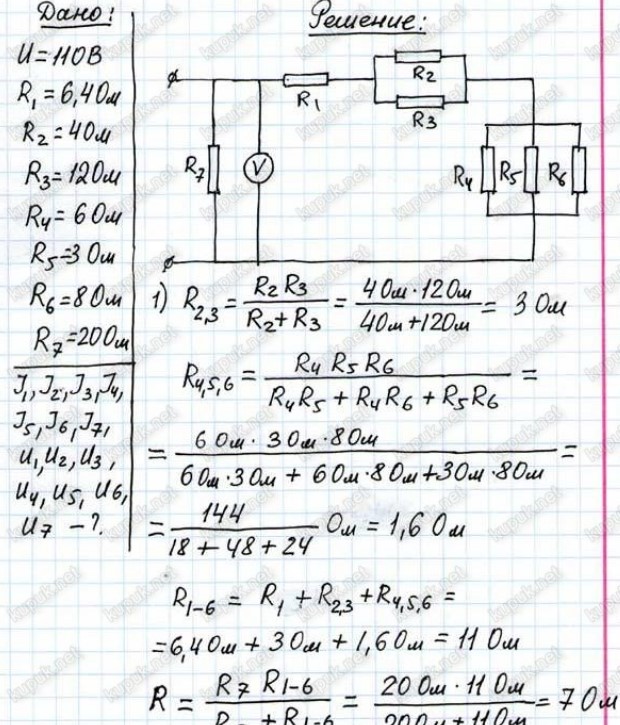 При этом необходимо будет использовать общее сопротивление и общее напряжение (или напряжение батареи).
При этом необходимо будет использовать общее сопротивление и общее напряжение (или напряжение батареи).
я до = 4 ампера
Расчет тока 4 А представляет собой ток в месте расположения батареи. Но резисторы R 1 и R 4 включены последовательно и ток в последовательно соединенных резисторах везде одинаков. Таким образом,
Для параллельных ветвей сумма токов в каждой отдельной ветви равна току вне ветвей. Таким образом, я 2 + I 3 должен равняться 4 Ампер. Существует бесконечное число возможных значений I 2 и I 3 , которые удовлетворяют этому уравнению. Поскольку значения сопротивлений равны, значения тока в этих двух резисторах также равны. Следовательно, ток в резисторах 2 и 3 равен 2 Ампер.
Теперь, когда ток в каждом отдельном резисторе известен, уравнение закона Ома (ΔV = I • R) можно использовать для определения падения напряжения на каждый резистор. Эти расчеты показаны ниже.
ΔV 1 = I 1 • R 1 = (4 А) • (5 Ом)ΔV 1 = 20 ВΔV 2 = I 2 • R 2 = (2 А) • (8 Ом)
ΔV 2 = 16 ВΔV 3 = I 3 • R 3 = (2 А) • (8 Ом)
ΔV 3 = 16 ВΔV 4 = I 4 • R 4 = (4 А) • (6 Ом)
ΔV 4 = 24 В
Анализ завершен, и его результаты представлены на диаграмме ниже.
Пример 2:
Второй пример является более сложным случаем — параллельно расположенные резисторы имеют разное значение сопротивления. Цель анализа та же — определить ток на входе и падение напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Эквивалентное сопротивление резистора 4 Ом и 12 Ом, включенного параллельно, можно определить по обычной формуле для эквивалентного сопротивления параллельных ветвей: 2 + 1 / R 3 …
1 / R eq = 1 / (4 Ом) + 1 / (12 Ом)
1 / R экв. = 0,333 Ом -1
R экв. = 1 / (0,333 Ом -1 )
R экв. = 3,00 Ом
На основании этого расчета можно сказать, что два ответвленных резистора (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 3 Ом.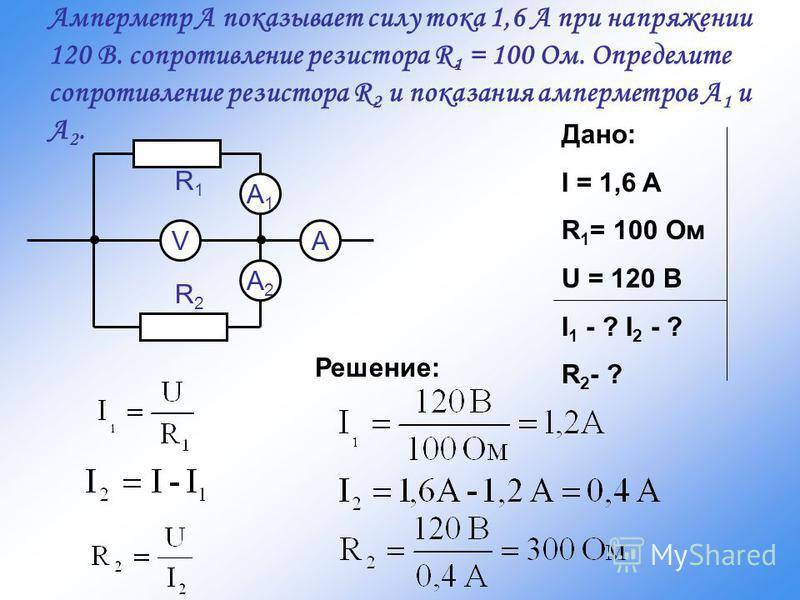 Этот резистор на 3 Ом включен последовательно с R 1 и R 4 . Таким образом, общее сопротивление равно
Этот резистор на 3 Ом включен последовательно с R 1 и R 4 . Таким образом, общее сопротивление равно
R до = 16 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи. При этом необходимо будет использовать общее сопротивление и общее напряжение (или напряжение батареи).
I to = 1,5 А
Расчет тока 1,5 А представляет собой ток в месте расположения батареи. Но резисторы R 1 и R 4 включены последовательно и ток в последовательно соединенных резисторах везде одинаков. Таким образом,
Для параллельных ветвей сумма токов в каждой отдельной ветви равна току вне ветвей.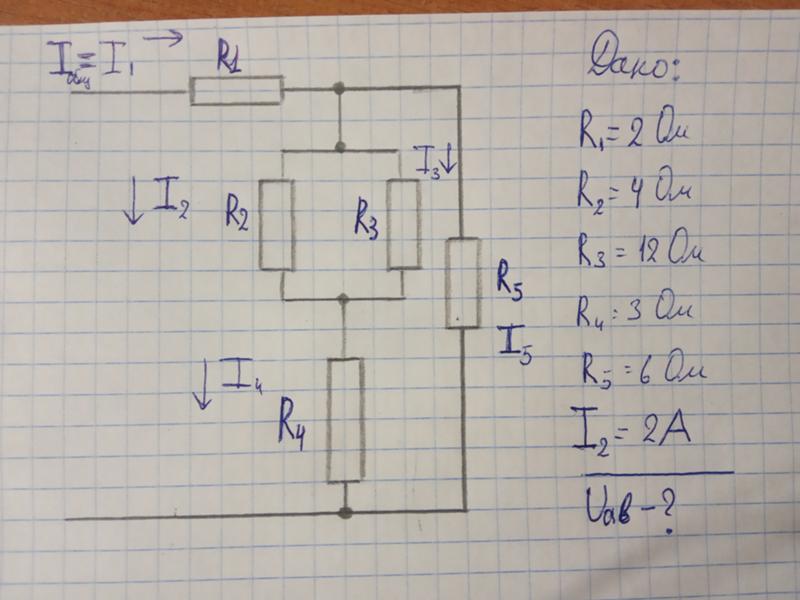 Таким образом, я 2 + I 3 должен равняться 1,5 Ампер. Существует бесконечное множество значений I 2 и I 3 , которые удовлетворяют этому уравнению. В предыдущем примере два резистора, включенных параллельно, имели одинаковое сопротивление; таким образом, ток распределялся поровну между двумя ветвями. В этом примере неравный ток в двух резисторах усложняет анализ. Ветвь с наименьшим сопротивлением будет иметь наибольший ток. Определение величины тока потребует использования уравнения закона Ома. Но чтобы его использовать, нужно сначала знать падение напряжения на ветвях. Таким образом, направление решения в этом примере будет немного отличаться от направления в более простом случае, показанном в предыдущем примере.
Таким образом, я 2 + I 3 должен равняться 1,5 Ампер. Существует бесконечное множество значений I 2 и I 3 , которые удовлетворяют этому уравнению. В предыдущем примере два резистора, включенных параллельно, имели одинаковое сопротивление; таким образом, ток распределялся поровну между двумя ветвями. В этом примере неравный ток в двух резисторах усложняет анализ. Ветвь с наименьшим сопротивлением будет иметь наибольший ток. Определение величины тока потребует использования уравнения закона Ома. Но чтобы его использовать, нужно сначала знать падение напряжения на ветвях. Таким образом, направление решения в этом примере будет немного отличаться от направления в более простом случае, показанном в предыдущем примере.
Для определения падения напряжения на параллельных ветвях сначала необходимо определить падение напряжения на двух последовательно соединенных резисторах (R 1 и R 4 ). Уравнение закона Ома (ΔV = I • R) можно использовать для определения падения напряжения на каждом резисторе.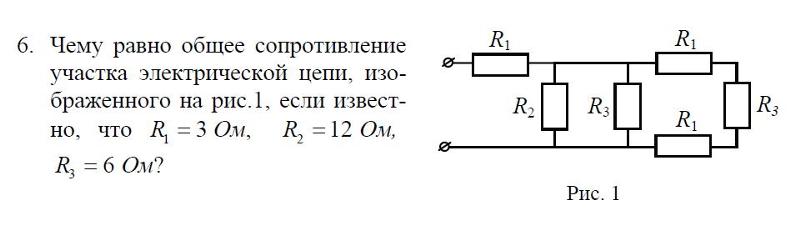 Эти расчеты показаны ниже.
Эти расчеты показаны ниже.
ΔV 1 = I 1 • R 1 = (1,5 А) • (5 Ом)ΔV 1 = 7,5 ВΔВ 4 = I 4 • R 4 = (1,5 А) • (8 Ом)
ΔV 4 = 12 В
Эта схема питается от источника 24 В. Таким образом, кумулятивное падение напряжения заряда, пересекающего петлю цепи, составляет 24 вольта. Будет падение 19,5 В (7,5 В + 12 В) в результате прохождения через два последовательно соединенных резистора (R 1 и R 4 ). Падение напряжения на ветвях должно составлять 4,5 вольта, чтобы компенсировать разницу между 24 вольтами и 19 вольтами.Падение 0,5 В на R 1 и R 4 . Таким образом,
Зная падение напряжения на параллельно включенных резисторах (R 1 и R 4 9002 6 ) позволяет использовать уравнение закона Ома ( ΔV = I • R) для определения тока в двух ветвях.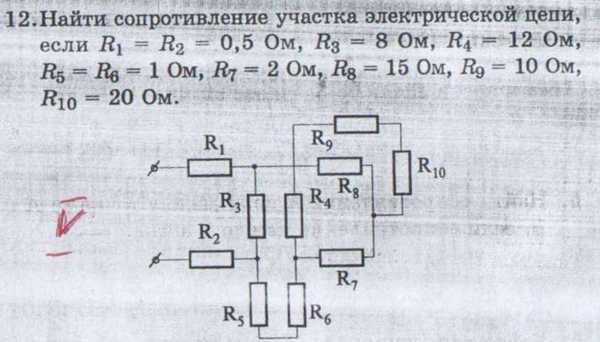
I 2 = ΔV 2 / R 2 = (4,5 В) / (4 Ом)I 2 = 1,125 АI 3 = ΔV 3 / R 3 = (4,5 В) / (12 Ом)
I 3 = 0,375 А
Анализ завершен, и его результаты представлены на диаграмме ниже.
Разработка стратегии
Два приведенных выше примера иллюстрируют эффективную концептуальную стратегию анализа комбинационных цепей. Подход требовал твердого понимания последовательностей и параллельных концепций, обсуждавшихся ранее. Такие анализы часто проводятся для решения физической задачи для заданного неизвестного. В таких ситуациях неизвестность обычно варьируется от проблемы к проблеме. В одной задаче номиналы резисторов могут быть заданы, а ток во всех ветвях неизвестен. В другой задаче можно указать ток в батарее и несколько номиналов резисторов, а неизвестная величина станет сопротивлением одного из резисторов.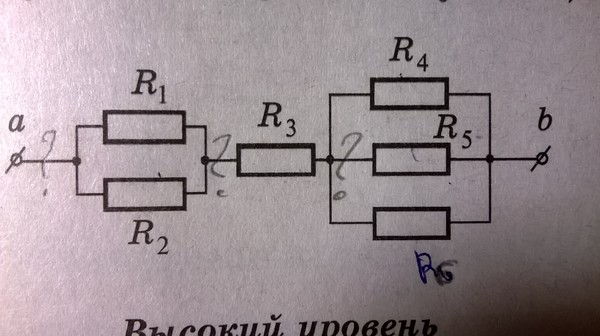 Различные проблемные ситуации, очевидно, потребуют небольших изменений в подходах. Тем не менее, каждый подход к решению проблем будет использовать те же принципы, что и при подходе к двум вышеприведенным примерам проблем.
Различные проблемные ситуации, очевидно, потребуют небольших изменений в подходах. Тем не менее, каждый подход к решению проблем будет использовать те же принципы, что и при подходе к двум вышеприведенным примерам проблем.
Начинающему ученику предлагаются следующие рекомендации по решению задач комбинированной схемы:
- Если схематическая диаграмма не предоставлена, найдите время, чтобы построить ее. Используйте схематические символы, подобные показанным в примере выше.
- Приступая к проблеме, связанной с комбинированной схемой, найдите время, чтобы организовать себя, записывая известные значения и приравнивая их к символу, такому как I tot , I 1 , R 3 , ΔV 2 и т. д. Схема организации, использованная в двух приведенных выше примерах, является эффективной отправной точкой.
- Знать и использовать соответствующие формулы эквивалентного сопротивления последовательно и параллельно соединенных резисторов.
 Использование неправильных формул гарантирует неудачу.
Использование неправильных формул гарантирует неудачу. - Превратите комбинированную цепь в строго последовательную, заменив (мысленно) параллельную часть одним резистором, сопротивление которого равно эквивалентному сопротивлению параллельной части.
- Используйте уравнение закона Ома (ΔV = I • R) часто и надлежащим образом. Большинство ответов будут определены с помощью этого уравнения. При его использовании важно подставлять в уравнение соответствующие значения. Например, при расчете I 2 важно подставить в уравнение значения ΔV 2 и R 2 .
Для дальнейшей практики анализа комбинированных цепей рассмотрите возможность анализа проблем в разделе «Проверьте свое понимание» ниже.
Мы хотели бы предложить … Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom.
 Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного конструктора цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Конструктор цепей постоянного тока предоставляет учащимся набор для создания виртуальных схем. Вы можете легко перетаскивать источники напряжения, резисторы и провода на рабочее место, располагать и соединять их так, как пожелаете. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Прикосновение к резистору или источнику напряжения позволяет изменить сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если только вы не используете его в ванной).
Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного конструктора цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Конструктор цепей постоянного тока предоставляет учащимся набор для создания виртуальных схем. Вы можете легко перетаскивать источники напряжения, резисторы и провода на рабочее место, располагать и соединять их так, как пожелаете. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Прикосновение к резистору или источнику напряжения позволяет изменить сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если только вы не используете его в ванной).
Посетите: DC Circuit Builder
1. Комбинированная схема показана на схеме справа. Используя схему, ответьте на следующие вопросы.
а. Ток в точке А равен _____ (больше, равно, меньше) току в точке В.
b. Ток в точке B равен _____ (больше, равно, меньше) току в точке E.
в. Ток в точке G равен _____ (больше, равно, меньше) току в точке F.
d. Ток в точке E равен _____ (больше, равно, меньше) току в точке G.
e. Ток в точке B равен _____ (больше, равно, меньше) току в точке F.
f. Ток в точке А равен _____ (больше, равно, меньше) тока в точке L.
g. Ток в точке H равен _____ (больше, равно, меньше) току в точке I.
2. Рассмотрим комбинированную цепь на схеме справа. Используя схему, ответьте на следующие вопросы. (Считать, что падение напряжения в самих проводах пренебрежимо мало.)
а. Разность электрических потенциалов (падение напряжения) между точками B и C составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками J и K.
b. Разность электрических потенциалов (падение напряжения) между точками B и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.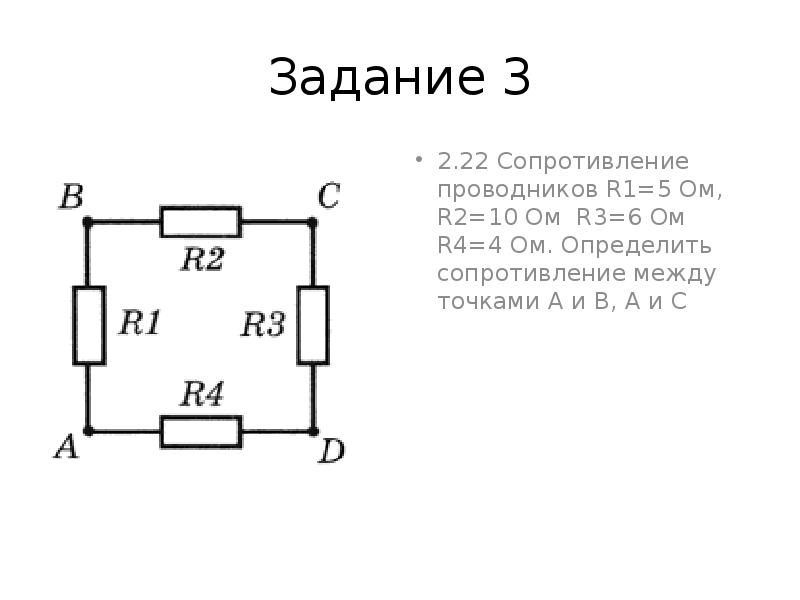
в. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками G и H.
d. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
e. Разность электрических потенциалов (падение напряжения) между точками J и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
ф. Разность электрических потенциалов между точками L и A равна _____ (больше, равно, меньше) разности электрических потенциалов (падению напряжения) между точками B и K.
3. Используйте понятие эквивалентного сопротивления, чтобы определить неизвестное сопротивление идентифицированного резистора, которое сделало бы схемы эквивалентными.
4. Проанализируйте следующую цепь и определите значения полного сопротивления, полного тока, а также падения тока и напряжения на каждом отдельном резисторе.
5. По схеме вопроса №4 определите …
а. … номинальная мощность резистора 4.б. … скорость, с которой энергия потребляется резистором 3.
Ответ: На рис. Найдите общее сопротивление…
Задача 10.1CYU: проверьте свое понимание. праздничные огни закорачивают, когда лампочка… Задача 10.3CYU: проверьте свое понимание Рассмотрим ту же разность потенциалов (V = 3,00 В), приложенную к тому же… Задача 10.4CYU: проверьте свое понимание Как бы вы использовали река и два водопада, чтобы смоделировать параллельную.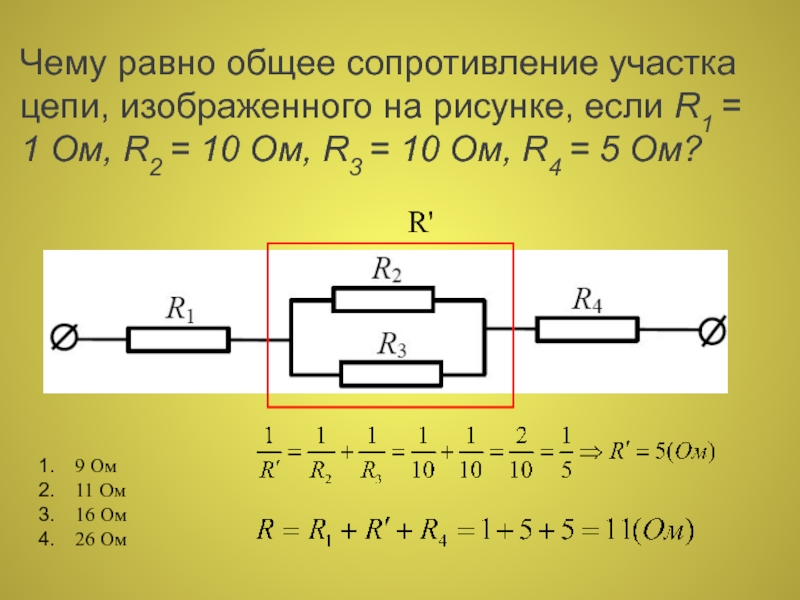 .. Задача 10.5CYU: проверьте свое понимание Рассмотрим электрические цепи в вашем доме. Назовите не менее двух из… Задача 10.6CYU: проверьте свое понимание При рассмотрении следующей схемы и подводимой и потребляемой мощности… Задача 10.7CYU: проверьте свое понимание При использовании законов Кирхгофа вам необходимо решить, какие контуры использовать и какие the… Задача 10.8CYU: проверьте свое понимание Цифровые счетчики способны определять меньшие токи, чем аналоговые счетчики… Задача 1CQ: Какое влияние окажет внутреннее сопротивление перезаряжаемой батареи на энергию, используемую для… Задача 2CQ : Батарея с внутренним сопротивлением r и ЭДС 10,00 В подключена к нагрузочному резистору R =… Задача 3CQ: Показать, что мощность, рассеиваемая нагрузочным резистором, максимальна, когда сопротивление нагрузки… Задача 4CQ: Напряжение возникает на разомкнутом переключателе. Какова мощность, рассеиваемая открытым выключателем? Задача 5CQ: Тяжесть удара током зависит от величины тока, протекающего через ваше тело.
.. Задача 10.5CYU: проверьте свое понимание Рассмотрим электрические цепи в вашем доме. Назовите не менее двух из… Задача 10.6CYU: проверьте свое понимание При рассмотрении следующей схемы и подводимой и потребляемой мощности… Задача 10.7CYU: проверьте свое понимание При использовании законов Кирхгофа вам необходимо решить, какие контуры использовать и какие the… Задача 10.8CYU: проверьте свое понимание Цифровые счетчики способны определять меньшие токи, чем аналоговые счетчики… Задача 1CQ: Какое влияние окажет внутреннее сопротивление перезаряжаемой батареи на энергию, используемую для… Задача 2CQ : Батарея с внутренним сопротивлением r и ЭДС 10,00 В подключена к нагрузочному резистору R =… Задача 3CQ: Показать, что мощность, рассеиваемая нагрузочным резистором, максимальна, когда сопротивление нагрузки… Задача 4CQ: Напряжение возникает на разомкнутом переключателе. Какова мощность, рассеиваемая открытым выключателем? Задача 5CQ: Тяжесть удара током зависит от величины тока, протекающего через ваше тело.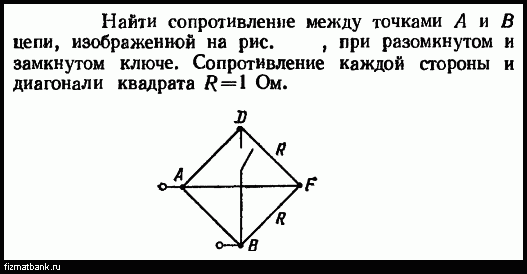 Вы бы предпочли… Задача 6CQ: Предположим, вы выполняете лабораторную работу по физике, в которой вас просят включить резистор в цепь, но все… Задача 7CQ: Некоторые лампочки имеют три уровня мощности (не считая нуля), полученные из нескольких нитей… Задача 8CQ: Могут ли все токи, входящие в соединение, показанное ниже, быть положительными? Объясните. Проблема 9CQ: Рассмотрим схему, показанную ниже. Требуется ли для анализа цепи метод Кирхгофа или… Задача 10CQ: Всегда ли батареи в цепи подают питание в цепь или они могут поглощать энергию в цепи?… Задача 11CQ: Каковы преимущества и недостатки последовательного соединения аккумуляторов? Параллельно? Задача 12CQ: Полуприцепы или грузовики используют четыре больших 12-вольтовых аккумулятора. Для пусковой системы требуется 24 В, в то время как в обычном режиме… Задача 13CQ: Что произойдет, если вы подключите вольтметр последовательно с проверяемым компонентом? Задача 14CQ: Какова основная операция омметра при измерении сопротивления? Задача 15CQ : Почему бы вам не подключить амперметр непосредственно к источнику напряжения, как показано ниже? Задача 16CQ: Батарея, переключатель, конденсатор и лампа соединены последовательно.
Вы бы предпочли… Задача 6CQ: Предположим, вы выполняете лабораторную работу по физике, в которой вас просят включить резистор в цепь, но все… Задача 7CQ: Некоторые лампочки имеют три уровня мощности (не считая нуля), полученные из нескольких нитей… Задача 8CQ: Могут ли все токи, входящие в соединение, показанное ниже, быть положительными? Объясните. Проблема 9CQ: Рассмотрим схему, показанную ниже. Требуется ли для анализа цепи метод Кирхгофа или… Задача 10CQ: Всегда ли батареи в цепи подают питание в цепь или они могут поглощать энергию в цепи?… Задача 11CQ: Каковы преимущества и недостатки последовательного соединения аккумуляторов? Параллельно? Задача 12CQ: Полуприцепы или грузовики используют четыре больших 12-вольтовых аккумулятора. Для пусковой системы требуется 24 В, в то время как в обычном режиме… Задача 13CQ: Что произойдет, если вы подключите вольтметр последовательно с проверяемым компонентом? Задача 14CQ: Какова основная операция омметра при измерении сопротивления? Задача 15CQ : Почему бы вам не подключить амперметр непосредственно к источнику напряжения, как показано ниже? Задача 16CQ: Батарея, переключатель, конденсатор и лампа соединены последовательно. Опишите, что происходит с лампой… Задача 17CQ: При измерении ЭКГ важно измерять колебания напряжения в течение короткого промежутка времени… Задача 18CQ: Почему короткое замыкание не обязательно представляет опасность поражения электрическим током? Задача 19CQ: Нам часто советуют не щелкать электрическими выключателями мокрыми руками, сначала высушить руки. Мы также… Проблема 20P: Автомобильный аккумулятор с ЭДС 12 В и внутренним сопротивлением 0,050 заряжается током… Проблема 21P: Наклейка на радиоприемнике с батарейным питанием рекомендует использовать перезаряжаемый аккумулятор. никель-кадмиевый элемент… Задача 22P: Автомобильный стартер имеет эквивалентное сопротивление 0,0500 и питается от сети 12,0 В… Задача 23P: (a) Каково внутреннее сопротивление источника напряжения, если его потенциал на клеммах падает на 2,00 В… Задача 24P: Человек с сопротивлением тела между руками 10,0 кОм случайно захватывает клеммы… Задача 25P: Автомобильный аккумулятор с ЭДС 12,0 В имеет напряжение на клеммах 16,0 В при зарядке ток .
Опишите, что происходит с лампой… Задача 17CQ: При измерении ЭКГ важно измерять колебания напряжения в течение короткого промежутка времени… Задача 18CQ: Почему короткое замыкание не обязательно представляет опасность поражения электрическим током? Задача 19CQ: Нам часто советуют не щелкать электрическими выключателями мокрыми руками, сначала высушить руки. Мы также… Проблема 20P: Автомобильный аккумулятор с ЭДС 12 В и внутренним сопротивлением 0,050 заряжается током… Проблема 21P: Наклейка на радиоприемнике с батарейным питанием рекомендует использовать перезаряжаемый аккумулятор. никель-кадмиевый элемент… Задача 22P: Автомобильный стартер имеет эквивалентное сопротивление 0,0500 и питается от сети 12,0 В… Задача 23P: (a) Каково внутреннее сопротивление источника напряжения, если его потенциал на клеммах падает на 2,00 В… Задача 24P: Человек с сопротивлением тела между руками 10,0 кОм случайно захватывает клеммы… Задача 25P: Автомобильный аккумулятор с ЭДС 12,0 В имеет напряжение на клеммах 16,0 В при зарядке ток .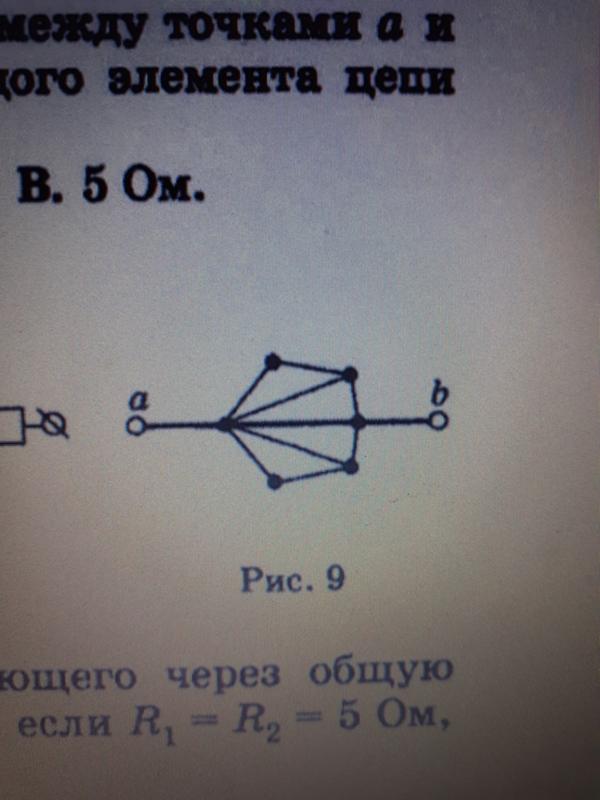 .. Задача 26P: (a) Каково сопротивление последовательно соединенных резисторов 1,00102, 2,50k и 4,00k? (b) В… Задача 27P: Какое наибольшее и самое маленькое сопротивления можно получить, соединив 36,0, 50,0 и… Задача 28P: Тостер мощностью 1800 Вт, динамик мощностью 1400 Вт и в эту же розетку включена лампа мощностью 75 Вт с предохранителем на 15 А… Задача 29P: Фара вашего автомобиля мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно соединены параллельно в 12,0-В… Задача 30P: (a) Учитывая аккумуляторную батарею на 48,0 В и резисторы на 24,0 и 96,0, найдите ток через кристалл и мощность для каждого при… Задача 31P: Ссылаясь на пример объединения последовательных и параллельных цепей и рисунок 10.16, рассчитайте в… Задача 32P: Ссылаясь на рисунок 10.16, (a) Вычислите P3 и обратите внимание, как оно сравнивается с P3, найденным в первом два… Задача 33P: Обратитесь к рисунку 10.17 и обсуждению затемнения света при включении тяжелого электроприбора. (a)… Задача 34P: Покажите, что если два резистора R1 и R2 объединены и один из них намного больше другого (R1R2) (a).
.. Задача 26P: (a) Каково сопротивление последовательно соединенных резисторов 1,00102, 2,50k и 4,00k? (b) В… Задача 27P: Какое наибольшее и самое маленькое сопротивления можно получить, соединив 36,0, 50,0 и… Задача 28P: Тостер мощностью 1800 Вт, динамик мощностью 1400 Вт и в эту же розетку включена лампа мощностью 75 Вт с предохранителем на 15 А… Задача 29P: Фара вашего автомобиля мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно соединены параллельно в 12,0-В… Задача 30P: (a) Учитывая аккумуляторную батарею на 48,0 В и резисторы на 24,0 и 96,0, найдите ток через кристалл и мощность для каждого при… Задача 31P: Ссылаясь на пример объединения последовательных и параллельных цепей и рисунок 10.16, рассчитайте в… Задача 32P: Ссылаясь на рисунок 10.16, (a) Вычислите P3 и обратите внимание, как оно сравнивается с P3, найденным в первом два… Задача 33P: Обратитесь к рисунку 10.17 и обсуждению затемнения света при включении тяжелого электроприбора. (a)… Задача 34P: Покажите, что если два резистора R1 и R2 объединены и один из них намного больше другого (R1R2) (a).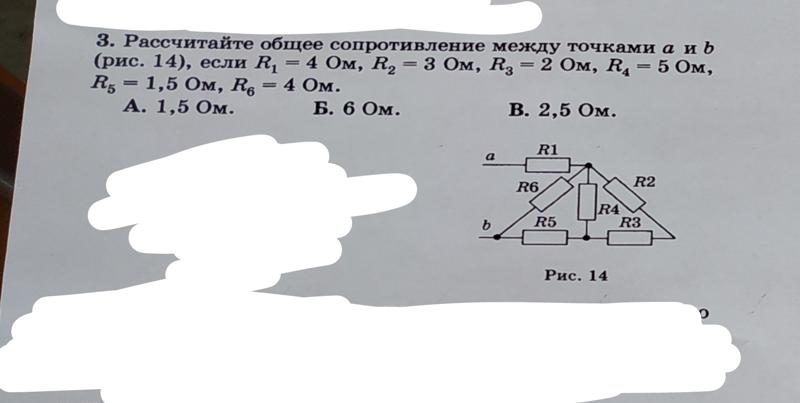 .. Задача 35P: Рассмотрим схему, показанную ниже. Напряжение на клеммах батареи V = 18,00 В. (a) Найдите… Задача 36P: Рассмотрите схему, показанную ниже. (a) Найдите напряжение на каждом резисторе. (b) Какова мощность… Задача 37P: Рассмотрите цепи, показанные ниже, (a) Каков ток через каждый резистор в части (a)? (b)… Задача 38P: Рассмотрим схему, показанную ниже. Найдите V1, I2 и I3. Задача 39.П: Рассмотрим схему, показанную ниже. Найдите V1, V2 и R4. Задача 40P. Рассмотрим схему, показанную ниже. Найдите I1, I2 и I3. Задача 41P: Рассмотрите схему, показанную ниже: (a) I1, I2, I3, I4 и I5 (b) Найдите мощность, обеспечиваемую напряжением… Задача 42P: Рассмотрим схему, показанную ниже. Напишите уравнения трех петель для показанных петель. Задача 43P: Рассмотрим цепь, показанную ниже. Напишите уравнения для трех токов через R и V. Задача 44P: Рассмотрим цепь, показанную в предыдущей задаче. Напишите уравнения для мощности, подаваемой… Задача 45P: Детская электронная игрушка питается от трех щелочных элементов на 1,58 В, имеющих внутреннее сопротивление.
.. Задача 35P: Рассмотрим схему, показанную ниже. Напряжение на клеммах батареи V = 18,00 В. (a) Найдите… Задача 36P: Рассмотрите схему, показанную ниже. (a) Найдите напряжение на каждом резисторе. (b) Какова мощность… Задача 37P: Рассмотрите цепи, показанные ниже, (a) Каков ток через каждый резистор в части (a)? (b)… Задача 38P: Рассмотрим схему, показанную ниже. Найдите V1, I2 и I3. Задача 39.П: Рассмотрим схему, показанную ниже. Найдите V1, V2 и R4. Задача 40P. Рассмотрим схему, показанную ниже. Найдите I1, I2 и I3. Задача 41P: Рассмотрите схему, показанную ниже: (a) I1, I2, I3, I4 и I5 (b) Найдите мощность, обеспечиваемую напряжением… Задача 42P: Рассмотрим схему, показанную ниже. Напишите уравнения трех петель для показанных петель. Задача 43P: Рассмотрим цепь, показанную ниже. Напишите уравнения для трех токов через R и V. Задача 44P: Рассмотрим цепь, показанную в предыдущей задаче. Напишите уравнения для мощности, подаваемой… Задача 45P: Детская электронная игрушка питается от трех щелочных элементов на 1,58 В, имеющих внутреннее сопротивление. .. Задача 46P: Примените правило соединения к соединению b, показанному ниже. Можно ли получить какую-либо новую информацию, применяя… Задача 47P: Примените правило цикла к Loop afedcba в предыдущей задаче. Задача 48P: Предположим, вы измеряете напряжение на клеммах щелочного элемента на 1,585 В, имеющего внутреннее сопротивление… Задача 49P: Таймер в системе прерывистого режима работы стеклоочистителей автомобиля основан на постоянной времени RC и… Задача 50P: Кардиостимулятор срабатывает 72 раза в минуту, каждый раз, когда заряжается конденсатор емкостью 25,0 нФ (аккумулятором в .. .Задача 51P: Продолжительность фотовспышки связана с постоянной времени RC, которая составляет 0,100F для… Задача 52P: Конденсаторы емкостью 2,00 и 7,50F могут быть соединены последовательно или параллельно, как и конденсатор емкостью 25,0F. — и 100 кОм… Задача 53P: Резистор 500 Ом, незаряженный конденсатор 1,50 Ф и ЭДС 6,16 В соединены последовательно, (a) Что такое… Задача 54P: На пациенте используется сердечный дефибриллятор имеет постоянную времени RC 10,0 мс из-за.
.. Задача 46P: Примените правило соединения к соединению b, показанному ниже. Можно ли получить какую-либо новую информацию, применяя… Задача 47P: Примените правило цикла к Loop afedcba в предыдущей задаче. Задача 48P: Предположим, вы измеряете напряжение на клеммах щелочного элемента на 1,585 В, имеющего внутреннее сопротивление… Задача 49P: Таймер в системе прерывистого режима работы стеклоочистителей автомобиля основан на постоянной времени RC и… Задача 50P: Кардиостимулятор срабатывает 72 раза в минуту, каждый раз, когда заряжается конденсатор емкостью 25,0 нФ (аккумулятором в .. .Задача 51P: Продолжительность фотовспышки связана с постоянной времени RC, которая составляет 0,100F для… Задача 52P: Конденсаторы емкостью 2,00 и 7,50F могут быть соединены последовательно или параллельно, как и конденсатор емкостью 25,0F. — и 100 кОм… Задача 53P: Резистор 500 Ом, незаряженный конденсатор 1,50 Ф и ЭДС 6,16 В соединены последовательно, (a) Что такое… Задача 54P: На пациенте используется сердечный дефибриллятор имеет постоянную времени RC 10,0 мс из-за. .. Задача 55P: Монитор ЭКГ должен иметь постоянную времени KC менее 1,00102 с, чтобы иметь возможность измерять изменения… Задача 56P: Используя точную экспоненциальную обработку, определить, сколько требуется время для первоначального заряда… Задача 57P: Если вы хотите сфотографировать пулю, летящую со скоростью 500 м/с, затем очень короткую вспышку света… Задача 58P: (a) Какова мощность рассеивается при коротком замыкании 240 В переменного тока через сопротивление 0,250 Ом. (б)… Задача 59P: Какое напряжение возникает при коротком замыкании мощностью 1,44 кВт через сопротивление 0,100 Ом? Задача 60P: Найдите ток, протекающий через человека, и определите вероятное воздействие на него, если он прикоснется к сети переменного тока 120 В… Задача 61P: Пока принимая ванну, человек касается металлического корпуса радиоприемника. Путь через человека к… Задача 62P: Человек по глупости пытается выловить горящий кусок хлеба из тостера металлическим ножом для масла и… Задача 63P: (a) Во время операции ток 20,0 А, приложенное непосредственно к сердцу, может вызвать желудочковый.
.. Задача 55P: Монитор ЭКГ должен иметь постоянную времени KC менее 1,00102 с, чтобы иметь возможность измерять изменения… Задача 56P: Используя точную экспоненциальную обработку, определить, сколько требуется время для первоначального заряда… Задача 57P: Если вы хотите сфотографировать пулю, летящую со скоростью 500 м/с, затем очень короткую вспышку света… Задача 58P: (a) Какова мощность рассеивается при коротком замыкании 240 В переменного тока через сопротивление 0,250 Ом. (б)… Задача 59P: Какое напряжение возникает при коротком замыкании мощностью 1,44 кВт через сопротивление 0,100 Ом? Задача 60P: Найдите ток, протекающий через человека, и определите вероятное воздействие на него, если он прикоснется к сети переменного тока 120 В… Задача 61P: Пока принимая ванну, человек касается металлического корпуса радиоприемника. Путь через человека к… Задача 62P: Человек по глупости пытается выловить горящий кусок хлеба из тостера металлическим ножом для масла и… Задача 63P: (a) Во время операции ток 20,0 А, приложенное непосредственно к сердцу, может вызвать желудочковый. .. Задача 64P: (a) Каково сопротивление короткого замыкания 220 В переменного тока, которое создает пиковую мощность 96,8 кВт? (b)… Задача 65P: Дефибриллятор сердца пропускает 10,0 А через туловище пациента в течение 5,00 мс, пытаясь восстановить… Проблема 66P: Короткое замыкание в шнуре прибора на 120 В имеет сопротивление 0,500 Ом. Рассчитайте повышение температуры… Задача 67AP: Цепь содержит батарею D-элемента, переключатель, резистор 20 Ом и четыре конденсатора емкостью 20 мФ… Задача 68AP: Цепь содержит батарею D-элемента, переключатель, резистор 20 Ом и три конденсатора по 20 мФ. … Проблема 69AP: Рассмотрим схему ниже. Аккумулятор имеет ЭДС = 30,00 В и внутреннее сопротивление r =… Задача 70AP: Самодельный конденсатор изготовлен из 2 листов алюминиевой фольги площадью 2,00 квадратных метра,… Задача 71AP: Учащийся делает самодельный резистор из графитового карандаша длиной 5,00 см, где графит 0,05… Задача 72AP: Довольно простая схема, показанная ниже, известна как делитель напряжения.
.. Задача 64P: (a) Каково сопротивление короткого замыкания 220 В переменного тока, которое создает пиковую мощность 96,8 кВт? (b)… Задача 65P: Дефибриллятор сердца пропускает 10,0 А через туловище пациента в течение 5,00 мс, пытаясь восстановить… Проблема 66P: Короткое замыкание в шнуре прибора на 120 В имеет сопротивление 0,500 Ом. Рассчитайте повышение температуры… Задача 67AP: Цепь содержит батарею D-элемента, переключатель, резистор 20 Ом и четыре конденсатора емкостью 20 мФ… Задача 68AP: Цепь содержит батарею D-элемента, переключатель, резистор 20 Ом и три конденсатора по 20 мФ. … Проблема 69AP: Рассмотрим схему ниже. Аккумулятор имеет ЭДС = 30,00 В и внутреннее сопротивление r =… Задача 70AP: Самодельный конденсатор изготовлен из 2 листов алюминиевой фольги площадью 2,00 квадратных метра,… Задача 71AP: Учащийся делает самодельный резистор из графитового карандаша длиной 5,00 см, где графит 0,05… Задача 72AP: Довольно простая схема, показанная ниже, известна как делитель напряжения. Символ, состоящий из трех… Задача 73AP: Три резистора на 300 Ом соединены последовательно с батареей типа ААА емкостью 3 ампер-часа. (a) Как… Задача 74AP: Рассмотрим схему, состоящую из реальной батареи с ЭДС и внутренним сопротивлением r… Задача 75AP: Рассмотрим схему, показанную ниже. Какова энергия, накопленная в каждом конденсаторе после того, как выключатель повернулся… Задача 76AP: Рассмотрим цепь, состоящую из батареи с ЭДС l и внутренним сопротивлением r, подключенной… Задача 77AP: Рассмотрим схему, показанную ниже. Показаны напряжения на клеммах батарей. (a) Найдите… Задача 78AP: Рассмотрите схему, показанную ниже. а) Чему равно напряжение на клеммах аккумулятора? (б) Что такое… Задача 79АП: Рассмотрим схему, показанную ниже. (a) Определить эквивалентное сопротивление и ток из… Задача 80AP: Два резистора, один из которых имеет сопротивление 145 Ом, соединены параллельно, чтобы получить общее… Задача 81AP: Два резистора, один из которых имеет сопротивление 900 кОм соединены последовательно, чтобы получить общее сопротивление.
Символ, состоящий из трех… Задача 73AP: Три резистора на 300 Ом соединены последовательно с батареей типа ААА емкостью 3 ампер-часа. (a) Как… Задача 74AP: Рассмотрим схему, состоящую из реальной батареи с ЭДС и внутренним сопротивлением r… Задача 75AP: Рассмотрим схему, показанную ниже. Какова энергия, накопленная в каждом конденсаторе после того, как выключатель повернулся… Задача 76AP: Рассмотрим цепь, состоящую из батареи с ЭДС l и внутренним сопротивлением r, подключенной… Задача 77AP: Рассмотрим схему, показанную ниже. Показаны напряжения на клеммах батарей. (a) Найдите… Задача 78AP: Рассмотрите схему, показанную ниже. а) Чему равно напряжение на клеммах аккумулятора? (б) Что такое… Задача 79АП: Рассмотрим схему, показанную ниже. (a) Определить эквивалентное сопротивление и ток из… Задача 80AP: Два резистора, один из которых имеет сопротивление 145 Ом, соединены параллельно, чтобы получить общее… Задача 81AP: Два резистора, один из которых имеет сопротивление 900 кОм соединены последовательно, чтобы получить общее сопротивление. .. Задача 82AP. Примените правило соединения в точке G, показанное ниже. Задача 83AP. Примените правило петли к Loop akledcba из предыдущей задачи. Задача 84AP. схема в предыдущей задаче. Явно покажите, как вы следуете… Задача 85AP: Рассмотрите схему, показанную ниже, (a) Найдите ток через каждый резистор, (b) Проверьте… Задача 86AP: Мигающая лампа в рождественской сережке основана на RC разряд конденсатора через его… Задача 87AP: Конденсатор 160F, заряженный до 450 В, разряжается через резистор 31,2k. (a) Найдите время… Задача 88CP: В некоторых фотовспышках используются лампы-вспышки, требующие высокого напряжения. Они получают высокое напряжение… Задача 89КП: Рассмотрим схему, показанную ниже. Каждая батарея имеет ЭДС 1,50 В и внутреннее сопротивление… Задача 90CP: Аналоговые счетчики используют гальванометр, который по существу состоит из катушки провода с небольшим… Задача 91CP: Аналоговые счетчики используют гальванометр, который по существу состоит из катушки провода с небольшим.
.. Задача 82AP. Примените правило соединения в точке G, показанное ниже. Задача 83AP. Примените правило петли к Loop akledcba из предыдущей задачи. Задача 84AP. схема в предыдущей задаче. Явно покажите, как вы следуете… Задача 85AP: Рассмотрите схему, показанную ниже, (a) Найдите ток через каждый резистор, (b) Проверьте… Задача 86AP: Мигающая лампа в рождественской сережке основана на RC разряд конденсатора через его… Задача 87AP: Конденсатор 160F, заряженный до 450 В, разряжается через резистор 31,2k. (a) Найдите время… Задача 88CP: В некоторых фотовспышках используются лампы-вспышки, требующие высокого напряжения. Они получают высокое напряжение… Задача 89КП: Рассмотрим схему, показанную ниже. Каждая батарея имеет ЭДС 1,50 В и внутреннее сопротивление… Задача 90CP: Аналоговые счетчики используют гальванометр, который по существу состоит из катушки провода с небольшим… Задача 91CP: Аналоговые счетчики используют гальванометр, который по существу состоит из катушки провода с небольшим.

 Найдите общее
сопротивление электрической цепи (рис. 7), если
Rx
= 2 Ом,
R2
= R3
= R4
= 3 Ом.
Найдите общее
сопротивление электрической цепи (рис. 7), если
Rx
= 2 Ом,
R2
= R3
= R4
= 3 Ом.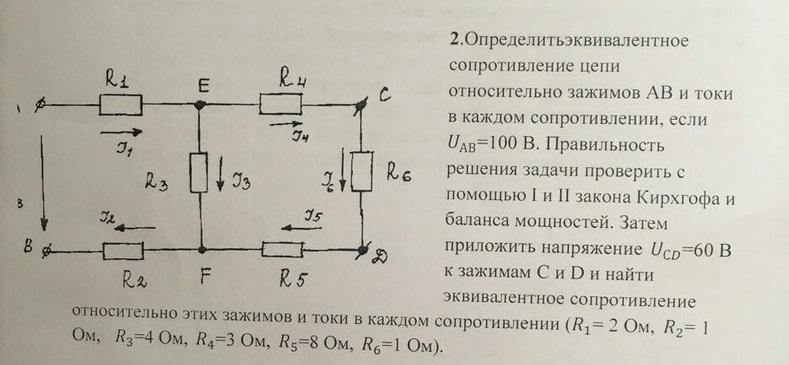 1 А. Б. 0,5
А. В. 2 А.
1 А. Б. 0,5
А. В. 2 А. Использование неправильных формул гарантирует неудачу.
Использование неправильных формул гарантирует неудачу.
Leave A Comment