Из ОГЭ на площадь прямоугольника

Площадь прямоугольника, квадрата, ромба.

1. Сто­ро­на квад­ра­та равна 10. Най­ди­те его пло­щадь.

2. Пе­ри­метр квад­ра­та равен 40. Най­ди­те пло­щадь квад­ра­та.

3.  Из квад­ра­та вы­ре­за­ли пря­мо­уголь­ник (см. ри­су­нок). Най­ди­те пло­щадь по­лу­чив­шей­ся фи­гу­ры.

4.  Пе­ри­метр квад­ра­та равен 160. Най­ди­те пло­щадь квад­ра­та.

5.  Най­ди­те пло­щадь квад­ра­та, если его диа­го­наль равна 1.

6.  Най­ди­те пло­щадь квад­ра­та, опи­сан­но­го во­круг окруж­но­сти ра­ди­у­са 83.

7. В пря­мо­уголь­ни­ке одна сто­ро­на равна 10, дру­гая сто­ро­на равна 12. Най­ди­те пло­щадь пря­мо­уголь­ни­ка.

ДЗ 8.  Най­ди­те пло­щадь пря­мо­уголь­ни­ка, если его пе­ри­метр равен 44 и одна сто­ро­на на 2 боль­ше дру­гой.

9.  В пря­мо­уголь­ни­ке одна сто­ро­на равна 96, а диа­го­наль равна 100. Най­ди­те пло­щадь пря­мо­уголь­ни­ка.

10.  На сто­ро­не BC пря­мо­уголь­ни­ка ABCD, у ко­то­ро­го AB = 12 и AD = 17, от­ме­че­на точка E так, что ∠EAB = 45°. Най­ди­те ED.(см.рис.)

1. Задание 18 

Найдите пло­щадь параллелограмма, изображённого на рисунке.

2. Задание 18 

Сторона ромба равна 5, а диа­го­наль равна 6. Най­ди­те площадь ромба.

3. Задание 18 

Периметр ромба равен 40, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

4. Задание 18 Периметр ромба равен 24, а синус од­но­го из углов равен .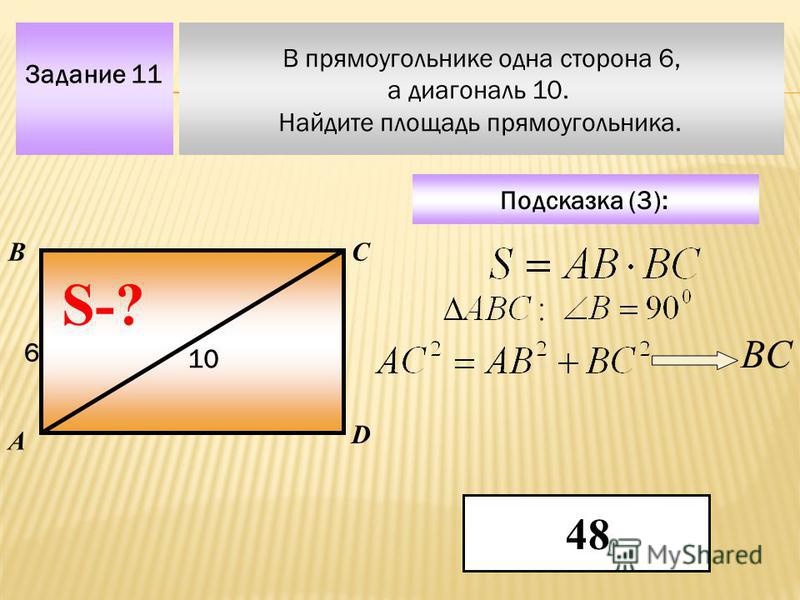 Най­ди­те площадь ромба.

5. Задание 18 Одна из сто­рон параллелограмма равна 12, а опу­щен­ная на нее вы­со­та равна 10. Най­ди­те площадь параллелограмма.

6. Задание 18  Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а один из углов — 45°. Най­ди­те площадь параллелограмма, делённую на .

7. Задание 18 Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а синус од­но­го из углов равен . Най­ди­те площадь параллелограмма.

8. Задание 18 Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а ко­си­нус одного из углов равен . Най­ди­те площадь параллелограмма.

9. Задание 18 Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а тан­генс одного из углов равен . Най­ди­те площадь параллелограмма.

10. Задание 18 № В ромбе сто­ро­на равна 10, одна из диагоналей — , а угол, ле­жа­щий напротив этой диагонали, равен 30°. Най­ди­те площадь ромба.

ДЗ 12. Задание 18 № 314870

Пло­щадь па­рал­ле­ло­грам­ма ABCD равна 56. Точка E — се­ре­ди­на сто­ро­ны CD. Най­ди­те пло­щадь тра­пе­ции AECB.

13. Задание 18

Най­ди­те пло­щадь ромба, если его диа­го­на­ли равны 14 и 6.

ДЗ14. Задание 18 

Сто­ро­на ромба равна 9, а рас­сто­я­ние от цен­тра ромба до неё равно 1. Най­ди­те пло­щадь ромба.

15. Задание 18 

Сто­ро­на ромба равна 50, а диа­го­наль равна 80. Най­ди­те пло­щадь ромба.

16. Задание 18 

Пе­ри­метр ромба равен 116, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

ДЗ 17. 

Высота BH па­рал­ле­ло­грам­ма ABCD делит его сто­ро­ну AD на от­рез­ки AH = 1 и HD = 28. Диа­го­наль параллелограмма BD равна 53. Най­ди­те площадь параллелограмма.

ДЗ 18. Задание

Высота BH ромба ABCD делит его сто­ро­ну AD на от­рез­ки AH = 5 и HD = 8. Най­ди­те площадь ромба.

19. Задание 18

Площадь ромба равна 54, а пе­ри­метр равен 36. Най­ди­те вы­со­ту ромба.

20. Задание 18 

Высота  ромба  делит его сторону  на отрезки  и . Найдите площадь ромба.

Площадь фигур — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

«Площадь
фигур»
Что такое площадь:
определение
Площадь
фигуры
плоскости,
ограниченная
кривой
или
—
ломаной
это
часть
замкнутой
линией.
Обозначается эта величина буквой S.
У разных фигур разные формулы для
нахождения их площади.

Прямоугольник
Площадь прямоугольника равна
произведению его смежных сторон:
Треугольник
Площадь треугольника равна половине
произведения его основания на высоту.
Прямоугольный треугольник
Площадь
прямоугольного
треугольника
равна половине произведения его катетов.
Равнобедренный треугольник
Площадь равнобедренного треугольника
равняется произведению высоты на
половину длины основания.
Трапеция
Площадь трапеции равна произведению
полусуммы оснований на высоту.
Параллелограмм
Площадь
параллелограмма
произведению основания и
опущенной на это основание.
равна
высоты
Практическая
часть
Квадрат
Задание № 1
Сторона квадрата равна 10. Найдите его
площадь.
Решение: Площадь квадрата равна квадрату
его стороны, поэтому она равна 100.
Ответ: 100.
Задание № 2
Периметр квадрата равен 40. Найдите площадь
квадрата.
Решение: Периметр квадрата равен сумме длин
всех его сторон. Таким образом, сторона
квадрата равна 10. Площадь квадрата равна
квадрату его стороны, поэтому она равна 100.
Ответ: 100.
Задание № 3
Периметр квадрата равен 160. Найдите площадь
квадрата.
Решение: Все стороны квадрата равны, поэтому
сторона длинны стороны квадрата равна 160/4 =
40. Найдем площадь квадрата как квадрат его
стороны: S=40*40=1600.
Ответ: 1600.
Прямоугольник
Задание №1
В прямоугольнике одна сторона равна 10, ругая
сторона 12. Найдите площадь прямоугольника.
Решение: Площадь треугольника равна
произведению его смежных сторон, поэтому она
равна 120.
Ответ: 120.
Задание №2
Найдите площадь прямоугольника, если его периметр равен 58 и одна
сторона на 5 больше другой.
Решение: Площадь прямоугольника равна произведению его сторон.
Найдём стороны прямоугольника. Пусть x — меньшая сторона
прямоугольника, тогда другая сторона равна х+5. Следовательно,
периметр прямоугольника равен 2*(х+х+5)=58
откуда 4х=48, следовательно х=12.
Поэтому площадь прямоугольника равна 12*(12+5)=204.
Ответ: 204.
Задание №3.
Найдите площадь прямоугольника, если его периметр
равен 44 и одна сторона на 2 больше другой.
Решение: Площадь прямоугольника равна произведению
его сторон. Найдём стороны прямоугольника. Пусть x
— меньшая сторона прямоугольника. Тогда периметр
прямоугольника равен 2*(х+(х+2))=44, откуда 2х=22-2,
следовательно х=10. Поэтому площадь
прямоугольника равна 10*12=120.

Ответ: 120.
Прямоугольный треугольник
Задание №1.
Два катета прямоугольного треугольника
равны 4 и 9. Найдите площадь этого
треугольника.
Решение: Площадь прямоугольного
треугольника равна половине произведения
катетов.
Таким образом: S=1/2*4*9=18.
Ответ: 18.
Задание №2.
В прямоугольном треугольнике один из катетов равен 10, а угол,
лежащий напротив него, равен 45°. Найдите площадь
треугольника.
Решение: Так как в прямоугольном треугольнике один из углов
равен 45°, то такой треугольник является равнобедренным.
Площадь прямоугольного треугольника равна половине
произведения катетов. Таким образом:
S=1/2*10*10=50.
Ответ: 50.
Задание № 3.
В прямоугольном треугольнике один из катетов равен 4, а острый угол,
прилежащий к нему, равен 45°. Найдите площадь треугольника.
Решение: Сумма углов в треугольнике равна 180°, поэтому второй острый
угол равен 180° − 90° − 45° = 45°. Оба острых угла равны, следовательно,
данный треугольник — равнобедренный, откуда получаем, что второй
катет равен 4. Площадь прямоугольного треугольника можно найти как
половину произведения катетов:
S=1/2*4*4=8.
Ответ: 8.
Равнобедренный треугольник
Задание №1.
Периметр равнобедренного треугольника равен 16, а боковая
сторона — 5. Найдите площадь треугольника.
Решение: Так как боковая сторона равнобедренного треугольника
равна 5, его основание равно 6, а полупериметр: 16/2=8, по
формуле Герона имеем:
Ответ: 12.
Задание №2.
Боковая сторона равнобедренного треугольника равна 34, а основание равно
60. Найдите площадь этого треугольника.
Решение: Пусть а — длина основания равнобедренного треугольника, b
— длина боковой стороны равнобедренного треугольника, h — высота,
проведенная к основанию . Высота равнобедренного треугольника,
проедённая к основанию, также является его биссектрисой и медианой.
Из прямоугольного треугольника найдём высоту по теореме Пифагора:
Площадь треугольника равна половине произведения основания на высоту:
S=1/2*ah=1/2*60*16=480
Ответ: 480.
Задание № 3.
Периметр равнобедренного треугольника равен 216, а боковая сторона
— 78. Найдите площадь треугольника.
Решение: Периметр треугольника равен сумме длин его сторон,
поэтому длина основания равна 216 − 78 − 78 = 60. Высота
проведённая к основанию равнобедренного треугольника, также
является его биссектрисой и медианой, поэтому (см. рис.) имеем:
Площадь треугольника равна половине произведения основания на
высоту:
S=1/2*60*72=2160.
Ответ: 2160.
Трапеция
Задание №1.
Найдите площадь трапеции, изображённой на рисунке.
Решение: Площадь трапеции равна произведению полусуммы оснований на
высоту:
S=(1/2*(7+9+12))*12=168
Ответ: 168.
Задание №2.
Найдите площадь трапеции, изображённой
на рисунке.
Решение: Площадь трапеции вычисляется по
формуле S= ((a+b)/2)*h, где a и b –
основания, а h – высота трапеции.
S=((5+7+15)/2)*24=324.
Ответ: 324.
Задание №3.
Основания равнобедренной трапеции равны 5 и 17, а ее
боковые стороны равны 10. Найдите площадь трапеции.
Решение:
Ответ: 88.
Треугольники общего вида
Задание №1.
В треугольнике одна из сторон равна 10, а опущенная
на нее высота — 5. Найдите площадь треугольника.
Решение: Площадь треугольника равна половине
произведения высоты на основание.
Таким образом: S=1/2*10*5=25
Ответ: 25.
Задание №2.
Найдите площадь треугольника,
изображённого на рисунке.
Решение: Площадь треугольника можно
найти как половину произведения
основания на высоту:
S=1/2*a*h=1/2*(32+10)*24=504.
Ответ: 504.
Задание №3.
Сторона треугольника равна 12, а высота, проведённая к этой
стороне, равна 33. Найдите площадь этого треугольника.
Решение: Площадь треугольника равна полупроизведению
стороны треугольника на высоту, проведенную к этой
стороне:
S=1/2*12*33=198
Ответ: 198.
Параллелограмм
Задание №1.
Найдите площадь параллелограмма,
изображённого на рисунке.
Решение: Площадь параллелограмма равна
произведению длины основания на высоту:
S=(3+7)*4=40
Ответ: 40.
Задание №2.
Сторона ромба равна 5, а диагональ равна 6.
Найдите площадь ромба.
Решение:
Площадь ромба равна половине произведения диагоналей:
½*8*6=24
Ответ: 24.
Задание №3.
Периметр ромба равен 40, а один из углов равен 30°.
Найдите площадь ромба.
Решение: Периметр ромба равен сумме длин всех его
сторон. Так как все стороны равны, сторона ромба
равна 10. Площадь ромба равна произведению сторон
на синус угла между ними. Таким образом,
S=10*10*1/2=50
Ответ: 50.
Задания для самостоятельной
проверки знаний
№1. Найдите площадь квадрата,
описанного вокруг окружности
радиуса 83.
№ 2. Найдите площадь квадрата, если
его диагональ равна 1.
№ 3. Из квадрата вырезали
прямоугольник (см. рисунок). Найдите
площадь получившейся фигуры.
№ 4. На стороне BC прямоугольника
ABCD, у которого AB = 12 и AD = 17,
отмечена точка E так, что ∠EAB = 45°.
Найдите ED.
№ 5. В прямоугольнике одна сторона
равна 96, а диагональ равна 100.

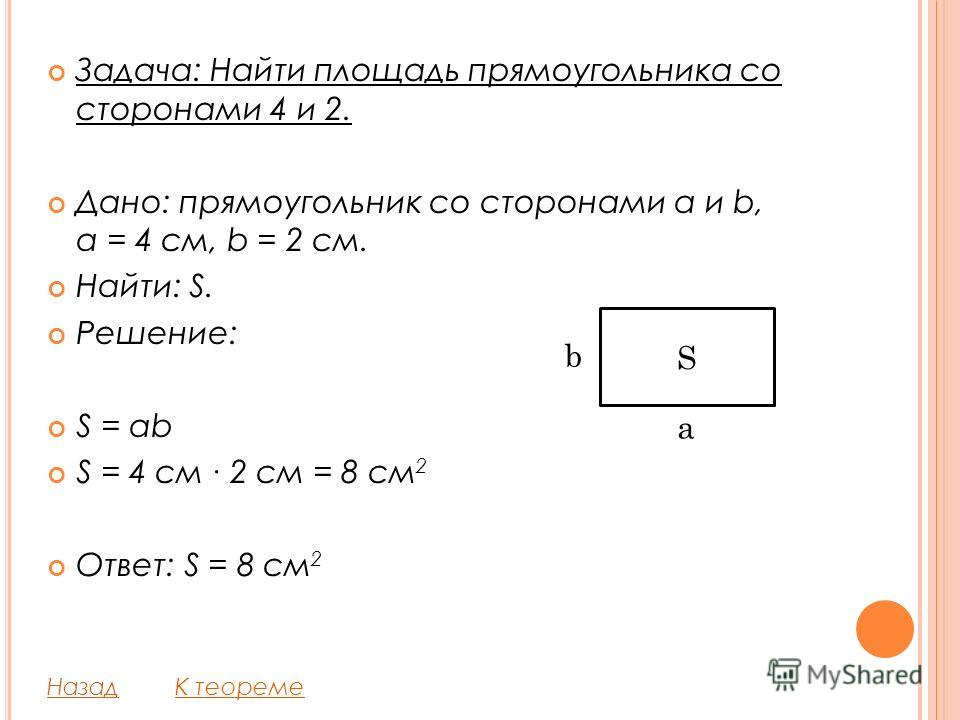
Найдите площадь прямоугольника.
№ 6. Два катета прямоугольного
треугольника равны 4 и 9. Найдите
площадь этого треугольника.
№ 7. В прямоугольном треугольнике
гипотенуза равна 70, а один из
острых углов равен 45°. Найдите
площадь треугольника.
№ 8. Боковая сторона равнобедренного треугольника
равна 34, а основание равно 60. Найдите площадь
этого треугольника.
№ 9. В треугольнике ABC отрезок DE — средняя линия.
Площадь треугольника CDE равна 97. Найдите
площадь треугольника ABC.
№ 10. Периметр ромба равен 116, а один из углов равен
30°. Найдите площадь ромба.
№ 11. Радиус круга равен 3, а длина ограничивающей
его окружности равна 6π. Найдите площадь круга. В
ответ запишите площадь, деленную на π.

English     Русский Правила

Q2 Диагональ прямоугольной доски 1 м, а длина 96 см. Найдите площадь доски…

Перейти к

  • Упражнение 20 (А)
  • Упражнение 20(Б)
  • Целые числа
  • Рациональное число
  • Фракции (включая задачи)
  • Десятичные дроби (десятичные дроби)
  • Показатели (включая законы показателей)
  • Соотношение и пропорция (включая долю в соотношении)
  • Унитарный метод (включая время и работу)
  • Процент и процент
  • Прибыль, убыток и дисконт
  • Простой интерес
  • Основные понятия (включая основные операции)
  • Простые линейные уравнения (включая текстовые задачи)
  • Понятия набора (некоторые простые деления по ведическому методу)
  • Линии и углы (включая построение углов)
  • Треугольники
  • Теорема Пифагора
  • Симметрия (включая отражение и вращение)
  • Распознавание твердых тел (представление 3D в 2D)
  • Конгруэнтность: конгруэнтные треугольники
  • Измерение
  • Обработка данных
  • Вероятность

Главная > Селина Солюшнс Класс 7 Математика > Глава 20 — Измерение > Упражнение 20(Б) > Вопрос 2

Вопрос 2 Упражнение 20(B)

В2) Диагональ прямоугольной доски равна 1 м, а ее длина 96 см. Найдите площадь доски.

Ответ:

Решение: 92

\sqrt{784}=BC

BC = 28 см

Площадь прямоугольной доски

= l x b или AB x BC

= 96 x 28 = 2688 см²

900 92

Стенограмма видео

«Привет, ребята. Какает у вас все хорошо. Надеюсь, у вас все хорошо. — Работайте, очень внимательно говоря о схеме. Самокат Тина Стиральная машина из телевизора. Диагональ прямоугольной доски равна 1 метру, а ее длина 26 метров, найдите площадь дороги. Диагональ решения равна 1 метру, что равно 200 сантиметрам, длина прямоугольника равна 96 сантиметров. Согласно теореме Пифагора, это равно p квадрату плюс обзоры, где в отличие от квадрата D квадрат равен квадрату движения вперед минус b квадрат для всего маршрута. То есть b квадрат B равен Вы должны прийти и найти на этой неделе. Ага. Принимая как в диаграмме b стороны. Треугольник ADC KD равен 600 метрам по переменному току чему равно b? Квадрат равен x в квадрате минус B в квадрате, что равно 200 в квадрате, равно минус 96, содержит 96 в квадрате. Это равно 10 000 — 9200, что равно циклу 784. Из 784 дней Группа 784 это Корень из 74 равен 28 сантиметрам. Итак, это идеальный квадрат, а затем площадь треугольника. Мы нашли хлеб. Мы нашли хлеб, значит площадь прямоугольника равна длине в ширину, то есть 96 на двадцать восемь девять шесть сантиметров на 28 сантиметров. Ответ 2680 H и сельское хозяйство для ответа 2688 Кинотеатр 20-метровая площадь. Спасибо.»

Похожие вопросы

1) Найдите площадь прямоугольника, длина и ширина которого равны 25 см и 16 см.

Q3) Стороны прямоугольного парка относятся как 4 : 3. Если его площадь 1728 кв.м, найдите (i) его площадь…

Q4) Пол имеет длину 40 м и ширину 15 м. Он покрыт плиткой, каждая размером 60 см на 50 см. Фи…

Q5) Длина и ширина прямоугольного участка земли находятся в соотношении 5 : 3. Если общая стоимость …

6) Найдите площадь квадрата, периметр которого равен 56 см.

Q7) Квадратный газон окружен дорожкой шириной 2,5 м. Найдите площадь пути 165 м…

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Упражнение 20(A)

Упражнение 20(B)

Главы

Целые числа

Рациональные числа

Дроби (включая задачи)

Десятичные дроби (десятичные)

Показатель степени (включая законы степени)

Соотношение и доля (включая долю в соотношении)

Унитарный метод (включая время и работу)

Проценты и проценты

Прибыль, убыток и дисконт

Простые проценты

Основные понятия (включая основные операции)

Простые линейные уравнения (включая текстовые задачи)

Набор понятий (S некоторые простые деления по ведическому методу)

строки и углы (включая построение углов)

Треугольники

Теорема Пифагора

Симметрия (включая отражение и вращение)

Распознавание твердых тел (представление 3D в 2D)

Конгруэнтность: конгруэнтные треугольники

Измерение

Обработка данных

Вероятность

Курсы

Быстрые ссылки

Условия и политика

Условия и политика

2022 © Quality Tutorials Pvt Ltd Все права защищены

How to Estimate — Wallcoverings Association (WA)

900 04
  • Точное измерение
  • Метод площади квадратных футов
  • Лестницы или стены собора
  • Оценка коммерческих квадратных метров

    • Измерение перед оценкой потребности в обоев

    Наиболее важным шагом в оценке обоев являются точные измерения. Используйте мерную линейку или стальную рулетку, а не тканевую рулетку. Снимите мерки в футах, округлив их до следующей по величине половины фута или фута. Нарисуйте схему комнаты с указанием дверей, окон и высоты потолка. Если стена необычно разбита камином, встроенными книжными шкафами и т. д., схема с подробными размерами будет полезна для расчета необходимых квадратных метров обоев.

    Измерьте высоту стены от пола до потолка. Исключить плинтуса и молдинги. Измерьте длину каждой стены, включая двери и окна. Найдите общую площадь стен в квадратных метрах, умножив высоту потолка на общую длину стены. Вычтите области, которые не будут покрыты. (Стандартные двери имеют размер около 3 x 7 футов или 21 квадратный фут; стандартные окна имеют размер около 3 x 4 или 12 квадратных футов.)

    Эти расчеты дают общее количество квадратных футов, которое необходимо закрыть. С его помощью можно определить количество рулонов или погонных метров обоев.

    Например:

    На приведенном выше рисунке каждая стена имеет длину 12 футов и высоту потолка 8 футов. Умножьте 12 x 8 = 96 квадратных футов для каждой стены, затем умножьте 96 x 4 (поскольку есть четыре стены по 96 квадратных футов каждая) = 384 квадратных фута для комнаты.

    Метрические одинарные рулоны

    Повторяющаяся длина Полезный ресурс
    от 0 до 6 дюймов 25 кв. футов
    от 7 до 12 дюймов 22 кв. фута
    от 13 до 18 дюймов 20 кв. футов
    от 19 до 23 дюймов 18 кв. футов

    Эти цифры хорошо подходят для стен нормального размера. На необычно короткие (менее 3 футов) или высокие (более 9 футов) они не распространяются.

    Наверх

    9009Метод определения площади в квадратных футах

    Используя приведенную выше диаграмму в качестве примера, подсчитайте количество обоев, которое потребуется, чтобы повесить комнату. Цифра в 384 квадратных фута не учитывает квадратные метры дверей и окон. Вычтите фактические квадратные метры каждого проема — 21 квадратный фут для двери и 12 квадратных футов для каждого из окон. 384 квадратных фута — 45 квадратных футов (21 + 12 + 12 = 45) = 339 квадратных футов площади стен, которые будут покрыты обоями. Если вы используете обои с повторением узора 8 дюймов, прикиньте, что каждый метрический рулон будет содержать 22 квадратных фута пригодного для использования покрытия для обоев, 339квадратных футов (пространство на стене сверху, которое будет подвешено), деленное на 22 квадратных фута (из таблицы полезной площади), что равно 15,4, или округлить до 16 метрических одинарных рулонов, которые потребуются для подвешивания примера тоже (8 метрических рулонов) .

    Уравнение будет выглядеть следующим образом:

    384 кв. фута (размер комнаты)
    -21 кв. фут (одна стандартная дверь)
    -12 кв.м (одно стандартное окно)
    -12 кв. футов (одно стандартное окно)

    = 339 кв. футов пространства на стене, которое будет подвешено

    339 кв. футов / 22 кв. фута = 15,4 кв. м для подвески комнаты, округляем до 16 кв. футов.

    Вернуться к началу

    Лестницы или стены собора

    При оценке стены, имеющей диагональ, помните, что будут дополнительные отходы, учитывающие наклон ступеней или высоту потолка. Есть два разных типа лестниц: одна с горизонтальной линией потолка, а вторая с диагональной линией потолка, которая параллельна падению ступеней.

    В обоих случаях первым делом нужно разделить стену на квадраты или прямоугольники, чтобы определить площадь в квадратных футах. На приведенном выше рисунке высота потолка на верхнем этаже составляет 8 дюймов, а высота потолка на нижнем этаже — 8 дюймов. Эти цифры и есть длина стены. Затем измерьте ширину стены по горизонтали от вершины лестницы до воображаемой вертикальной линии, начинающейся внизу лестницы, которая в примере равна 15 дюймам. Взяв верхний прямоугольник, цифра 8 x 15 дюймов = 120 кв. футов. Затем вычислите нижний прямоугольник, 8 x 15 дюймов = 120 кв. футов, но, поскольку часть этой площади стены находится под лестницей, умножьте квадратные метры нижнего прямоугольника на 65%, что является отраслевым стандартом. Сложите две цифры. вместе, чтобы получить площадь в квадратных футах, которая должна быть покрыта обоями.Уравнение будет выглядеть следующим образом:

    8 x 15 дюймов = 120 кв. футов (верхний прямоугольник)
    8 x 15 дюймов = 120 кв. футов x 65% = 78 кв. футов (нижний прямоугольник)
    120 кв. футов + 78 кв. футов = 198 кв. футов. из Таблицы полезной доходности, а затем разделив общее количество квадратных футов на это число.

    Например, при использовании настенного покрытия с повторением 14 дюймов каждый msr будет содержать 20 квадратных футов полезного настенного покрытия. Уравнение будет выглядеть следующим образом: 198 кв. футов / 20 кв. футов = 9,9 мср, округленное до 10 мср. Если лестница имеет наклонный потолок, выполните первый пример при нахождении ширины и длины воображаемого прямоугольника или квадрата. Следующим шагом будет умножение обеих этих фигур прямоугольника/квадрата на 65%, чтобы найти квадратные футы площади стены. Уравнение будет выглядеть следующим образом:

    8 x 15 дюймов = 120 кв. футов (верхний прямоугольник)
    8 x 15 дюймов = 120 кв. футов (нижний прямоугольник)
    120 кв. футов + 120 кв. футов = 240 кв. футов
    240 кв. футов x 65% = 156 кв. футов площади стены, которую необходимо покрыть

    При использовании того же шаблона с повторением 14 дюймов каждый мср будет содержать 20 квадратных футов полезного покрытия для стен, и уравнение будет выглядеть следующим образом:

    156 кв. футов / 20 кв. футов = 7,8 мср, округленное до 8 msr

    Потолок собора будет оцениваться таким же образом, возведя верхний прямоугольник в квадрат, умножив квадратные футы на 65%, а затем прибавив это число к квадратным футам нижнего прямоугольника

    Вернуться к началу

    Оценка коммерческого помещения Квадратные метры

    После того, как покрытие для обоев было определено по спецификации, прикиньте площадь в квадратных футах и ​​сколько потребуется для работы. Как только ширина известна, можно определить количество квадратных футов в линейном ярде для этой конкретной ширины обоев. Важно помнить следующую формулу:

    • Ширина, деленная на 12 = количество футов
      • .
    • Количество футов, умноженное на 3 (1 ярд) = квадратные футы/ширина (квадратные футы на линейный ярд)
    • Разделите квадратные футы площади стены на квадратные футы/ширину

    Например:

    • Материал шириной 54 дюйма, используемый для покрытия 1500 квадратных футов, обозначен цифрой
      • .
    • 54 разделить на 12 = 4,5
    • 4,5 умножить на 3 = 13,5 квадратных футов на погонный ярд
    • 1500 разделить на 13,5 = 111,11

    1500 квадратных футов площади стены потребовали бы 112 ярдов без отходов.

    Когда известна ширина и квадратные метры для ширины, можно определить любую сумму. Если метраж для определенной ширины известен, а ширина материала изменена, чтобы преобразовать одну ширину в другую, действуйте в обратном порядке, чтобы определить метраж.