Урок алгебры в 9-м классе по теме «Задачи на движение»
Цель:
- обобщение знаний учащихся, связанных с решением задач на движение,
- подготовка к экзамену;
- воспитание умения навыков коммуникативности;
- воспитание самостоятельности.
Ход урока
Приложение.
1. Актуализация знаний учащихся:
(Скорость, время, расстояние)
Как найти скорость, если известно расстояние и время? время, если известно расстояние и скорость? расстояние, если известно время и скорость?
2. Устно: Условие задачи на экране.
Задача 1: Геологи 4 часа летели на вертолете со скоростью 80км/ч, а затем ехали верхом 2часа со скоростью 12 км/ч. Какой путь проделали геологи за это время?
В задаче два процесса: движение на вертолете и
движение верхом.
| Процессы | Скорость (км/ч) | Время (ч) | Расстояние (км) | |
| На вертолете | ||||
| Верхом | ||||
Задача 2:
Решение:
В задаче путь, проделанный теплоходом, состоит
из двух частей: по озеру и по реке. Для того чтобы
найти расстояние, надо знать скорость и время.
Время движения известно, скорость теплохода по
озеру известна, а скорость по реке нет.
Краткую запись можно сделать так: (заготовка таблицы на экране)
| Время | Расстояние | |||
| По озеру | ||||
| По реке | ||||
| Время | Скорость | Расстояние | ||
| По озеру | 3 ч | 23км/ч | ? | ? |
| По реке | 4 ч | на 3 км/ч > | ? | |
Решение:
1. Найдем расстояние по озеру 23·3=69 (км)
Найдем расстояние по озеру 23·3=69 (км)
2. Найдем скорость по реке 23+3=26 (км/ч)
3. Найдем расстояние по реке 26 * 4 =104 (км)
4. Найдем все пройденное теплоходом расстояние 69 +104=173 (км)
Задача 3:
Моя задача напомнить, что существует несколько случаев, а значит и несколько решений.
На доске сделаны 4 одинаковых рисунка.
Учащиеся должны дорисовать его, чтобы рассмотреть 4 возможных случая.
1.
Решение:
1) 70 + 90 = 160 (км) на 160 км увеличивается расстояние между машинами за 1ч.
2) 400 + 160 =560 (км) будет между машинами через 1ч.
Ответ: 560 км
2.
Решение:
1) 70 + 90 = 160 (км) на 160 км уменьшается расстояние между машинами за 1 ч.
2) 400 — 160 = 240 (км) будет между машинами через 1 ч.
Ответ: 240 км
3.
Решение:
1) 90 — 7 0 = 20 (км) на 20 км увеличивается расстояние
между машинами за 1 ч.
2) 400 + 20 = 420 (км) будет между машинами через 1 ч.
Ответ: 420 км
4.
Решение:
1) 90 — 7 0 = 20 (км) на 20 км уменьшается расстояние между машинами за 1 ч.
2) 400 — 20 = 380 (км) будет между машинами через 1 ч.
Ответ: 380 км.
3) Решите самостоятельно
С последующей устной проверкой.
Прочитайте задачу и выберите уравнение, отвечающее условию задачи, в котором неизвестной обозначена скорость автомобиля:
а) Скорость автомобиля на 20 км/ч больше скорости мотоцикла. Они едут навстречу друг другу из двух пунктов, расстояние между которыми 280 км. Найдите скорость автомобиля, если в момент встречи автомобиль был в пути 3 часа, а мотоциклист — 2 часа.
1) 3х + 2(х + 20) = 280
2) 3(х — 20) + 2х = 280
3) 3х + 2(х — 20) = 280
4) 3(х + 20) + 2х = 280
б) Прочитайте задачу и выберите уравнение, отвечающее условию задачи, в котором
переменной t обозначено время движения велосипедиста (в часах):
Расстояние от поселка до станции автомобиль
проехал на 1 час быстрее велосипедиста,
проделавшего тот же путь.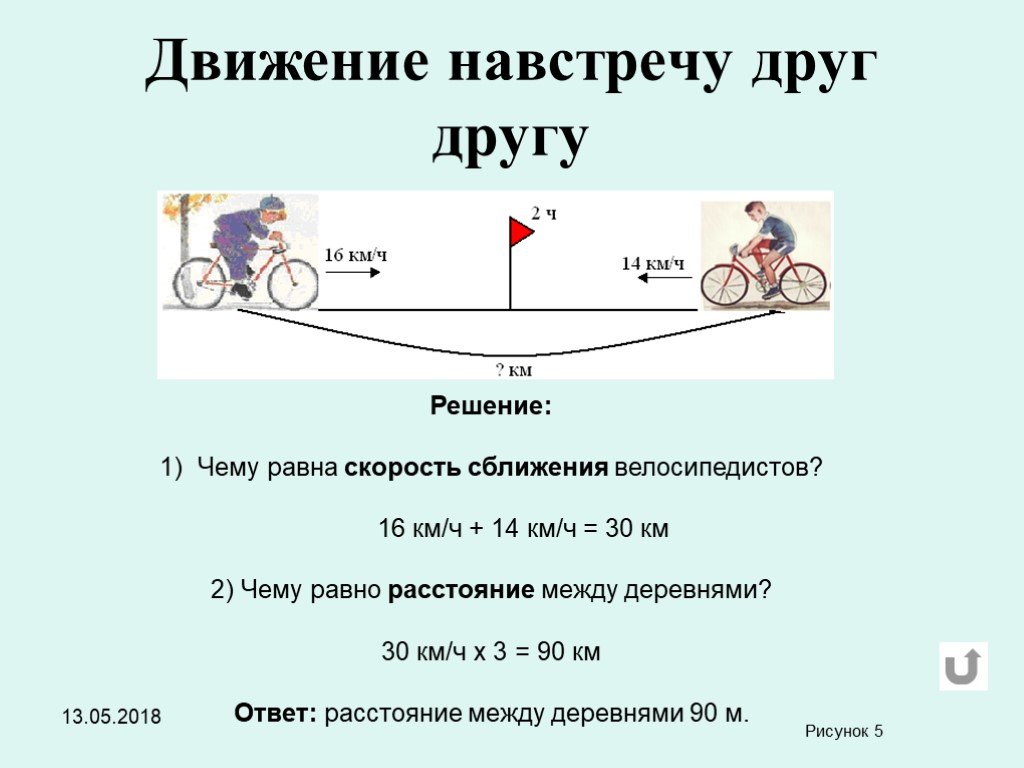
1) 60(t + 1) — 15t = 0
2) 60t — 15(t + 1) = 0
3) 60t — 15(t — 1) = 0
4) 60(t — 1) — 15t = 0
в) Прочитайте задачу и выберите уравнение, отвечающее условию задачи, в котором переменной t обозначено искомое время:
Скорость автомобиля 60 км/ час, а скорость велосипедиста — 15 км/ час.
Велосипедист выезжает из пункта А, а через 40 минут следом за ним из того же пункта выезжает автомобиль. Найдите время, прошедшее после выезда автомобиля из пункта А, за которое автомобиль, обогнав велосипедиста, удалится от него на 30 км.
1) 60t — 5(3t + 2) = 30
2) 60t — 15(t — 40) = 30
3) 60(t + 40) — 15t = 30
4) 60(t — 40) — 15t = 30
4) Практикум по решению задач
Решите задачу арифметическим способом, условие открыто, а решение закрыто «шторкой»)
5) Решение задач 2 уровня
(условия задач на карточках, которые учащиеся получают после решения задач первого уровня)
Из пункта А в пункт В расстояние между которыми
18 км, одновременно выезжают два велосипедиста. Скорость одного из них на 5 км/ч меньше скорости
другого. Велосипедист, который первым прибыл в В,
сразу же повернул обратно и встретил другого
велосипедиста через 1ч 20мин после выезда из А. На
каком расстоянии от пункта В произошла встреча?
Скорость одного из них на 5 км/ч меньше скорости
другого. Велосипедист, который первым прибыл в В,
сразу же повернул обратно и встретил другого
велосипедиста через 1ч 20мин после выезда из А. На
каком расстоянии от пункта В произошла встреча?
Два пешехода выходят навстречу друг другу из двух пунктов, расстояние между которыми 30 км. Если первый выйдет на 2 ч раньше второго, то он встретит второго пешехода через 4,5 ч после своего выхода. Если второй выйдет на 2 ч раньше первого, то он встретит первого пешехода через 5 ч после своего выхода. С какой скоростью идет каждый пешеход?
Тетради с решением этих задач учащиеся сдают на проверку.
Итог урока.
Домашнее задание.
Готовимся к ГИА «Задачи на движение по воде» ( 9, 11 классы)
Областное государственное бюджетное учреждение
дополнительного профессионального образования
«Курский институт развития образования»
(ОГБУ ДПО КИРО)
Задачи
на движение по воде.
(курсовая работа в рамках курсов повышения квалификации по ДПП ПК/ ПП «Проектирование педагогической деятельности по подготовке обучающихся к ГИА по математике»)
Выполнила учитель математики
МОКУ « Нижне – Реутчанская СОШ»
Медвенского района
Шеверёва Марина Викторовна
2020 год
Текстовые задачи. ЕГЭ (профиль) №11 и ОГЭ №22.
Сортировка по темам:
Тема1: Проценты.
Тема 2: Движение.
Тема 3: Движение по воде.
Тема 4: Средняя скорость.
Тема 5: Движение длинных тел.
Тема 6: Движение по кругу.
Тема 7: Совместная работа.
Тема 8: Сплавы, растворы (концентрация).
Тема 9: Прогрессии.
Задачи на движение по воде из открытого банка ЕГЭ на ФИПИ:
1. Моторная лодка проплыла против течения реки 20 км. После этого мотор вышел из строя, и лодку отнесло течением реки на место старта. На весь путь туда и обратно лодка затратила 6 часов. Найдите скорость лодки в стоячей воде, если скорость течения реки 5 км/ч. Ответ дайте в км/ч.
2. Моторная лодка отчалила от пристани и проплыла против течения реки 40 км. После остановки на 30 минут лодка повернула обратно. В пункт отправления лодка приплыла через шесть с половиной часов после отплытия. Найдите скорость лодки в стоячей воде, если скорость течения реки 5 км/ч. Ответ дайте в км/ч.
3. Моторная
лодка проплыла по течению реки 10 км. После этого мотор вышел из строя, и лодку
несло течением еще 2 километра. На весь путь лодка затратила 1,5 часа. Найдите
скорость течения реки, если скорость лодки по течению реки 20 км/ч. Ответ дайте
в км/ч.
На весь путь лодка затратила 1,5 часа. Найдите
скорость течения реки, если скорость лодки по течению реки 20 км/ч. Ответ дайте
в км/ч.
4. Первую половину пути катер прошел по течению узкой части реки с большой скоростью течения. После излучины русло реки расширилось, и течение стало в два раза медленнее. Найдите скорость течения в начале пути, если на первую половину потребовалось в 1,2 раза меньше времени. Скорость катера в стоячей воде 20 км/ч. Ответ дайте в км/ч.
5. Моторная лодка отчалила от пристани и проплыла по течению реки 61,5 км. После остановки на 30 минут лодка повернула обратно. Через 5,5 часов после начала движения от пристани лодке оставалось плыть до нее 30,5 километров. Скорость лодки в стоячей воде 18 км/ч. Найти скорость течения реки, если известно, что она менее 3 км/ч. Ответ дайте в км/ч.
Задание №22 на ОГЭ из открытого банка на ФИПИ.
1. (352848) Баржа прошла по течению реки 72 км
и, повернув обратно, прошла ещё 54 км, затратив на весь путь 9 часов. Найдите
собственную скорость баржи, если скорость течения реки равна 5 км/ч.
Найдите
собственную скорость баржи, если скорость течения реки равна 5 км/ч.
2. (311660) Пристани А и В расположены на реке, скорость течения которой на этом участке равна 4 км/ч. Лодка проходит туда и обратно без остановок со средней скоростью 6 км/ч. Найдите собственную скорость лодки.
3. (314488) Рыболов проплыл на лодке от пристани некоторое расстояние вверх по течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся обратно через 5 часов от начала путешествия. На какое расстояние от пристани он отплыл, если скорость реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?
4. (314487) Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 2 часа, вернулись обратно через 6 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость реки равна 3 км/ч, а собственная скорость лодки 6 км/ч?
5. (341534) Теплоход проходит по течению реки до пункта
назначения 76 км и после стоянки возвращается в пункт отправления. Найдите
скорость теплохода в неподвижной воде, если скорость течения равна 3 км/ч,
стоянка длится 1 час, а в пункт отправления теплоход возвращается через 20
часов после отплытия из него.
Найдите
скорость теплохода в неподвижной воде, если скорость течения равна 3 км/ч,
стоянка длится 1 час, а в пункт отправления теплоход возвращается через 20
часов после отплытия из него.
Текстовые задачи (разных видов) входят в ОГЭ и ЕГЭ, поэтому, данная тема имеет важнейшее значение в обучении математике. Решение текстовых задач вызывает затруднения у обучающихся и следует больше уделять внимание их решению. Следует сформировать у учащихся представление о способах решения задач, так как решение задач на экзамене способствует набору большего количества баллов, например задание №22 на ОГЭ и задание №11 на ЕГЭ( профиль). Для текстовых задач не существует единого алгоритма решения – в этом вся их сложность. Тем не менее существуют типовые задачи, которые вполне решаются стандартно. В моей работе рассмотрены задачи на движение по воде.
Объект исследования: подготовка обучающихся к экзамену по математике в формате ОГЭ и ЕГЭ.
Предмет исследования: текстовые задачи на
движение по воде.
Цель исследования: — выбрать текстовые задачи данного типа;
— разобрать цепочку задач данного типа;
— проанализировать задачи данного типа;
— просмотреть задачи в учебниках с 5 по 9 классы, а также в открытых банках ОГЭ и ЕГЭ в на ФИПИ.
Классификация задач.
Задачи на движение по реке можно классифицировать
По направлению течения:
— Задачи на движение в стоячей воде.
— Задачи на движение по течению.
— Задачи против течения.
При решении задач на движение по воде необходимо помнить следующее:
Данный тип задач начинает изучаться в начальной школе.
Все текстовые математические
задачи по числу действий, выполняемых для их решения, делятся на простые
и составные. Простые задачи в системе обучения математике играют чрезвычайно
важную роль. С помощью решения простых задач формируется одно из главных
понятий начального курса математики – понятие об арифметических действиях.
Умение решать простые задачи является подготовительной ступенью овладения
учащимися умением решать составные задачи, так как решение составной задачи
сводится к решению ряда простых задач. Таким образом, для решения составной
задачи, надо установить систему связей между данными и искомым, а затем
выполнить арифметические действия.
Таким образом, для решения составной
задачи, надо установить систему связей между данными и искомым, а затем
выполнить арифметические действия.
Для решения текстовых задач в школе применяют два основных метода: арифметический и алгебраический. Рассмотрим каждый из этих методов.
Арифметический метод решения задач преимущественно используется в 5-6 классах. Задачи на движение по реке, решаемые арифметическим методом, служат для отработки вычислительных навыков и навыка решения задач на движение, готовят к пониманию текстов алгебраических задач, служат пропедевтикой для изучения алгебры.
Простые задачи позволяют учащимся усвоить понятия «собственная скорость»; «скорость в стоячей воде»; «скорость течения»; «скорость плота», «скорость по течению»; «скорость против течения», выработать навыки нахождения этих видов скоростей.
Простые задачи встречаются при изучении
следующих тем: « Сложение и вычитание натуральных чисел», « Составление
буквенных выражений» , « Формулы», « Сложение и вычитание обыкновенных дробей с
одинаковыми знаменателями», « Сложение и вычитание десятичных дробей», «
Сложение и вычитание дробей с разными знаменателями».
Примеры простых задач на движение по реке ( для устного счёта) :
1. Собственная скорость моторной лодки 17 км/ч. Скорость течения реки 2 км/ч. Найдите скорость моторной лодки по течению реки.
17+2 =19(км/ч)
Ответ: скорость моторной лодки по течению 19км/ч.
2. Скорость теплохода при движении по озеру 32 км/ч. Скорость течения реки 3 км/ч. Найдите скорость теплохода против течения реки.
32-3=29(км/ч)
Ответ: скорость теплохода против течения 29км/ч.
3. Скорость лодки по течению реки 8 км/ч. Собственная скорость лодки 5 км/ч. Найдите скорость течения реки.
8-5=3(км/ч)
Ответ: скорость течения реки 3 км/ч.
4. Скорость катера в стоячей воде 12 км/ч, а по течению реки -14 км/ч. Найдите скорость течения плота, плывущего по этой же реке.
14-12=2(км/ч)
Ответ: скорость течения реки 2 км/ч.
5. Скорость
лодки вверх по реке 4,2 км/ч. Собственная скорость лодки 5,8 км/ч. Найдите
скорость плота, спускающегося по этой реке.
Найдите
скорость плота, спускающегося по этой реке.
5,8-4,2=1,5(км/ч)
Ответ: скорость течения реки 1,5 км/ч.
6. Скорость моторной лодки вниз по реке- 25,5 км/ч. Скорость течения реки 3,7 км/ч. Найдите собственную скорость моторной лодки.
25,5-3,7=21,8(км/ч)
Ответ: собственная скорость моторной лодки 21,8 км/ч.
7. По течению реки катер за 1 ч проходит 32 км. Найдите собственную скорость катера, если скорость течения реки 4 км/ч.
32-4=28(км/ч)
Ответ: собственная скорость катера 28 км/ч.
8. Скорость катера в стоячей воде 12 км/ч. Скорость течения реки v км/ч. Составьте буквенное выражение для нахождения скорости катера по течению реки и найдите её значение при v=1;3.
12+v;
v=1; 12+1=13
v=3; 12+3=15
9. Скорость
моторной лодки по течению реки m км/ч. Скорость течения реки 3 км/ч.
Составьте буквенное выражение для нахождения собственной скорости моторной
лодки и найдите её значение при m=17;
15,7.
m-3;
m=17; 17-3=14
m=15,7; 15,7-3=12,7
Задания на составление буквенных выражений позволяют провести исследования о возможных значениях собственной скорости и скорости течения.
Составные арифметические задачи на движение по реке, включая в себя простые задачи, отражающие особенности этого типа задач, в остальном сходны с задачами на движение по земле. Особо можно выделить только задачи, в которых надо найти ни одну, а несколько скоростей: скорость не только по течению, но и против, среднюю скорость движения и т.п.
1. Собственная скорость катера 12 км/ч. Скорость течения реки 3 км/ч. Найдите скорость катера по течению и против течения реки.
1) 12+3=15(км/ч)
2) 12-3=9(км/ч)
Ответ: скорость катера по течению реки 15км/ч, скорость катера против течения 9 км/ч.
2. Собственная скорость катера 21,7 км/ч, а его скорость по течению реки — 24,2 км/ч. Найдите скорость катера против течения реки.
1) 24,2-21,7=2,5(км/ч)-скорость течения реки;
2) 21,7-2,5=19,2(км/ч)
Ответ: скорость катера против течения 19,2
км/ч.
3. Собственная скорость теплохода 41,2 км/ч, а его скорость против течения реки — 37,6 км/ч. Найдите скорость теплохода по течению реки.
1) 41,2 — 37,6=3,6(км/ч)-скорость течения реки;
2) 41,2+3,6=44,8 (км/ч)
Ответ: скорость теплохода по течению реки 44,8 км/ч.
4. Скорость теплохода по течению реки 53,1 км/ч. Скорость течения реки 3,6 км/ч. Найдите собственную скорость теплохода и его скорость против течения реки.
1) 53,1- 3,6=49,5(км/ч)- собственная скорость катера.
2) 49,5-3,6=45,9 (км/ч)
Ответ: скорость теплохода против течения 45,9 км/ч.
5. Скорость катера по течению реки 19 км/ч, а против течения -14 км/ч. Найдите скорость течения реки. Какова скорость плота, плывущего по этой реке?
1) (19-14) : 2= (19-14) :2=4 :2=2,2: 2=1,1 (км/ч)
Ответ: скорость плота 1,1 км/ч.
Примеры
задач на движение по реке, решаемых арифметическим способом с использованием
общего правила решения задач на движение: путь = скорость*время.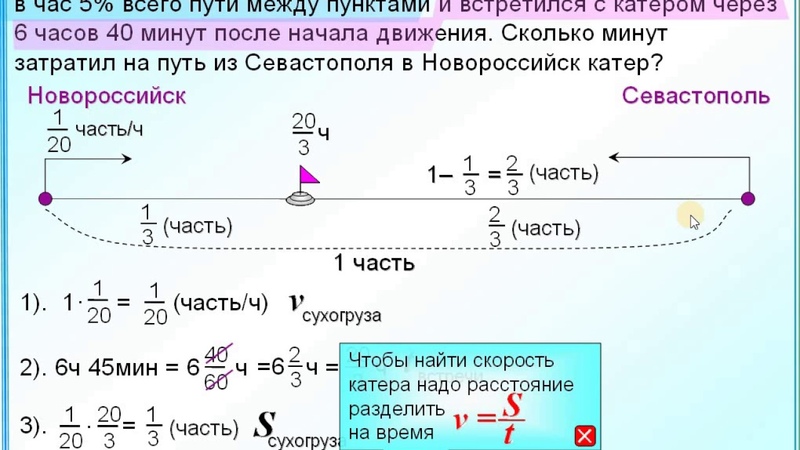
1. Собственная скорость теплохода 48,2 км/ч, а его скорость против течения реки — 45,5 км/ч. Какое расстояние пройдет теплоход по течению реки за 5 ч?
1) 48,2-45,5=2,7 (км/ч) скорость течения реки;
2) 48,2+2,7=50,9(км/ч) скорость теплохода по течению реки;
3) 50,9*5=254,5(км)
Ответ: теплоход по течению реки пройдет 254,5 км.
2. Моторная лодка, собственная скорость которой 12,6 км/ч, прошла за 3 ч по течению реки 46,2 км. Найдите скорость течения реки.
1) 46,2 : 3=15,4 (км/ч) –скорость моторной лодки по течению реки.
2) 15,4-12,6=2,8 (км/ч)
Ответ: 2,8 км/ч–скорость течения реки.
3. Скорость течения реки 4,6 км/ч. Теплоход за 4 ч прошел против течения 154,4 км. Какова собственная скорость теплохода?
1) 154,4 :4 =38,6(км/ч)- скорость теплохода против течения реки;
2) 38,6+4,6=43,2(км/ч)
Ответ: собственная скорость теплохода 43,2 км/ч.
4. Туристы проплыли на лодке 24 км вниз по реке до острова и, побыв
там, вернулись в лагерь. Скорость течения реки 2 км/ч, собственная скорость
лодки 8 км/ч. Сколько времени туристы были в пути?
Скорость течения реки 2 км/ч, собственная скорость
лодки 8 км/ч. Сколько времени туристы были в пути?
1) 8+2=10(км/ч)-скорость лодки вниз по реке;
2) 8-2=6(км/ч)-скорость лодки вверх по реке;
3) 24: 10=2,4 (ч)- время движения вниз по реке;
4) 24: 6= 4 (ч)- время движения вверх по реке;
5) 2,4+4=6,4(ч)
Ответ: время туристов в пути 6,4 ч.
5. Собственная скорость моторной лодки 17,2 км/ч. Скорость течения реки 2,7 км/ч. Сначала лодка плыла 1,5 ч против течения реки, а потом 3,2 ч — по озеру. Какое расстояние прошла моторная лодка за это время?
Алгебраический метод решения задач используется в 7-9
классах при изучении тем: 7 класс: « Системы двух линейных уравнений с двумя
переменными как математические модели реальных ситуаций»; 8 класс: «Алгебраические
дроби», «Первые представления о рациональных уравнениях», « Рациональные
уравнения как математические модели реальных ситуаций»; 9 класс: «Системы
уравнений. Основные понятия», «Системы уравнений как математические модели
реальных ситуаций».
Основные понятия», «Системы уравнений как математические модели
реальных ситуаций».
Рассмотрим примеры решения таких задач:
Пример 1 ( 8 класс Мордкович А.Г.)
Катер прошел 10 км по течению реки и 6 км против течения, затратив на весь путь 2 часа. Чему равна собственная скорость катера, если скорость течения равна 2 км/ч? ( 8 класс Мордкович А.Г.)
Решение:
1 этап. Составление математической модели.
Пусть х км/ч – собственная скорость лодки, тогда по течению реки она плывёт со скоростью ( х + 2 ) км/ч, а против течения – со скоростью ( х – 2) км/ч. Значит, ч – время, затраченное на путь по течению, а ч – время, затраченное на путь против течения. По условию задачи известно, что на весь путь затрачено 2 часа, получим уравнение: + = 2.
2 этап. Работа с составленной моделью.
+ = 2.
+ — 2 = 0
= 0
= 0
-2х2 + 16х =0
х( х – 8) = 0
х1 =0, х2 = 8
0 и 8 удовлетворяют условию
3
этап.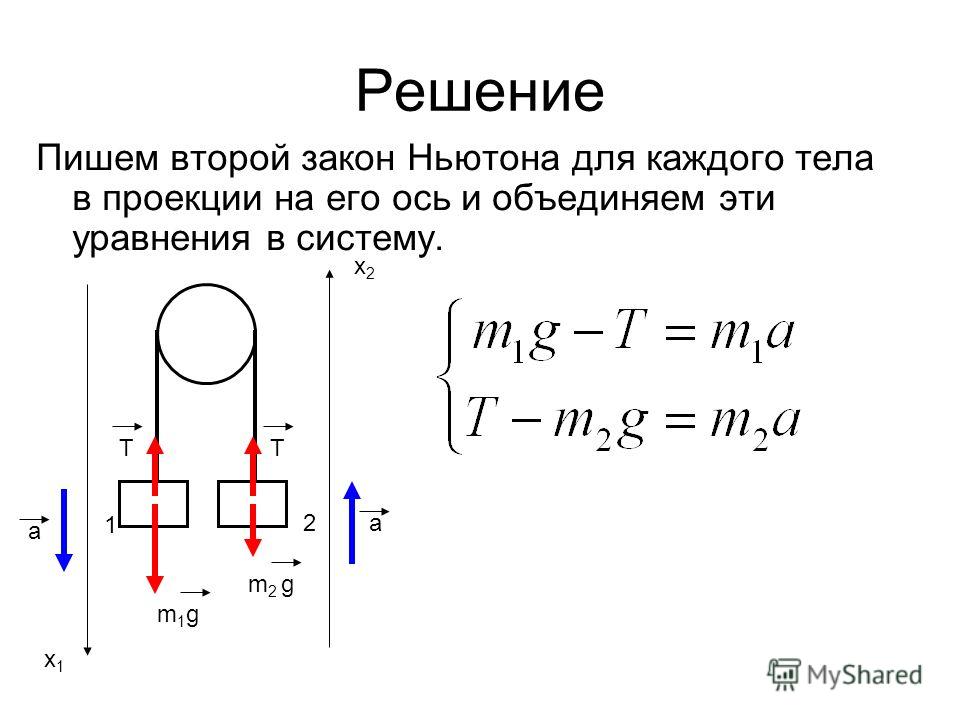 Ответ на вопрос задачи.
Ответ на вопрос задачи.
Надо выяснить , чему равна собственная скорость лодки, т.е. чему равно значение х. Мы получили, что либо х =0, либо х = 8. Первое значение нас не устраивает: собственная скорость лодки не может быть равной 0 км/ч( по условию лодка плывёт). Значит, собственная скорость лодки равна 8 км/ч.
Ответ: 8 км/ч.
Пример 2 ( 9 класс Мордкович А.Г.)
Пристани В и С находятся ниже пристани А по течению реки на 30 км и 45 км соответственно. Моторная лодка отходит от пристани А, доходит до С, сразу поворачивает назад и приходит в В, затратив на весь путь 4 ч 40 мин. В другой раз эта же лодка отошла от пристани С, дошла до А , сразу повернула назад и пришла в В, затратив на весь путь 7 ч. Чему равна собственная скорость лодки и скорость течения реки?
Решение:
1
этап. Составление математической модели.
Пусть х км/ч — собственная скорость лодки, у км/ч – скорость течения реки. Тогда (х + у) км/ч – скорость движения лодки по течению реки, а (х — у) км/ч – скорость движения лодки против течения реки. Далее получаем ч – время движения лодки от А до С, ч – время движения лодки от С до В. Всего на первый рейс лодка затратила 4 ч 40 мин, т.е. 4 ч = ч. Получаем первое уравнение системы: + = . Рассмотрим второй рейс лодки:
ч – время движения лодки от С до А, ч – время движения лодки от А до В. Всего на второй рейс затрачено 7 ч. Получаем второе уравнение:
+ = 7. Итак, получаем систему двух уравнений:
2 этап. Работа с составленной моделью.
Решим методом введения новых переменных.
Пусть = a, = b. Получаем систему:
Решив эту систему, получим а = 1, b = .
Итак, = 1, т.е. х + у =1; = , т.е. х – у = 9.
Получаем х =12, у = 3.
3
этап. Ответ на вопрос задачи.
Собственная скорость лодки 12 км/ч, скорость течения реки 3 км/ч.
Ответ: 12км/ч; 3 км/ч.
Делаем вывод, что для достижения высокого уровня освоения навыка решения задач на движение по реке необходима систематичность в решении задач этого типа.
Текстовые задачи занимают значительное место в школьной программе математики. Их особенностью является то, что они увязывают упрощенное описание действительности и ее математической модели. В процессе решения текстовых задач у обучающихся формируется умение моделировать реальные объекты и явления
Формула для класса 9 Глава — Движение
- Движение означает движение.
- Движение объекта воспринимается, когда его положение непрерывно изменяется относительно некоторого неподвижного объекта.
- В определенных ситуациях движение выводится по косвенным признакам
- Состояния покоя и движения относительны.
 Объект может казаться движущимся по отношению к одному человеку, и тот же объект может казаться неподвижным по отношению к другому человеку.
Объект может казаться движущимся по отношению к одному человеку, и тот же объект может казаться неподвижным по отношению к другому человеку. - Чтобы определить положение объекта, мы должны выбрать подходящую точку отсчета, называемую началом координат.
Расстояние и перемещение
- Расстояние, пройденное объектом, — это длина фактического пути, пройденного объектом во время движения.
- Перемещение объекта в движении – это кратчайшее расстояние между начальным положением и конечным положением объекта.
- Расстояние — это скалярная величина, имеющая только величину. Перемещение — это векторная величина, имеющая как величину, так и направление.
- Расстояние, пройденное движущимся объектом, никогда не может быть нулевым или отрицательным. Смещение может быть положительным, нулевым или отрицательным.
- Когда конечное положение движущегося объекта совпадает с его начальным положением, перемещение равно нулю, но пройденное расстояние не равно нулю.

- Между двумя заданными положениями пройденное расстояние никогда не может быть меньше смещения.
Скорость и Скорость
Скорость тела есть мера скорости движения тела . Он равен расстоянию, пройденному телом за единицу времени.
Измеряется в м/с, см/с или км/ч.
Скорость тела определяется как расстояние, пройденное телом в заданном направлении в единицу времени. Таким образом,
Решенные примеры
Q1. Вычислите скорость тела z в м/с и км/ч, если оно проходит 30 км за 6 часов
Решение: Расстояние (с) = 30 км
Время (t) = 6 часов
скорость (в км/ч) = общее расстояние/общее время = 30/6 = 5 км/ч
30 км = 30 х 1000 м = 30 000 м
6 часов = 6 х 60 х 60 с
скорость (им м/с) = (30 х 1000)/ (4 х 60 х 60) = 1,6 м/с
Q2. Первую половину пути тело движется со скоростью 60 км/ч, а вторую половину — со скоростью 10 км/ч. Вычислите среднюю скорость на всем пути.
Вычислите среднюю скорость на всем пути.
Решение: Скорость в первой половине (v1) = 60 км/ч
Скорость во второй половине (v 2 ) = 10 км/ч
Средняя скорость = (v1+v2)/2 = (60+10)/2 = 70/2 = 35
Средняя скорость объекта (тела) = 35 км/час.
Q3. Автомобиль проехал 30 км за первый час, 60 км за второй час и 10 км за третий час. Вычислите среднюю скорость поезда.
Решение: Скорость в I час = 30 км/ч
Расстояние, пройденное за 1 час = 1×30= 30 км
Скорость за 2 часа = 40 км/ч
Расстояние, пройденное за 2 часа = 1×60= 60 км
Скорость через 3 часа = 30 км/ч
Расстояние, пройденное за 3 часа = 1×10= 10 км
Средняя скорость = Общее пройденное расстояние/Общее затраченное время
= (30+60+10)/3 = 100/3 = 33,3 км/ч
Ускорение
Ускорение тела определяется как скорость изменения скорости тела во времени.
Единица ускорения = м/с 2 , см/с 2 , км/ч 2
Примеры:
Q1. Скорость автомобиля увеличивается с 30 км/ч до 50 км/ч за 4 секунды. Вычислите ускорение автомобиля.
Скорость автомобиля увеличивается с 30 км/ч до 50 км/ч за 4 секунды. Вычислите ускорение автомобиля.
Решение: u = 30 км/ч = (30×5)/18 = 25/3 = 8,33 м/с
v = 50 км/ч = (50×5)/18 = 150/9 = 13,8 м/с
т = 4 сек
а = (v-u)/t = (13,8 — 8,33)/5
= 5,47/5 = 1,094 мс-2
Q2. Автомобиль, движущийся со скоростью 30 км/ч, останавливается через 0,5 ч. Какова будет величина его замедления?
Решение: v = 0 км/ч
u = 30 км/ч
t = 0,5 часа
Запаздывание, а’ = (v-u)/t = (0-30)/0,5
= -300/5 = -60 км ч-2
В физике уравнения движения — это уравнения, описывающие поведение физической системы с точки зрения ее движения как функции времени. В частности, уравнения движения определяют поведение физической системы как набор математических функций, зависящих от переменных.
- v = u + at
- s = ut + 1/2at 2
- v 2 = u 2 + 2as
Команда Physics Wallah и преподаватели подготовили все необходимые Physics Formula для класса физики 9 главы Motion в листе pdf. Учебник NCERT настоятельно рекомендуется учащимся 9-го класса решать числовые задачи и использовать их в качестве справочных решений NCERT для 9-го класса. Студенты также могут посетить CBSE класс 9 Заметки по физике , так как им будет очень полезно понять концепции.
Учебник NCERT настоятельно рекомендуется учащимся 9-го класса решать числовые задачи и использовать их в качестве справочных решений NCERT для 9-го класса. Студенты также могут посетить CBSE класс 9 Заметки по физике , так как им будет очень полезно понять концепции.
Также проверьте
- Рабочий лист для класса 9
- Вопросы MCQ для класса 9 по естественным наукам с ответами
Скачать бесплатно PDF лист со всеми формулами главы — Motion Class 9 ниже.
Богатые задачи — математика для любви
Богатые задачи
Каждый учащийся заслуживает возможности решать задачи и заниматься подлинным математическим мышлением. Расширенные задачи предназначены для того, чтобы сделать этот богатый опыт обучения возможным. Мы написали эти задания для быстрого запуска, вовлечения учащихся и развития навыков мышления, необходимых математикам: настойчивость и поиск закономерностей, смелость и любознательность, организованность и общение.

 Объект может казаться движущимся по отношению к одному человеку, и тот же объект может казаться неподвижным по отношению к другому человеку.
Объект может казаться движущимся по отношению к одному человеку, и тот же объект может казаться неподвижным по отношению к другому человеку.
Leave A Comment