1. Найдите объем выпукло-вогнутой линзы, у которой радиусы поверхностей… Самостоятельные работы. С-19. В-6. Зив Б.Г. 11 класс Геометрия ГДЗ.
1. Найдите объем выпукло-вогнутой линзы, у которой радиусы поверхностей… Самостоятельные работы. С-19. В-6. Зив Б.Г. 11 класс Геометрия ГДЗ. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?1. Найдите объем выпукло-вогнутой линзы, у которой радиусы поверхностей равны 25 и 29, а расстояние между
центрами 6.
ответы
ответ
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЮморОлимпиадыЕГЭКомпьютерные игрыпохожие вопросы 5
Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.Привет. Запуталась при решении, нужна помощь знатоков!!!
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)
ГДЗГеометрия11 класс10 классАтанасян Л.С.
Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный переносИспользуя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости.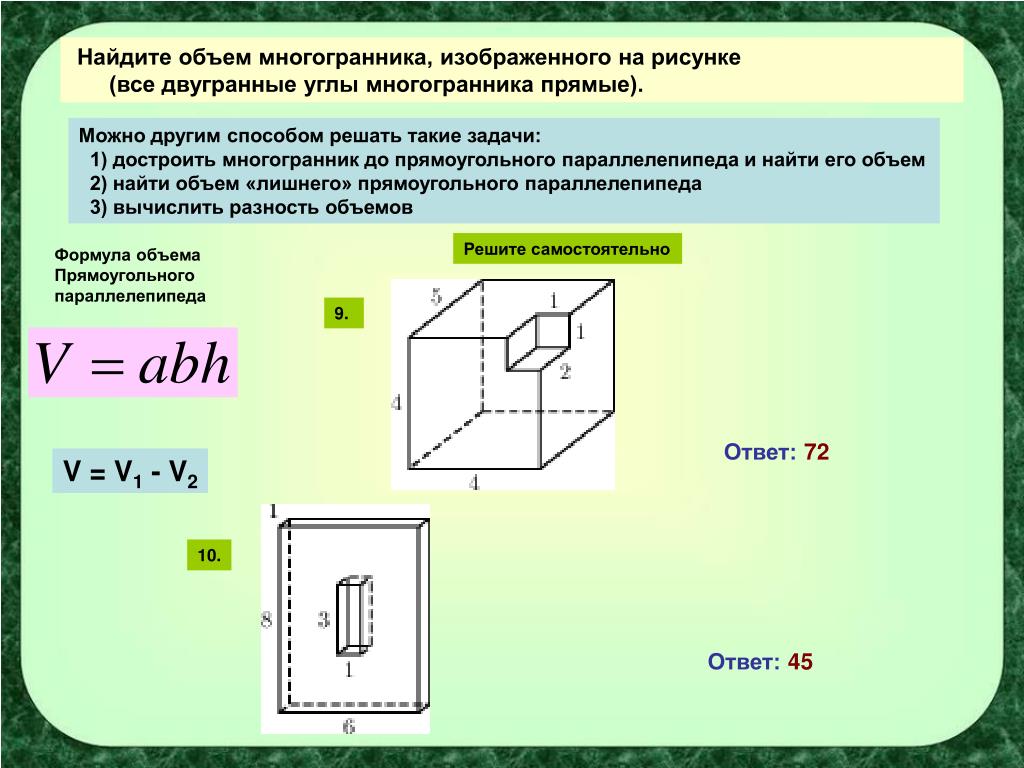
(Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?С чем связано окончание приема учащихся в Московский институт телевидения и радиовещания «Останкино»? (Подробнее…)
ВузыПоступление11 классНовости
Какой был проходной балл в вузы в 2017 году?Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее…)
Поступление11 классЕГЭНовости
Объем. 11 класс
ОБЪЕМ ФИГУР В ПРОСТРАНСТВЕ
Объем – величина, аналогичная площади и сопоставляющая фигурам в пространстве неотрицательные действительные числа. За единицу объема принимается куб, ребро которого равно единице измерения длины.
Для объемов пространственных фигур справедливы свойства, аналогичные свойствам площадей плоских фигур, а именно:
1. Объем фигуры в пространстве является неотрицательным числом.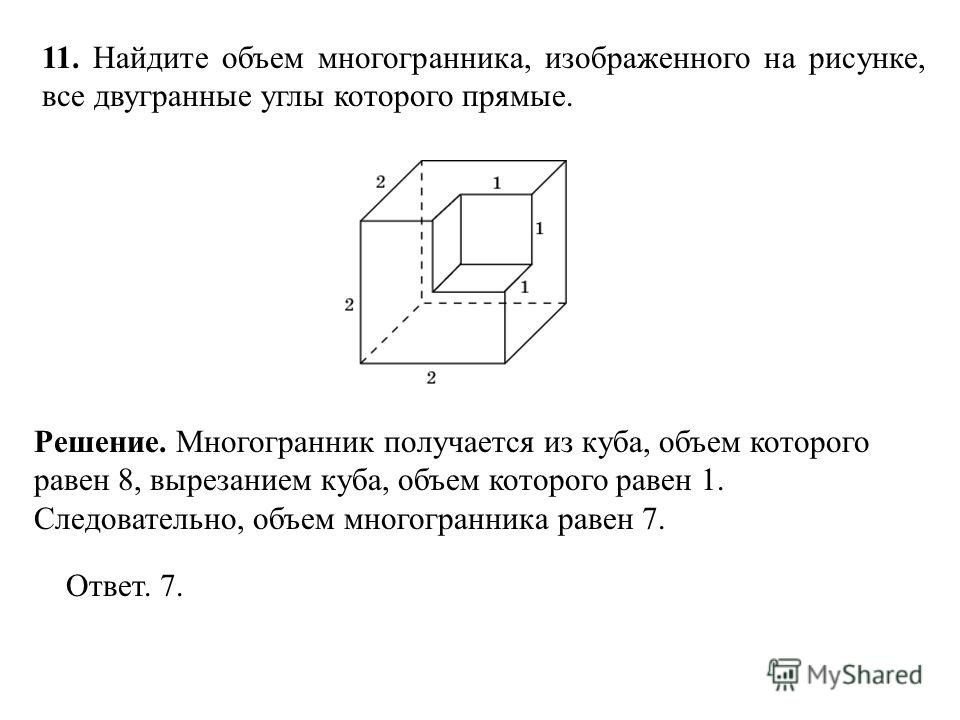
2. Равные фигуры имеют равные объемы.
3. Если фигура Ф составлена из двух неперекрывающихся фигур Ф 1 и Ф 2 , то объем фигуры Ф равен сумме объемов фигур Ф 1 и Ф 2 , т.е.
V ( Ф )= V ( Ф 1 )+ V ( Ф 2 ).
Две фигуры, имеющие равные объемы, называются равновеликими.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Объем прямой призмы
Объем прямоугольного параллелепипеда равен произведению трех его измерений, т. е. имеет место формула
где a , b , c
Объем прямой призмы равен произведению площади ее основания на высоту, т. е. имеет место формула
где S – площадь основания, h – высота призмы.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Объем цилиндра и шара
Объем цилиндра, высота которого равна h и радиус основания R , выражается формул ой
Объем шара радиуса R выражается формулой
В режиме слайдов ответы и решения появляются после кликанья мышкой
Упражнение 1
Как относятся объемы двух кубов: данного и его модели, уменьшенной в масштабе: а) 1 : 2; б) 1 : 3; в) 1 : n ?
Ответ: а) 1 : 8;
б) 1 : 27;
в) 1 : n 3 .
Упражнение 2
Площадь поверхности куба равна 24. Найдите его объем.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: 8 .
Упражнение 3
Если каждое ребро куба увеличить на 2 см, то его объем увеличится на 98 см 3 . Определите ребро куба.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 3 см.
Упражнение 4
Как изменится объем прямого параллелепипеда, если: а) одно из его измерений увеличить в 2 раза, в 3 раза, в n раз; б) если два его измерения увеличить, причем каждое из них в 2, 3, n раз; в) если все три его измерения увеличить в 2, 3, n раз?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: а) Увеличится в 2 раза, в 3 раза, в n раз;
б) увеличится в 4 раза, в 9 раза, в n 2 раз;
в) увеличится в 8 раз, в 27 раз, в n 3 раз.
Упражнение 5
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 3. Каким должно быть третье ребро, выходящее из той же вершины, чтобы объем этого параллелепипеда равнялся 30?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 5.
Упражнение 6
Основанием аквариума является прямоугольник со сторонами 40 см и 50 см. Уровень воды в нем находится на высоте 80 см. Эту воду перелили в другой аквариум, основанием которого является прямоугольник со сторонами 80 см и 100 см. На какой высоте будет находиться уровень воды?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 20 см .
Упражнение 7
Сколько коробок в форме прямоугольного параллелепипеда размерами 30х40х50 (см) можно поместить в кузов машины размерами 2х3х1,5 (м)?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 150.
Упражнение 8
Чему равен объем пространственного креста, если ребра образующих его кубов равны единице?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 7 .
Упражнение 9
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение 1. М ногогранник состоит из двух прямоугольных параллелепипедов , объемы которых равн ы 2 и 4 . Следовательно, объем многогранника рав ен 6 .
Решение 2. М ногогранник получается из куба, объем которого равен 8, вырезанием прямоугольного параллелепипеда, объем которого равен 2. Следовательно, объем многогранника рав ен 6 .
Ответ. 6.
Упражнение 10
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение 1. М ногогранник состоит из двух прямоугольных параллелепипедов , объемы которых равн ы 2 и 4 .
Решение 2. М ногогранник получается из куба, объем которого равен 8, вырезанием прямоугольного параллелепипеда, объем которого равен 2. Следовательно, объем многогранника рав ен 6 .
Ответ. 6.
Упражнение 11
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение 1. М ногогранник состоит из двух прямоугольных параллелепипедов , объемы которых равн ы 2 и 4 . Следовательно, объем многогранника рав ен 6 .
Решение 2. М ногогранник получается из куба, объем которого равен 8, вырезанием прямоугольного параллелепипеда, объем которого равен 2. Следовательно, объем многогранника рав ен 6 .
Ответ. 6.
Упражнение 1 2
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение. М ногогранник составлен из двух прямоугольных параллелепипедов, объемы которых равны 9 и 1.
Следовательно, объем многогранника рав ен 10 .
Ответ. 10.
Упражнение 1 3
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение. М ногогранник получается из куба, объем которого равен 8, вырезанием куба, объем которого равен 1. Следовательно, объем многогранника рав ен 7 .
Ответ. 7.
Упражнение 1 4
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение. М ногогранник получается из прямоугольного параллелепипеда, объем которого равен 48, вырезанием прямоугольного параллелепипеда, объем которого равен 8. Следовательно, объем многогранника рав ен 40 .
Ответ. 48.
Упражнение 15
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Ответ. 12.
Упражнение 16
Дан куб с ребром 3 см.
В каждой грани проделано сквозное квадратное отверстие со стороной 1 см. Найдите объем оставшейся части.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 20 см 3 .
Упражнение 17
Найдите объем правильной четырехугольной призмы, сторона основания которой 5 см и высота 8 см.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 200 см 3 .
Упражнение 18
Найдите высоту правильной четырехугольной призмы, если сторона ее основания 20 см и объем 4800 см 3 .
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 12 см.
Упражнение 19
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 см и 4 см, высота призмы равна 10 см. Найдите объем данной призмы.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 60 см 3 .
Упражнение 20
Найдите объем правильной 6 -угольной призмы, высота которой равна h , а сторона основания равна a .
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ:
Упражнение 21
Объем правильной шестиугольной призмы равен V . Определите объем призмы, вершинами оснований которой являются середины сторон оснований данной призмы.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ:
Упражнение 2 2
Найдите объем общей части (пересечения) двух единичных кубов, вершина одного из которых расположена в центре другого, как показано на рисунке.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 1/8
Упражнение 2 3
Найдите объем фигуры, составленной из двух единичных кубов, две вершины одного из которых расположены в центрах граней другого.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 1,75.
Упражнение 2 4
Осевое сечение прямого кругового цилиндра — квадрат со стороной 1 см. Найдите объем цилиндра.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: см 3 .
Упражнение 2 5
Одна кружка вдвое выше другой, зато другая в полтора раза шире. Какая кружка вместительнее?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: Та, которая шире.
Упражнение 26
Найдите объем части цилиндра, изображенной на рисунке , если объем всего цилиндра равен 8.
Ответ. 2.
Упражнение 27
Найдите объем части цилиндра, изображенной на рисунке , если объем всего цилиндра равен 12 .
Ответ. 9.
Упражнение 28
Найдите объем части цилиндра, изображенной на рисунке , если объем всего цилиндра равен 12 .
Ответ. 2.
Упражнение 29
Найдите объем части цилиндра, изображенной на рисунке , если объем всего цилиндра равен 9 .
Ответ. 7,5.
Упражнение 30
Найдите объем части цилиндра, изображенной на рисунке , если объем всего цилиндра равен 4 .
Ответ. 3.
Упражнение 31
Найдите объем части цилиндра, изображенной на рисунке , если объем всего цилиндра равен 8 .
Ответ. 6.
Упражнение 32
Площадь боковой поверхности и объем цилиндра выражаются одним и тем же числом. Найдите диаметр основания цилиндра.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: 4.
Упражнение 33
Во сколько раз объем цилиндра, описанного около правильной четырехугольной призмы, больше объема цилиндра, вписанного в эту же призму?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: В 2 раза.
Упражнение 34
В цилиндрический сосуд, диаметр которого равен 9 см, опущена деталь. При этом уровень жидкости в сосуде поднялся на 12 см. Чему равен объем детали?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 243 см 3 .
Упражнение 35
В цилиндрическом сосуде уровень жидкости достигает 18 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого?
Ответ. 2 см.
Упражнение 36
Объём шара равен 288 дм 3 . Найдите площадь его поверхности.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: 144 дм 2 .
Упражнение 37
Около шара описан цилиндр. Найдите отношение их площадей поверхностей и объемов.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: 2:3; 2:3.
Упражнение 38
Вишня имеет форму шара.
Диаметр косточки равен толщине мякоти. Во сколько раз объем мякоти больше объема косточки?
Решение. Диаметр вишни в три раза больше диаметра косточки. Следовательно, объем вишни в 27 раз больше объема косточки. Значит, объем мякоти в 26 раз болше объема косточки.
В режиме слайдов ответ появляется после кликанья мышкой
Упражнение 39
Одним из пространственных аналогов ковра Серпинского является губка Менгера. Она получается, если из куб разбить на 27 кубиков, вырезать центральный кубик и еще 6 кубиков, прилегающих к его граням. Затем повторить эту операцию к оставшимся кубикам и т.д. Найдите ее объем, считая исходный куб единичным.
Решение. На первом шаге выреза е тся пространственный крест, состоящий из семи кубиков, объемом 7 / 27 . На каждом следующем шаге число вырезаемых пространственных крестов увеличивается в 20 раз, а объем каждого из них уменьшается в 27 раз. Таким образом, общ ий объем вырезаемых пространственных представляет собой сумму геометрической прогрессии с начальном членом 7 /27 и знаменателем 20/27 .
По формуле суммы геометрической прогрессии находим, что это число равно единице . Следовательно, объем губки Менгера равн ен нулю.
Калькулятор объема
Ниже приведен список калькуляторов объема для нескольких распространенных форм. Пожалуйста, заполните соответствующие поля и нажмите кнопку «Рассчитать».
Калькулятор объема сферы
Калькулятор объема конуса
Калькулятор объема куба
Калькулятор объема цилиндра
Калькулятор объема прямоугольного резервуара
|
Калькулятор объема капсулы
Калькулятор объема сферической крышки
Для расчета укажите любые два значения ниже.
|
Калькулятор объема усеченного конуса
|
Калькулятор объема эллипсоида
|
Калькулятор объема квадратной пирамиды
Калькулятор объема пробирки
|
Связанные Калькулятор площади поверхности | Калькулятор площади
Объем – это количественная оценка трехмерного пространства, занимаемого веществом.
Единицей объема в системе СИ является кубический метр или 9.0253 м 3 . По соглашению объем контейнера обычно представляет собой его вместимость и количество жидкости, которое он может вместить, а не объем пространства, которое вытесняет фактический контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы можно разбить на более простые совокупные формы, и сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм, можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы. Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Сфера
Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, равноудаленных от заданной точки в его центре, где расстояние между центром и любой точкой на сфере равно радиусу r . Вероятно, наиболее известным сферическим объектом является идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и вычисление их объемов одинаково. Как и в случае с окружностью, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром, д . Уравнение для расчета объема сферы приведено ниже:
| объем = | πr 3 |
EX: Клэр хочет наполнить идеально сферический водяной шар радиусом 0,15 фута уксусом, чтобы использовать его в битве с водяным шаром против ее заклятого врага Хильды в ближайшие выходные.
Необходимый объем уксуса можно рассчитать по приведенному ниже уравнению:
объем = 4/3 × π × 0,15 3 = 0,141 фута 3
Конус
Конус представляет собой трехмерную форму, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус образован подобно кругу набором отрезков, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или какое-либо другое основание). На этой странице рассматривается только случай конечного прямого кругового конуса. Конусы, состоящие из полулиний, некруглых оснований и т. д., которые простираются до бесконечности, рассматриваться не будут. Уравнение для расчета объема конуса выглядит следующим образом:
| объем = | πr 2 ч |
где r — радиус, а h — высота конуса
ПРИМЕР: Беа полна решимости выйти из магазина мороженого с хорошо потраченными 5 долларами, заработанными тяжелым трудом.
Хотя она предпочитает обычные сахарные рожки, вафельные рожки, бесспорно, крупнее. Она определяет, что на 15 % предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15 % объем сахарного рожка. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью приведенного ниже уравнения:
объем = 1/3 × π × 1,5 2 × 5 = 11,781 дюйма 3
Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет < 15%, и решает купить сахарный рожок. . Теперь все, что ей нужно сделать, это использовать свою ангельскую детскую привлекательность, чтобы заставить персонал опустошить контейнеры с мороженым в ее рожок.
Куб
Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых сходятся в каждой из его вершин и все перпендикулярны соответствующим соседним граням.
Куб является частным случаем многих классификаций фигур в геометрии, включая квадратный параллелепипед, равносторонний кубоид и правильный ромбоэдр. Ниже приведено уравнение для расчета объема куба:
объем = а 3
где a — длина ребра куба
ПРИМЕР: Боб, родившийся в Вайоминге (и никогда не покидавший штат), недавно посетил родину своих предков в Небраске. Потрясенный великолепием Небраски и окружающей средой, непохожей ни на что другое, с чем он когда-либо сталкивался ранее, Боб понял, что ему нужно привезти часть Небраски домой с собой. У Боба есть чемодан кубической формы с краями длиной 2 фута, и он вычисляет объем земли, который он может унести с собой домой, следующим образом:
объем = 2 3 = 8 футов 3
Цилиндр
Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от заданной прямой оси. Однако в обычном употреблении «цилиндр» относится к прямолинейному круговому цилиндру, основаниями которого являются окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой 90 253 h 90 256 и радиусом 90 253 r 90 256.
. Уравнение для расчета объема цилиндра показано ниже:
объем = πr 2 ч
где r — радиус, а h — высота резервуара
ПРИМЕР: Кэлум хочет построить замок из песка в гостиной своего дома. Поскольку он решительно выступает за переработку отходов, он нашел три цилиндрические бочки с незаконной свалки и очистил их от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя приведенное ниже уравнение:
объем = π × 3 2 × 4 = 113,097 фута 3
Он успешно строит замок из песка в своем доме, и в качестве дополнительного бонуса ему удается экономить электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым в темноте. темнота.
Прямоугольный резервуар
Прямоугольный резервуар представляет собой обобщенную форму куба, стороны которого могут иметь различную длину.
Он ограничен шестью гранями, три из которых сходятся в его вершинах и все перпендикулярны соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
объем= длина × ширина × высота
ПРИМЕР: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к тортам. Она планирует пройти по тропе Калалау на Кауаи, и, хотя Дарби в отличной форме, она беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет наполнить свой идеально прямоугольный пакет длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может поместить в свою упаковку, рассчитывается ниже:
объем = 2 × 3 × 4 = 24 фута 3
Капсула
Капсула представляет собой трехмерную геометрическую форму, состоящую из цилиндра и двух полусферических концов, где полусфера представляет собой половину сферы.
Отсюда следует, что объем капсулы можно рассчитать, комбинируя уравнения объема для сферы и прямого кругового цилиндра:
| объем = πr 2 ч + | πr 3 = πr 2 ( | р + ч) |
где r радиус и h высота цилиндрической части
Джо может взять с собой капсулу времени, которую он хочет похоронить для будущих поколений в своем путешествии самопознания через Гималаи:
объем = π × 1,5 2 × 3 + 4/3 × π ×1,5 3 = 35,343 футов 3
Сферическая крышка
Сферическая крышка представляет собой часть сферы, отделенную от остальной части сферы плоскостью. Если плоскость проходит через центр сферы, сферическая шапка называется полусферой. Существуют и другие различия, в том числе сферический сегмент, где сфера сегментирована двумя параллельными плоскостями и двумя разными радиусами, где плоскости проходят через сферу.
Уравнение для расчета объема сферической шапки получено из уравнения для сферического сегмента, где второй радиус равен 0. Относительно сферической шапки, показанной в калькуляторе:
| объем = | πh 2 (3R — h) |
Имея два значения, предоставленный калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:
Дано r и R : h = R ± √R 2 — r 2
Он отрезает идеальный сферический колпачок от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимого для замены сферического колпачка и смещения веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:0003
Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее и откусывает часть нижней части рожка, которая идеально параллельна ранее единственному отверстию. Беа теперь осталась с протекающим мороженым в правом коническом усеченном конусе, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма и радиусы 1,5 дюйма и 0,2 дюйма:
Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может поместить в свой бутерброд. Учитывая, что осевая длина его булочки составляет 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат вычисляет объем мяса, который он может поместить в каждую выдолбленную булочку, следующим образом:
Будучи старшим из своих братьев и сестер Ту, Три и Форе, он может легко загнать их в загон и использовать по своему желанию. Воспользовавшись этим, Ван решает воспроизвести древние египетские времена и попросить своих братьев и сестер выступить в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать с помощью уравнения для квадрата. пирамида:
С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:
Объем запатентованного ударопрочного бетона, необходимый для строительства трубы с внешним диаметром 3 фута, внутренним диаметром 2,5 фута и длиной 10 футов, можно рассчитать следующим образом:
Leave A Comment