В параллелограмме диагонали являются биссектрисами: Решение №3156 В параллелограмме ABCD диагонали являются биссектрисами его углов, AB = 45, AC = 72.

Параллелограмм — Умскул Учебник

Математика

10.5.2022

22382

Поделитесь статьей в социальных сетях:

На этой странице вы узнаете

• Чем отличаются признаки от свойств?
• Сколько крыс у биссектрисы?
• Гибридом чего будет квадрат?

Когда мы видим изображение с множеством деталей, наш мозг автоматически раскладывает их на простые фигуры. Этот процесс занимает доли секунды. Разные геометрические фигуры вызывают у нас разные ощущения, эмоции и ассоциации.А что будет, если мы задержим взгляд на одной из них и разберем подробнее? Давайте сделаем так с параллелограммом.

Параллелограмм

Параллелограмм – это четырёхугольник, чьи стороны попарно параллельны и равны. 

Параллелограмм мы видим достаточно часто.

Признаки параллелограмма

У параллелограмма есть три основных признака. Если для четырехугольника выполняется хотя бы один из признаков, такой четырехугольник можно называть параллелограммом.

Признаки параллелограмма:

1. Две противоположные стороны четырехугольника параллельны и равны.

2. Противоположные стороны четырехугольника попарно равны.

3. Диагонали четырехугольника пересекаются и в точке пересечения делятся пополам.

Свойства параллелограмма

Чем отличаются признаки от свойств? Свойства нельзя путать с признаками, хоть они и очень похожи. Свойствами параллелограмма обладает фигура, уже являющаяся параллелограммом, тогда как признаки предназначены для выявления параллелограммов среди четырехугольников.

Свойства параллелограмма:

1. Противолежащие стороны равны.

2. Противолежащие стороны параллельны.

3. Противолежащие углы равны.

4. Сумма всех углов 360⁰.

5. Диагонали пересекаются и точкой пересечения делятся пополам.

6. Сумма углов, прилежащих к любой стороне, равна 180⁰.

7. Сумма квадратов диагоналей равна сумме квадратов всех сторон.

8. Диагонали делят параллелограмм на четыре треугольника с одинаковой площадью.

9. Каждая диагональ делит параллелограмм на два равных треугольника

Биссектриса в параллелограмме

Можно ли провести биссектрису в параллелограмме? Да. Биссектриса параллелограмма – это луч, исходящий из вершины угла параллелограмма, делящий этот угол на два равных угла и пересекающий одну из сторон параллелограмма.

Сколько крыс у биссектрисы? Значение биссектрисы легко запомнить, используя фразу “Биссектриса – это крыса, она бегает по углам и делит угол пополам”. Так как у треугольника три угла – соответственно, и крыс-биссектрис тоже три.

 Два факта связанные с биссектрисой в параллелограмме:

1. Биссектриса, проведенная из угла параллелограмма, отсекает от него равнобедренный треугольник.

2. Биссектрисы углов, принадлежащих одной стороне параллелограмма, пересекаются под прямым углом.

Площадь параллелограмма

Есть три формулы площади параллелограмма, которые применяются в зависимости от известных величин

1. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

2. Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними.

3. Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.

Прямоугольник

Как параллелограмм связан с прямоугольником?

Прямоугольник – это параллелограмм, углы которого по 900.   

Данную фигуру часто называют частным случаем параллелограмма. Из этого следует, что для прямоугольника применимы те же признаки и свойства, что для параллелограмма, но и имеется ряд собственных.

В жизни прямоугольником можно назвать дверь, картину или фотографию:

Признаки прямоугольника

1. Параллелограмм, имеющий хотя бы один прямой угол.

2. Параллелограмм, все углы которого равны.

3. Параллелограмм, диагонали которого равны.

4. Четырехугольник, у которого три прямых угла.

Свойства прямоугольника

1. Все углы прямые.

2. Диагонали равны.

3. Стороны прямоугольника одновременно являются и его высотами.
4. Сумма квадратов двух прилежащих сторон равна квадрату диагонали.

Биссектриса и площадь прямоугольника

Биссектриса делит угол прямоугольника на два угла по 45⁰ и пересекает одну из сторон прямоугольника.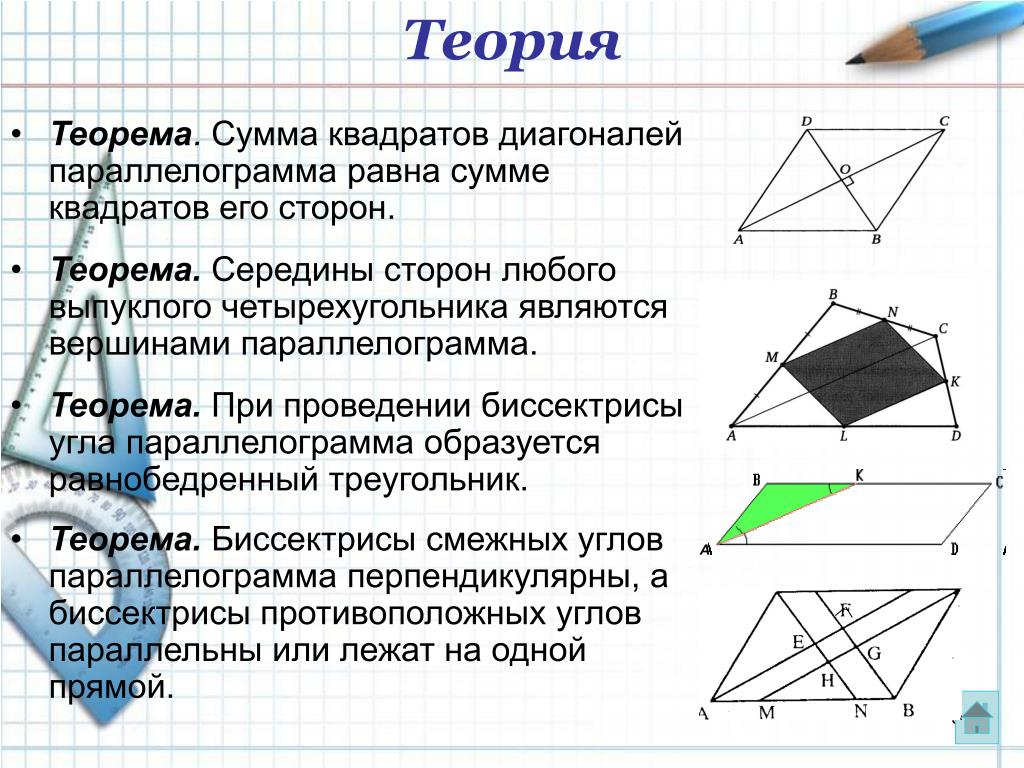

Теперь рассмотрим два способа нахождения площади прямоугольника:

1. Площадь прямоугольника равна произведению двух соседних сторон.

2. Площадь прямоугольника равна половине произведения квадрата диагонали на синус угла между диагоналями.

Ромб

Пожалуй, это самая неустойчивая фигура.

Ромб – это параллелограмм, у которого все стороны равны. 

Ромб можно увидеть на знаке машины “Митсубиси”, их там целых три.

А также в игровых наградах:

Также является частным случаем параллелограмма и обладает его признаками и свойствами, но имеет и собственные.

Всё о ромбе

Признаки ромба:

1. Две смежные стороны параллелограмма равны.
2. Диагонали параллелограмма пересекаются под прямым углом.
3. Диагональ параллелограмма делит каждый угол пополам.
4. Четырехугольник, у которого все стороны равны.

Свойства ромба:

1. Все стороны равны.

2. Диагонали пересекаются под прямым углом и точкой пересечения делятся пополам.

3. Диагонали являются биссектрисами.

4. Высоты в ромбе равны.

Как уже отмечено в свойствах ромба, биссектрисой ромба является диагональ.

Как найти площадь ромба?

Для нахождения площади ромба есть три разные формулы:

1. Площадь ромба равна произведению стороны и высоты ромба.

2. Площадь ромба равна половине произведения его диагоналей.

3. Площадь ромба равна произведению квадрата стороны на синус угла ромба.

Квадрат

А вот квадрат, наоборот, достаточно устойчив.

Квадрат – это четырехугольник, у которого все углы и стороны равны. 

Гибридом чего будет квадрат? Если внимательно посмотреть на определение, то можно заметить, что квадрат объединяет в себе и параллелограмм, и прямоугольник, и ромб. Нечто, сочетающее в себе разнородные элементы, называют гибридом. Квадрат будет иметь все признаки и свойства родительских фигур:параллелограмма, прямоугольника и ромба.

Квадратом может быть крышка подарочной коробки или окно.

Рассмотрим признаки и свойства данной фигуры.

Всё о квадрате

Признаки квадрата:

1. Ромб, у которого хотя бы один угол прямой.
2. Ромб, у которого все углы равны.
3. Ромб, у которого диагонали равны.
4. Четырехугольник, диагонали которого равны и перпендикулярны.

Свойства квадрата:

1. Диагональ квадрата равна 2 стороны квадрата.

2. Диагонали делят квадрат на четыре равных треугольника.

Биссектрисой квадрата, как и у ромба, является диагональ.

Рассмотрим формулы для нахождения площади квадрата:

1. Площадь квадрата равна квадрату его стороны.

2. Площадь квадрата равна половине квадрата диагонали.

Фактчек

• Параллелограмм – это четырёхугольник, чьи стороны попарно параллельны и равны.
• Прямоугольник – это параллелограмм, углы которого по 900 и диагонали которого равны.
• Ромб – это параллелограмм, у которого все стороны равны, а также диагонали перпендикулярны друг другу
• Квадрат – это четырехугольник, у которого все углы и стороны равны. Квадрат является гибридом параллелограмма, прямоугольника и ромба.

Проверь себя

Задание 1.
Найдите площадь параллелограмма, если его стороны 5 и 8, а угол между ними 30⁰ 

1. 40
2. 20
3. 10
4. 25

Задание 2.
Найдите площадь прямоугольника, если его диагональ 12, а угол между диагоналями 60⁰

1. 83
2. 6
3. 63
4. 4

Задание 3.
Найдите площадь ромба, если его диагонали 6 и 10

1. 30
2. 60
3. 15
4. 25

Задание 4.
У четырехугольника диагонали пересекаются под углом 30⁰, а его стороны попарно параллельны и равны. Что это за фигура?

1. Квадрат
2. Ромб
3. Прямоугольник
4. Параллелограмм

Задание 5.
У четырехугольника две противоположные стороны параллельны и равны и есть один прямой угол. Что это за фигура?

1. Квадрат
2. Ромб
3. Прямоугольник
4. Параллелограмм

Ответы: 1. – 2; 2. – 3; 3. – 1; 4. – 4; 5. – 3

Математика Параллелограмм

Поделитесь статьей в социальных сетях:

Понравилась статья? Оцени:

Читайте также:

Параллелограмм

Чему равна наименьшая из сторон параллелограмма, если его периметр равен 36 см, а одна из сторон в два раза больше другой:

6 см

12 см

18 см

 

Если в параллелограмме ABCD угол А  угол В  угол D = 252°, тогда угол А равен:

90°

108°

72°

 

В параллелограмме ABCD диагональ АС со сторонами АВ и ВС образует углы 45° и 25° соответственно. Величина угла С равна:

45°

25°

70°

 

Четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых:

параллелограмм

ромб

квадрат

 

Частным случаем параллелограмма является:

треугольник

сфера

ромб

 

Частным случаем параллелограмма является:

круг

квадрат

сфера

 

Частным случаем параллелограмма является:

круг

треугольник

прямоугольник

 

Противолежащие стороны параллелограмма:

равны

не равны

зависит от условий

 

Противолежащие углы параллелограмма:

зависит от условий

не равны

равны

 

Сумма углов, прилежащих к одной стороне, равна:

90°

180°

45°

 

Точка пересечения диагоналей является … параллелограмма:

центром симметрии

сферой симметрии

основой симметрии

 

Параллелограмм диагональю делится на два … треугольника:

не равных

равных

оба варианта верны

 

Аффинное преобразование всегда переводит параллелограмм в:

параллелограмм

ромб

круг

 

У четырёхугольника без самопересечений две противоположные стороны:

только параллельны

только равны

одновременно равны и параллельны

 

У четырёхугольника без самопересечений все противоположные стороны попарно:

равны

параллельны

оба варианта верны

 

Площадь параллелограмма равна произведению его основания:

на одну из сторон

на высоту

оба варианта верны

 

Площадь параллелограмма равна произведению его сторон на … угла между ними:

косинус

тангенс

синус

 

Средние линии параллелограмма пересекаются в точке пересечения:

его высоты

его диагоналей

его основания

 

Одно из равенств в векторной алгебре и векторном анализе:

природа параллелограмма

свойство параллелограмма

тождество параллелограмма

 

Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна:

его периметру

его полупериметру

его основанию

 

В параллелограмме ABCD биссектриса угла А пересекает сторону ВС в точке К так, что ВК = 7 см, КС = 3 см. Периметр параллелограмма равен:

34 см

30 см

38 см

 

В параллелограмме ABCD высота, опущенная на сторону CD, делит ее пополам и образует с диагональю BD угол 30°, АВ = 10 см. Необходимо найти периметр параллелограмма:

28 см

40 см

30 см

 

В параллелограмме ABCD биссектрисы углов B и D пересекают стороны AD и ВС в точках М и К соответственно так, что MD = 5 см, КС = 7 см. Необходимо найти периметр ABCD:

32 см

24 см

38 см

 

Периметр параллелограмма равен 32 см, а две из его сторон относятся как 3 : 1. Наибольшая из его сторон равна:

22 см

12 см

8 см

 

Если в параллелограмме ABCD угол А  угол В  угол С = 237°, тогда угол В равен:

79°

29°

123°

 

В параллелограмме ABCD диагональ BD со сторонами АВ и AD образует углы, равные соответственно 52° и 26°. Величина угла В равна:

26°

78°

52°

 

В параллелограмме ABCD биссектриса угла В пересекает сторону AD в точке М так, что АМ = 8 см, MD = 4 см. Периметр параллелограмма равен:

40 см

12 см

24 см

 

В параллелограмме ABCD отрезки AC и BD являются:

соседними сторонами

противоположными сторонами

диагоналями

 

Дайте название следующему утверждению: в параллелограмме противоположные стороны равны:

свойство параллелограмма

определение параллелограмма

признак параллелограмма

 

Если в четырехугольнике диагонали пересекаются и в точке пересечения делятся пополам, то это параллелограмм:

свойство параллелограмма

признак параллелограмма

определение параллелограмма

 

Обычная страница без названия

Обычная страница без названия

---

«Диагонали ромба делят углы ромба пополам. » Схема проверки
Использование Блокнот геометра
Дэвида Уайза

---

Примечание. Я рекомендую распечатать эту страницу, чтобы инструкциям легче следовать.

---

Чтобы успешно завершить доказательство, важно подумать над определением и построением ромба.
В следующем плане я приведу утверждения, вы указать причины .

---

Докажите: если четырехугольник — ромб, то диагонали делят углы пополам.

Дано: ромб ABCD с диагоналями BD и AC.

Докажите: отрезок AC делит углы пополам БАД и ДКБ. Отрезок DB делит пополам углы ADC и CBA.

---

• Ромб — это параллелограмм, поэтому определение а свойства параллелограмма применимы к ромбу.
• Рассмотрим, как устроен ромб——параллельно линии.
• Учитывать свойства параллельных прямых и вертикальные углы.
• Каждая диагональ образует пару треугольников.
• Учитывать свойства конгруэнтности треугольников.
• Рассмотрим равнобедренные треугольники и их свойства.
• Нажмите здесь , чтобы исследовать этот эскиз, чтобы помочь с шагами доказательства.

---

Доказательство :

Сначала будем использовать только диагональный AC.

1. Отрезок DA конгруэнтен отрезку AB.
2. Сегмент CD конгруэнтен сегменту CB.
3. Сегмент CA конгруэнтен сегменту CA.
4. Треугольник DAC равен треугольнику BAC.
5. Угол CAD равен углу BAC. Угол DCA равен углу ACB.
6. Отрезок AC делит пополам углы BAD и ДКБ.

Тогда будем использовать только диагональные BD.

 

1. Сегмент DA конгруэнтен сегменту DC.
2. Отрезок AB конгруэнтен отрезку BC.
3. Отрезок BD конгруэнтен отрезку BD.
4. Треугольник DAB равен треугольнику DCB.
5. Угол ADB равен углу BDC. Угол DBA равен углу CBD.
6. Отрезок BD делит пополам углы ADC и ЦБ.

---

Внутренний номер :

1. Преобразование двухколонного доказательство в доказательство абзаца.
2. Найдите альтернативный способ докажите, что диагонали параллелограмма делят друг друга пополам.

---

Если у вас возникнут вопросы при попытке завершить это расследование, или предложения, которые были бы полезны, особенно для использования на уровень средней школы, пожалуйста, отправьте электронное письмо по адресу [email protected] .

Возврат в Содержание.

---

Balbharati Solutions for Mathematics 2 Geometry 9th Standard Maharashtra State Board

Mathematics 2 Geometry 9th Standard Maharashtra State Board

Автор: Balbharati/>Издатель: Бюро производства учебников и учебных программ штата Махараштра/>Язык: английский/>/>

Shaalaa предоставляет решения для 9-го стандарта Balbharati и содержит все ответы на вопросы, заданные в Математика 2 Геометрия 9-й стандарт Государственного совета Махараштры . Shaalaa — это, безусловно, сайт, который используют большинство ваших одноклассников, чтобы хорошо сдать экзамены.

Вы можете решить вопросы учебника Mathematics 2 Geometry 9th Standard Maharashtra State Board и использовать решения Shaalaa Balbharati для 9th Standard Geometry, чтобы проверить свои ответы.

Появляется в

• SSC (английский средний) 9th Standard Maharashtra State Board

Balbharati 9th Стандартные решения по другим предметам

Мы также предлагаем решения по другим предметам, которые помогут вам лучше сдать экзамены. Эти решения Balbharati специально подобраны с учетом шаблонов экзаменов и старых работ. Найдите лучшие вопросы и решения здесь. Нажмите сейчас, чтобы получить к нему доступ.

• Решения Balbharati для английского языка kumarbharati 9th Standard Maharashtra State Board
• Решения Balbharati для хинди — Lokbharati 9th Standard Maharashtra State Board ९ वीं कक्षा]
• Решения Balbharati для маратхи — Государственный совет штата Махараштра, 9-й стандарт Акшарбхарати
• Решения Бальбхарати для математики 1 Алгебра 9-го стандарта Правление штата Махараштра
• Решения Бальбхарати для санскритского композита — Ананд 9-й стандарт (सयुक्त-सस्कृतम्‌ — आनन्दः नवमी कक्षा)
• Решения Balbharati для всего санскрита — Amod 9th Standard (सम्पूर्ण-संस्क ृतम् — आमोदः नवमी कक्षा)
• Решения Balbharati для науки и техники 9th Standard Maharashtra State Board
• Решения Balbharati для географии социальных наук 9th Standard Maharashtra State Board
• Balbharati решения для социальных наук, истории и политических наук 9th Standard Maharashtra State Board

Board

Решения Бальбхарати для 9-й стандартной геометрии (математика 2, 9) Глава 1: Основные понятия геометрии

Понятия, описанные в разделе «Основные понятия геометрии», включают в себя промежуточность, понятие линии, понятие сегмента линии, понятие плоскости, понятие точек, понятие луча, условные операторы и обратное, координаты точек и расстояние, введение в основы Понятия геометрии, доказательства

Балбхарати 9-я Стандартная геометрия (Математика 2, 9) Глава 1: Основные понятия геометрии, упражнения

9020 8 6

Упражнение	Количество вопросов	Страницы
Практический набор 1. 1	19	5
Практический набор 1.2	7–8
Практический набор 1.3	6	11
Набор задач 1	33	11–12

Решения Бальбхарати для 9-й стандартной геометрии (математика 2, 9) Глава 2: Параллельные прямые 9 0053

Концепции, охватываемые параллельными линиями, — это тест альтернативных углов, теоремы об альтернативных углах, проверка параллельных линий, следствие параллельных линий, тест соответствующих углов, теорема о соответствующем угле, тест внутренних углов, теорема о внутренних углах, пары линий — пересечение параллельных линий, параллельность Линии, свойства параллельных линий, тест на параллельные линии, использование свойств параллельных линий

Балбхарати 9-я стандартная геометрия (математика 2, 9) Глава 2: Параллельные прямые, упражнения

Упражнение	Количество вопросов	Страницы
Практический набор 2. 1	5	от 17 до 18
Практический набор 2.2	6	от 21 до 22
Набор задач 2	12	от 22 до 23

Реклама Удалить все объявления

Balbharati Solutions for 9th Standard Geo метрия (Математика 2, 9th) Глава 3: Треугольники

Понятия, изложенные в треугольниках, — это теорема о биссектрисах угла, понятия треугольников — стороны, углы, вершины, внутренние и внешние стороны треугольника, конгруэнтность треугольников, обратная теорема о равнобедренном треугольнике, следствие треугольника, внешний вид Угол треугольника и его свойство, Теорема о равнобедренных треугольниках, Медиана треугольника, Теорема о перпендикулярной биссектрисе, Свойства неравенств сторон и углов треугольника, Свойство 30°-60°-90° Теорема о треугольнике, Свойство 45°- 45°- 9Теорема о треугольнике 0°, свойство медианы, проведенной на гипотенузе прямоугольного треугольника, теорема об отдаленных внутренних углах треугольника, подобие треугольников, подобные треугольники

Балбхарати 9-я стандартная геометрия (математика 2, 9)

Упражнение Количество вопросов Страницы Практический набор 3. 1 10 27 до 28 Практический набор 3.2 10 от 31 до 33 Практический набор 3.3 4 38 Практический набор 3.4 8 от 43 до 44 Практический набор 3,5 3 47 Набор задач 3 10 от 49 до 50

Решения Бальбхарати для 9-го стандарта геометрии (математика) 2, 9) Глава 4: Построение треугольников

Концепции, изложенные в Построении треугольников, включают построение треугольников, теорему о перпендикулярной биссектрисе, построение треугольника, если известны его периметр, основание и углы, включающие основание. Построение треугольника, когда к его основанию примыкает угол. к основанию и дана сумма длин остальных сторон. Построить треугольник, зная его основание, угол, прилежащий к основанию, и разность между остальными сторонами.

Балбхарати 9th Стандартная геометрия (математика 2, 9) Глава 4: Построение треугольников упражнения

90 208 Практический набор 4.1

Упражнение	Количество вопросов	Страницы
4	53
Практический набор 4.2	3	54
Практический набор 4.3	3	56
Набор задач 4	4	56

Реклама Удалить все объявления

Решения Бальбхарати для 9-й стандартной геометрии (математика 2, 9) Глава 5: Четырехугольники rilaterals — Стороны, Смежные стороны, Противоположные стороны, Угол , Смежные углы и противоположные углы, Обращение к теореме о середине, Свойства параллелограмма, Свойства квадрата, Свойства равнобедренной трапеции, Свойства прямоугольника, Свойства ромба, Свойства трапеции, Свойство: диагонали ромба делят его противоположность пополам Углы. , Свойство: Диагонали квадрата равны., Свойство: Диагонали квадрата делят противоположные углы пополам., Свойство: Смежные углы параллелограмма дополнительные., Свойство: Диагонали параллелограмма делят друг друга пополам. (в точке их пересечения), Свойство: Диагонали прямоугольника имеют одинаковую длину., Свойство: Диагонали ромба являются взаимно перпендикулярными биссектрисами., Свойство: Диагонали квадрата являются перпендикулярными биссектрисами друг к другу. ., Свойство: Противоположные углы параллелограмма равны., Свойство: Противоположные стороны параллелограмма имеют одинаковую длину., Признаки параллелограмма, Теорема: Если каждая пара противоположных сторон четырехугольника равна, то она является параллелограммом., Теорема: Если в четырехугольнике каждая пара противоположных углов равна, то он является параллелограммом., Теорема: Если одна пара противоположных сторон четырехугольника равны и параллельны, то он является параллелограммом., Теорема. : Если диагонали четырехугольника делят друг друга пополам, то это параллелограмм, Теорема о серединах двух сторон треугольника

Балбхарати 9-я Стандартная Геометрия (Математика 2, 9) Глава 5: Четырехугольники упражнения

90 197

Упражнение	Количество вопросов	Страницы
Тренировочный набор 5. 1	7	62
Практический набор 5.2	5	67
Практический набор 5.3	10	69
Практический набор 5.4	3	71
Практический набор 5.5	4	73
Набор задач 5	11	от 73 до 74

Решения Бальбхарати для 9-й стандартной геометрии (математика 2, 9-я ) Глава 6: Окружность

Понятия, охватываемые в круге, включают центр окружности треугольника, понятие круга — центр, радиус, диаметр, дугу, сектор, хорду, сегмент, полуокружность, окружность, внутреннюю и внешнюю сторону, концентрические окружности, построение Окружность треугольника, Построение вписанной окружности треугольника, Вписанная окружность треугольника, Свойства хорды, Свойства конгруэнтных хорд, Связь между конгруэнтными хордами окружности и их расстояниями от центра, Теорема: перпендикуляр, проведенный из центра окружности, делящей хорду пополам. Теорема: равные хорды окружности равноудалены от центра. Теорема: хорды окружности, равноудаленные от центра, равны. Теорема: отрезок, соединяющий центр круг и середина его хорды перпендикулярна хорде.

Балбхарати 9-я Стандартная Геометрия (Математика 2, 9) Глава 6: Круговые упражнения

902 05 901 97

Упражнение	Количество вопросов	Страницы
Тренировочный набор 6.1	6	79
Практический набор 6.2	3	82
Практический набор 6.3	5	86
Набор задач 6	12	86 — 87

Реклама Удалить все объявления

Решения Бальбхарати для 9-й стандартной геометрии (математика 2, 9) Глава 7: Координатная геометрия

-ординатная геометрия — это координатная геометрия, координаты точек на осях, уравнения прямых, параллельных оси X и оси Y, графики линейных уравнений, построение точки на плоскости, если ее координаты заданы. , координаты точки на плоскости, График линейного уравнения в общем виде

Balbharati 9th Standard Geometry (Mathematics 2, 9th) Глава 7: Координатные геометрические упражнения

Упражнение	Количество вопросов	Страницы
Тренировочный набор 7.1	3	93
Практический набор 7.2	14	От 97 до 98
Набор задач 7	17	от 98 до 99

Решения Бальбхарати для 9-й стандартной геометрии (Математика 2, 9) Глава 8: Тригонометрия

Понятия, охватываемые тригонометрией, являются важными уравнениями в тригонометрии, отношением между тригонометрическими отношениями, терминами, относящимися к прямоугольному треугольнику, тригонометрическими отношениями и их обратными значениями, тригонометрическими отношениями углов 30° и 60°, тригонометрическая таблица, тригонометрия

Балбхарати 9-я стандартная геометрия (математика 2, 9) Глава 8: Тригонометрические упражнения

Упражнение	Количество вопросов	Страницы
Практический набор 8. 1	4	104
Практический набор 8.2	9	112
Набор задач 8	10	113

Решения Бальбхарати для 9-й стандартной геометрии (математика 2, 9) Глава 9: Площадь поверхности и объем 900 16 Концепции, охватываемые в разделе «Площадь поверхности» и «Объем», — это «Концепция конуса», «Площадь поверхности a куб, площадь поверхности кубоида, площадь поверхности прямого кругового конуса, площадь поверхности сферы, площадь поверхности цилиндра, объем прямоугольного параллелепипеда, объем цилиндра, объем прямого кругового конуса, объем сферы, Объем куба

Балбхарати 9-я стандартная геометрия (математика 2, 9) Глава 9: Площадь поверхности и объем упражнения

Упражнение	Количество вопросов	Страницы
Тренировочный набор 9.1	8	115
Практический набор 9. 2	10	119
Практический набор 9.3	7	123
Набор задач 9	9	123

Правление штата Махараштра 9 математические решения часть 2 Геометрия была очень умно создана Шаала.

Поиск лучших решений 9-й стандартной геометрии (математика 2, 9) Бальбхарати очень важен если вы хотите полностью подготовиться к экзамен. Крайне важно убедиться, что вы полностью готовы к любым проблемам, которые могут возникнуть, и это почему тяжелый, профессиональный акцент на геометрии Balbharati 9th Standard решения могут быть очень хорошей идеей. Как вы узнаете решения, вам намного проще получить желаемые результаты, а сам опыт может быть ошеломляет каждый раз.

Балбхарати 9-я стандартная геометрия (математика 2, 9) Путеводитель Назад Ответы

Мы надеемся, что следующая книга Государственного совета Махараштры Балбхарати 9-я стандартная геометрия (математика 2, 9) Ответы Руководство по решениям Pdf Free Download in English Medium будет вам полезен.

Ответный материал разработан в соответствии с последний шаблон экзамена и является частью Balbharati 9th Standard Books Solutions. Вы не пропустите ни одного темы или концепции, обсуждаемые в книге, и получат больше концептуальных знаний из учебного материала. Если у вас есть какие-либо вопросы о Совете штата Махараштра Новая программа 9th Standard 9th Standard Geometry (Mathematics 2, 9th) Guide Pdf of Text Book Back Вопросы и ответы, примечания, важные вопросы по главам, типовые вопросы и т. д., пожалуйста, свяжитесь с нами.

Комплексные решения Бальбхарати для математики 2, геометрия, 9-й стандарт Государственного совета Махараштры

Очень важно иметь решения Бальбхарати для математики 2, геометрия, 9-й стандарт, Государственный совет Махараштры. поскольку они могут предложить хорошее руководство в относительно того, что вам нужно улучшить. Если вы хотите становиться все лучше и лучше, вам нужно подталкивать границы и выйти на новый уровень. Это, безусловно, очень помогает и может привести к огромное количество преимуществ каждый раз.

Это выводит опыт на новый уровень, а отдача в одиночку может быть экстраординарным.

Что вы хотите от решения Бальбхарати по геометрии (математика 2, 9) 9-го стандарта это большая точность. Без точные решения, вы никогда не получите желаемых результатов и ценности. Вот почему вам нужно качество, надежность и согласованность с чем-то вроде этого. Если он у вас есть, все, безусловно, будет удивительным и вы получите, чтобы преследовать свои мечты.

Правильное форматирование

Если вы приобрели решения Geometry Balbharati 9th Standard на этой странице, они полностью отформатированы и готовы к использовать. Это помогает сделать опыт проще и удобнее, предлагая результаты и ценность. тебе нужно. Это то, к чему вы стремитесь, — истинный акцент на качество и ценность, и отдача может быть отличной. благодаря этому.

Все решения Balbharati Mathematics 2 Geometry 9th Standard Maharashtra State Board охватывают все 9 глав. В результате вы сможете полностью подготовьтесь к экзамену должным образом и не беспокойтесь о том, что что-то упустите.