Интегрирование — один из важнейших математических инструментов, особенно в численном моделировании. Например, дифференциальные уравнения в частных производных обычно выводятся из интегральных уравнений сохранения. Когда возникает необходимость численного решения уравнения в частных производных, интегрирование также играет важную роль. В этой статье приведен обзор методов и подходов интегрирования, доступных в COMSOL Multiphysics, а также конкретные примеры их использования.
Важность интегралов
В COMSOL используется метод конечных элементов, который преобразует описывающее некоторый процесс уравнение в частных производных в интегральное уравнение — другими словами, в слабую форму (weak form). При детальном и глубоком изучении формулировок, используемых в интерфейсах COMSOL, вы обнаружите, что множество граничных условий реализованы через интегралы. В качестве наиболее характерных примеров можно привести условия
Вычисление интегралов в узле Derived Values
Интеграл общего вида имеет форму
\int_{t_0}^{t_1}\int_{\Omega}F(u)\ \mathrm{d A} \mathrm{d} t
где [t_0,t_1] — это временной интервал, \Omega — это пространственная область, а F(u) — это произвольное выражение, включающее зависимую переменную u и произвольные функции от нее, в том числе производные по пространству, времени, а также любой другой величине.
Наиболее удобный способ вычисления интегралов — использование узла Derived Values (Расчет выражений) в разделе Results (Результаты) ленты Ribbon или дерева модели (Лента Ribbon отсутствует в том случае, если ваш компьютер работает не под управлением ОС Windows®).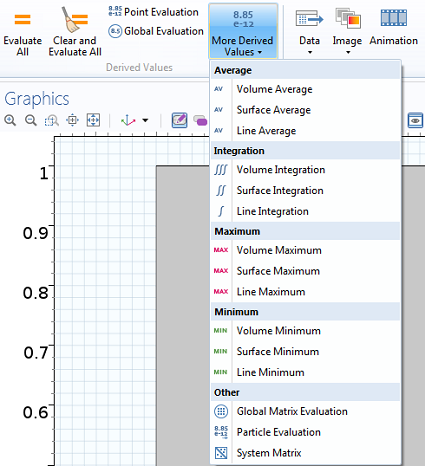
Добавление операций расчета пространственных интегралов по объему, поверхности или линии в узле Derived Values (Расчет выражений)
Вы можете обратиться к любому доступному решению, выбрав соответствующий набор данных (data set). В поле Expression (Выражение) вводится подынтегральная функция, включающая зависимые или производные переменные. Для данных расчета во временной области пространственный интеграл вычисляется на каждом временном шаге. В качестве альтернативы, в окне Settings (Настройки) узла Data Series Operations (Операции с массивами данных) можно выбрать опцию Integral (Интегрирование), что позволит вычислить общий пространственно-временной интеграл.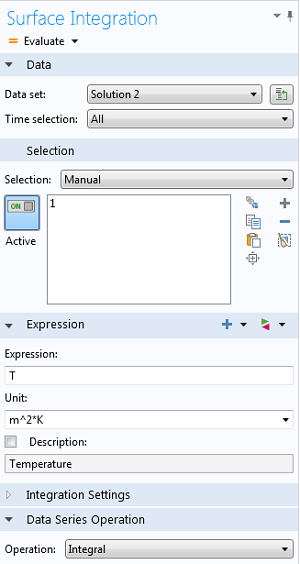
Пример настроек вычисления интегралов по поверхности (Surface Integration) с дополнительным вычислением интеграла по времени в разделе Data Series Operations.
Оператор Average (Усреднение) — еще одна операция в разделе Derived Values, связанная с вычислением интегралов. Оператор вычисляет интеграл и делит его на объем, площадь или длину выбранной области. Операция Average
Вычисление пространственного и временного интегралов для демо-модели из области теплопередачи
Рассмотрим простую модель теплопередачи: двумерный единичный квадрат из алюминия в (x,y)-плоскости. Температура верхней и правой сторон постоянна и равна комнатной (293.15 K), в то время как для левой и нижней границы задан общий входящий тепловой поток (General inward heat flux), составляющий 5 000 W/m^2. Стационарное и нестационарное решение (в момент времени 100 секунд) представлены на иллюстрациях ниже.
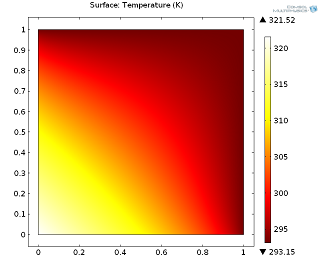
Стационарное решение, нажмите на изображение для увеличения.
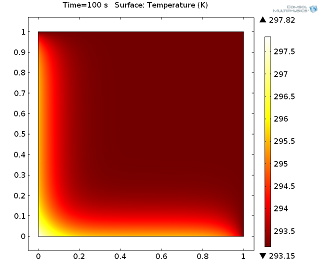
Нестационарное решение (для момента времени 100 секунд), нажмите на изображение для увеличения.
Вычисление пространственного интеграла с использованием операторов узла Component Coupling
Операторы узла Component Coupling (Сопряжение компонентов) используются в тех случаях, когда, например, в одном выражении объединяются несколько интегралов, или интегралы требуются в процессе вычислений, или требуется множество контурных интегралов. Операторы данного узла определяются в разделе Definitions (Определения). На этом этапе режультат использования оператора не просчитывается, а указываются только их название и выборки областей.
Добавление операторов через узел Component Couplings
В нашем примере мы для начала хотим вычислить пространственный интеграл для стационарного распределения температуры, равный
\int_{\Omega}T(x,y)\ \mathrm{d}x\mathrm{d}y = 301.65
В пакете COMSOL оператор вычисления интеграла по умолчанию получает имя intop1.
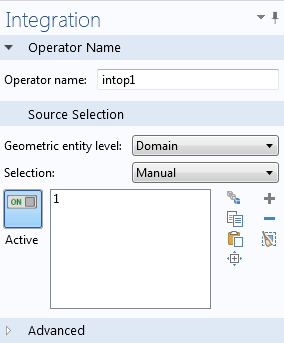
Окно настроек оператора интегрирования.
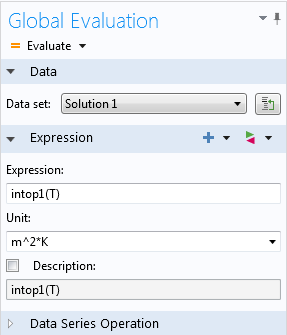
Расчет результата интегрирования через оператор.
Теперь давайте рассмотрим, как оператор интегрирования может использоваться непосредственно в процессе расчета модели. С его помощью мы могли бы, например, выяснить, какая нагревательная мощность потребуется для получения средней температуры 303.15 К, то есть температуры, на 10 К превышающей температуру окружающей среды. Прежде всего нам необходимо вычислить разницу между требуемым и действительным средними значениями. Среднее значение вычисляется путем деления интеграла от T на интеграл от постоянной функции 1, который равен площади области. Нетрудно догадаться, что вычисление подобного вида легко выполнить с помощью представленного в COMSOL оператора Average (Усреднение), см. комментарии выше. По умолчанию данный оператор получает название aveop1. Обратите внимание, что среднее значение для области в нашем примере совпадает с интегралом, т.к. область имеет единичную площадь. Соответствующая разность равна
303.15-\int_{\Omega}T(x,y)\mathrm{d} x\mathrm{d} y = 1.50
Далее нам необходимо найти значение General heat flux (Общий тепловой поток) на левой и нижней границах, при котором была бы достигнута требуемая средняя температура. Для этого мы введем дополнительную степень свободы под названием q_hot и дополнительное ограничение в качестве глобального уравнения (Global Equation). Общий входящий тепловой поток (General inward heat flux) тогда перезадается через переменную

Добавление дополнительной степени свободы (переменной) и глобального уравнения, для неяного подбора средней температуры, равной 303.15 K.
Решение данной сопряженной системы с помощью стационарного исследования дает значение q_{hot}=5 881.30 W/m^2. Т.е. полученное значение можно задать в качестве граничного условия для общего входящего теплового потока, чтобы средняя температура в рассматриваемой области стала равна 303.15 К.
Вычисление неопределенного интеграла посредством оператора интегрирования
В своих обращениях в службу поддержки пользователи часто задают один и тот же вопрос: как рассчитать неопределенный пространственный интеграл? Для этой цели нам также пригодится оператор интегрирования, задаваемый через Component Couplings. Нахождение неопределенного интеграла — операция, обратная дифференцированию. Неопределенный интеграл позволяет вычислять площади произвольных областей, ограниченных графиками функций. Одна из самых важных прикладных задач — вычисление вероятностей в статистическом анализе. Для того чтобы это продемонстрировать, мы зафиксируем y=0 и обозначим неопределенный интеграл от T(x,0) как u(x). Это значит, что \frac{\partial u}{\partial x}=T(x,0). Тогда неопределенный интеграл имеет вид
u(\bar x) = \int_0^{\bar x}T(x,0)\mathrm{d} x
Здесь мы используем \bar x, чтобы отличать переменную интегрирования от внешней переменной. В отличие от представленных выше интегралов, результатом интегрирования является функция, а не скалярная величина. Нам необходимо указать для ПО, что для каждого значения \bar x\in[0,1] соответствующее значение u(\bar x) вычисляется при помощи интеграла. В среде COMSOL это можно легко сделать всего за три шага. Во-первых, потребуется логическое выражение для переписывания интеграла в виде
u(\bar x) = \int_0^1T(x,0)\cdot(x\leq\bar x)\ \mathrm{d} x
Во-вторых, нам понадобится оператор вычисления интеграла, который будет действовать на нижней границе области из примера. Давайте обозначим его как intop2. В-третьих, мы должны отличать переменную интегрирования от внешней переменной. Принятые обозначения для такого случая: x называется источником (source), а \bar x — точкой назначения (destination). При использовании операторов интегрирования доступен встроенный оператор dest, который позволяет явно оглашать, что соответствующее выражение не относится к переменным интегрирования. Точнее, это значит, что в COMSOL \bar x=dest(x). Объединив логическое выражение с оператором dest, мы получим выражение вида T*(x<=dest(x)), которое является именно тем входным выражением, которое требуется для intop2. Объединив все вместе, мы можем вычислить неопределенный интеграл, воспользовавшись выражением intop2(T*(x<=dest(x))). Результат данной операции можно проиллюстрировать следующим графиком:
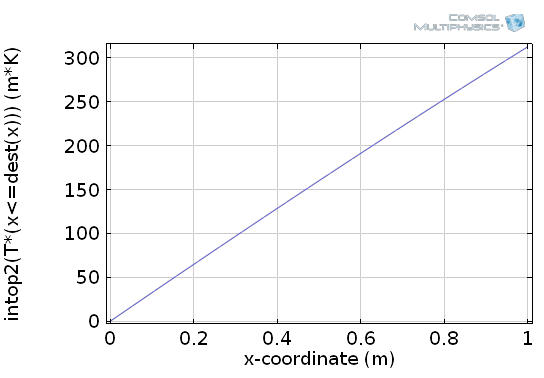
Как построить график неопределенного интеграла с помощью оператора интегрирования, оператора dest и логического выражения.
В пакете COMSOL дополнительно доступны еще два оператора вычисления интеграла, а именно общая проекция (general projection) и линейная проекция (linear projection). Эти операторы можно использовать для получения множества контурных интегралов в любом направлении в области. Другими словами, вычисление интеграла производится только вдоль одного измерения. В результате мы получаем функцию размерности на единицу меньше, чем размерность области. Для двухмерного примера результатом будет одномерная функция, которая может быть рассчитана на любой границе. Более подробная информация об использовании данных операторов будет представлена в одной из следующих публикаций в нашем компоративном блоге.
Вычисление пространственного интеграла посредством дополнительного физического интерфейса
Наиболее гибким способом вычисления пространственных интегралов является техника с добавлением дополнительного PDE-интерфейса. Давайте вспомним пример выше с неопределенным интегралом и предположим, что мы хотим вычислить неопределенный интеграл не только для y=0. Данная задача может быть сформулирована в виде дифференциального уравнения в частных производных
\frac{\partial u}{\partial x}=T(x,y)
с граничным условием типа Дирихле u=0 на левой границе. Расчет такого уравнения проще всего реализовать в физическом (математическом) интерфейсе Coefficient Form PDE (Дифференциальное уравнение в частных производных, коэффициентная форма записи), который потребует следующих настроек:

Вычисление пространственного интеграла посредством дополнительного PDE-интерфейса.
Зависимая переменная u представляет собой неопределенный интеграл по x и доступна в процессе расчета модели и в постобработке. Помимо гибкости, дополнительным преимуществом данного подхода является точность, так как интеграл рассчитывается не вспомогательными инструментами на основе уже определенного распределения переменной, а непосредственно в процессе расчета с учетом алгоритмов оценки погрешностей и т.п.
Вычисление временного интеграла посредством встроенных операторов
Мы уже упоминали узел Data Series Operations, который можно использовать для вычисления интеграла по времени. Другой крайне полезный способ вычисления интеграла по времени обеспечивается встроенными операторами timeint и timeavg для вычисления интеграла или среднего значения по времени, соответственно. Данные инструменты доступны при постобработке результатов, используются для вычисления интеграла от любого выражения (зависящего от времени) на заданном временном интервале. В нашем примере мы рассчитаем среднее значение температуры в диапазоне от 90 до 100 секунд, то есть:
\frac{1}{10}\int_{90}^{100}T(x,y,t)\ \mathrm{d} t
На поверхностном графике ниже представлен результирующий интеграл, являющийся функцией пространственных переменных (x,y):
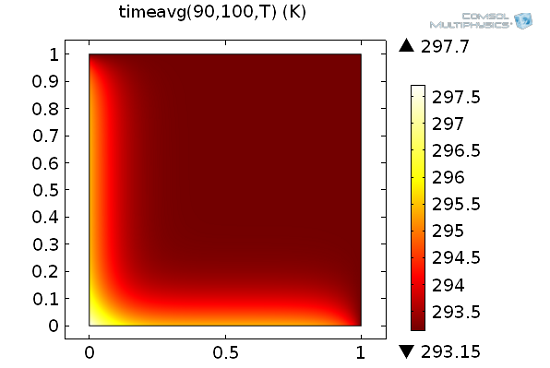
Использование оператора timeavg – оператора вычисления интеграла по времени.
Схожие операторы существуют для вычисления интегралов на сферических зонах, а именно ballint, circint, diskint и sphint.
Вычисление временного интеграла посредством дополнительного физического интерфейса
В случае если временные интегралы нужно использовать непосредственно в модели в процессе расчета, вам будет необходимо задать их как дополнительные зависимые переменные. Аналогично представленному выше примеру с интерфейсом Coefficient Form PDE, это можно сделать, добавив ODE-интерфейс из раздела Mathematics. Предположим, например, что на каждом временном шаге требуется вычислять интеграл от величины общего теплового потока на промежутке от старта до текущего момента, который показывает накопленную энергию. Переменная для общего теплового потока рассчитывается в COMSOL автоматически и называется ht.tfluxMag. Интеграл может быть вычислен как дополнительная зависимая переменная с помощью узла Distributed ODE (Распределенное обыкновенное дифференциальное уравнение) интерфейса Domain ODEs and DAEs. Правой частью (источниковым членом) для доменного ОДЕ должна выступать подынтегральная функция, что и показано на иллюстрации ниже.
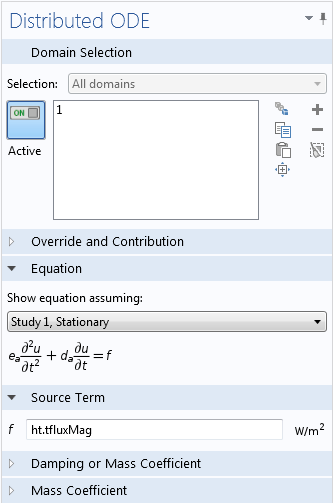
Использование дополнительного ODE-интерфейса для вычисления интеграла по времени.
В чем польза подобной техники? Полученный интеграл можно повторно использовать в других физических интерфейсах, поля в которых могут зависеть от накопленной в системе энергии. Более того, полученный резултат будет мгноменно доступен для всех видов постобработки, что удобнее и быстрее, чем использование встроенных операторов. Рекомендуем ознакомится с моделью Carbon Deposition in Hetereogeneous Catalysis (Образование сажевых отложений при гетерогенном катализе), в которой ОДЕ в области используется для вычисления пористости катализатора при наличии химических реакций в виде нестационарной полевой переменной.
Вычисление интеграла от аналитических функций и выражений
До сих пор мы демонстрировали, каким образом вычислять интеграл от искомых переменных в процессе расчета или при постобработке. Но не касались случая взятия интегралов от аналитических функций или выражений. Для этой операции в среде COMSOL доступен встроенный оператор integrate(expression, integration variable, lower bound, upper bound).
Выражение может представлять собой любую одномерную функцию, например sin(x). При этом допускается включение дополнительных переменных, например sin(x*y). Второй параметр определяет, по какой переменной вычисляется интеграл. Например, integrate(sin(x*y),y,0,1) выдает функцию переменной x, потому что интегрирование выполняется только по переменной y. Обратите внимание, что данный оператор также может использоваться для работы с аналитическими функциями, заданными в узле Definitions (Определения) текущего компонента.
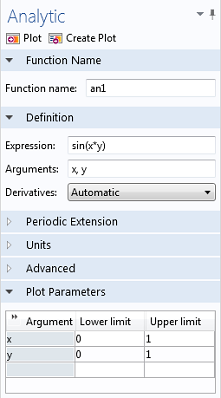
Добавление аналитической функции.
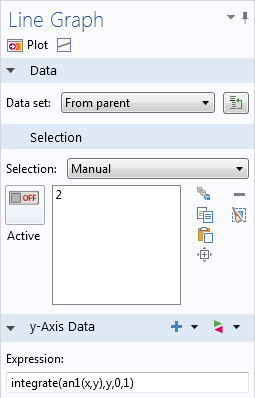
Вычисление интеграла от аналитической функции.
Материалы для дальнейшего изучения
В отличие от других ответчиков я начну с интеграла, а не с производной. Интеграл в жизни имеет конкретный физический смысл. Это площадь фигуры ограниченной осью абцисс Х и графиком функции. Далеко от жизни? Сейчас приблизим. Представим себе машину, которая едет. Отложим по оси Х время в пути, а по Y — скорость в каждый, конкретный момент времени, и начертим график скорости от времени. Если скорость постоянная — это будет горизонтальная прямая. Фигура ограниченная этой прямой и осью Х — будет прямоугольником. Ширина прямоугольника — время в пути, а высота — скорость машины. Ширина*высота=площадь. Но при этом время*скорость=расстояние. Т.е. расстояние равно площади! И пройденное расстояние — это интеграл скорости.
А теперь начинается магия математики. Как посчитать путь, который пройдет машина, если у неё непрерывно меняется скорость, и её график извилистая кривая? А очень просто. Ведь ничего не изменилось — надо только найти площадь фигуры на графике! Как мы будем искать эту площадь — не важно. Можно просто посчитать клеточки на бумаге (это будет численным интегрированием, которое всегда приблизительное). А если скорость описана функцией от времени — можно найти её интеграл и сразу получить точный ответ.
А диференцирование — это это действие обратное интегрированию. Если продиференцировать функцию расстояния от времени, которую получили интегрированием скорости — мы обратно получим скорость. Ту самую скорость, с которой меняется пройденный путь машины. Сейчас скорость большая, километровые столбы мелькают, и пройденный путь быстро растет, а когда скорость падает и пройденные километры набираются медленно. На графике пути от времени, скорость это наклон самого графика. Грфик идет вверх — скорость положительная, мы едем вперед и расстояние растет. График пошел вниз — скорость отрицательная, мы едем обратно, а расстояние до точки старта уменьшается. График горизонтальная линия (наклона нет) -скорость равна нулю, мы стоим и расстояние неизменно.
Немного решил дописать.
Вообще интеграл в изменяющихся физических процессах очень востребован. А любой процесс описывает какую-то жизненную ситуацию.
Это сколько воды натекло через трубу в пресловутый бассейн при переменном напоре. Сколько киловатт накрутил электросчетчик при переменной нагрузке на сеть. До какой температуры нагрелась вода в кастрюле, если в процессе нагрева мы регулировали мощность плиты.
Любой процесс изменяемый во времени можно интегрировать и получить полезный результат. То же касается и дифенциала, который показывает скорость изменения общего результата.
Физические основы механики
Скорость частицы может изменяться со временем, как по величине, так и по направлению.
Быстрота изменения вектора скорости называется ускорением.
Быстрота (скорость) изменения во времени любой величины определяется производной по времени от этой величины. Это общее правило касается и вектора скорости.
Ускорение равно производной вектора по времени t, или, что то же самое — второй производной по времени радиус-вектора :
Рис. 2.9. Тангенциальное и нормальное ускорения.
Если известны зависимость от времени ускорения а = a(t) и начальная скорость v0 (при t = t0), то значение скорости в любой момент времени t равно
Если известно также положение тела в начальный момент t = t0 , то мы можем найти не только скорость, но и положение тела в любой момент времени:
При равноускоренном движении ( ) интегралы легко вычисляются и мы получаем:
Вычисление последнего интеграла приводит к закону равноускоренного движения материальной точки
При прямолинейном движении векторы перемещения, скорости и ускорения направлены вдоль одной и той же прямой, совпадающей с траекторией. Поэтому направление прямой можно принять за ось x и оперировать с ускорением и скоростью как с проекциями векторов на эту ось, то есть как с алгебраическими величинами. При этом индекс, обозначающий проекцию вектора на ось, опускают.
Видео 2.2. Скатывание тележки с наклонной плоскости как пример равноускоренного движения.
Физические основы механики
Если путь , пройденный материальной точкой за промежуток времени от t1 до t2, разбить на достаточно малые участки , то для каждого го участка выполняется условие
Тогда весь путь приближенно равен сумме
При стремлении всех к нулю это приближенное равенство становится точным, то есть
Подчеркнем, что здесь речь идет о модуле скорости. Если зависимость модуля скорости от времени выразить графически, то путь, пройденный материальной точкой за время от t2 до t1, численно равен площади фигуры, ограниченной кривой , осью времени и вертикальными прямыми, проходящими через точки с абсциссами и (рис. 2.7.).
Рис. 2.7. Определение пройденного пути по графику зависимости скорости от времени
При равномерном движении величина скорости постоянна и может быть вынесена из-под знака интеграла:
Так как модуль скорости , то пройденный телом путь с течением времени может только возрастать (или быть постоянным, когда тело покоится).
Если нас интересует перемещение материальной точки за то же время, то мы так же разбиваем траекторию на малые участки, но суммируем теперь векторы перемещения:
Учитывая связь перемещения с вектором скорости
получаем
В отличие от выражения для пройденного пути под интегралом здесь стоит не модуль, а вектор скорости. Точно так же при равномерном прямолинейном движении, когда , мы можем вынести скорость из-под знака интеграла:
Чтобы практически найти перемещение, интеграл, представленный в векторной форме, необходимо записать в виде интегралов для проекций
Здесь x1, y1, z1 — координаты точки в момент времени t1, а x2, y2, z2 — координаты точки в момент времени t2, соответственно величина перемещения при этом равна
а направление вектора перемещения определяется соотношением:
Пример. Пункт A находится на бетонированном аэродроме, пункт B — на примыкающем к нему поле, на котором скорость машины в n раз меньше. Для того, чтобы за кратчайшее время добраться из в , был выбран оптимальный маршрут, показанный на рис. 2.8. Найти соотношение между синусами углов α и β.
Рис. 2.8. Оптимальный маршрут из пункта А в пункт В
Все расстояния указаны на рисунке. Время , затрачиваемое на путь , преодолеваемый со скоростью , равно
Время t2, затрачиваемое на путь , преодолеваемый со скоростью , равно
Полное время в пути, будет
Поскольку точка 0 была выбрана так, что на путь затрачивалось минимальное время, должна быть равна нулю производная времени по координате точки перехода с бетона на траву:
Поскольку
находим, что
то есть
Сходство с известным законом преломления света на границе двух сред не случайно: природа устроена так, что свет выбирает путь, требующий минимального времени. Это так называемый принцип Ферма, который мы подробно рассмотрим в соответствующем разделе.
     Определенный интеграл. Теорема существования.
     Решение многих важных задач геометрии и физики (определение площади, работы, массы, пути) приводит к одной и той же последовательности действий над известными функциями и их аргументами.
     Если отвлечься от физического смысла переменных и от их обозначений, то указанная последовательность действий состоит в следующем:
     1) Интервал \([a, b]\), в котором задана непрерывная функция \(f(x)\), разбивается на \(n\) частичных интервалов при помощи точек $$x_{0}=a,x_{1},x_{2},…,x_{n-1},x_{n}=b.$$
     2) Значение функции \(f(\xi _{i})\) в какой-нибудь точке \(\xi _{i}\in [x_{i-1},x_{i}]\) умножается на длину этого интервала \(x_{i}-x_{i-1}\), т.е. составляется произведение \(f(\xi _{i})(x_{i}-x_{i-1}).\)
     3) Берется сумма \(I_{n}\) всех этих произведений $$I_{n}=f(\xi _{1})(x_{1}-x_{0})+f(\xi _{2})(x_{2}-x_{1})+…+f(\xi _{n})(x_{n}-x_{n-1})=\sum_{i=1}^{n}{f(\xi _{i})(x_{i}-x_{i-1})}$$
или, если обозначить \(x_{i}-x_{i-1}\) через \(\Delta x_{i}\),
$$I_{n}=\sum_{i=1}^{n}{f(\xi _{i})\Delta x_{i}}.$$ | (1) |
     4) Находится предел \(I\) суммы \(I_{n}\) при стремлении к нулю длины наибольшего частичного интервала, и следовательно, при \(n\rightarrow \propto\), т.е. $$I=\lim I_{n}=\lim \sum_{i=1}^{n}{f(\xi _{i})\Delta x_{i}}.$$
     В рассмотренных выше четырех конкретных задачах этот предел \(I\) измеряет соответственно площадь, работу, путь, массу. В общем слк=учае он называется определенным интегралом или просто интегралом от функции \(f(x)\) в пределах от \(a\) до \(b\) и обозначается так: $$I=\int_{a}^{b}{f(x)dx}$$
и читается: интеграл от от \(a\) до \(b\) \(f(x)\) на \(dx\). Следовательно, по определению $$\int_{a}^{b}{f(x)dx}=\lim \sum_{i=1}^{n}{f(\xi _{i})\Delta x_{i}}.$$
Сумма (1) называется \(n\)-й интегральной суммой.
     Определение. Определенным интегралом называется предел, к которому стремится \(n\)-я интегральная сумма (1) при стремлении к нулю длины наибольшего частичного интервала.
     Как и в неопределенном интеграле, функция \(f(x)\) — подынтегральная функция, выражение \(f(x)dx\) — подынтегральное выражение и переменная \(x\) — переменная интегрирования. Интервал \([a, b]\) называется интервалом интегрирования, число \(a\) — нижний, а число \(b\) — верхний пределы интеграла.
     Сам процесс образования определенного интеграла показывает, что символ \(\int_{a}^{b}{f(x)dx}\) есть некоторе число. Величина его зависит только от вида подынтегральной функции и от чисел \(a\) и \(b\), определяющих интервал интегрирования. Переменная интегрирования \(x\) служит лишь для удобного обозначения определенного интеграла; ничего не изменится, если переменную интегрирования обозначить другой буквой, например \(t\) или \(u\): $$\int_{a}^{b}{f(x)dx}=\int_{a}^{b}{f(t)dt}=\int_{a}^{b}{f(u)du}.$$
     Внешняя общность записи определенного и неопределенного интегралов подчеркивает тесную связь между ними, хотя определенный интеграл есть число, а неопределенный интеграл — совокупность первообразных функций.
     Итак, совершенно очевидный результат $$\int_{a}^{b}{dx}=b-a,$$ который следует из того, что любая интегральная сумма для функции \(f(x)\equiv 0\) равна \(b-a\): $$\sum_{i=1}^{n}{\Delta x_{i}}=x_{1}-x_{0}+x_{2}-x_{1}+…+x_{n}-x_{n-1}=x_{n}-x_{0}=b-a.$$
     Применяя определение интеграла, можно сделать такие выводы:
     1) Площадь криволинейной трапеции равна интегралу от ординаты линии, ограничивающей трапецию, взятому по основанию: $$s=\int_{a}^{b}{f(x)dx}.$$
     2) Работа, произведенная силой, равна интегралу от силы, взятому по пути: $$A=\int_{0}^{S}{f(S)dS}.$$
     3) Путь, пройденный телом, равен интегралу от скорости, взятому по времени: $$S=\int_{T_{1}}^{T_{2}}{f(t)dt}.$$
     4) Масса, распределенная на линии, равна интегралу от плотности, взятому по длине линии: $$m=\int_{0}^{s}{f(s)ds}.$$
     Теорема существования определенного интеграла. Если функция \(f(x)\) непрерывна в замкнутом интервале \([a, b]\), то ее \(n\)-я интегральная сумма стремится к пределу при стремлении к нулю длины наибольшего частичного интервала. Этот предел, т.е. определенный интеграл \(\int_{a}^{b}{f(x)dx}\), не зависит от способа разбиения интервала интегрирования на частичные интервалы и от выбора в них промежуточных точек.
     Интегральные суммы, составленные при различных разбиениях интервала интегрирования и различных выборах точек \(\xi\), могут отличаться друг от друга весьма значительно. Сформулированная выше теорема показывает, что для непрерывных функций разница между этими суммами стирается по мере возрастания числа точек деления и убывания длины наибольшего частичного интервала, совсем исчезая в пределе.
2012-11-04 • Просмотров [ 5992 ]
Урок 6: Интеграл и первообразная
План урока:
Понятие первообразной
Бесконечное количество первообразных
Неопределенный интеграл
Таблица первообразных
Правила вычисления интегралов
Физический смысл неопределенного интеграла
Понятие первообразной
Ранее мы познакомились с важнейшим понятием математического анализа – производной. Она имеет большое практическое значение, в частности, с ее помощью можно определить скорость тела, если известен закон его передвижения. Например, если путь, пройденный автомобилем, можно вычислить с помощью функции S = t2, то его скорость в любой момент времени может быть рассчитана по формуле

Однако на практике значительно чаще встречается прямо противоположная задача. Известно, как меняется скорость тела, и найти требуется путь, пройденный им. В таком случае необходимо по производной определить ту функцию, которая «подверглась» дифференцированию.
Задание. Известна производная функции у(х):

В этом примере мы выполнили операцию, обратную дифференцированию. В математическом анализе он называется интегрированием. Если интегрируют некоторую произвольную функцию f(х), то в итоге получают новую функцию, которую чаще всего обозначают как F(x). Её называют первообразной функции f(x).

Приведем несколько примеров первообразной:

Последний пример показывает, что иногда первообразная может и совпадать с исходной функцией.
Задание. Докажите, что функция

Первообразные встречаются и в ряде практических задач, особенно в тех, где рассматривается движение тел.
Задание. Автомобиль Buggati Veyron разгоняется от 0 до 40 м/с за 4 секунды. Какое расстояние проедет эта машина за эти 4 секунды, если разгон осуществляется равномерно?
Решение: Если за 4 секунды машина разгоняется до 30 м/с, то за одну секунду она увеличивает скорость на

Примечание – в будущем мы научимся более строго решать такие задачи, и «угадывать» подходящую первообразную не придётся.

Эффективно подготовиться к ЕГЭ по математике помогут тщательно продуманные онлайн-курсы
Перейти
Бесконечное количество первообразных
Рассмотрим функцию

Оказывается, что g1 также является первообразной для у. То есть у одной функции у = 4х3 есть сразу две первообразных:g = x4и g = x4 + 1! Более того, можно доказать, что у любой функции есть бесконечное количество первообразных!
Действительно, рассмотрим сразу все функции

где С – некоторая константа, то есть параметр. В данном случае можно сказать, что мы рассматриваем не одну функцию, а семейство функций. Продифференцируем g:

Мы видим, что у всех функций из этого семейства, независимо от значения параметра С, производная одинакова. Здесь С может принимать любое действительное значение. Так как действительных чисел бесконечно много, то и количество функций, образующих семейство, также бесконечно. И все они являются первообразными для у = 4х3.
Данная особенность операции интегрирования может быть сформулирована в виде следующей теоремы:

Можно дать и графическую иллюстрацию этого правила. Построим произвольный график g = F(x). Далее построим ещё один график

Очевидно, что он может быть получен параллельным переносом первого графика на С единиц вверх:

Теперь в какой-нибудь точке х0 проведем касательные к обоим графикам первообразных. Очевидно, что они будут иметь одинаковый угол наклона, так как по сути тоже могут быть получены параллельным переносом:

Если же углы наклона касательных совпадают, то и производные в этих точках также равны.
В связи с наличием у каждой функции бесконечного количества первообразных их часто записывают в общем виде. Например, пусть надо записать первообразную для

Однако 2х2 – это лишь одна из бесконечного множества первообразных. Все вместе они образуют семейство, которое записывается так:
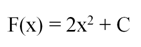
Неопределенный интеграл
Каждая математическая операция имеет какое-то особое обозначение. Например, чтобы показать, что мы дифференцируем некоторую функцию, мы ставим после неё штрих (и при необходимости берем в скобки):

Напомним, что операция нахождения первообразной называется интегрированием. Для ее обозначения используется особый знак – интеграл. Например, мы знаем, что первообразная для у = х2 – это семейство функций вида

Рассмотрим элементы записанного нами равенства:

Исходная функция – это та самая функция, для которой необходимо найти первообразную, то есть интегрируемая функция. Справа от знака «равно» как раз записывается первообразная. Сразу после первообразной надо писать «+ С». Тем самым мы показываем, что у интегрируемой функции есть бесконечное количество первообразных.
После интегрируемой функции стоит так называемый дифференциал dх (читается как «дэ икс»). В данном случае он указывает, что именно буквой х мы обозначаем переменную в интегрируемой функции. Его значение мы разберем несколько позже. Пока что надо запомнить, что после интегрируемой функции необходимо писать «dx». В целом вся запись

читается так: «интеграл от два икс по дэ икс равен икс в квадрате плюс цэ».
В чем разница между первообразной и интегралом? Первообразная – это функция, при дифференцировании которой получается исходная функция. Интеграл же – это не функция, а целое семейство функций (или их множество), которое включает в себя сразу все первообразные интегрируемой функции.
Так как интегрирование – это действие, обратное дифференцированию, то мы можем проверить результат своих вычислений. Пусть мы записали, что

Получили подынтегральное выражение. Значит, мы всё сделали правильно.
Здесь важно заметить, что в математике существует сразу несколько видов интегралов, каждый из которых имеет разное определение. Здесь описан так называемый «неопределенный интеграл». Несложно догадаться, что существует ещё и «определенный интеграл», который мы рассмотрим на следующих уроках. Теперь можно дать следующее определение:

Задание. Найдите неопределенный интеграл
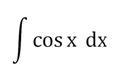
Решение. Вспомним таблицу производных элементарных функций. Производная синуса равна косинусу:

Заметим, что непосредственно из определения следует важное свойство неопределенного интеграла – производная интеграла равна его подынтегральному выражению:

Грубо говоря, операции интегрирования дифференцирования «сокращают» друг друга.
Задание. Вычислите производную:


Только усвоенная информация становится знанием. В этом вам помогут онлайн-курсы
Перейти
Таблица первообразных
Как же вычислять интегралы? Проще всего начать с тех функций, которые уже есть в таблице производных. Напомним, как она выглядит:

Из определения первообразной следует, что для тех функций, которые указаны во втором столбце таблицы, одной из первообразных является соответствующая функция из первого столбца. То есть можно составить такую таблицу первообразных:

Обратите внимание на третью строку снизу. Здесь произошло небольшое изменение – вместо первообразной lnx мы записали ln |x|, то есть использовали модуль числа. Дело в том, что функция

определена при любом значении аргумента, кроме нуля. В то же время функция

не определена при отрицательных значениях х, так как под знаком логарифма не может стоять отрицательное число. Однако области определения интегрируемой функции и ее первообразной должны совпадать. Использование модуля обеспечивает выполнение этого условия.
Полученная нами таблица интегралов не совсем удобна. Предположим, нам надо проинтегрировать функцию

отличающуюся от интересующей нас функции лишь множителем перед х5.
Однако можно догадаться, что в качестве подходящей первообразной можно взять функцию

В связи с этим есть смысл немного подкорректировать таблицу первообразных таким образом, чтобы в первом столбце стояли стандартные функции без неудобных множителей. В результате таблица примет следующий вид:

Можно доказать, что каждое равенство в третьем столбце является справедливым. Возьмем, например, равенство

Получили подынтегральное выражение, а это значит, что равенство справедливо. Таким же образом можно доказать и все остальные равенства в таблице.
Задание. Вычислите неопределенный интеграл:

Решение. Этот интеграл присутствует в таблице (7-ая строка), а потому мы просто переписываем равенство из неё:
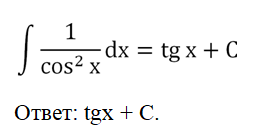
Задание. Найдите первообразную функции


Для достижения наилучшего результата важно структурировать знания. В этом вам помогут онлайн-курсы по математике
Перейти
Правила вычисления интегралов
Что делать в том случае, если надо вычислить интеграл, которого нет в таблице? Существует три несложных правила интегрирования, которые могут помочь в такой ситуации.

Докажем это правило. Для этого просто продифференцируем правую часть равенства:

Получили именно то выражение, которое стоит под знаком интеграла в левой части равенства. Это значит, что формула справедлива.
Рассмотрим пример использования этого правила. Пусть надо найти первообразную функции

Здесь мы представили исходный интеграл как сумму двух более простых интегралов, которые являются табличными
Обратите внимание, что мы не стали складывать константы интегрирования С как подобные слагаемые и писать 2С. Дело в том, что С – это некоторое произвольное число. Но если сложить два произвольных числа, то в итоге получится третье произвольное число, которое также будет обозначаться как С! Поэтому обычно константу С просто дописывают в самом конце решаемого примера.
Естественно, что правило сложения интегралов работает и в случае суммы не двух, а большего количества слагаемых.
Задание. Вычислите неопределенный интеграл

Возможна ситуация, когда мы не уверены в правильности полученного решения. В таком случае можно легко проверить себя, просто продифференцировав получившийся интеграл. В итоге мы должны получить исходную функцию (подынтегральное выражение):
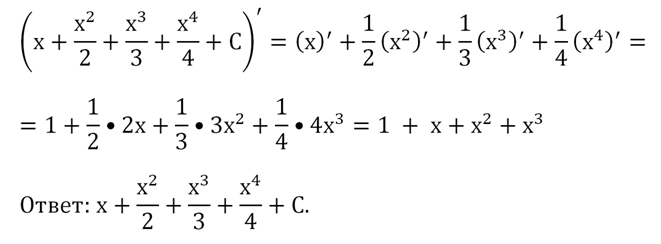
Следующее правило позволяет выносить множитель из-под знака интеграла.

Для доказательства тождества снова продифференцируем его левую часть:

Получили как раз то выражение, которое стоит под интегралом справа. Следовательно, формула верна.
Рассмотрим несколько простейших примеров использования этого метода интегрирования неопределенных интегралов:

Естественно, что правила 1 и 2 можно комбинировать друг с другом, решая более сложные примеры.
Задание. Вычислите неопределенный интеграл от квадратичной функции

Первые два правила достаточно просты и напоминают аналогичные правила дифференцирования. А вот третий метод вычисления неопределенного интеграла более сложный.

Проиллюстрируем его на примере. Пусть надо найти первообразную для функции

Но в нашем случае под знаком косинуса стоит не х, а выражение 5х + 7, являющееся линейной функцией. Поэтому, согласно правилу, мы должны написать впервообразной не sinx, а sin (5x + 7), то есть изменить аргумент. Также надо добавить перед синусом «поправочный множитель», равный 1/k, то есть в нашем случае 1/5:

Проверим себя. Продифференцируем получившуюся первообразную. При этом мы используем правило дифференцирования сложной функции:
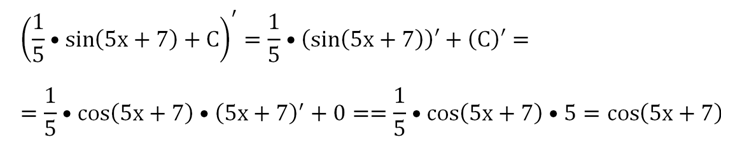
Получили ту самую функцию, которую и надо было проинтегрировать.
Приведем ещё несколько примеров использования правила 3:

Напомним, что при изучении производной мы познакомились также с правилами дифференцирования произведения, дроби и сложной функции. Используя их, мы могли найти производную для почти любой функции, которую только могли записать. С решением неопределенных интегралов ситуация значительно сложнее. С помощью приведенных трех правил не получится вычислить такие интегралы, как

Более того, в записанной нами таблице интегралов отсутствует ряд элементарных функций, поэтому мы не сможем даже проинтегрировать такую простую функцию, как

Дело в том, что задача интегрирования является значительно более сложной, чем задача дифференцирования. Отметим три момента. Во-первых, в нашей школьной таблице интегралов, содержащей всего 11 формул, указаны лишь самые простые элементарные функции. Существуют справочники, где в качестве табличных указаны интегралы десятков, а то и сотен функций. Во-вторых, есть и более сложные правила интегрирования, которые изучаются уже в институте. В-третьих, существуют такие элементарные функции, первообразную которых в принципе невозможно записать, используя элементарные функции (синус, косинус, логарифм и т.п.). В связи с этим приходится вводить в рассмотрение новые специальные функции, а также использовать приближенные методы вычислений.
Физический смысл неопределенного интеграла
Напомним физический смысл производной – если известен закон движения материальной точки, то есть некоторая функция S(t), то производная этого закона будет выражать скорость тела в момент времени t:

Отсюда прямо вытекает физический смысл первообразной. Если известен закон изменения скорости v(t), то его первообразная будет являться законом движения S(t). Точнее говоря, законом движения будет являться только одна из первообразных, так как их существует бесконечно много.
Задача. Скорость тела в произвольный момент времени t может быть вычислена по закону

Найдите закон движения материальной точки S(t). Известно, что в начальный момент времени тело находилось в точке с координатой 1,5, то есть S(0) = 1,5.
Решение. Нам надо просто проинтегрировать функцию v(t):

Интеграл вычислен, но это ещё не закон движения, ведь в нем присутствует константа интегрирования. Как от неё избавиться? Надо использовать условие, согласно которому S(0) = 1,5. В общем виде закон движения имеет вид
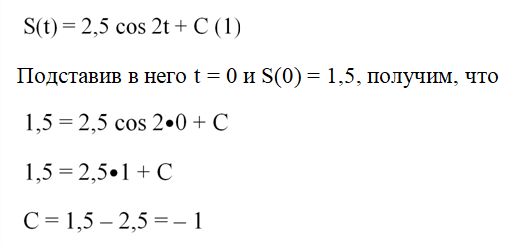
Мы нашли конкретное значение константы интегрирования. С учетом этого закон движения (1) примет вид:


Мы сделали подборку лучших онлайн-курсов по школьным предметам
Перейти
Неопределенный интеграл онлайн
В школе говорят, интеграл – это значок ∫, а вычисление интеграла, то есть процесс интегрирования, – это операция обратная дифференцированию. Согласитесь скучно!
Разумеется, у школьников возникает резонный вопрос: а нафиг он нам нужен?
Но если бы учитель уделил несколько минут на вводную про интегралы, такой вопрос всё равно бы возник, но уже не у всех!
Вводная к интегралам
В далеком 17 веке были на тот момент нерешенные насущные проблемы, а именно изучались закономерности движения тел. Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее.
Допустим, мы знаем закон изменения скорости тела – это некая функция. Тогда площадь фигуры, ограниченная этой кривой и осью координат, будет равна пройденному пути. Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.
В этом заключается один из физических смыслов интеграла.
Как вы уже поняли, геометрический смысл интеграла – это площадь криволинейной трапеции. Соответственно с помощью кратного интеграла вычисляется объем тела.
Решение интегралов
Лейбниц и Ньютон заложили основы дифференциального и интегрального исчисления. В последующие десятилетия было много великих открытий, связанных с вычислением интегралов.
Поскольку подынтегральная функция может принимать различные виды, естественно это привело к разделению интегралов на свои типы, а главное были отрыты многочисленные методы решения интегралов.
Но не все так безоблачно. На практике часто происходит так, что в аналитическом виде вычислить интегралы невозможно, то есть используя какой-либо известный метод. Конечно, получить аналитическое решение это здорово, но, с другой стороны, главное ведь вычислить точное значение интеграла. В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека.
Калькулятор решения интегралов
Теперь самое интересное. Еще каких-то 15 лет назад школьник и помыслить не мог, что под рукой будут такие калькуляторы интегралов, как, например, наш. Это безусловно облегчает процесс обучения. Можно проверять свои решения, находить допущенные ошибки и лучше усваивать образовательный курс.
И тут в который раз повторяем, калькулятор решения интегралов – это только ваш безотказный помощник, к которому можете обратиться в любое время. Но никак не подмена вашей головы. Старайтесь самостоятельно решать задачи, только так можно развивать мышление, а компьютер будет в помощь.
90000 integral time — це … Що таке integral time? 90001 90002 90003 90004 Time-Domain Thermoreflectance 90005 — is a method by which the thermal properties of a material can be measured, most importantly thermal conductivity. This method can be applied most notably to thin film materials (up to hundreds of nanometers thick), which have properties that vary … Wikipedia 90006 90007 90002 90003 90004 Time’s Up! 90005 — is a grassroots environmental group that seeks to promote a more sustainable, less toxic New York City.{T} v (t), … … Wikipedia 90006 90007 90002 90003 90004 Integral 90005 — This article is about the concept of integrals in calculus. For the set of numbers, see integer. For other uses, see Integral (disambiguation). A definite integral of a function can be represented as the signed area of the region bounded by its … … Wikipedia 90006 90007 90002 90003 90004 Integral transform 90005 — In mathematics, an integral transform is any transform T of the following form :: (Tf) (u) = int {t 1} ^ {t 2} K (t, u), f (t ), dt.The input of this transform is a function f, and the output is another function Tf. An integral transform is a … … Wikipedia 90006 90007 90002 90003 90004 Time-scale calculus 90005 — In mathematics, time scale calculus is a unification of the theory of difference equations with that of differential equations, unifying integral and differential calculus with the calculus of finite differences, offering a formalism for studying … Wikipedia 90006 90007 90002 90003 90004 integral reality 90005 — by William Pawlett The notion of integral reality appeared relatively late in Baudrillard s career, becoming important thematically in The Perfect Crime (1996c [1995a]) and discussed in detail in his final major work The Intelligence of Evil … The Baudrillard dictionary 90006 90007 90002 90003 90004 Integral movement 90005 — This article is about the integral movement in philosophy and psychology.See Integral (disambiguation) for other uses. The integral movement (also called the integral paradigm, integral philosophy, the integral worldview, or the integral … … Wikipedia 90006 90007 90002 90003 90004 Integral Systems 90005 — Infobox Company company name = Integral Systems company company type = Public (nasdaq2 | ISYS) foundation = Lanham, Maryland, USA (1982) location city = Lanham, Maryland location country = United States key people = John Higginbotham , CEO William … … Wikipedia 90006 90007 90002 90003 90004 Time dependent vector field 90005 — In mathematics, a time dependent vector field is a construction in vector calculus which generalizes the concept of vector fields.It can be thought of as a vector field which moves as time passes. For every instant of time, it associates a … … Wikipedia 90006 90007 90002 90003 90004 Integral curve 90005 — In mathematics, an integral curve for a vector field defined on a manifold is a curve in the manifold whose tangent vector (i.e. time derivative) at each point along the curve is the vector field itself at that point. Intuitively, an integral … … Wikipedia 90006 90007 .90000 integral time — це … Що таке integral time? 90001 90002 90003 90004 Time-Domain Thermoreflectance 90005 — is a method by which the thermal properties of a material can be measured, most importantly thermal conductivity. This method can be applied most notably to thin film materials (up to hundreds of nanometers thick), which have properties that vary … Wikipedia 90006 90007 90002 90003 90004 Time’s Up! 90005 — is a grassroots environmental group that seeks to promote a more sustainable, less toxic New York City.{T} v (t), … … Wikipedia 90006 90007 90002 90003 90004 Integral 90005 — This article is about the concept of integrals in calculus. For the set of numbers, see integer. For other uses, see Integral (disambiguation). A definite integral of a function can be represented as the signed area of the region bounded by its … … Wikipedia 90006 90007 90002 90003 90004 Integral transform 90005 — In mathematics, an integral transform is any transform T of the following form :: (Tf) (u) = int {t 1} ^ {t 2} K (t, u), f (t ), dt.The input of this transform is a function f, and the output is another function Tf. An integral transform is a … … Wikipedia 90006 90007 90002 90003 90004 Time-scale calculus 90005 — In mathematics, time scale calculus is a unification of the theory of difference equations with that of differential equations, unifying integral and differential calculus with the calculus of finite differences, offering a formalism for studying … Wikipedia 90006 90007 90002 90003 90004 integral reality 90005 — by William Pawlett The notion of integral reality appeared relatively late in Baudrillard s career, becoming important thematically in The Perfect Crime (1996c [1995a]) and discussed in detail in his final major work The Intelligence of Evil … The Baudrillard dictionary 90006 90007 90002 90003 90004 Integral movement 90005 — This article is about the integral movement in philosophy and psychology.See Integral (disambiguation) for other uses. The integral movement (also called the integral paradigm, integral philosophy, the integral worldview, or the integral … … Wikipedia 90006 90007 90002 90003 90004 Integral Systems 90005 — Infobox Company company name = Integral Systems company company type = Public (nasdaq2 | ISYS) foundation = Lanham, Maryland, USA (1982) location city = Lanham, Maryland location country = United States key people = John Higginbotham , CEO William … … Wikipedia 90006 90007 90002 90003 90004 Time dependent vector field 90005 — In mathematics, a time dependent vector field is a construction in vector calculus which generalizes the concept of vector fields.It can be thought of as a vector field which moves as time passes. For every instant of time, it associates a … … Wikipedia 90006 90007 90002 90003 90004 Integral curve 90005 — In mathematics, an integral curve for a vector field defined on a manifold is a curve in the manifold whose tangent vector (i.e. time derivative) at each point along the curve is the vector field itself at that point. Intuitively, an integral … … Wikipedia 90006 90007 .
Leave A Comment