Изображение предмета в плоском зеркале – построение
4.5
Средняя оценка: 4.5
Всего получено оценок: 158.
4.5
Средняя оценка: 4.5
Всего получено оценок: 158.
В быту широко используются различные зеркала. Однако мало кто задумывается, почему в зеркале возникает изображение, и почему оно находится именно в данном месте. Разберем явление возникновения изображения в зеркале подробнее.
Действие плоского зеркала
Идеальное плоское зеркало – это плоскость, полностью отражающая все падающие на нее лучи света в соответствии законом отражения. Напомним, закон отражения гласит, что отраженный луч лежит в плоскости, задаваемой падающим лучом и перпендикуляром к зеркалу, восстановленным из точки падения луча; угол между перпендикуляром и отраженным лучом равен углу между перпендикуляром и падающим лучом.
Рис. 1. Падающий, отраженный лучи и перпендикулярДля построения отраженного изображения точки достаточно проследить путь двух произвольных лучей, которые вышли в разных направлениях из этой точки, и отразились в зеркале.
Два луча обязательно пересекутся либо до, либо после отражения в плоском зеркале, это определяется законом отражения и тем, что оба они вышли из одной точки, а значит, изначально лежали в одной плоскости.
Изображение точки в зеркале
Для построения изображения точки S в зеркале, проследим за двумя лучами, выходящими из этой точки в разных направлениях.
После отражения оба лучи расходятся, следовательно, зеркало не даст реального изображения.
Используя закон отражения, можно доказать, что треугольник, образованный лучами до отражения и треугольник, образованный продолжением лучей «в зазеркалье» равны по двум углам и общей стороне (зеркалу, от которого происходит отражение).
А значит, и треугольник, образованный лучом, вышедшим из S, зеркалом и перпендикуляром к зеркалу, опущенным из S, равен треугольнику, образованному продолжением отраженного луча, приходящим в S’, зеркалом и перпендикуляром к зеркалу, опущенным из S’. Отсюда следует, что перпендикуляры из S и из S’ равны и представляют собой одну прямую.
Таким образом, изображение в плоском зеркале S’ точки S будет мнимым, оно будет находиться «в зазеркалье», на продолжении перпендикуляра к зеркалу, опущенному из S, на таком же расстоянии (симметрично относительно зеркала).
Изображение предмета в зеркале
Зная процесс формирования изображения для одной точки, можно построить изображение любого объекта, построив изображение всех его точек.

Хотя кажется, что изображение, которое дает зеркало, идентично исходному предмету, это не совсем так. Отраженное изображение меняет местами правую и левую стороны. Посмотрите циферблат часов, отражающихся в зеркале, на буквы в отражении книг – вы увидите разницу. Наконец, попытайтесь писать текст, глядя в зеркало, так, чтобы в зеркале читались слова – убедитесь, что это не так-то просто.
Что мы узнали?
Изображение точки в плоском зеркале является мнимым, и находится на линии перпендикуляра, опущенного из точки к плоскости зеркала на расстоянии равном расстоянию от зеркала до точки. Изображение объекта в зеркале также мнимое, зеркально симметричное и находится на таком же расстоянии от зеркала, как и исходный объект. Оно одинакового с исходным объектом размера и не имеет искажений, но зеркально обращено.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Егор Князев
3/5
Александр Коновалов
5/5
Оценка доклада
4. 5
5
Средняя оценка: 4.5
Всего получено оценок: 158.
А какая ваша оценка?
Плоское зеркало • 8 класс • Физика
Содержание
Из прошлых уроков вы уже знаете, что свет распространяется прямолинейно в однородной среде, а при столкновении с какой-либо поверхностью — отражается.
Один из видов отражения называется зеркальным. При слове «зеркало» мы представляем себе плоское стекло, на одну сторону которого нанесено специальное покрытие, содержащее серебро. Но в физике зеркалом может считаться любой предмет, имеющий гладкую плоскую поверхность.
У зеркал есть одна интересная особенность, которая нас и будет интересовать в этом уроке. Мы видим в зеркале отражения — себя и окружающих нас предметов.
Мы же видим предметы благодаря свету, но предметы в зеркале — ненастоящие. Что происходит на самом деле? Как это объясняет физика? На данном уроке вы узнаете много нового и интересного о, казалось бы, такой простой и привычной вещи, как зеркало.
Изображение в плоском зеркале
Плоское зеркало — это плоская поверхность, зеркально отражающая свет.
Рассмотрим изображение, которые мы получаем с помощью него.
Возьмем плоское зеркало $MN$ (рисунок 1). У нас есть источник света $S$, от которого идет расходящийся пучок света. Мы изобразим его с помощью расходящихся лучей $SO$, $SO_1$ и $SO_2$.
Рассмотрим все лучи по очереди:
- Луч $SO$
Луч достигает зеркала и отражается. Угол падения равен $0 \degree$, значит (по закону отражения света) угол отражения тоже будет равен $0 \degree$. Отраженный луч $OS$ совпадает с лучом $SO$, но имеет другое направление
- Луч $SO_1$
Этот луч падает на зеркало под углом $\alpha_1$ и отражается под углом $\beta_1$. По закону отражения: $\angle \beta_1 = \angle \alpha_1$
- Луч $SO_2$
Данный луч падает на плоское зеркало под углом $\alpha_2$ и отражается под углом $\beta_2$ ($\angle \beta_2 = \angle \alpha_2$)
Мы видим, что в глаз попадет расходящийся пучок света, который определяют лучи $SO_1$ и $SO_2$.
А теперь продолжим все отраженные лучи за зеркало. Они сойдутся в точке $S_1$. Эта точка называется мнимым изображением точки $S$.
Изображение в плоском зеркале называют мнимым, так как оно получается в результате пересечения не реальных лучей света, а их воображаемых продолжений.
{"questions":[{"content":"Мнимое изображение образуется[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["За плоским зеркалом","Перед плоским зеркалом","На плоском зеркале"],"answer":[0]}}}]}В итоге, получается, что в глаз попадает расходящийся пучок света, исходящий как будто бы из точки $S_1$. Но в этой точке сходятся не сами лучи, а только их продолжения. В действительности изображения в этой точке нет: нам только кажется, что из этой точки исходят лучи.
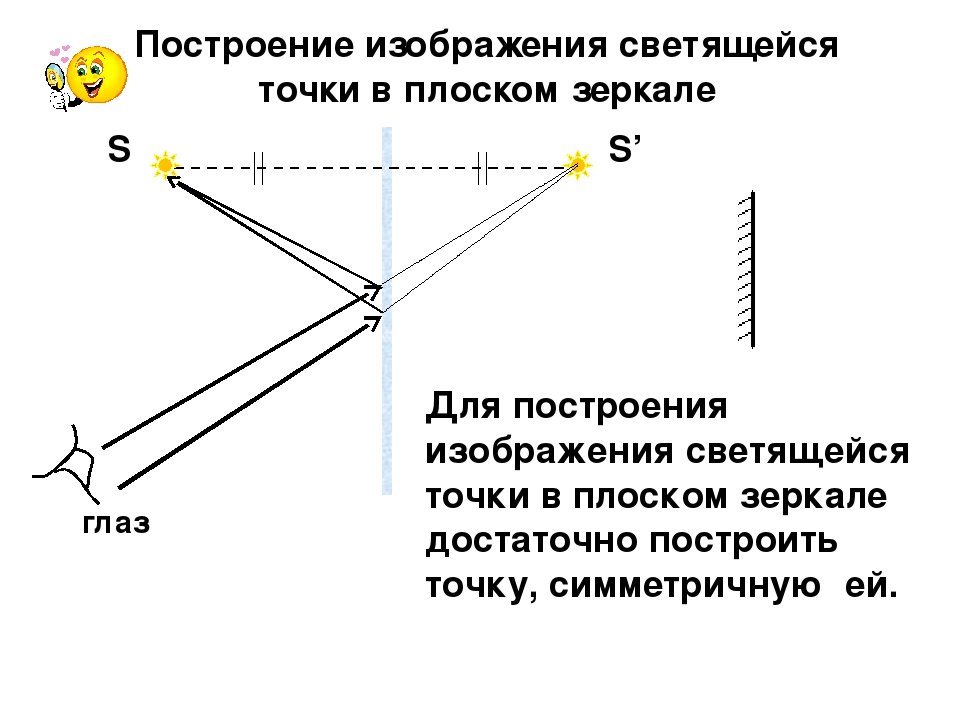
Построение мнимого изображения светящейся точки
Источник света, подобный тому, что мы рассмотрели выше, принято называть светящейся точкой (точка $S$ на рисунке 1).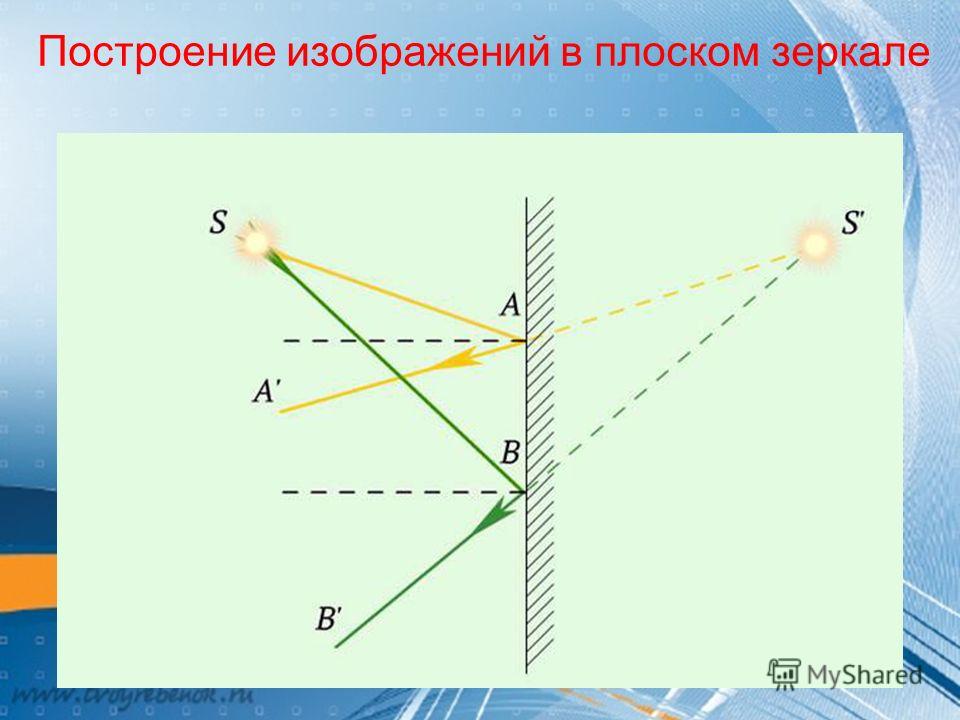 Построить мнимое изображение такой точки очень просто.
Построить мнимое изображение такой точки очень просто.
На рисунке 1 мы описали пучок света с помощью трех лучей, чтобы обратить ваше внимание на то изображение, которое попадает в глаза. Для построения такого изображения на чертеже нам хватит выделить всего два луча:
1. Луч, перпендикулярный зеркалу
2. Луч, падающий под углом
Второй луч мы выбираем удобным для нас образом, чтобы он попадал на зеркало под каким-то углом падения $\alpha$.
Итак, возьмем светящуюся точку $S$ и плоское зеркало $MN$ (рисунок 2).
Рисунок 2. Построение мнимого изображения светящейся точки в плоском зеркалеИз точки $S$ опустим перпендикуляр на зеркало. Мы отметили первый луч $SA$. Отраженный луч будет совпадать с ним, но иметь обратное направление — $AS$.
Отметим второй луч — $SB$, он падает на поверхность зеркала под углом $\alpha$. Опустим на поверхность зеркала перпендикуляр $BC$ и отложим от него угол $\beta$, по закону отражения света равный углу $\alpha$. Мы получили отражённый луч $CD$.
Мы получили отражённый луч $CD$.
Теперь необходимо продолжить лучи $AS$ и $CD$ за зеркало до их пересечения. Точка их пересечения $S_1$ — это мнимое изображение светящейся точки $S$.
Расположение и размеры предмета и его мнимого изображения относительно зеркала
Используя признаки равенства треугольников на рисунке 1, мы можем доказать, что $S_1O = OS$. То же самое можно проделать и с отрезками $AS$ и $AS_1$ на рисунке 2. Значит, изображение предмета находится на таком же расстоянии за зеркалом, на каком предмет расположен перед зеркалом.
Подтвердим этот факт простым, но очень показательным опытом. Возьмем обычную линейку и вертикально укрепим на ней кусок плоского стекла, как на рисунке 3.
Стекло будет являться полупрозрачным зеркалом. С одной его стороны мы видим зеркальное отражение предметов, а с другой — то, что происходит за этим стеклом.
Рисунок 3. Получение мнимого изображения в плоском зеркалеТакже у нас имеются две одинаковые свечи. Одну поставим на расстоянии 3 см от зеркала и зажжем. Мы видим ее отражение в зеркале. Кажется, что оно находится позади стекла.
Одну поставим на расстоянии 3 см от зеркала и зажжем. Мы видим ее отражение в зеркале. Кажется, что оно находится позади стекла.
Наша задача — разместить вторую свечу с другой стороны зеркала так, чтобы она тоже казалась зажженой. Передвигая ее, найдем это положение.
Что мы получили? Незажженная свеча находится именно в том месте, где наблюдается изображение горящей свечи (рисунок 3, а). А теперь взгляните на линейку — за зеркалом свеча находится тоже на 3 см от него. Расстояние от свечи до стекла и от ее изображения до стекла одинаковы.
Итак, мы подошли к интересному выводу.
Мнимое изображение предмета в плоском зеркале находится на том же расстоянии от зеркала, на каком находится сам предмет.
Из этого опыта также очевидно, что высота изображения свечи равна высоте самой свечи (рисунок 3, б). Ведь, передвигая свечу за зеркалом, мы добились того, что она полностью совпала с изображением зажженной свечи.
Размеры изображения предмета в плоском зеркале равны реальным размерам предмета.
Из своего жизненного опыта каждый из нас знает, что когда мы смотрим на изображение предмета в зеркале, мы видим его симметричную форму (рисунок 4).
Рисунок 4. Зеркальное отражениеЭто означает, что в зеркале «право» и «лево» меняются местами. Например, зеркальное изображение левой руки представляет для нас как бы правую руку.
{"questions":[{"content":"Какие свойства изображения предмета в плоском зеркале отличают его от самого предмета?[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["Другой размер и другая удаленность от зеркала","Его мнимость и симметричность предмету","Его мнимость и другой размер","У них нет различий"],"explanations":["Размер изображения и его удаленность от зеркала соответствуют действительным.","","Размер изображения идентичен реальному предмету.",""],"answer":[1]}}}]}Давайте подведем итоги.
Изображение предмета в плоском зеркале:
- Мнимое (находится на пересечении продолжений лучей, а не самих лучей)
- Прямое (не перевернутое)
- Равное по размеру самому предмету
- Находится за зеркалом на таком же расстоянии, как и предмет перед ним
- Симметричное предмету
Построение мнимого изображения предмета
Вы уже узнали определение плоского зеркала и установили его свойства. Теперь давайте рассмотрим, как самостоятельно построить мнимое изображение любого предмета в зеркале.
Теперь давайте рассмотрим, как самостоятельно построить мнимое изображение любого предмета в зеркале.
На чертеже у нас есть плоское зеркало и предмет $AB$ (рисунок 5).
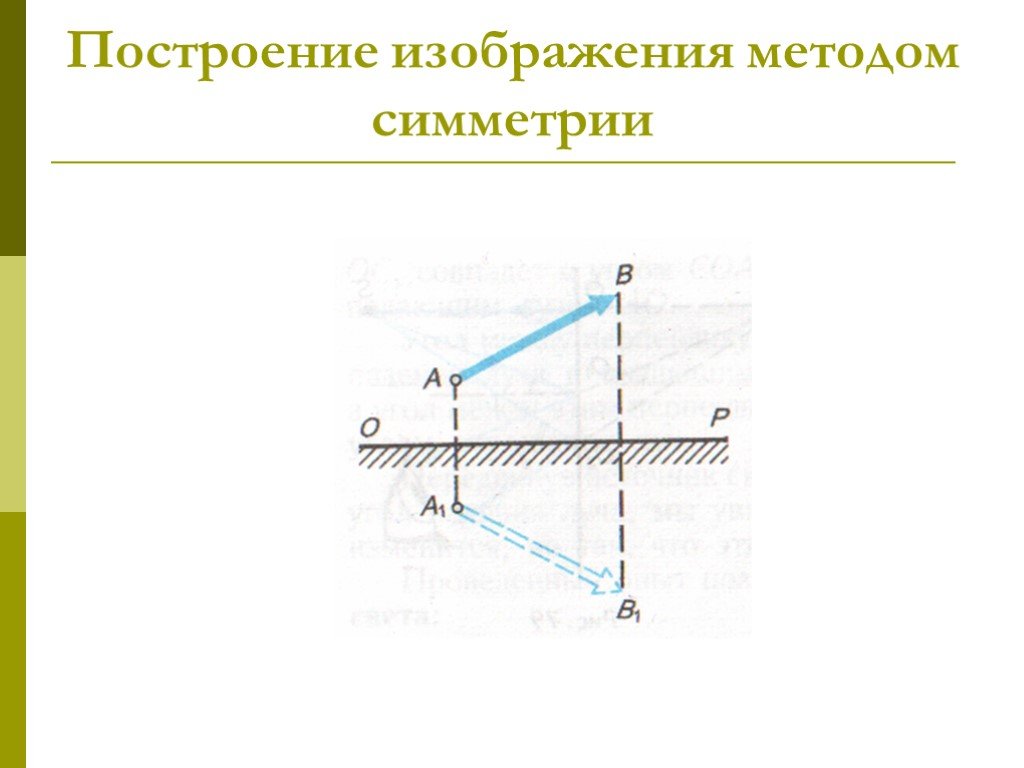
Рисунок 5. Построение мнимого изображения предмета в плоском зеркалеНачнем построение изображения. Для этого опустим из точки $A$ перпендикуляр $АС$ на плоское зеркало. Теперь измерим и зафиксируем длину этого отрезка ($AC$).
Продлим отрезок $AC$ за зеркало и отложим расстояние, равное его длине. Так мы получили точку $A_1$ — мнимое изображение точки $A$.
Проделаем то же самое с точкой $B$. Опустим перпендикуляр на зеркало, продолжим и на определенном расстоянии отметим точку $B_1$.
Теперь осталось только соединить две полученные точки. Так мы получили мнимое изображение $A_1B_1$ предмета $AB$.
Пример задачи
Солнечные лучи при падении образуют с горизонтом угол $\varphi = 40 \degree$. Под каким углом к горизонту нужно расположить плоское зеркало, чтобы отраженные лучи пошли вертикально вверх?
Дано:
$\varphi = 40 \degree$
$\eta — ?$
Для решения задачи нам понадобится рисунок 6.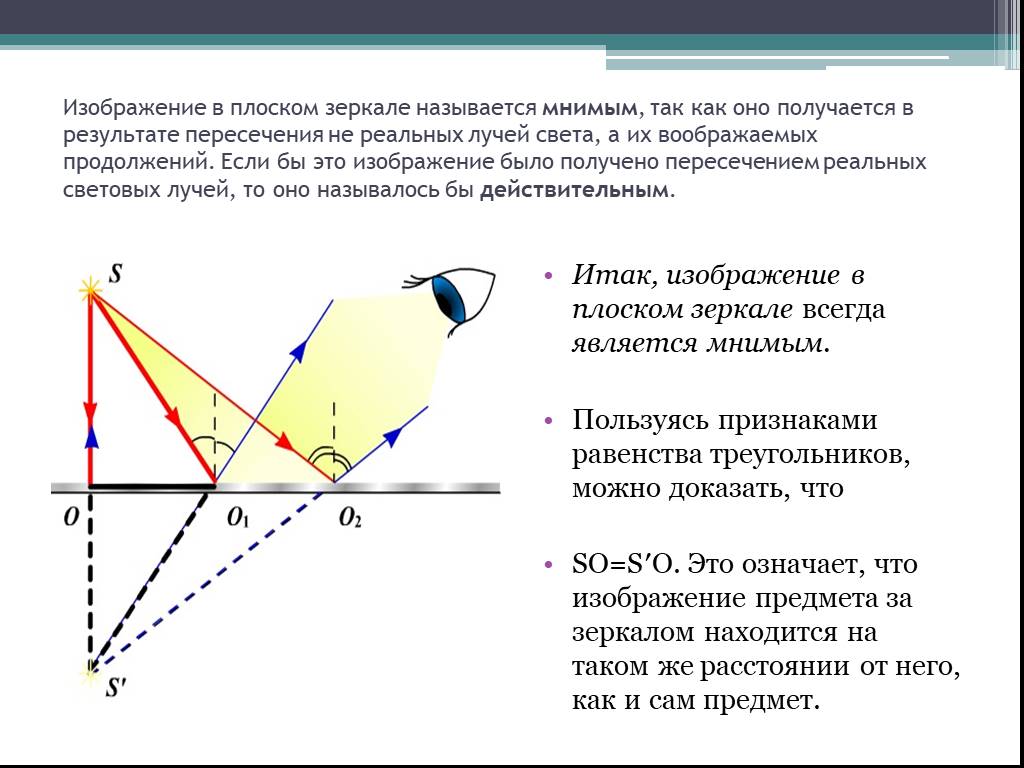
Как мы получили такую картинку? Давайте разберемся.
Первым делом проводим линию горизонта $MN$ и отмечаем наш источник света ($S$). Солнечные лучи представим в виде одного падающего луча $SO$. Отмечаем угол между падающим лучом и линией горизонта — угол $\varphi$.
Теперь нарисуем отраженный луч $OD$. По условию задачи $OD \perp MN$.
По закону отражения света угол падения равен углу отражения. Поэтому мы разделим угол, образованный на картинке падающим и отраженными лучами, пополам — проведем биссектрису $OC$. Отметим угол падения $\alpha$ и угол отражения $\beta$.
Теперь вспомните, как мы строим отражённый луч. Для этого мы проводим перпендикуляр к отражающей поверхности. В нашем случае, эта поверхность — это зеркало, а перпендикуляр у нас уже есть — $OC$. Значит, поверхность зеркала должна располагаться перпендикулярно этому отрезку.
Таким образом изобразим на рисунке зеркало и отметим искомый угол $\eta$.
Теперь можно приступать к решению задачи.
Посмотреть решение и ответ
Скрыть
Решение:
Из условия задачи $OD \perp MN$, $\angle MOD = 90 \degree$.
Из рисунка мы видим, что $\angle MOD$ составляют два угла: $\angle MOS$ и $\angle SOD$.
Значит, $\angle SOD = 90 \degree — \varphi$.
$\angle SOD = 90 \degree — 40 \degree = 50 \degree$.
По закону отражения света $\angle \alpha = \angle \beta$. Именно эти два угла и составляют $\angle SOD$. Выразим этот угол через углы падения и отражения:
$\angle SOD = \alpha + \beta = 2\alpha$.
Теперь мы можем найти угол $\alpha$:
$\alpha = \frac{\angle SOD}{2} = \frac{50 \degree}{2} = 25 \degree$.
Рассмотрим прямоугольный треугольник $OCA$.
$\angle COA = 90 \degree$.
С другой стороны:
$\angle COA = \eta + \varphi + \alpha$.
Отсюда найдем угол $\eta$:
$\eta = \angle COA — \varphi — \alpha = 90 \degree — 40 \degree — 25 \degree = 25 \degree$.
Ответ: $\eta = 25 \degree$.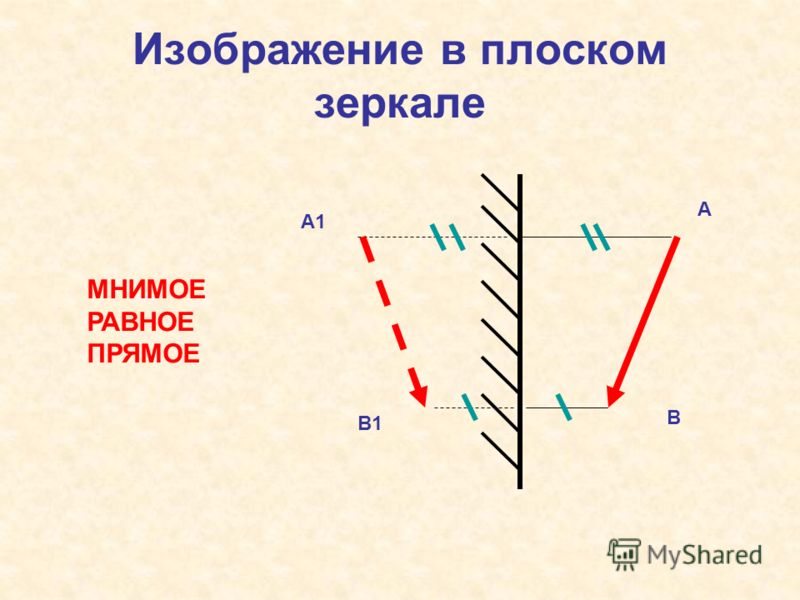
Применение плоских зеркал
В повседневной жизни нас окружает множество плоских зеркал. Они нашли очень широкое применение как в быту, так и в технике.
Например, плоские зеркала используют в фарах различных автомобилей, прожекторов. И помимо этого, мы можем упомянуть и о дорожных и автомобильных зеркалах (боковых и заднего вида). Многие оптические приборы содержат в своем устройстве одно или несколько зеркал: объективы фотоаппаратов, лазеры, телескопы, перископы).
Перископ — это специальный прибор для наблюдения за поверхностью моря с подводной лодки, идущей на небольшой глубине (рисунок 7).
Рисунок 7. ПерископПростейший перископ представляет собой трубу, в углах которой расположены зеркала. Они наклонены относительно трубы на $45 \degree$. Сделано это для изменения хода световых лучей. Благодаря этому человек, находящийся у нижнего края трубы может видеть то, что находится у ее верхнего края.
Также в настоящее время зеркала используются в дизайне интерьеров. С их помощью создается иллюзия пространства — большой объем в небольших помещениях.
С их помощью создается иллюзия пространства — большой объем в небольших помещениях.
Интересный прием с зеркалами используют в магазинах. Один предмет помещают между несколькими зеркальным поверхностями, и создается впечатление, что предмет не один, а их много. Это возможно, если установить зеркала под определенным углом $\alpha$ друг к другу. Здесь работает формула, позволяющая рассчитать количество изображений $n$: $n = \frac{360 \degree — \alpha}{\alpha}$.
Характеристики изображения плоских зеркал
Как обсуждалось в предыдущем разделе Урока 2, положение изображения — это место в пространстве, от которого, по-видимому, расходится весь отраженный свет. Поскольку кажется, что свет от объекта отклоняется от этого места, человек, который смотрит вдоль линии в этом месте, увидит копию или подобие реального объекта.
В случае плоских зеркал изображение называется виртуальный образ .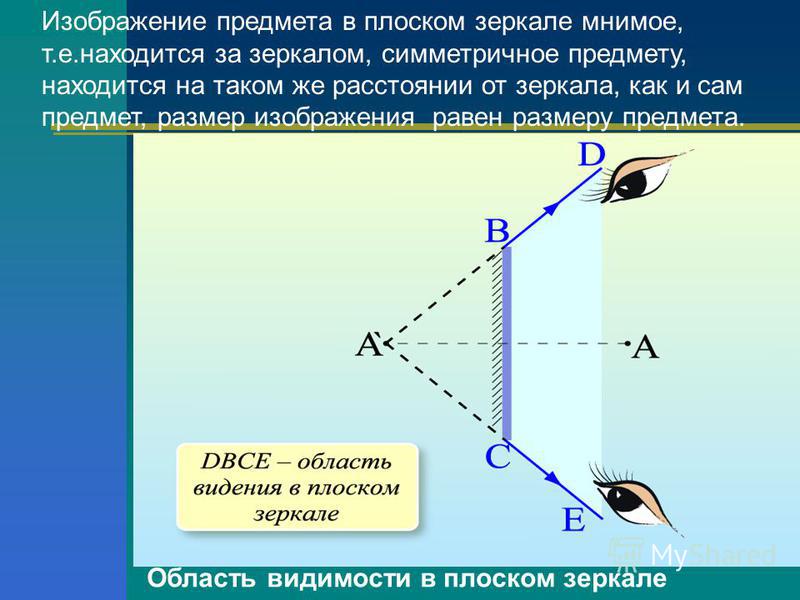 Виртуальные изображения — это изображения, которые формируются в местах, куда на самом деле не попадает свет. Свет на самом деле не проходит через место по другую сторону зеркала; наблюдателю только кажется, что свет исходит из этого места. Всякий раз, когда зеркало (будь то плоское или другое) создает виртуальное изображение, оно будет располагаться за зеркалом, откуда на самом деле не исходит свет. Позже в этом разделе мы будем изучать случаи, когда реальные изображения формируются криволинейными зеркалами. Такие изображения формируются на той же стороне зеркала, что и объект, и свет проходит через реальное местоположение изображения.
Виртуальные изображения — это изображения, которые формируются в местах, куда на самом деле не попадает свет. Свет на самом деле не проходит через место по другую сторону зеркала; наблюдателю только кажется, что свет исходит из этого места. Всякий раз, когда зеркало (будь то плоское или другое) создает виртуальное изображение, оно будет располагаться за зеркалом, откуда на самом деле не исходит свет. Позже в этом разделе мы будем изучать случаи, когда реальные изображения формируются криволинейными зеркалами. Такие изображения формируются на той же стороне зеркала, что и объект, и свет проходит через реальное местоположение изображения.
Помимо того факта, что плоские зеркальные изображения являются виртуальными, следует отметить несколько других характеристик. Вторая характеристика связана с ориентацией изображения. Если вы посмотрите на свое изображение в плоском зеркале (например, в зеркале в ванной), вы быстро заметите, что изображение переворачивается слева направо. То есть, если вы поднимете левую руку, то заметите, что на изображении поднимается то, что казалось бы правой рукой. Если вы поднимете правую руку, изображение поднимет то, что кажется его левой рукой. Это часто называют переворот влево-вправо . Эта характеристика становится еще более очевидной, если вы носите рубашку с надписью. Например, рубашка со словом «NIKE» будет читаться как «EKIN», если смотреть в зеркало; на рубашке со словом «ILLINOIS» будет написано «SIONILLI»; а на рубашке со словом «BOB» будет написано «BOB». (ПРИМЕЧАНИЕ. Мало того, что порядок букв будет изменен на противоположный, реальная ориентация самих букв также будет изменена. Конечно, это немного сложно сделать при наборе текста с клавиатуры.) правое изменение ориентации изображения, нет вертикального обращения сверху вниз. если вы встать на ноги перед плоским зеркалом, изображение не встать на голову . Точно так же потолок не становится этажом . Говорят, что изображение прямое , а не перевернутое .
То есть, если вы поднимете левую руку, то заметите, что на изображении поднимается то, что казалось бы правой рукой. Если вы поднимете правую руку, изображение поднимет то, что кажется его левой рукой. Это часто называют переворот влево-вправо . Эта характеристика становится еще более очевидной, если вы носите рубашку с надписью. Например, рубашка со словом «NIKE» будет читаться как «EKIN», если смотреть в зеркало; на рубашке со словом «ILLINOIS» будет написано «SIONILLI»; а на рубашке со словом «BOB» будет написано «BOB». (ПРИМЕЧАНИЕ. Мало того, что порядок букв будет изменен на противоположный, реальная ориентация самих букв также будет изменена. Конечно, это немного сложно сделать при наборе текста с клавиатуры.) правое изменение ориентации изображения, нет вертикального обращения сверху вниз. если вы встать на ноги перед плоским зеркалом, изображение не встать на голову . Точно так же потолок не становится этажом . Говорят, что изображение прямое , а не перевернутое .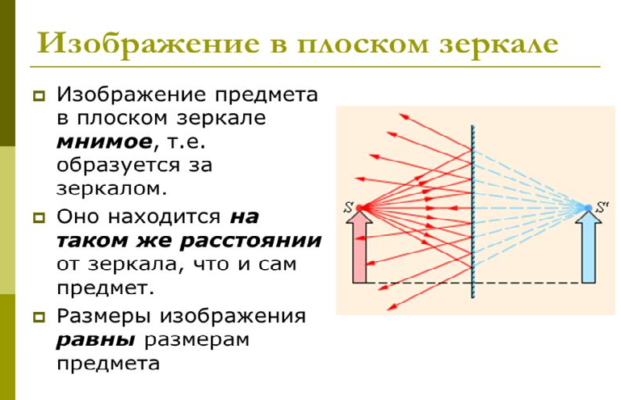
Студентов, изучающих физику, обычно очень заинтриговала эта кажущаяся перестановка влево-вправо. Что именно происходит, из-за чего ILLINOIS читается как SIONILLI? И почему переворот наблюдается в направлении слева направо, а не в направлении головы к пальцам ног? Эти вопросы побуждают нас к более глубокому осмыслению ситуации. Предположим на мгновение, что мы можем напечатать название вашего любимого школьного предмета на вашей рубашке и попросить вас посмотреть в зеркало. Все мы знаем, что когда вы посмотрите в зеркало, вы увидите буквы SCISYHP, написанные на рубашке вашего изображения — перевернутая форма PHYSICS. Но можем ли мы действительно сказать, что слово, появившееся на вашей рубашке, — это слово ФИЗИКА (буквы не перевернуты)? Ответ — нет! (Но вам пока не обязательно в это верить. Продолжайте читать… и размышляйте.)
Чтобы глубже изучить причину появления перестановки левого и правого, давайте предположим, что мы напишем слово PHYSICS на прозрачной пленке и подержим ее перед собой перед плоским зеркалом. Если мы посмотрим на изображение транспаранта в зеркале, то увидим ожидаемое — SCISYHP. Буквы написаны наоборот если смотреть в зеркало. А что, если мы посмотрим на буквы на транспаранте? Как ориентированы эти буквы? Когда мы стоим перед зеркалом и смотрим на буквы на транспаранте, мы наблюдаем неожиданное — SCISYHP. Если смотреть с точки зрения человека, держащего транспарант (и стоящего лицом к зеркалу), буквы демонстрируют такое же переворачивание влево-вправо, как и зеркальное отражение. Буквы кажутся перевернутыми на изображении, потому что они на самом деле перевернуты на рубашке. По крайней мере, они перевернуты, если смотреть с точки зрения человека, стоящего лицом к зеркалу. Представьте себе! Все это время вы думали, что зеркало переворачивает буквы на вашей рубашке. Но дело в том, что буквы уже были перевернуты на вашей рубашке, по крайней мере они были перевернуты от лица, которое стоит за футболкой . Люди, которые смотрят на вашу рубашку спереди, имеют другую систему отсчета и поэтому не видят буквы перевернутыми.
Если мы посмотрим на изображение транспаранта в зеркале, то увидим ожидаемое — SCISYHP. Буквы написаны наоборот если смотреть в зеркало. А что, если мы посмотрим на буквы на транспаранте? Как ориентированы эти буквы? Когда мы стоим перед зеркалом и смотрим на буквы на транспаранте, мы наблюдаем неожиданное — SCISYHP. Если смотреть с точки зрения человека, держащего транспарант (и стоящего лицом к зеркалу), буквы демонстрируют такое же переворачивание влево-вправо, как и зеркальное отражение. Буквы кажутся перевернутыми на изображении, потому что они на самом деле перевернуты на рубашке. По крайней мере, они перевернуты, если смотреть с точки зрения человека, стоящего лицом к зеркалу. Представьте себе! Все это время вы думали, что зеркало переворачивает буквы на вашей рубашке. Но дело в том, что буквы уже были перевернуты на вашей рубашке, по крайней мере они были перевернуты от лица, которое стоит за футболкой . Люди, которые смотрят на вашу рубашку спереди, имеют другую систему отсчета и поэтому не видят буквы перевернутыми.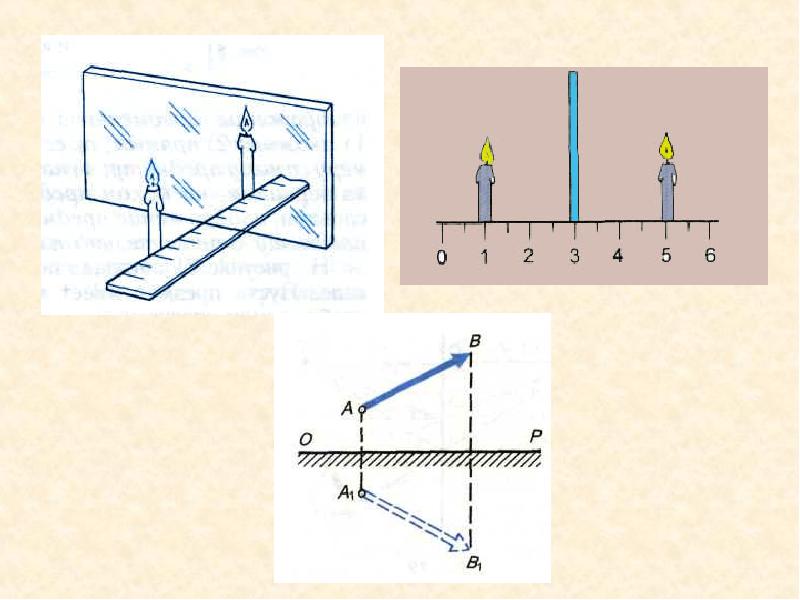 Кажущееся переворачивание изображения влево-вправо — это просто феномен системы отсчета. Когда вы смотрите на свою рубашку в плоском зеркале (или в любой части мира), вы смотрите на свою рубашку спереди. Это переключение систем отсчета.
Кажущееся переворачивание изображения влево-вправо — это просто феномен системы отсчета. Когда вы смотрите на свою рубашку в плоском зеркале (или в любой части мира), вы смотрите на свою рубашку спереди. Это переключение систем отсчета.
Третья характеристика плоских зеркальных изображений относится к соотношению между расстоянием объекта до зеркала и расстоянием изображения до зеркала. Для плоских зеркал расстояние до объекта (часто обозначается символом d o ) равно расстоянию до изображения (часто обозначается символом d i ). То есть изображение находится за зеркалом на том же расстоянии, что и объект перед зеркалом. Если вы стоите на расстоянии 2 метров от плоского зеркала, вы должны сфокусироваться на месте, находящемся на расстоянии 2 метров за зеркалом, чтобы увидеть свое изображение.
Относительный размер изображения и объекта
Четвертая и последняя характеристика плоских зеркальных изображений заключается в том, что размеры изображения совпадают с размерами объекта. Если перед зеркалом встанет человек ростом 1,6 метра, то он увидит изображение высотой 1,6 метра. Если перед плоским зеркалом поставить монету диаметром 18 мм, то изображение монеты будет иметь диаметр 18 мм. Отношение размеров изображения к размерам объекта называется увеличение . Плоские зеркала дают изображения с увеличением 1.
Если перед зеркалом встанет человек ростом 1,6 метра, то он увидит изображение высотой 1,6 метра. Если перед плоским зеркалом поставить монету диаметром 18 мм, то изображение монеты будет иметь диаметр 18 мм. Отношение размеров изображения к размерам объекта называется увеличение . Плоские зеркала дают изображения с увеличением 1.
В заключение, плоские зеркала дают изображения с рядом отличительных характеристик. Изображения, формируемые плоскими зеркалами, являются виртуальными, прямыми, перевернутыми влево-вправо, на таком же расстоянии от зеркала, как и расстояние до объекта, и того же размера, что и объект.
Flickr Physics Photo Изображение свечи в плоском зеркале. Изображение имеет те же размеры, что и объект, и находится за зеркалом на том же расстоянии, что и объект перед зеркалом.
1.

Leave A Comment