Дано: AC делит пополам \угол BAD
Геометрические доказательства
Эмма Р.
спросил 06.11.15 Дано: AC делит пополам \угол BAD
\угол ABC=\угол ADC
Напишите доказательство в два столбца, чтобы доказать= BC=DC
Подписаться І 3
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Санита М. ответил 06.11.15
Репетитор
4.7 (11)Математика и геология
Смотрите таких репетиторов
Смотрите таких репетиторов
AC делит пополам ∠BAD, => ∠BAC=∠CAD ….. (1)
, таким образом, в ΔABC и ΔADC, ∠ABC=∠ADC (дано),
∠BAC=∠CAD [из (1) ],
AC (противоположная сторона ∠ABC) = AC (противоположная сторона ∠ADC), общая сторона между ΔABC и ΔADC сторона сторона ∠BAC) = DC (противоположная сторона ∠CAD), поскольку (1)
Следовательно, BC=DC доказано.
Подробнее
Отчет
Сьюзен С. ответил 06.11.15
Репетитор
5 (31)Я люблю математику и люблю ее преподавать.
Смотрите таких репетиторов
Дорогая Эмма,
Вот что вам нужно сделать, чтобы построить доказательство. Разделение пополам и два отрезка, равенство которых они хотят, чтобы вы доказали, составляют два треугольника. Вам нужно сначала доказать, что эти треугольники, треугольник ABC и треугольник ADC равны по углу-углу-стороне. Тогда вы можете сказать, что два отрезка, BC и DC, равны на основании того, что «соответствующие части конгруэнтных треугольников конгруэнтны» (CPCTC). Между прочим, оба этих треугольника имеют одну общую сторону, AC. ___Заявления___________________________Причины_________________________ 1. Сегмент. AC делит пополам ∠BAD 1. Дано 2. (m=мера) m∠BAC=∠CAD 2. Определение биссектрисы угла Следовательно, m∠BAC≅∠CAD. 3. AC=AC 3. Рефлексивное свойство 4. ∠A BC =∠ADC 4. Дано 5. Треугольник ABC≅ Треугольник ADC 5. Угол-Угол-Сторона (постулат AAS). 6. Следовательно, BC=DC 6. CPCTC Примечание: ( Соответствующие части конгруэнтных треугольников конгруэнтны.) A-A-S= Две пары углов соответствуют, но есть общая сторона, которая не находится между углами. Надеюсь, я вам помог. Если у меня есть, пожалуйста, дайте мне палец вверх. 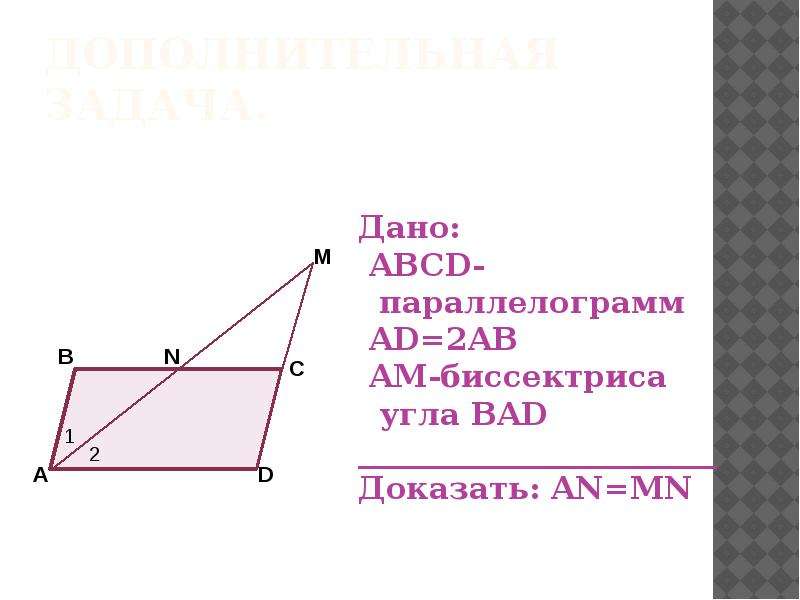 Вы должны нарисовать рисунок, прежде чем начать доказательство. 9
Вы должны нарисовать рисунок, прежде чем начать доказательство. 9
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчасВыберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Доказательств свойства воздушного змея
Доказательство свойства воздушного змеяСодержание: Три доказательства | Комментарии: Другой случай | Возможные ошибки | Использовать для подтверждения SSS
Для воздушного змея ABCD, где AB = AD и CB = CD, верно следующее.
- Диагональная прямая AC является серединным перпендикуляром к BD.
- Пересечение E линии AC и линии BD является серединой BD.
- Углы AED, DEC, CED, BEA прямые.
- Треугольник ABC равен треугольнику ADC.
- Следовательно, угол ABC = угол ADC.
- Прямая AC делит пополам углы BAD и BCD.
Два утверждения выделены жирным шрифтом, потому что эти утверждения включают в себя другие, из определений или серединного перпендикуляра и конгруэнтности треугольников. (Конечно, чтобы доказать смелые утверждения, возможно, придется доказать некоторые другие первый.
На уроке ученикам было предложено доказать это:
Дан воздушный змей ABCD с AB = AD и CB = CD, тогда треугольника ABC конгруэнтны в треугольник ADC.
Вот два доказательства, которые были найдены в классе (моя формулировка). (Примечание: это
пример, который показывает, что существует не обязательно только одно хорошее доказательство геометрическая теорема.
Доказательство 1: (основная идея: показать угол BAC = угол DAC)
- Пусть M — середина BD. Поскольку треугольник ABD равнобедренный, луч AM делится пополам. угол BAD, поэтому угол BAM = угол DAM.
- Также, поскольку треугольник ABD равнобедренный, прямая AM перпендикулярна BD.
- Так как треугольник CDB также равнобедренный, то прямая CM перпендикулярна BD для та же причина. Так как через М проходит только одна прямая, перпендикулярная к BD (аксиома транспортира), тогда линия AM = линия CM, поэтому A, M, C коллинеарны и эта линия является линией AC.
- Угол BAM = угол BAC и угол DAM = угол DAC (одинаковые лучи).
- Таким образом, треугольник ABC равен треугольнику ADC по SAS, так как два угла BAC и DAC, указанные выше, конгруэнтны, а также AB = AD (по гипотезе) и AC = переменного тока.
QED (почти см. комментарии ниже о другом случае).
Доказательство 2: (ключевая идея: показать угол BAC = угол DAC)
- Пусть m — серединный перпендикуляр к BD.
 По определению перпендикуляра
биссектриса m пересекает BD в точке M, середине BD.
По определению перпендикуляра
биссектриса m пересекает BD в точке M, середине BD. - Треугольник ABD равнобедренный. По свойствам симметрии равнобедренного треугольника прямая AM является серединным перпендикуляром к BD = m. Таким образом, А есть на м.
- Кроме того, поскольку треугольник ABD равнобедренный, луч AM делит угол BAD пополам, поэтому угол BAM = угол DAM.
- Угол BAM = угол BAC и угол DAM = угол DAC (одинаковые лучи)
- Таким образом, треугольник ABC равен треугольнику ADC по SAS, так как два угла BAC и DAC, указанные выше, конгруэнтны, а также AB = AD (по гипотезе) и AC = переменного тока.
QED (почти см. комментарии ниже о другом случае).
Доказательство 3: (ключевая идея: показать угол ABC = угол ADC)
- Треугольник ABD равнобедренный, поэтому угол ABD = углу ADB.
- Треугольник CBD равнобедренный, поэтому угол CBD = угол CDB.

- Угол ABC = угол ABD + угол DBC
- Угол ADC = угол ADB + угол BDC
- Поскольку суммы справа равны из-за конгруэнтности углов, тогда угол ABC = угол ADC.
- Таким образом, треугольник ABC равен треугольнику ADC по SAS, так как два угла ABC = ADC конгруэнтны, а также AB = AD и CB = CD (по условию).
QED (почти см. комментарии ниже о другом случае).
Комментарии: Хорошие доказательства, но есть еще одно (невыпуклое) дело
Все доказательства хороши и действительны для фигуры, показанной в верхней части страница. Однако есть еще один рисунок, показывающий другой случай воздушного змея. доказательства которых почти верны, но нуждаются в некоторых дополнительных комментариях. Этот это тот случай, когда A и C находятся на одной стороне линии BD, как на этом рисунке.
Так что не так с пруфами?
В Доказательство 1 и Доказательство 2 , важный шаг был
- Угол BAM = угол BAC и угол DAM = угол DAC (одинаковые лучи).

Но на этом рисунке это не так. Но еще не все потеряно. Мы просто должны обоснуйте угол BAC = угол DAC и в этом случае. Тогда доказательства верны для остальных шагов. Мы действительно можем установить и установить равенство пары способов.
- По-прежнему верно, что луч CM = луч CA, поэтому мы можем поменять роли A и C и работаем с делением пополам угла C вместо угла A. Мы не приходится заново писать все доказательство; мы можем просто переобозначить ABCD так, чтобы A было вершина, наиболее удаленная от М.
- Второй подход состоит в том, чтобы работать с фигурой так, как она помечена, но утверждать, что Два угла равны, если они смежны с равными углами. В этом случае, угол BAC и угол BAM являются дополнительными, а также угол DAC является дополнительным к углу DAM, который равен углу BAM. Таким образом, угол BAC = угол DAC.
В Proof 3 шаг которые не соответствуют действительности в этом уходе
- Угол ABC = угол ABD + угол DBC
- Угол ADC = угол ADB + угол BDC
Но что, если мы вычтем вместо сложения, тогда мы все равно получим правильные утверждения
который можно использовать в остальной части доказательства.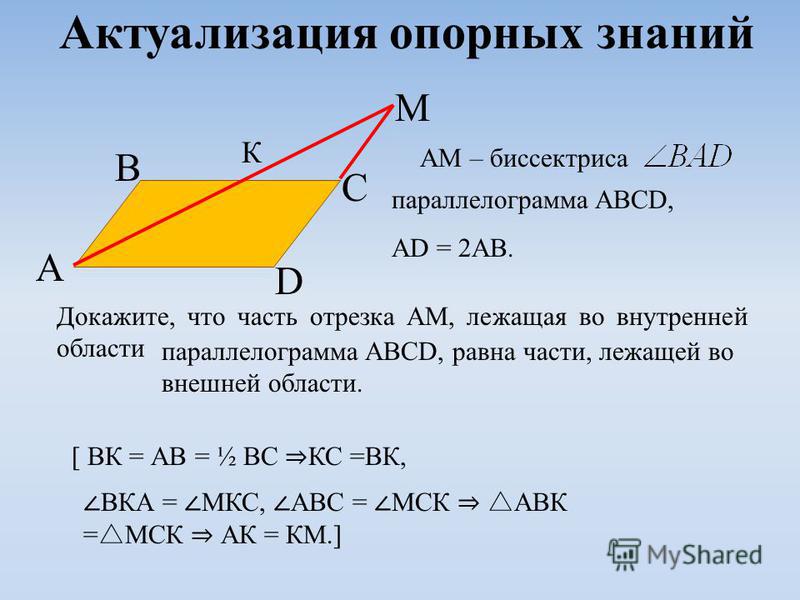
- Угол ABC = угол DBC — угол ABD
- Угол ADC = угол BDC — угол ADB
Возможные ошибки в доказательствах
Несмотря на то, что существует несколько правильных способов доказать приведенную выше теорему, также ряд ошибочных подходов. Как правило, к ним относятся замаскированные способ сделать вывод. Вот несколько примеров начала таких доказательства того, что треугольник ABC равен треугольнику ADC

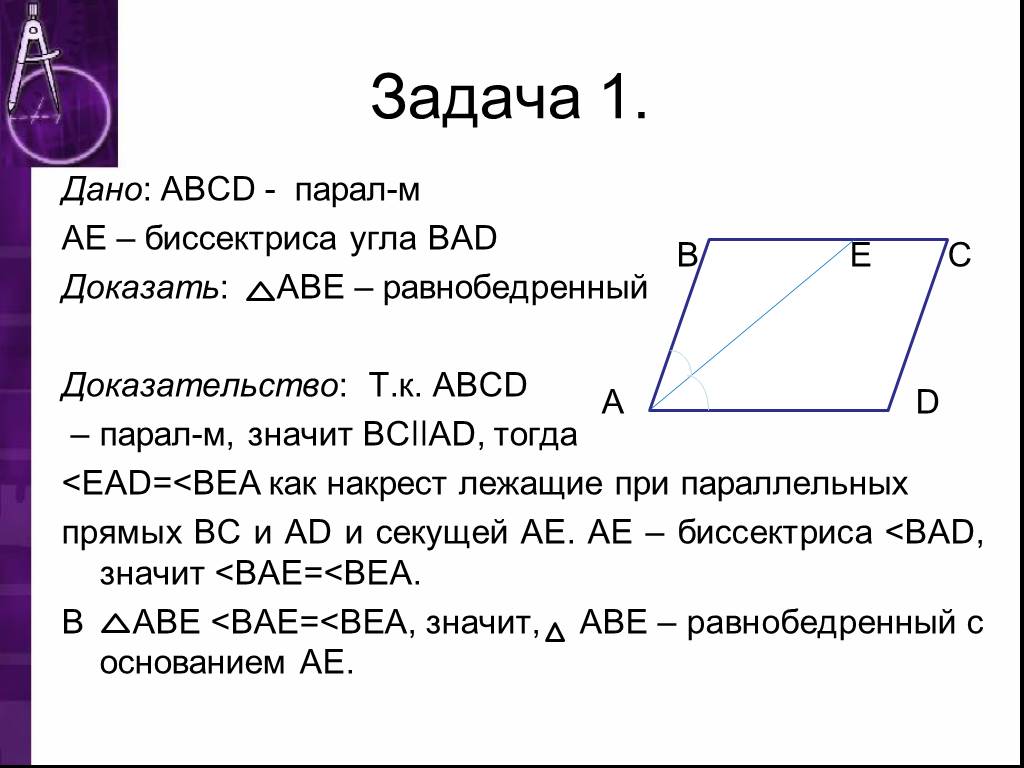 По определению перпендикуляра
биссектриса m пересекает BD в точке M, середине BD.
По определению перпендикуляра
биссектриса m пересекает BD в точке M, середине BD.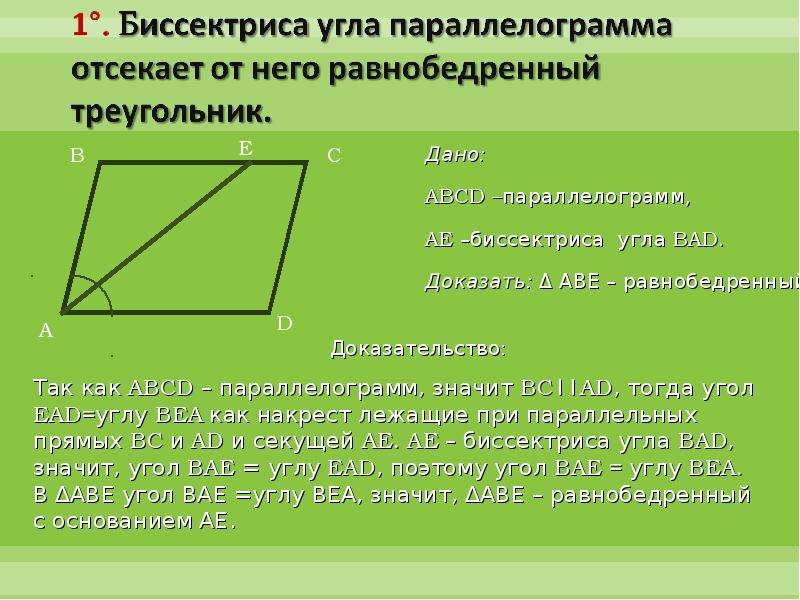


Leave A Comment