Если диагонали параллелограмма перпендикулярны то этот параллелограмм является ромбом: Если у параллелограмма диагонали перпендикулярны

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Поиск по сайту:

Справочник по математике

Геометрия (Планиметрия)

Четырехугольники

Свойства и признаки параллелограмма

Свойства и признаки прямоугольника

Свойства и признаки ромба

Свойства и признаки квадрата

Замечание. Мы рассматриваем только выпуклые четырёхугольникивыпуклые четырёхугольники.

Свойства и признаки параллелограмма

Тип утверждения	Фигура	Рисунок	Формулировка
Определение	Параллелограмм		Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны
Определение	Диагонали параллелограмма		Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины
Определение	Высота параллелограмма		Высотой параллелограмма называют перпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение
Свойство	Равенство противолежащих сторон		Если четырёхугольник является параллелограммом, то его противолежащие стороны равны
Признак	Равенство противолежащих сторон		Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом
Признак	Равенство и параллельность двух противолежащих сторон		Если у четырёхугольника *две* противолежащие стороны равны и параллельны, то он является параллелограммом
Свойство	Диагонали точкой пересечения делятся пополам		Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам
Признак	Диагонали точкой пересечения делятся пополам		Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом
Свойство	Суммы углов, прилежащих к сторонам		Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180°
Признак	Суммы углов, прилежащих к сторонам		Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом
Свойство	Равенство противолежащих углов		Если четырёхугольник является параллелограммом, то его противолежащие углы равны
Признак	Равенство противолежащих углов		Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом
Свойство	Два треугольника, на которые каждая диагональ делит четырёхугольник		Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника
Признак			Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом
Свойство	Четыре треугольника, на которые диагонали делят четырёхугольник		Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника)
Признак			Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом

Определение: параллелограмм
	Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны
Определение: диагонали параллелограмма
	Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины
Определение: высота параллелограмма
	Высотой параллелограмма называютперпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение
Свойство: равенство противолежащих сторон
	Если четырёхугольник является параллелограммом, то его противолежащие стороны равны
Признак: равенство противолежащих сторон
	Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом
Признак: равенство и параллельность двух противолежащих сторон
	Если у четырёхугольника *две* противолежащие стороны равны и параллельны, то он является параллелограммом
Свойство: диагонали точкой пересечения делятся пополам
	Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам
Признак: диагонали точкой пересечения делятся пополам
	Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом
Свойство: суммы углов, прилежащих к сторонам
	Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180°
Признак: суммы углов, прилежащих к сторонам
	Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом
Свойство: равенство противолежащих углов
	Если четырёхугольник является параллелограммом, то его противолежащие углы равны
Признак: равенство противолежащих углов
	Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом
Свойство: два треугольника, на которые каждая диагональ делит четырёхугольник
	Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника
Признак: два треугольника, на которые каждая диагональ делит четырёхугольник
	Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом
Свойство: четыре треугольника, на которые диагонали делят четырёхугольник
	Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника)
Признак: четыре треугольника, на которые диагонали делят четырёхугольник
	Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом

Параллелограмм

Определение: Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны

Диагонали параллелограмма

Определение: Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины

Высота параллелограмма

Определение: Высотой параллелограмма называют перпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение

Равенство противолежащих сторон

Свойство: Если четырёхугольник является параллелограммом, то его противолежащие стороны равны.

Признак: Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом.

Равенство и параллельность двух противолежащих сторон

Признак: Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом.

Диагонали точкой пересечения делятся пополам

Свойство: Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам.

Признак: Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом.

Суммы углов, прилежащих к сторонам

Свойство: Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180°.

Признак: Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом.

Равенство противолежащих углов

Свойство: Если четырёхугольник является параллелограммом, то его противолежащие углы равны.

Признак: Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом.

Два треугольника, на которые каждая диагональ делит четырёхугольник

Свойство: Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника.

Признак: Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом.

Четыре треугольника, на которые диагонали делят четырёхугольник

Свойство: Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника)

Признак: Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом.

Свойства и признаки прямоугольника

Тип утверждения	Фигура	Рисунок	Формулировка
Определение	Прямоугольник		Прямоугольником называют параллелограмм, у которого все углы прямые
Свойство	Равенство диагоналей		Если параллелограмм является прямоугольником, то его диагонали равны
Признак	Равенство диагоналей		Если у параллелограмма диагонали равны, то он является прямоугольником

Определение: прямоугольник
	Прямоугольником называют параллелограмм, у которого все углы прямые
Свойство: равенство диагоналей
	Если параллелограмм является прямоугольником, то его диагонали равны
Признак: равенство диагоналей
	Если у параллелограмма диагонали равны, то он является прямоугольником

Прямоугольник

Определение: Прямоугольником называют параллелограмм, у которого все углы прямые.

Равенство диагоналей

Свойство: Если параллелограмм является прямоугольником, то его диагонали равны.

Признак: Если у параллелограмма диагонали равны, то он является прямоугольником.

Свойства и признаки ромба

Тип утверждения	Фигура	Рисунок	Формулировка
Определение	Ромб		Ромбом называют параллелограмм, у которого все стороны равны
Свойство	Биссектрисы углов диагонали		Если параллелограмм является ромбом, то его диагонали является биссектрисами углов
Признак	Биссектрисы углов диагонали		Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом
Свойство	Перпендикулярность диагоналей		Если параллелограмм является ромбом, то его диагонали перпендикулярны
Признак	Перпендикулярность диагоналей		Если у параллелограмма диагонали перпендикулярны, то он является ромбом

Определение: ромб
	Ромбом называют параллелограмм, у которого все стороны равны
Свойство: биссектрисы углов и диагонали
	Если параллелограмм является ромбом, то его диагонали являются биссектрисами углов
Признак: биссектрисы углов и диагонали
	Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом
Свойство: перпендикулярность диагоналей
	Если параллелограмм является ромбом, то его диагонали перпендикулярны
Признак: перпендикулярность диагоналей
	Если у параллелограмма диагонали перпендикулярны, то он является ромбом

Ромб

Определение: Ромбом называют параллелограмм, у которого все стороны равны

Биссектрисы углов и диагонали

Свойство: Если параллелограмм является ромбом, то его диагонали являются биссектрисами углов

Признак: Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом

Перпендикулярность диагоналей

Свойство: Если параллелограмм является ромбом, то его диагонали перпендикулярны

Признак: Если у параллелограмма диагонали перпендикулярны, то он является ромбом

Свойства и признаки квадрата

Тип утверждения	Фигура	Рисунок	Формулировка
Определение	Квадрат		Квадратом называют параллелограмм, у которого все стороны равны и все углы равны
Свойство	Перпендикулярность и равенство диагоналей		Если параллелограмм является квадратом, то его диагонали перпендикулярны и равны
Признак	Перпендикулярность и равенство диагоналей		Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом
Свойство	Перпендикулярность диагоналей		Если прямоугольник является квадратом, то его диагонали перпендикулярны
Признак	Перпендикулярность диагоналей		Если у прямоугольника диагонали перпендикулярны, то он является квадратом
Свойство	Равенство диагоналей		Если ромб является квадратом, то его диагонали равны
Признак	Равенство диагоналей		Если у ромба диагонали равны, то он является квадратом

Определение: квадрат
	Квадратом называют параллелограмм, у которого все стороны равны и все углы равны
Свойство: перпендикулярность и равенство диагоналей
	Если параллелограмм является квадратом, то его диагонали перпендикулярны и равны
Признак: перпендикулярность и равенство диагоналей
	Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом
Свойство: перпендикулярность диагоналей
	Если прямоугольник является квадратом, то его диагонали перпендикулярны
Признак: перпендикулярность диагоналей
	Если у прямоугольника диагонали перпендикулярны, то он является квадратом
Свойство: равенство диагоналей
	Если ромб является квадратом, то его диагонали равны
Признак: равенство диагоналей
	Если у ромба диагонали равны, то он является квадратом

Квадрат

Определение: Квадратом называют параллелограмм, у которого все стороны равны и все углы равны

Перпендикулярность и равенство диагоналей

Свойство: Если параллелограмм является квадратом, то его диагонали перпендикулярны и равны

Признак: Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом

Перпендикулярность диагоналей

Свойство: Если прямоугольник является квадратом, то его диагонали перпендикулярны

Признак: Если у прямоугольника диагонали перпендикулярны, то он является квадратом

Равенство диагоналей

Свойство: Если ромб является квадратом, то его диагонали равны

Признак: Если у ромба диагонали равны, то он является квадратом

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Ромб

Содержание

Определение ромба
Свойства ромба
Признаки ромба

Определение ромба

Определение 1. Ромб − это параллелограмм, у которого все стороны равны.

На рисунке 1 изображен ромб ABCD.

Определение 2. Ромб − это четырехугольник, у которого все стороны равны.

Ромб разделяет плоскость на две части, одна из которых называется внутренней областью ромба, а другая внешней областью ромба.

Объединение ромба и ограниченной им части плоскости также называют ромбом.

Свойства ромба

Поскольку ромб является параллелограммом, то имеет следующие свойства:

1. У ромба противолежащие углы равны (\( \small \angle A = \angle C, \; \angle B = \angle D.\) )
2. У ромба противолежащие стороны равны (\( \small AB = DC, \; BC=AD. \) )
3. У ромба противолежащие стороны параллельны \( \small( AB \ || \ DC, \; BC \ || \ AD).\)
4. У ромба соседние углы дополняют друг друга до 180° \( \small ( \angle A +\angle B=180°, \) \( \small \angle C + \angle D=180°).\)
5. Диагонали ромба точкой пересечения делятся пополам \( \small ( AO = OC, \) \( \small BO=OD).\)

Ромб имеет также и следующие свойства:

6. Диагонали ромба пересекаются под прямым углом (\( \small AC \perp BD.\) )
7. Диагонали ромба являются биссектрисами его углов (\( \small \angle ABD = \angle CBD, \) \( \small \angle ADB = \angle CDB, \) \( \small \angle DAC = \angle BAC, \) \( \small \angle BCA = \angle DCA. \))
8. В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
9. Сумма квадратов диагоналей ромба равна квадрату стороны, умноженная на четыре \( \small (AC^2+BD^2=4AB^2). \)

Докажем свойства 6 и 7, сформулировав следующую теорему:

Теорема 1. Диагонали ромба перпендикулярны и являются биссектрисами его углов.

Доказательство. По определению 1, \( \small AD = DC \) (Рис.2). Следовательно треугольник \( \small DAC \) равнобедренный. Тогда \( \small \angle DCO = \angle DAO. \) Учитывая, что \( \small AO = OC \) (свойство 5 ромба), получим, что треугольники \( \small DOA \) и \( \small DOC \) равны по двум сторонам и углу между ними (см. статью Треугольники. Признаки равенства треугольников). Тогда равны углы DOC и DOA. Но эти углы смежные и их сумма равна 180°. Следовательно \( \small \angle DOC= \angle DOA=90°. \) То есть диагонали AC и BD перпендикулярны.

Из равенства треугольников \( \small DOA \) и \( \small DOC \) также следует, что \( \small \angle CDO= \angle ADO,\) следовательно BD является биссектрисой угла ADС, то есть BD является биссектрисой ромба ABCD.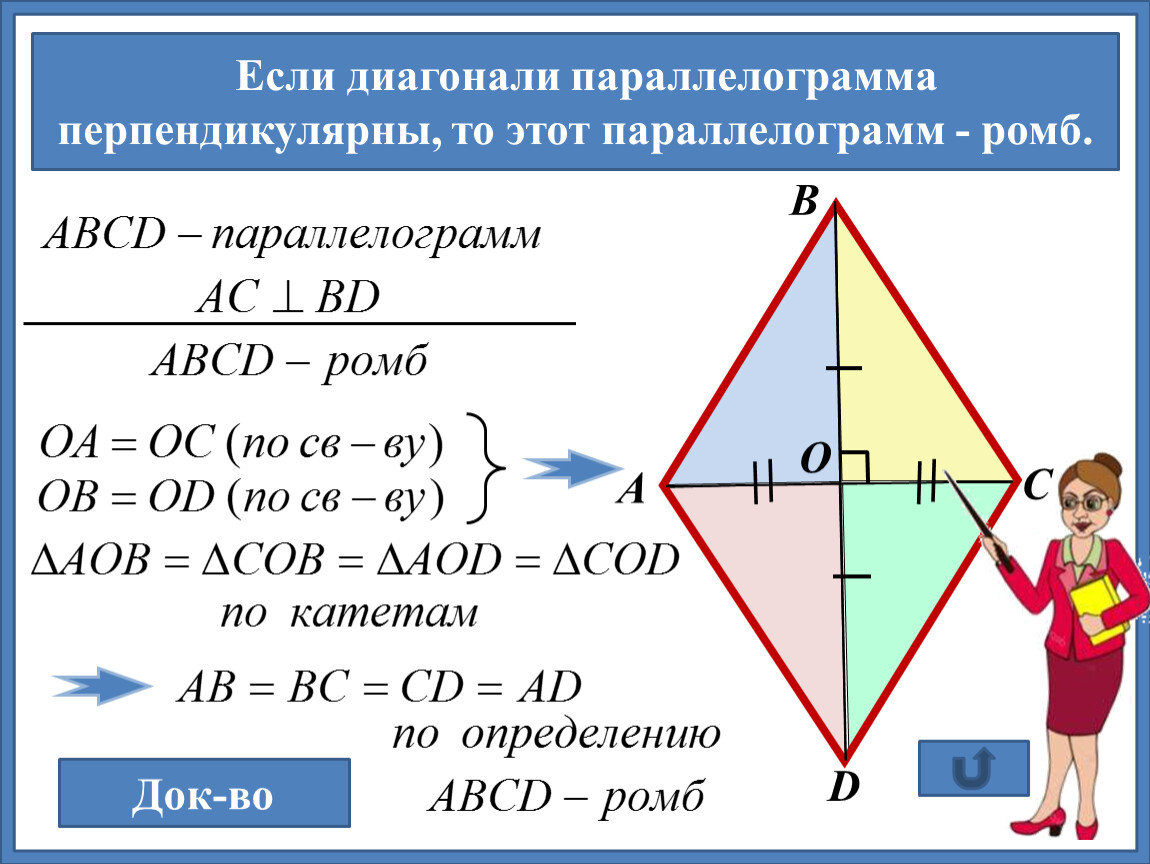

Признаки ромба

Признак 1. Если смежные стороны параллелограмма равны, то этот параллелограмм − ромб.

Доказательство. Пусть смежные стороны параллелограмма ABCD равны. То есть имеем: AB=BC (Рис.3). У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда DC=AB=BC=AD. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.

Признак 2. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм − ромб.

Доказательство. Пусть диагонали параллелограмма ABCD перпендикулярны (Рис.3). Рассмотрим прямоугольные треугольники AOB и COB. Так как у параллелограмма диагонали точкой пересечения разделяются пополам (Свойство 2 статьи Параллелограмм), то AO=OC. Тогда прямоугольные треугольники AOB и COB равны по двум катетам (AO=OC, BO общий катет (см. статью Прямоугольный треугольник. Свойства, признаки равенства)). Следовательно AB=BC. Тогда по признаку 1 этот параллелограмм является ромбом.

Признак 3. Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм − ромб.

Доказательство. Пусть диагональ AC параллелограмма ABCD является биссектрисой угла BAD (Рис.4). Тогда \( \small \angle 1= \angle 2 .\) У параллелограмма ABCD \( \small AB \ || \ DC .\) Тогда для параллельных прямых AB и DC и секущей AC справедливо равенство \( \small \angle 1= \angle 4 .\) (см теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично, для параллельных прямых BC и AD и секущей AC справедливо равенство \( \small \angle 2= \angle 3 .\) Так как \( \small \angle 1= \angle 2 ,\) то \( \small \angle 1= \angle 2=\angle 3= \angle 4 .\) Из \( \small \angle 1= \angle 3\) следует, что треугольник ABC равнобедренный (Признак 2 статьи Равнобедренный треугольник). Тогда AB=BC.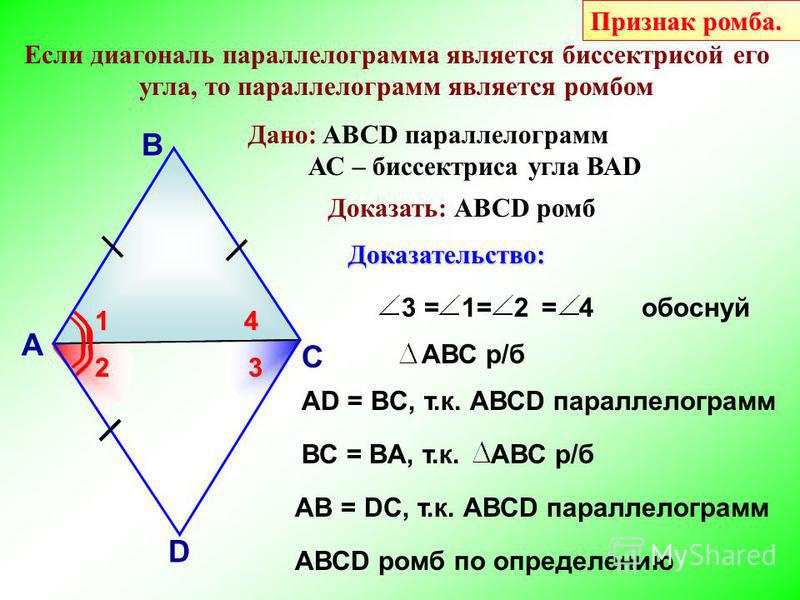 У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда AB=BC=CD=DA. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.

Признак 4. Если стороны четырехугольника равны, то этот четырехугольник − ромб.

Доказательство. Пусть у четырехугольника все стороны равны. Тогда этот четырехугольник является параллелограммом (признак 2 статьи Параллелограмм). А по определению 1, этот параллелограмм является ромбом.

Ромб

Горячая математика

А ромб это параллелограмм с четырьмя конгруэнтный стороны. Множественное число слова ромб ромбы . (Я люблю это слово.)

Формула для область формула ромба аналогична формуле параллелограмма:

А «=» б час ,

где б это длина основания и час это высота.

Область «=» 5 ⋅ 4 «=» 20 см 2 .

Диагонали ромба

Если параллелограмм является ромбом, то его диагонали перпендикулярны.

Например: Если п Вопрос р С является ромбом, то п р ¯ ⊥ Вопрос С ¯ .

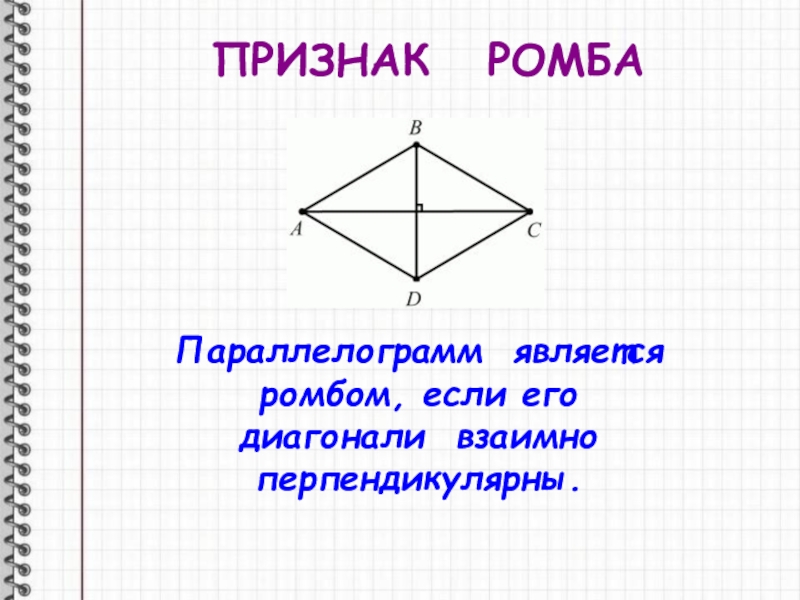
Если параллелограмм является ромбом, то каждая диагональ делит пополам пару противоположных углов.

Например: Если п Вопрос р С является ромбом, то

∠ 1 ≅ ∠ 2 , ∠ 3 ≅ ∠ 4 , ∠ 5 ≅ ∠ 6 , и ∠ 7 ≅ ∠ 8 .

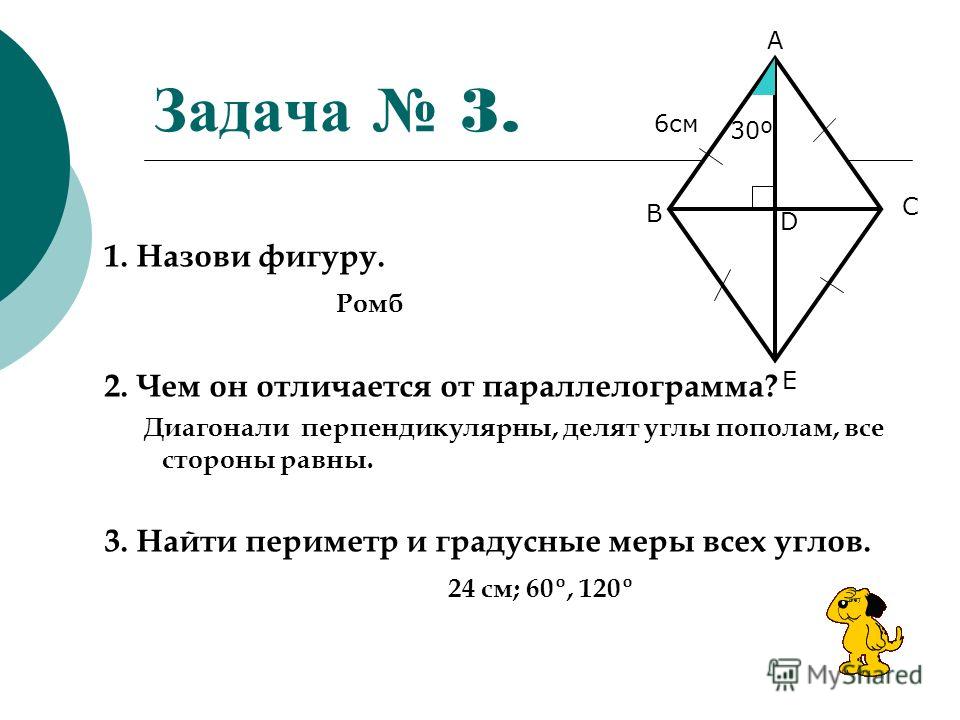
Пример 1:

В ромбе А Б С Д , м ∠ А Б С «=» 2 Икс − 7 и м ∠ Б С Д «=» 2 Икс + 3 . Находить м ∠ Д А Б .

В ромбе последовательные внутренние углы являются дополнительными. Так,

м ∠ А Б С + м ∠ Б С Д «=» 180 ° .

Подставьте меры и решите Икс .

2 Икс − 7 + 2 Икс + 3 «=» 180 ° 4 Икс «=» 184 Икс «=» 46

Используйте значение Икс найти м ∠ Д А Б .

Каждая пара противоположных углов ромба конгруэнтна. Так,

м ∠ Д А Б «=» м ∠ Б С Д «=» 2 ( 46 ) + 3 «=» 95 ° .

Пример 2:

В ромбе Икс Д Z Вт , м ∠ Вт Д Z «=» 63 ° . Находить м ∠ Д Z В .

Диагонали ромба перпендикулярны.

Так, м ∠ Д В Z «=» 90 ° и Δ Д В Z это прямоугольный треугольник .

Используйте теорему о сумме углов.

м ∠ Д Z В + м ∠ Z В Д + м ∠ В Д Z «=» 180 °

Подставьте меры и решите.

м ∠ Д Z В + 90 ° + 63 ° «=» 180 °

м ∠ Д Z В + 153 ° «=» 180 ° м ∠ Д Z В «=» 27 °

Когда параллелограмм является ромбом?

Я думаю о параллелограмме, диагонали которого перпендикулярны.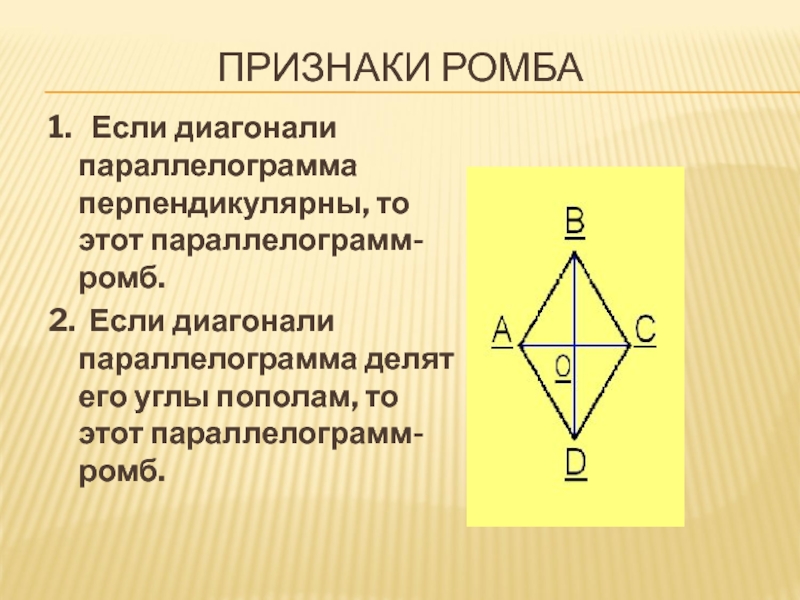 Назовите этот параллелограмм.

Если вы догадались, что это квадрат, то вы плохо читали заголовок этого раздела. Это ромб! Хорошая вещь в работе с параллелограммами заключается в том, что диагонали создают множество треугольников, просто умоляющих, чтобы их конгруэнтность была доказана. На рис. 16.6 диагонали параллелограмма ABCD перпендикулярны. Конгруэнтные треугольники пытаются общаться с вами. Слушайте внимательно.

Рисунок 16.6 Параллелограмм ABCD с ¯AC ¯BD.

Теорема 16.6 : Если диагонали параллелограмма перпендикулярны, то параллелограмм является ромбом.

Давайте сразу перейдем к плану игры. Вы знаете, что ¯AC ¯BD, поэтому mAMB = 90º и mCMB = 90º. Поскольку диагонали параллелограмма делят друг друга пополам, вы знаете, что ¯AM ~= ¯MC. Рефлексивное свойство ~= позволяет писать ¯BM ~= ¯BM. По постулату SAS вы знаете, что AMB ~= CMB. По CPOCTAC вы знаете, что ¯AB ~= ¯BC. Поскольку ¯AB ~= ¯BC и ¯AB ~= ¯BC являются смежными сторонами, у вас есть параллелограмм с конгруэнтными смежными сторонами, он же ромб.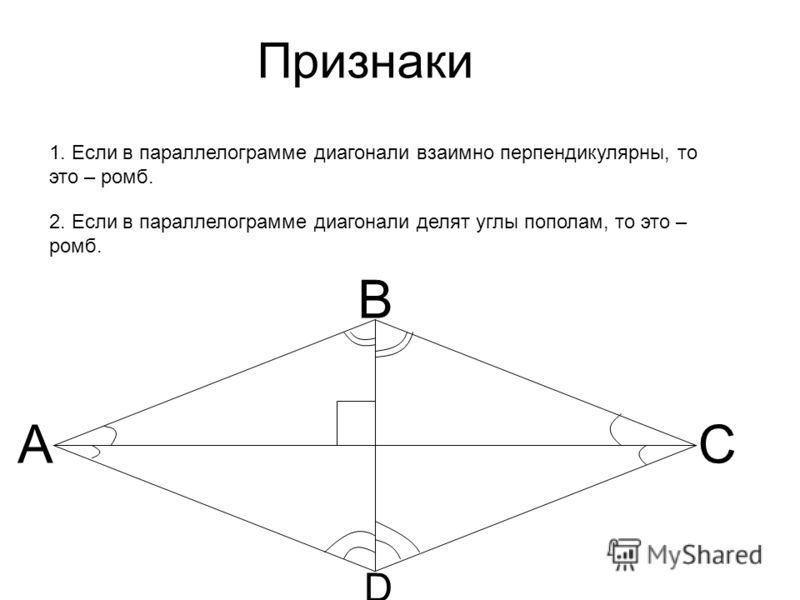

СМБ

	Заявления	Причины
1.	Параллелограмм ABCD имеет ¯AC ¯BD	Учитывая
2.	AMB и CMB верны	Определение
3.	mAMB = 90° и mCMB = 90°	Определение прямого угла
4.	АМБ ~= СМБ	Определение ~=
5.	¯AM ~= ¯MC	Теорема 15.6
6.	¯BM ~= ¯BM	Рефлексивное свойство ~=
7.	АМБ ~=	Постулат SAS
8.	¯AB ~= ¯BC	КПОКТАК
9.	Параллелограмм ABCD является ромбом	Определение ромба

А теперь немного посложнее. Предположим, у вас есть прямоугольник ABCD. Найдите середины каждой стороны прямоугольника и последовательно соедините их, чтобы получился четырехугольник MNOP, как показано на рис. 16.7. Какой четырехугольник получился?

Рис. 16.7 Прямоугольник ABCD, середины каждой стороны которого последовательно соединены вместе, образуя четырехугольник MNOP.

Судя по картинке, это похоже на параллелограмм. Но нужно быть осторожным, потому что внешность может быть обманчивой. Также похоже, что диагонали вновь созданного четырехугольника перпендикулярны. Если рисунок точен, у вас может возникнуть соблазн заключить, что четырехугольник является ромбом. Давайте докажем это.

Теорема 16.7 : Если середины сторон прямоугольника соединить по порядку, то образовавшийся четырехугольник будет ромбом.

Для этого нужен серьезный план игры. Поскольку M, N, O и P являются серединами ¯AB, ¯BC, ¯CD и ¯AD, вы знаете, что ¯BN ~= ¯NC ~= ¯AP ~= ¯PD и ¯AM ~= ¯MB ~= ¯OD ~= ¯CO. Поскольку вы имеете дело с прямоугольником, вы знаете, что mA = 90°, mB = 90°, mC = 90° и mD = 90°. Итак, согласно постулату SAS, PAM ~= NBM ~= PDO ~= NCO. Применяя принцип CPOCTAC ¯MN ~= ¯MP ~= ¯PO ~= ¯NO. Значит противоположные стороны равны и четырехугольник MNOP является параллелограммом. Кроме того, смежные стороны равны, поэтому параллелограмм MNOP является ромбом.

	Заявления	Причины
1.	Прямоугольник ABCD, середины каждой стороны которого последовательно соединены вместе, образуя четырехугольник MNOP	Дано
2.	¯BC ~= ¯NC, ¯AP ~= ¯PD, и ¯OD ~= ¯CO	Определение средней точки
3.	¯AB ~= ¯CD и ¯BC ~= ¯AD	Теорема 15.4
4.	БН = ¹ / ₂ ВС, АП = ¹ / ₂ АД, АМ = ¹ / ₂ AB и CO = ¹ / ₂ CD	Теорема 9. 1
5.	BN = NC = AP = PD и AM = MB = OD = CO	Замена (шаги 2, 3, 4)
6.	¯BN ~= ¯NC ~= ¯AP ~= ¯PD и ¯AM ~= ¯MB ~= ¯OD ~= ¯CO	Определение ~=
7.	мА = 90°. mB = 90°, mC = 90° и mD = 90°	Определение прямоугольника
8.	PAM ~= NBM ~= PDO ~= NCO	Постулат SAS
9.	¯MN ~= ¯MP ~= ¯PO ~= ¯NO	CPOCTAC
10.	Четырехугольник MNOP — параллелограмм	Теорема 16.2 0116 Определение ромба

Выдержки из Полное руководство по геометрии для идиотов © 2004 г. Дениз Сечеи, доктор философии. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.

Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476.