Смешали 3 литра 35 процентного водного раствора некоторого вещества с 12: Решение №1831 Смешали 3 литра 25-процентного водного раствора некоторого вещества с 12 литрами 15-процентного водного раствора этого же вещества.

1. мольной доли количества присутствующего растворенного вещества и
2. исходное давление паров (чистый растворитель).

При любой заданной температуре конкретного твердого вещества или жидкости существует давление, при котором пар, образующийся над веществом, находится в динамическом равновесии с его жидкой или твердой формой. Это давление паров вещества при данной температуре. В состоянии равновесия скорость испарения твердого вещества или жидкости равна скорости конденсации газа обратно в его первоначальную форму. У всех твердых и жидких тел есть давление пара, и это давление постоянно, независимо от того, сколько вещества присутствует.

Идеальные и неидеальные решения

Закон Рауля работает только для идеальных решений. «Идеальный раствор показывает термодинамические характеристики смешения, идентичные характеристикам идеальных газовых смесей, [за исключением] идеальных растворов, которые имеют межмолекулярные взаимодействия, равные взаимодействиям чистых компонентов». ² Как и многие другие понятия, изучаемые в химии, закон Рауля применяется только в идеальных условиях в идеальном растворе. Тем не менее, он по-прежнему работает достаточно хорошо для растворителя в разбавленных растворах. Однако в действительности уменьшение давления пара будет больше, чем рассчитанное по закону Рауля для чрезвычайно разбавленных растворов. ³

Почему работает закон Рауля

Если вы просмотрите концепции коллигативных свойств, вы обнаружите, что добавление растворенного вещества снижает давление пара, потому что дополнительные частицы растворенного вещества заполняют промежутки между частицами растворителя и занимают место. Это означает, что меньшее количество растворителя будет находиться на поверхности и меньшее количество растворителя сможет вырваться и перейти в газовую фазу, что приведет к более низкому давлению пара. Есть два способа объяснить, почему работает закон Рауля — простой визуальный способ и более сложный способ, основанный на энтропии. Ниже приведен простой подход.

Помните, что давление насыщенного пара — это то, что вы получаете, когда жидкость находится в герметичном контейнере. Равновесие устанавливается, когда число частиц, отрывающихся от поверхности, точно равно числу частиц, вновь прилипающих к поверхности.

Теперь предположим, что молекулы растворенного вещества были добавлены таким образом, что молекулы растворителя заняли только 50% поверхности раствора.

Определенная часть молекул растворителя будет иметь достаточную энергию, чтобы уйти с поверхности (например, 1 на 1000 или 1 на миллион). Если вы уменьшите количество молекул растворителя на поверхности, вы уменьшите количество молекул, которые могут ускользнуть за любой момент времени. Но это не будет иметь никакого значения для способности молекул пара снова прилипать к поверхности. Если молекула растворителя в паре коснется части поверхности, занятой частицами растворенного вещества, она вполне может прилипнуть. Очевидно, что между растворителем и растворенным веществом существует притяжение, иначе у вас не было бы решения.

Чистый эффект этого заключается в том, что, когда установится равновесие, в паровой фазе будет на меньше молекул растворителя — менее вероятно, что они собираются отделиться, но нет никаких проблем с их возвращением. Однако, если в равновесном паре меньше частиц, давление насыщенного пара ниже.

Ограничения закона Рауля

На практике идеального решения не существует! Однако особенности одного включают:

• Идеальные решения удовлетворяют закону Рауля. Решение на последней диаграмме рисунка \(\PageIndex{3}\) выше на самом деле не подчинялось бы закону Рауля — оно слишком концентрированное, но оно было нарисовано настолько концентрированным, чтобы подчеркнуть суть.
• В идеальном растворе требуется точно такое же количество энергии, чтобы молекула растворителя оторвалась от поверхности раствора, как и в чистом растворителе. Силы притяжения между растворителем и растворенным веществом точно такие же, как и между исходными молекулами растворителя — маловероятно!

Предположим, что в чистом растворителе 1 из 1000 молекул обладает достаточной энергией, чтобы преодолеть межмолекулярные силы и оторваться от поверхности в любой момент времени. В идеальном растворе это все равно будет точно такой же пропорцией. Оторвалось бы, конечно, меньше, потому что теперь молекул растворителя на поверхности меньше, но из тех, что находятся на поверхности, отрывается еще та же пропорция. Если имело место сильное притяжение растворителя к растворенному, эта пропорция может быть уменьшена до 1 на 2000, или 1 на 5000, или чего-то еще.

В любом реальном растворе, скажем, соли в воде существует сильное притяжение между молекулами воды и ионами. Это, как правило, замедляет потерю молекул воды с поверхности. Однако, если раствор достаточно разбавлен, на поверхности будут области хорошего размера, где у вас все еще есть молекулы воды. Тогда решение будет приближаться к идеальному поведению.

Природа растворенного вещества

Есть еще одна вещь, с которой вы должны быть осторожны, если собираетесь делать какие-либо расчеты по закону Рауля. Возможно, вы заметили в небольшом расчете молярной доли выше на странице, что сахар является растворенным веществом, а не солью. На самом деле важно не количество молей вещества, которое вы помещаете в раствор, а

Итак, если вы добавите 0,1 моля хлорида натрия, в растворе будет фактически 0,2 моля частиц — и это значение вам придется использовать при расчете мольной доли.

На самом деле имеет значение не количество молей вещества, которое вы поместили в раствор, а число молей образовавшихся частиц.

Закон Рауля и коллигативные свойства

Действие закона Рауля заключается в том, что давление насыщенного пара раствора будет ниже, чем у чистого растворителя при любой конкретной температуре. Это оказывает важное влияние на фазовую диаграмму растворителя. На следующей диаграмме показана фазовая диаграмма чистой воды в области ее нормальных температур плавления и кипения. Линия 1 атмосфера показывает условия для измерения нормальных температур плавления и кипения.

Линия, разделяющая области жидкости и пара, представляет собой набор условий, при которых жидкость и пар находятся в равновесии. Его можно рассматривать как влияние давления на температуру кипения воды, но это также кривая, показывающая влияние температуры на давление насыщенного пара воды. Эти два способа взглянуть на одну и ту же линию кратко обсуждаются в примечании примерно на полпути вниз по странице о фазовых диаграммах (перейдите по последней ссылке выше).

Если построить кривую давления насыщенного пара для раствора нелетучего вещества в воде, она всегда будет ниже, чем кривая для чистой воды.

Если вы внимательно посмотрите на последнюю диаграмму, вы увидите, что точка, в которой кривая равновесия жидкость-пар встречается с кривой твердого тела-пар, сместилась. Эта точка является тройной точкой системы — уникальным набором условий температуры и давления, при которых возможно получить твердое, жидкое и парообразное состояние в равновесии друг с другом в одно и то же время.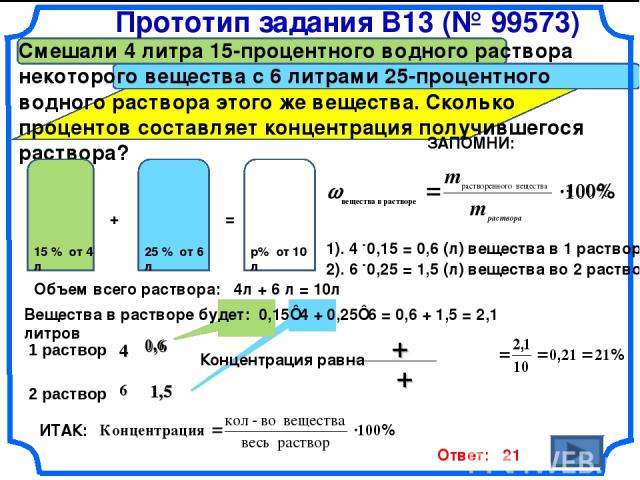 Поскольку в тройной точке присутствует равновесие твердой и жидкой фаз (среди других равновесий), она также является точкой плавления системы, хотя и не нормальной точкой плавления, потому что давление не равно одной атмосфере.

Кривые для чистой воды и для раствора часто проводят параллельно друг другу. Это должно быть неправильно! Предположим, у вас есть раствор, в котором молярная доля воды равна 0,99, а давление паров чистой воды при этой температуре равно 100 кПа. Давление паров раствора будет 99 кПа — падение на 1 кПа. При более низкой температуре, когда давление паров чистой воды составляет 10 кПа, падение составит всего 0,1 кПа. Чтобы кривые были параллельными, падения должны быть одинаковыми во всем диапазоне температур. Это не так!

Это должно означать, что на фазовой диаграмме нужна новая линия точки плавления (линия равновесия твердого тела и жидкости), проходящая через новую тройную точку. Это показано на следующей диаграмме.

Теперь мы, наконец, можем увидеть, какое влияние оказывает нелетучее растворенное вещество на точки плавления и замерзания раствора. Посмотрите, что происходит, когда вы проводите линию давления в 1 атмосферу, которая позволяет вам измерять точки плавления и кипения. Диаграмма также включает точки плавления и кипения чистой воды из исходной фазовой диаграммы для чистой воды (черные линии).

Из-за изменений на фазовой диаграмме видно, что:

• температура кипения растворителя в растворе выше, чем у чистого растворителя;
• температура замерзания (плавления) растворителя в растворе ниже, чем у чистого растворителя.

Мы рассмотрели это с водой в качестве растворителя, но использование другого растворителя не изменило бы аргумент или выводы. Единственная разница заключается в наклоне линий равновесия твердой и жидкой фаз. Для большинства растворителей они наклонены вперед, тогда как ватерлиния наклонена назад. Вы можете доказать себе, что это не влияет на то, на что мы смотрели, перерисовав все эти диаграммы с изменением наклона этой конкретной линии. Вы обнаружите, что это не имеет никакого значения.

Как рассчитать давление паров раствора

Мы можем рассчитать давление паров раствора двумя способами, в зависимости от летучести растворенного вещества. Если растворенное вещество является летучим, оно будет создавать собственное давление паров, и это количество является значительным вкладом в общее давление паров раствора и, следовательно, должно быть включено в расчеты. С другой стороны, если это нелетучее вещество, растворенное вещество не будет создавать давление пара в растворе при этой температуре.

Нелетучие растворенные вещества

Эти расчеты довольно просты, если вы знакомы со стехиометрическими преобразованиями. Поскольку растворенное вещество нелетуче, вам нужно только определить изменение давления паров растворителя. Используя уравнение для закона Рауля, вам нужно будет найти мольную долю растворителя, и обычно дается давление паров чистого растворителя.

Пример \(\PageIndex{1}\): Kool-Aid

1,5 моля вишневого Kool-Aid добавляют в кувшин с 2 литрами воды в погожий день при 25°C. 0046 o C. Давление паров только воды составляет 23,8 мм рт.ст. при 25 ^o C. Каково новое давление паров Kool-Aid?

Раствор

\(P_{H_2O}\) = 23,8 мм рт. ст.

Чтобы найти молярную долю, необходимо сначала преобразовать 2 л воды в моли:

1 л = 1000 мл = 1000 г

Зная это, можно перевести массу воды (2000 г) в моли:

2000 г / 18,02 г (молярная масса воды) = 110,9 моль H ₂ O

Решите для молярной доли, \(\chi_{H_2O}\):

\(\chi_{H_2O}\) = моль H ₂ O / общее количество молей
= 110,9 моль / 110,9 + 1,5 моль = 0,979

Наконец, примените закон Рауля

\(P_{Kool-Aid} = \chi_{H_2O} \, P_{H_2O}\) = (0,979)(23,8 мм рт.ст.) = 23,3 мм рт.ст.

Пример \(\PageIndex {2A}\): Неэлектролит

Рассчитайте давление паров раствора, полученного путем растворения 50,0 г глюкозы \(C_6H_{12}O_6\) в 500 г воды. Давление паров чистой воды 47,1 Торр при 37°С

Раствор

Чтобы использовать закон Рауля (уравнение \(\ref{RLaw}\)), нам нужно рассчитать молярную долю воды (растворителя) в этом сахарно-водном растворе.

\[ \chi_{растворитель} = \dfrac{ \text{моли воды}}{\text{моли растворенного вещества} + \text{моли растворителя}} \nonumber \]

\[ \chi_{растворитель } = \dfrac{ n_{вода}}{ n_{глюкоза} + n_{вода} } \nonumber\]

Молярная масса глюкозы 180,2 г/моль, а воды 18 г/моль. Итак,

\[n_{вода} = \dfrac{500\,g}{18\,g/mol} = 27,7 \,mol \nonnumber\]

и

\[n_{глюкоза} = \dfrac{50\,г}{180,2\,г/моль} = 0,277 \,моль \номер\]

и

\[ \chi_{растворитель} = \dfrac{ 27,7 \,mol}{ 0,277 \,mol + 27,7 \,mol } = 0,99 \nonumber\]

Обратите внимание, что это все еще относительно разбавленный.

\[ P_{раствор} = 0,99 \умножить на 47,1 = 46,63 \, торр \номер\]

совсем не большое изменение.

Пример \(\PageIndex{2B}\): Электролит

Рассчитайте давление паров раствора, полученного путем растворения 50,0 г CaCl ₂ , \(C_6H_{12}O_6\), в 500 г воды. Давление паров чистой воды составляет 47,1 Торр при 37°C.

Раствор

соляно-водный раствор.

\[ \chi_{растворитель} = \dfrac{ \text{моли воды}}{\text{моли растворенного вещества} + \text{моли растворителя}} \nonumber\]

\[ \chi_{растворитель } = \dfrac{ n_{вода}}{ n_{растворенные вещества} + n_{вода} } \nonumber\]

и

\[ \chi_{растворитель} = \dfrac{ 27,7 \,mol}{ 0,45 \,mol + 0,9 \,mol + 27,7 \,mol } = 0,953 \nonnumber\]

Обратите внимание, что это все еще относительно разбавить.

\[ P_{раствор} = 0,953 \умножить на 47,1 = 44,88\, торр \нечисло\]

Большее изменение, чем в примере с глюкозой выше.

Летучие растворенные вещества

Единственная разница между летучими и нелетучими растворенными веществами заключается в том, что необходимо учитывать парциальное давление, создаваемое давлением пара летучего растворенного вещества, и давлением пара растворителя. Сумма двух даст вам общее давление паров раствора.

Пример \(\PageIndex{3}\)

Каково парциальное давление бензола и толуола в растворе, в котором мольная доля бензола равна 0,6? Каково общее давление пара? Давление паров чистого бензола равно 95,1 мм рт. ст., а давление паров чистого толуола 28,4 мм рт.ст. при 25 ^o С. {толуол} = 0,4\), так как \(1 — 0,6 = 0,4\).

Теперь, когда мы знаем молярные доли и давления паров, решить эту задачу несложно.

P _бензол = x _бензол P _бензол = (0,6)(95,1 мм рт.ст.) = 57,1 мм рт.ст.
P _толуол = x _{толуол 9009 1 P толуол = (0,4)(28,4 мм рт.ст. ) = 11,4 мм рт.ст.}

Общее давление паров представляет собой просто сумму парциальных давлений:

P _общее = P _бензол + P _туол = 57,1 мм рт.ст. + 11,4 мм рт.ст. = 68,5 мм рт.ст.

Упражнения

*MM = молярная масса

1. Каково давление паров раствора при 25 ^o C, содержащий 78,0 г глюкозы (MM = 180,16 г/моль) в 500 г воды? Давление пара чистой воды при этой температуре равно 23,8 мм рт.
2. 25 г циклогексана (P _o = 80,5 торр, MM = 84,16 г/моль) и 30 г этанола (P _o = 52,3 торр, MM = 92,14 г/моль) являются летучими компонентами, присутствующими в растворе . Каково парциальное давление этанола?
3. Каково давление паров чистого бутана при 20 ^o С, если его парциальное давление равно 69о = (0,985)(23,8\; мм рт.ст.) = 23,4\; мм рт. ст.]

   2.

   Рассчитайте количество молей каждого компонента.

   • Моли циклогексана: \(\dfrac{25\; г}{84,16\; г/моль} = 0,297 \; \text{моли циклогексана}\)
   • Моль этанола: \(\dfrac{30\; г}{92,14 \;г/моль} = 0,326 \; \text{моль этанола}\)

   Определите мольную долю этанола и примените закон Рауля.

   _{Xэтанол} = 0,326 моль / (0,326 + 0,297) моль = 0,523 9о = \dfrac{P}{X} = \dfrac{698\; мм рт.ст.}{0,423} = 1650\; мм рт. ст.]

   Ссылки

   1. Petrucci, et al. Общие принципы химии и современные приложения. 9-е изд. Река Аппер-Сэдл, Нью-Джерси: Pearson Prentice Hall, 2007.
   .
   2. Кугель, Роджер В. «Закон Рауля: бинарные фазовые диаграммы жидкость-пар» Journal of Chemical Education 75. 9 (1998): 1125.
   3. П. Циас, К. Трейнер и М. Чемла. «Применимость закона Рауля в неидеальных смешанных растворителях» Journal of Solution Chemistry 6.6 (1977): 393-402.

   ---

   Закон Рауля распространяется под лицензией CC BY-NC-SA 4.0, авторами, ремиксами и/или кураторами являются Джим Кларк, Ирен Ли, Санна Хан и Санна Хан.

   1. Наверх
   • Была ли эта статья полезной?

   1. Тип изделия

      Раздел или страница

      Лицензия

      CC BY-NC-SA

      Версия лицензии

      4,0

      Показать страницу TOC

      № на стр.

   2. Теги

      1. автор @ Ирэн Ли
      2. автор @ Джим Кларк
      3. автор@Санна Хан
      4. идеальное решение
      5. Закон Рауля

   Приготовление химических растворов

   Лабораторные эксперименты и исследования часто требуют приготовления химических растворов. Мы рассмотрим приготовление этих химических растворов по весу (масса/объем) и по объему (объем/объем). В приведенном ниже глоссарии приводятся определения, чтобы знать, когда ваша работа требует их создания, а также наиболее точные молярные растворы.

   К этому мы добавляем информацию, предназначенную для понимания того, как использовать шкалу рН при измерении кислотности или щелочности раствора.

   Глоссарий, основные термины для понимания…

   Растворенное вещество — Вещество, которое растворяется в растворе

   Растворитель — Вещество, которое растворяет другое с образованием раствора. Например, в растворе сахара и воды вода является растворителем; сахар является растворенным веществом.

   Раствор — Смесь двух или более чистых веществ. В растворе одно чистое вещество растворено в другом чистом веществе гомогенно. Например, в растворе сахара и воды раствор имеет одинаковую концентрацию повсюду, т.е. оно однородно.

   Моль — Фундаментальная единица массы (например, «дюжина» для пекаря), используемая химиками. Этим термином обозначают большое количество элементарных частиц (атомов, молекул, ионов, электронов и т. д.) любого вещества. 1 моль равен 6,02 х 10 ²³ молекул этого вещества. (номер Авогадро).М

   Введение в приготовление растворов.

   Многие эксперименты с химическими веществами требуют их использования в виде растворов. То есть два или более вещества смешиваются вместе в известных количествах. Это может включать взвешивание точного количества сухого материала или измерение точного количества жидкости. Точная подготовка растворов повысит безопасность эксперимента и шансы на успех.

   Раствор 1: Использование весовых процентов (вес/объем)

   Формула

   Формула весовых процентов (вес/объем): [Масса растворенного вещества (г) / Объем раствора (мл)] x 100

   Пример

   10% раствор NaCl содержит десять граммов хлорида натрия, растворенных в 100 мл раствора.

   Процедура

   Взвесить 10 г хлорида натрия. Перелейте его в мерный цилиндр или мерную колбу, содержащую примерно 80 мл воды. После полного растворения хлорида натрия (при необходимости осторожно встряхните колбу) добавьте воды, чтобы довести объем до окончательных 100 мл. Внимание: не просто измеряйте 100 мл воды и добавить 10 г хлорида натрия. Это приведет к ошибке, потому что добавление твердого вещества изменит конечный объем раствора и отбросит окончательный процент.

   ---

   Решение 2: использование объемных процентов (об./об.)

   Когда растворенное вещество представляет собой жидкость, иногда удобно выражать концентрацию раствора в объемных процентах.

   Формула

   Формула для объемного процента (об./об.): [Объем растворенного вещества (мл) / Объем раствора (мл)] x 100

   Пример

   Приготовьте 1000 мл 5% по объему раствора этиленгликоля в воде.

   Процедура

   Сначала выразите процент растворенного вещества в виде десятичной дроби: 5% = 0,05

   Умножьте эту десятичную дробь на общий объем: 0,05 x 1000 мл = 50 мл (необходим этиленгликоль).

   Вычесть объем растворенного вещества (этиленгликоль) из общего объема раствора:

   1000 мл (общий объем раствора) — 50 мл (объем этиленгликоля) = 950 мл (необходимая вода)

   Растворите 50 мл этиленгликоля в чуть менее чем 950 мл воды. Теперь доведите окончательный объем раствора до 1000 мл , добавив еще воды. (Это исключает любую ошибку, поскольку конечный объем раствора может не совпадать с рассчитанной суммой отдельных компонентов).

   Итак, 50 мл этиленгликоля / 1000 мл раствора x100 = 5% (об./об.) раствора этиленгликоля.

   ---

   Раствор 3: Молярные растворы

   Молярные растворы наиболее полезны при расчетах химических реакций, поскольку они напрямую связывают количество молей растворенного вещества с объемом раствора.

   Формула

   Формула молярности (М): количество молей растворенного вещества на 1 л раствора или грамм-молекулярная масса растворенного вещества на 1 л раствора.

   Примеры

   Молекулярная масса молекулы хлорида натрия (NaCl) равна 58,44, поэтому один грамм молекулярной массы (=1 моль) равен 58,44 г. Мы знаем это, глядя на периодическую таблицу. Атомная масса (или вес) Na равна 22,99, атомная масса Cl равна 35,45, поэтому 22,99 + 35,45 = 58,44.

   Если растворить 58,44 г NaCl в конечном объеме 1 литр , вы сделали 1M раствор NaCl , 1-молярный раствор.