По графику производной найти наибольшее значение функции
Рассмотрим задания, в которых дан график производной функции и требуется найти, в какой точке данного отрезка эта функция принимает наибольшее значение.
№1
На рисунке изображён график производной функции f(x), определённой на интервале (-14;8). В какой точке отрезка [-11;-8] функция f(x) принимает наибольшее значение?
Решение:
Выделяем отрезок [-11;-8].
На этом отрезке производная f'(x) принимает положительные значения.
Следовательно, функция f(x) на этом отрезке возрастает, то есть бо́льшему значению аргумента соответствует бо́льшее значение функции:
x1,x2 ∈[-11;-8], x2>x1, ⇒ f(x2)>f(x1).
Поэтому наибольшее значение функция f(x) на отрезке принимает при наибольшем значении аргумента, то есть на правом конце отрезка, при x=-8.
Ответ: -8.
№2
На рисунке изображён график производной функции f(x), определённой на интервале (-7;9).
Решение:
Выделяем отрезок [4;8].
Так как этом отрезке производная f'(x)<o, то функция f(x) на [4;8] убывает, то есть бо́льшему значению аргумента соответствует меньшее значение функции:
x1,x2 ∈[4;8], x2>x1, ⇒ f(x2)<f(x1).
Поэтому наибольшее значение f(x) принимает в этом случае при наименьшем значении аргумента, то есть на левом конце отрезка, при x=4.
Ответ: 4.
№3
Функция y=f(x) определена на промежутке (-5;9). На рисунке изображён график её производной. Найти абсциссу точки, в которой функция y=f(x) принимает наибольшее значение.
Решение:
В точке с абсциссой x=6 производная меняет знак с плюса на минус.
Следовательно, x=6 — точка максимума.
Производная f'(x) существует на всём интервале (-5;9), следовательно, функция f(x) непрерывна на (-5;9).
Если непрерывная функция f(x) имеет на заданном интервале (a;b) только одну точку экстремума xo и это точка максимума, то на (a;b) функция принимает своё наибольшее значение в точке xo.
Таким образом, функция f(x) на интервале (-5;9) принимает наибольшее значение в точке x=6.
Ответ: 6.
№4
Функция y=f(x) определена и непрерывна на отрезке [-1;9]. На рисунке изображён график её производной. Найти точку xo, в которой функция принимает наибольшее значение, если f(-1)≥f(9).
Решение:
На промежутках (-1;3) и (8;9) производная f'(x)>0, поэтому на этих промежутках функция f(x) возрастает.
На промежутке (3;9) производная f'(x)<0, поэтому на (3;9) функция f(x) убывает.
Так как функция определена и непрерывна на отрезке [-1;9], то точки -1, 3, 8 и 9 можно включать в промежутки монотонности.
Следовательно, на отрезках [-1;3] и [8;9] функция f(x) возрастает, на отрезке [3;8] — убывает.
На промежутках возрастания наибольшее значение функция принимает на правом конце отрезка. На [-1;3] наибольшее значение f(x) принимает в точке x=3 (точке максимума), на [8;9] — в точке x=9.
Так как на [-1;3] f(x) возрастает, то f(3)>f(-1). По условию, f(-1)≥f(9), значит f(3)>f(9).
Таким образом, наибольшее значение функции f(x) принимает в точке x=3.
Ответ: 3.
В какой точке значение производной набольшее
Дорогие друзья! В группу заданий связанных с производной входят задачи — в условии дан график функции, несколько точек на этом графике и стоит вопрос:
В какой точке значение производной наибольшее (наименьшее)?
Данные задачи очень просты, не требуется никаких вычислений, решаются устно. Главное что необходимо – это понимать геометрический смысл производной, свойства производной для исследования функций. По представленным ссылкам вы можете повторить (изучить) материал на сайте, также краткая информация есть в справочнике.
Кратко повторим:
Производная в точке равна угловому коэффициенту касательной проходящей через эту точку графика.
Угловой коэффициент касательной в свою очередь равен тангенсу угла наклона этой касательной.
*Имеется ввиду угол между касательной и осью абсцисс.
Далее:
1. На интервалах возрастания функции производная имеет положительное значение.
2. На интервалах её убывания производная имеет отрицательное значение.
Рассмотрим следующий эскиз:
В точках 1,2,4 производная функции имеет отрицательное значение, так как данные точки принадлежат интервалам убывания.
В точках 3,5,6 производная функции имеет положительное значение, так как данные точки принадлежат интервалам возрастания.
Как видим, со значением производной всё ясно, то есть определить какой она имеет знак (положительный или отрицательный) в определённой точке графика совсем несложно.
При чём, если мы мысленно построим касательные в этих точках, то увидим, что прямые проходящие через точки 3, 5 и 6 образуют с осью оХ углы лежащие в пределах от 0 до 90о, а прямые проходящие через точки 1, 2 и 4 образуют с осью оХ углы в пределах от 90о до 180о.
*Взаимосвязь понятна: касательные проходящие через точки принадлежащие интервалам возрастания функции образуют с осью оХ острые углы, касательные проходящие через точки принадлежащие интервалам убывания функции образуют с осью оХ тупые углы.
Теперь важный вопрос!
А как изменяется значение производной? Ведь касательная в разных точках графика непрерывной функции образует разные углы, в зависимости от того, через какую точку графика она проходит.
*Или, говоря простым языком, касательная расположена как бы «горизонтальнее» или «вертикальнее». Посмотрите:
Прямые образуют с осью оХ углы в пределах от 0 до 90о
Прямые образуют с осью оХ углы в пределах от 90о до 180о
Поэтому, если будут стоять вопросы:
— в какой из данных точек графика значение производной имеет наименьше значение?
— в какой из данных точек графика значение производной имеет наибольшее значение?
то для ответа необходимо понимать, как изменяется значение тангенса угла касательной в пределах от 0 до 180о.
*Как уже сказано, значение производной функции в точке равно тангенсу угла наклона касательной к оси оХ.
Значение тангенса изменяется следующим образом:
При изменении угла наклона прямой от 0о до 90о значение тангенса, а значит и производной, изменяется соответственно от 0 до +∞;
При изменении угла наклона прямой от 90о до 180о значение тангенса, а значит и производной, изменяется соответственно –∞ до 0.
Наглядно это видно по графику функции тангенса:
Говоря простым языком:
При угле наклона касательной от 0о до 90о
Чем он ближе к 0о, тем больше значение производной будет близко к нулю (с положительной стороны).
Чем угол ближе к 90о, тем больше значение производной будет увеличиваться к +∞.
При угле наклона касательной от 90о до 180о
Чем он ближе к 90о, тем больше значение производной будет уменьшаться к –∞.
Чем угол будет ближе к 180о, тем больше значение производной будет близко к нулю (с отрицательной стороны).
317543. На рисунке изображен график функции y = f(x) и отмечены точки –2, –1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Имеем четыре точки: две из них принадлежат интервалам на которых функция убывает (это точки –1 и 1) и две интервалам на которых функция возрастает (это точки –2 и 2).
Можем сразу же сделать вывод о том, что в точках –1 и 1 производная имеет отрицательное значение, в точках –2 и 2 она имеет положительное значение. Следовательно в данном случае необходимо проанализировать точки –2 и 2 и определить в какой из них значении будет наибольшим. Построим касательные проходящие через указанные точки:
Значение тангенса угла между прямой a и осью абсцисс будет больше значения тангенса угла между прямой b и этой осью. Это означает, что значение производной в точке –2 будет наибольшим.
Ответим на следующий вопрос: в какой из точек –2, –1, 1 или 2 значение производной является наибольшим отрицательным? В ответе укажите эту точку.
Производная будет иметь отрицательное значение в точках, принадлежащим интервалам убывания, поэтому рассмотрим точки –2 и 1. Построим касательные проходящие через них:
Видим, что тупой угол между прямой b и осью оХ находится «ближе» к 180о, поэтому его тангенс будет больше тангенса угла, образованного прямой а и осью оХ.
Таким образом, в точке х = 1, значение производной будет наибольшим отрицательным.
317544. На рисунке изображен график функции y = f(x) и отмечены точки –2, –1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Имеем четыре точки: две из них принадлежат интервалам, на которых функция убывает (это точки –1 и 4) и две интервалам, на которых функция возрастает (это точки –2 и 1).
Можем сразу же сделать вывод о том, что в точках –1 и 4 производная имеет отрицательное значение, в точках –2 и 1 она имеет положительное значение. Следовательно, в данном случае, необходимо проанализировать точки –1 и 4 и определить – в какой из них значении будет наименьшим. Построим касательные проходящие через указанные точки:
Следовательно, в данном случае, необходимо проанализировать точки –1 и 4 и определить – в какой из них значении будет наименьшим. Построим касательные проходящие через указанные точки:
Значение тангенса угла между прямой a и осью абсцисс будет больше значения тангенса угла между прямой b и этой осью. Это означает, что значение производной в точке х = 4 будет наименьшим.
Ответ: 4
Надеюсь, что «не перегрузил» вас количеством написанного. На самом деле, всё очень просто, стоит только понять свойства производной, её геометрический смысл и как изменяется значение тангенса угла от 0 до 180о.
Общие рекомендации:
1. Сначала определите знаки производной в данных точках (+ или -) и выберете необходимые точки (в зависимости от поставленного вопроса).
2. Постройте касательные в этих точках.
3. Пользуясь графиком тангесоиды, схематично отметьте углы и отобразите соответствующие им значения.
4. Далее в зависимости от поставленного вопроса в задаче, вы без труда определите точку.
*Если вы понимаете, как изменяется значение тангенса, то можно обойтись без графика.
На этом всё. Успехов Вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Определение локального максимума или минимума — задача с производной формулировкой
Задавать вопрос
спросил
Изменено 8 лет, 11 месяцев назад
Просмотрено 289 раз
$\begingroup$
Кубическая функция имеет правило $y=f(x).$ График производной функции $f’$ пересекает ось $x$ в точках $(2,0)$ и $(-3,0). $ Максимальное значение производной функции $10$.
Значение $x$, при котором график $y=f(x)$ имеет локальный максимум, равно
$\eqalign{&{\bf A.} \ \ -2 \\ & {\ бф Б. } \ \ 2 \\ &{\bf С.} \ \ -3 \\ &{\bf D.} \ \ 3 \\ &{\bf E. } \ \ -\dfrac12 }$
Что мне делать с информацией «максимальное значение производной функции $10$? Означает ли это максимальное значение диапазона $f'(x) = 10$. Как мне узнать, где эта точка лежит на График $f'(x)$?
Все, что я знаю, это:
- $f'(2) = 0$, что означает стационарную точку для $f(x)$.
- $f'(-3) = 0$, что означает еще одну стационарную точку для $f(x)$.
Очень запутался. Может кто-нибудь, пожалуйста, помогите мне интерпретировать вопрос, а затем решить для локального максимума.
Ответ: B:2
- производные
$\endgroup$
Ответ: $x = 2$. 92$ срок. Из них должно быть возможно решить вопрос.
PS: я не проверял, верен ли ваш ответ.
$\endgroup$
$\begingroup$
то, что $f’$ имеет максимум, подразумевает, что $f’$ является квадратичным полиномом с отрицательным опережающим коэффициентом
поэтому $f$ является кубическим полиномом с отрицательным опережающим коэффициентом (вы знаете, как это выглядит ?)
следует наличие локального минимума при $x=-3$ и локального максимума при $x=2$
3
$\begingroup$
Производная кубической функции является квадратичной функцией.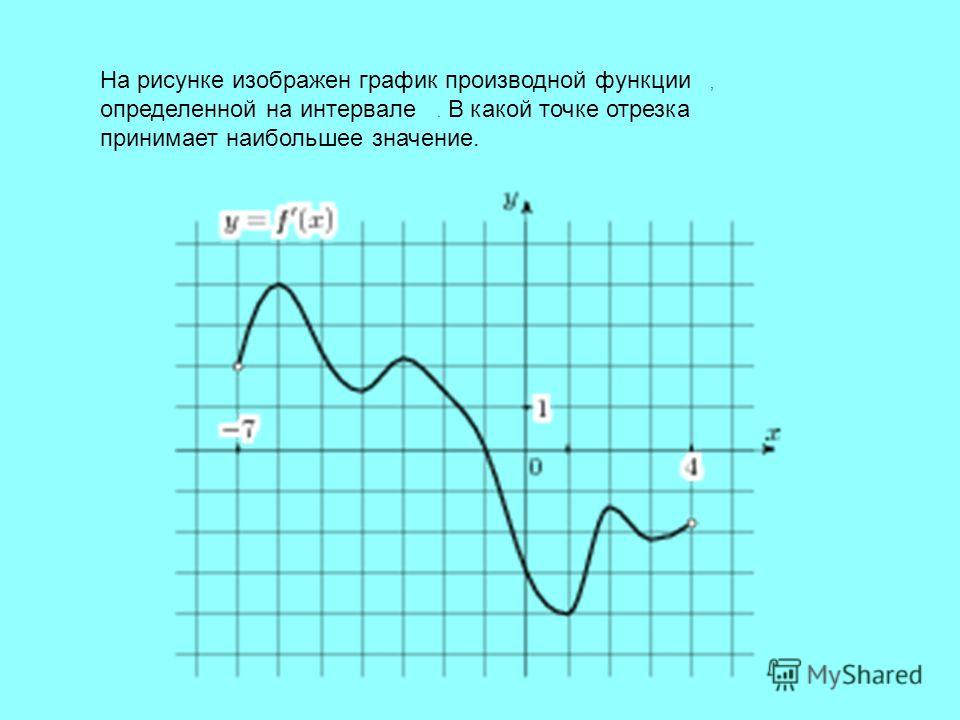 Квадратичная функция ограничена с одной стороны, то есть принимает значения в $[min,\ +\infty[$ или $]-\infty,\ max]$ в зависимости от знака старшего члена (2-й степени).
Квадратичная функция ограничена с одной стороны, то есть принимает значения в $[min,\ +\infty[$ или $]-\infty,\ max]$ в зависимости от знака старшего члена (2-й степени).
«Максимальное значение функции производной равно 10» — это информация об этом знаке, которая поможет вам определить, какие корни производной соответствуют минимумам/максимумам кубической.
тригонометрия — исчисление одной переменной: максимальная скорость изменения: триггерные функции
Задавать вопрос
спросил
Изменено 4 года, 1 месяц назад
Просмотрено 1к раз
$\begingroup$
У меня есть вопрос по исчислению, который я покажу здесь в виде изображения:
Мне интересно понять часть (b) этого вопроса.
Надеюсь получить дополнительную информацию от других участников форума.
- исчисление
- тригонометрия
$\endgroup$
$\begingroup$
Когда я думаю о второй производной, я представляю касательную к кривой в точке $x$ и позволяю $x$ возрастать. Вторая производная говорит вам об изменении наклона касательной. Таким образом, если 2-я производная положительна, наклон увеличивается, и поэтому касательная вращается против часовой стрелки (по мере увеличения $x$). Аналогично, отрицательная 2-я производная показывает, что касательная вращается по часовой стрелке.
Вторая производная говорит вам об изменении наклона касательной. Таким образом, если 2-я производная положительна, наклон увеличивается, и поэтому касательная вращается против часовой стрелки (по мере увеличения $x$). Аналогично, отрицательная 2-я производная показывает, что касательная вращается по часовой стрелке.
Точка перегиба — это точка, в которой касательная пересекает график, а также точка, в которой вращение изменяется с по часовой стрелке на против часовой стрелки, или vv.
Таким образом, вы получаете максимальный наклон именно тогда, когда вращение меняется с CCW на CW. Именно это и есть точки перегиба.
$\endgroup$
7
$\begingroup$
Первая производная любой функции $y=f(x)$ в точке $x$ дает наклон касательной в этой точке или скорость изменения функции $y=f(x)$ в точке $х$. Если производная положительная или отрицательная, наклон соответственно положительный или отрицательный.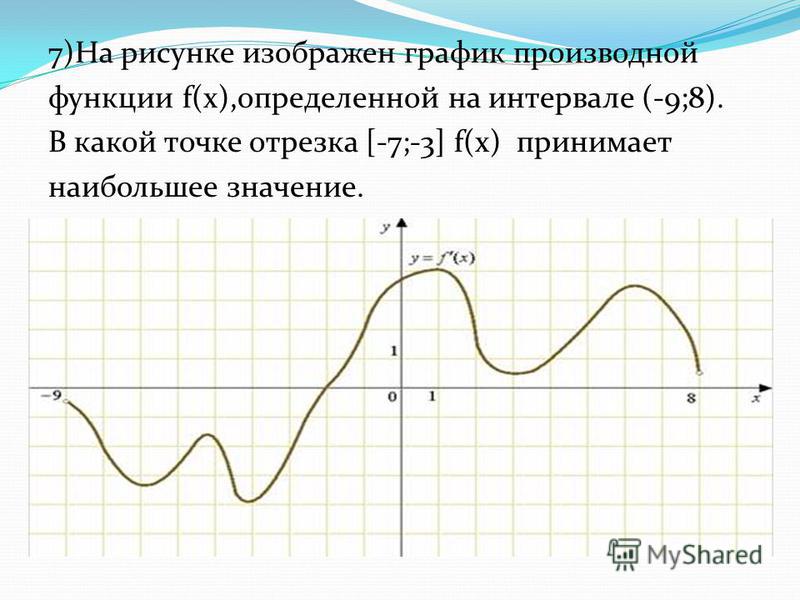

 } \ \ -2 \\
& {\ бф Б. } \ \ 2 \\
&{\bf С.} \ \ -3 \\
&{\bf D.} \ \ 3 \\
&{\bf E. } \ \ -\dfrac12
}$
} \ \ -2 \\
& {\ бф Б. } \ \ 2 \\
&{\bf С.} \ \ -3 \\
&{\bf D.} \ \ 3 \\
&{\bf E. } \ \ -\dfrac12
}$
Leave A Comment