Закрепление новых знаний — Студопедия
Поделись с друзьями:
А класс Геометрия
Урок № 23
Тема урока:
Средняя линия трапеции, ее свойства.
Записать в тетради число, тему урока
Актуализация опорных знаний учащихся
Вопросы классу
1. Дайте определение трапеции.
2. Какие стороны трапеции называются основаниями?
3. Что называется средней линией треугольника?
4. Сформулируйте свойство средней линии треугольника.
Изучение нового материала
План изложения темы
1. Определение средней линии трапеции.
2. Формулировка и доказательство теоремы о средней линии трапеции.
Определение средней линии трапеции
нарисовать трапецию ABCD и ее среднюю линию — отрезок MN.
Вопрос:
• Как расположена средняя линия трапеции по отношению к ее основаниям?
Теорема о средней линии трапеции
Для определения длины средней линии измерьте длины оснований и сопоставьте их полусумму с длиной средней линии.
Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Работа с учебником
Изучить с.97-98
Закрепление новых знаний
Выполнение устных упражнений
1. Основания трапеции равны 5 см и 9 см. Чему равна средняя линия трапеции? (Ответ: 7 см.)
2. Отрезок MN — средняя линия трапеции ABCD (рис. 1). Через точку N проведена прямая, параллельная стороне AB и пересекающая сторону AD в точке L. Докажите, что AMNL — параллелограмм.
3. В трапеции ABCD AB =4 см, BC =6 см, CD =5 см, AD=10 см,
MN — средняя линия. Чему равны стороны трапеции AMND.
4. Каждая из боковых сторон трапеции ABCD (AD ǁ BC) разделена
на четыре равные части (рис. 2). Чему равны отрезки EF, MN и QP, если AD =11 см, BC =3 см? (Ответ: EF =9 см; MN =7 см; QP =5 см.)
5. Средняя линия трапеции равна 8 см, а одно из оснований равно 6 см. Найдите второе основание трапеции. (Ответ: 10 см).
(Ответ: 10 см).
Выполнение письменных упражнений
1. Средняя линия трапеции равна 24 см. Основания трапеции относятся как 3:5. Найдите основания трапеции. (Ответ: 18 см, 30 см.)
2. Основания трапеции равны 8 см и 14 см. Найдите отрезки, на которые диагональ делит среднюю линию трапеции. (Ответ: 4 см и 7 см.)
3. Большее основание трапеции равно 8 см, а меньшее — на 3 см
меньше средней линии. Найдите меньшее основание и среднюю
линию трапеции. (Ответ: 2 см, 5 см.)
4. В трапеции ABCD боковая сторона AB перпендикулярна основаниям, а боковая сторона CD равна диагонали AC. Найдите среднюю линию трапеции, если BC =1 м. (Ответ: 1,5 м.)
5. В равнобокой трапеции диагональ является биссектрисой острого
угла, одно из оснований на 6 см больше другого. Найдите среднюю линию трапеции, если ее периметр равен 74 см.
Решение
Пусть ABCD (рис. 3) — равнобокая трапеция (AB =CD), AC —биссектриса угла A. Пусть BC =x см, тогда (x +6) см —нижнее основание трапеции.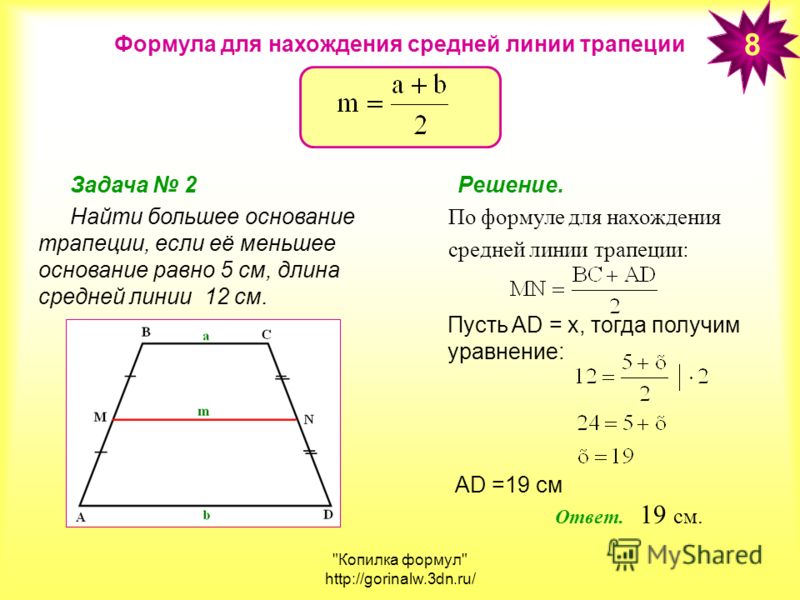
4x =68,
x =17.
Следовательно, BC =17 см, AD =17 +6 =23 (см). Значит, средняя линия трапеции равна = 20 (см).
Ответ: 20 см.
6. Боковая сторона равнобокой трапеции равна 18 см, а большее
основание — 32 см. Угол между ними равен 60º. Найдите среднюю линию трапеции.
Решение
Пусть ABCD (рис. 4) — равнобокая трапеция, AB =CD =18 см, AD =32 см, ∠BAD=60º. Из вершин B и C трапеции проведем высоты BK и CM (BK ⊥AD, CM⊥AD). Тогда в треугольнике ABK AK = AB = 9 см (как катет, лежащий
против угла в 30º). Значит, и MD =9 см. Тогда KM=AD−2⋅AK =32−18 =14 (см). Отсюда BC=KM=14 см. Следовательно, средняя линия трапеции ABCD равна = 23 (см).
Ответ: 23 см.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Трапеция.
 Теорема о средней линии трапеции
Теорема о средней линии трапеции1. Трапеция
Трапецией называется четырехугольник, у которого двестороны параллельны, а две другие не параллельны.
Параллельные стороны трапеции называются ее
основаниями, а непараллельные стороны – боковыми
сторонами.
Трапеция называется равнобедренной, если ее боковые
стороны равны.
Трапеция называется прямоугольной, если один из ее
углов прямой.
2. Средняя линия трапеции
Средней линией трапеции называетсясоединяющий середины ее боковых сторон.
отрезок,
3. Теорема о средней линии трапеции
Теорема. Средняя линия трапеции параллельна основаниям иравна их полусумме.
Доказательство. Пусть EF – средняя
линия трапеции ABCD (AB || CD).
Проведем прямую DF и ее точку
пересечения с прямой AB обозначим G.
Треугольники DFC и GFB равны по второму признаку равенства
треугольников (CF = BF по условию, угол 1 равен углу 2, как
вертикальные, угол 3 равен углу 4, как накрест лежащие углы).
 Из
Изравенства этих треугольников следует, что DF = GF и, значит, EF средняя линия треугольника AGD. Из теоремы о средней линии
треугольника следует, что EF параллельна AB и EF = AG. Так как
AB || CD, то EF будет параллельна обоим основаниям и кроме того,
EF = AG/2 = (AB + BG)/2 = (AB + CD)/2.
4. Вопрос 1
Какой четырехугольник называется трапецией?Ответ: Трапецией называется четырехугольник,
у которого две стороны параллельны, а две
другие не параллельны.
5. Вопрос 2
Какие стороны трапеции называются:основаниями; б) боковыми сторонами?
а)
Ответ: а) Основаниями трапеции называются ее
параллельные стороны;
б) боковыми сторонами трапеции
называются ее непараллельные стороны.
6. Вопрос 3
Какая трапеция называется: а) равнобедренной;б) прямоугольной?
Ответ: а) Трапеция называется равнобедренной,
если ее боковые стороны равны;
б) трапеция называется прямоугольной,
если один из ее углов прямой.

7. Вопрос 4
Что называется средней линией трапеции?Ответ: Средней линией трапеции называется
отрезок, соединяющий середины ее боковых
сторон.
8. Вопрос 5
Сформулируйтетрапеции.
Вопрос 5
теорему
о
средней
линии
Ответ: Средняя линия трапеции параллельна
основаниям и равна их полусумме.
9. Упражнение 1
Изобразите равнобедренную трапецию ABCD,три вершины которой даны на рисунке, а
четвертая находится в одном из узлов сетки.
Ответ:
10. Упражнение 2
Изобразите прямоугольную трапецию ABCD,три вершины которой даны на рисунке, а
четвертая находится в одном из узлов сетки.
Ответ:
11. Упражнение 3
Могут ли углы, прилежащие к основаниютрапеции, быть один острым, а другой тупым?
Ответ: Да.
12. Упражнение 4
Может ли у трапеции быть: а) три прямых угла;б) три острых угла?
Ответ: а) Нет; б) нет.
13. Упражнение 5
Докажите,что
углы
при
равнобедренной трапеции равны.
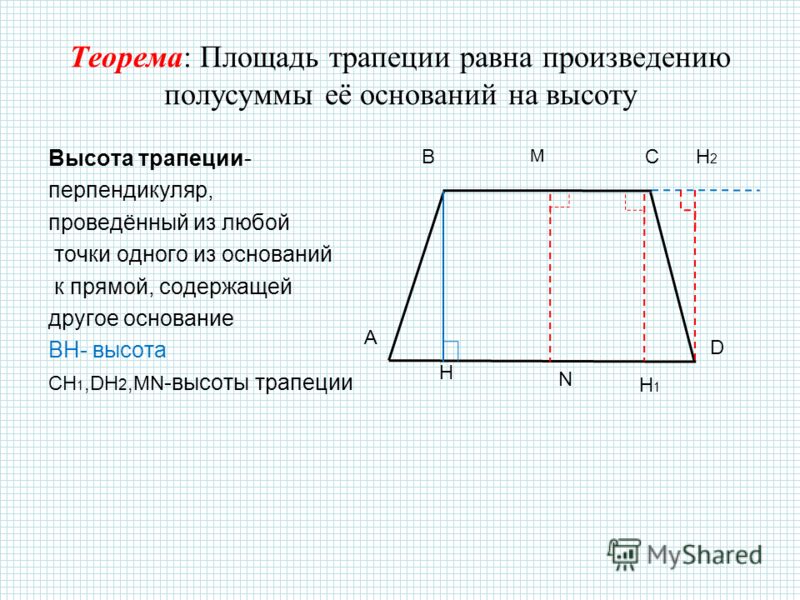
основании
Доказательство. Пусть ABCD –
трапеция, AD не параллельна BC.
Докажем, что углы A и B равны.
Через вершину C проведем прямую, параллельную AD и
обозначим E ее точку пересечения с прямой AB.
Четырехугольник AECD – параллелограмм,
следовательно, угол BAD равен углу BEC. Треугольник
BCE – равнобедренный, следовательно, угол BCE равен
углу BEC. Таким образом, в трапеции ABCD угол A равен
углу B.
14. Упражнение 6
Верно ли, что если два угла трапеции равны, тоона равнобедренная?
Ответ. Нет, она может быть прямоугольной.
15. Упражнение 7
Верно ли, что если два угла при основаниитрапеции равны, то она равнобедренная?
Ответ. Да.
16. Упражнение 8
Докажите, что сумма двух противоположныхуглов равнобедренной трапеции равна 180о.
Доказательство. Пусть ABCD – трапеция, AD не
параллельна BC. Докажем, что сумма углов A и С равна
180о. Действительно, Сумма углов B и C равна 180о.
Угол A равен углу B.
 Следовательно, сумма углов A и С
Следовательно, сумма углов A и Сравна 180о.
17. Упражнение 9
Чему равны углы равнобедренной трапеции,если известно, что разность противолежащих
углов равна 40о?
Ответ: 70о, 110о, 70о, 110о.
18. Упражнение 10
Докажите, чтотрапеции равны.
диагонали
равнобедренной
Доказательство. Пусть ABCD – равнобедренная
трапеция. Треугольники ABC и BAD равны (AB –
общая сторона, BC = AD, угол ABC равен углу
BAD. Следовательно, AC = BD.
19. Упражнение 11
Верно ли, что если диагонали трапеции равны,то она равнобедренная?
Ответ. Да.
20. Упражнение 12
Определите вид четырехугольника, которыйполучится, если последовательно соединить
отрезками середины сторон равнобедренной
трапеции.
Ответ: Ромб.
21. Упражнение 13
Прямая, проведенная параллельно боковойстороне трапеции через конец меньшего
основания, равного 3 см, отсекает треугольник,
периметр которого равен 15 см.
 Найдите
Найдитепериметр трапеции.
Ответ: 21 см.
22. Упражнение 14
Проведитесреднюю
линию
изображенной на рисунке.
Ответ:
трапеции,
23. Упражнение 15
Проведитесреднюю
линию
изображенной на рисунке.
Ответ:
трапеции,
24. Упражнение 16
Основания трапеции относятся как 5:2, а ихразность равна 18 см. Найдите среднюю линию
трапеции.
Ответ: 21 см.
25. Упражнение 17
Периметр трапеции равен 50 см, а сумманепараллельных сторон равна 20 см. Найдите
среднюю линию трапеции.
Ответ: 15 см.
26. Упражнение 18
Средняя линия трапеции равна 30 см, а меньшееоснование равно 20 см. Найдите большее
основание.
Ответ: 40 см.
27. Упражнение 19
Периметр равнобедренной трапеции равен 80 см,ее средняя линия равна боковой стороне.
Найдите боковую сторону данной трапеции.
Ответ: 20 см.
28. Упражнение 20
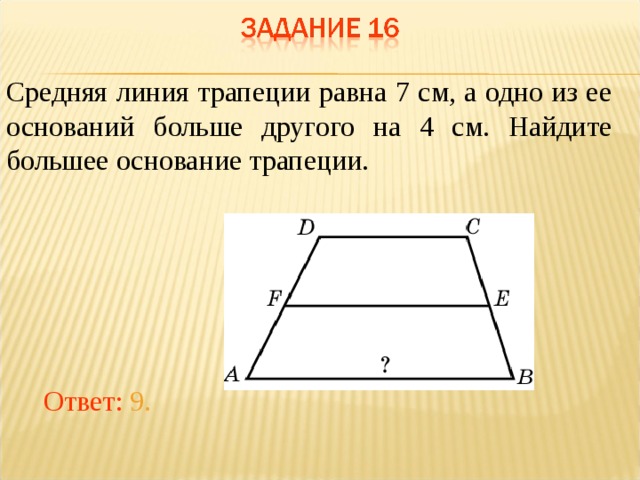
Средняя линия трапеции равна 7 см, а одно из ееоснований больше другого на 4 см.
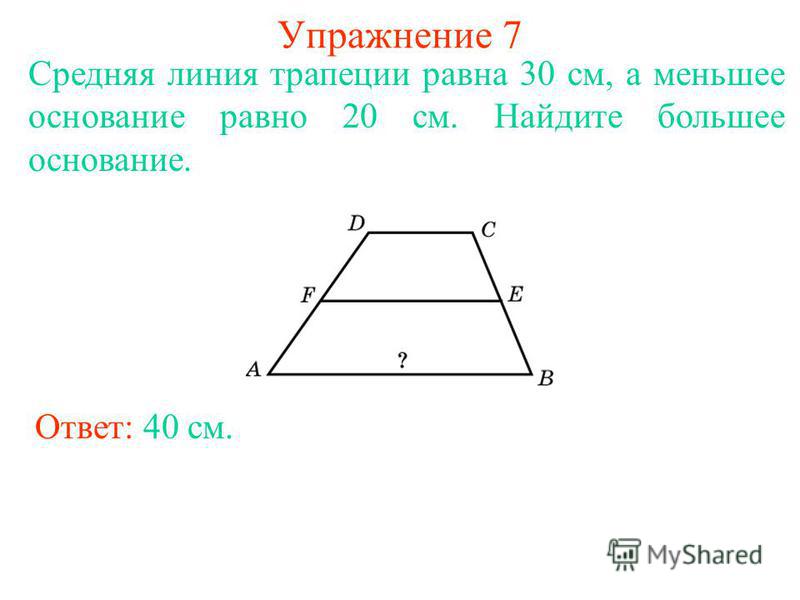 Найдите
Найдитеоснования трапеции.
Ответ: 5 см и 9 см.
29. Упражнение 21
Основания трапеции относятся как 2 : 3, асредняя линия равна 5 м. Найдите основания.
Ответ: 4 м и 6 м.
30. Упражнение 22
Перпендикуляр, опущенный из вершины тупогоугла на большее основание равнобедренной
трапеции, делит его на части, имеющие длины 5
см и 2 см. Найдите среднюю линию этой
трапеции.
Ответ: 5 см.
31. Упражнение 23
В равнобедренной трапеции большее основаниеравно 2,7 м, боковая сторона равна 1 м, угол
между ними 60о. Найдите меньшее основание.
Ответ: 1,7 м.
32. Упражнение 24
Cредняя линия трапеции равна 10 см. Одна издиагоналей делит ее на два отрезка, разность
которых равна 2 см. Найдите основания этой
трапеции.
Ответ: 8 см и 12 см.
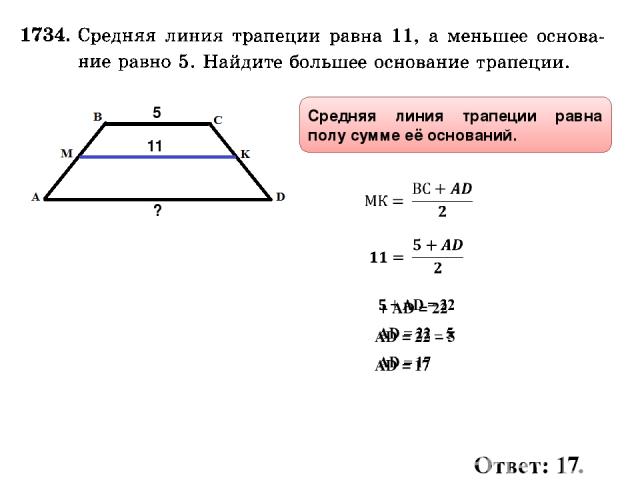
33. Упражнение 25
Основания трапеции равны 4 см и 10 см.Найдите отрезки, на которые делит среднюю
линию этой трапеции одна из ее диагоналей.
Ответ: 2 см и 5 см.
34. Упражнение 26
Меньшее основание равнобедренной трапецииравно
боковой
стороне,
а
диагональ
перпендикулярна боковой стороне. Найдите углы
трапеции.
Ответ: 60о, 120о, 60о, 120о.
35. Упражнение 27*
Может ли средняя линия трапеции пройти черезточку пересечения диагоналей?
Решение: Нет. Действительно, пусть ABCD – трапеция, EF
– средняя линия, G, H – ее точки пересечения с
диагоналями. Тогда EG – средняя линия треугольника
ACD и, следовательно, равна половине CD. FH – средняя
линия треугольника BCD и, следовательно, равна
половине CD. Если бы точки G и H совпадали, то средняя
линия EF была бы равна CD. В этом случае трапеция была
бы параллелограммом.
36. Упражнение 28*
В выпуклом пятиугольнике ABCDE AE = 4.Середины сторон AB и CD, BC и ED соединены
отрезками. Середины H и K этих отрезков снова
соединены отрезками. Найдите длину отрезка
HK.
Решение: Пусть M, N, P, R, L – середины
соответствующих сторон.
 Тогда HK = 1 ML = 1 AE = 1.
Тогда HK = 1 ML = 1 AE = 1.2
4
Математическая задача: Трапеция — центральная медиана
Центральная медиана делит трапецию на две меньшие трапеции. Найдите отношение его площадей.
Правильный ответ:
p = (3a+c)/(a+3c)Пошаговое объяснение:
S1 = ((a+c)/2+c)h/2 S2 = ( (a+c)/2+a)h/2 p = S2:S1 = ((a+c)/2+a)/ ((a+c)/2+c) p = (1,5a+ 0,5c)/(0,5a+1,5c) p=(3a+c)/(a+3c)
Нашли ошибку или неточность? Не стесняйтесь
пишите нам. Спасибо!
Советы по использованию связанных онлайн-калькуляторов
Воспользуйтесь нашим калькулятором коэффициентов.
Для решения данной словесной задачи по математике необходимо знать следующие знания:
- алгебра
- выражение переменной из формулы
- планиметрика 900 27
- площадь формы
- трапеция
- основные функции
- отношение
Уровень задачи:
- практика для 14-летних
- старшая школа
Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: video1
- Длина 26
Длина медианы трапеции составляет 10 дюймов. Медиана делит трапецию на две части, соотношение которых равно 3:5. Длина меньшего основания:
Медиана делит трапецию на две части, соотношение которых равно 3:5. Длина меньшего основания: - Внутренние углы
Величина внутреннего угла при центральной вершине C равнобедренного треугольника ABC равна 72°. Прямая p, параллельная основанию этого треугольника, делит треугольник на трапецию и меньший треугольник. Каковы внутренние углы трапеций - Стороны 2
Соотношение сторон трапеции 2:5:8:5. Площадь трапеции равна 245. Найдите высоту и периметр трапеции. - Герб
Класс создал свой герб, который имел форму, состоящую из равнобедренной трапеции ABCD (более короткое основание а = 4,5 см в длину, более длинное 2а = 9 см, высота трапеции 6 см) и полукруга с центром S и диаметр АВ. Три одинаковых равнобедренных треугольника fo - Трети трапеции
Трапеция ABCD имеет параллельные стороны AB и CD. Точка Е лежит на стороне АВ. Отрезок DE делит трапецию на две части одинаковой площади. Найдите длину отрезка AE. - Концентрический 6751
Дана окружность K с радиусом r = 8 см. Какого радиуса должна быть меньшая концентрическая окружность, которая делит окружность K на две части одинаковой площади?
Какого радиуса должна быть меньшая концентрическая окружность, которая делит окружность K на две части одинаковой площади? - МО Z9–I–2 — 2017
VO является более длинным основанием в трапеции VODY, а диагональное пересечение K делит линию VD в отношении 3:2. Площадь треугольника КОВ равна 13,5 см². Найдите площадь всей трапеции. - MO Z8–I–6 2018
Трапеция KLMN, KL имеет основание 40 см и MN 16 см. Точка P лежит на прямой KL так, что отрезок NP делит трапецию на две части одинаковой площади. Найдите длину линии КП. - Трапеции
В равнобедренной трапеции ABCD мы знаем: AB||CD, |CD| = c = 8 см, высота h = 7 см, |∠CAB| = 35°. Найдите площадь трапеции. - Концентрические окружности
Дана окружность K радиусом r = 8 см. Насколько большим должен быть радиус меньшей концентрической окружности, которая делит окружность К на две части одинаковой площади? - Круги
Площади двух кругов находятся в соотношении 2:20. Диаметр большего круга равен 20. Вычислите радиус меньшего круга.
Вычислите радиус меньшего круга. - Разделить равнобедренный треугольник
Как разделить равнобедренный треугольник на две части с равными площадями, перпендикулярными оси симметрии (на трапецию и треугольник)? - Трапеция KLMN
Трапеция KLMN имеет основания KL 40см и MN 16см. В основании KL находится точка P. Отрезок NP делит трапецию на звенья одинаковой площади. На каком расстоянии точка P от точки K? - См. гармоники
Верно ли, что размер центрального сегмента любой трапеции равен среднему гармоническому размеру ее оснований? Докажите это. Центральный отрезок пересекает пересечение диагоналей и параллелен основаниям. - Два земельных участка
Общая площадь двух соседних земельных участков составляет 964 м². Второй участок меньше на 77 м 2 , вдвое больше первого участка. Найдите площади каждой земли. - Отношение площадей треугольников
В равностороннем треугольнике ABC точка T является его центром тяжести, точка R является образом точки T в осевой симметрии вдоль линии AB, а точка N является образом точки T в осевой симметрии вдоль линии BC. Найдите отношение площадей
Найдите отношение площадей - Прямоугольные треугольники
Длины соответствующих сторон двух прямоугольных треугольников относятся как 2:5. При каком отношении медианы относятся к гипотенузе этих прямоугольных треугольников? В каком отношении находятся площади этих треугольников? Меньший прямоугольный треугольник имеет стороны 6 и 8 c
Математическая задача: Длина 26 — вопрос № 68714, статистика, среднее
Длина медианы трапеции равна 10 дюймам. Медиана делит трапецию на две части, соотношение которых равно 3:5. Длина более короткого основания:
Правильный ответ:
c = 5 вПошаговое объяснение:
m=10 in S1:S2 = 3:5 (a+c)/2 = m a+c = 2⋅ m = 20 in h2=h3 h2+h3=h S1 = h2⋅ (a+m)/2 S2 = h3⋅ (c+m)/2 = h2⋅ (c+m )/2 h2⋅ (c+m)/2 : h2⋅ (a+m)/2 = 3:5 (c+m) : (a+m) = 3:5 (c+m)=53 ⋅ (а+m) (a+c)/2=m (c+10)=53⋅ (a+10) (a+c)/2=10 (c+10)=3/5⋅ ( a+10) (a+c)/2=10 3a−5c=20 a+c=20 Row2−31⋅ Row1→Row2 3a−5c=20 2,67c=13,33 c=2,6666666713,33333333=5 a= 320+5c=320+5⋅ 5=15 a=15 c=5=5 в
Нашли ошибку или неточность? Не стесняйтесь
пишите нам . Спасибо!
Спасибо!
Советы по использованию связанных онлайн-калькуляторов
Нужна помощь в вычислении среднего арифметического?
Ищете статистический калькулятор?
Воспользуйтесь нашим калькулятором коэффициентов.
У вас есть линейное уравнение или система уравнений и вы ищете ее решение? Или у вас есть квадратное уравнение?
См. также наш калькулятор тригонометрического треугольника.
Для решения этой математической задачи вам необходимо знать следующие знания:
- статистика
- среднее
- геометрия
- подобие треугольников 900 24 алгебра
- уравнение
- система уравнений
- выражение переменной из формулы
- контуры
- площадь фигуры
- треугольник
- трапеция
- основные функции
- отношение
Единицы физических величин:
- площадь
Уровень словесной задачи:
- практика для 14-летних 900 44
- Трапеция — центральная медиана
Центральная медиана делит трапецию на две меньшие трапеции. Найдите отношение его площадей. - МО Z9–I–2 — 2017
VO является более длинным основанием в трапеции VODY, а диагональное пересечение K делит линию VD в отношении 3:2. Площадь треугольника КОВ равна 13,5 см². Найдите площадь всей трапеции. - Вычислить 47763
Вычислить площадь равнобедренной трапеции ABCD, длинное основание которой равно 48 см, меньшее основание составляет 3/4 наибольшего основания, а катет трапеции составляет 2/3 наибольшего основания. Результат округляется до сотых.
Трапеция KLMN имеет основания KL 40см и MN 16см. В основании KL находится точка P. Отрезок NP делит трапецию на звенья одинаковой площади. На каком расстоянии точка P от точки K?- Герб
Класс создал свой герб, который имел форму, состоящую из равнобедренной трапеции ABCD (более короткое основание а = 4,5 см в длину, более длинное 2а = 9 см, высота трапеции 6 см) и полукруга с центром S и диаметр АВ. Три одинаковых равнобедренных треугольника fo
Три одинаковых равнобедренных треугольника fo - MO Z8–I–6 2018
Трапеция KLMN, KL имеет основание 40 см и MN 16 см. Точка P лежит на прямой KL так, что отрезок NP делит трапецию на две части одинаковой площади. Найдите длину линии КП. - Внутренние углы
Величина внутреннего угла при центральной вершине C равнобедренного треугольника ABC равна 72°. Прямая p, параллельная основанию этого треугольника, делит треугольник на трапецию и меньший треугольник. Насколько велики внутренние углы трапеций - Разрез куба
Ребро СС’ направляет куб ABCDA’B’C’D’, плоскость, которая делит куб на две перпендикулярные четырехгранные и треугольные призмы, объемы которых составляют 3:2. Определите, в каком отношении ребро AB делит эту плоскость. - Терции трапеции
Трапеция ABCD имеет параллельные стороны AB и CD. Точка Е лежит на стороне АВ. Отрезок DE делит трапецию на две части одинаковой площади. Найдите длину отрезка AE. - Равнобедренная трапеция
Какова высота равнобедренной трапеции, длина основания которой 11 см и 8 см, а длина катетов 2,5 см? - Тимоти
Рост Тимоти 56 4/5 дюймов. Тереза на 1 1/6 дюйма ниже Тимоти, а Джейн на 1 1/3 дюйма ниже Терезы. Какой рост у Джейн?
Тереза на 1 1/6 дюйма ниже Тимоти, а Джейн на 1 1/3 дюйма ниже Терезы. Какой рост у Джейн? - Рассчитать 3993
Медиана трапеции p равна 18,6 см, а основание a = 29,8 см. Вычислите размер второго основания c. - Томас 2
Рост Томаса 56 3/4 дюйма. Джиллиан на 1 3/8 дюйма ниже Томаса, а Джейн на 1 1/5 дюйма ниже Джиллиан. Какой рост у Джейн? Подпишите имена на диаграмме ленты, чтобы представить эту проблему. Джейн Джиллиан Томас Отлично! - Трапеция
Длина основания и высота основания трапеции находятся в соотношении 5:3:2. Площадь трапеции 128 см². Вычислите длину основания и высоту трапеции. - Разделить равнобедренный треугольник
Как разделить равнобедренный треугольник на две части с равными площадями, перпендикулярными оси симметрии (на трапецию и треугольник)? - Золотое сечение
Разделите линию длиной 14 см на две части так, чтобы отношение меньшей части к большей было равно отношению большей части ко всей длине линии.
Рекомендуем посмотреть это обучающее видео по этой математической задаче.

 Медиана делит трапецию на две части, соотношение которых равно 3:5. Длина меньшего основания:
Медиана делит трапецию на две части, соотношение которых равно 3:5. Длина меньшего основания: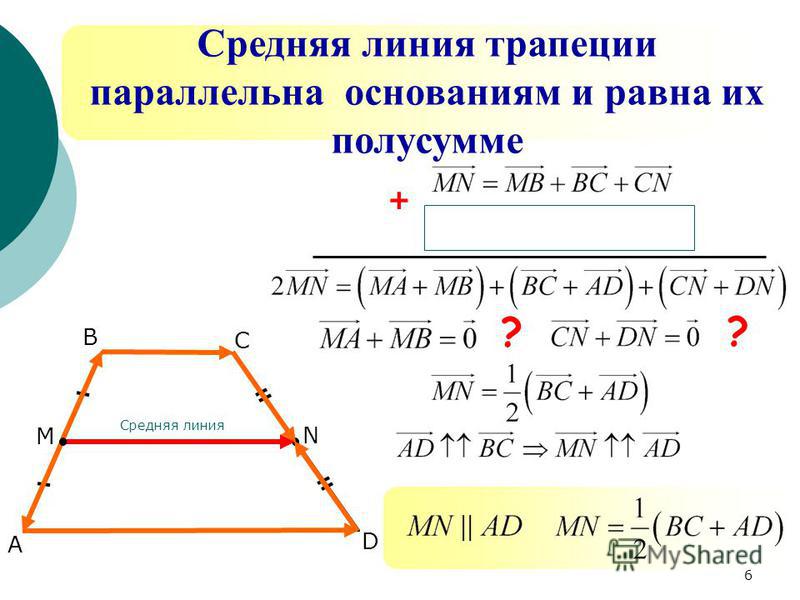 Какого радиуса должна быть меньшая концентрическая окружность, которая делит окружность K на две части одинаковой площади?
Какого радиуса должна быть меньшая концентрическая окружность, которая делит окружность K на две части одинаковой площади?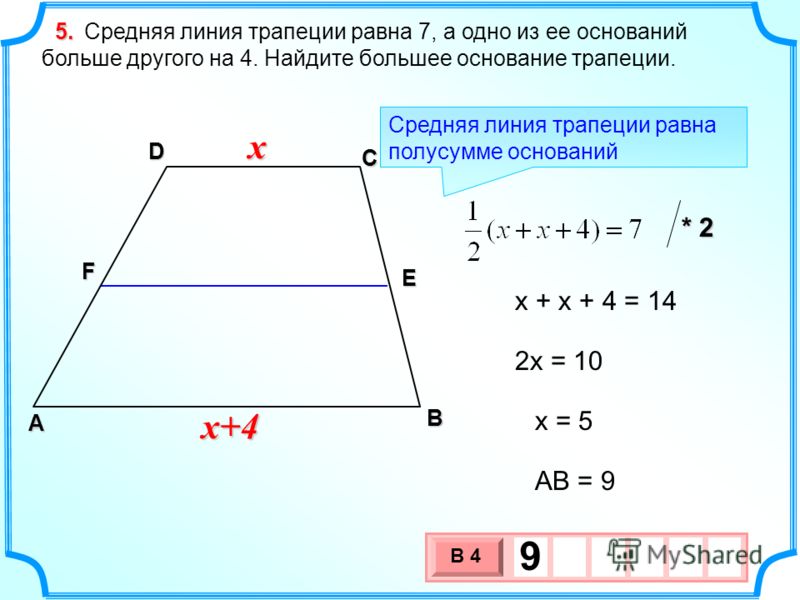 Вычислите радиус меньшего круга.
Вычислите радиус меньшего круга.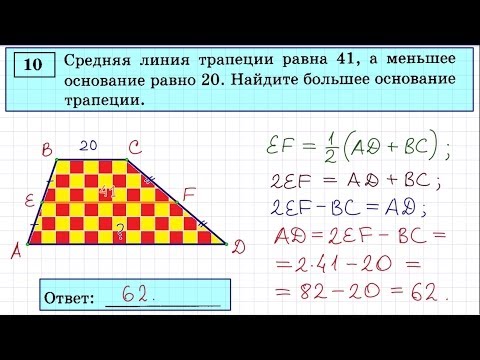 Найдите отношение площадей
Найдите отношение площадей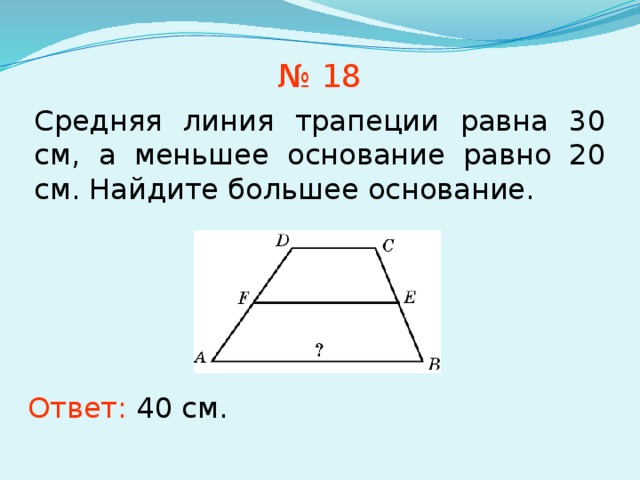 Три одинаковых равнобедренных треугольника fo
Три одинаковых равнобедренных треугольника fo Тереза на 1 1/6 дюйма ниже Тимоти, а Джейн на 1 1/3 дюйма ниже Терезы. Какой рост у Джейн?
Тереза на 1 1/6 дюйма ниже Тимоти, а Джейн на 1 1/3 дюйма ниже Терезы. Какой рост у Джейн?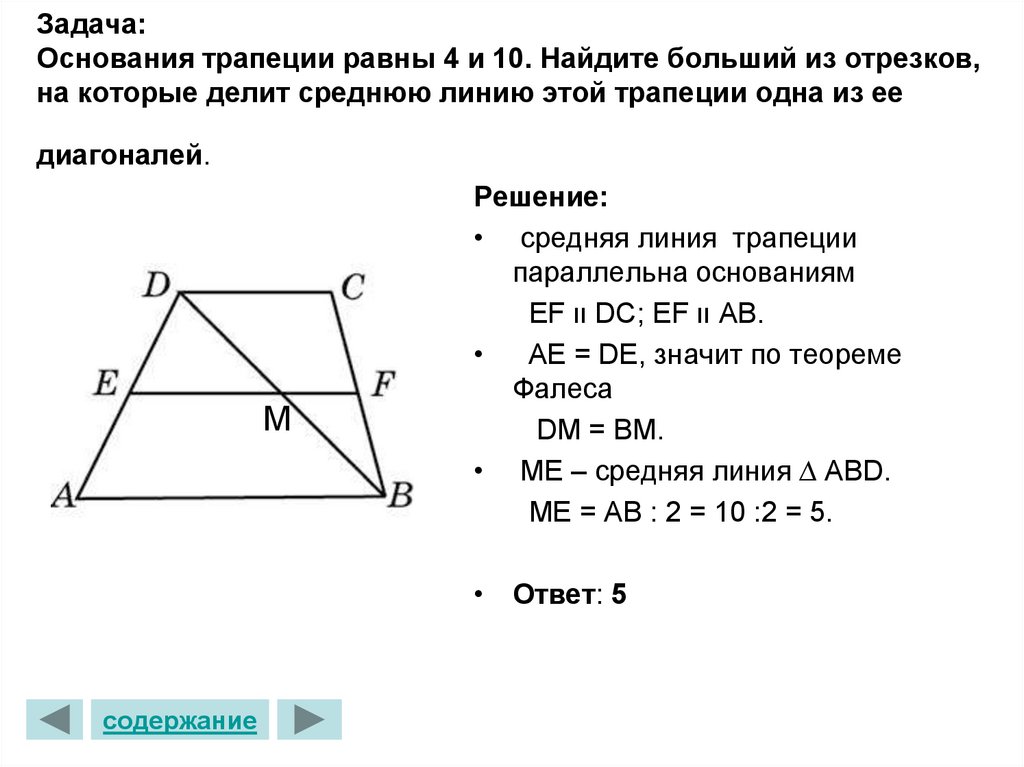
Leave A Comment