Как найти большую высоту параллелограмма. Параллелограмм
Найдите диагональ параллелограмма, проведенную из вершины тупого угла и углы, которые она образует со сторонами параллелограмма. Используя теорему косинусов, можно найти биссектрисы параллелограмма через стороны. Если известна величина угла (α) в какой-либо из вершин параллелограмма, а также длины сторон (a и b), образующих этот угол, найти большую из высот тоже будет не очень несложно.
Если кроме длины самой короткой из сторон треугольника (a) в условиях приведена площадь (S) фигуры, формула расчета большей из высот (Hₐ) будет достаточно проста. Не зная площади, но имея длины всех сторон треугольника (a, b и c), тоже можно найти самую длинную из его высот, однако математических операций будет значительно больше. Начните с вычисления вспомогательной величины — полупериметра (р). Для этого сложите длины всех сторон и разделите результат пополам: р = (a+b+c)/2.
Из полученного значения извлеките квадратный корень √(р*(р-a)*(р-b)*(р-c)) и не удивляйтесь — вы использовали формулу Герона для нахождения площади треугольника. Для определения длины наибольшей высоты осталось заменить полученным выражением площадь в формуле из второго шага: Hₐ = 2*√(р*(р-a)*(р-b)*(р-c))/a.
Для определения длины наибольшей высоты осталось заменить полученным выражением площадь в формуле из второго шага: Hₐ = 2*√(р*(р-a)*(р-b)*(р-c))/a.
Примечание. Это часть урока с задачами по геометрии (раздел параллелограмм). См. также: Свойства и площадь параллелограмма. Затем, зная один из углов, в зависимости от того, какая высота была дана, отнимаем его из 180 градусов, чтобы найти второй. Используя эту же теорему косинусов, можно найти угол между диагоналями в одном из четырех треугольников, образованных ими, где сторонами являются половины диагоналей и одна из сторон параллелограмма.
У нас есть много людей, которые помогут Вам здесь Кроме того, мой последний вопрос был решен менее чем за 10 минут:D Во всяком случае, Вы можете просто войти и попробовать добавить свой вопрос. Параллелограмм — это один из видов четырехугольников, а высота — это перпендикуляр, опущенный из вершины к противолежащей стороне.
Трижды умножьте полупериметр на разность между ним и каждой из сторон: р*(р-a)*(р-b)*(р-c). Для этого величину длинной стороны умножьте на синус известного угла, а результат разделите на длину короткой стороны: Hₐ = b*sin(α)/a. Результаты ЕГЭ зависят не только от знаний и умений выпускника: немаловажным является также правильное заполнение…
Для этого величину длинной стороны умножьте на синус известного угла, а результат разделите на длину короткой стороны: Hₐ = b*sin(α)/a. Результаты ЕГЭ зависят не только от знаний и умений выпускника: немаловажным является также правильное заполнение…
Бесплатная помощь с домашними заданиями
Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Тебе необходимо научиться правильно и ПОЛНОСТЬЮ формулировать вопрос. Надо написать полностью условие задачи. Треугольник считается равнобедренным, так как из свойств биссектрисы и суммы углов в треугольнике следует, что углы при основании такого треугольника конгруэнтны. Помогите,пожалуйста, решить одну задачу.
Поэтому в задачах из курса геометрии иногда требуется определить длину большей высоты, например, треугольника или параллелограмма. Периметр параллелограмма, зная стороны, выглядит как их удвоенная сумма, а площадь является произведением высоты и стороны, на которую она опущена.
У которого противоположные стороны параллельны.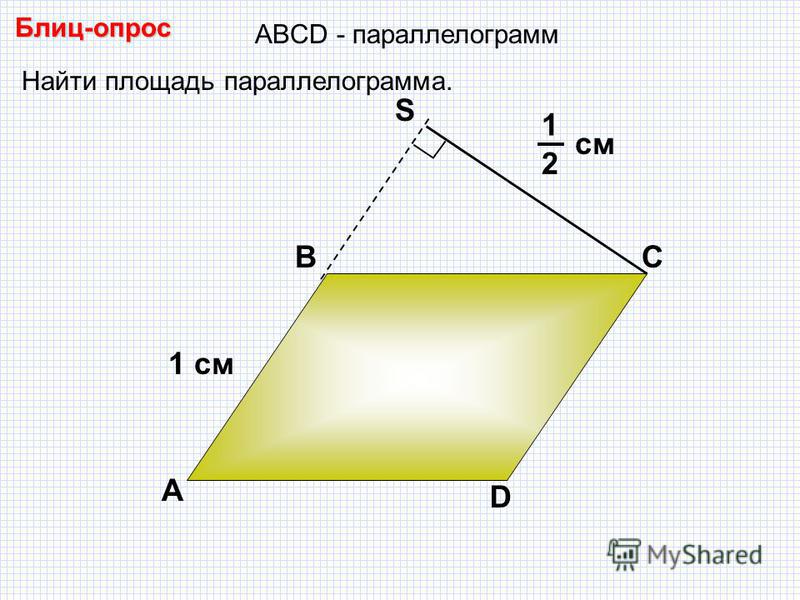 Если у параллелограмма все углы прямые, то такой параллелограмм называется прямоугольником , а прямоугольник, у которого все стороны равны, называется квадратом.
Если у параллелограмма все углы прямые, то такой параллелограмм называется прямоугольником , а прямоугольник, у которого все стороны равны, называется квадратом.
Все параллелограммы обладают следующими свойствами:
- противоположные стороны равны:
AB = CD и BC = DA
- противолежащие углы равны:
∠ABC = ∠CDA и ∠DAB = ∠BCD
- сумма углов, прилежащих к одной стороне, равна 180°:
∠ABC + ∠BCD = 180°
∠BCD + ∠CDA = 180°
∠CDA + ∠DAB = 180°
∠DAB + ∠ABC = 180° - в точке пересечения диагонали делятся пополам:
AO = OC и BO = OD
- каждая диагональ делит параллелограмм на два равных треугольника :
ΔABC = ΔCDA и ΔABD = ΔBCD
- точка пересечения диагоналей — это центр симметрии параллелограмма:
Точка O — это центр симметрии.

Высота
Нижняя сторона параллелограмма называется его основанием , а перпендикуляр, опущенный на основание из любой точки противоположной стороны, — высотой .
AD — это основание параллелограмма, h — высота.
Высота выражает расстояние между противоположными сторонами, поэтому определение высоты можно сформулировать ещё так: высота параллелограмма — это перпендикуляр, опущенный из любой точки одной стороны на противоположную ей сторону.
Площадь
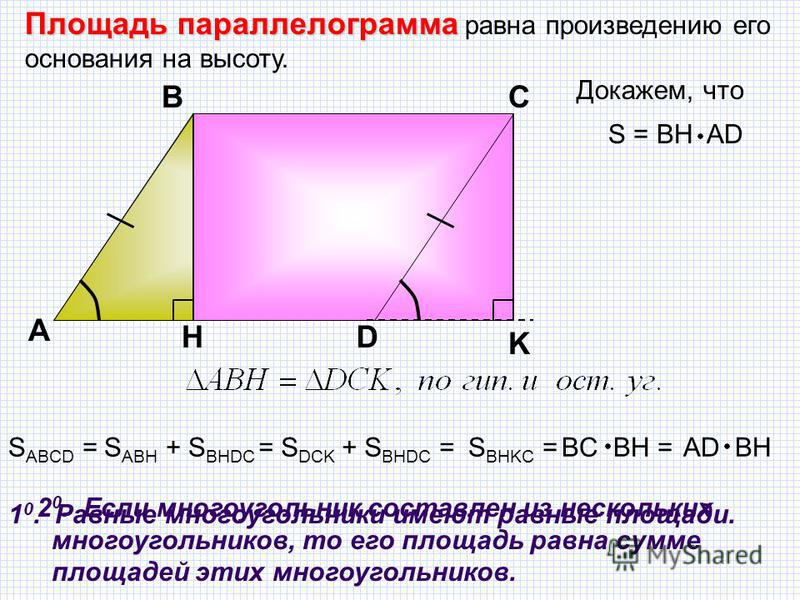
Для измерения площади параллелограмма можно представить его в виде прямоугольника. Рассмотрим параллелограмм ABCD :
Построенные высоты BE и CF образуют прямоугольник EBCF и два треугольника: ΔABE и ΔDCF . Параллелограмм ABCD состоит из четырёхугольника EBCD и треугольника ABE , прямоугольник EBCF состоит из того же четырёхугольника и треугольника DCF . Треугольники ABE и DCF равны (по четвёртому признаку равенства прямоугольных треугольников), значит и площади прямоугольника с параллелограммом равны, так как они составлены из равных частей.
Итак, параллелограмм можно представить в виде прямоугольника, имеющего такое же основание и высоту. А так как для нахождения площади прямоугольника перемножаются длины основания и высоты, значит и для нахождения площади параллелограмма нужно поступить также:
площадь ABCD = AD · BE
Из данного примера можно сделать вывод, что площадь параллелограмма равна произведению его основания на высоту . Общая формула:
S = ah
где S — это площадь параллелограмма, a — основание, h — высота.
Как определить высоту параллелограмма, зная некоторые из его остальных параметров? Таких, как площадь, длины диагоналей и сторон, величины углов.
Вам понадобится
- калькулятор
Инструкция
1. В задачах по геометрии, вернее по планиметрии и тригонометрии, изредка требуется обнаружить высоту параллелограмма, исходя из заданных значений сторон, углов, диагоналей и т. п.Дабы обнаружить высоту параллелограмма, зная его площадь и длину основания, нужно воспользоваться правилом определения площади параллелограмма. Площадь параллелограмма, как вестимо, равняется произведению высоты на длину основания:S=a*h, где:S – площадь параллелограмма,а – длина основания параллелограмма,h – длина опущенной на сторону а высоты, (либо на ее продолжение).Отсель получаем, что высота параллелограмма будет равняться площади, поделенной на длину основания:h=S/aНапример,дано: площадь параллелограмма равняется 50 кв.см., основание – 10 см.;обнаружить: высоту параллелограмма.h=50/10=5 (см).
п.Дабы обнаружить высоту параллелограмма, зная его площадь и длину основания, нужно воспользоваться правилом определения площади параллелограмма. Площадь параллелограмма, как вестимо, равняется произведению высоты на длину основания:S=a*h, где:S – площадь параллелограмма,а – длина основания параллелограмма,h – длина опущенной на сторону а высоты, (либо на ее продолжение).Отсель получаем, что высота параллелограмма будет равняться площади, поделенной на длину основания:h=S/aНапример,дано: площадь параллелограмма равняется 50 кв.см., основание – 10 см.;обнаружить: высоту параллелограмма.h=50/10=5 (см).
2. Потому что высота параллелограмма, часть основания и прилежащая к основанию сторона образуют прямоугольный треугольник, то для нахождения высоты параллелограмма дозволено применять некоторые соотношения сторон и углов прямоугольных треугольников.Если знамениты прилежащая к высоте h (DE) сторона параллелограмма d (AD) и противоположный высоте угол A (BAD), то расчета высоты параллелограмма необходимо умножить длину прилежащей стороны на синус противоположного угла:h=d*sinA,скажем, если d=10 см, а угол А=30 градусов, тоH=10*sin(30?)=10*1/2=5 (см).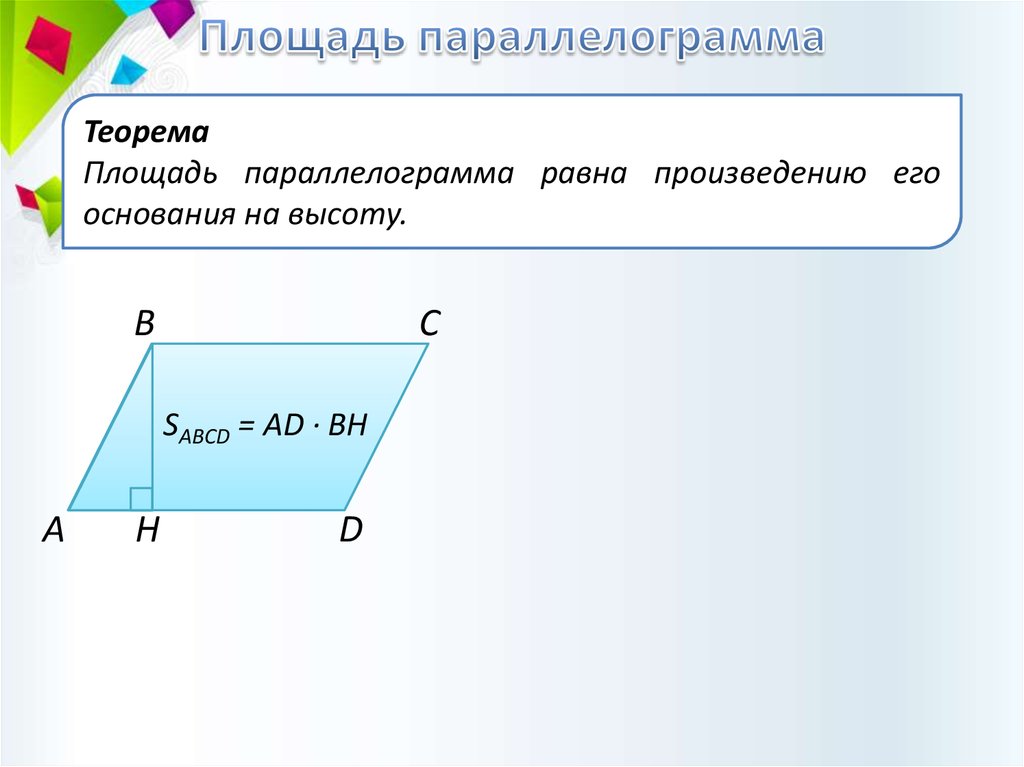
Высотой многоугольника называют перпендикулярный одной из сторон фигуры отрезок прямой, тот, что соединяет ее с вершиной противолежащего угла. Таких отрезков в плоской выпуклой фигуре существует несколько, и длины их не идентичны, если хоть одна из сторон многоугольника имеет хорошую от других величину. Следственно в задачах из курса геометрии изредка требуется определить длину большей высоты, скажем, треугольника либо параллелограмма.
Инструкция
1. Определите, которая из высот многоугольника должна иметь крупнейшую длину. В треугольнике это отрезок, опущенный на самую короткую сторону, следственно если в начальных условиях даны размеры всех 3 сторон, то гадать не придется.
2. Если помимо длины самой короткой из сторон треугольника (a) в условиях приведена площадь (S) фигуры, формула расчета большей из высот (H?) будет довольно примитивна. Удвойте площадь и поделите полученное значение на длину короткой стороны – это и будет желанная высота: H? = 2*S/a.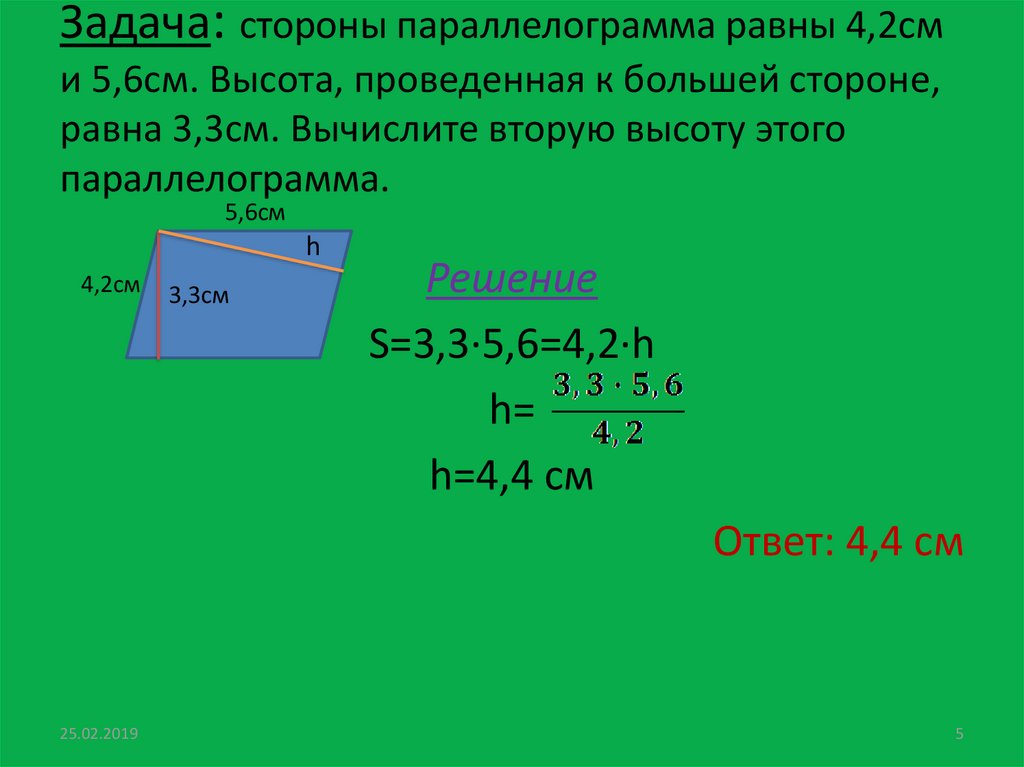
3. Не зная площади, но имея длины всех сторон треугольника (a, b и c), тоже дозволено обнаружить самую длинную из его высот, впрочем математических операций будет гораздо огромнее. Начните с вычисления вспомогательной величины – полупериметра (р). Для этого сложите длины всех сторон и поделите итог напополам: р = (a+b+c)/2.
4. Трижды умножьте полупериметр на разность между ним и всякой из сторон: р*(р-a)*(р-b)*(р-c). Из полученного значения извлеките квадратный корень?(р*(р-a)*(р-b)*(р-c)) и не изумляйтесь – вы применяли формулу Герона для нахождения площади треугольника. Для определения длины наибольшей высоты осталось заменить полученным выражением площадь в формуле из второго шага: H? = 2*?(р*(р-a)*(р-b)*(р-c))/a.
5. Огромная высота параллелограмма (H?) вычисляется еще проще, если знаменита площадь этой фигуры (S) и длина ее короткой стороны (a). Поделите первое на второе и получите надобный итог: H? = S/a.
6. Если вестима величина угла (?) в какой-нибудь из вершин параллелограмма, а также длины сторон (a и b), образующих данный угол, обнаружить крупную из высот тоже будет не дюже нетрудно.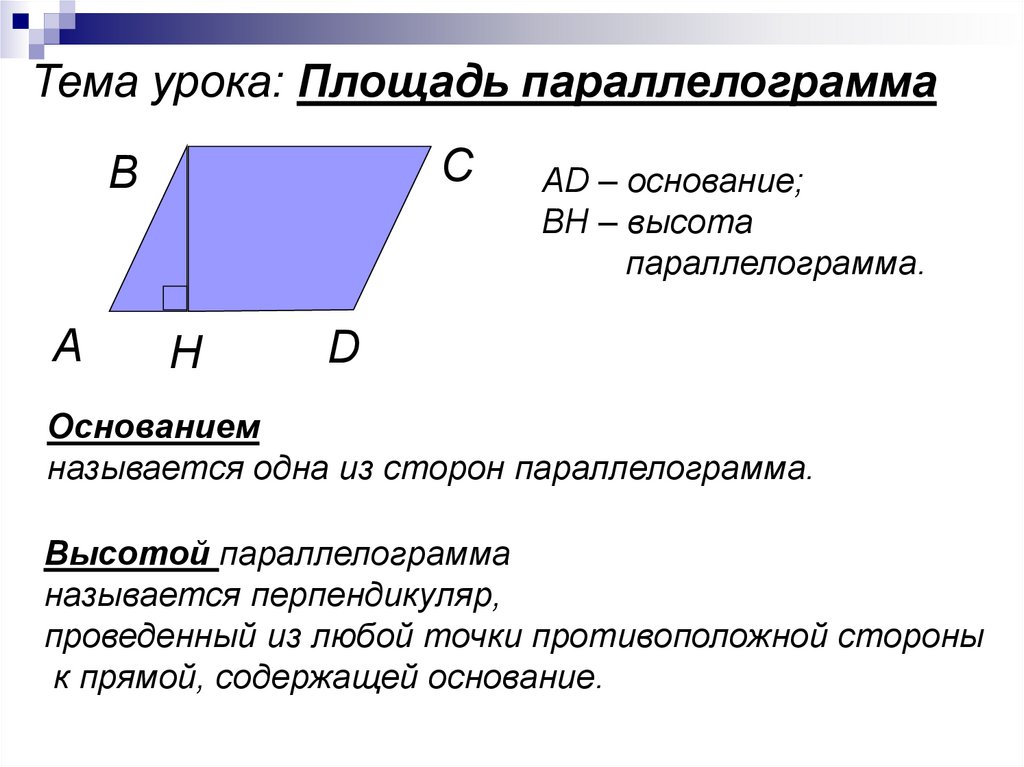 Для этого величину длинной стороны умножьте на синус знаменитого угла, а итог поделите на длину короткой стороны: H? = b*sin(?)/a.
Для этого величину длинной стороны умножьте на синус знаменитого угла, а итог поделите на длину короткой стороны: H? = b*sin(?)/a.
Видео по теме
Параллелограмм — это четырехугольник с противолежащими и попарно параллельными друг другу сторонами.
Высота параллелограмма — это линия, перпендикулярная одной из сторон параллелограмма и соединяющая эту сторону с противолежащим углом.
Для того чтобы узнать, как найти длину высоты параллелограмма, обратимся к формулам. Высота чаще всего обозначается буквой h.
Способ нахождения высоты зависит от известных нам величин в задании. Рассмотрим разные способы на конкретных примерах.
Пример 1
Даны площадь (S) и длина основания (a).
- Формула: h=S/a
Пример: Площадь параллелограмма равна 100 см 2 , основание, к которому проведена высота, равно 20 см. Найдите высоту.
- h= 100/20 =5
- Ответ: 5 см
Пример 2
Даны длина прилежащей к высоте стороны параллелограмма (b) и угол, противоположный самой высоте (a).
- Формула: h = b* sin a
Пример: Обозначим наш параллелограмм буквами ABCD, высота BE проходит из угла ABC к стороне AD. Длина стороны AB равна 20 см, угол BAD равен 30 градусов. Найдите высоту.
- h = 20 * sin 30° = 20 * 0,5 = 10
Ответ: 10 см
Пример 3
Даны длина стороны параллелограмма, прилегающая к высоте (n) и длина отсекаемой от основания части стороны (m).
- h = корень из (n 2 — m 2)
Пример: в параллелограмме ABCD высота BE проходит из угла ABC к стороне AD. Длина AB равна 5 см, длина АЕ равна 3 см. Найдите высоту.
- h = корень из (AD 2 — AB 2)
- h = корень из (5 2 -3 2) = 4
- Ответ: 4 см
Пример 4
Даны длина диагонали, выходящей из того же угла, что и высота (d), и длина отсекаемой от основания части стороны (m).
- h= корень из (d 2 — m 2)
Пример: в параллелограмме ABCD высота BE проходит из угла ABC к стороне AD. Диагональ BD равна 5 см, длина ED = 4 см.
- h = корень из (BD 2 — ED 2)
- h= корень из (5 2 — 4 2) = 3
- Ответ: 3 см
Если в задании требуется найти большую высоту параллелограмма, то необходимо посчитать длины обеих высот и выбрать наибольшее значение.
Как определить высоту параллелограмма, зная некоторые из его остальных параметров? Таких, как площадь, длины диагоналей и сторон, величины углов.
Вам понадобится
- калькулятор
Инструкция
В задачах по геометрии, точнее по планиметрии и тригонометрии, иногда требуется найти высоту параллелограмма, исходя из заданных значений сторон, углов, диагоналей и т.п.
Чтобы найти высоту параллелограмма, зная его площадь и длину основания, необходимо воспользоваться правилом определения площади параллелограмма. Площадь параллелограмма, как известно, равняется произведению высоты на длину основания:
S — площадь параллелограмма,
а — длина основания параллелограмма,
h — длина опущенной на сторону а высоты, (или на ее продолжение).
Отсюда получаем, что высота параллелограмма будет равняться площади, разделенной на длину основания:
Например,
дано: площадь параллелограмма равняется 50 кв.см., основание — 10 см.-
найти: высоту параллелограмма.
h=50/10=5 (см).
Так как высота параллелограмма, часть основания и прилежащая к основанию сторона образуют прямоугольный треугольник, то для нахождения высоты параллелограмма можно использовать некоторые соотношения сторон и углов прямоугольных треугольников.
Если известны прилежащая к высоте h (DE) сторона параллелограмма d (AD) и противоположный высоте угол A (BAD), то расчета высоты параллелограмма нужно умножить длину прилежащей стороны на синус противоположного угла:
например, если d=10 см, а угол А=30 градусов, то
H=10*sin(30?)=10*1/2=5 (см).
Если в условиях задачи заданы длина прилежащей к высоте h (DE) стороне параллелограмма d (AD) и длина отсекаемой высотой части основания (АЕ), то высоту параллелограмма можно найти воспользовавшись теоремой Пифагора:
|AE|^2+|ED|^2=|AD|^2, откуда определяем:
h=|ED|=?(|AD|^2-|AE|^2),
т. 2)=3 (см).
2)=3 (см).
Высотой многоугольника называют перпендикулярный одной из сторон фигуры отрезок прямой, который соединяет ее с вершиной противолежащего угла. Таких отрезков в плоской выпуклой фигуре существует несколько, и длины их не одинаковы, если хоть одна из сторон многоугольника имеет отличную от других величину. Поэтому в задачах из курса геометрии иногда требуется определить длину большей высоты, например, треугольника или параллелограмма.
Инструкция
Определите, которая из высот многоугольника должна иметь наибольшую длину. В треугольнике это отрезок, опущенный на самую короткую сторону, поэтому если в исходных условиях даны размеры всех трех сторон, то гадать не придется.
Если кроме длины самой короткой из сторон треугольника (a) в условиях приведена площадь (S) фигуры, формула расчета большей из высот (H?) будет достаточно проста. Удвойте площадь и разделите полученное значение на длину короткой стороны — это и будет искомая высота: H? = 2*S/a.
Не зная площади, но имея длины всех сторон треугольника (a, b и c), тоже можно найти самую длинную из его высот, однако математических операций будет значительно больше. Начните с вычисления вспомогательной величины — полупериметра (р). Для этого сложите длины всех сторон и разделите результат пополам: р = (a+b+c)/2.
Начните с вычисления вспомогательной величины — полупериметра (р). Для этого сложите длины всех сторон и разделите результат пополам: р = (a+b+c)/2.
Трижды умножьте полупериметр на разность между ним и каждой из сторон: р*(р-a)*(р-b)*(р-c). Из полученного значения извлеките квадратный корень?(р*(р-a)*(р-b)*(р-c)) и не удивляйтесь — вы использовали формулу Герона для нахождения площади треугольника. Для определения длины наибольшей высоты осталось заменить полученным выражением площадь в формуле из второго шага: H? = 2*?(р*(р-a)*(р-b)*(р-c))/a.
Большая высота параллелограмма (H?) вычисляется еще проще, если известна площадь этой фигуры (S) и длина ее короткой стороны (a). Разделите первое на второе и получите нужный результат: H? = S/a.
Если известна величина угла (?) в какой-либо из вершин параллелограмма, а также длины сторон (a и b), образующих этот угол, найти большую из высот тоже будет не очень несложно. Для этого величину длинной стороны умножьте на синус известного угла, а результат разделите на длину короткой стороны: H? = b*sin(?)/a.
По какой формуле вычисляется высота параллелограмма? Геометрия / Справочник :: Бингоскул
К параллелограммам относят четырёхугольники с попарно параллельными сторонами. Частными случаями таких геометрических фигур являются квадраты, ромбы и прямоугольники. В публикации рассмотрим, что такое высота параллелограмма, как её провести и вычислить через стороны, диагонали и углы. Рассмотрим признаки и свойства фигуры.
Особенности геометрической фигуры
Рассматриваемый 4-угольник обладает рядом присущих только ему свойств. У него одинаковые противоположные стороны и углы. Сумма последних, примыкающих к одной стороне, равняется 180°. Место пересечения диагоналей делит их пополам, является центром симметрии параллелограмма и точкой пересечения средних линий. Также диагональ образует два одинаковых треугольника.
Определение высоты параллелограмма
Высота параллелограмма – это перпендикуляр – линия, опущенная из одной стороны на другую, противоположную или параллельную ей.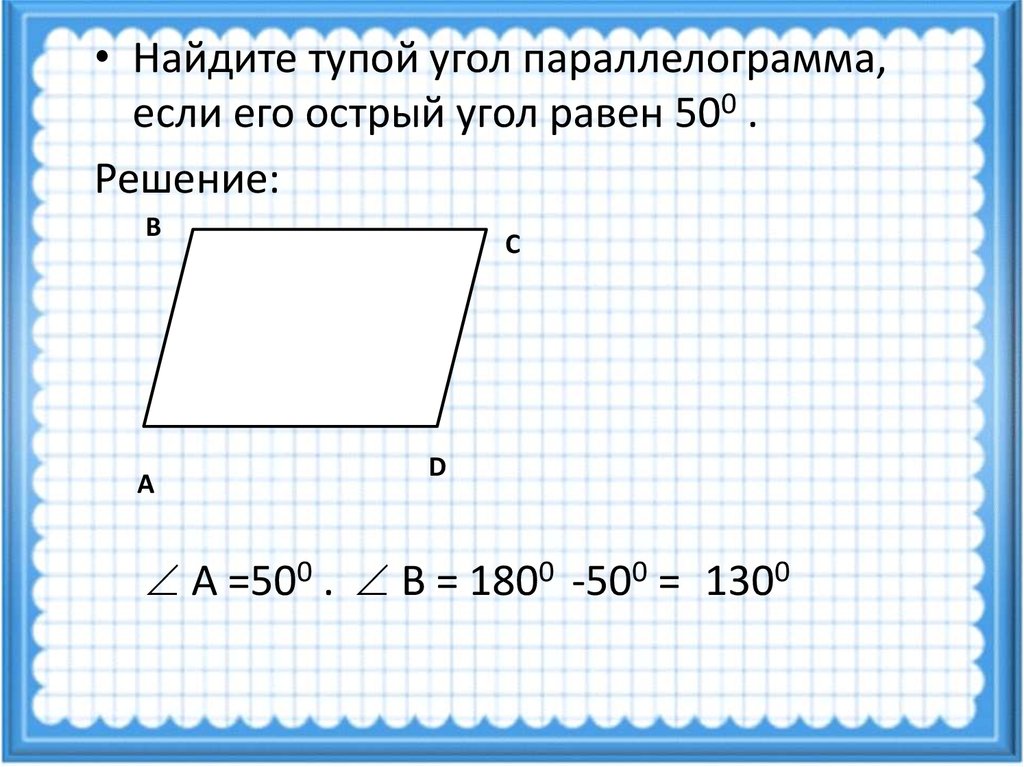 Обозначится двумя буквами, например, DE, либо одной – h.
Обозначится двумя буквами, например, DE, либо одной – h.
Перпендикуляр проводится не из каждой точки геометрической фигуры, ведь иногда находится за её пределами. Тогда высоту (BE) опускают на продолжение стороны (CE).
Как провести высоту в параллелограмме
Для построения высоты одна сторона угольника ставится на основание, перпендикулярная ей пересекает противоположную в месте, где будет проводиться перпендикуляр. Точки, принадлежащие параллелограмму, соединяются.
В итоге получается высота FG.
Также она может проводиться с одной боковой стороны на вторую.
Все формулы высоты параллелограмма
Рассмотрим способы вычислить длину перпендикуляра четырёхугольника.
Как найти высоту параллелограмма, зная его стороны
Высота – отношение площади геометрической фигуры к длине стороны, из которой опущен перпендикуляр:
h = S / a,
- S = площадь фигуры;
- a – размер основания, на который опущен перпендикуляр.
 2 }.
2 }.Существует более сложная формула, позволяющая найти одну высоту параллелограмма через другую и стороны. Обратно пропорциональное отношение одной высоты ко второй равно соотношению длин оснований:
\frac { a } { b } = \frac { 1 } { h_a} : \frac { 1 } { h_b }.
Задача
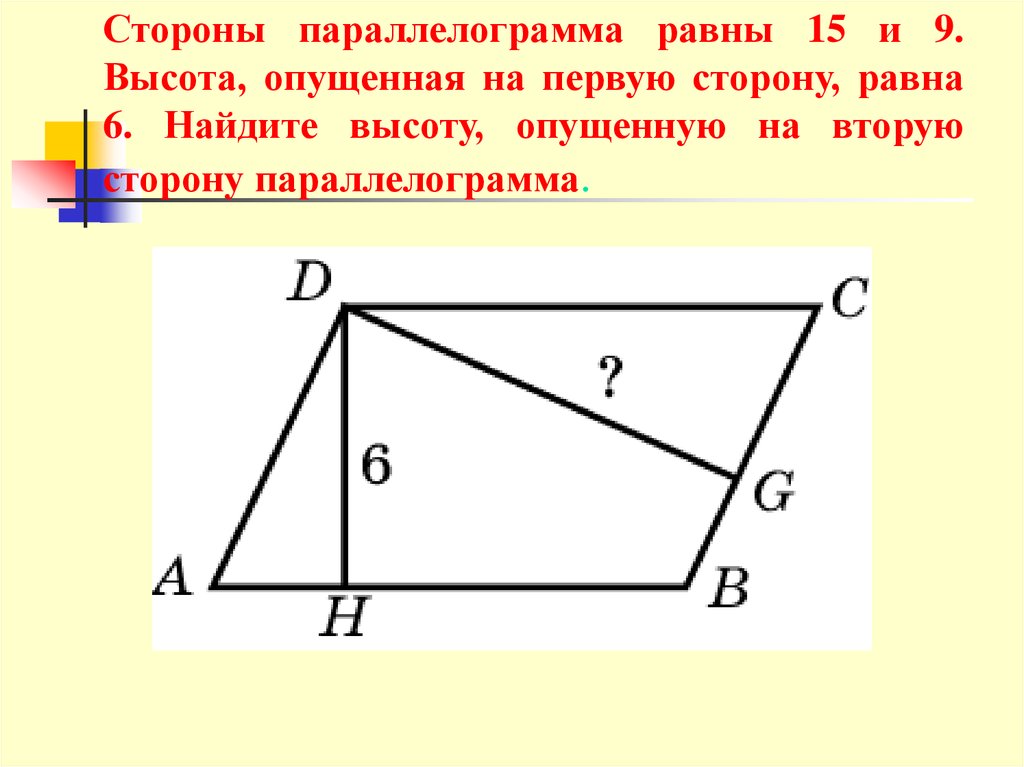
Дан параллелограмм с высотой BE, проведённой из тупого угла 4-угольника. Она делит основание на равные отрезки. Острый угол между ней и стороной равен 30°, а диагональ, проведённая между вершинами тупых углов – 10 см. Вычислить h геометрической фигуры и градусную меру ∠ABD.
Начнём из рассмотрения получившихся треугольников: ABE, BED – в соответствии с первым признаком их равенства, эти 3-угольники равны между собой: имеют равные катеты AE = ED и углы BEA = BED = 90°. Отсюда следует, что AB = BD. Получим равнобедренный треугольник BDA с равными 30° углами при основании: BAD = BDA.
Расположенный накрест угол при параллельных отрезках DA с CB тоже равняется 30°.
Присмотримся к треугольнику ABE.
 Сумма углов равна 180°. Если один угол прямой, второй – 30°, значит третий – ABE – находится по формуле: ABE = 80 – 90 – 30 = 60°. Он такой, как DBE = 60°.
Сумма углов равна 180°. Если один угол прямой, второй – 30°, значит третий – ABE – находится по формуле: ABE = 80 – 90 – 30 = 60°. Он такой, как DBE = 60°.∠ABD = ∠ABE + ∠DBE = 60 = 60 = 120°.
∠CDB = ∠ABD = 120° ведь он внутренний накрест лежащий.
Для нахождения высоты параллелограмма подойдёт формула:
EB / DB = cos (EBD), градусная мера EBD = 60°.
EB / DB = cos (60) = ½.
DB из условий задачи равняется 10 см. Подставим в формулу.
EB / 10 = ½.
EB = 10 * ½ = 5 (см).
Ответ: ∠ABD, EB = 5 (см).
Высота параллелограмма — Формула и примеры решения
Формула высоты параллелограмма полезна при вычислении высоты параллелограмма. Высота параллелограмма — это расстояние по перпендикуляру между стороной основания и противоположной ему параллельной стороной.
Параллелограмм можно определить как четырехугольник, у которого противоположные стороны параллельны и длины этих противоположных сторон также равны. Его противоположные углы также равны.

Какова высота формулы параллелограмма?
Высота параллелограмма рассчитывается по формуле Площадь равна Основанию, умноженному на Высоту, поэтому, если известна площадь параллелограмма, его высота рассчитывается путем деления площади на его Основание.
Формула высоты параллелограмма
Формула высоты параллелограмма получается из формулы площади, площадь параллелограмма можно найти, используя длину основания и высоту параллелограмма.
Периметр параллелограммаПлощадь = основание × высота
Высота = Площадь/Основание
Периметр определяется как сумма всех сторон, по которым построена замкнутая фигура. В случае параллелограмма у него 4 стороны, из которых противоположные стороны равны, поэтому периметр равен сумме всех четырех сторон.
Возьмем противоположные стороны как X и Y, следовательно,
Периметр параллелограмма = X + Y + X + Y = 2X + 2Y = 2(X + Y)
Периметр = 2(X + Y)
Пример решения для высоты параллелограмма
Пример 1: Найдите высоту параллелограмма, если его площадь 625 см 2 и длина основания 25 см .

Решение:
Высота параллелограмма может быть рассчитана по формуле высоты параллелограмма
Высота = Площадь / Основание
Высота = 625/25 5 см.
Отсюда высота параллелограмма 25 см
Пример 2: Найдите площадь параллелограмма, основание которого 20 см, а высота 15 см.
Решение:
Площадь параллелограмма = Основание × Высота
Основание и высота равны 20 см и 15 см соответственно.
Площадь = 20 × 15
Площадь = 300 см.
Пример 3. Периметр параллелограмма равен 226 см, а длина одной стороны параллелограмма 12 см. Найдите другую сторону.
Решение:
Периметр параллелограмма = 2 (x + y)
, где x — длина одной стороны, а y — длина другой стороны, так что дайте x = 12 см
226 = 2 (x — это длина другой стороны, так что дайте x = 12 см
226 = 2 (x + Y)
2(X + Y) = 226
2(12 + Y) = 226
24 + 2Y = 226
2Y = 226 – 24
2Y = 202 90 003
Д = 202/2
Y = 101 см.

Пример 4. Найдите высоту параллелограмма, если его площадь 800 см 2 и длина основания 40 см.
Решение
Высота параллелограмма может быть рассчитана по формуле высоты параллелограмма
Высота = Площадь / Основание
Высота = 800/40
Высота = 20 см.
Отсюда высота параллелограмма 20 см
Пример 5: Периметр параллелограмма равен 400 см, а длина одной стороны параллелограмма 80 см, найдите другую сторону.
Решение:
Периметр параллелограмма = 2(X + Y)
Где X — длина одной стороны, а Y — длина другой стороны, поэтому пусть X = 80 см
400 = 2(X + Y)
2(X + Y) = 400
2(80 + Y) = 400
160 + 2Y =400
2Y = 400 – 160
2Y = 240
Y = 120 см.
Часто задаваемые вопросы о высоте параллелограмма
Вопрос 1: Что такое основание и высота параллелограмма?
Ответ:
«Основание» относится к длине стороны, а «Высота» — это длина перпендикуляра между двумя параллельными линиями.

Вопрос 2: Что такое высота параллелограмма?
Ответ:
Высота параллелограмма называется расстоянием по перпендикуляру между двумя параллельными линиями параллелограмма.
Вопрос 3: Какова площадь параллелограмма?
Ответ:
Площадью параллелограмма называют пространство внутри границы параллелограмма.
Связанные ресурсы
- Параллельные линии
- Площадь прямоугольника
- Периметр прямоугольника
Площадь параллелограмма – шаги, примеры и рабочий лист
Введение
Чему равна площадь параллелограмма?
Как найти площадь параллелограмма
Площадь рабочего листа параллелограмма
Распространенные заблуждения
Практика Область параллелограмма вопросы
Площадь параллелограмма GCSE вопросы
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Еженедельные онлайн-уроки повторения математики GCSE теперь доступны
Узнать больше
Введение
Чему равна площадь параллелограмма?
Как найти площадь параллелограмма
Площадь рабочего листа параллелограмма
Распространенные заблуждения
Практика Область параллелограмма вопросы
Площадь параллелограмма GCSE вопросы
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы научимся находить площадь параллелограмма, включая вопросы о сложной площади, вопросы с недостающими длинами сторон и вопросы, связанные с преобразованием единиц измерения.

Кроме того, есть область рабочей таблицы параллелограмма, основанная на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные указания о том, что делать дальше, если вы все еще застряли.
Какова площадь параллелограмма?
Площадь параллелограмма 9{2} и т.д.)
Параллелограмм представляет собой четырехугольник (четырехгранный) с 2 парами параллельных сторон . Параллельные стороны равны , а противоположные углы равны . внутренних угла параллелограмма в сумме дают 360°.
Площадь параллелограмма вычисляется путем умножения основания параллелограмма на его перпендикулярную высоту .
Площадь параллелограмма формула:
\[\begin{выровнено} \text {Площадь} _{\text {параллелограмм}}&=\text {база} \times \text {перпендикулярная высота} \\ \text {Площадь} _{\text {параллелограмм}}&=b \times h \end{aligned}\]
Давайте посмотрим, почему это работает:
Если мы отрежем треугольник на одном конце параллелограмма и присоединим его к другому, мы получим прямоугольник.
 Формула площади прямоугольника: длина х ширина (или в данном случае основание х высота).
Формула площади прямоугольника: длина х ширина (или в данном случае основание х высота).Наш окончательный ответ должен быть в единицах, возведенных в квадрат 9{2} ) и т.д.
Какова площадь параллелограмма?
Параллелограмм
Параллелограмм — это двумерная фигура, противоположные стороны которой параллельны и равны по длине. Диагонали параллелограмма делят друг друга пополам. Мы можем классифицировать их как четырехугольники, потому что у них 4 стороны.Нам нужно определить три специальных типа параллелограммов.
Параллелограмм, у которого все стороны равны, равен ромб .
Параллелограмм, у которого все углы прямые, а диагонали равны, называется прямоугольником .
Параллелограмм, у которого все стороны равны, все углы равны 90 градусам, а диагонали равны , является квадратом .
Параллелограмм, по сути, представляет собой наклонный прямоугольник, поэтому мы можем использовать те же вычисления для нахождения площади параллелограмма, что и для вычисления площади прямоугольника, если вы используете высоту перпендикуляра, а не наклонную длину.

Напр.
Вычислите площадь параллелограмма.
Площадь = 10 x 6 = 60
Ниже мы рассмотрим параллелограммы подробнее.
Как найти площадь параллелограмма
Чтобы найти площадь параллелограмма:
- Найдите основание и высоту перпендикуляра параллелограмма .
- Запишите формулу площади параллелограмма .
- Подставить данные значения и вычислить .
- Запишите свой окончательный ответ в единицах, возведенных в квадрат .
Как найти площадь параллелограмма
Площадь рабочего листа параллелограмма
Получите бесплатную площадь рабочего листа параллелограмма из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксПлощадь рабочего листа параллелограмма
Получите бесплатную площадь рабочего листа параллелограмма из 20+ вопросов и ответов.
 Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.СКАЧАТЬ БЕСПЛАТНО
Примеры площади параллелограмма
Пример 1: нахождение площади по основанию и высоте перпендикуляра
Найдите площадь приведенного ниже параллелограмма:
- Определите основание и высоту перпендикуляра параллелограмма .
Основание = 10 м
Высота перпендикуляра = 6 м
2 Запишите формулу площади параллелограмма .
\text { Площадь }_{ \text { параллелограмм }}=\text { Основание } \times \text { Перпендикулярная высота } 9{2}
Пример 2: нахождение площади параллелограмма, требующее преобразования единиц измерения
Найдите площадь параллелограмма ниже:
Определите высоту основания и перпендикуляра параллелограмма.
У нас есть две разные единицы измерения высоты основания и перпендикуляра, поэтому нам нужно изменить единицы измерения на общую единицу измерения.

Переведем обе меры в метры.
В метре 100 см, поэтому если мы разделим основание на 100, получим 8 м
Основание = 8 м
Высота по перпендикуляру = 6 м
ПРИМЕЧАНИЕ: Важно отметить, что 6,3 м — это длина диагонали, а , а не — высота по перпендикуляру.
Запишите формулу площади параллелограмма.
\text { Площадь }_{ \text { параллелограмм }}=\text { Основание } \times \text { Перпендикулярная высота }
Подставляем данные значения и вычисляем.
\begin{выровнено} \text { Площадь }_{ \text { параллелограмм }}&=\text { Основание } \times \text { Перпендикулярная высота }\\ &=8\times6\\ &=48\ \end{выровнено} 9{2} . Сколько будет стоить нанесение логотипа?
Определите основание и перпендикулярную высоту параллелограмма .
Основание = 4 м
Высота перпендикуляра = 2 м (8\div4 параллелограмма)
Запишите формулу площади параллелограмма .

\text { Площадь }_{ \text { параллелограмм }}=\text { Основание } \times \text { Перпендикулярная высота }
Поскольку в логотипе 4 одинаковых параллелограмма, нам нужно умножить площадь на 4 . 9{2} нам нужно разделить 2,5 на 32 .
32 \дел 2,5=12,8 банок
Так как вы не можете купить 0,8 баночки, нужно округлить количество банок до 13 .
Каждая банка стоит 1,20 фунта стерлингов, поэтому 13 х 1,2 = 15,60 фунтов стерлингов
Таким образом, общая стоимость нанесения логотипа составляет 15,60 фунтов стерлингов .
Пример 4: расчет длины основания по площади
Найдите длину основания параллелограмма ниже:
Определите высоту основания и перпендикуляра параллелограмма 9{2} , который мы можем использовать для вычисления базы.
Запишите формулу площади параллелограмма .
\text { Площадь }_{ \text { параллелограмм }}=\text { Основание } \times \text { Перпендикулярная высота }
Подставьте данные значения и вычислите .

\[\begin{выровнено} \text { Площадь }_{ \text { параллелограмм }} &=\text { Основание } \times \text { Перпендикуляр Высота } \\ 242 &=\текст {база} \times 11 \\ \text { База } &=\frac{242}{11} \\ \текст { База } &=22 \конец{выровнено}\]
Запишите свой окончательный ответ.
Длина основания = 22 см
Пример 5: составная площадь
Вычислите площадь заштрихованной области ниже:
Определите высоту основания и перпендикуляра параллелограмма .
Прежде чем найти площадь заштрихованной области, нам нужно разбить фигуру на два параллелограмма. Мы можем разрезать фигуру пополам, потому что оба параллелограмма идентичны.
Каждый параллелограмм имеет высоту перпендикуляра 5 см и длину основания 8 см.
Основание = 8 см
Высота по перпендикуляру = 5 см
Примечание : Нам также нужно вычесть площадь квадрата, так как он не закрашен.
Запишите формулу площади параллелограмма .
 {2}: 9{2}
{2}: 9{2}Запишите формулу площади параллелограмма .
\text { Площадь }_{ \text { параллелограмм }}=\text { Основание } \times \text { Перпендикулярная высота }
Подставьте данные значения и вычислите .
\text {Площадь} _{\text {Параллелограмм}}=\text {Основание} \times \text {Перпендикулярная высота}
\[\begin{align} &14=2(2 х+3) \\ &14=4 х+6 \\ &4 х=8 \\ &х=2 \end{aligned}\]
Запишите свой окончательный ответ .
x=2
Распространенные заблуждения
- Использование неправильных единиц измерения для ответа
Распространенная ошибка заключается в том, что при вычислении площади забывают включить единицы измерения в квадрате.
- Забвение приведения мер к общей единице
Прежде чем использовать формулу для вычисления площади параллелограмма, мы должны убедиться, что используемые единицы измерения одинаковы.
 Если даны разные единицы измерения (например, длина = 4 м и ширина = 3 см), мы должны преобразовать их обе в сантиметры или обе в м. 9{2}
Если даны разные единицы измерения (например, длина = 4 м и ширина = 3 см), мы должны преобразовать их обе в сантиметры или обе в м. 9{2}Преобразование всех мер в см. Сначала найдите площадь параллелограмма, умножив основание на высоту. Добавьте площадь прямоугольника, которая рассчитывается путем умножения длины и ширины.
Умножьте основание на высоту перпендикуляра. Не забудьте умножить два на оба члена. Измените уравнение, чтобы вычислить x . Подставьте значение x обратно в 4x-11, чтобы вычислить базовую длину.
Площадь параллелограмма GCSE вопросы 9{2}
(1)
(б)
78,25\дел3 = 26,08 рулонов травы(1)
27\х14,5
(1)
391,50 фунтов стерлингов
(1)
3. Рассчитайте значение x на диаграмме ниже:
Показать ответ
6 \раз (3x-9)
(1)
18х-54=36
(1)
Свидетельство перестановки уравнения для решения x
(1)
х = 5
(1)
Контрольный список для обучения
Теперь вы научились:
- Вычислять и сравнивать площади параллелограммов с использованием стандартных единиц
- Вычисление площади параллелограмма и связанных с ним составных фигур
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning.



 2 }.
2 }. Сумма углов равна 180°. Если один угол прямой, второй – 30°, значит третий – ABE – находится по формуле: ABE = 80 – 90 – 30 = 60°. Он такой, как DBE = 60°.
Сумма углов равна 180°. Если один угол прямой, второй – 30°, значит третий – ABE – находится по формуле: ABE = 80 – 90 – 30 = 60°. Он такой, как DBE = 60°.

 Формула площади прямоугольника: длина х ширина (или в данном случае основание х высота).
Формула площади прямоугольника: длина х ширина (или в данном случае основание х высота).
 Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.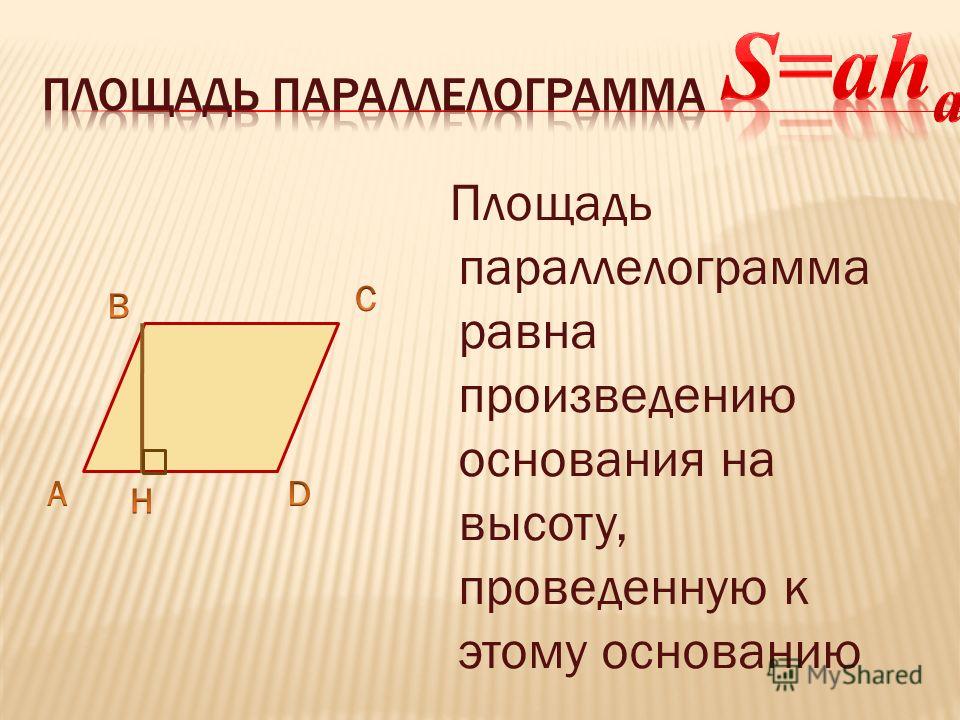


 {2}: 9{2}
{2}: 9{2} Если даны разные единицы измерения (например, длина = 4 м и ширина = 3 см), мы должны преобразовать их обе в сантиметры или обе в м. 9{2}
Если даны разные единицы измерения (например, длина = 4 м и ширина = 3 см), мы должны преобразовать их обе в сантиметры или обе в м. 9{2}
Leave A Comment