Узнаем как найти объем правильной шестиугольной призмы (формула расчета)
Определение объемов геометрических тел является одной из важных задач пространственной геометрии. В данной статье рассматривается вопрос, что такое призма с шестиугольным основанием, а также приводится формула объема правильной шестиугольной призмы.
Определение призмы
С точки зрения геометрии призмой называется фигура в пространстве, которая образована двумя одинаковыми многоугольниками, расположенными в параллельных плоскостях. А также несколькими параллелограммами, которые эти многоугольники соединяют в единую фигуру.
В трехмерном пространстве призму произвольной формы можно получить, если взять любой многоугольник и отрезок. Причем последний плоскости многоугольника принадлежать не будет. Тогда, располагая этот отрезок от каждой вершины многоугольника, можно получить параллельный перенос последнего в другую плоскость. Образованная таким способом фигура будет призмой.
Чтобы иметь наглядное представление о рассматриваемом классе фигур, приведем рисунок четырехугольной призмы.
Многие знают эту фигуру под названием параллелепипеда. Видно, что два одинаковых многоугольника призмы представляют собой квадраты. Их называют основаниями фигуры. Остальные четыре ее стороны — прямоугольники, то есть это частный случай параллелограммов.
Шестиугольная призма и ее основные характеристики
Изучением призм занимается пространственная геометрия. Важными их характеристиками являются…
Прежде чем приводить формулу, как определяется объем шестиугольной правильной призмы, необходимо четко понять, о какой фигуре пойдет речь. Шестиугольная призма имеет в основаниях шестиугольник. То есть, плоский многоугольник с шестью сторонами, углов столько же. Боковые стороны фигуры так же, как и для любой призмы, в общем случае являются параллелограммами. Сразу отметим, что шестиугольное основание может быть представлено как правильным, так и неправильным шестиугольником.
Расстояние между основаниями фигуры — это ее высота. Далее мы будем обозначать ее буквой h.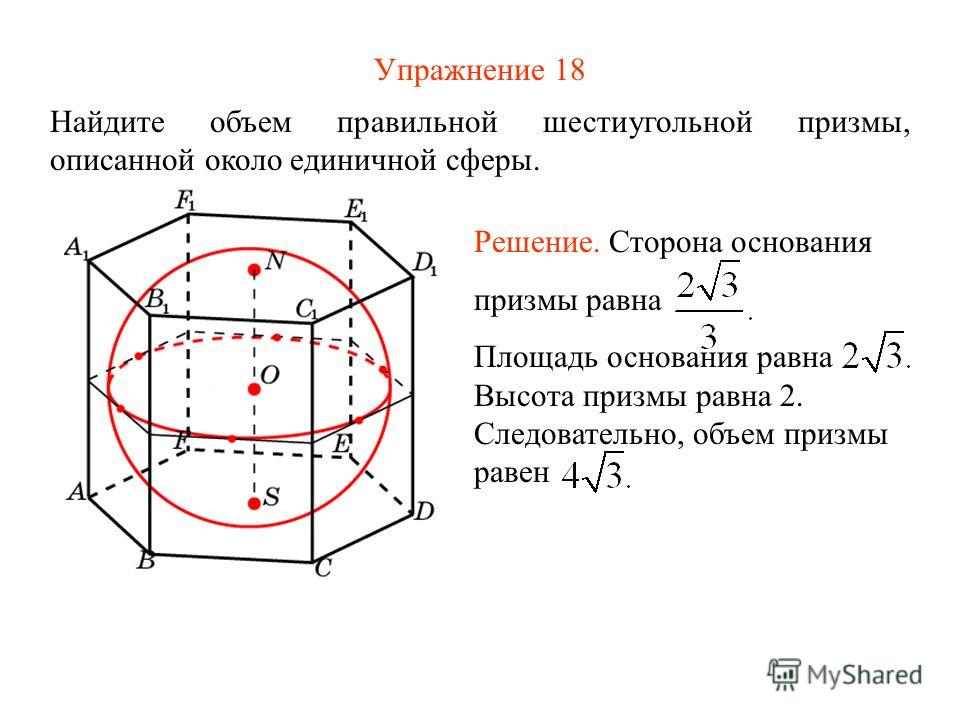 Геометрически высота h представляет собой отрезок, перпендикулярный обоим основаниям. Если этот перпендикуляр:
Геометрически высота h представляет собой отрезок, перпендикулярный обоим основаниям. Если этот перпендикуляр:
- опущен с геометрического центра одного из оснований;
- пересекает второе основание также в геометрическом центре.
Фигура в этом случае называется прямой. В любом другом случае призма будет косоугольной или наклонной. Разницу между этими видами шестиугольной призмы можно увидеть с первого взгляда.
Прямая шестиугольная призма — это фигура, имеющая в основании правильные шестиугольники. При этом она является прямой. Рассмотрим подробнее ее свойства.
Шестиугольная призма и ее основные характеристики
Изучением призм занимается пространственная геометрия. Важными их характеристиками являются…
Элементы правильной шестиугольной призмы
Чтобы понять, как вычислить объем правильной шестиугольной призмы (формула приведена ниже в статье), необходимо также разобраться, из каких элементов состоит фигура, а также какими свойствами она обладает.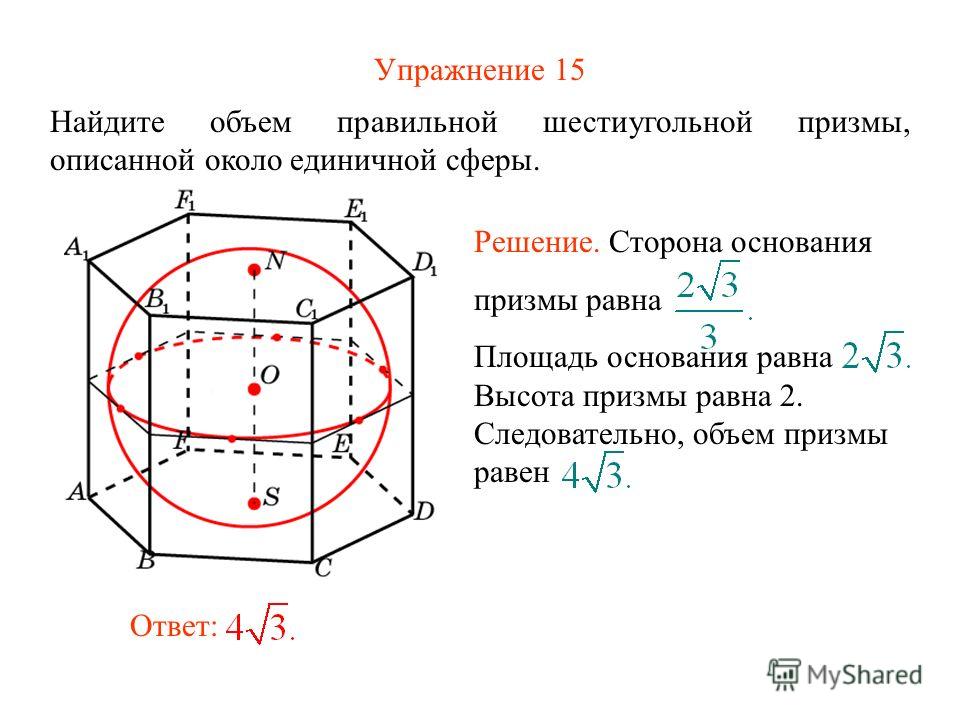 Чтобы было легче анализировать фигуру, покажем ее на рисунке.
Чтобы было легче анализировать фигуру, покажем ее на рисунке.
Главными ее элементами являются грани, ребра и вершины. Количества этих элементов подчиняется теореме Эйлера. Если обозначить Р — число ребер, В — количество вершин и Г — граней, тогда можно записать равенство:
Р = Г + В — 2.
Проверим его. Число граней рассматриваемой фигуры равно 8. Две из них — это правильные шестиугольники. Шесть граней представляет собой прямоугольники, это видно из рисунка. Число вершин составляет 12. Действительно, 6 вершин принадлежат одному основанию, и 6 другому. Согласно формуле, число ребер должно равняться 18, что является справедливым. 12 ребер лежат в основаниях и 6 образуют параллельные друг другу стороны прямоугольников.
Переходя к получению формулы объема правильной шестиугольной призмы, следует остановить свое внимание на одном важном свойстве этой фигуры: прямоугольники, образующие боковую поверхность, равны между собой и перпендикулярны обоим основаниям.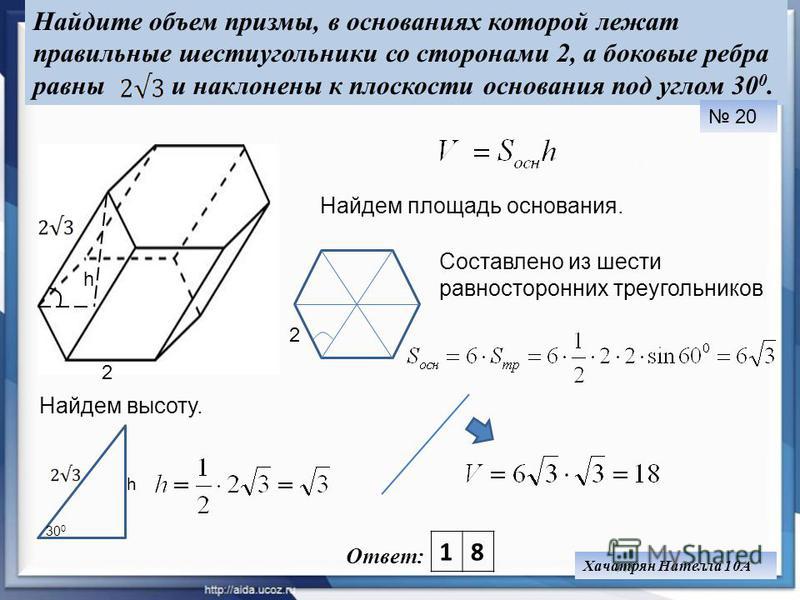 Это приводит к двум важным следствиям:
Это приводит к двум важным следствиям:
Узнаем как вычислить объем призмы четырехугольной? Формулы…
Стереометрия является важной частью общего курса геометрии, которая рассматривает характеристики…
- Высота фигуры равна длине ее бокового ребра.
- Любое сечение боковой поверхности пирамиды, выполненное с помощью секущей плоскости, которая параллельна основаниям, является правильным шестиугольником, равным этим основаниям.
Площадь шестиугольника
Можно интуитивно догадаться, что эта площадь основания фигуры появится в формуле объема правильной призмы шестиугольной. Поэтому в данном пункте статьи найдем эту площадь. Правильный шестиугольник, разделенный на 6 одинаковых треугольников, вершины которых пересекаются в его геометрическом центре, показан ниже:
Каждый из этих треугольников является равносторонним. Доказать это не очень сложно. Поскольку вся окружность имеет 360o, то углы треугольников вблизи геометрического центра шестиугольника равны 360o/6=60o.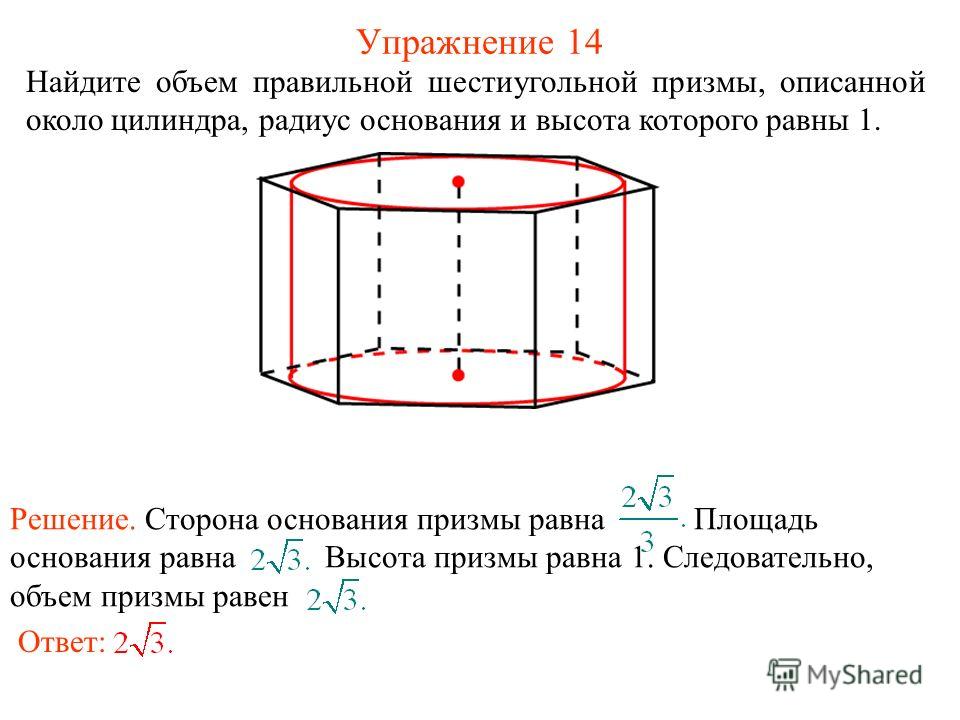 Расстояния от геометрического центра до вершин шестиугольника являются одинаковыми.
Расстояния от геометрического центра до вершин шестиугольника являются одинаковыми.
Последнее означает, что все 6 треугольников будут равнобедренными. Поскольку один из углов равнобедренных треугольников равен 60o, значит, два остальных угла тоже равны по 60o. ((180o-60o)/2) — треугольники равносторонние.
Обозначим длину стороны шестиугольника буквой a. Тогда площадь одного треугольника будет равна:
S1 = 1/2*√3/2*a*a = √3/ a2.
Формула получена на основании стандартного выражения для площади треугольника. Тогда площадь S6 для шестиугольника будет:
S6 = 6*S1 = 6*√3/ a2 = 3*√3/2*a2.
Формула определения объема правильной шестиугольной призмы
Чтобы записать формулу для объема рассматриваемой фигуры, следует учесть приведенную выше информацию. Для произвольной призмы объем пространства, ограниченный ее гранями, вычисляется так:
V = h*So.
То есть, V равен произведению площади основания So на высоту h. Поскольку мы знаем, что высота h равна длине бокового ребра b для шестиугольной правильной призмы, а площадь ее основания соответствует S6, то формула объема правильной шестиугольной призмы примет вид:
V6 = 3*√3/2*a2*b.
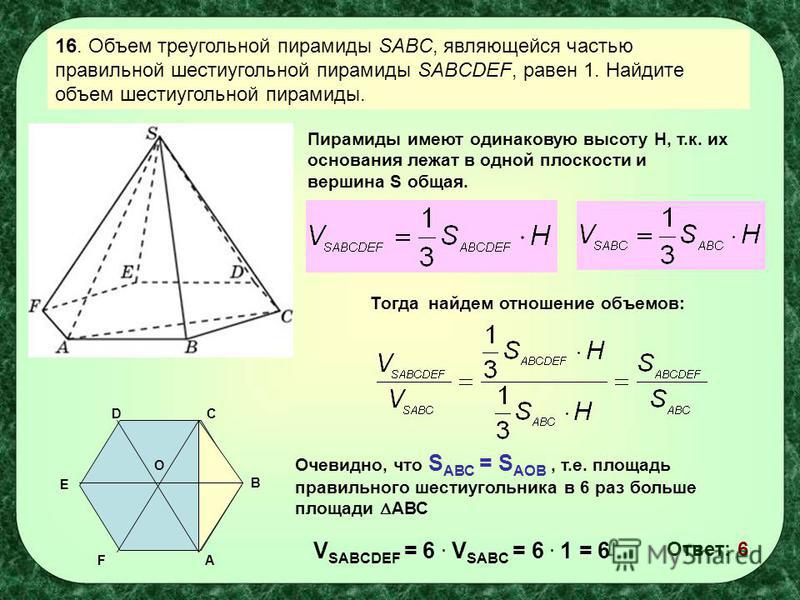
Пример решения геометрической задачи
Дана шестиугольная правильная призма. Известно, что она вписана в цилиндр радиусом 10 см. Высота призмы в два раза больше стороны ее основания. Необходимо найти объем фигуры.
Чтобы найти требуемую величину, необходимо знать длину стороны и бокового ребра. При рассмотрении правильного шестиугольника было показано, что его геометрический центр расположен в середине описанной вокруг него окружности. Радиус последней равен расстоянию от центра до любой из вершин. То есть он равен длине стороны шестиугольника. Эти рассуждения приводят к следующим результатам:
a = r = 10 см;
b = h = 2*a = 20 см.
Подставляя эти данные в формулу объема правильной шестиугольной призмы, получим ответ: V6≈5196 см3 или около 5,2 литра.
Банк ЕГЭ | Открытый банк заданий
Банк ЕГЭ Банк решенных | ЕГЭ по математике В1 ● В2 ● В3 ● В4 ● В5 ● В6 ● В7 |
Полезные советы | Лента задачек | |
| С4 {\circ}$ больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах. [посмотреть решение] {\circ}$ больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах. [посмотреть решение]В7Найдите, если $\operatorname{tg}\alpha=-4$ [посмотреть решение] |
Шестиугольная призма
– определение, формула, примеры, часто задаваемые вопросы
Шестиугольная призма представляет собой трехмерную геометрическую структуру с двумя шестиугольными основаниями, соединенными шестью прямоугольными гранями. Это многогранник с восемью гранями, двенадцатью вершинами и восемнадцатью ребрами. Он также известен как октаэдр, поскольку у него восемь граней; две из восьми граней — шестиугольники, являющиеся основаниями призмы, а остальные шесть граней — прямоугольники, являющиеся боковыми (или) боковыми гранями призмы. Верхняя и нижняя грани шестиугольной призмы имеют форму шестиугольника и конгруэнтны друг другу.
Верхняя и нижняя грани шестиугольной призмы имеют форму шестиугольника и конгруэнтны друг другу.
Существует два вида шестиугольных призм, а именно: правильная шестиугольная призма и неправильная шестиугольная призма.
- Правильная шестиугольная призма — это призма, имеющая два шестиугольных основания, все стороны которых имеют одинаковую длину. В правильной шестиугольной призме углы также измеряются одинаково.
- Неправильная шестиугольная призма представляет собой призму с двумя неправильными шестиугольными основаниями. Все стороны основания не имеют одинаковой длины, и меры каждого угла различны.
Площадь поверхности шестиугольной призмы
Общая площадь, покрываемая поверхностями шестиугольной призмы, называется площадью ее поверхности. Площадь поверхности призмы измеряется в квадратных единицах, таких как кв. м, кв. см, кв. дюйм и т. д. Шестиугольная призма имеет два типа площадей, как и другие трехмерные фигуры: площадь боковой поверхности (LSA).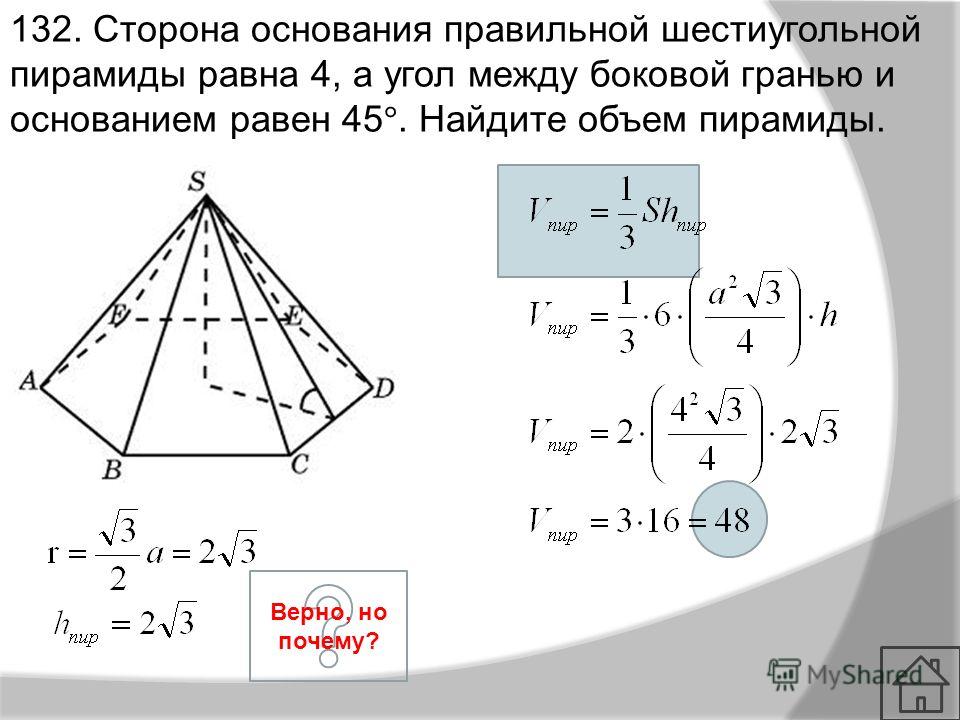 ) и общей площади поверхности (TSA).
) и общей площади поверхности (TSA).
Рассмотрим шестиугольную призму с длиной апофемы «a», длиной основания «s» и высотой «h». Мы знаем, что общая формула для вычисления площади боковой поверхности призмы представляет собой произведение ее основания на высоту. Так, площадь боковой поверхности призмы шестиугольной призмы определяется путем вычисления произведения периметра основания шестиугольной призмы на ее высоту.
Формула для определения площади боковой поверхности шестиугольной призмы равна сумме площадей шести ее прямоугольных граней. Таким образом,
Площадь боковой поверхности шестиугольной призмы (LSA) = 6sh кв. единиц.
Где «s» — длина ребра основания, а
«h» — высота призмы.
Формула для определения площади поверхности шестиугольной призмы выглядит следующим образом: + ч).
Общая площадь поверхности шестиугольной призмы (TSA) = 6s(a + h) кв. единиц.

Где «a» — длина апофемы,
«s» — длина ребра основания, а
«h» — высота призмы.
Формула для определения площади поверхности шестиугольной призмы в случае правильной шестиугольной призмы, TSA = 6sh + 3√3s 2 .
Общая площадь поверхности шестиугольной призмы (TSA) = 6sh + 3√3s 2 кв.ед.
Где «s» — длина ребра основания, а
«h» — высота призмы.
Объем шестиугольной призмы
Объем шестиугольной призмы — это количество пространства, ограниченное ею в трехмерном пространстве. Его также называют количеством вещества, которое он может удерживать, что является вместимостью шестиугольной призмы. Формула объема шестиугольной призмы эквивалентна произведению площади ее основания на высоту, которая измеряется в кубических единицах, таких как см 3 , m 3 , in 3 и т. д.
Формула для нахождения объема шестиугольной призмы дается следующим образом:
Объем шестиугольной призмы (V) = основание площадь × высота
Формула для расчета объема шестиугольной призмы, когда известны длина ребра основания и высота призмы, приведена ниже.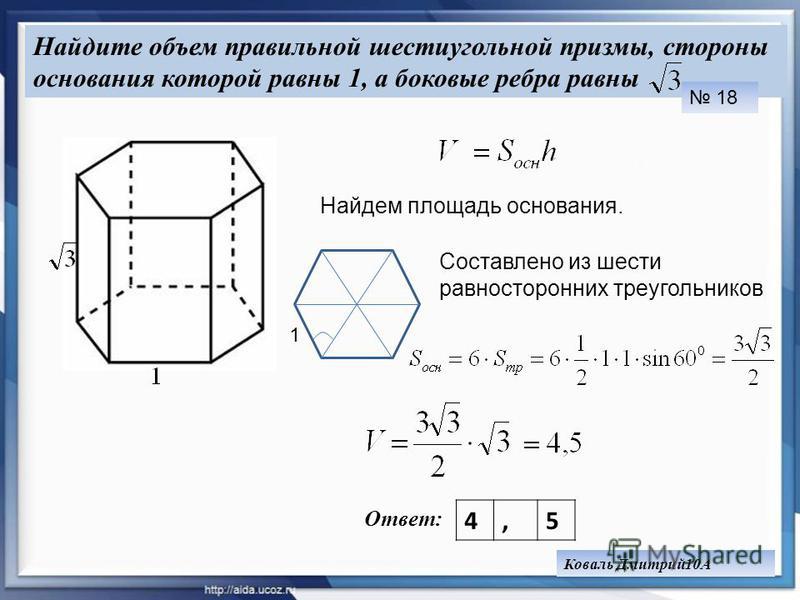
Объем шестиугольной призмы (V) = [(3√3)/2] с 2 h
Где «s» — длина ребра основания, а
«h» — высота призмы.
Формула для расчета объема шестиугольной призмы при известных длине апофемы, длине ребра основания и высоте призмы приведена ниже.
Объем шестиугольной призмы (V) = 3ash
Где «a» — длина апофемы,
«s» — длина ребра основания, а
«h» — высота призмы.
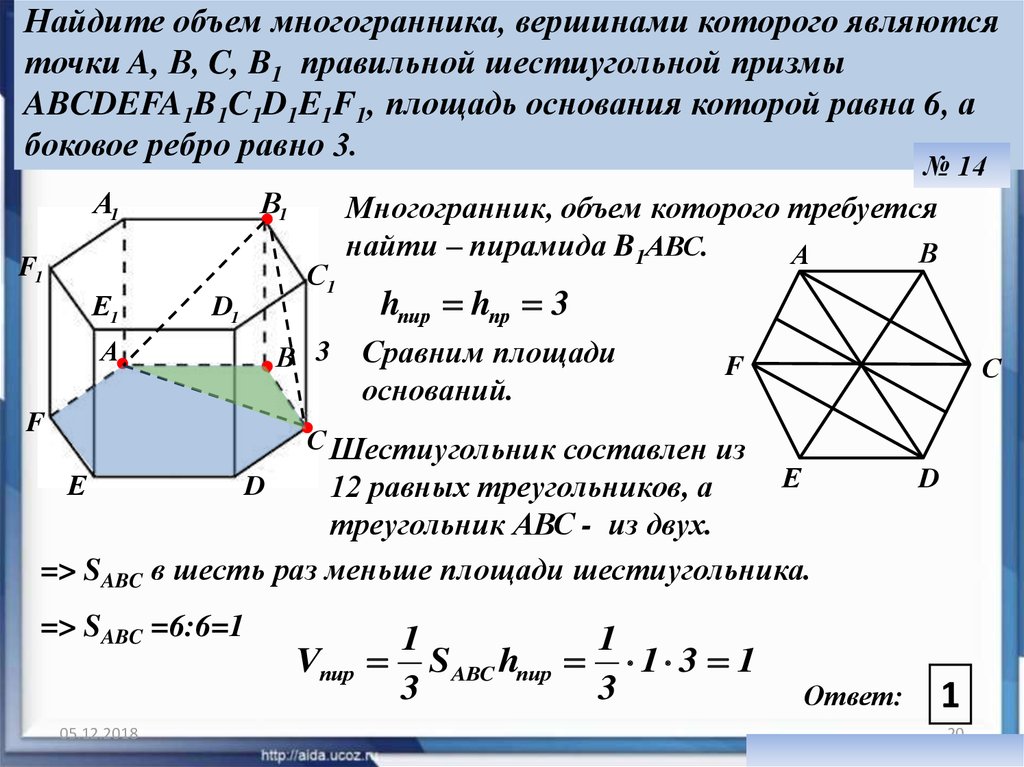
Решенный пример объема шестиугольной призмы
Пример 1: Вычислите объем шестиугольной призмы с длиной ребра основания 15 см и высотой 12 см.
Решение:
Приведенные данные,
Длина ребра основания (s) = 15 см
Объем шестиугольная призма = [(3√3)/2]s 2 h
= (3/2) × (1,732) × (15) 2 × 12
= 7 014,805 куб. см
Отсюда объем шестиугольной призмы равен 7014,805 куб.
см.
Пример 2. Определите объем шестиугольной призмы, если ее высота равна 10 дюймам, а площадь основания равна 60 кв. дюймам. 5 Базовая площадь = 60 кв. дюймов Высота призмы (h) = 10 дюймов Мы знаем, что Объем шестиугольной призмы (V) = площадь основания × высота = 60×10 = 600 куб. в Отсюда объем шестиугольной призмы равен 600 куб. дюймов Пример 3: Рассчитайте объем шестиугольной призмы, если ее высота 13 см, длина каждой стороны основания 10 см, а длина апофемы 8 см. Решение: Приведенные данные, Длина ребра основания (s) = 10 см Длина апофемы (a) = 8 см Высота призмы ( ч) = 13 см Мы знаем, что Объем шестиугольной призмы (V) = 3 зольных кубических единиц = 3 × 8 × 10 × 13 = 3120 куб. см Отсюда объем шестигранной призмы равен 3120 куб. см. Пример 4: Найдите общую площадь поверхности шестиугольной призмы, если длина каждой стороны основания 8 см, а высота 10 см. Решение: Приведенные данные, Длина базового ребра (ов) = 8 см Высота призмы (H) = 10 см Мы знаем, что Общая площадь поверхности гексагональной призмы = 6sh + 3√3s 2 = 6 × 8 × 10 + 3√3 × (8) 2 = 480 + 3√3 × 64 = 480 + 332,554 = 812,554 кв. см Таким образом, общая площадь поверхности шестиугольной призмы равна 812,554 кв. см. Пример 5: Определить площадь боковой поверхности шестиугольной призмы с длиной основания 12 см и высотой 9см. Решение: Приведенные данные, Длина основания длина ребра (s) = 12 см Высота призмы (h) = 9 см Мы знаем, что, Боковой площадь поверхности шестиугольной призмы = 6ш кв. ед. LSA = 6 × 12 × 9 LSA = 648 кв.см Отсюда объем шестиугольной призмы равен 648 кв. Вопрос 1: Каков объем шестиугольной призмы? Ответ: Объем шестиугольной призмы – это количество заключенного ею пространства в трехмерном пространстве. Его также называют количеством вещества, которое он может удерживать, что является вместимостью шестиугольной призмы. Формула объема шестиугольной призмы эквивалентна произведению площади ее основания на высоту, которая измеряется в кубических единицах, таких как см 3 , м 3 , 3 дюймов и т. д. Формула для нахождения объема прямоугольной призмы выглядит следующим образом: Объем шестиугольной призмы (V) = площадь основания × высота Вопрос 2: Как определить объем шестиугольной призмы? Ответ: Чтобы определить объем шестиугольной призмы, выполните следующие действия: Шаг 1: Рассчитайте площадь основания призмы по соответствующей формуле. Вопрос 3: Как определить объем шестиугольной призмы, зная площадь основания и высоту? Ответ: Мы знаем, что общая формула для вычисления объема любой призмы — это произведение площади ее основания на высоту. Шестиугольная призма – это призма, в основании которой находится шестиугольник. Таким образом, мы можем использовать ту же формулу для определения объема шестиугольной призмы. Поскольку даны и площадь основания, и высота шестиугольной призмы, формула для определения объема шестиугольной призмы дается следующим образом: Объем шестиугольной призмы = площадь основания × высота. Вопрос 4: Что произойдет с объемом шестиугольной призмы, если ее высоту уменьшить вдвое? Ответ: Мы знаем, что формула для вычисления объема шестиугольной призмы V = 3abh. Вопрос 5: Что означает площадь поверхности шестиугольной призмы? Ответ: Общая площадь, покрытая поверхностями шестиугольной призмы, называется площадью ее поверхности. Площадь поверхности призмы измеряется в квадратных единицах, таких как кв. м, кв. см, кв. дюйм и т. д. Формула для определения площади поверхности шестиугольной призмы дается следующим образом: Общая площадь поверхности , TSA = 2 (площадь основания шестиугольника) + 6 (площадь граней прямоугольника) = 6s (a + h), где «a» — длина апофемы призмы, «s» — длина ребра основания, а «h» — высота призмы. Формула для определения площади поверхности шестиугольной призмы в случае правильной шестиугольной призмы, TSA = 6sh + 3√3s 2 . Вопрос 6: Как определить площадь боковой поверхности шестиугольной призмы? Ответ: Чтобы определить площадь боковой поверхности шестиугольной призмы, выполните шаги, описанные ниже: Призма представляет собой трехмерную объемную фигуру с плоскими гранями и двумя одинаковыми основаниями. Например, треугольная призма имеет в основании два треугольника. Прямоугольная призма имеет в основании два прямоугольника. Исходя из этого, можете ли вы догадаться, что такое шестиугольная призма ? Шестиугольная призма определяется как призма с шестиугольным основанием и вершиной. Шестиугольная призма имеет 8 граней, 18 ребер и 12 вершин. Из 8 граней 6 параллелограммов и 2 шестиугольника, поэтому призма называется шестиугольной. Эти шестиугольники находятся в основании и наверху, поскольку противоположные грани призмы одинаковы. Альтернативный тег: твердая шестиугольная призма, отмеченная основанием, гранью и вершиной Шестиугольные призмы могут быть не так распространены, как другие призмы, но их все же можно найти вокруг нас. Мы можем сформировать шестиугольную призму, используя ее сетку, как показано ниже. Сеть 3D-объекта показывает грани этого объекта, когда он открыт плоско. Сворачивая сетку, мы получаем 3D-объект. Объем шестиугольной призмы относится к пространству, которое она занимает. Объем любой призмы можно рассчитать с помощью следующего уравнения: Объем = площадь основания × высота призмы Площадь основания — это площадь поверхности основания многоугольника. В данном случае это шестиугольник. Измеряется в квадратных единицах (например, в квадратных дюймах или квадратных футах), поскольку описывает площадь поверхности. Высота столбца, соединяющего два основания призмы. Он измеряется в отдельных единицах (например, в дюймах или футах), поскольку описывает длину колонны. При умножении базовой площади на высоту результирующее значение выражается в кубических единицах, таких как кубические дюймы, кубические ярды, кубические футы или кубические метры. Эти единицы измеряют объем трехмерной фигуры. Шестиугольная грань шестиугольной призмы может быть правильным или неправильным шестиугольником. Если это правильный шестиугольник, то все углы шестиугольника равны. Если это неправильный шестиугольник, то углы шестиугольника различны. Пример 1. Сколько всего граней имеет шестиугольная призма ? Альтернативный тег: Шестиугольная призма Ответ. Шестиугольная призма имеет всего 8 граней — два основания и 6 сторон. Пример 2. Какие многоугольники составляют стороны шестиугольной призмы ? Ответ. Стороны шестиугольной призмы представляют собой параллелограммы или прямоугольники. Пример 3 . Основание шестиугольной призмы имеет площадь поверхности 475 дюймов². Высота 8 дюймов. Рассчитайте объем. Ответ. Объем = площадь основания × высота Площадь основания = 475 дюймов² Высота = 8 дюймов Объем = 475 × 8 = 3800 дюймов³ м составляет 150 дюймов³. Площадь поверхности основания составляет 10 дюймов². Какова высота? Ответ. Объем = площадь основания x высота Объем = 150 дюймов³ Площадь поверхности = 10 дюймов² 150 = 10 × высота Высота = 150/10 = 15 Итак, высота равна 15 дюймам. 1 24 ребра и 36 вершин 18 ребер и 12 вершин 12 ребер и 18 вершин 24 ребра и 30 вершин Правильный ответ: 18 ребер и 12 вершин айс 2 12,5 дюймов³ 5000 дюймов³ 4625 дюймов³ 3341 дюймов² Правильный ответ: 5000 дюймов³ 3 2500 см 25 см² 0,65 м² 250 см Правильный ответ: 250 см Почему шестиугольную призму называют многогранником? Многогранник — это трехмерная фигура, у которой все грани — многоугольники.
 см.
см. Часто задаваемые вопросы о шестиугольной призме
Шаг 2: Запишите значение высоты данной шестиугольной призмы.
Шаг 3: Подставьте значения заданных размеров в формулу V = [(3√3)/2]s 2 h
Шаг 4: Наконец, запишите окончательное значение в соответствующих кубических единицах.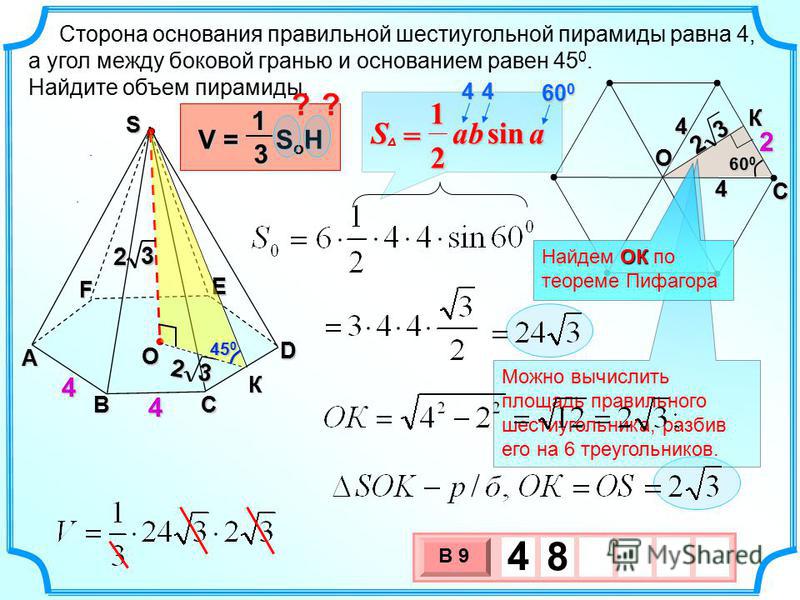 Где «а» — длина апофемы, «s» — длина ребра основания, а «h» — высота призмы. Итак, объем призмы прямо пропорционален ее высоте. Итак, если высоту уменьшить наполовину, новая высота станет равной (h/2). Итак, объем новой шестиугольной призмы будет 3ab (h/2) = (1/2) (3abh) = V/2. Таким образом, мы можем сделать вывод, что объем также будет уменьшен вдвое.
Где «а» — длина апофемы, «s» — длина ребра основания, а «h» — высота призмы. Итак, объем призмы прямо пропорционален ее высоте. Итак, если высоту уменьшить наполовину, новая высота станет равной (h/2). Итак, объем новой шестиугольной призмы будет 3ab (h/2) = (1/2) (3abh) = V/2. Таким образом, мы можем сделать вывод, что объем также будет уменьшен вдвое.
Что такое шестиугольная призма? Определение, примеры решений, факты
Что такое призма?
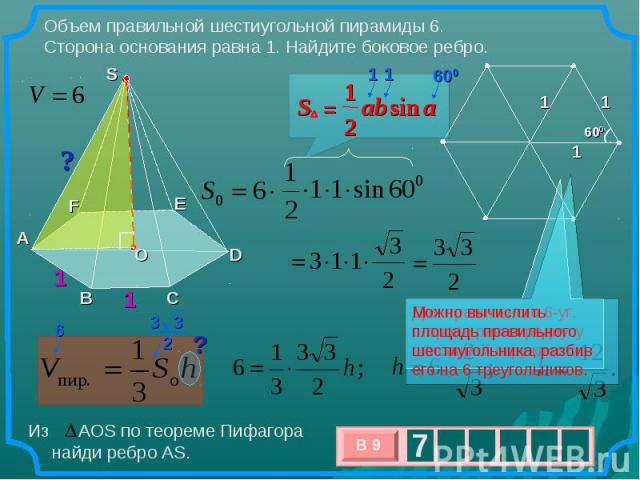 Два основания призмы представляют собой многоугольники, такие как треугольник, квадрат, прямоугольник или гексаграмма. Призму обычно называют в честь многоугольника, образующего ее основание.
Два основания призмы представляют собой многоугольники, такие как треугольник, квадрат, прямоугольник или гексаграмма. Призму обычно называют в честь многоугольника, образующего ее основание. Что такое шестиугольная призма?
Реальные примеры шестиугольных призм
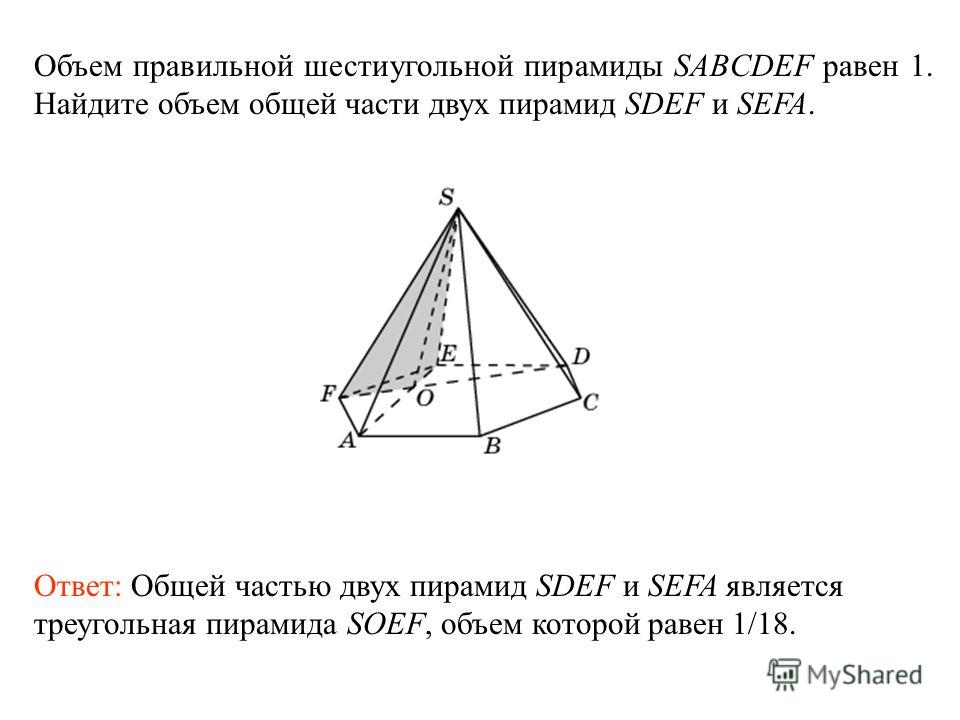 Некоторые из его примеров: коробки, орехи, карандаши, гири, здания, вазы и т. д.
Некоторые из его примеров: коробки, орехи, карандаши, гири, здания, вазы и т. д. Сеть шестиугольной призмы
Как рассчитать объем шестиугольной призмы?
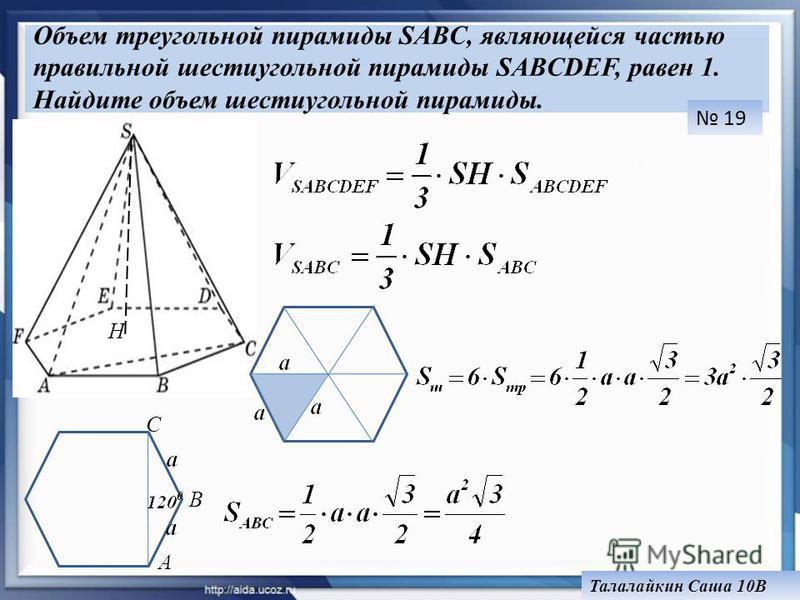
Забавный факт
Решенные примеры
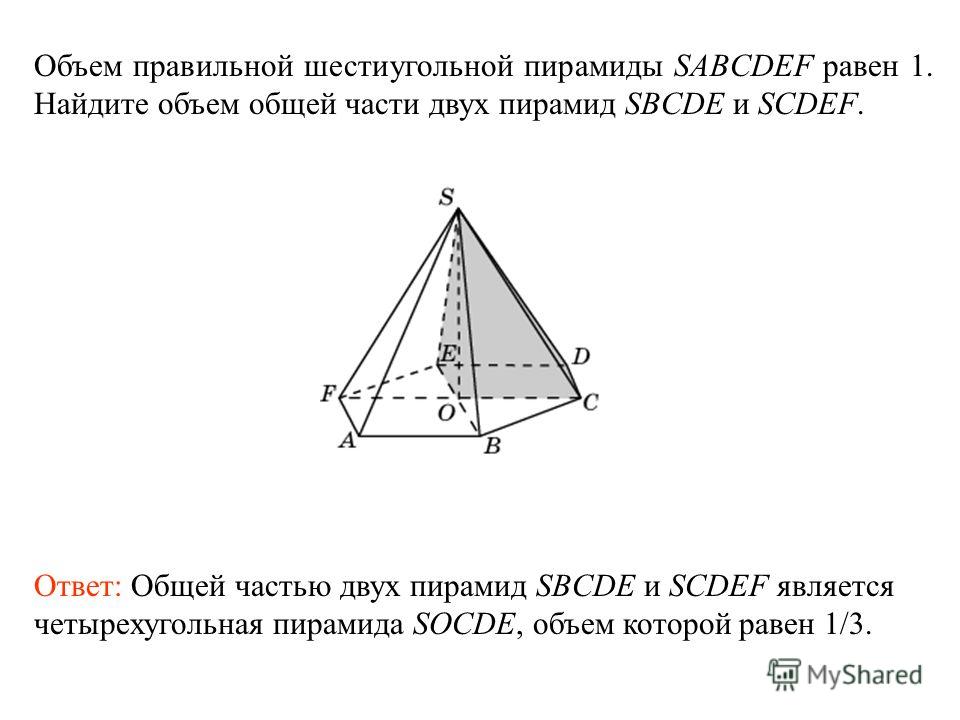
Практические задачи
Сколько ребер и вершин у шестиугольной призмы?
Шестиугольная призма имеет 18 ребер и 12 вершин.
Основание шестиугольной призмы имеет площадь поверхности 250 дюймов². Высота 20 дюймов. Рассчитайте объем.
Площадь основания = 250 дюйм²
Высота = 20 дюймов
Объем = площадь основания x высота
= 250 × 20
Объем = 5000 дюймов³ Объем шестиугольной призмы составляет 250000 см³. Площадь поверхности основания составляет 1000 см². Какова высота?
Объем = 250000 см³
Площадь основания = 100 0 см
Объем = площадь основания × высота
250000 = 1000 × высота
Высота = 250000/1000
= 250 см Часто задаваемые вопросы




 wolframalpha.com/. На этом сайте вы можете: решать не слишком сложные уравнения и системы уравнений (неравенств), брать производные от функций, стоить графики этих функций и так далее. Во время подготовки к ЕГЭ, этот сайт можно использовать для: проверки отсутствия арифметических ошибок, вычисления громоздких выражений, решения промежуточных систем уравнений, и еще для огромного количества других полезных вещей. Более подробную информацию о том, как пользоваться сайтом wolframalpha.com, можно получить в соответствующей статье.
wolframalpha.com/. На этом сайте вы можете: решать не слишком сложные уравнения и системы уравнений (неравенств), брать производные от функций, стоить графики этих функций и так далее. Во время подготовки к ЕГЭ, этот сайт можно использовать для: проверки отсутствия арифметических ошибок, вычисления громоздких выражений, решения промежуточных систем уравнений, и еще для огромного количества других полезных вещей. Более подробную информацию о том, как пользоваться сайтом wolframalpha.com, можно получить в соответствующей статье. Мы рекомендуем просматривать этот форум именно через браузер Firefox, потому что отображение в нем MathML-формул самое лучшее.
Мы рекомендуем просматривать этот форум именно через браузер Firefox, потому что отображение в нем MathML-формул самое лучшее.
 см.
см.
Leave A Comment