ТЕСТ по теме «Параллельность прямых и плоскостей»
ГД 114 выполнить тест! Прислать на почту [email protected]u
Вариант 1 – фамилия начинаются с А-К, вариант 2 – Л-Я
Практическое занятие: Параллельность прямых и плоскостей
Цели занятия:
— проверить степень усвоения обучающимися изученного материала и умения применять его к решению задач;
— способствовать развитию логического мышления и пространственного воображения обучающихся
Вариант 1.
1. Раздел геометрии, в котором изучаются свойства фигур в пространстве,
называется…
а). планиметрией в). видеометрией
б). стереометрией г). сферометрией
2. Какие из фигур являются основными в пространстве
а). прямая в). отрезок
б). точка г). плоскость
3. Какое наименьшее число точек определяет прямую в пространстве?
а). одна точка в). три точки
одна точка в). три точки
б). две точки г). четыре точки
4. Выберите верные утверждения.
а). Если прямая АВ лежит в плоскости и точка С принадлежит прямой АВ, то прямая АС лежит в плоскости .
б). Если прямая АВ лежит в плоскости , а прямая CD пересекает АВ, то CD лежит в плоскости .
в). Если прямые АВ и CD пересекаются в точке О, то точка D лежит в плоскости АОС.
г). Если прямые АВ и СD не пересекаются, то прямая АС лежит в плоскости АВС.
5. Через конец М отрезка MN проведена плоскость . Через точку K— середину отрезка MN, и точку N проведены параллельные прямые, пересекающие плоскость в точках K1 и N1 соответственно. Найдите NN1, если KK1 меньше NN1 на 8,4 см.
6. Отрезок АВ разделили точкой С так, что АС : ВС=3:4. Через точку В проведена плоскость . Через точки С и А проведены параллельные прямые, пересекающие плоскость соответственно в точках С1 и А1. Найдите ВА1, если ВС1=16 см.
7. Выберите верные утверждения.
а). прямая лежит в плоскости
б). прямая и плоскость имеют одну общую точку
в). прямая пересекает плоскость в двух точках
г). прямая и плоскость не имеют ни одной общей точки
8. Плоскость пересекает треугольник АВС по прямой KD. KD АС. Найдите BD, если АС : KD=7:3, ВС=35 см .
9. Два треугольника АВС и ADC имеют общую сторону АС, точка D не лежит в плоскости АВС, MN— средняя линия треугольника ADC.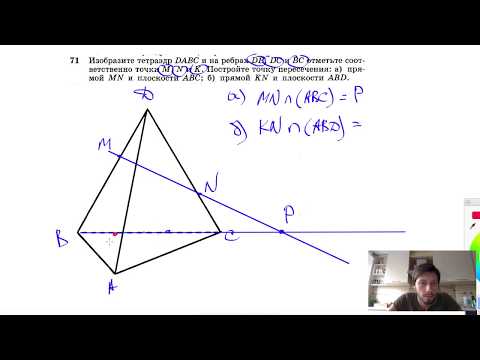 Отметьте скрещивающиеся прямые.
Отметьте скрещивающиеся прямые.
а). АС и MN г). АВ и DN
б). MD и AC д). MN и ВС
в). АМ и BC
10. Параллельные плоскости и пересекают стороны угла АОВ в точках А1, В1 и А2, В2
соответственно. Найдите ОВ1, если ОВ2 =15 см и ОА1:А1А2=2:3.
Вариант 2.
1. Стереометрия — это раздел геометрии, в котором изучаются свойства…
а). прямых в пространстве в). фигур на плоскости
б). фигур в пространстве г). плоскостей в пространстве
2. Какие из фигур не являются основными в пространстве
а). треугольник в). плоскость
б). отрезок г). куб
3. Какое наименьшее число точек определяет плоскость в пространстве?
Какое наименьшее число точек определяет плоскость в пространстве?
а). одна точка в). три точки
б). две точки г). четыре точки
4. Выберите верные утверждения.
а). Если прямая KM лежит в плоскости , а прямая NL пересекает KM, то NL лежит в плоскости .
б). Если прямая KL лежит в плоскости и точка М принадлежит KL, то прямая LM лежит в плоскости .
в). Если прямые KL и MN не пересекаются, то прямая KM лежит в плоскости KLM.
г). Если прямые KL и MN пересекаются в точке O, то точка N лежит в плоскости KOM.
5. Через конец A отрезка AB проведена плоскость . Через точку C— середину отрезка AB, и точку B проведены параллельные прямые, пересекающие плоскость в точках C1 и B1 соответственно. Найдите ВВ1, если ВВ1 больше СС1 на 7,8 см.
Найдите ВВ1, если ВВ1 больше СС1 на 7,8 см.
6. Точка S делит отрезок РQ так, что PS : SQ=5:2. Точка P лежит в плоскости . Через точки S и Q проведены параллельные прямые, пересекающие плоскость соответственно в точках S1 и Q1. Найдите PQ1, если PS1=15 см.
7. Продолжите, чтобы получилось верное высказывание.
Прямая и плоскость называются параллельными, если…
а). они имеют общую точку
б). прямая лежит в плоскости
в). они не имеют общих точек
г). они имеют две общие точки
8. Плоскость пересекает стороны треугольника MNK в точках P и Q, причём PQ параллельна MK. Найдите PN, если PQ : MK=5:9, MN=27см .
9. Два треугольника ABC и ADC имеют общую сторону AC, точка B не лежит в плоскости ADC, EF— средняя линия треугольника ABC. Отметьте скрещивающиеся прямые.
а). АС и BF г). EF и AC
б). BE и DC д). EF и AD
в). AD и FC
10. Параллельные плоскости и пересекают стороны угла POQ в точках P1, P2 и Q1, Q2
соответственно. Найдите QQ1, если QQ2 =21 см и OP1 : P1P2=3:4.
Ответить на вопросы:
Что изучает стереометрия?
Какие основные (простейшие) фигуры в пространстве?
Сформулировать аксиомы стереометрии.
Какое взаимное расположение прямых, прямой и плоскости в пространстве?
Основные признаки параллельности прямых и плоскостей в пространстве.
Работы по начертательной геометрии 1 курс, скачивание примеров чертежей с решениями задач.
Работы по начертательной геометрии 1 курс, скачивание примеров чертежей с решениями задач.Цена Заказать Примеры Форум
Готовые варианты задач по начертательной геометрии 1 курса. Для бесплатного скачивания задачи в нормальном разрешении, нажмите на пример чертежа.
На форуме предлагаются бесплатные консультации по основам начертательной геометрии, методам решений, основным построениям, типовым задачам и контрольным работам.
Пересечение прямой и плоскости
На эпюре плоскость определена треугольником. В основе метода решения задачи лежит использование плоскости посредника.
В примере эпюра, плоскость посредник Альфа проведена через прямую l перпендикулярно горизонтальной плоскости проекций П1.
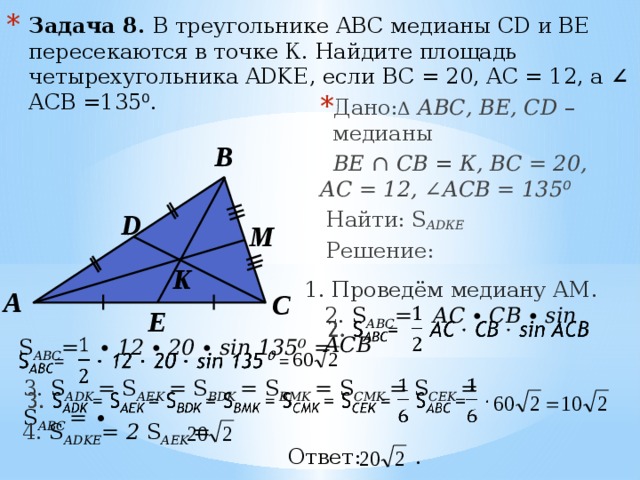
Прямая l пересекающая плоскость треугольника лежит в плоскости Альфа. Прямая 12 также принадлежит Альфа, т.к. это
пересечение Альфа и плоскости треугольника. Следовательно, l и 12 пересекаются и точка N
В качестве плоскости посредника, можно выбрать вариант фронтально проецирующей плоскости. Для понимания метода решения задачи поверните эпюр ↻.
 Аналогично,
вертикальное направление V показывает на горизонтальной проекции то, что прямая l выше точки плоскости треугольника.
Видимость прямой l меняется в точке N пересечения плоскости.
Аналогично,
вертикальное направление V показывает на горизонтальной проекции то, что прямая l выше точки плоскости треугольника.
Видимость прямой l меняется в точке N пересечения плоскости.Пересечение треугольников
Аналогично примеру задачи пересечения прямой и плоскости, через  Посредник Альфа пересекает плоскость АВС по прямой 12. Точки 1 и 2 соответствуют пересечению отрезков
Посредник Альфа пересекает плоскость АВС по прямой 12. Точки 1 и 2 соответствуют пересечению отрезков
Для построения второй точки пересечения, построена плоскость 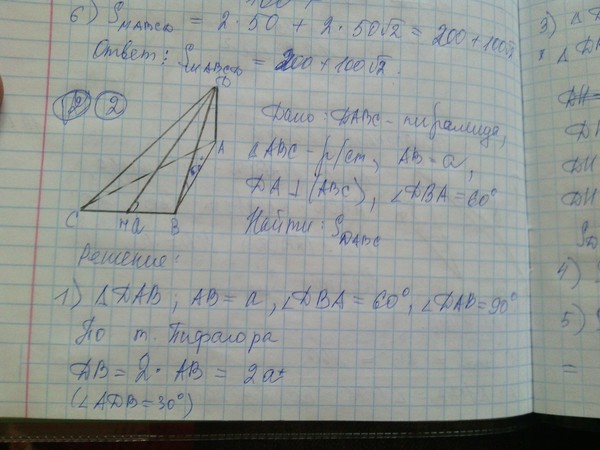
Точки N и M одновременно принадлежат обеим треугольникам и, следовательно, определяют прямую пересечения плоскостей.
Решение задачи видимости поверхностей решается методом конкурирующих точек. Вертикальное направление луча V показывает на горизонтальной проекции перекрытие отрезком BC отрезка DK. Следовательно, в окрестности этого луча, плоскость треугольника АВС перекрывает DEK до их пересечения. Аналогично, фронтально проецирующий луч F показывает, что KE находится перед BC, и на фронтальной проекции правая часть треугольника DEK перекрывает плоскость АВС.
Эту задачу можно решить выполнив преобразование способом замены плоскостей проекций. Но это преобразование целесообразно в задаче пересечения пирамиды плоскостью и связанных с множеством построений точек пересечения прямых с плоскостью.
Сечение и развёртка пирамиды
SABCПостроение сечения пирамиды выполняется по условию принадлежности точки прямой. На фронтальной плоскости проекций,
пересечения рёбер пирамиды и секущей плоскости Альфа очевидно представлены пересечениями проекций 12,
22 и 32. Горизонтальная проекция точек сечения определяется по проекционным связям.
На фронтальной плоскости проекций,
пересечения рёбер пирамиды и секущей плоскости Альфа очевидно представлены пересечениями проекций 12,
22 и 32. Горизонтальная проекция точек сечения определяется по проекционным связям.
Построение развёртки пирамиды SABC выполняется методом триангуляции. Определение натуральных величин боковых рёбер выполняется методом плоскопараллельного перемещения этих рёбер до положения фронталей. Натуральная величина сечения определена методом вращения вокруг горизонтального следа секущей плоскости до совмещения с горизонтальной плоскостью проекций.
Пересечение поверхностей Конуса и Цилиндра
Основа метода построения пересечения поверхностей конуса и цилиндра заключается в использовании метода плоскостей
посредников. Фронтальная проекция пересечения соответствует проекции боковой поверхности цилиндра, которая на примере
чертежа занимает фронтально проецирующее положение и содержит линию пересечения с любой другой поверхностью.
Серия горизонтальных плоскостей пересекает конус по горизонтальным окружностям и цилиндр по парам фронтально проецирующих образующих. Пересечение горизонтальных проекций этих окружностей и образующих определяет точки пересечения поверхностей.
Решение вопроса видимости линии пересечения на горизонтальной плоскости проекций, начинается с верхней точки, которая видима, и далее, видимость меняется при переходе линии пересечения через очерковую образующую цилиндра.
Построение сопряжений
Построение прямых линий сопряжения окружностей, определение периметра сечения, определение площади фигуры сечения.
Примеры решения задач 1 курса по начертательной геометрии.
Примеры по начертательной геометрии

Эван Чен • 404 Not Found
Запрошенный URL-адрес не найден. Извини за это.
00440400 00440000 00440400 00444040 00400000 04040000 04400004 04400444 04400404 00400000 04004440 04404444 04440400 00400000 04000440 04404444 04440404 04404440 04400400 00400004 00004404 00004040 00004404 00004040 00440400 00444000 00400000 00440440 00440004 00400000 00440444 00440440 00400000 00440440 00440404 00400000 00440040 00440000 00400000 00440440 00440004 00400000 00440040 00440000 00400000 00440440 00440444 00400000 00440440 00440404 00400000 00440440 04400440 00400000 00440440 04400400 00400000 00440440 00440404 00400000 00440444 00440400 00400000 00440444 00440040 00400000 00440444 00444004 00400000 00440040 00440000 00400000 00440444 00440000 00400000 00440444 00440040 00400000 00440440 04400440 00400000 00440440 00440040 00400000 00440440 04400044 00400000 00440440 00440404 00400000 00440440 04400400 00400000 00440044 04400004 00400000 00440000 04400400 00400000 00440000 04400004 00400000 00440000 04400400 00400000 00440000 04400004 00400000 00440404 00440444 00400000 00440044 00440004 00400000 00440404 00440040 00400000 00440440 00444000 00400000 00440440 00440004 00400000 00440404 00444000 00400000 00440440 00440400 00400000 00440440 00444000 00400000 00440440 00440040 00400000 00440440 00444004 00400000 00440400 00440040 00400000 00440404 00440404 00400000 00440404 00440404 00400000 00440044 00440004 00400000 00440404 00440004 00400000 00440440 00440444 00400000 00440400 04400400 00400000 00440440 04400004 00400000 00440400 00440004 00400000 00440444 00444000 00400000 00440400 04400440 00400000 00440404 00440440 00400000 00440044 00440000 00400000 00440440 00440444 00400000 00440404 00440440 00400000 00440400 00444000 00400000 00440400 04400004 00400000 00440444 00440000 00400000 00440404 00444004 00400000 00440404 00440444 00400000 00440044 00440404 00400000 00440440 04400404 00400000 00440440 00440040 00400000 00440400 00440444 00400000 00440404 00440404 00400000 00440440 00440444 00400000 00440400 04400004 00400000 00440400 00440404 00400000 00440400 00440440 00400000 00440400 00440044 00400000 00440404 00440004 00400000 00440444 00444004 00400000 00440404 00440004 00400000 00440440 00440444 00400000 00440440 00440004 00400000 00440404 00444000 00400000 00440400 04400400 00400000 00440440 00440444 00400000 00440440 00440004 00400000 00440404 00440444 00400000 00440044 00440404 00400000 00440444 04400004 00400000 00440404 00444004 00400000 00440044 00440044 00400000 00440400 04400004 00400000 00440444 00440000 00400000 00440404 00444004 00400000 00440440 04400400 00400000 00440404 00440440 00400000 00440440 04400040 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440440 04400044 00400000 00440444 00440404 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440400 00440440 00400000 00440444 00440404 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440404 00440440 00400000 00440444 00440044 00400000 00440440 00440040 00400000 00440400 00440444 00400000 00440440 04400044 00400000 00440444 00440444 00400000 00440440 00440044 00400000 00440044 00440040 00400000 00440404 00440404 00400000 00440440 00440444 00400000 00440440 00440400 00400000 00440044 00440040 00400000 00440440 04400044 00400000 00440044 00440000 00400000 00440440 00440004 00400000 00440400 00440044 00400000 00440400 00440040 00400000 00440440 04400400 00400000 00440440 00440040 00400000 00440044 00440040 00400000 00440400 04400404 00400000 00440444 00440000 00400000 00440400 00444004 00400000 00440400 00440044 00400000 00440404 00440040 00400000 00440400 00444004 00400000 00440400 04400004 00400000 00440400 00440044 00400000 00440400 00440040 00400000 00440440 00444000 00400000 00440440 00440040 00400000 00440440 04400400 00400000 00440404 00440004 00400000 00440440 00440444 00400000 00440400 04400004 00400000 00440400 00440404 00400000 00440444 00440044 00400000 00440440 04400040 00400000 00440400 04400044 00400000 00440440 00444004 00400000 00440400 00440040 00400000 00440404 00440004 00400000 00440440 00440044 00400000 00440440 04400400 00400000 00440044 00444004 00400000 00440044 00440040 00400000 00440404 04400004 00400000 00440404 00440044 00400000 00440400 00440040 00400000 00440044 00440000 00400000 00440440 00440004 00400000 00440400 00440444 00400000 00440400 00440440 00400000 00440044 00440000 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440440 04400044 00400000 00440440 04400400 00400000 00440400 00444004 00400000 00440400 00440044 00400000 00440404 00440040 00400000 00440400 00444004 00400000 00440400 04400004 00400000 00440400 00440044 00400000 00440400 00440040 00400000 00440444 00440000 00400000 00440440 00440044 00400000 00440444 00444004 00400000 00440400 00440040 00400000 00440044 00440000 00400000 00440440 00440004 00400000 00440400 00440444 00400000 00440404 00440404 00400000 00440440 00440444 00400000 00440440 00440040 00400000 00440044 00440044 00400000 00440400 04400004 00400000 00440044 00440000 00400000 00440440 00440004 00400000 00440400 00440444 00400000 00440044 00444004 00400000 00440440 04400004 00400000 00440404 04400004 00400000 00440404 00440444 00400000 00440044 00440404 00400000 00440044 00440000 00400000 00440404 04400004 00400000 00440404 00444000 00400000 00440400 00444004 00400000 00440440 00440444 00400000 00440440 00440040 00400000 00440044 00440040 00400000 00440404 00444004 00400000 00440440 00440444 00400000 00440400 04400004 00400000 00440400 00440440 00400000 00440444 00444000 00400000 00440044 00440000 00400000 00440440 00440044 00400000 00440440 04400400 00400000 00440440 04400044 00400000 00440440 00444000 00400000 00440440 00440040 00400000 00440440 04400400 00400000 00440440 00440400 00400000 00440444 00440044 00400000 00440404 04400004 00400000 00440404 00440044 00400000 00440400 00440040 00400000 00440400 00440040 00400000 00440404 00440004 00400000 00440440 04400040 00400000 00440400 04400400 00400000 00440440 04400040 00400000 00440400 00444004 00400000 00440400 00444000 00400000 00440404 00440040 00400000 00440440 04400440 00400000 00440404 04400004 00400000 00440404 00440444 00400000 00440044 00440400 00400000 00440440 00440444 00400000 00440440 00440400 00400000 00440400 00440444 00400000 00440440 00444000 00400000 00440440 04400044 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440440 04400044 00400000 00440444 00440404 00400000 00440404 00444004 00400000 00440044 00440040 00400000 00440404 00440440 00400000 00440444 00440404 00400000 00440440 00440400 00400000 00440400 00440444 00400000 00440404 00440440 00400000 00440444 00444004 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440044 00444004 00400000 00440440 04400400 00400000 00440400 00444004 00400000 00440400 00440044 00400000 00440404 00440040 00400000 00440440 00440044 00400000 00440440 00440400 00400000 00440400 00444000 00400000 00440400 04400004 00400000 00440444 00440000 00400000 00440404 00444004 00400000 00440404 00440444 00400000 00440044 00440404 00400000 00440440 04400404 00400000 00440440 00440040 00400000 00440400 00440444 00400000 00440404 00440404 00400000 00440440 00440444 00400000 00440404 00440004 00400000 00440404 00440404 00400000 00440400 04400004 00400000 00440400 00440400 00400000 00440400 04400004 00400000 00440400 00440044 00400000 00440400 00440040 00400000 00440444 00440044 00400000 00440440 00440004 00400000 00440404 00440444 00400000 00440404 00440440 00400000 00440444 04400004 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440044 00444004 00400000 00440444 00440404 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440444 00444000 00400000 00440444 00440000 00400000 00440440 00440040 00400000 00440440 04400400 00400000 00440404 00440404 00400000 00440440 00440444 00400000 00440400 04400004 00400000 00440400 00440404 00400000 00440440 00444000 00400000 00440400 04400044 00400000 00440400 04400004 00400000 00440400 00440044 00400000 00440044 00440400 00400000 00440400 04400404 00400000 00440400 00440044 00400000 00440440 00440444 00400000 00440044 00440000 00400000 00440400 04400040 00400000 00440400 00440400 00400000 00440404 00440004 00400000 00440440 04400440 00400000 00440044 04400400 00400000
Основные уравнения прямых и плоскостей
Основные уравнения прямых и плоскостейУравнение прямой
Важным предметом школьной алгебры является «уравнение прямой».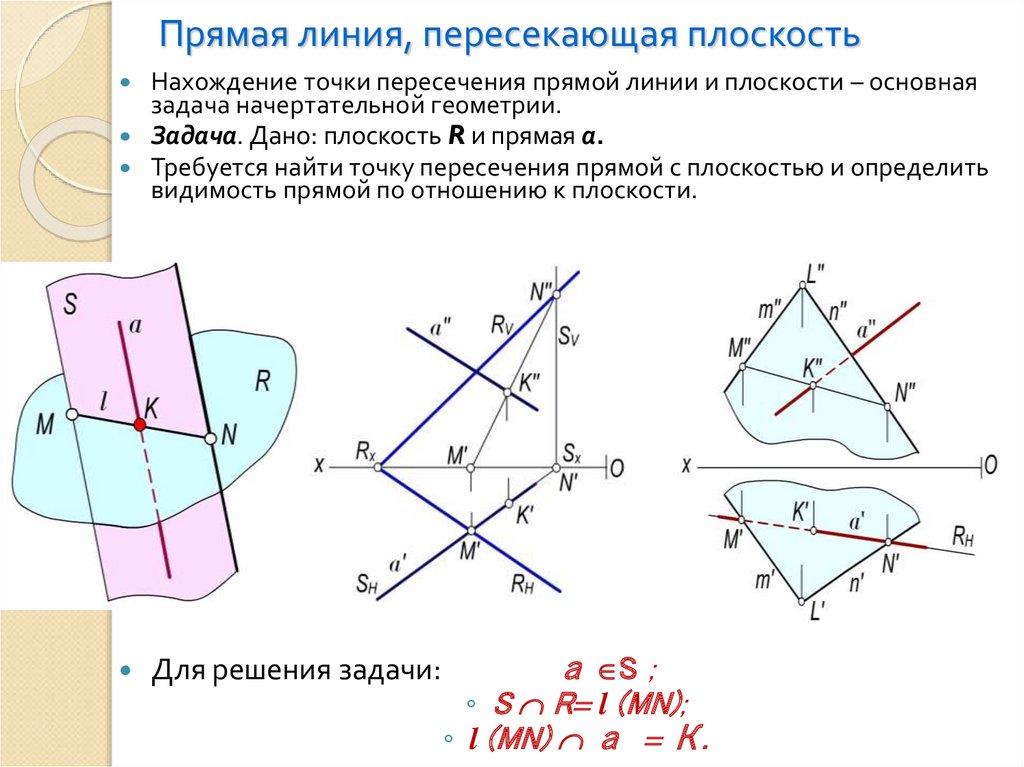 Это означает уравнение относительно x и y, набор решений которого представляет собой линию в (x, y)
самолет.
Это означает уравнение относительно x и y, набор решений которого представляет собой линию в (x, y)
самолет.
Самая популярная форма в алгебре — это форма «пересечение наклона».
у = тх + б.
Это фактически использует x как параметр и записывает y как функцию x: y = f(x) = мх+б. Когда x = 0, y = b и точка (0,b) является пересечением прямой с осью Y.
Думая о линии как о геометрическом объекте, а не о графике функции, имеет смысл относиться к x и y более беспристрастно. Общее уравнение для строка (нормальная форма)
топор + по = с,
с условием, что по крайней мере один из a или b отличен от нуля. Это может легко преобразовать в форму пересечения наклона, решив для y:
у = (-а/б) + с/б,
, за исключением особого случая b = 0, когда линия параллельна оси y.
Если коэффициенты в нормальной форме умножаются на ненулевую константу,
множество решений точно такое же, поэтому, например, все эти уравнения
имеют ту же строку, что и решение.
2x + 3 y = 4
4x + 6y = 8
-x — (3/2) y = -2
(1/2)x + (3/4)y = 1
В общем случае, если k — ненулевая константа, то это уравнений для одна и та же строка , так как они имеют одинаковые решения.
ax + by = c
(ka)x + (kb)y = kc.
Популярный выбор для k в случае, когда c не равно нулю, это k = (1/с). Тогда уравнение становится
(а/с)х + (б/с)у = 1.
Другой полезной формой уравнения является деление на |(a,b)|, квадратный корень из 2 + b 2 . Этот выбор будет объяснен в разделе Normal Vector.
Упражнение . Если на прямой стоит О, покажите, что уравнение принимает вид ax + by = 0 или y = mx.
Упражнение: Найдите точки пересечения этой прямой с координатные оси.
Упражнение : Уравнение прямой, проходящей через (0,0) и точка (h,k)?
Нахождение уравнения прямой через 2 точки на плоскости
Для любых двух точек P и Q через эти точки проходит ровно одна прямая PQ. Если известны координаты точек P и Q, то коэффициенты a, b, c
уравнение для прямой можно найти, решив систему линейных уравнений.
Если известны координаты точек P и Q, то коэффициенты a, b, c
уравнение для прямой можно найти, решив систему линейных уравнений.
Пример : Для P = (1, 2), Q = (-2, 5) найдите уравнение ax + by = c строки PQ.
Поскольку точка P находится на прямой, ее координаты удовлетворяют уравнению: a1 + b2 = c,
или а + 2b = с.
Поскольку Q находится на прямой, его координаты удовлетворяют уравнению: a(-2) + b5 = c,
или -2 а + 5b = с.
Умножьте первое уравнение на 2 и прибавьте, чтобы исключить a из уравнения: 4b + 5b = 9b = 2c + c = 3c, поэтому b = (1/3)c. Затем подставляя в первый уравнение, a = c — 2b = c — (2/3)c = (1/3)c.
Это дает уравнение [(1/3)c]x + [(1/3)c}y = c . Почему нет с
решено для? Помните, что существует бесконечное количество уравнений для
линии, каждая из которых кратна другой. Мы можем вынести c (или положить c
= 1 для того же результата) и получить (1/3)x + (1/3)y =1 как один из вариантов
уравнение для прямой. Другим вариантом может быть c = 3: x+y = 3 , что
очистил знаменатели.
Другим вариантом может быть c = 3: x+y = 3 , что
очистил знаменатели.
Этот метод всегда работает для любых различных P и Q. Конечно, существует формула также для а, б, в. Это можно найти в виде определители , или перекрестное произведение .
Упражнения : Найдите уравнения этих линий. Обратите внимание на особые случаи.
Линия через (3, 4) и (1, -2).
Линия через (3, 4) и (-6, -8).
Линия через (3, 4) и (3, 7).
Соединение с параметрической формой линии
Для двух точек P и Q точки прямой PQ можно записать как F(t) = (1-t)P + tQ, поскольку t охватывает все действительные числа. Если и P, и Q удовлетворяют одному и тому же уравнение ax+by = c, то вычисление показывает, что это верно и для (1-t)P + tQ для любого выбора t.
Вот это вычисление. Пусть P = (p 1 , p 2 ), Q = (q 1 , q 2 ). Тогда, поскольку точки лежат на прямой, мы знаем, что оба
ap 1 + bp 2 = c
aq 1 + bq 2 = c.
Для точки F(t) мы должны проверить a[(1-t)p 1 +tq 1 ] + b[(1-t)p 2 +tq 2 ] = с. Но левую часть можно переставить как (1-t)(ap 1 + bp 2 ) + t(aq 1 + bq 2 ), и это равно (1-t)c + tc = c. Итак равенство выполняется. Сравните это явное вычисление с вычислением, данным для плоскости, использующей скалярное произведение. Вычисления те же, но показывает больше деталей, а один скрывает координаты и показывает более концептуальный картина.
Уравнение плоскости
Плоскость в трехмерном пространстве имеет уравнение
топор+бы+ч=д,
, где хотя бы одно из чисел a, b, c должно быть ненулевым.
Что касается линии, если уравнение умножить на любую ненулевую константу k до получаем уравнение kax+kby+kcz=kd, плоскости решений совпадают.
Если с не равно нулю, часто полезно думать о плоскости как о графике
функция z от x и y. Уравнение можно переставить так:
Уравнение можно переставить так:
z = -(a/c)x + (-b/c)y + d/c
Еще один полезный вариант, когда d не равен нулю, — разделить на d так, чтобы константа срок = 1,
(a/d)x + (b/d)y + (c/d)z = 1.
Другой полезной формой уравнения является деление на |(a,b,c)|, квадрат корень a 2 + b 2 + c 2 . Этот выбор будет объяснено в разделе «Вектор нормали».
Упражнение: Где плоскость ax + by + cz = d пересекает координату топоры?
Упражнение: Что особенного в уравнении плоскости, проходящей через 0,
Нахождение уравнения плоскости через 3 точки в пробел
Учитывая точки P, Q, R в пространстве, найдите уравнение плоскости через 3 точки.
Пример : P = (1, 1, 1), Q = (1, 2, 0), R = (-1, 2, 1). Ищем коэффициенты уравнения ax + by + cz = d, где P, Q и R удовлетворяют уравнениям, таким образом:
а + b + с = d
а + 2b + 0с = d
-а + 2b + с = d
Вычитание первого уравнения из второго и последующее сложение первого уравнения к третьему, мы исключаем a, чтобы получить
б — в = 0
4б + в = 2d
Сложение уравнений дает 5b = 2d или b = (2/5)d, затем решение для c = b =
(2/5)d и тогда a = d — b — c = (1/5)d.
Таким образом, уравнение (с ненулевой константой, оставленной для выбора) имеет вид d(1/5)x + d(2/5)y + d(2/5)z = d, поэтому один выбор константы дает
х + 2у + 2г = 5
или другой вариант: (1/5)x + (2/5)y + (2/5)z = 1
Учитывая координаты P, Q, R, есть формула для коэффициентов плоскость, которая использует определители или перекрестное произведение .
Упражнение. Какое уравнение плоскости через точки I, J, K?
Упражнение: Какое уравнение плоскости через (1, 1, 1), (-1, 1, -1) и (1, -1, -1)?
Упражнение: Сравните этот метод нахождения уравнения плоскости с векторным произведением метод.
Соединение с параметрической формой плоскости
Для 3 точек P, Q, R все точки плоскости можно записать в параметрическом форма F(s,t) = (1 — s — t)P + sQ + tR, где s и t варьируются по всем действительным числам.
Вычисление, подобное приведенному выше для уравнения прямой, показывает, что если P,
Q, R удовлетворяют одному и тому же уравнению ax + by + cz = d, тогда все точки F(s,t)
также удовлетворяют тому же уравнению.

Leave A Comment