Квадратичная функция: ее график и свойства 9 класс онлайн-подготовка на Ростелеком Лицей
Тема 1: Функции и их свойства
- Видео
- Тренажер
- Теория
Заметили ошибку?
Тема 4.
Всем привет! Сегодня мы поговорим об одной из самых важных функций, о квадратичной функции.
Квадратичной функцией называется функция, которую можно задать y = ax2 + bx + c, где x – переменная, a, b и c – некоторые числа, причем a ≠ 0.
Изучение квадратичной функции мы начнем с частного случая, а именно с функции y = ax2. Мы уже встречались с функцией y = x2, когда a = 1. Ее графиком является парабола.
Построим в одной системе координат
y = x2; y = 2x2; y = 3x2.
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
y = 2x2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
18 |
8 |
2 |
0 |
2 |
8 |
18 |
При любом x ≠ 0 значение функции y = 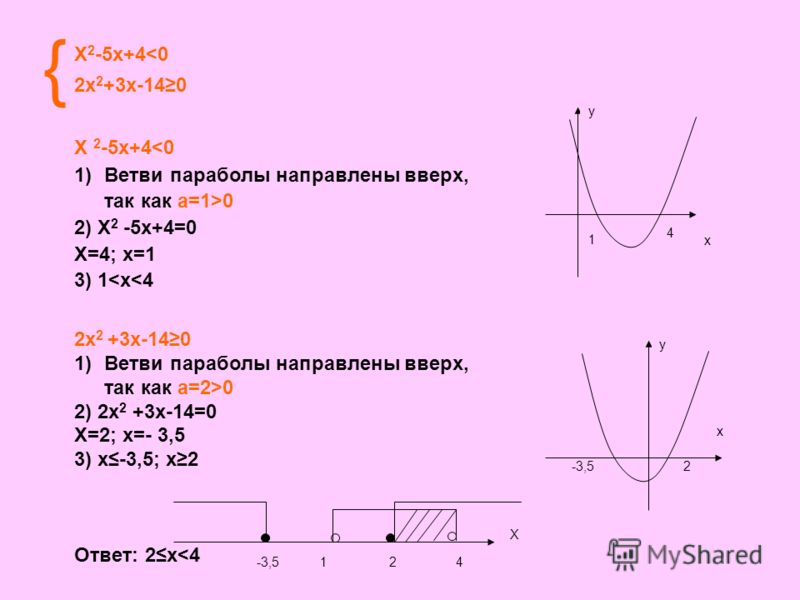 То есть график функции y = x2 можно получить из параболы y = x2 растяжением от оси x в 2 раза.
То есть график функции y = x2 можно получить из параболы y = x2 растяжением от оси x в 2 раза.
Аналогично, график функции y = 3x2 можно получить из графика функции y = x2 растяжением от оси x в 3 раза.
Построим теперь в одной системе координат графики функции y = x2, y=12×2, y=13×2.
y=12×2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
4,5 |
2 |
|
0 |
0,5 |
2 |
4,5 |
Заметим, что при любом x ≠ 0 значения функции y=12×2меньше соответствующих значений функции y = x2 в 2 раза.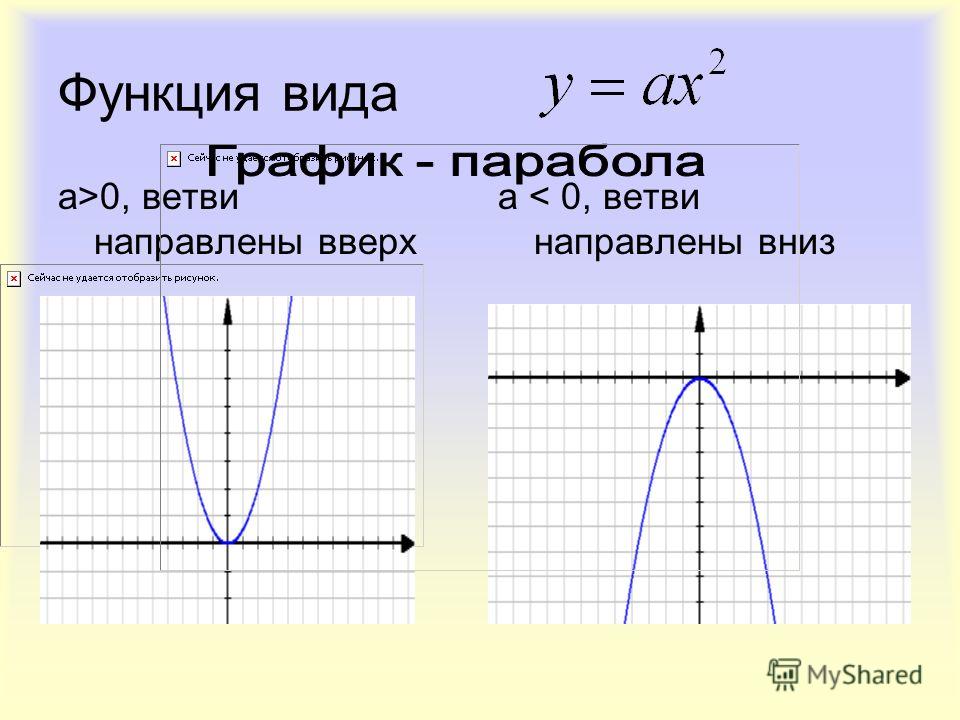
Таким образом, график функции y=12×2 можно получить из параболы y = x2 сжатием к оси x в 2 раза.
y=13×2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
3 |
43 |
|
0 |
13 |
43 |
3 |
Аналогично график функции y=13×2 можно получить из графика функции = x2 сжатием к оси x в 3 раза.
Давай сделаем вывод:
График функции y = ax2 можно получить из параболы
Рассмотрим теперь случай, когда a y=-13×2. Составим таблицу значений:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
-3 |
-43 |
-13 |
0 |
-13 |
-43 |
-3 |
Сравним графики функций y=13×2 и y=-13×2. При любом
При любом
То есть графики функций y = ax2 и y = —ax2 при a ≠ 0 симметричны относительно оси x. Графиком функции y = ax2, как и графиком функции y = x2 является парабола
Сформулируем свойства функции y = ax2 при a > 0.
- Область определения -∞;+∞;
- Область значений функций 0;+∞
-
Если x
- Если x ≠ 0, то y > 0. График функции расположен в верхней полуплоскости.
-
График функции симметричен относительно оси y.

- Функция убывает в промежутке -∞;0 и возрастает в промежутке 0;+∞.
- При x = 0 функция принимает наименьшее значение, равное 0. Наибольшего значения функции нет.
Сформулируем свойства функции y = ax
- Область определения -∞;+∞;
- Область значений функций -∞;0
- Если x = 0, то y = 0, т.е. график функции проходит через начало координат.
- Если x ≠ 0, то y
- График функции симметричен относительно оси y.
- Функция убывает в промежутке 0;+∞ и возрастает в промежутке -∞;0.
- При x = 0 функция принимает наибольшее значение, равное 0. Наименьшего значения функции нет.
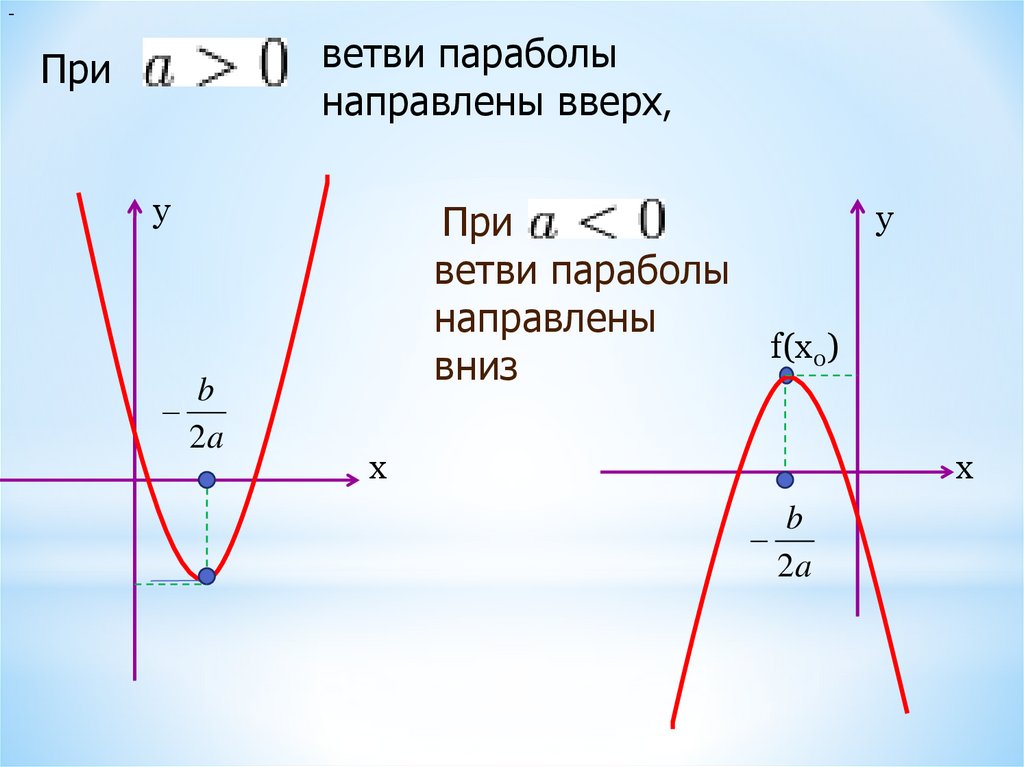
От коэффициента a зависит направление ветвей параболы. Если a > 0, то ветви параболы направлены вверх, если a
Если a > 0, то ветви параболы направлены вверх, если a
Построение графика, симметричного данному относительно оси x, или сжатие к оси x – различные виды преобразований графиков функций. Преобразования графиков функции, рассмотренные нами сегодня для функций y = ax2, применимы к любой функции.
График функции y=-fx можно получить из графика функции y=fx с помощью симметрии относительно оси абсцисс.
График функции y=afx можно получить из графика функции y=fx с помощью растяжения от оси x в a раз, если a > 1, и сжатием к оси x в 1a раз, если 0
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.Квадратичная функция и её график
Вершина этой параболы находится в точке (0; 0). И не забудь про то, что ветви параболы бесконечно поднимаются ввысь и не ограничены точками с координатами (3; 9) и (3; -9).
Еще одна стандартная парабола задается функцией y = —x2 (в этом случае а = -1). Для этого графика я тоже напишу табличку:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -9 | -4 | -1 | 0 | -1 | -4 | -9 |
Начало координат тоже является вершиной этой параболы, как и в предыдущем случае, но ветви уже будут направлены вниз:
Сразу напрашивается вывод: если перед х2 стоит положительное число, то ветви параболы направлены вверх, если отрицательное — то вниз.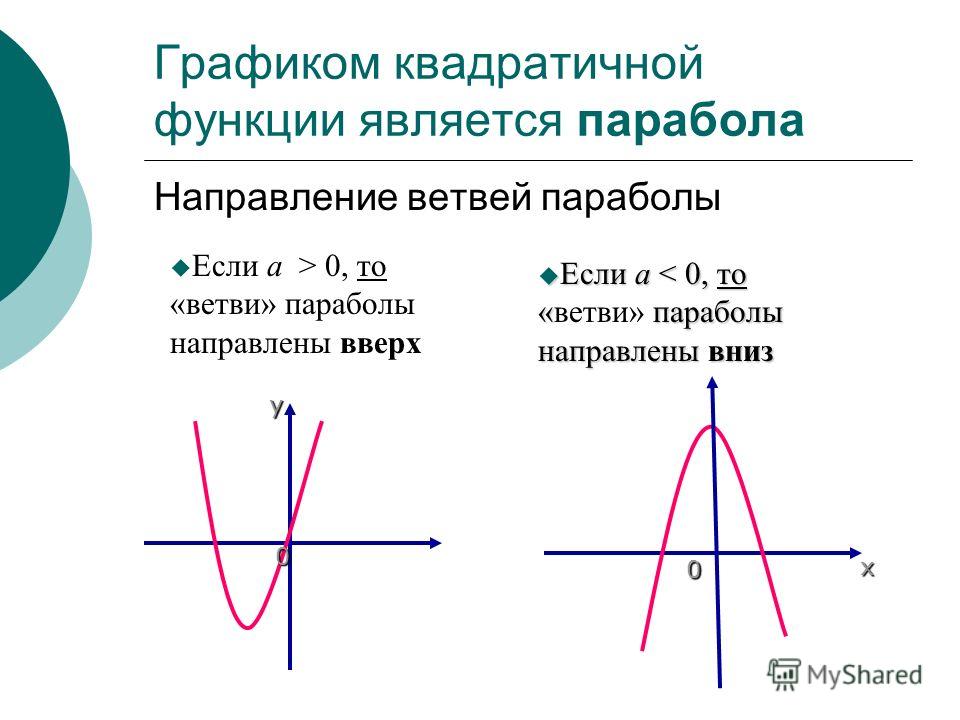
Если у тебя черный пояс по рисованию стандартных парабол, то следующий раздел пройдет у тебя «на ура».
Параболы со смещенной вершиной.
Зачем я начала статью со стандартной параболы? Ответ прост. Графиком любой квадратичной функции y = ±x2 + bx + c (обязательно коэффициент перед х2 должен равняться ±1) является стандартной параболой, только вот вершины этих парабол не будут находится в начале координат.
Чтобы начертить подобные параболы нужно сначала узнать, где находится вершина.
Пусть вершиной параболы будет точка О с координатами (x1; y1). Тогда найти эти координаты можно по формулам:
Кстати, можно найти координаты вершины и другим способом.
Координату хО находим по той же формуле, а координату уО можно найти подстановкой координаты хО в функцию.
Без примера не обойтись)
Пример 1.
Дана функция y = x2 — 4x + 4. Найдите вершину параболы и постройте график.
Найдем сначала вершину параболы двумя способами, чтобы убедится, что оба способа рабочие.
1 способ: по формулам.
2 способ: подстановкой.
Одну координаты мы уже нашли по формуле. Подставляем ее в исходную функцию.
Итак, получили, что О(2; 0) — вершина параболы. Отмечаем ее на координатной плоскости.
Перед х2 стоит положительное число, значит ветви параболы направлены вверх. Наша задача: нарисовать стандартную параболу, представив, что точка О — начало координат. Если тебе это сложно сделать, то необходимо начертить таблицу значений и уже по ней рисовать параболу.
Параболы-стройняшки и параболы-пухляшки.
Удивительно, но числовой коэффициент перед х2 оказывается влияет на стройность и полноту парабол.
Если числовой коэффициент лежит в промежутке (-1; 0) ∪ (0; 1), то парабола будет более обширно смотреться на координатной плоскости.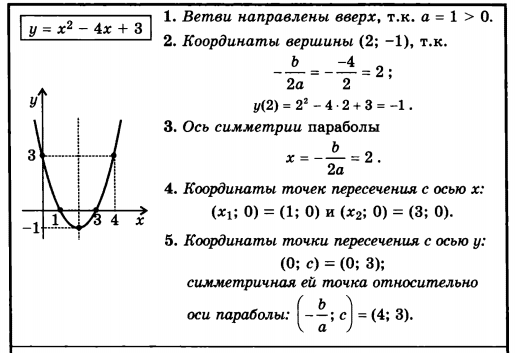
А если числовой коэффициент лежит в промежутке (-∞; -1) ∪ (1; +∞), то парабола будет прижиматься к оси Оу и занимать меньше места на плоскости.
Не веришь? Давай проверим! Для примера возьмем две функции:
К сожалению, здесь схитрить не получится: обе параболы нестандартные и для обеих необходимо создать таблицы значений. Но перед эти определимся с их вершинами.
Пусть вершиной первой параболы будет точка А(хА; уА), а вершиной второй параболы — точка B(хB; уB). Вершины буду находить по второму способу (см. выше).
Переходим к таблицам значений.
Голубая парабола.
| x | 0 | 2 | 4 | 6 | 8 |
| y | 3 | 6 | 7 | 6 | 3 |
Зеленая парабола.
| x | -1,5 | -1 | -0,25 | 0 | 1 |
| y | -3 | 1 | 4,5 | 3 | -3 |
Чертим обе параболы по получившимся координатам.
Вот о чем я и говорила) Перед тобой парабола-стройняшка и парабола-пухляшка во всей красе.
А ты заметил, что свободный член в уравнении функции — это точка пересечения графика с осью Оу? В обеих функциях свободный член равен 3 и графики пересекают ось Оу в точке с координатами (0; 3).
Практикум по параболам.
Теорию о параболах можно еще писать и дальше, но тебя, скорее всего, интересует практика по графикам.
Поскольку речь идет о параболах, то с параболами мы и будем сейчас возиться.
Задание 1. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
Решение. Коэффициент а, стоящий перед х2, отвечает за направление ветвей параболы, а свободный член с — за пересечение графика с осью Оу.
А) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с отрицателен, то график пересекает ось Оу ниже нуля. Подходит график 1.
Б) Если коэффициент а отрицателен, то ветви направлены вниз; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 3.
В) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с положителен, то график пересекает ось Оу выше нуля.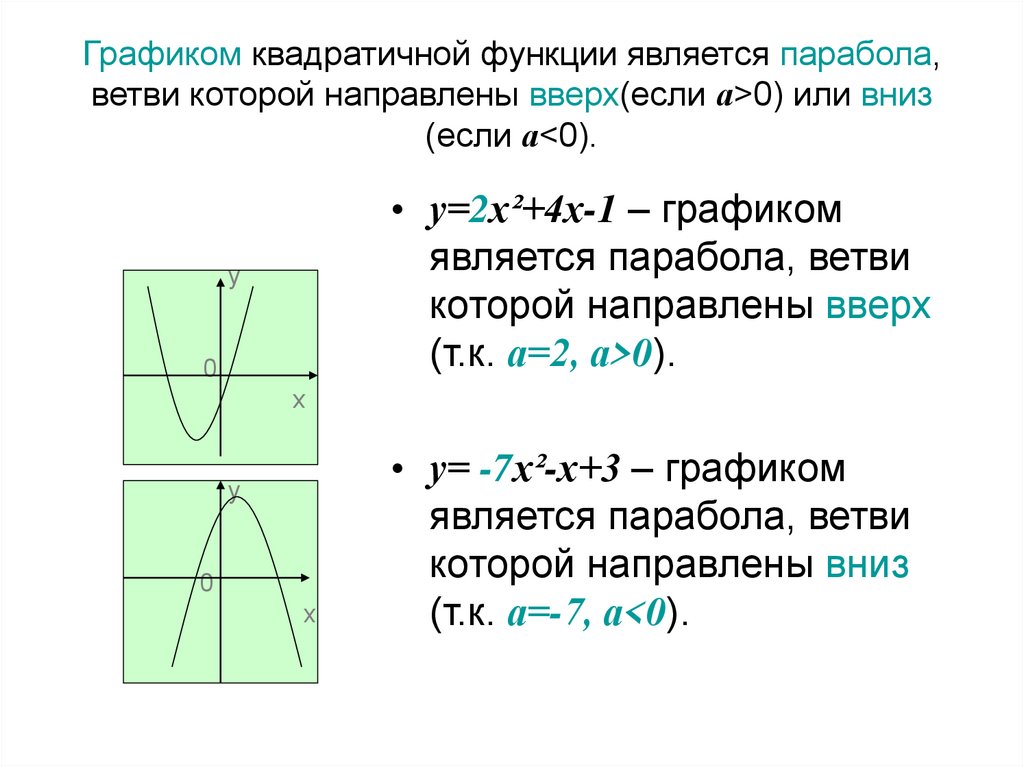 Подходит график 2.
Подходит график 2.
Задание 2 (наоборот). На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
А) Ветви направлены вверх, значит а > 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 3.
Б) Ветви направлены вверх, значит а > 0; график пересекает ось Оу ниже нуля, значит и с < 0. Подходит вариант под номером 1.
В) Ветви направлены вниз, значит а < 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 2.
Задание 3. Установите соответствие между графиками и их функциями.
График В отличается от остальных тем, что его ветви направлены вниз. За направление ветвей отвечает коэффициент перед х2 — он отрицательный.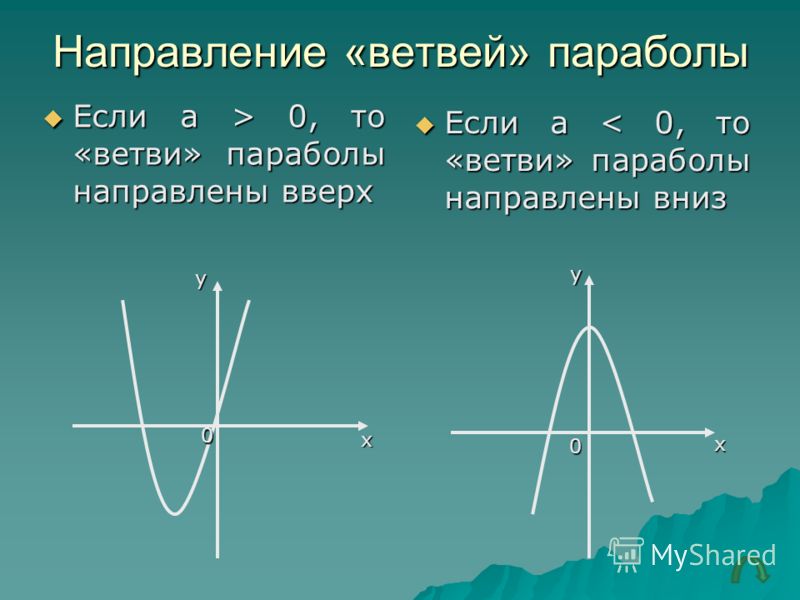 Отрицательный коэффициент только в функции под номером 3. Значит В-3.
Отрицательный коэффициент только в функции под номером 3. Значит В-3.
Дальше рекомендую отработанную годами технику. Она минимизирует твои ошибки, если ты, конечно, умеешь считать)
Итак, рассматриваем график А и выбираем на нем точку с красивыми координатами (красивые значит не дробные). Мне нравится тут вершина. Ее координаты (4; -3). Даже не спрашивайте почему не прорисованы оси; эти задания взяты с сайта ФИПИ)
Теперь эти координаты подставляем в оставшиеся функции: вместо у подставляем -3, а вместо х подставляем 4.
Подставляем в первую функцию: -3 = 2 · 42 — 16 · 4 + 29; -3 = -3 — верно. Значит, А-1.
И остается Б-2.
Задание 4 (наоборот, но принципе тот же). Установите соответствие между функциями и их графиками.
Очевидно, что В-2.
На графике 1 выбираем точку. Вершина снова четкая, но для разнообразия давайте возьмем другую точку, например, точку с координатами (-4; 1). Будь внимателен и смотри, чтобы точно такой же точки не было на третьем графике!
Подставляем в функцию А: 1 = (-4)2 + 4 · (-4) + 1; 1 = 1 — верно.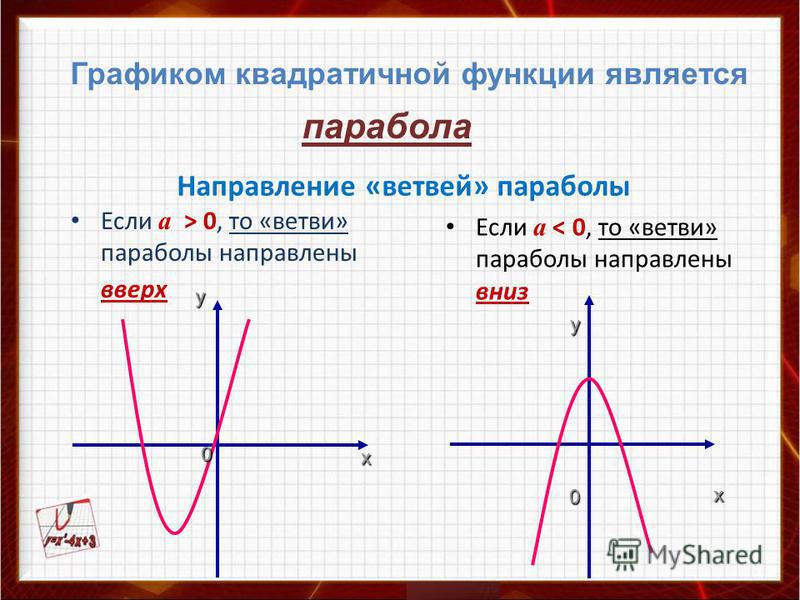 Значит, А-1.
Значит, А-1.
Соответственно, Б-3.
Если ты считаешь, что чего-то не хватает или у тебя есть ещё задания из первой части, связанные с параболами, — напиши мне в VK)
Как построить параболу
Что такое парабола? Как нарисовать его график? Это вопросы для этого раздела. Наброски парабол обычно задают в домашних заданиях по алгебре, поэтому некоторые советы будут полезны. Мы обсудим основные понятия и покажем на простых примерах, как работать с параболами.
Начнем. Проще говоря, парабола — это U-образная кривая с некоторыми специфическими свойствами. Однако обратите внимание, что не всякую U-образную кривую можно назвать параболой. Общеизвестно, что математика любит все описывать формулами. Здесь нет ничего удивительного, мы также можем написать формулу для параболы. В принципе, любая парабола описывается некоторым квадратным уравнением. 92
Сначала нарисуем. Для этого нам нужно заполнить таблицу значений x,y. Мы просто берем каждое значение x и подставляем его в уравнение, чтобы получить соответствующее значение y:
\begin{matrix} x&y\\ \\ {-3}&9\\-2&4 \\-1&1 \\0&0 \\ 1&1\\2&4\\3&9\end{matrix}
Теперь мы можем отметить все точки на координатной плоскости:
Наконец, мы нарисуем нашу параболу, соединяя точки. 2\\
у=к+2ат
\end{случаи}
$$ 92,k+2at)$ на второй параболе. Заметить, что
$$ P'(t)=P(t)+\mathbf{v}\qquad\forall t\in\mathbb{R}$$
2\\
у=к+2ат
\end{случаи}
$$ 92,k+2at)$ на второй параболе. Заметить, что
$$ P'(t)=P(t)+\mathbf{v}\qquad\forall t\in\mathbb{R}$$
Устранение ваших сомнений
Значения $x$ и $y$ равны координаты в $xy$-плоскости. Помещаете ли вы их в уравнение параболы или получаете из параметрических уравнений, $(x,y)$ являются координатами.
Уравнение параболы дает прямую связь между $x$ и $y$. Каждая точка параболы должна удовлетворять этому соотношению (кривая — это геометрическое место, определяемое ее уравнением).
С другой стороны, параметрические уравнения представляют каждую точку параболы как функцию параметра $t$. Думайте о $t$ как о времени, тогда $P(t)$ — это ваша траектория на плоскости. Конечно, изменение параметрических уравнений изменит начальную точку и скорость вашей траектории, но путь останется прежним.
При переносе вектором $\mathbf{v}=(h,k)$ все сдвигается на $h$ в направлении $x$ и на $k$ в направлении $y$ . Вот почему $P’=(x_{P’},y_{P’})=(x_P+h,y_P+k)=P+\mathbf{v}$.

Leave A Comment