Шестиугольная призма — геометрическое тело
Шестиугольная призма — геометрическое тело — Mnogogranniki.ru- Вы здесь:
- Главная
- Правильная шестиугольная призма
Правильная шестиугольная призма — это шестиугольная призма у которой основания правильные шестиугольники (все стороны которых равны, углы между сторонами основания составляют 120 градусов), а боковые грани прямоугольники.
Основания призмы являются равными правильными шестиугольниками.
Боковые грани призмы являются прямоугольниками.
Боковые рёбра призмы параллельны и равны.
Размеры призмы можно выразить через длину стороны a и высоту h.
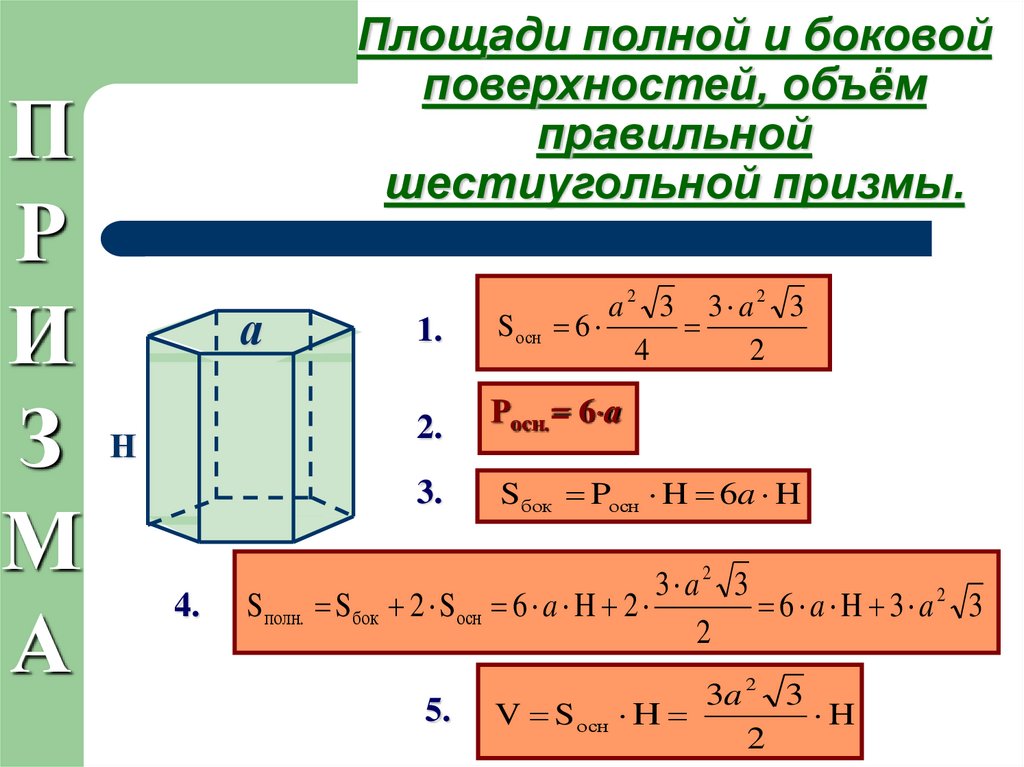
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Формула площади поверхности шестиугольной призмы:
Объём призмы равен произведению её высоты на площадь основания.
Формула объема правильной шестиугольной призмы:
Правильная шестиугольная призма может быть вписана в цилиндр.
Формула радиуса цилиндра вписанной шестиугольной призмы:
Двойственным многогранником прямой призмы является бипирамида.
Исторически понятие «призма» возникло из латыни и означало — нечто отпиленное.
Анимация демонстрирует как две параллельные плоскости отрезая лишнее формируют два основания призмы. Из одной заготовки можно получить как правильную призму, так и наклонную призму.
Скачать развертку правильной шестиугольной призмы для печати на листе А4
Геометрические размеры готовой призмы (мм):
Длина = 90
Ширина = 78
Высота = 45
Скачать развертку правильной шестиугольной призмы для печати на листе А4
Геометрические размеры готовой призмы (мм):
Длина = 73
Ширина = 64
Высота = 73
Скачать развертку правильной шестиугольной призмы для печати на листе А4
Геометрические размеры готовой призмы (мм):
Длина = 62
Ширина = 54
Высота = 93
youtube.com/embed/ifaUmy2cJO8?wmode=transparent» allowfullscreen=»»>
Популярное
Как освоить стереометрию?
Раздел геометрии, в котором изучаются фигуры в пространстве именуется стереометрия. Происхождение слова стереометрия относится к Древней Греции – от слов «stereos» —…
Заметка об Архимеде — древнегреческом ученом
АРХИМЕД (287 — 212 до н.э.) — древнегреческий математик, физик и механик. Архимед — автор многочисленных открытий и изобретений: машины для…
Развертки тел вращения
Что будет, если плоскую геометрическую фигуру, например прямоугольник, начать быстро вращать относительно одной из его сторон? Одним лишь вращением мы можем…
Что такое многогранник? Примеры
Многогранник — (определение) геометрическое тело, ограниченное со всех сторон плоскими многоугольниками — гранями.
Как собирать многогранники без клея?
До сих пор мы активно применяли для сборки многогранников из наборов «Волшебные грани» клей. Более того, настоятельно рекомендовали применять именно клей Супер-ПВА. Есть ли…
Головоломка звёздчатый октаэдр
Это новый, весьма необычный способ создать модель Звёздчатого многогранника открытого 1619 году немецким математиком и астрономом Иоганном Кеплером.
Колючие звезды на башнях
Представьте себе историческое здание, архитектурный ансамбль, который украшают звёздчатые многогранники. И не просто здание, а целый дворец! Возможно ли такое?
Площадь основания правильной шестиугольной призмы. Формулы площади правильного шестиугольника
В школьном курсе геометрии изучаются свойства различных видов призм, включая шестиугольную. Последняя часто встречается при рассмотрении кристаллических решеток металлов, поэтому знание ее характеристик важно при определении свойств этого класса материалов. Данная статья посвящена вопросу площади основания правильной шестиугольной призмы.
Данная статья посвящена вопросу площади основания правильной шестиугольной призмы.
Объемная фигура — призма
В геометрии под призмой понимают такую фигуру, которая образована двумя одинаковыми многоугольниками, расположенными параллельно друг другу, и некоторым числом параллелограммов, соединяющих вершины названных многоугольников. Если основание образовано многоугольником с n вершинами, то количество параллелограммов также будет равно n.
Призмы характеризуются по типу многоугольника в основании (правильные и неправильные треугольные, четырехугольные и так далее), который может быть вогнутым и выпуклым, и по углу между боковыми гранями (параллелограммами) и основанием (прямоугольные и косоугольные).
Основными элементами любой призмы являются ее грани (Г), ребра (Р) и вершины (В). На рисунке выше приведена для примера треугольная призма. Как видно, она имеет 6 вершин (по 3 для каждого основания). Ниже приведена развертка этой призмы. Рисунок показывает, что она состоит из 5 граней: 2 треугольника и 3 прямоугольника.
Узнаем как вычислить объем призмы четырехугольной? Формулы…
Стереометрия является важной частью общего курса геометрии, которая рассматривает характеристики…
Чтобы посчитать число ребер рассматриваемой фигуры, следует применить теорему Эйлера:
Р = В + Г — 2
Это выражение дает число ребер для этой призмы, равное 9. Действительно, если обратиться к трехмерному изображению призмы выше, то можно увидеть, что 6 ребер образуют основания фигуры, и еще 3 ребра являются результатом пересечения прямоугольников.
Призма шестиугольная
Перед рассмотрением вопроса площади основания правильной шестиугольной призмы, сначала познакомимся с этой фигурой. Из названия и приведенной выше классификации призм понятно, что речь пойдет о фигуре, в основании которой лежит шестиугольник. Это означает, что число сторон в такой призме будет равно 8 (два основания и шесть параллелограммов), а число вершин составит 12 (6 + 6). Тогда количество ребер будет равно:
Р = 12 + 8 — 2 = 18
Из этих 18-ти ребер основаниям принадлежат 12.
Если в основании находится правильный шестиугольник, а углы между боковыми сторонами (параллелограммами) и основаниями равны 90o, то такая фигура будет называться прямоугольной призмой с правильным шестиугольником в основании, или просто правильной шестиугольной призмой. Ее схематическое изображение приводится ниже.
Узнаем как вычислить объем призмы четырехугольной? Формулы…
Стереометрия является важной частью общего курса геометрии, которая рассматривает характеристики…
В правильной шестиугольной призме все ребра равны только в том случае, если c = a, где c — высота (длина бокового ребра) и a — длина стороны шестиугольника. В общем случае c ≠ a.
Далее приведем формулы для расчета площади поверхности и объема рассматриваемой призмы. Чтобы это сделать, необходимо знать площадь основания правильной шестиугольной призмы.
Площадь шестиугольника
Получим формулу площади правильного шестиугольника. Для этого рассмотрим эту плоскую фигуру, которая изображена на рисунке ниже.
Видно, что многоугольник состоит из шести одинаковых сторон, которые образуют угол 120o. Поскольку этих углов шесть, то их сумма составит 720o.
Рисунок также показывает, что правильный шестиугольник гармонично вписывается в окружность. Если соединить центр окружности с каждой вершиной фигуры, то получим 6 одинаковых треугольников. Поскольку угловая мера всей окружности составляет 360o, то соответствующие углы треугольника равны 60o (360o/6). Они обозначены на рисунке. Поскольку каждый серый отрезок делит угол шестиугольника пополам, то оставшиеся два треугольника также равны по 60o. Это означает, что изображенные 6 треугольников являются равносторонними. Длина каждой из их сторон равна стороне шестиугольника, обозначим ее буквой a.
Правильная треугольная призма: определение, формулы для…
Во всех школах в старших классах проходят курс стереометрии, в котором рассматривают характеристики…
Из курса геометрии известно, что площадь S3 любого треугольника равна произведению его высоты h на сторону a, к которой она проведена, деленному пополам, то есть:
S3 = h*a/2
Длину h легко вычислить, используя понятие о тригонометрической функции.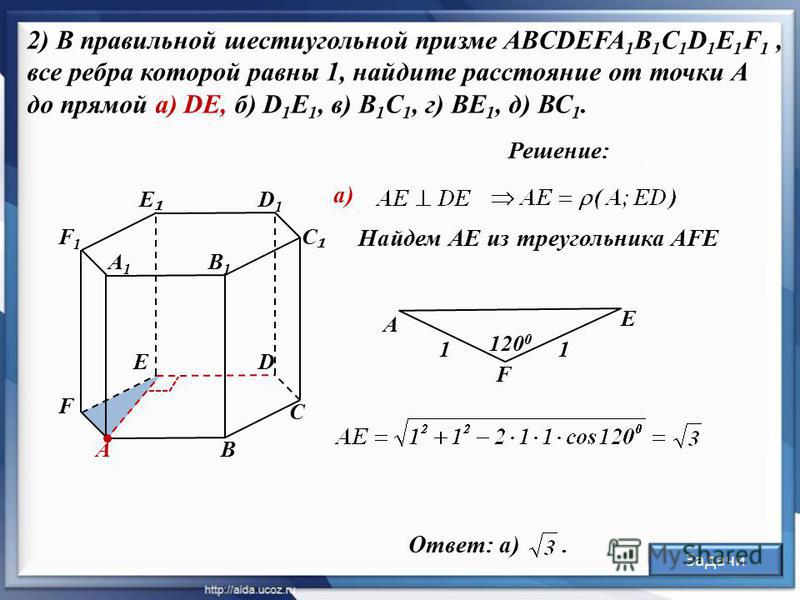 Она равна:
Она равна:
h = a*cos(30o) = a*√3/2
Тогда площадь всего треугольника равна:
S3 = √3*a2/4
Умножая эту площадь на 6, получаем формулу площади правильного шестиугольника:
S6 = 6*S3 = 3*√3*a2/2
Для полноты информации следует отметить, что существует формула площади правильного многоугольника с произвольным количеством сторон n. Ниже приведено соответствующее выражение:
Sn = n/ a2*ctg(pi/n)
Если подставить в это выражение значение n = 6, то мы получим формулу площади основания правильной шестиугольной призмы, которая совпадет с приведенной выше.
Заметим, что деление шестиугольника на 6 равносторонних треугольников означает, что шестиугольная призма состоит из 6 правильных треугольных призм.
Площадь поверхности
Полная площадь поверхности любой призмы может быть получена, если сложить соответствующие площади So для двух оснований и для боковой поверхности Sb, представленной параллелограммами:
S = 2*So + Sb
Изучим развертку рассматриваемого вида призмы, которая приведена на рисунке ниже.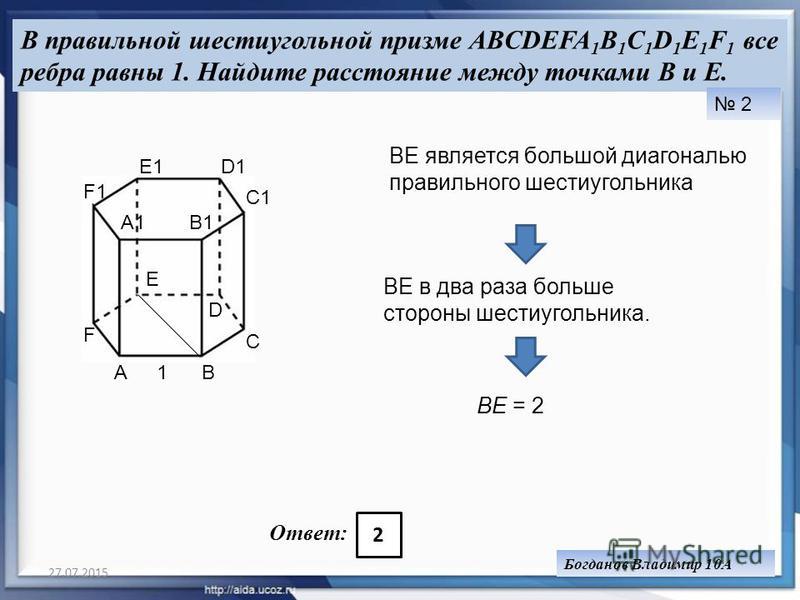
Мы видим, что призма состоит из двух одинаковых шестиугольников и 6 прямоугольников. Обозначим сторону основания буквой a, а стороны прямоугольников буквами a и c (сторона a является общей для шестиугольника и прямоугольника). В таком случае площадь полной поверхности шестиугольной призмы будет составлять:
S = 2*3*√3*a2/2 + 6*a*c = 3*a*(√3*a + 2*c)
Объем призмы
Эта важная величина для любого реального объекта в случае призмы находится просто: необходимо лишь умножить площадь основания на высоту фигуры, то есть:
V = So*h
Поскольку мы рассматриваем прямоугольную призму, то ее высота равна длине бокового ребра, то есть h = c. Тогда формула для объема правильной шестиугольной призмы запишется в виде:
V = 3*√3*a2*c/2
Таким образом, для определения площади и объема рассматриваемой фигуры необходимо знать длину ее ребра в основании и на боковой поверхности.
Для чего нужно знать свойства шестиугольной призмы?
Как было сказано во введении, эти призмы встречаются в природе в металлах. В частности, кристаллическая атомная упаковка титана, цинка, циркония, магния и некоторых других металлов имеет форму шестиугольной призмы, в основании которой лежат 7 атомов (6 в вершинах и 1 в центре). От соотношения длины ребра этой фигуры к длине стороны основания зависят многие механические свойства этих металлов (деформационные и упругие характеристики).
Выше приведен пример этой упаковки атомов, который носит сокращенное название ГПУ (гексагональная плотная упаковка).
Площадь поверхности шестиугольной призмы – формула, определение и примеры
Площадь поверхности призмы – это количество пространства, занимаемого поверхностью призмы. Шестиугольная призма представляет собой призму, состоящую из двух шестиугольных оснований и шести прямоугольных сторон. Это октаэдр. Это трехмерная фигура с шестиугольным основанием и шестиугольной вершиной.
| 1. | Что такое площадь поверхности шестиугольной призмы? |
| 2. | Формула площади поверхности шестиугольной призмы |
| 3. | Расчет площади поверхности шестиугольной призмы |
| 4. | Как найти площадь поверхности шестиугольной призмы? |
| 5. | Часто задаваемые вопросы о площади поверхности шестиугольной призмы |
Что такое площадь поверхности шестиугольной призмы?
Площадь поверхности шестиугольной призмы определяется как общая площадь, покрытая поверхностями шестиугольной призмы. Поскольку он имеет плоское основание, он имеет общую площадь поверхности, а также площадь изогнутой/боковой поверхности.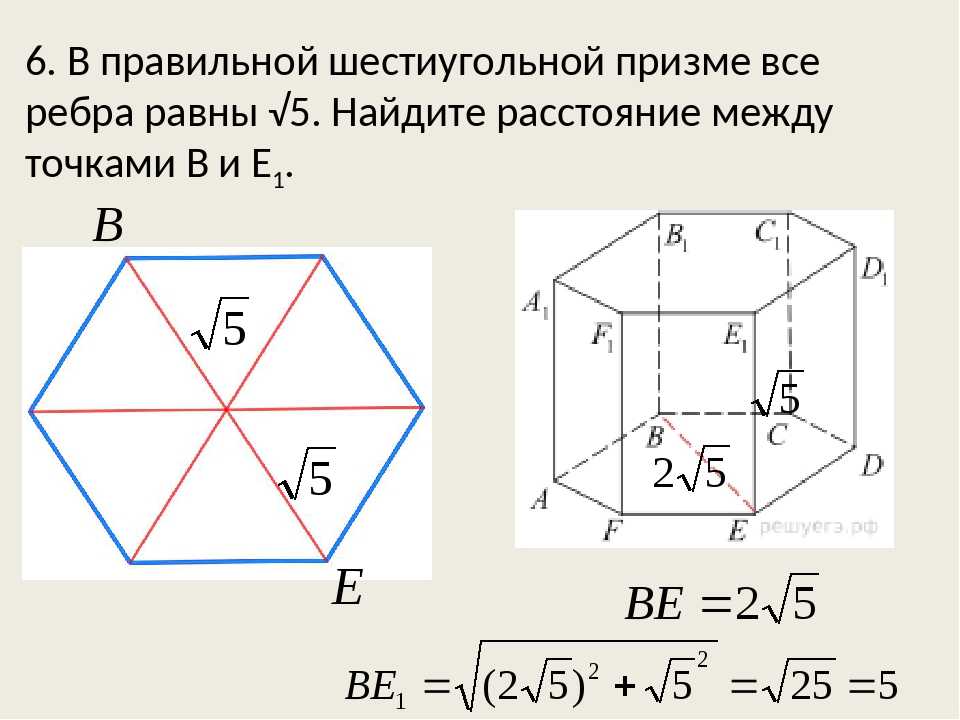 Шестиугольная призма имеет 8 граней, 18 ребер и 12 вершин. Он имеет равные верхнее и нижнее основания с диагоналями, пересекающими центральную точку правильного шестиугольника.
Шестиугольная призма имеет 8 граней, 18 ребер и 12 вершин. Он имеет равные верхнее и нижнее основания с диагоналями, пересекающими центральную точку правильного шестиугольника.
Площадь поверхности шестиугольной призмы выражается в квадратных единицах, распространенными единицами измерения являются квадратные метры, квадратные сантиметры, квадратные дюймы и т. д. Как и другие трехмерные формы, шестиугольная призма также может иметь два типа площадей:
- Общая площадь поверхности (TSA)
- Площадь боковой поверхности (LSA)
Формула площади поверхности шестиугольной призмы
Площадь поверхности шестиугольной призмы равна сумме площадей ее граней и основания. Площадь поверхности шестиугольной призмы дает площадь каждой грани призмы. Если длина апофемы призмы равна «а», длина основания призмы равна «b», а высота призмы равна «h», площадь поверхности шестиугольной призмы определяется как:
Общая площадь поверхности, TSA = 2 (площадь основания шестиугольника) + 6 (площадь грани прямоугольника) кв.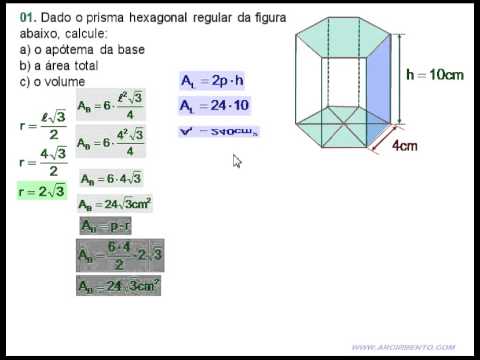
Площадь боковой поверхности, LSA = Ph = 6 (площадь прямоугольника) = 6ah кв. единиц
- a = длина основания
- а = длина апофемы
- ч = высота
В случае правильной шестиугольной призмы общая площадь поверхности, TSA = 6ah + 3√3a 2 , где a = длина основания и h = высота призмы. Формула шестиугольной призмы для расчета площади поверхности остается одинаковой для всех видов шестиугольных призм. Шестиугольные призмы могут быть правильными или неправильными.
- Правильная шестиугольная призма представляет собой шестиугольную призму, имеющую в основании правильные шестиугольники и все стороны одинаковой длины.
- Неправильная шестиугольная призма имеет неправильные шестиугольные основания, поэтому стороны ее шестиугольных оснований не имеют одинаковой длины.
Расчет площади поверхности шестиугольной призмы
Возьмем шестиугольную призму, имеющую длину апофемы «а», длину основания «b» и высоту «h». Для определения разрезаем шестигранную призму на ее сетку и вскрываем ее. Общая формула площади боковой поверхности призмы – это произведение ее основания на высоту. Таким образом, площадь боковой поверхности шестиугольной призмы можно определить, найдя периметр основания призмы, умноженный на ее высоту. Мы знаем, что основание шестиугольной призмы имеет форму шестиугольника.
Для определения разрезаем шестигранную призму на ее сетку и вскрываем ее. Общая формула площади боковой поверхности призмы – это произведение ее основания на высоту. Таким образом, площадь боковой поверхности шестиугольной призмы можно определить, найдя периметр основания призмы, умноженный на ее высоту. Мы знаем, что основание шестиугольной призмы имеет форму шестиугольника.
Площадь боковой поверхности шестиугольной призмы
Площадь боковой поверхности шестиугольной призмы равна сумме площадей шести прямоугольных граней. Таким образом, площадь боковой поверхности, L = 6ah = 6ah кв. единиц
Общая площадь поверхности шестиугольной призмы
Общая площадь поверхности, T = 6 (площадь прямоугольной грани) + 2 (площадь основания шестиугольника) кв. единиц . = 6ah + 3√3a 2
Как найти площадь поверхности шестиугольной призмы?
Для расчета площади поверхности шестиугольной призмы используются следующие шаги:
- Шаг 1: Вычислите площадь шестиугольного основания по формуле 3√3a 2
- Шаг 2: Найдите площадь шести прямоугольных граней.

- Шаг 3: Сложите все площади вместе, чтобы получить общую площадь поверхности квадратной призмы, а площадь 6 прямоугольных граней дает боковую площадь квадратной призмы.
Таким образом, общая площадь поверхности шестиугольной призмы равна 6ah + 3√3a 2 , а площадь боковой поверхности равна 6ah в квадратных единицах.
Пример: Определите общую площадь поверхности и площадь боковой поверхности шестиугольной призмы с длиной основания 4 дюйма и высотой 11 дюймов.
Решение: Учитывая A = 4 дюйма и H = 11 дюймов
Боковая площадь поверхности гексагональной призмы = 6AH = 6 × 4 × 11 = 264 квадратных дюймов
Общая площадь гексагональной PRISM = LSA + 3√ 3а 2 = 264 + 3√3 × (4) 2
⇒ АСП = 264 + 83,136
.
⇒ TSA = 347,136 квадратных дюймов
Таким образом, общая площадь поверхности шестиугольной призмы составляет 347,136 квадратных дюймов.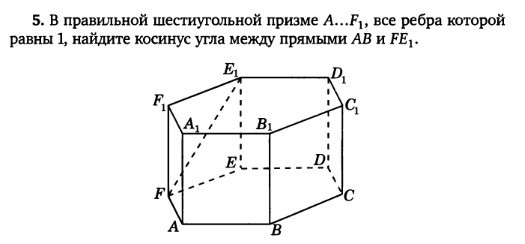
Часто задаваемые вопросы о площади поверхности шестиугольной призмы
Какова площадь поверхности шестиугольной призмы?
Площадь поверхности шестиугольной призмы относится к общей площади, покрытой поверхностями шестиугольной призмы. Площадь поверхности шестиугольной призмы дает площадь каждой грани призмы. Единица площади поверхности призмы выражается в квадратных единицах, таких как квадратные метры, квадратные сантиметры, квадратные дюймы и т. д.
По какой формуле найти площадь поверхности шестиугольной призмы?
Площадь поверхности шестиугольной призмы определяется как общая площадь поверхности, T = 2 (площадь основания шестиугольника) + 6 (площадь грани прямоугольника) кв. единиц. = 6b(a + h), где длина апофемы призмы равна «a», длина основания призмы равна «b», а высота призмы равна «h». В случае правильной шестиугольной призмы TSA = 6ah + 3√3a 2
Как найти общую площадь поверхности шестиугольной призмы?
Чтобы найти общую площадь поверхности шестиугольной призмы, выполните шаги, указанные ниже:
- Шаг 1: Проверьте предоставленную информацию.
 Определите значения длины апофемы, длины основания и высоты призмы.
Определите значения длины апофемы, длины основания и высоты призмы. - Шаг 2: Подставьте эти значения в формулу площади поверхности шестиугольной призмы, TSA = 6b(a + h)
- Шаг 3: Запишите значение площади поверхности шестиугольной призмы в соответствующих единицах измерения.
Как найти площадь боковой поверхности шестиугольной призмы?
Чтобы найти площадь боковой поверхности шестиугольной призмы, выполните следующие действия:
- Шаг 1: Найдите значения длины апофемы, длины основания и высоты шестиугольной призмы.
- Шаг 2: Подставьте эти значения в формулу площади боковой поверхности шестиугольной призмы, LSA = 6ah
- Шаг 3: Запишите полученное значение в кубических единицах
Как найти высоту шестиугольной призмы, зная площадь ее боковой поверхности и длину апофемы?
Формула для расчета площади боковой поверхности шестиугольной призмы: 6ah.
- Шаг 1: Проверьте площадь боковой поверхности и определите длину апофемы.

- Шаг 2: Разделите площадь боковой поверхности на 6а, чтобы найти высоту призмы.
Что произойдет с площадью боковой поверхности шестиугольной призмы, если ее высоту удвоить?
Мы знаем, что площадь боковой поверхности шестиугольной призмы равна 6ah. Если его высоту увеличить вдвое, площадь его боковой поверхности будет равна 6a(2h), то есть 2(6ah). Таким образом, можно сделать вывод, что площадь его боковой поверхности также увеличится вдвое.
Что произойдет с общей площадью поверхности шестиугольной призмы, если длину апофемы удвоить?
Мы знаем, что общая площадь поверхности шестиугольной призмы равна 6b(a + h). Удвоение длины апофемы обязательно приведет к увеличению значения площади, но площадь не удвоится.
Шестиугольная призма – формула, свойства, примеры, определение
Шестиугольная призма представляет собой шестиугольник с основанием и вершиной в форме шестиугольника. В нашей повседневной жизни мы сталкиваемся с различными примерами шестиугольной призмы, такими как карандаши, орехи, подарочные коробки, здания и т. Д. У нее 8 граней, 12 вершин и 18 ребер. Мы видим различные призматические примеры, но не все они шестиугольные. Давайте узнаем больше о шестиугольной призме в этой статье.
Д. У нее 8 граней, 12 вершин и 18 ребер. Мы видим различные призматические примеры, но не все они шестиугольные. Давайте узнаем больше о шестиугольной призме в этой статье.
| 1. | Что такое шестиугольная призма? |
| 2. | Свойства шестиугольной призмы |
| 3. | Сеть шестиугольной призмы |
| 4. | Площадь поверхности шестиугольной призмы |
| 5. | Объем шестиугольной призмы |
| 6. | Часто задаваемые вопросы о шестиугольной призме |
Что такое шестиугольная призма?
Шестиугольная призма представляет собой трехмерную призму с двумя параллельными концами одинакового размера и формы, называемыми основаниями. Шестиугольная призма имеет 6 сторон, известных как грани, которые имеют форму параллелограмма. По определению, шестиугольная призма — это призма с двумя основаниями в форме шестиугольников и 6 гранями в форме прямоугольников.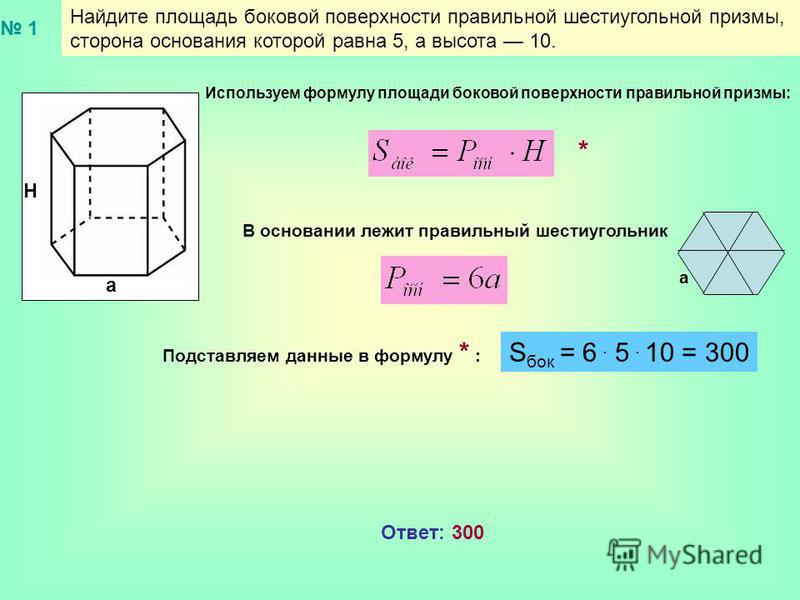 Существует 2 различных типа шестиугольных призм: правильные шестиугольные призмы и неправильные шестиугольные призмы. Правильная шестиугольная призма — это призма, основания которой имеют форму шестиугольника со всеми сторонами одинаковой длины (или состоят из правильного шестиугольника). Принимая во внимание, что неправильная шестиугольная призма — это призма, у которой стороны шестиугольных оснований не имеют одинаковой длины. Углы правильной шестиугольной призмы одинаковы, тогда как у неправильной призмы углы разные.
Существует 2 различных типа шестиугольных призм: правильные шестиугольные призмы и неправильные шестиугольные призмы. Правильная шестиугольная призма — это призма, основания которой имеют форму шестиугольника со всеми сторонами одинаковой длины (или состоят из правильного шестиугольника). Принимая во внимание, что неправильная шестиугольная призма — это призма, у которой стороны шестиугольных оснований не имеют одинаковой длины. Углы правильной шестиугольной призмы одинаковы, тогда как у неправильной призмы углы разные.
Шестиугольная призма Определение
Шестиугольная призма представляет собой многогранник с 8 гранями, 18 ребрами и 12 вершинами, где из 8 граней 6 граней имеют форму прямоугольников, а 2 грани имеют форму шестиугольников. Верх и низ шестиугольной призмы имеют форму шестиугольника и равны друг другу. В шестиугольной призме длинные диагонали всегда пересекают центральную точку шестиугольника, начиная с вершины основания, тогда как короткие диагонали не пересекают центральную точку, поскольку диагональ проходит от одной вершины основания к другой.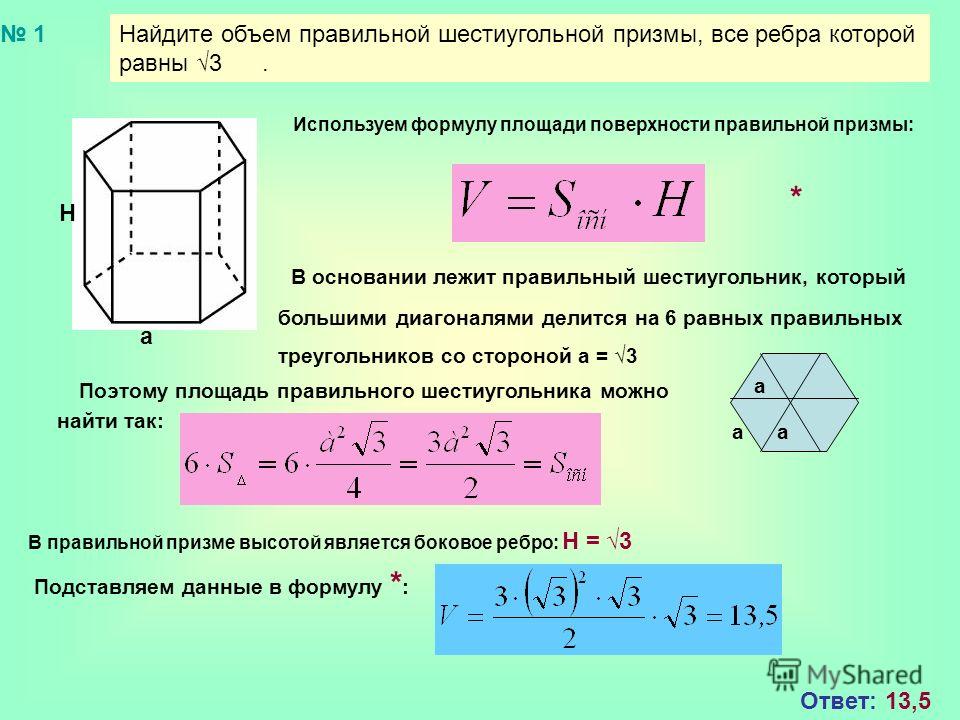
Свойства шестиугольной призмы
Шестиугольная призма представляет собой призму с двумя шестиугольными основаниями и шестью прямоугольными гранями. Свойства шестиугольной призмы:
- У нее 8 граней, 18 ребер и 12 вершин
- Верхнее и нижнее основания равны друг другу по длине
- Диагонали пересекают центр правильной шестиугольной призмы
- В правильной шестиугольной призме все углы шестиугольника равны
- В неправильной шестиугольной призме все углы шестиугольника различны
Сеть шестиугольной призмы
Шестиугольная призма может быть сформирована из сетки. Когда объект открывается плоско, сетка шестиугольной призмы ясно показывает грани формы. После складывания шестиугольной призмы становится видна трехмерная версия призмы. Для формы может быть несколько сеток, ниже приведена одна из сеток шестиугольной призмы.
Площадь поверхности шестиугольной призмы
Площадь поверхности представляет собой сумму поверхностей всего 3D-объекта. Следовательно, площадь поверхности шестиугольной призмы представляет собой комбинацию длины основания и высоты шестиугольной призмы. Следовательно,
Следовательно, площадь поверхности шестиугольной призмы представляет собой комбинацию длины основания и высоты шестиугольной призмы. Следовательно,
Площадь поверхности шестиугольной призмы = 6ah + 3√3a 2 квадратных единиц , где a — длина основания, а h — высота.
Объем шестиугольной призмы
Объем шестиугольной призмы находится путем вычисления площади основания, высоты и длины. Следовательно, формула для нахождения объема:
Объем шестиугольной призмы = [(3√3)/2]a 2 h кубических единиц , где a — длина основания, а h — высота призмы.
Связанные темы
Ниже перечислены несколько интересных тем, связанных с шестиугольной призмой, проверьте!
- Площадь поверхности прямоугольной призмы
- Площадь полигона
- Площадь прямоугольника
Примеры шестиугольной призмы
Пример 1: Найдите объем шестиугольной призмы с длиной основания 5 единиц и высотой 10 единиц.

Решение: Дано, a = 5 и h = 10, где a — длина основания, а h — высота шестиугольной призмы.
Объем шестиугольной призмы = [(3√3)/2]a 2 ч
Объем = [(3√3)/2] × 5 2 × 10
Объем = [(3√3)/2] × 250
Объем = 649,51 кубических единиц
90 002 Следовательно, объем шестигранной призмы равен 649,51 кубических единиц.Пример 2: Найдите площадь поверхности шестиугольной призмы с основанием, равным 5 единицам, и высотой, равной 10 единицам.
Решение: Даны a = 5 и h = 10, где a — длина основания, а h — высота шестиугольной призмы.
Площадь поверхности шестиугольной призмы = 6ah + 3√3a 2
Площадь = 6 × 5 × 10 + 3√3 × (5) 2
Площадь = 300 + 129,9 9 0003
Площадь = 429,9 квадратных единиц
Следовательно, площадь поверхности шестиугольной призмы составляет 429,9 квадратных единиц.
Пример 3: Найдите высоту шестиугольной призмы, если площадь ее поверхности 396 квадратных футов, длина апофемы 3 фута, длина основания 6 футов.

Решение:
Дано, Общая площадь поверхности = 396 квадратных футов, длина апофемы, a = 3 фута, и длина основания, b = 6 футов
Общая площадь поверхности шестиугольной призмы = 6b(a+h)
⇒ 6 × 6 (3 + ч) = 396
⇒ 36(3 + ч) = 396
. ⇒ 3 + ч = 396/36
⇒ h = 11 — 3 = 8 футовСледовательно, высота шестиугольной призмы равна 8 футам.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по шестиугольной призме
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о шестиугольной призме
Что такое шестиугольная призма?
Шестиугольная призма представляет собой трехмерную фигуру, верхняя и нижняя части которой имеют форму шестиугольника. Это многогранник с 8 гранями, 18 ребрами и 12 вершинами, где из 8 граней 6 граней имеют форму прямоугольников, а 2 грани имеют форму шестиугольников. Некоторыми из реальных примеров шестиугольной призмы являются карандаши, коробки, орехи и т. д.
Это многогранник с 8 гранями, 18 ребрами и 12 вершинами, где из 8 граней 6 граней имеют форму прямоугольников, а 2 грани имеют форму шестиугольников. Некоторыми из реальных примеров шестиугольной призмы являются карандаши, коробки, орехи и т. д.
Из скольких вершин и ребер состоит шестиугольная призма?
Шестиугольная призма состоит из 12 вершин и 18 ребер. Вершины находятся как в верхней, так и в нижней части шестиугольной призмы и объединяются вместе, образуя призму с 18 ребрами.
Какая формула используется для расчета площади поверхности шестиугольной призмы?
Для расчета площади поверхности шестиугольной призмы используется формула Площадь поверхности шестиугольной призмы = 6ah + 3√3a 2 квадратных единиц, где a — длина основания, а h — высота.
По какой формуле вычисляется объем шестиугольной призмы?
Для расчета объема шестиугольной призмы используется формула: Объем шестиугольной призмы = [(3√3)/2]a 2 h кубических единиц, где a — длина основания, а h — высота призмы
Что такое Сеть шестиугольной призмы?
Сеть шестиугольной призмы — это 2D-изображение, из которого формируется шестиугольная призма путем соединения краев сетки.

 Определите значения длины апофемы, длины основания и высоты призмы.
Определите значения длины апофемы, длины основания и высоты призмы.
Leave A Comment