ЕГЭ Информатика Тест задание 15 Поиск путей в графе
ЕГЭ Информатика Тест задание 15 Поиск путей в графе| Правильно | Ошибки | Пустые ответы |
|---|---|---|
×

 Вычисление количества информации
Вычисление количества информации Анализ программ с циклами и подпрограммами
Анализ программ с циклами и подпрограммамиПодготовка к ЕГЭ по Информатике
Задания на тему «Поиск путей в графе».
Категория вопросов: Все категории задания Подсчет количества маршрутов 1)
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М.
Сколько существует различных путей из города А в город М, проходящих через город Л?
Ваш ответ:
2) На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует способов добраться из пункта А в пункт З?
Ваш ответ:
3) На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует способов добраться из пункта А в пункт Л?
Ваш ответ:
4)
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует способов добраться из пункта А в пункт Л?
Ваш ответ:
5) На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует способов добраться из пункта А в пункт Л?
Ваш ответ:
6)
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует способов добраться из пункта А в пункт М?
Ваш ответ:
7) На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует способов добраться из пункта А в пункт Ж?
Ваш ответ:
8) На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О, П, Р, С.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует способов добраться из пункта А в пункт С?
Ваш ответ:
9)
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует способов добраться из пункта А в пункт О?
Ваш ответ:
10) На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует способов добраться из пункта А в пункт Л?
Ваш ответ:
11) На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует способов добраться из пункта А в пункт К?
Ваш ответ:
12)
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует способов добраться из пункта А в пункт М?
Ваш ответ:
13) На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует способов добраться из пункта А в пункт Н?
Ваш ответ:
14) На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О, П, Р, С, Т.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует способов добраться из пункта А в пункт Т?
Ваш ответ:
15)
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О, П, Р, С.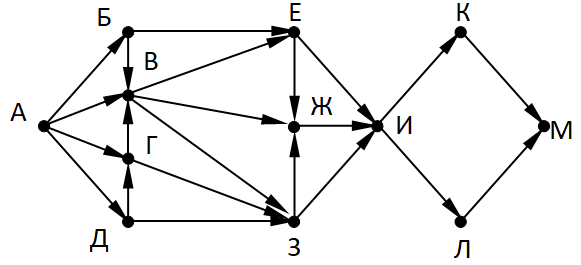
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует способов добраться из пункта А в пункт С?
Ваш ответ:
16) На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н, О, П
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует способов добраться из пункта А в пункт П?
Ваш ответ:
Задача 15 — разбор задания ЕГЭ по предмету Информатика
- Newtonew
- ProTeachers
- MOOC 2016
- Большая переменная
Мы в соц.сетях:
- Статьи
- ·
- Разборы
- ·
- Новости
Написать статью
Решение №1
Будем решать задачу от обратного: будем последовательно у каждой вершины указывать, сколько из этой вершины существует путей в М. При этом мы будем пользоваться следующей логикой:
При этом мы будем пользоваться следующей логикой:
Допустим, у нас есть вершины А, Б, В и Г. И нам надо посчитать количество путей из А в Г. При этом из А есть дороги только в Б и В. При этом из Б в Г существует 5 маршрутов, а из В в Г — 7. Тогда количество маршрутов из А в Г равно количеству маршрутов из Б в Г плюс количество маршрутов из В в Г: 5+7=12.
Воспользуемся этим правилом:
Из К в М, очевидно, ведёт одна дорога. Равно как и из Л в М. Значит, из И в М будут вести две дороги: 1+1=2.
Из Ж есть путь только в И, поэтому кол-во маршрутов из Ж в М также равно 2. Следовательно, количество маршрутов из З в М равно 4, так как из З можно попасть в Ж (2 маршрута) или в И (2 маршрута): 2+2=4. Аналогично из Е: количество маршрутов равно также 4.
- Теперь посчитаем количество маршрутов из точки В (Б и Г мы не можем посчитать из-за незнания маршуртов в точке В, а точку Д — из-за незнания точки Г).
- Из точки В можно попасть в Е (4 маршрута), или в Ж (2 маршрута) или в З (4 маршрута), то есть 4+2+4=10 всего.

- Значит, из Б будет 4 (точка Е) + 10 (точка В) = 14 маршрутов.
- Из точки Г — 4 (точка З) + 10 (точка В) = 14 маршрутов.
- Значит, из точки Д будет 14 (точка Г) + 4 (точка З) = 18 маршрутов.
- Значит, из точки А будет 14 (Б) + 10 (В) + 14 (Г) + 18 (Д) = 56 маршрутов.
Ответ: 56 маршрутов.
Сообщение:
Запрос успешно отправлен. В ближайшее время расширенный доступ будет предоставлен.
– Oбразование как Стиль Жизни
Присылайте свои колонки
и предложения
У вас есть интересная новость
или материал из сферы образования
или популярной науки?
Расскажите нам!
[email protected]
© 2014-2023 Newtonew. 12+
Просветительский медиа-проект об образовании,
посвящённый самым актуальным и полезным
концепциям, теориям и методикам, технологиям
и исследованиям, продуктам и сервисам. Мы
говорим о том, как развиваются и изменяются
образование и наука.
Мы
говорим о том, как развиваются и изменяются
образование и наука.
Копирование материалов возможно только
с разрешения редакции Newtonew.
ЕГЭ спецпроект ProTeachers
MOOC 2016 Большая переменная
Физика: игра света
Маршрут в будущее
Считаные годы
Образование XXI века
Мы используем файлы cookie для улучшения пользовательского опыта. Подробнее вы можете посмотреть в нашем пользовательском соглашении.
App Store Google Play
Подписаться на рассылку
Подписаться на рассылку
Авторизация на сайте
Вход через соц.сети:
ВКонтакте Facebook Google
Новый пользователь
Введите ваш email:
Введите пароль:
Повторите пароль:
назад
Напомнить пароль
Введите email, на который вы зарегистрированы:
назад
Пароль выслан
Мы выслали ваш пароль для входа в систему на указанный email.
Не забывайте о том, что вы можете авторизоваться в системе через социальные сети. Если при регистрации в соц.сетях вы указывали тот же email что и на нашем сайте, то после авторизации вы попадете в свой профиль.
Вход через соц.сети:
ВКонтакте Facebook Google
Подтвердите регистрацию
На указанный e-mail было отправлено письмо со ссылкой. Пожалуйста, перейдите по ссылке для подтверждения.
Вход через соц.сети:
ВКонтакте Facebook Google
Регистрация подтверждена
Вы успешно зарегистрировались
2}\], где ‘\[a\]’ — длина любой стороны восьмиугольника и далее, взяв разность площадей внутреннего и внешнего восьмиугольника, получим требуемое решение. Полный пошаговый ответ:
В геометрии площадь можно определить как область или пространство, занимаемое геометрической фигурой или формой. Правильный восьмиугольник — это тип многочлена, у которого восемь сторон равны по длине, а восемь углов имеют одинаковую меру. 2}\] 92}\] ———(2)
2}\] 92}\] ———(2)
Площадь данного правильного восьмиугольного кадра:
\[ \Стрелка вправо \,\,\,\]Площадь внешнего восьмиугольника \[ — \] Площадь внутреннего восьмиугольника
\[ \Rightarrow \,\,\,A = 392\left( {1 + \sqrt 2 } \right) — 288\left( {1 + \sqrt 2 } \right)\]
Take общий терм \[\left( {1 + \sqrt 2 } \right)\], затем
\[ \left( {1 + \sqrt 2 } \right)\left( {392 — 288} \right)\ ]
\[ \Rightarrow \,\,\,\left( {1 + \sqrt 2 } \right)\left( {104} \right)\]
Применение распределительного свойства 92}\].
Примечание: Помните, что в многоугольнике правильной формы длина всех сторон и углы между любыми двумя сторонами всегда равны, и в вопросах, основанных на измерениях, вы не должны забывать указывать единицу измерения с окончательным ответом. Тогда как единицей площади будет квадрат единицы длины стороны многоугольника.
На рисунке показано устройство, в котором используется принцип передачи давления…
Перейти к
- Упражнение 4А
- Упражнение 4Б
- Глава 1 – Измерения и эксперименты
- Глава 2.
 Движение в одном измерении
Движение в одном измерении - Глава 3 Законы движения
- Глава 4 Давление в жидкостях и атмосферное давление
- Глава 5. Аптраст в жидкости. Принцип Архимеда и плавучесть.
- Глава 6 Тепло и энергия
- Глава 7 Отражение света
- Глава 8 Распространение звуковых волн
- Глава 9 Текущее электричество
- Глава 10 Магнетизм
Главная > Селина Солюшнс Класс 9 Физика > Глава 4 — Глава 4 Давление в жидкостях и атмосферное давление > Упражнение 4А > Вопрос 30
Вопрос 30. Упражнение 4A
Упражнение 4A
На рисунке показано устройство, использующее принцип передачи давление.
(i) Назовите части, обозначенные буквами X и Y.
(ii) Опишите, что происходит с клапанами A и B и с количество воды в двух цилиндрах, когда плечо рычага опущено.
(iii) Объясните, что происходит с клапанами A и B в Часть II).
(iv) Что происходит, когда открывается выпускной клапан?
(v) Что происходит с клапаном В в цилиндре Р, когда рычаг рука поднята?
(vi) Обоснуйте свой ответ в части (v)
(vii) Укажите один случай использования вышеуказанного устройства.
Ответ:
(i) X – нажимной плунжер
Y – плунжер насоса
(ii) Когда плечо рычага перемещается вниз, клапан A открывается, а клапан В закрывается. Благодаря этому вода из цилиндра Р выбрасывается в цилиндр Q
(iii) Клапан B закрывается. Именно из-за увеличения
давление в цилиндре P. Давление передается на соединительную трубу, и когда давление в
трубе выше, чем давление в цилиндре Q, клапан А раскрывает.
(iv) Плунжер Q опущен, и вода в цилиндре Q высвобождается в резервуаре при открытии выпускного клапана.
(v) Клапан B открывается вверх.
(vi) Это связано с тем, что давление в цилиндре P уменьшается
(vii) Одно применение – используется для выдавливания масла из льняного семена хлопка
Похожие вопросы
Дайте определение термину тяга. Укажите его единицу СИ.
Что понимается под давлением? Укажите его единицу СИ.
а) Какая физическая величина измеряется в бруске? (b) Как единица бар связана с единицей СИ p…
Определить один паскаль (Па) как единицу давления в системе СИ.
Укажите, является ли тяга скаляром или вектором?
Укажите, является ли давление скаляром или вектором?
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 4A
Упражнение 4B
Главы
Глава 1 – Измерения и эксперименты
Глава 2 Движение в одном измерении
Глава 3.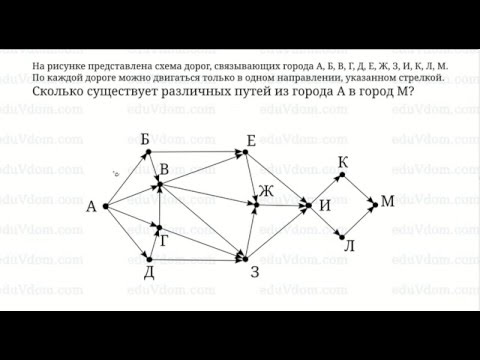


 Движение в одном измерении
Движение в одном измерении
Leave A Comment