Механическая работа — определение, формула, виды, свойства
Покажем, как применять знание физики в жизни
Начать учиться
121.5K
Работа — не волк! А еще и не мощность и не энергия. В этой статье разберемся, что же такое механическая работа в физике, а помогут нам в этом древнегреческие мифы.
Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.
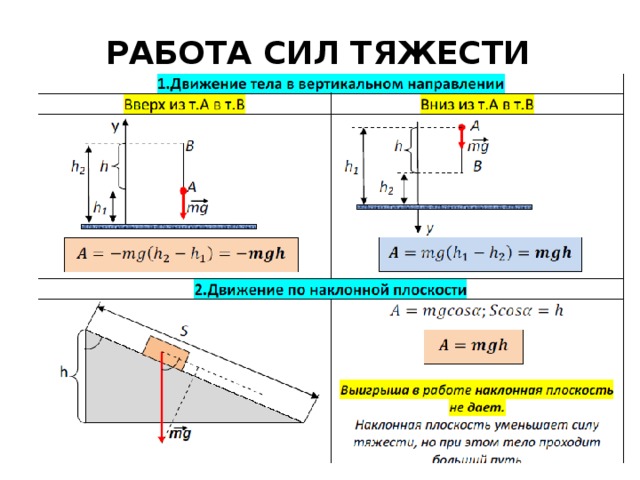
Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.
Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.
Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.
Механическая работа А = FS A — механическая работа [Дж] S — путь [м] |
Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.
Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.
Механическая работа А = FScosα A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] α — угол между векторами силы и перемещения [°] |
 Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.
Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.Для совершения работы необходимы два условия:
- чтобы на тело действовала сила,
- чтобы происходило перемещение тела.
Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.
Запомнить!
Работа равна нулю, если:
- при приложенной силе перемещение отсутствует;
- сила не приложена и тело перемещается по инерции;
- угол между векторами силы и перемещения равен 90°.

Полезная и затраченная работа
Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».
Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.
Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.
Потенциальная энергия Еп = mgh m — масса тела [кг] g — ускорение свободного падения [м/с2] На планете Земля g ≈ 9,8 м/с2 |
Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] |
И как же достоверно определить, какая работа полезная, а какая затраченная?
Все очень просто! Задаем два вопроса:
За счет чего происходит процесс?
Ради какого результата?
В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).
Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.
Мощность
На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.
Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
Мощность N = A/t N — мощность [Вт] A t — время [с] |
Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.
Также для мощности справедлива другая формула:
Мощность N = Fv F — приложенная сила [Н] v — скорость [м/с] |
Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.
Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:
Мощность N = Fvcosα N — мощность [Вт] F — приложенная сила [Н] v — скорость [м/с] α — угол между векторами силы и скорости [°] |
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Примеры решения задач
Задача 1
Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:
На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:
Выталкивающая сила.
Сила вязкого трения.
Сила тяжести.
Ни одна из перечисленных сил.
Решение
Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.
Ответ: 3.
Задача 2
Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?
Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?
Решение
Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:
Ответ: 3200 Дж.
Задача 3
Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?
Решение
В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.
Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.
Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:
A = Fl = 30 * 5 = 150 Дж
Ответ: 150 Дж.
Задача 4
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости vx тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение
На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.
Мощность можно найти по формуле N = Fv.
N = FV = 2×5 = 10 Вт
Ответ: 10 Вт.
Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!
Карина Хачатурян
К предыдущей статье
Поверхностное натяжение
К следующей статье
Идеальный газ
Получите индивидуальный план обучения физике на бесплатном вводном уроке
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Глава 14. Термодинамика
Изучение энергетических превращений в молекулярных системах составляет содержание термодинамики. Для решения задач на термодинамику необходимо знать определения внутренней энергии, количества теплоты, теплоемкости и ряда других величин. Необходимо также понимать и уметь использовать в простейших случаях первый закон термодинамики как балансовое соотношение, описывающее процессы превращения энергии из одних форм в другие. Также нужно знать основные свойства процессов перехода вещества из одних агрегатных состояний в другие. Рассмотрим эти вопросы.
Для решения задач на термодинамику необходимо знать определения внутренней энергии, количества теплоты, теплоемкости и ряда других величин. Необходимо также понимать и уметь использовать в простейших случаях первый закон термодинамики как балансовое соотношение, описывающее процессы превращения энергии из одних форм в другие. Также нужно знать основные свойства процессов перехода вещества из одних агрегатных состояний в другие. Рассмотрим эти вопросы.
Внутренней энергией тела называется сумма кинетической энергии молекул и потенциальной энергии их взаимодействия друг с другом. Для жидкостей и твердых тел из-за сильного взаимодействия молекул друг с другом вычислить внутреннюю энергию не удается. Внутреннюю энергию можно вычислить только для идеальных газов, в которых можно пренебречь энергией взаимодействия молекул друг с другом и считать, что внутренняя энергия равна сумме кинетических энергий молекул. Для одноатомного газа (т.е. газа, каждая молекула которого состоит из одного атома) внутренняя энергия определяется соотношением
(14. |
где — количество вещества газа (число молей), — универсальная газовая постоянная, — абсолютная температура. Заметим, что с помощью закона Клапейрона-Менделеева формула (14.1) может быть преобразована к виду
(14.2) |
где — давление, — объем газа.
Внутренняя энергия тела может измениться при теплообмене, когда молекулы тела сталкиваются с более быстрыми или более медленными молекулами других тел и получают от них или отдают им энергию, или в процессе совершения механической работы над этим телом внешними силами. В связи с эти вводят следующие определения. Количеством теплоты, переданным некоторому телу, называют энергию, переданную этому телу в процессе хаотических столкновений молекул. Процесс передачи энергии в виде теплоты называют процессом теплопередачи. Если внешние силы не совершают над телом работы, для процесса теплопередачи справедливо следующее балансовое соотношение
(14. |
где — изменение внутренней энергии тела, — количество переданной этому телу теплоты. Поскольку изменение внутренней энергии тела может быть и положительным , и отрицательным , из закона (14.3) следует, что количеству теплоты следует придать алгебраический смысл: если энергия передается телу, количество переданной этому телу теплоты нужно считать положительным , если забирается — отрицательным .
Внутренняя энергия тела изменяется при сжатии тела, трении и ряде других механических процессах. В этом случае на изменение внутренней энергии расходуется работа , совершаемая над телом внешними силами
(14.4) |
(конечно, здесь подразумевается, что работа не расходуется на энергию движения тела как целого, а только на изменение внутреннего движения, т.е. все перемещения тела как целого или его макроскопических частей должны происходить бесконечно медленно). Очевидно, работа внешних сил положительна, если эти силы сжимают тело и его объем уменьшается, и отрицательна — если объем тела увеличивается. В первом случае, как это следует из (14.4), внутренняя энергия тела возрастает (), во втором убывает ().
Очевидно, работа внешних сил положительна, если эти силы сжимают тело и его объем уменьшается, и отрицательна — если объем тела увеличивается. В первом случае, как это следует из (14.4), внутренняя энергия тела возрастает (), во втором убывает ().
Одновременно с внешними силами при сжатии или расширении тел совершают работу и сами эти тела. Рассмотрим, например, газ, находящийся в цилиндрическом сосуде и отделенный от атмосферы поршнем (см. рисунок). И при сжатии, и при расширении газа силы, действующие на поршень со стороны газа, совершают над ним работу (в первом случае отрицательную, во втором положительную). При этом, поскольку поршень перемещается бесконечно медленно, силы, действующие на него со стороны газа и внешние силы практически равны друг другу как при сжатии, так и при расширении газа (в противном случае в балансе энергии необходимо было учитывать кинетическую энергию, приобретенную поршнем). Поэтому работа, совершенная газом и внешними силами над газом равны по величине, но отличаютсязнаком1. Очевидно, работа газа положительна, если газ расширяется, и отрицательна, если газ сжимается.
Очевидно, работа газа положительна, если газ расширяется, и отрицательна, если газ сжимается.
При решении задач на термодинамику следует помнить одно важное свойство работы газа, которое во многих случаях позволяет ее легко вычислить. Работа газа в некотором процессе численно равна площади фигуры под графиком зависимости давления от объема в этом процессе. В частности в изобарическом процессе при давлении , в котором объем газа изменился от значения до значения , газ совершает работу (см. рисунок; площадь графика, соответствующая работе, выделена):
(14.5) |
где — количество вещества газа, — изменение температуры в рассматриваемом процессе.
Если газ участвует в процессе, в котором одновременно имеет место и теплообмен, и совершается работа, то справедливо соотношение
(14.6) |
которое называется первым законом термодинамики (здесь — работа газа).
Закон (14.6) позволяет найти одну из входящих в него величин, если заданы две других. Если задается только одна из величин, входящих в закон (14.6), но как-то определяется процесс, происходящий с газом, то две остальные величины могут быть определены. Например, в изохорическом процессе не совершается работа, поэтому
(14.7) |
В изотермическом процессе не меняется внутренняя энергия газа, поэтому
(14.8) |
В адиабатическом процессе (процессе без теплообмена с окружающей средой) , поэтому
(14.9) |
В изобарическом процессе есть связь между изменением внутренней энергии газа и его работой. Из формул (14.1) и (14.5) заключаем, что работа одноатомного идеального газа и изменение его внутренней энергии в изобарическом процессе связаны соотношением
(14. |
Для характеристики процессов нагрева-остывания тела вводят понятие теплоемкости тела , которая определяется как
(14.11) |
где — количество теплоты, сообщенное телу в некотором процессе, — изменение его температуры в этом процессе. Подчеркнем, что и в формуле (14.11) не независимы, а связаны друг с другом: — это то изменение температуры, которое происходит благодаря сообщению телу количества теплоты . Поэтому теплоемкость (14.11) не зависит от и , а зависит от свойств тела и происходящего с ним процесса.
Если тело однородно, то его теплоемкость пропорциональна его массе . Поэтому отношение является характеристикой вещества тела и называется его удельной теплоемкостью. Удельная теплоемкость представляет собой экспериментально измеряемую (табличную) характеристику веществ. Из определения удельной теплоемкости следует, что если телу массой , изготовленному из вещества с удельной теплоемкостью , сообщить количество теплоты , то будет справедливо соотношение
(14. |
где — изменение температуры тела.
Приведем теперь решения данных в первой части задач.
В задаче 14.1.1 внутренняя энергии газа увеличится согласно формуле (14.1) — ответ 1.
Для ответа на вопрос задачи 14.1.2 удобно использовать формулу для внутренней энергии газа в виде (14.2). По этой формуле находим, что внутренняя энергия увеличилась в 3/2 раза (ответ 2). Обратим внимание читателя, что причина изменения давления и объема может быть любой — ответ от этого не зависит. Может измениться или температура газа, или количество вещества, или и то и другое одновременно.
Поскольку температура и количество вещества газа не изменялись в рассматриваемом в задаче 14.1.3 процессе, внутренняя энергия газа не изменилась (ответ 3).
В задаче 14.1.4 следует воспользоваться определением теплоемкости (14. 11). Для этого рассмотрим, например, ин-тервал времени , выделенный жирным на оси времени (см. рисунок). За этот интервал оба тела получили одинаковое количество теплоты , поскольку нагреватели одинаковы. Изменение температур тел и можно определить по графику — эти величины отмечены фигурными скобками на оси температур. Поскольку из формулы (14.11) заключаем, что — ответ 2.
11). Для этого рассмотрим, например, ин-тервал времени , выделенный жирным на оси времени (см. рисунок). За этот интервал оба тела получили одинаковое количество теплоты , поскольку нагреватели одинаковы. Изменение температур тел и можно определить по графику — эти величины отмечены фигурными скобками на оси температур. Поскольку из формулы (14.11) заключаем, что — ответ 2.
В задаче 14.1.5 следует воспользоваться определением удельной теплоемкости. По формуле (14.12) находим
(ответ 1).
Для совершения работы необходимо механическое движение. Поскольку объем газа в задаче 14.1.6 не меняется, механическое движение отсутствует, работа газа равна нулю (ответ 4).
Применяя к рассматриваемому в задаче 14.1.7 процессу первый закон термодинамики (14.6) и учитывая, что в изохорическом процессе работа газа равна нулю, заключаем, что (ответ 3).
В изотермическом процессе не меняется внутренняя энергия идеального газа. Поэтому , и работа , совершенная над газом, определяется соотношением (14.4), (14.6): (задача 14.1.8 — ответ 2).
Поэтому , и работа , совершенная над газом, определяется соотношением (14.4), (14.6): (задача 14.1.8 — ответ 2).
Адиабатический процесс происходит без теплообмена с окружающими телами: . Поэтому из первого закона термодинамики (14.6) получаем в задаче 14.1.9 для работы газа (ответ 2).
Применяя первый закон термодинамики (14.6) к процессу, происходящему с газом в задаче 14.1.10, найдем, что внутренняя энергия газа увеличилась на 10 Дж (ответ 2).
Для решения задачи 14.2.1 можно использовать то обстоятельство, что работа газа численно равна площади фигуры, ограниченной графиком зависимости давления от объема и осью объемов. Из рисунка следует, что наибольшей является площадь под графиком процесса 1. Поэтому бóльшую работу газ совершает в процессе 1 (ответ 1).
В задаче 14.2.2 следует применить ко всем трем процессам, графики которых даны на рисунке к решению предыдущей задачи, первый закон термодинамики (14. 6) . Учитывая, что начальная и конечная температура газа во всех трех процессах одинакова, и, следовательно, одинаковы изменения внутренней энергии газа , а работа наибольшая в процессе 1 (см. решение предыдущей задачи), заключаем, что газ получил большее количество теплоты в процессе 1 (ответ 1).
6) . Учитывая, что начальная и конечная температура газа во всех трех процессах одинакова, и, следовательно, одинаковы изменения внутренней энергии газа , а работа наибольшая в процессе 1 (см. решение предыдущей задачи), заключаем, что газ получил большее количество теплоты в процессе 1 (ответ 1).
Работа газа положительна, если газ расширяется. Для доказательства этого утверждения представим газ в сосуде, ограниченном подвижным поршнем. Если газ расширяется, то и перемещение поршня и сила, действующая на него со стороны газа, направлены одинаково, поэтому работа газа положительна. При сжатии газа его работа отрицательна. Поэтому в задаче 14.2.3 работа газа положительна в процессе 3 (ответ 3).
Так как графики процессов 1–2 и 3–4 в задаче 14.2.4 — прямые, проходящие через начало координат, эти процессы — изохорические, и газ не совершает в них работу. А поскольку изменение внутренней энергии газа в этих процессах одинаково, то одинаковы и количества теплоты, сообщенные газу в этих процессах (ответ 3).
Задача 14.2.5 аналогична предыдущей. Рассматриваемый процесс — изохорический, поэтому изменение внутренней энергии газа равно сообщенному количеству теплоты = 100 кДж (ответ 2).
Вычисляя площадь под графиком процесса в задаче 14.2.6, находим работу газа (ответ 2).
В условии задачи 14.2.7 дано количество теплоты , которое забрали у газа. Первый закон термодинамики, в который входит эта величина, имеет вид
где — работа, совершенная над газом в рассматриваемом процессе. Подставляя в эту формулу данные в условии величины, находим = –5 Дж (ответ 1).
Чтобы понять, расширялся или сжимался газ в рассматриваемом в задаче 14.2.8 процессе, из первого закона термодинамики найдем работу газа: если она окажется положительной, газ расширялся, если отрицательной — сжимался. Из закона (14.6) находим
Поэтому газ сжимался (ответ 1).
Чтобы найти долю количества теплоты, которая пошла на увеличение внутренне энергии газа в изобарическом процессе (задача 14.2.9) воспользуемся формулой (14.5) для работы газа в этом процессе . Поскольку изменение внутренней энергии одноатомного идеального газа равно , заключаем, что изменение внутренней энергии газа составляет 3/2 от его работы. Поэтому 2/5 количества теплоты, сообщенного газу в изобарическом процессе тратится на работу, 3/5 — на изменение внутренней энергии газа (ответ 3).
Чтобы найти теплоемкость газа в изотермическом процессе (задача 14.2.10), применим к этому процессу определение теплоемкости (14.11)
Поскольку в изотермическом процессе при ненулевом количестве сообщенной теплоты, то теплоемкость газа равна бесконечности. Это означает следующее — в изотермическом процессе газу сообщают теплоту, а он не нагревается, что и означает бесконечную теплоемкость газа (теплота расходуется только на совершение работы).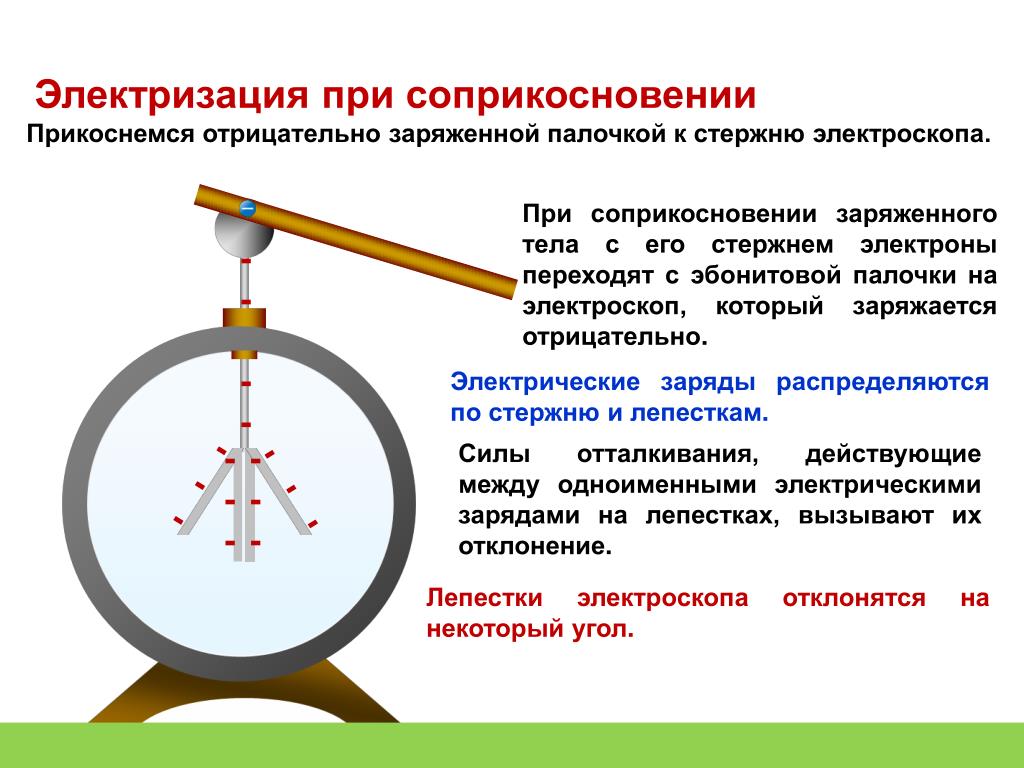
11 фактов (прочитайте сначала) —
В этой статье мы обсудим 11 фактов, связанных с тем, может ли смещение быть отрицательным или нет.
Ответ на вопрос, может ли смещение быть отрицательным или нет, – да. Уточним, почему смещение является отрицательным. Кратчайшее расстояние между начальным и конечным положением тела можно определить как его перемещение. Перемещение — это всегда прямой путь. Поскольку перемещение является векторной величиной, оно имеет определенное направление.
По этой причине смещение может быть отрицательным. Перемещение любого движущегося тела всегда зависит от его начального и конечного положения, а не от пути, по которому оно шло. На примере покажем, как смещение становится отрицательным. Частица движется вдоль отрицательной оси x, скажем, она переместилась на 50 м вдоль отрицательной оси x. Величина расстояния в данном случае – 50 м. Теперь возникает вопрос, как это было возможно?
Изначально частица находилась в начале координат.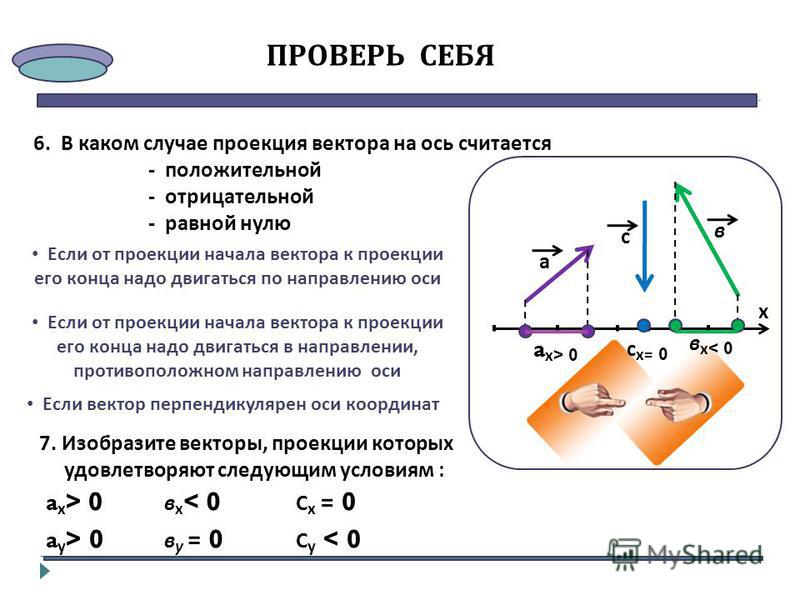 Это означает, что х i = 0, но, в конце концов, он переместился на 50 м по отрицательной оси x. Это означает, что x f = – 50 м, т. е. x f < 0. Отсюда по определению перемещение = конечное положение (x f ) – начальное положение (x i ) = x f – х i = -50 – 0 = – 50 м. В некоторых случаях смещение может быть отрицательным – такой вывод сделан на примере, приведенном выше.
Это означает, что х i = 0, но, в конце концов, он переместился на 50 м по отрицательной оси x. Это означает, что x f = – 50 м, т. е. x f < 0. Отсюда по определению перемещение = конечное положение (x f ) – начальное положение (x i ) = x f – х i = -50 – 0 = – 50 м. В некоторых случаях смещение может быть отрицательным – такой вывод сделан на примере, приведенном выше.
Если тело выбрало движение в отрицательном направлении, т. е. оно движется вдоль отрицательной оси x, отрицательной оси y или отрицательной оси z в трехмерной плоскости, то его перемещение можно назвать отрицательным. Точно так же, если начальное положение тела находится в гораздо более положительном направлении, чем конечное положение, тогда мы также можем сказать, что смещение отрицательно. Теперь опишем это отрицательное смещение на простом математическом примере.
Гусеница идет по стене вниз. Если вначале она была на высоте 57 см, а пройдя расстояние до 20 см, остановилась, то какова будет величина водоизмещения этой гусеницы?
Ответ:
xi = начальное положение гусеницы
xf = конечное положение гусеницы
Итак, изначально гусеница была на высоте 57 см. Значит, х i = 57 см, а гусеница остановилась на 20 см. Следовательно, x f = 20 см
Мы знаем, что перемещение Δ x = x f – x i = 20 см – 57 см = – 37 см
Поскольку мы знаем, что при отрицательном результате, это означает отрицательное смещение. Следовательно, это случай отрицательного смещения.
Когда смещение отрицательное? Существует несколько условий, когда смещение становится отрицательным. Прежде всего, нам нужно понять одну вещь: когда тело опускается ниже точки, из которой оно изначально начало свое путешествие, тогда такой тип смещения называется отрицательным смещением этого тела.
Теперь мы должны прояснить еще одну вещь. Когда тело движется влево от начала координат, это отрицательное смещение, и если тело падает вниз, пересекая начальную точку в направлении вниз, то это смещение также отрицательно. Как мы знаем, смещение является произведением скорости и времени, следовательно, скорость и ускорение являются факторами смещения. Здесь мы поговорим еще о нескольких условиях, когда смещение отрицательно.
- При скорости = 0 и ускорении = – ve
В этом случае сначала тело остается в покое. После этого было выбрано отрицательное направление движения. Итак, это случай отрицательного смещения.
- 2. Скорость = – ve и ускорение = +ve
Здесь скорость уменьшается. Таким образом, тело будет двигаться в отрицательном направлении после отрицательного смещения.
- 3. Скорость = – ve и ускорение = 0
В этом случае отрицательного смещения скорость продолжает уменьшаться, и тело движется в отрицательном направлении.
- 4. Скорость = – ve и ускорение = – ve
В этом случае тело также движется в отрицательном направлении после отрицательного смещения.
Почему смещение отрицательное?Давайте рассмотрим простой пример, чтобы понять, почему смещение отрицательно. Допустим, автомобиль покоится в точке P. Теперь он начинает двигаться в правую сторону до точки Q, которая находится в 10 м справа от точки P, после чего снова начинает двигаться в обратном направлении, то есть в сторону точки P. и достигает точки P. В этом случае автомобиль имеет нулевое водоизмещение. Потому что сначала он переместился на 10 м в правую сторону, а потом снова на 10 м в левую. Отсюда перемещение автомобиля = PQ = 10 – 10 = 0 м.
Теперь, если автомобиль начинает двигаться влево в направлении R, то смещение будет отрицательным. Наверняка возникает вопрос, а почему? Поскольку мы приняли смещение в правой части точки P как положительное смещение, следовательно, смещение вдоль левой стороны точки P должно быть отрицательным. Допустим, R находится в 5 м от P с левой стороны. Отсюда PR = -5 – 0 = – 5 м
Допустим, R находится в 5 м от P с левой стороны. Отсюда PR = -5 – 0 = – 5 м
Возможны два случая, когда смещение не является отрицательным. Первый случай имеет нулевое смещение, а второй случай — положительное смещение. Теперь давайте обсудим эти два случая:
- Нулевое смещение
- Положительное смещение
1.
Нулевое смещениеЭто случай, когда начальное положение и конечное положение тела накладываются друг на друга. Если xi обозначает начальное положение тела, а xf обозначает конечное положение тела, то перемещение будет = Δ x = x f – x i
В этом случае x i = x f отсюда Δ x = x f – x i = 0
Пример нулевого смещения: если человек начинает двигаться из положения на круглом парке и через некоторое время возвращается в то же положение, то ее начальная и конечная позиция совпадают. Поэтому ее водоизмещение равно нулю.
Поэтому ее водоизмещение равно нулю.
2.
Положительное смещениеВ положительном направлении, если конечное положение тела далеко от начального положения, этот случай будет рассматриваться как случай положительного смещения. В этом случае х f > 0 и x i = 0 или x i < 0 или x i >0 (но должно иметь меньшее положительное значение, чем x f ). В качестве примера положительного перемещения можно рассматривать тело, продолжающее движение вдоль положительной оси x.
Как смещение может быть положительным или отрицательным?- Положительное смещение
В положительном направлении, если конечное положение тела далеко от начального положения, этот случай будет рассматриваться как случай положительного смещения В этом случае x f > 0 и x i = 0 или x i < 0 или x i >0 (но должно иметь меньшее положительное значение, чем x f ).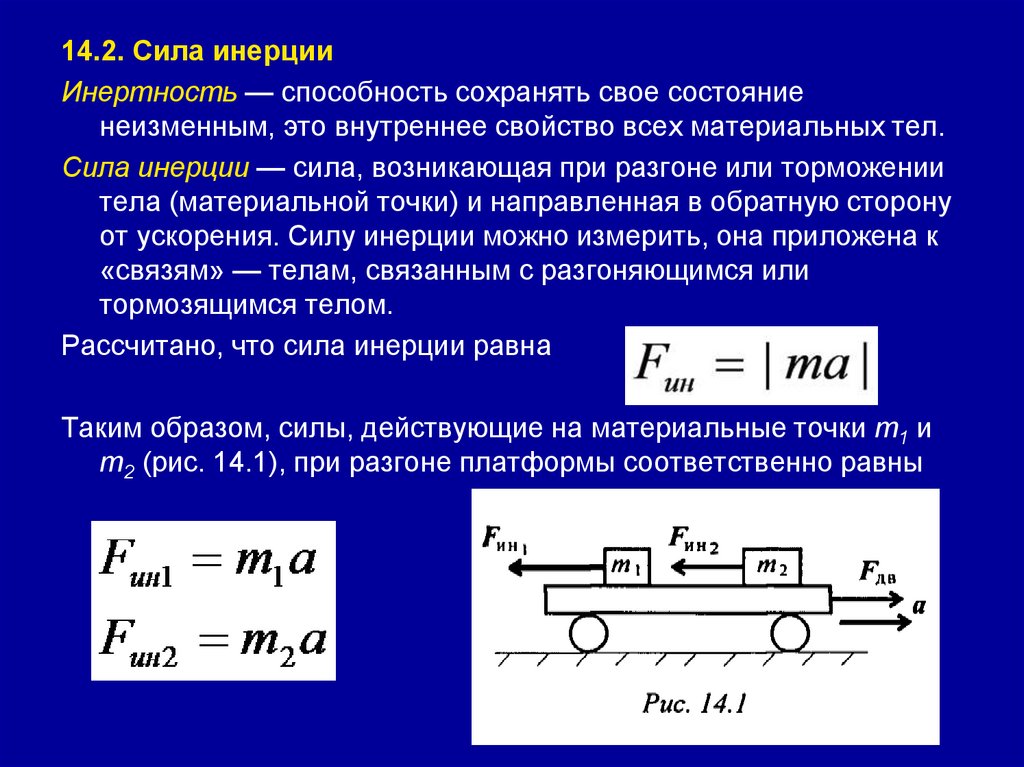 В качестве примера положительного перемещения можно рассматривать тело, продолжающее движение вдоль положительной оси x.
В качестве примера положительного перемещения можно рассматривать тело, продолжающее движение вдоль положительной оси x.
- Отрицательное смещение
Первый случай
Это случай, когда начальное положение тела далеко от конечного положения в положительном направлении. х i >0 и x f > 0
Δ x = x f – x i < 0
Второй случай
Могут быть другой случай отрицательного смещения, когда начальное положение тело находится в положительном направлении (положительная ось x), а конечное положение находится в начальной точке (начало координат). x i > 0,x f = 0, Δ x = x f – x i < 0
Третий случай
Когда начальное положение тела в начале координат и финал position находится вдоль отрицательной оси x системы координат. х i = 0,x f < 0, Δ x = x f – x i < 0
Четвертый случай
900 02 Когда начальное положение тела вдоль положительной оси x и конечное положение вдоль отрицательной оси x. х i >0,x f <0,
х i >0,x f <0,Δ x = x f – x i < 0
Может ли перемещение быть положительным?Это тот случай, когда конечное положение тела далеко от начального положения в положительном направлении. Должен быть другой случай. если тело падает, но не может пересечь начальную точку в направлении вниз, то это перемещение также положительно. В этом случае х f > 0 и x i = 0 или x i < 0 или x i >0 (но должно иметь меньшее положительное значение, чем x f ). Пример: частица движется вдоль положительной оси x.
Почему смещение положительное?Существует несколько условий, при которых смещение может быть положительным.
- Когда конечное положение тела далеко от начального положения тела в положительном направлении, то это смещение является положительным смещением.

xi> 0, xf> 0 Δ x = xf – xi > 0
- Когда конечное положение тела находится далеко от начального положения в положительном направлении, а начальное положение тела находится на отправная точка, то это случай положительного смещения. x i = 0, x f > 0, Δ x = x f – x i > 0
- Когда конечное положение тела положительное, а начальное положение тела в отрицательном направлении. х i < 0, x f > 0
Δ x = x f – x i > 0
- Когда конечное положение тела находится в исходной точке и в исходном положении из тело находится в отрицательном направлении. x i < 0, x f = 0
Δ x = x f – x i > 0
Примеры отрицательного смещения 90 035Есть несколько примеров отрицательного смещения.
- Частица движется вдоль отрицательной оси x, отрицательной оси y или отрицательной оси z.
 Смещение этой частицы является примером отрицательного смещения.
Смещение этой частицы является примером отрицательного смещения. - Нили бросила камень вверх. Камень достиг высоты 20 м в направлении вверх, а затем начал падать на землю. Если он достиг земли, находящейся в 30 м от точки броска вниз, то каково будет его перемещение? Здесь х я = 20 м > 0 и x f = -30 м < 0
Δ x = x f – x i = – 30 – 20 = –50 м < 0. Следовательно, перемещение камень можно назвать отрицательным смещением.
Примеры положительного смещения- Частица движется вдоль любой из ортогональных осей в положительном направлении, т.е. положительная ось x или положительная ось y или положительная ось z. Смещение этой частицы является примером положительного смещения.
- Возьмем автомобиль, который решил двигаться вдоль отрицательной оси x. Сначала он продвинулся на 10 м, затем снова начал двигаться вправо и достиг 30 м по положительной оси абсцисс.
 Каким будет его водоизмещение?
Каким будет его водоизмещение?
Начальное положение автомобиля, x i = – 10 м < 0
Конечное положение автомобиля, x f = 30 м > 0
Следовательно, перемещение автомобиля равно, Δ х = х f – х i
= 30 – (-10) м
= 40 м
Постановка задачи с решением 900 72 затем снова эта частица переместилась в точку E вдоль отрицательной оси y на расстояние 5 м и, наконец, достигла точки F. каково будет ее полное перемещение?
затем снова эта частица переместилась в точку E вдоль отрицательной оси y на расстояние 5 м и, наконец, достигла точки F. каково будет ее полное перемещение? Ответ:
Первоначально частица находилась в точке А вдоль отрицательной оси y. Отсюда его водоизмещение – 5 м. После этого он переместился в точку B вдоль положительной оси y. Теперь его перемещение равно + 5 м, значит, оно достигло точки С по отрицательной оси ординат, значит, его перемещение равно – 5 м.
Начав с точки C, он переместился в точку D вдоль положительной оси y, поэтому перемещение равно + 5 м. Затем он переместился в точку Е по отрицательной оси у, следовательно, перемещение равно – 5 м. наконец она переместилась в точку F. Следовательно, перемещение частицы = (-5 + 5 – 5 + 5 – 5) м = -5 м
Диаграмма для постановки задачи Заключение Здесь, в этой статье, мы подробно обсудили, может ли смещение быть отрицательным или нет. Помимо этого, мы объяснили отрицательное и положительное смещение с помощью подходящих примеров и математических задач.
Помимо этого, мы объяснили отрицательное и положительное смещение с помощью подходящих примеров и математических задач.
Может ли смещение быть отрицательным?
Ответить
Проверено
217,5 тыс.+ просмотров
Подсказка: Чтобы ответить на поставленный выше вопрос, мы поймем, что такое расстояние и смещение. Разберемся, что это за величины расстояние и перемещение и чем они отличаются. Наконец, мы ответим на наш вопрос, может ли смещение быть отрицательным или нет.
Полный ответ:
Нам часто приходит в голову, что расстояние и перемещение — это два термина, которые кажутся синонимами, но имеют несколько разные значения и определения. Термин «расстояние» относится к тому, «сколько земли объект преодолел во время своего движения», а «смещение» относится к тому, «насколько далеко находится объект».
РАССТОЯНИЕ: Общее перемещение объекта, независимо от направления, называется расстоянием. Мы можем описать расстояние как площадь земли, покрытую объектом, независимо от его начальной или конечной точки.
Мы можем описать расстояние как площадь земли, покрытую объектом, независимо от его начальной или конечной точки.
ПЕРЕМЕЩЕНИЕ: Термин «перемещение» относится к смещению местоположения объекта. Это векторная величина с величиной и направлением. Это проиллюстрировано стрелкой, указывающей от начальной точки к месту назначения. Например, если объект перемещается из положения А в положение В, его положение изменяется. Смещение — это термин, обозначающий изменение местоположения объекта.
Утверждение о том, что перемещение является векторной величиной, само по себе достаточно для обоснования нашего ответа.
В физике вектор — это величина, имеющая как величину, так и направление. Обычно он представлен стрелкой с тем же направлением, что и количество, и длиной, равной величине количества. Вектор может иметь значения, содержащие положительные, отрицательные и нулевые значения.
Поэтому мы можем сказать, что: Да, смещение может иметь отрицательные значения.


 1)
1) 3)
3) 10)
10) 12)
12)
 Смещение этой частицы является примером отрицательного смещения.
Смещение этой частицы является примером отрицательного смещения.  Каким будет его водоизмещение?
Каким будет его водоизмещение?
Leave A Comment