100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
Для начинающих водителей выбор покрышек для автомобиля может быть очень сложным. Ведь среди огромного ассортимента, необходимо выбрать подходящие изделия с учетом размера колес (ширины и высоты), типа шины, параметров нагрузки и скорости.
Однако учитывая основные характеристики, совершить покупку будет гораздо проще. При этом рекомендуется совершать покупку в крупной торговой сети, где профессиональные консультанты помогут совершить выбор.
Как правильно выбрать покрышки для автомобиля
Решив купить покрышки, в первую очередь определяют сезонность. В регионах, где летом жарко, а зимой холодно, требуется иметь летние и зимние шины. Последние имеют маркировку в виде снежинки или букв M.S. Для регионов с переменным климатом, можно выбрать всесезонные изделия. Далее уделяют внимание следующим характеристикам.
- Типу протектора. В зависимости от рисунка, шины бывают симметричными или ассиметричными.
 От этого зависит эффективность отвода влаги и, соответственно, устойчивость авто. Шины с симметричным рисунком имеют доступную стоимость и пользуются популярностью у водителей. Ассиметричные более дорогие, зато они лучше отводят воду.
От этого зависит эффективность отвода влаги и, соответственно, устойчивость авто. Шины с симметричным рисунком имеют доступную стоимость и пользуются популярностью у водителей. Ассиметричные более дорогие, зато они лучше отводят воду.
- Размеру. Покрышки должны соответствовать размеру колес автомобиля. Данное значение указывается производителем авто и его важно выдерживать.
- Конструкции. Шины могут быть камерными или бескамерными. Многие современные покрышки являются бескамерными. На это указывает маркировка TL или Tubeless.
- Если предстоит покупка только шин без дисков, учитывают посадочный диаметр. Значение должно соответствовать диаметру диска.
- Нагрузка. Шины имеют допустимый индекс нагрузки. Суммарно, он должен превышать массу автомобиля, при этом значение нагрузки каждой покрышки умножают на число 4.
- Скорость. Покрышки одного размера могут иметь разные индексы скорости. Это допустимое значение, при котором шины сохраняют свои эксплуатационные характеристики.
 Если Вы предпочитаете быстрое движение, то нужно выбрать покрышки с более высоким уровнем скорости.
Если Вы предпочитаете быстрое движение, то нужно выбрать покрышки с более высоким уровнем скорости.
Как продлить ресурс использования покрышек
Существует несколько правил, соблюдая которые, можно значительно продлить время использования шин.
- Поддерживать давление воздуха. Это значительно снижает износ покрышек.
- Контролировать вес, который перевозится в автомобиле. Избыточный вес создает дополнительный износ покрышек и увеличивает расход топлива.
- Рекомендуется периодически менять передние и задние покрышки местами, чтобы уравновесить износ.
- Выбирать покрышки надо правильно. Когда шины соответствуют климатическим условиям и стилю вождения, уменьшается их износ.
- Важно регулярно проверять шины на предмет повреждений, таких как порезы и проколы. В случае образования дефекта, его необходимо сразу устранить.
- Вождение без резких торможений и ускорений, помогает продлить срок службы покрышек.

Качественное обслуживание и уход за покрышками продлевают срок их службы, увеличивает безопасность во время поездок.
Путь и перемещение – чем отличается, формулы
4.2
Средняя оценка: 4.2
Всего получено оценок: 131.
4.2
Средняя оценка: 4.2
Всего получено оценок: 131.
Важнейшими понятиями кинематики являются понятия пути и перемещения. Рассмотрим их подробнее, а также узнаем, чем отличается путь от перемещения.
Траектория пути
Кинематика изучает движение тел безотносительно причин этого движения. Главной задачей кинематики является математическое описание положения тела в принятой системе отсчета и изменение этого положения со временем.
Положение тела в системе отсчета задается одной или несколькими координатами (в зависимости от числа измерений) и временем.
Рис. 1. Координаты тела в пространстве.Если тело движется, то в разные моменты времени координаты тела будут различны. Умножая скорость тела на время движения, можно найти длину пройденного пути:
$$s=vt$$
Однако, даже зная точку, где находилось тело в нулевой момент времени, мы далеко не всегда можем определить, в какой точке тело будет находиться в другой произвольный момент времени.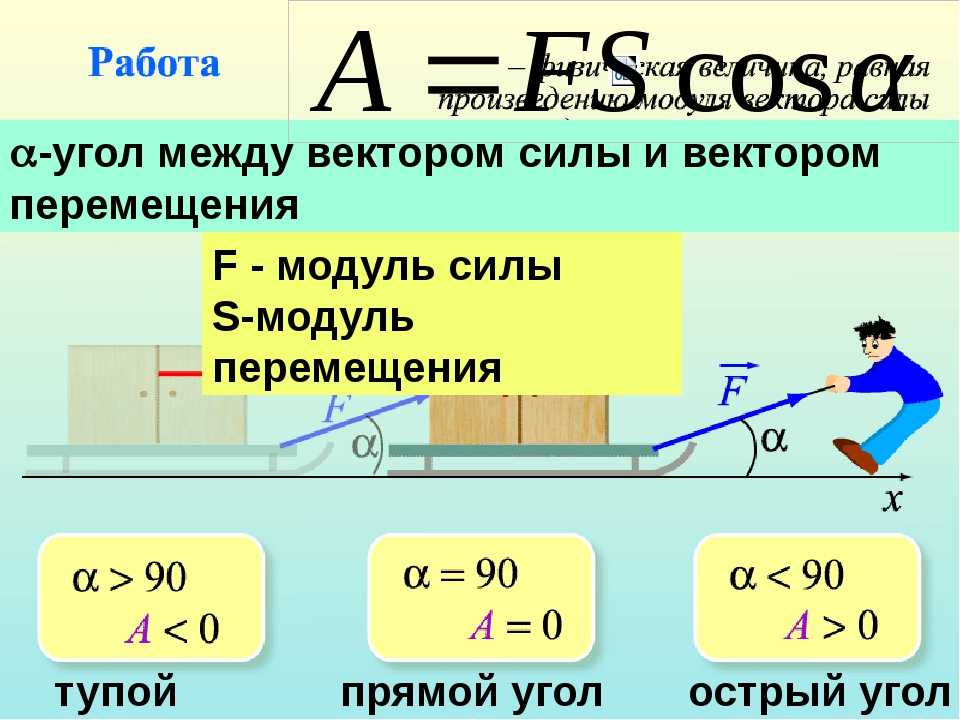
Дело в том, что с помощью приведенной формулы можно найти длину пройденного пути. А сам путь при этом может иметь любую, сколь угодно сложную форму. Линия, вдоль которой перемещается тело, вовсе необязательно будет прямой, она может быть и окружностью, и ломанной, и более сложной фигурой, состоящих из многих частей.
Линия, вдоль которой двигалось тело на рассматриваемом участке времени, называется траекторией пути или просто траекторией.
Перемещение
Чтобы всегда знать, в какой точке находится тело в заданный момент времени, необходимо знать не длину пройденного пути, а другую кинематическую характеристику – перемещение.
Перемещение – это вектор, соединяющий начальное положение тела с его конечным положением.
Зная начальную точку в нулевой момент времени и перемещение за некоторое время, можно всегда найти координату тела в конце пути.
Рис. 2. Путь и перемещение.Сходство и различие.
Путь и перемещение – это не одно и то же. Если движение происходит на плоскости или в пространстве и криволинейно, то длина траектории всегда будет больше модуля перемещения.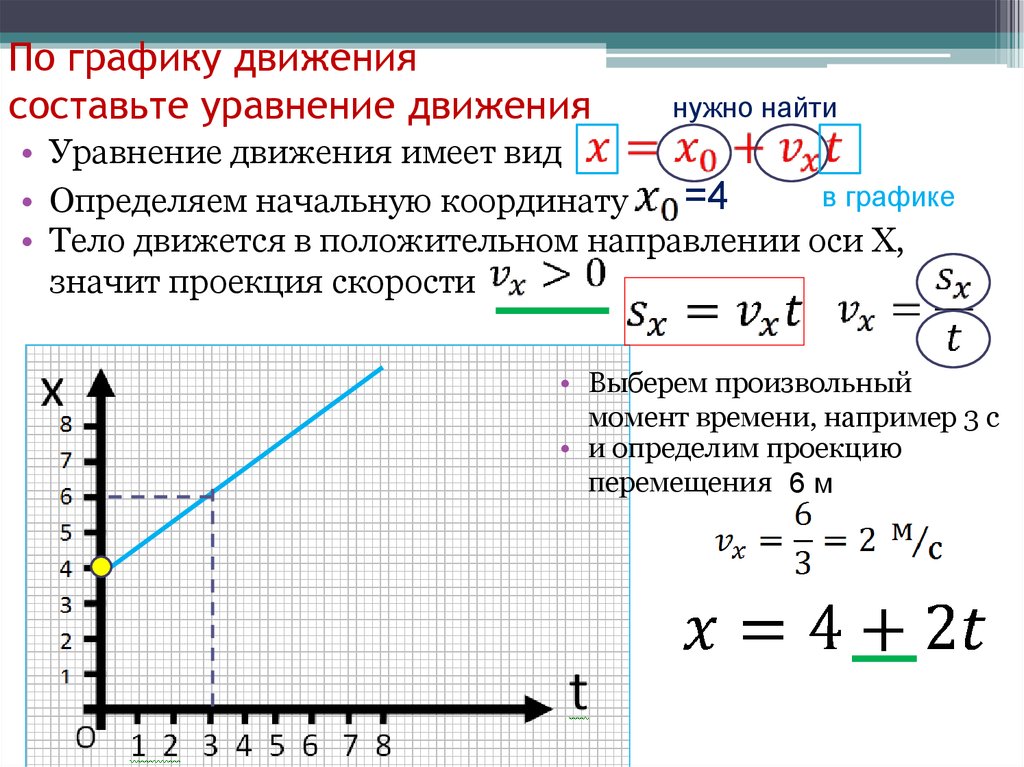 Происходит этот потому, что вектор является прямой, то есть, кратчайшим расстоянием между двумя точками. Криволинейная траектория же прямой не является.
Происходит этот потому, что вектор является прямой, то есть, кратчайшим расстоянием между двумя точками. Криволинейная траектория же прямой не является.
Более того, перемещение может быть равно нулю, несмотря на то, что путь будет иметь большую длину. Например, планеты, двигаясь по окружностям, проходят за каждый оборот большой путь, однако, перемещение при этом никогда не превышает диаметра орбиты, и может быть равно нулю, если планета делает полный оборот.
Рис. 3. Орбиты планет.Однако, и перемещение и траектория пути служат одной и той же цели – описанию движения. Обе этих величины измеряются в единицах длины, к обоим могут быть применены формулы движения.
Но, если траектория описывает весь путь, пройденный телом, то перемещение акцентирует внимание на разнице положения тела между первым и последним моментами движения. Поэтому большинство формул в кинематике, в которые входит время, работают именно с перемещением.
Единственный случай, когда путь и перемещение равны – это случай прямолинейного движения, при условии, что скорость движения не меняла знак.
Что мы узнали?
Траектория пути – это линия, вдоль которой перемещалось тело во время своего движения. Перемещение – это вектор, направленный из точки начала движения в точку конца движения. Длина пути всегда равна или больше, чем длина перемещения.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 131.
А какая ваша оценка?
Смещение: определение, формула и примеры
Смещение: определение, формула и примеры | StudySmarterВыберите язык
Предлагаемые языки для вас:
Немецкий (DE)
Дойч (Великобритания)
Европа
- английский (DE)
- английский (Великобритания)
StudySmarter — универсальное учебное приложение.
4.8 • Рейтинг +11k
Более 3 миллионов загрузок
Бесплатно
смещение
СОДЕРЖАНИЕ :
ОГЛАВЛЕНИЕ
Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persönlichen Lernstatistiken
Jetzt kostenlos anmelden
Nie wieder prokastinieren mit unseren Lernerinnerungen.
Jetzt kostenlos anmelden
Вы когда-нибудь ходили буквально где-нибудь? Тогда угадайте, что вы используете измерение, которое мы знаем как смещение. Смещение используется повсеместно в области физики: если что-то движется, нужно найти его смещение, чтобы знать об этом все остальное. Это переменная, без которой мы просто не можем жить! Но что такое смещение и как его решить? Давай выясним.
Определение смещения
Предположим, что объект меняет положение: он перемещается из положения \(A\) в положение \(B\).
Смещение объекта — это вектор, указывающий из позиции \(A\) в позицию \(B\): это разница между этими позициями.
Если что-то начиналось в начальном положении, двигалось в любом направлении, в течение любого промежутка времени и различными способами и заканчивалось в конечном положении, можно провести линию от начального до конечного положения. Если мы превратим эту линию в стрелку, указывающую на конечное положение, мы получим графическое представление вектора смещения.
Перемещение является векторной величиной. Как вектор, смещение имеет как величину, так и направление. Из определения, являющегося разницей в позициях, мы видим, что перемещение измеряется метрами.
Величина смещения
Смещение, как мы знаем, является вектором. Это означает, что у нас есть и величина, и направление. Если мы уберем смещение и оставим только величину, вместо этого мы получим расстояние от одной точки до другой, превратив наше векторное смещение в скалярное расстояние.
Расстояние между положениями \(A\) и положением \(B\) является величиной смещения между этими двумя положениями.
Расстояние против смещения
Как вы знаете, прямая линия от начального положения до конечного положения — не единственный способ измерения длины. Что, если человек, путешествующий между этими точками, выбрал менее прямой путь? Если вы измеряете весь путь от точки \(A\) до точки \(B\), игнорируя направление, вместо этого вы будете измерять пройденное расстояние. Расстояние — это скаляр, который, в отличие от вектора, не учитывает направление, то есть не может быть отрицательным. Например, если кто-то путешествовал налево на \(9\,\mathrm{ft}\), их смещение будет \(-9\,\mathrm{ft}\), если мы выберем левое отрицательное направление. Однако расстояние этого человека до начальной точки будет равно \(9\,\mathrm{ft}\), так как направление, в котором он двигался, совершенно не имеет значения для расстояния. Простой способ понять это так: если вы возьмете свое перемещение и отбросите информацию о направлении, у вас останется только информация о расстоянии.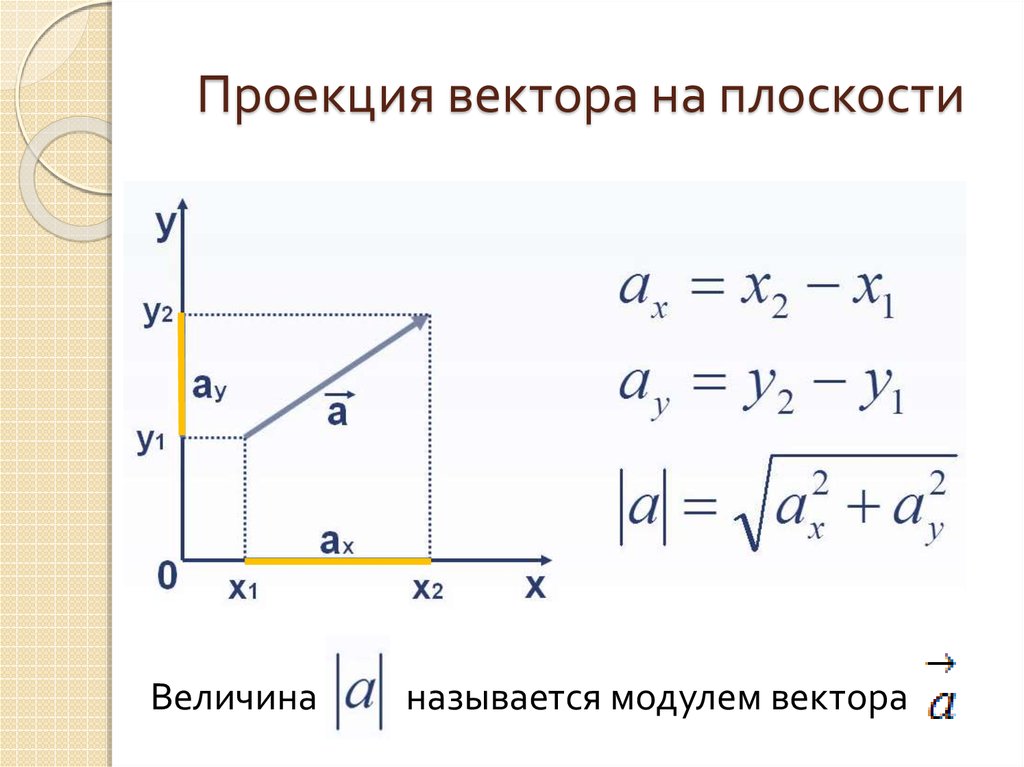
Перемещение населения: в данном контексте важно, в каком направление движения человек, а не только то, как далеко они уходят от своей отправной точки, Wikimedia Commons Public Domain
Что такое формула смещения?
Как указывалось ранее, смещение — это вектор, идущий от начальной позиции \(x_\text{i}\) к конечной позиции \(x_\text{f}\). Следовательно, уравнение для расчета смещения \(\Delta x\) выглядит так:
\[\Delta\vec{x}=\vec{x}_\text{f}-\vec{x}_\ text{i}.\]
Важно знать, что когда речь идет о смещении, значение может быть отрицательным в зависимости от направления смещения. Если мы выберем положительное значение вверх, то смещение парашютиста между прыжком и приземлением будет отрицательным. Однако, если мы выберем отрицательное значение вверх, то их смещение будет положительным! При этом расстояние между их прыжком и приземлением в обоих случаях будет положительным.
Примеры смещения
Вот несколько примеров, которые мы можем использовать, чтобы попрактиковаться в том, как можно использовать смещение для решения проблем.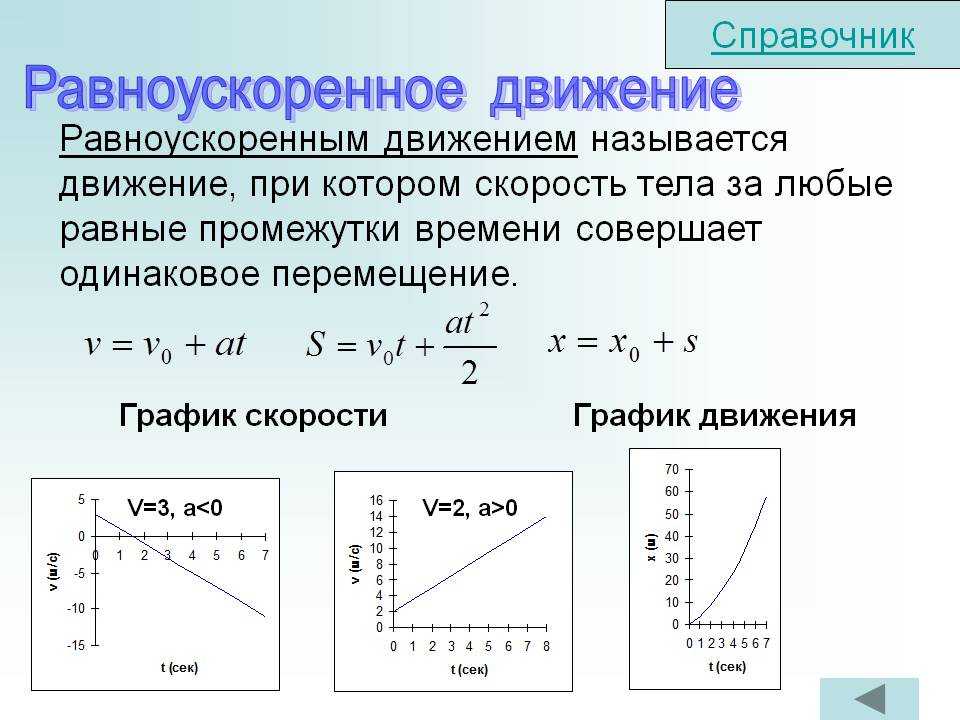
Джеймс движется \(26\,\mathrm{ft}\) на восток через футбольный стадион, прежде чем двигаться \(7\,\mathrm{ft}\) на запад. Затем он перемещается еще на \(6\,\mathrm{ft}\) на запад, а затем возвращается на \(15\,\mathrm{ft}\) на восток. Каково перемещение Джеймса после того, как он проделает описанное путешествие? Каково расстояние до его начального положения?
Во-первых, мы решили для себя сделать восток положительным направлением. Джеймс смещается на \(26\,\mathrm{ft}\) на восток, поэтому после этого шага смещение Джеймса составляет \(26\,\mathrm{ft}\) на восток. Затем он перемещается на \(7\,\mathrm{ft}\) на запад, что равно \(-7\,\mathrm{ft}\) на восток. Это означает, что мы вычитаем \(7\) из \(26\), что дает нам общее смещение \(19\,\mathrm{ft}\) теперь на восток. Затем Джеймс перемещается еще на \(6\,\mathrm{ft}\) на запад, что дает нам смещение \(19\,\mathrm{ft}-6\,\mathrm{ft}=13\,\mathrm{ футов}\) на восток. Наконец, Джеймс перемещается на \(15\,\mathrm{ft}\) на восток, совершая окончательное полное перемещение \(28\,\mathrm{ft}\) на восток.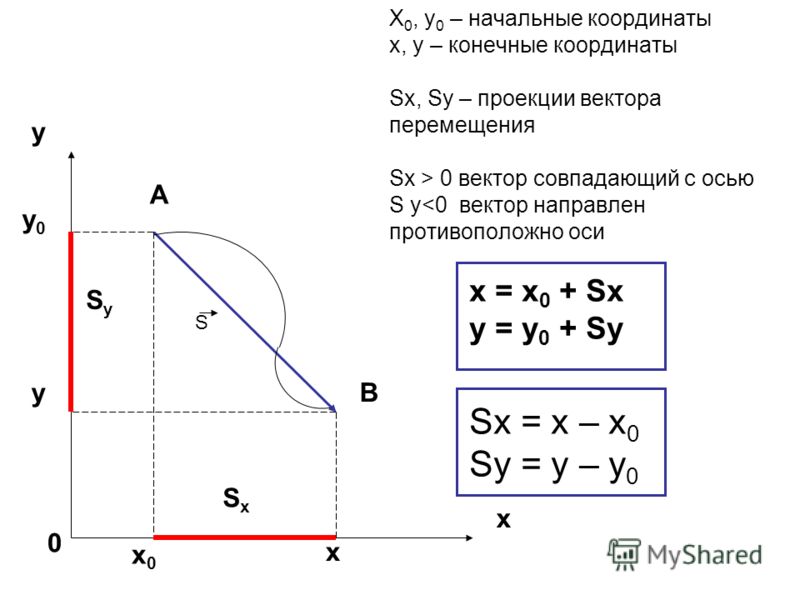
Расстояние между его конечной и начальной позицией равно \(28\,\mathrm{ft}\).
София идет на север вверх по улице на \(50\,\mathrm{ft}\). Затем она путешествует \(20\,\mathrm{ft}\) на запад через улицу, затем еще \(25\,\mathrm{ft}\) на север. Каким будет ее двухмерное перемещение, когда она прибудет в пункт назначения?
Поскольку это расчет двумерного смещения, мы выбираем направления на восток и север как положительные. Мы считаем, что София начинается со смещения \((0,0)\,\mathrm{ft}\) на восток и север соответственно. Во-первых, она перемещается на север за \(50\,\mathrm{ft}\), и, поскольку смещение с севера на юг идет последним в наших координатах, мы называем ее смещением после этого перемещения \((0,50)\,\mathrm{ футов}\). Далее, \(20\,\mathrm{ft}\) west дает нам отрицательное значение смещения с востока на запад, делая общее смещение равным \((-20,50)\,\mathrm{ft}\) . Наконец, она перемещается на \(25\,\mathrm{ft}\) на север.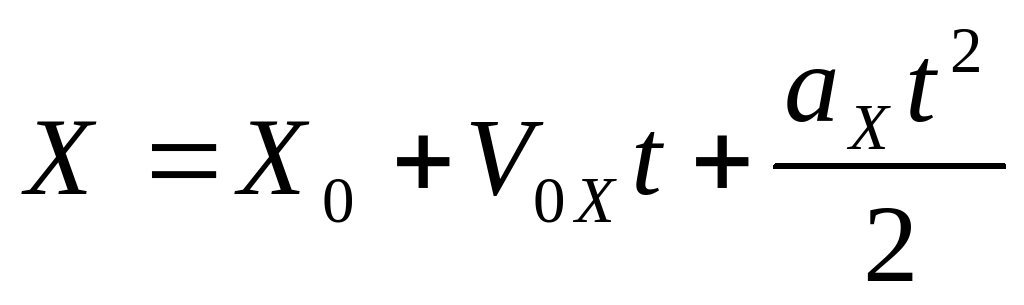 Добавление этого к нашему смещению с севера на юг дает нам окончательное смещение \((-20,75)\,\mathrm{ft}\) в наших координатах. Чтобы ответить на вопрос, вернем наши координаты обратно в реальность и придем к выводу, что София смещается на \(75\,\mathrm{ft}\) на север и на \(20\,\mathrm{ft}\) на запад.
Добавление этого к нашему смещению с севера на юг дает нам окончательное смещение \((-20,75)\,\mathrm{ft}\) в наших координатах. Чтобы ответить на вопрос, вернем наши координаты обратно в реальность и придем к выводу, что София смещается на \(75\,\mathrm{ft}\) на север и на \(20\,\mathrm{ft}\) на запад.
Расстояние от начальной точки до конечной можно рассчитать с помощью теоремы Пифагора.
Пример того, как перемещение может выглядеть в реальной жизни. В городском квартале есть четкие и конкретные пути для передвижения, а это означает, что расстояние, которое вы путешествуете, может включать в себя извилистые улицы. Однако смещение между двумя точками всегда будет прямой линией, направленной из одной точки в другую, Wikimedia Commons CC BY-SA 4.0
Вектор смещения
Мы рассмотрели смещение и знаем, что это вектор, а это означает, что смещение имеет как величину, так и направление, когда мы его описываем. Вектор, который мы называем смещением, может быть задан в одном, двух или трех измерениях.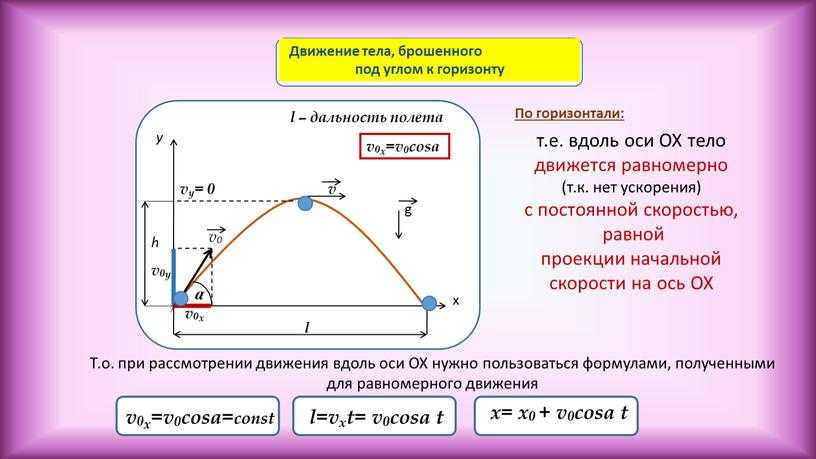 Мы уже рассмотрели смещение в двух измерениях, но что, если мы добавим третье? Мы живем в трехмерном пространстве, поэтому важно знать, как используется смещение в трех измерениях.
Мы уже рассмотрели смещение в двух измерениях, но что, если мы добавим третье? Мы живем в трехмерном пространстве, поэтому важно знать, как используется смещение в трех измерениях.
В трех измерениях вектор изображается в виде матрицы: \(\begin{pmatrix}i\\ j\\ k\end{pmatrix}\). Здесь \(i\) представляет смещение в направлении \(x\), \(j\) представляет смещение в направлении \(y\), а \(k\) представляет смещение в \( г\) направление.
С точки зрения сложения и вычитания в векторах это довольно просто. Все, что вам нужно сделать, это взять значения \(i\), \(j\) и \(k\) одного вектора и добавить или вычесть их из соответствующих значений другого вектора. Это полезно при смещении, поскольку смещение между двумя позициями равно разнице между позициями.
Вам явно нужно смещение с вертикальным компонентом, чтобы достичь вершины этой горы, Wikimedia Commons Public Domain
Предположим, вы поднялись на самую высокую точку США, Денали, и хотите узнать свое перемещение между началом восхождения (в координатах \((62.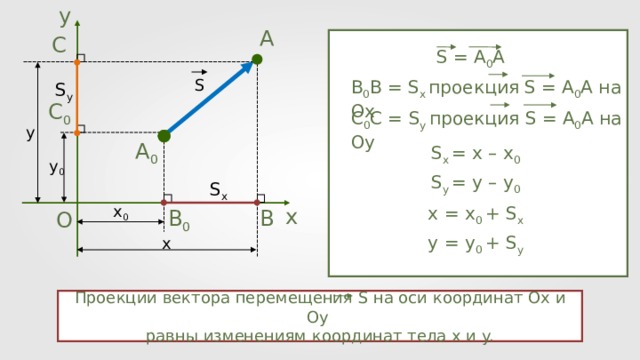 966284,\,-151.156684)\,\text{градус}\) и высота \(7500\,\mathrm{ft}\)) и вершина (в координатах \((63.069042,\,-151.006347)\,\text{градус}\) и высота \(20310\,\mathrm{ft }\)). Что вы делаете, так это вычисляете разницу между этими двумя векторами, чтобы получить вектор смещения \(\Delta\vec{x}\):
966284,\,-151.156684)\,\text{градус}\) и высота \(7500\,\mathrm{ft}\)) и вершина (в координатах \((63.069042,\,-151.006347)\,\text{градус}\) и высота \(20310\,\mathrm{ft }\)). Что вы делаете, так это вычисляете разницу между этими двумя векторами, чтобы получить вектор смещения \(\Delta\vec{x}\):
\[\Delta\vec{x}=\begin{pmatrix}63,069042\,\mathrm{град} — 62.966284\,\mathrm{град} \\ -151.006347\,\mathrm{град}+151.156684\,\mathrm{град} \\ 20310\,\mathrm{ft}-7500\ ,\mathrm{ft}\end{pmatrix} =\begin{pmatrix}0.102758\,\mathrm{deg} \\ 0.150337\,\mathrm{deg} \\ 12810\,\mathrm{ft} \end{pmatrix} .\]
Конечно, это удобно перевести в метры, и мы получим
\[\Delta\vec{x}=\begin{pmatrix} 11,5 \\ 7,6 \\ 3,9 \end{pmatrix}\ ,\mathrm{км}.\]
Теперь у нас есть смещение в виде вектора, поэтому мы можем разобрать его и сделать вывод, что ваше смещение было \(11,5\,\mathrm{км}\) на север, \( 7,6\,\mathrm{км}\) на восток и \(3,92}=14.3\,\mathrm{км}.\]
Смещение — основные выводы
Смещение — это вектор, описывающий разницу между начальным и конечным положениями.

Формула смещения: \(\Delta\vec{x}=\vec{x}_\text{f}-\vec{x}_\text{i}\).
Расстояние — это длина или величина вектора смещения.
Перемещение и расстояние различаются тем, что они являются вектором и скаляром соответственно.
Расстояние не может быть отрицательным.
Часто задаваемые вопросы о смещении
Смещение — это измерение величины и направления от начальной начальной точки до конечной точки.
Формула смещения представляет собой начальное положение, вычтенное из конечного положения.
Всякий раз, когда вы перемещаетесь из одного места в другое, вы «перемещаете» себя, то есть вы создаете смещение между тем, с чего вы начали, и тем, где вы оказались. Это смещение зависит от того, в каком направлении вы пошли и как далеко вы пошли.
Это смещение зависит от того, в каком направлении вы пошли и как далеко вы пошли.
Первая производная смещения по времени — это скорость, а вторая производная смещения по времени — это ускорение.
Уравнение для расчета смещения объекта состоит в том, чтобы умножить его скорость на время, затраченное на перемещение с этой скоростью.
Заключительный опрос о перемещении
Опрос о перемещении — Teste dein Wissen
Вопрос
Является ли перемещение векторной или скалярной величиной?
Показать ответ
Ответ
Вектор.
Показать вопрос
Вопрос
Кратко опишите, что такое смещение.
Показать ответ
Ответ
Смещение — это разница между двумя местоположениями в пространстве, принимая во внимание как величину, так и направление разницы/изменения местоположения.
Показать вопрос
Вопрос
Что такое скалярный эквивалент перемещения?
Показать ответ
Ответ
Расстояние.
Показать вопрос
Вопрос
В чем разница между смещением и расстоянием?
Показать ответ
Ответ
Перемещение — это вектор, а расстояние — это скаляр. Расстояние — это длина вектора смещения.
Показать вопрос
Вопрос
Какое уравнение используется для расчета смещения?
Показать ответ
Ответ
\(\Delta x=x_f-x_i\).
Показать вопрос
Вопрос
Если мы знаем смещение, мы всегда знаем расстояние.
Показать ответ
Ответ
Показать вопрос
Вопрос
В какой ситуации это правильное предложение?
«Мое водоизмещение было 5 метров.»
Показать ответ
Ответ
Во всех ситуациях.
Показать вопрос
Вопрос
Автомобиль находится в начальной позиции в 5 футах справа от вас и проезжает 7 футов вправо от вас. Каков его водоизмещение по сравнению с вами?
Показать ответ
Ответ
12 футов вправо.
Показать вопрос
Вопрос
Автобус стартует в 3 футах слева от вас и проезжает 10 футов вправо от вас.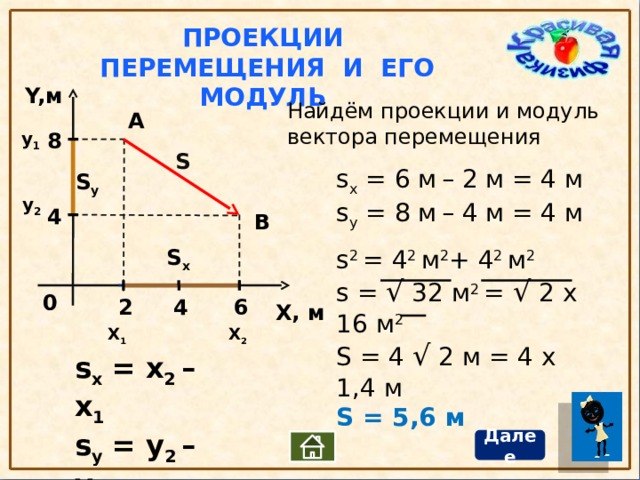 Каков его водоизмещение по сравнению с вами?
Каков его водоизмещение по сравнению с вами?
Показать ответ
Ответ
7 футов вправо от вас.
Показать вопрос
Вопрос
Поезд имеет смещение относительно вас -12 футов после движения -6 футов. Какова была его исходная позиция по сравнению с вами?
Показать ответ
Ответ
-6 футов.
Показать вопрос
Вопрос
Смещение имеет максимальное количество измерений, в которых оно может произойти.
Показать ответ
Ответ
Неверно.
Показать вопрос
Вопрос
Может ли составляющая вектора смещения быть меньше величины смещения?
Показать ответ
Ответ
Показать вопрос
Вопрос
Если вы куда-то едете, совпадает ли расстояние между начальной и конечной точкой с расстоянием, которое проехала ваша машина?
Показать ответ
Ответ
Показать вопрос
Вопрос
Если вы занимаетесь подводным плаванием, что вы можете сказать о своем вертикальном смещении между вашим положением на пляже и вашим положением под водой?
Показать ответ
Ответ
Это вниз.
Показать вопрос
Вопрос
Как складывать и вычитать векторы?
Показать ответ
Ответ
Возьмите каждый соответствующий компонент и сложите или вычтите их друг из друга, чтобы сформировать компоненты нового вектора, который является ответом на сложение или вычитание.
Показать вопрос
Подробнее о смещении
Откройте для себя подходящий контент для ваших тем
Не нужно обманывать, если у вас есть все необходимое для успеха! Упаковано в одно приложение!
Учебный план
Будьте идеально подготовлены вовремя с индивидуальным планом.
Тесты
Проверьте свои знания с помощью игровых тестов.
Карточки
Создавайте и находите карточки в рекордно короткие сроки.
Заметки
Создавайте красивые заметки быстрее, чем когда-либо прежде.
Учебные наборы
Все учебные материалы в одном месте.
Документы
Загружайте неограниченное количество документов и сохраняйте их в Интернете.
Study Analytics
Определите сильные и слабые стороны вашего исследования.
Еженедельные цели
Ставьте индивидуальные учебные цели и зарабатывайте баллы за их достижение.
Умные напоминания
Хватит откладывать на потом наши напоминания об учебе.
Награды
Зарабатывайте очки, открывайте значки и повышайте уровень во время учебы.
Волшебный маркер
Создавайте карточки в заметках полностью автоматически.
Интеллектуальное форматирование
Создавайте самые красивые учебные материалы, используя наши шаблоны.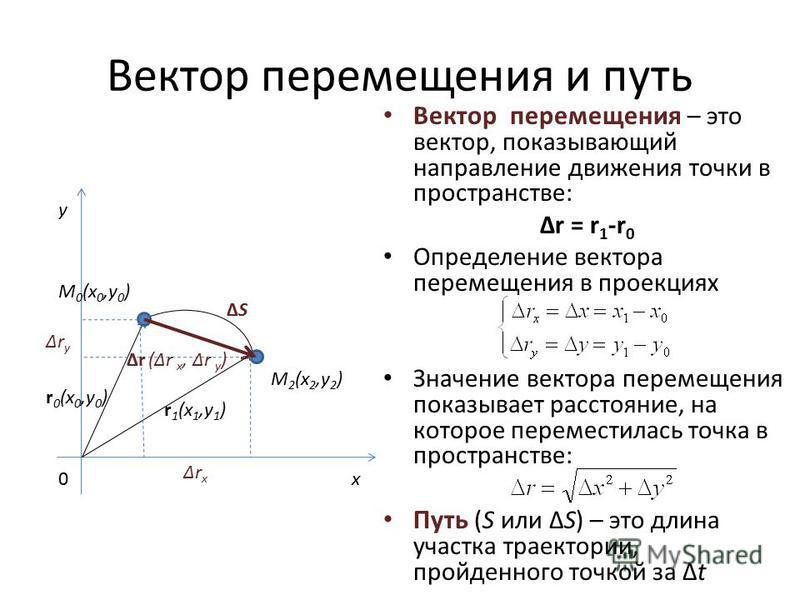
Физика — Модуль Юнга — Бирмингемский университет
Одним из самых важных тестов в технике является знание того, когда объект или материал согнется или сломается, и свойство, которое говорит нам об этом, — модуль Юнга. Это мера того, насколько легко материал растягивается и деформируется.
Введение | Видео | В фокусе | Заключение | Следующие шаги |
Согнется или сломается?
Провода подчиняются закону Гука, как и пружины. Когда приложена сила F , она распространяется на некоторое расстояние x , которое можно просто описать уравнением F = kx
В то время как k для пружины — это жесткость пружины, степень удлинения проволоки зависит от ее площади поперечного сечения, длины и материала, из которого она изготовлена. Модуль Юнга ( E ) — это свойство материала, которое говорит нам, насколько легко он может растягиваться и деформироваться, и определяется как отношение растягивающего напряжения ( σ ) к деформации растяжения ( ε ). Где напряжение представляет собой количество силы, приложенной к единице площади ( σ = F/A ), а деформация представляет собой удлинение на единицу длины ( ε = дл/л ).
Модуль Юнга ( E ) — это свойство материала, которое говорит нам, насколько легко он может растягиваться и деформироваться, и определяется как отношение растягивающего напряжения ( σ ) к деформации растяжения ( ε ). Где напряжение представляет собой количество силы, приложенной к единице площади ( σ = F/A ), а деформация представляет собой удлинение на единицу длины ( ε = дл/л ).
Поскольку сила F = мг , мы можем получить модуль Юнга проволоки, измерив изменение длины ( dl ), так как применяются гири массой м (при условии, что г = 9,81 метра в секунду в квадрате).
Относится ли модуль Юнга к исследованиям?
Имеет ли модуль Юнга отношение к исследованиям?
Что важно знать?
Для разных типов материалов графики напряжения-деформации могут выглядеть очень по-разному. Хрупкие материалы, как правило, очень прочные, потому что они могут выдерживать большие нагрузки, они не сильно растягиваются и могут внезапно сломаться. Пластичные материалы имеют большую область упругости, где зависимость между напряжением и деформацией является линейной, но при первом обороте (предел упругости) линейность нарушается, и материал больше не может вернуться к своей первоначальной форме. Второй пик — это предел прочности при растяжении, и он говорит нам о максимальном напряжении, которое материал может выдержать до разрыва. Пластмассовые материалы не очень прочные, но выдерживают большую нагрузку. Модуль Юнга задается градиентом линии на графике напряжения-деформации.
Пластичные материалы имеют большую область упругости, где зависимость между напряжением и деформацией является линейной, но при первом обороте (предел упругости) линейность нарушается, и материал больше не может вернуться к своей первоначальной форме. Второй пик — это предел прочности при растяжении, и он говорит нам о максимальном напряжении, которое материал может выдержать до разрыва. Пластмассовые материалы не очень прочные, но выдерживают большую нагрузку. Модуль Юнга задается градиентом линии на графике напряжения-деформации.
В эксперименте на видео выше мы измерили модуль Юнга некоторого медного провода, который не очень сильно удлиняется. Таким образом, можно использовать реперный маркер, например, ленту, чтобы определить исходную и увеличенную длину. Выполнение многократных измерений с различными массами увеличит количество точек на графике напряжения-деформации и сделает расчет модуля Юнга более надежным. Еще одна вещь, о которой нужно позаботиться, — это измерение площади поперечного сечения провода. Дефекты проволоки могут означать, что диаметр не является абсолютно постоянным по всей ее длине, поэтому может помочь среднее значение нескольких показаний микрометра.
Дефекты проволоки могут означать, что диаметр не является абсолютно постоянным по всей ее длине, поэтому может помочь среднее значение нескольких показаний микрометра.
Как это применимо ко мне?
Изучение механических свойств материалов важно, потому что оно помогает нам понять, как ведут себя материалы, и позволяет нам разрабатывать новые продукты и улучшать существующие. В качестве примера темы исследования в Бирмингеме рассматривалась разработка шестов для прыжков, используемых спортсменами, занимающимися прыжками в высоту, для достижения максимальной производительности. Эти шесты должны быть легкими, чтобы обеспечить быстрый разбег, но также должны сохранять энергию упругой деформации при изгибе шеста. Шест должен преобразовывать энергию упругости в кинетическую энергию по мере выпрямления шеста и быть в состоянии выдерживать нагрузку, вызванную весом прыгуна, а также выдерживать многократное использование спортсменом.
В небольших масштабах существует много продуктов, содержащих биологические (например, фармацевтические препараты, препараты для лечения бесплодия, тканевая инженерия) и небиологические микрочастицы (например, химикаты, сельское хозяйство, товары для дома).

 От этого зависит эффективность отвода влаги и, соответственно, устойчивость авто. Шины с симметричным рисунком имеют доступную стоимость и пользуются популярностью у водителей. Ассиметричные более дорогие, зато они лучше отводят воду.
От этого зависит эффективность отвода влаги и, соответственно, устойчивость авто. Шины с симметричным рисунком имеют доступную стоимость и пользуются популярностью у водителей. Ассиметричные более дорогие, зато они лучше отводят воду.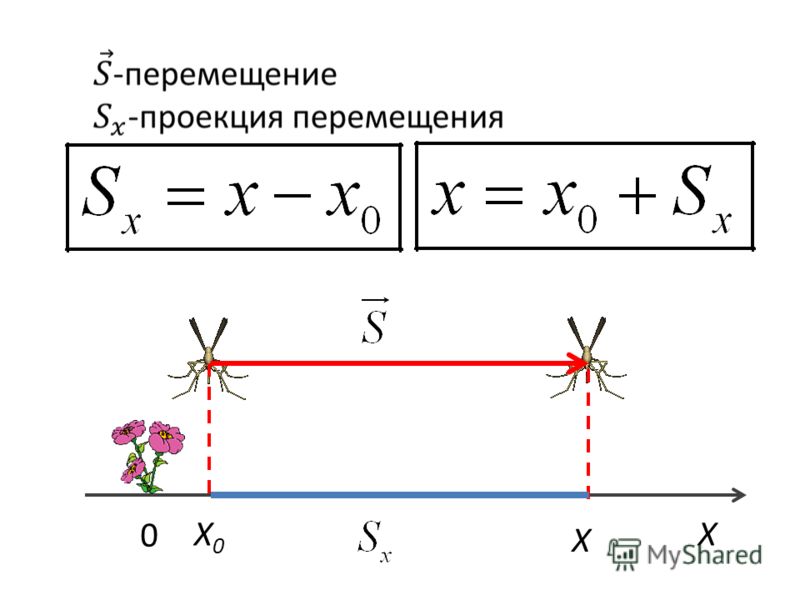 Если Вы предпочитаете быстрое движение, то нужно выбрать покрышки с более высоким уровнем скорости.
Если Вы предпочитаете быстрое движение, то нужно выбрать покрышки с более высоким уровнем скорости.
Leave A Comment