Найдите углы §11 №32 ГДЗ Геометрия 7-9 класс Погорелов А.В. – Рамблер/класс
Найдите углы §11 №32 ГДЗ Геометрия 7-9 класс Погорелов А.В. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
В остроугольном треугольнике АВС проведены высоты AD, BE, CF. Найдите углы треугольника DEF, зная углы треугольника АВС.
Найдите углы треугольника DEF, зная углы треугольника АВС.
ответы
Из предыдущей задачи получаем, что ΔFBD ~ ΔАВС, следовательно, ∠BDF = ∠A, ∠BFD = ∠C.
Далее ΔDCE ~ ΔАВС так, что ∠CDE = ∠A и ∠CED = ∠B.
∠D = 180°- (∠BDF + ∠CDE) = 180°- (∠A + ∠A) = 180°- 2∠A.
Так как ΔAEF ~ ΔАВС, то ∠AEF = ∠B, ∠AFE = ∠C. Так что:
∠E = 180°- (∠CED + ∠AEF) = 180°- (∠B + ∠B) = 180°- 2∠B. ∠F = 180°- (∠AFE + ∠BFD) = 180°- (∠C + ∠C) = 180°- 2∠C. Ответ. ∠D = 180°- 2∠A; ∠E = 180°- 2∠B, ∠F = 180°- 2∠C.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Досуг
Химия
похожие вопросы 5
Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.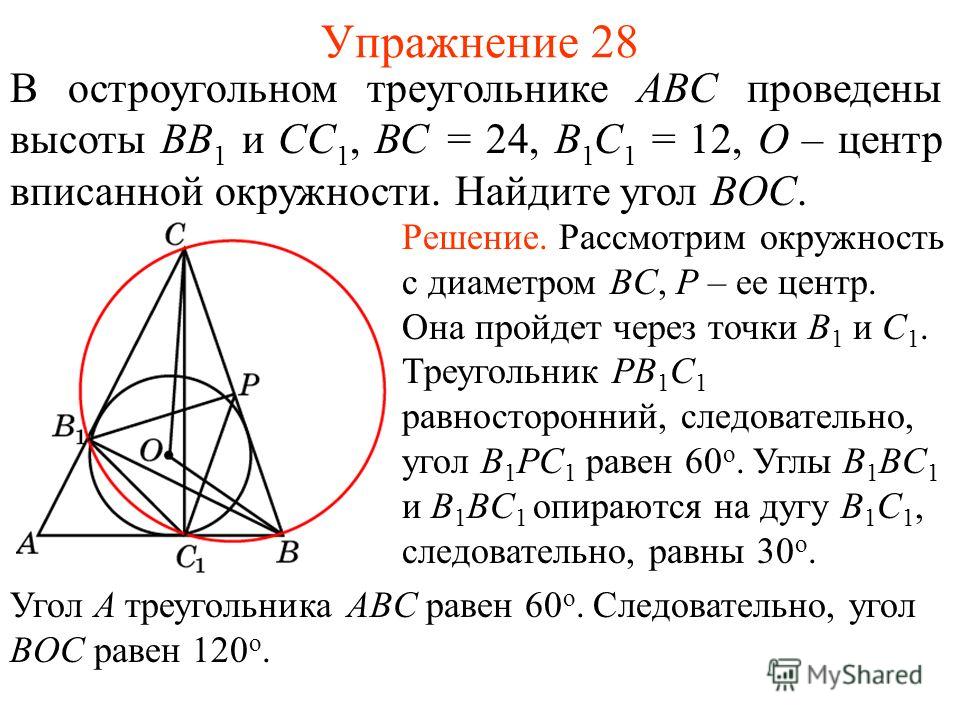 Г. Помогите доказать, используя параллельный перенос
Г. Помогите доказать, используя параллельный перенос
Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
ГДЗФизикаПерышкин А.В.Школа7 класс
Дадут ли аттестат после второй пересдачи.?
Мне сказала подруга,что аттестат не дадут после второй пересдачи,дадут только справку и всё,так ли это?
9 класс
Ребята нужны ответы на пересдачу по математике 9 класс 11 регион. Срочно!
ГИА9 класс
Не могу справиться с заданием, §8№26. Какой высоты должна быть….Геометрия 11 класс ГДЗ Погорелов
Не могу справиться с заданием, §8№26.
Сосуд имеет форму полушара радиуса R, дополненного ци-
линдром. Какой высоты должна (Подробнее…)
ГДЗ11 классГеометрияПогорелов А.В.
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
Пользуйтесь нашим приложением
Математическая задача: Найдите — вопрос № 46091, контурометрия, угол
Найдите третий внутренний угол треугольника ABC, где: α = 48°, γ = 65°.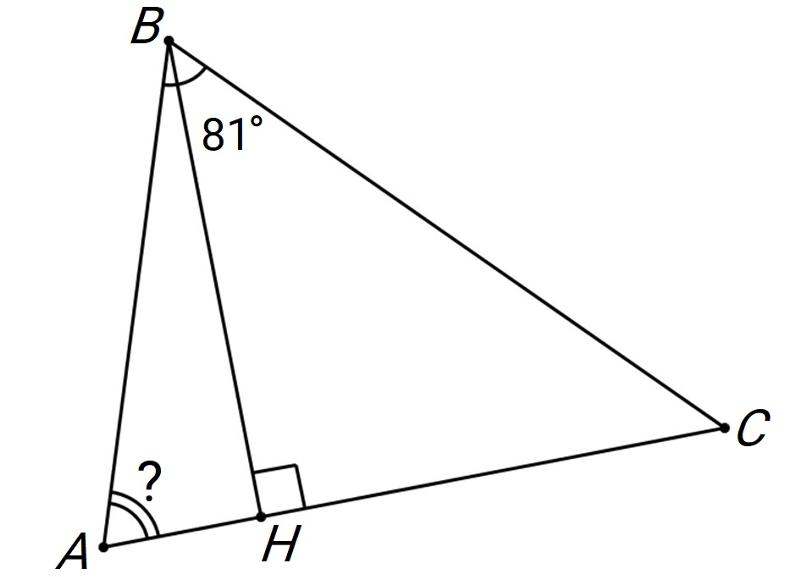
Правильный ответ:
β = 67 °Пошаговое объяснение:
α=48 ∘ γ=65 ∘ α+β+γ=180° β=180−α−γ=180−48− 65=67∘
Нашли ошибку или неточность? Не стесняйтесь
пишите нам. Спасибо!
Советы по использованию связанных онлайн-калькуляторов
См. также наш тригонометрический калькулятор треугольников.
Для решения этой словесной математической задачи необходимы следующие знания:
- планиметрия
- треугольник
Единицы физических величин:
- угол 22 Класс словесной задачи:
- Практика для 11-летних
- Практика для 12-летних
Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: video1
- Вычислите 8059
Вычислите величину третьего внутреннего угла в треугольнике ABC при альфа = 30°, бета = 60° - Вычислите 6678
Вы знаете величину двух внутренних углов треугольника альфа = 40° бета = 60° . Вычислить размер третьего внутреннего угла.
Вычислить размер третьего внутреннего угла. - В треугольнике
В треугольнике ABC величина внутреннего угла гамма равна одной трети угла альфа. Размер угла бета на 80 градусов больше размера угла гамма. Вычислите величины внутренних углов треугольника ABC. - Площадь и два угла
Вычислите величину всех сторон и внутренних углов треугольника ABC, если он задан площадью S = 501,9; и два внутренних угла α = 15°28′ и β = 45°. - Величины 24271
В треугольнике ABC величина внутреннего угла бета составляет одну треть величины угла альфа и на 20° больше величины угла гамма. Определить величины внутренних углов этого треугольника. - Треугольники
Выяснить, могут ли заданные величины углов быть внутренними углами треугольника: а) 23°10′,84°30′,72°20′ б) 90°,41°33′,48°37′ c) 14°51′,90°,75°49′ d) 58°58′,59°59′,60°3′ - Конструкция 25851
A. Конструкция ∆ABC такой, что c = 55 мм, α = 45°, β = 60°. Б. Нарисуйте любой остроугольный треугольник и постройте его высоты.
- Коэффициент подобия
Треугольники ABC и A’B’C’ подобны с коэффициентом подобия 2. Величина углов треугольника ABC равна α = 35° и β = 48°. Найдите величины всех углов треугольника A’B’C’. - Гамма-угол
Найдите модуль гамма-угла в треугольнике ABC, если: α = 38° 56′ и β = 47° 54′. - Величины 64704
Треугольник ABC определяет размеры сторон a и b и величины внутренних углов β и γ при условии, что c = 1,86 м, прямая на стороне c равна 2,12 м, а угол альфа равен 40°. ° 12′. - Трапеция — конструкция
Построить трапецию KLMN, где: k = 9 см, l = 4 см, m = 5 см и угол α = 45° - S=(n−2)⋅180 65054
Для суммы s внутренних углов многоугольника, где n — количество его сторон, применяется соотношение s=(n−2)⋅180 градусов. Сколько сторон у многоугольника, если сумма его внутренних углов равна 9?00°? - Биссектрисы
Как показано, в △ ABC, ∠C = 90°, AD делит пополам ∠BAC, DE⊥AB и E, BE = 2, BC = 6. Найдите периметр треугольника △ BDE.
- Величина 29891
В треугольнике ABC модуль внутреннего угла α на 12° меньше угла β, а угол γ в четыре раза больше угла α. Каковы размеры этих внутренних углов в треугольнике? - Линейка и циркуль
Используйте линейку и циркуль, чтобы построить треугольник ABC с AB 5см BAC 60° и ACB 45°. - Одна четверть 13953
Вычислите величину внутренних углов треугольника ABC, если альфа = две пятых бета и альфа = одна четверть гамма. - Треугольники
Треугольники ABC и A’B’C’ подобны, с коэффициентом подобия 2. Углы треугольника ABC равны альфа = 35° и бета = 48°. Определить величины всех углов треугольника A’B’C’.
Математическая сцена — Треугольники — Урок 1
Урок 1 Правила для треугольников
Вершины треугольника принято обозначать заглавными буквами. буквы и стороны с маленькими буквами.
Также принято маркировать сторону, противоположную углу А, знаком малый a, сторона противоположная углу B с малым b и сторона противоположная углу C с маленькой с (см.

Стороны, образующие стороны угла А, называются смежными с А. Сторона, на которой стоит треугольник, называется основанием треугольника.
сумма углов треугольника равна 180°. В этом легко убедиться, проведя прямую прямую, проходящую через угол B и параллельную стороне b. (см. схему).
Углы, образованные этой прямой, равны A, B и C (по правилу что противоположные углы между параллельными прямыми равны).
Также A + B + C = 180, так как вместе они образуют прямую линию.Прямая линия, проведенная из угла B перпендикулярно базовой линии b, называется высота треугольника. На приведенной ниже диаграмме высота обозначена буквой h.
Ранее вы узнали, что площадь треугольника определяется формула.
Площадь F = ×b×h
Буква G используется здесь для обозначения точки, где высота и основание пересекается. Эту точку иногда называют перпендикулярной проекцией точку B на линию b.

Два треугольники называются подобными, если все углы одного треугольника равны все углы другого. Если мы хотим показать, что два треугольника подобны достаточно показать, что два угла равны. Если два угла равны, то очевидно, что третий угол в каждом должен быть равен.
Треугольники на приведенной выше диаграмме похожи. Отсюда следует, что отношения между соответствующими сторонами равны такой же.
Другими словами:и Теперь мы сделаем несколько примеров, используя эти соотношения.
Пример 1Треугольники на схеме подобны с равными углы отмечены таким же образом. Мы хотим вычислить длину сторон обозначены х и у.
Начнем с обозначения треугольников, чтобы лучше видеть легко, какие стороны соответствуют друг другу.
Мы можем записать следующие отношения:
б/к = 36/33 = 24/г = б/к
Это означает, что у/24 = 33/36
и, следовательно, y = 24×33/36 = ·22 см.
Также a/b = х/36 = 20/24 = а/б
Что дает нам x = 36×20/24 = 30 см.Другое правило, использующее пропорции в треугольниках можно вывести.
Проводим прямую линию, пересекающую две стороны треугольника и параллельна третьей стороне. Эта линия разделяет треугольник на две части, верхняя часть представляет собой треугольник, подобный АВС, оригинальный треугольник. Обозначим стороны этого меньшего треугольника знаком буквы x, y и z. Следующее теперь правда:
Проведенная линия делит сторону c на две части, x и r, а сторону a на z и t. Подставляя x + r вместо c и z + t in для a в приведенном выше уравнении мы получаем следующий результат:
Мы показали, что любая линия через две стороны треугольника и параллельно третьей стороне делит эти две стороны в том же соотношении.
Пример 2
Две стороны треугольника ABC, AB и BC равны 30 см.
 длина и третья сторона АС, линия основания, 42 см. Через точку X на АВ проведем прямую, параллельную основанию и длиной 14 см. Найдите длину линий BX
и АКС.
длина и третья сторона АС, линия основания, 42 см. Через точку X на АВ проведем прямую, параллельную основанию и длиной 14 см. Найдите длину линий BX
и АКС.14 / 42 = XB / 30
XB = 30×14 / 42 = 10 см
АХ = 30 — 10 = 20 см
В большинстве случаев, если мы хотим найти размер углов треугольника нам нужно либо нарисовать точную диаграмму, либо измерить углы или воспользоваться правилами тригонометрии.
Равносторонний. Равнобедренный. Прямоугольный.
В равностороннем треугольник все стороны равны и все углы равны 60.
В равнобедренном треугольнике две стороны имеют одинаковую длину и два угла (углы, образованные с основанием линия) равны. Зная один угол в равнобедренном треугольнике, мы можем найти другие углы. Перпендикуляр из вершины к базовой линии (высоте) в равнобедренный треугольник делит треугольник на два равных прямоугольных треугольники.

Стороны справа треугольник ABC удовлетворяет правилу Пифагора, то есть a 2 + b 2 = c 2 .
Также обратное истинный. Если выполняется правило Пифагора, то треугольник прямоугольный.
Мы можем проверить, что Третий треугольник на приведенной выше диаграмме является прямым углом по правилу Пифагора.
5 2 + (53) 2 = 10 2
25 + 75 = 100
Обратите внимание, что длина гипотенуза (10 см) в этом треугольнике в два раза больше длины самой короткой стороны (5 см).
Пример 3
В этом случае углы треугольника всегда равны 30, 60 и 90°.Найдите площадь равностороннего треугольника со стороной 20 см.
Начнем с рисования высоты h треугольника. Это разделяет треугольник на два равных прямоугольных треугольника. Используя правило Пифагора, мы можем рассчитать ч.
ч 2 + 5 2 = 10 2
ч 2 = 10 2 − 5 2 = 100 − 25 = 75 = 5 2 × 3
ч = 53 ≈ 8,7
Площадь A = ×10×h ≈ ×10×8,7 ≈ 43 см 2
Пример 4
Длина сторон равнобедренного треугольника 30 см.
 в длину, а базовая линия 42
см. Найдите длину прямой, проведенной через две равные стороны параллельно
основания и 10 см от основания.
в длину, а базовая линия 42
см. Найдите длину прямой, проведенной через две равные стороны параллельно
основания и 10 см от основания.Сначала делим треугольник на два прямоугольных угловые треугольники, рисуя высоту h от вершины до основания. Сейчас мы используем правило Пифагора, чтобы вычислить высоту.
ч 2 + 21 2 = 30 2
ч 2 = 30 2 − 21 2 = 459
ч ≈ 21,4
у = ч — 10 ≈ 21,4 — 10 ≈ 11,4 см
Используя правило соотношения для подобных треугольников получаем:
г / ч = x / 21
x ≈ 21×11,4 / 21,4 ≈ 11 см
Следовательно, длина параллельная линия 22 см .
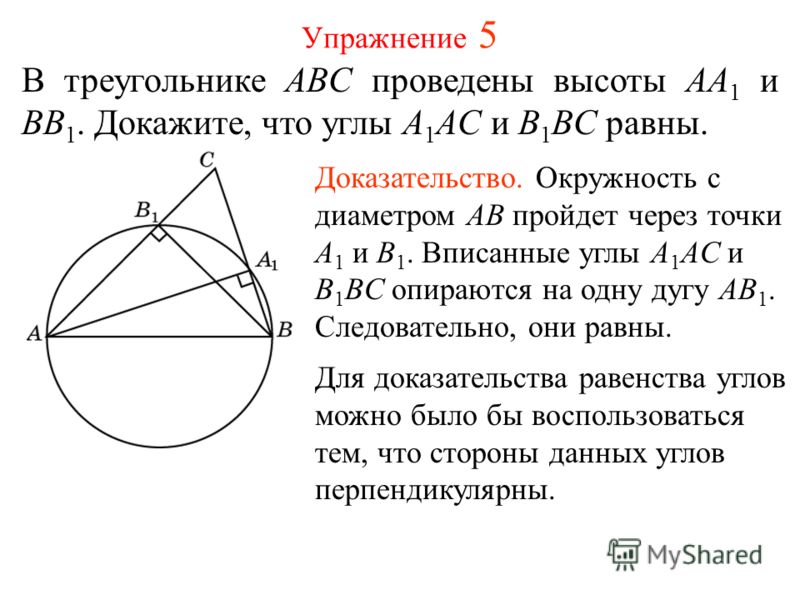
Хорошо нарисуйте прямоугольный треугольник, используя гипотенуза AB в качестве базовой линии, так что угол при вершине C равен 90.
 Мы
затем проведите высоту от C до AB, как показано на диаграмме:
Мы
затем проведите высоту от C до AB, как показано на диаграмме:Эта линия делит угол при вершине на два частей (не равны, если треугольник не равнобедренный). Если одна часть равна х, тогда другое должно быть 90−x. Легко видеть, что два угла при основании должны быть равны 90 − x (на справа) и x (слева) как сумма углов любого треугольника всегда равна 180.
Обратите внимание, что все углы как в меньшем, так и в треугольников, а также в исходном треугольнике ABC равны и равны 90, х и 90 — х. Следовательно, эти три треугольника подобны.
Следующее правило верно для всех прямоугольных треугольники:
высота, проведенная из вершины к гипотенузе, делит прямоугольный треугольник на два треугольника, которые оба подобны исходному треугольнику.
Это приводит к трем наборам соотношений.
Используя греческие буквы а для обозначения стороны, противоположной уголс маркировкой x и b для стороны, противоположной углу с маркировкой 90− х, как показано на на диаграмме получаем следующее:
Два меньших треугольника подобны, поэтому
Исходный треугольник и треугольник с углом x при вершине похожи поэтому
Исходный треугольник и треугольник с углом 90−x аналогичный поэтому
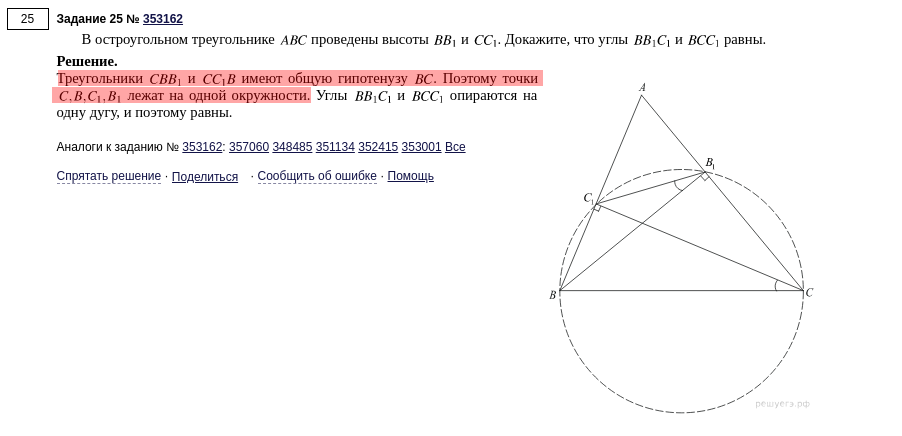
Пример 5
Дан прямоугольный треугольник с две более короткие стороны длиной 7 см и 10 см.



 Вычислить размер третьего внутреннего угла.
Вычислить размер третьего внутреннего угла.



 длина и третья сторона АС, линия основания, 42 см. Через точку X на АВ проведем прямую, параллельную основанию и длиной 14 см. Найдите длину линий BX
и АКС.
длина и третья сторона АС, линия основания, 42 см. Через точку X на АВ проведем прямую, параллельную основанию и длиной 14 см. Найдите длину линий BX
и АКС.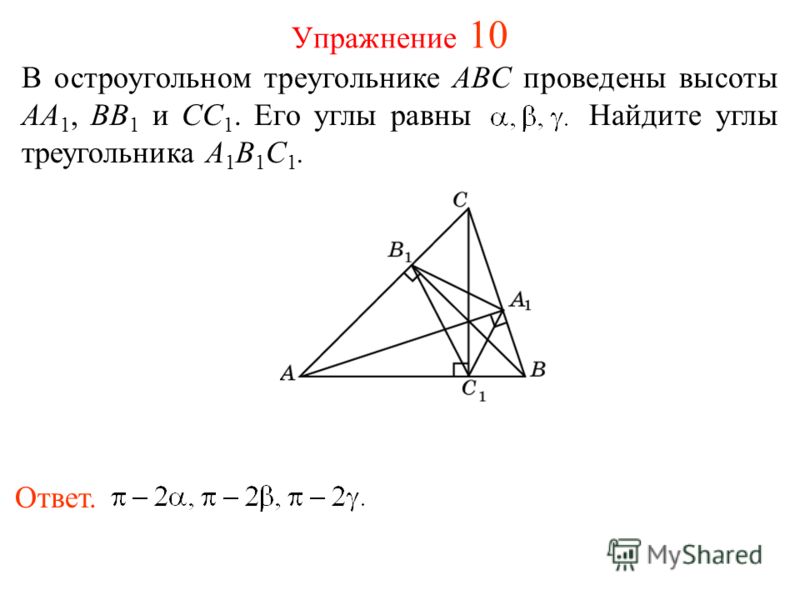
 в длину, а базовая линия 42
см. Найдите длину прямой, проведенной через две равные стороны параллельно
основания и 10 см от основания.
в длину, а базовая линия 42
см. Найдите длину прямой, проведенной через две равные стороны параллельно
основания и 10 см от основания.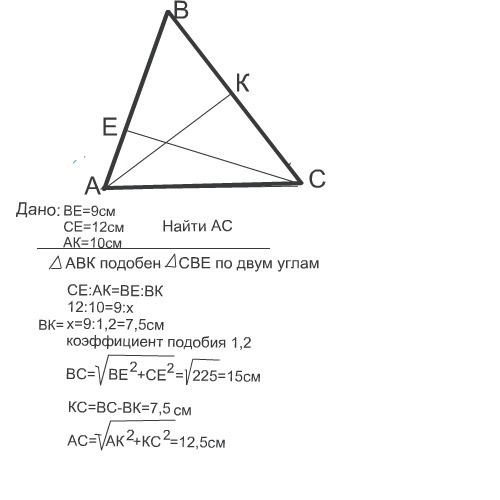 Мы
затем проведите высоту от C до AB, как показано на диаграмме:
Мы
затем проведите высоту от C до AB, как показано на диаграмме:
Leave A Comment