[PDF] Презентация к уроку на тему \»Четырехугольники\»

Четырехугольники

• Углы выпуклого четырехугольника относятся как 10:13:18:19. Найдите меньший угол. Ответ дайте в градусах.

• ABCDEFGHI — правильный девятиугольник. Найдите угол BAG. Ответ дайте в градусах.

• В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 8.

• В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DE параллельны.

• Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A = 75°. Ответ дайте в градусах.

• Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.

• Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.

• На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = DE.

Найдите больший угол параллелограмма ABCD, если ∠DEC = 53°. Ответ дайте в градусах.

Прямая, параллельная основаниям МР и NК трапеции МNКР , проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны MN и КР в точках А и В соответственно. Найдите длину отрезка АВ , если МР=24 см, NК=16см .

Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.

• В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 6.

• В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

• Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK = 7, CK = 12.

• Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.

• Диагонали АС и ВD трапеции АВСD пересекаются в точке О. Площади треугольников ВОС и АОD равны соответственно 25 и 16 . Найдите площадь трапеции.

Середины сторон параллелограмма является вершинами ромба. Докажите, что данный параллелограмм — прямоугольник.

• Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.

• Точка O — центр окружности, на которой лежат точки S, T и V таким образом, что OSTV — ромб. Найдите угол OVT. Ответ дайте в градусах.

• Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.

• Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 7:29. Ответ дайте в градусах.

• Каждое основание АD и ВС трапеции АВСD продолжено в обе стороны. Биссектрисы внешних углов А и В этой трапеции пересекаются в точке К , биссектрисы внешних углов С и D пересекаются в точке Е. Найдите периметр трапеции , если длина отрезка КЕ равна 28.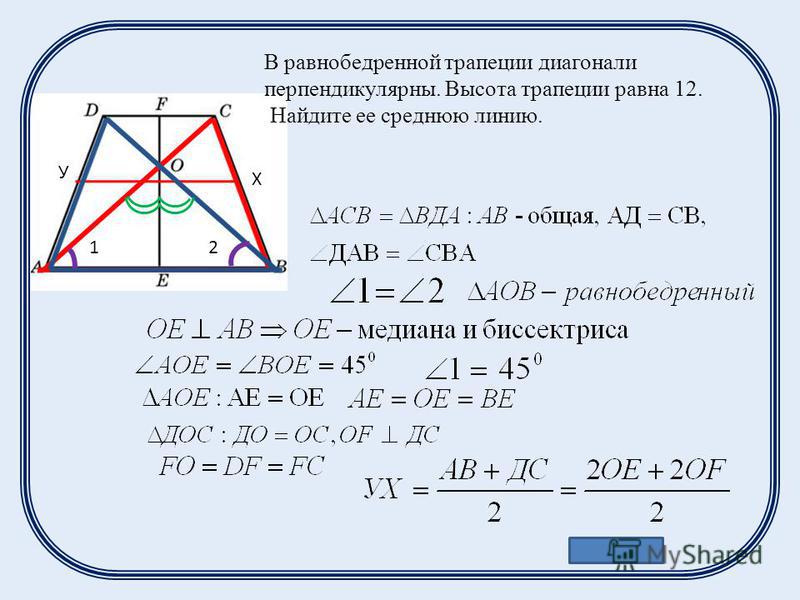

• В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.

• Тангенс острого угла прямоугольной трапеции равен 2. Найдите её большее основание, если меньшее основание равно высоте и равно 78.

• Основания трапеции равны 3 и 14. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

• Основания равнобедренной трапеции равны 62 и 92, боковая сторона 39. Найдите длину диагонали трапеции.

• Около трапеции, один из углов которой равен 52°, описана окружность. Найдите остальные углы трапеции.

• В трапецию, сумма длин боковых сторон которой равна 18, вписана окружность. Найдите длину средней линии трапеции.

• В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.

• В трапеции ABCD AD = 5, BC = 2, а её площадь равна 28.