Тесты

 

        		 Тесты по физике взяты из сборника экзаменационных заданий физика ЕГЭ 2008 г.
МЕХАНИКА
А. Простые задания с вариантами ответов
Задание 1.1-А1. Поставлены две задачи:
1) рассчитать маневр стыковки двух космических кораблей;
2) рассчитать период обращения космических кораблей вокруг Земли.
В каком случае космические корабли можно рассматривать как материальные точки?
1. Только в первом случае.
2. Только во втором случае.
3. В обоих случаях.
4. Ни в первом, ни во втором случае.   Рекомендация по решению
Задание 1.1-А2. Камень брошен из окна второго этажа с высоты 4 м и падает на землю на расстоянии 3 м от стены дома. Чему равен модуль перемещения камня?
1.
3 м.   2. 4 м.   3. 5 м.   4. 7 м.   Рекомендации по решению
Задание 1.1-АЗ.
На рисунке представлен график зависимости координаты движущегося тела от времени. Сравните скорости v1, v2 и v3 тела в моменты времени t1, t2, t3.
1. v1>v2=v3   2. v1>v2>v3   3. v1<v2<v3   4. v1=v2>v3   Рекомендации по решению
Задание 1.1-А4. По графику зависимости модуля скорости от времени, представленному на рисунке, определите ускорение пря­молинейного движения в момент времени t = 2 с.
1. 2 м/с2.   2. 3м/с2.   3. 9 м/с2.   4. 27 м/с2.   Рекомендации по решению
 
Задание 1.1-А5. На рисунке показаны три равные по модулю силы, действующие на тело, и его мгновенная скорость. Куда направлено ускорение тела?
1. 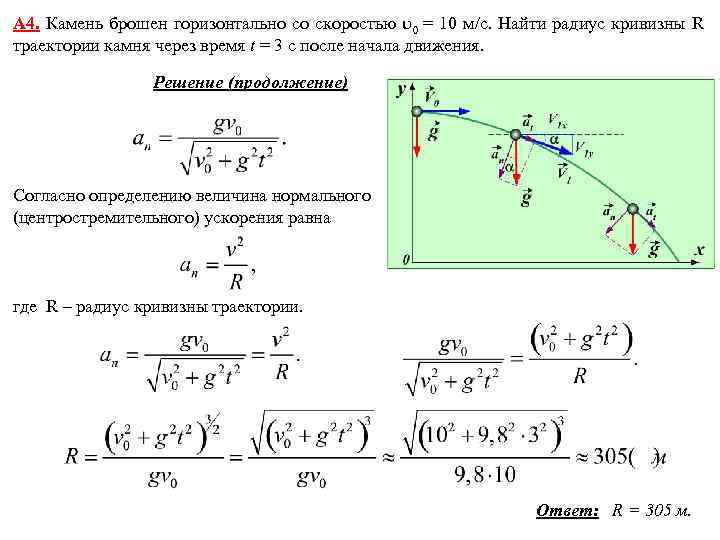Вверх.   2. Влево.   3. Вправо.   4. Направление ускорения по условию задачи определить нельзя.   Рекомендации по решению

 
Задание 1.1-А6. Шарик, брошенный из точки А под углом к горизонту, проходит верхнюю точку полета. Какая стрелка правильно указывает направление ускорения тела, если сопротивлением воздуха можно пренебречь?
1. 1   2. 2   3. 3   4. 4    Рекомендации по решению
Задание 1.1-А7. Книга лежит на столе. На каком рисунке верно представлены силы взаимодействия книги и крышки стола?   Рекомендации по решению
Задание 1.1-А8. Ученик провел опыты с двумя разными пружинами, измеряя силы упругости при разных деформациях пружин. Результаты экспериментов приведены в таблице.
Закон Гука в условиях проведенных опытов. ..
1. …подтверждается только для первой пружины.
2. …подтверждается только для второй пружины.
3. …подтверждается для обеих пружин.
4. … не подтверждается ни для одной из пружин.   Рекомендации по решению
Задание 1.1-А9. На рисунке представлен график зависимости силы трения FTp от модуля силы нормального давления N. Определить коэффициент трения скольжения.
1. 0,1.   2. 0,2.   3. 0,25.   4. 0,5.     Рекомендации по решению
 
Задание 1.1-А10. В 1798 г. Генри Кавендиш провел измерение G-гравитационной постоянной. Этот научный факт позволяет определить…
1. …массу Земли.
2. …период вращения Земли вокруг Солнца.
3. …период вращения Земли вокруг своей оси.
4. …расстояние от Земли до Солнца. Рекомендации по решению
Задание 1.1-А11. Какое из приведенных ниже утверждений является определением, а какое — законом?
1. Импульс р равен произведению массы тела m на его скорость v .
2. Изменение импульса пропорционально силе F и времени t ее действия.
1. 1 — определение, 2 — закон.
2. 1 — закон, 2 — определение.
3. 1 и 2 — определения.
Среди утверждений 1 и 2 нет ни определения, ни закона.  
Задание 1.1-А12. Тележка массой т, движущаяся со скоростью v, сталкивается с неподвижной тележкой такой же массы и сцепляется с ней. Скорость тележек после взаимодействия равна…
1. …v/√2
2. …v/2
3. …v
4. …2v Рекомендации по решению
Задание 1.1-А13. Кинетическая энергия тела измеряется в тех же единицах, что и…
1. …работа силы.
2. …импульс силы.
3. …мощность силы.
4. …давление.   
Задание 1.1-А14. Кинетическая энергия тела равна 8 Дж, а величина импульса 4 Н*с. Масса тела равна…
1. …0,5 кг.
2. …1 кг.
3. …2 кг.
4. …32 кг.   Рекомендации по решению
Задание 1.1-А15. Подъемный кран поднимает вертикально вверх равномерно груз весом 1000 Н на высоту 5 м за 5 с. Какую механическую мощность развивает подъемный кран за время этого подъема?
1. 0 Вт.
2. 5000 Вт
3. 25 000 Вт.
4. 1000 Вт.   Рекомендации по решению
Задание 1.1-А16. Какое из значений для КПД наклонной плоскости, полученных учащимися при выполнении лабораторной работы, является заведомо неверным?
1. 1,5.
2. 0,75.
3. 0,60.
4. 0,33   Рекомендации по решению
Задание 1.1-А17. Какие величины сохраняются для системы тел при упругом и неупругом ударах?
1. Суммарная механическая энергия и импульс шаров.
2. Только суммарная механическая энергия шаров.
3. Только суммарный импульс шаров.
4. Только суммарная скорость шаров.   Рекомендации по решению
Задание1.1-А18. Тормозной путь увеличивается при уменьшении…
1. …угла наклона дороги к горизонту во время движения под гору.
2. …коэффициента трения шин о дорогу.
3. …скорости перед торможением.
4. …массы автомобиля.   Рекомендации по решению
Задание 1.1-А19. Парашютист движется вертикально вниз с постоянной скоростью. При этом его…
1. …потенциальная энергия превращается в кинетическую.
2. …потенциальная энергия превращается во внутреннюю энергию системы «парашютист — воздух».
3. …кинетическая энергия превращается в потенциальную.
4. …кинетическая энергия превращается во внутреннюю энергию системы «парашютист — воздух».   Рекомендации по решению
Задание 1.1-А20. На рычаг действуют две перпендикулярные рычагу силы, плечи которых равны 0,1 м и 0,3 м. Сила, действующая на короткое плечо, равна 3 Н. Чему должна быть равна сила, действующая на длинное плечо, чтобы рычаг был в равновесии?
1. 1 Н.   2. 6 Н.   3. 9 Н.   4. 12 Н.   Рекомендации по решению
Задание 1.1-А21. Чему примерно равна архимедова сила, действующая на тело объемом 2 м3, наполовину погру­женное в жидкость плотностью 1000 кг/м3?
1. 2000 Н.   2. 5000 Н.   3. 10 000 Н.   4. 20 000 Н.   Рекомендации по решению
Задание 1.1-А22. Груз на нитке (см. рис.) начинает двигаться из точки А и далее совершает колебания, проходя после­довательно точки А-Б-В-Б-А и т. д. Период колебания — это время его движения…
1. …от точки А до точки Б.
2. …от точки Б до точки В.

3. …от точки А до точки В.
4. …от точки А до точки В и обратно до точки А.
Задание 1.1-А23. Тело колеблется вдоль оси х так, что его координата меняется во времени по закону х = 5cos(πt) м. Период колебаний тела равен…
1. …0,5 с.
2. …2 с.
3. …л с.
4. …5 с.   Рекомендации по решению
Задание 1.1-А24. Если массу груза уменьшить в 4 раза, то период колебаний груза на пружине…
1. …увеличится в 4 раза.
2. …увеличится в 2 раза.
3. …уменьшится в 2 раза.
4. …уменьшится в 4 раза.   Рекомендации по решению
Задание 1.1-А25. Вы услышали звуковой сигнал от источника, скрытого за препятствием. Этот факт можно объяснить, рассматривая звук как…
1. …механическую волну.
2. …поток частиц, вылетающих из источника звука.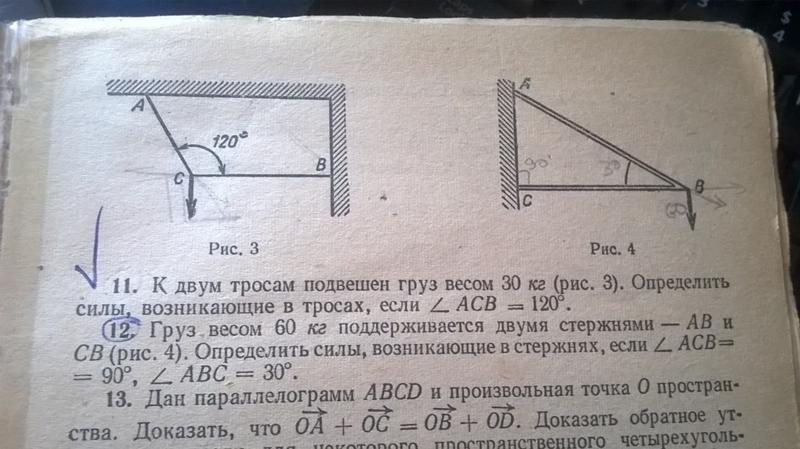
3. …поток молекул, составляющих воздух и движущихся от источника поступательно.
4. …вихревой поток воздуха, идущий из источника звука.
Задание 1.1-А26. Уравнение зависимости проекции скорости движущегося тела от времени: vx=2+3t(м/с). Каково соответствующее уравнение проекции перемещения тела?
1. rx = 2t + 3t2 (м).   2. rх = 1,5t2 (м).   3. rx = 2t + 1,5t2(м).   4. rx = 3t + t2 (м).    Рекомендации по решению
Задание 1.1-А27. Специальный фотоаппарат зафиксировал два положения падающего в воздухе из состояния покоя шарика: в начале движения и через 0,31с (см. рис.). Ускорение свободного падения по результатам такого опыта приблизительно равно…
1. …10,0 м/с2.
2. …10,5 м/с2.
3. …9,2 м/с2.
4. …11,0 м/с2.
Рекомендации по решению
 
Задание 1. 1-А28. Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рисунке. В какой из указанных точек траектории центростремительное ускорение максимально?
1. 1.
2. 2.
3. 3.
4. Во всех точках одинаково.   Рекомендации по решению
Задание 1.1-А29. Два школьника тянут динамометр в противоположные стороны, прикладывая силы по 2 Н каждый. Чему равно показание неподвижного динамометра?
1. 0 Н.   2. 4 Н.   3. 2 Н.   4. Ответ неоднозначен.   Рекомендации по решению
Задание 1.1-АЗО. Модуль скорости автомобиля массой 500 кг изменяется в соответствии с графиком, приведенным на рисунке. Определите модуль равнодействующей силы в момент времени t = 3 с.
1. 0 Н.
2. 500 Н.
3. 1000 Н.
4. 2000 Н.   Рекомендации по решению
РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ТЕСТОВЫХ ЗАДАНИЙ
Задание 1.1-А1. Воспользоваться определением материальной точки — тело, размерами которого можно пренебречь по сравнению с другими размерами в данной задаче.    К задаче
Задание 1.1-А2. Сделать рисунок. Использовать определение вектора перемещения -это вектор, соединяющий начальное и конечное положение тела. Воспользоваться теоремой Пифагора для сторон прямоугольного треугольника: r2 = h3 + S2.    К задаче

 
Задание 1.1-A3. На графике зависимости координаты тела от времени проекция вектора скорости в данный момент времени численно равна тангенсу угла наклона графика (чем «круче» к оси абсцисс расположен график, тем проекция скорости больше; проекция скорости равна нулю, если график расположен параллельно оси времени, координата при этом не меняется — тело покоится).    К задаче
Задание 1.1-А4. При прямолинейном равноускоренном движении (из графика видно, что скорость тела увеличивается) модуль ускорения равен отношению изменения скорости к промежутку времени, за которое это изменение произошло:a=Δv/Δt. По графику определяют, что, например, за промежуток времени 3 с (от 0 до 3 с) модуль скорости увеличился с 3 до 9 м/с, т. е. на 6 м/с.   К задаче
Задание 1.1-А5. Воспользоваться вторым законом Ньютона: ускорение тела прямо пропорционально действующей на него равнодействующей силе и обратно пропорционально массе тела. Равнодействующая сила — векторная сумма всех сил, действующих на тело.   К задаче
Задание 1.1-А6. При отсутствии сопротивления воздуха на шарик действует только сила тяжести, направленная вниз. Далее надо применить второй закон Ньютона.   К задаче
Задание 1.1-А7. Применить третий закон Ньютона: силы взаимодействия двух тел равны по модулю, противоположны по направлению, приложены к взаимодействующим телам и направлены вдоль одной прямой. 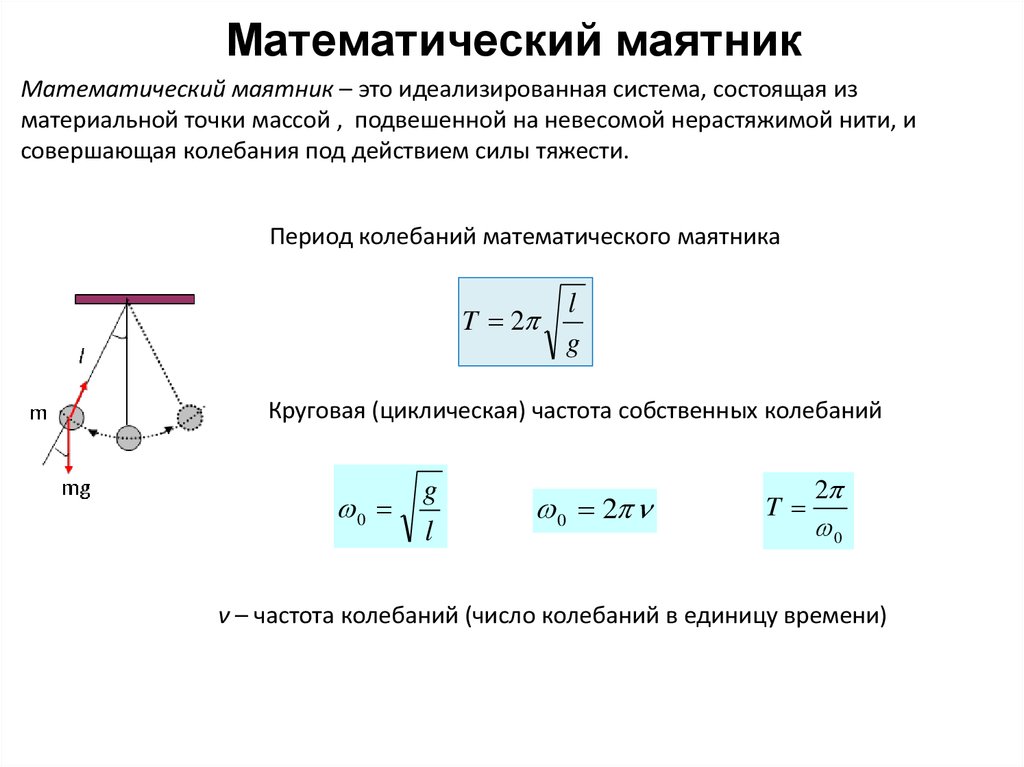     К задаче
Задание 1.1-А8. Воспользоваться законом Гука: модуль силы упругости Fynp прямо пропорционален деформации х пружины Fynp = kx, где k — коэффициент пропорциональности.   К задаче
Задание 1.1-А9. Применить закон для модуля силы трения скольжения FTp: FTp = μN, где μ — коэффициент трения; N — модуль силы нормальной реакции опоры. По приведенному графику определить, что, например, при N = 40 Н и FTP = 10 Н.   К задаче
Задание 1.1-А10. Использовать закон всемирного тяготения для модуля силы F взаимодействия Земли массой М3 с телом массой т, расположенным на ее поверхности:
F =GMз*m/R2з , где R3 — радиус Земли.   К задаче
Задание 1.1-А12. Применить закон сохранения импульса системы тел в проекции на координатную ось, направленную вдоль направления движения тележки: m1v1 + m2v2 = (т1 + т2)и, где т1 = т — масса движущейся тележки; v1=v — ее скорость; т2 = т — масса неподвижной тележки; v2 = 0 — ее скорость; и — скорость тележек после их взаимодействия (абсолютно неупругого удара).     К задаче
Задание 1.1-А14. Воспользоваться формулами кинетической энергии тела Ek=mv2/2 и модулем (величиной) импульса р = mv, и решить полученную систему уравнений относительно искомой величины m.   К задаче
Задание 1.1-А15. При равномерном подъеме груза поднимающая сила равна по модулю силе тяжести, которая равна по модулю весу груза: F = Р = 1000 Н. Работа поднимающей силы равна А = FScosa = Ph, где S = h = 5 м — высота подъема груза; а = 0 — угол между направлением поднимающей силы и направлением перемещения груза. Мощность крана равна N=A/t, где t = 5 с — время подъема груза.   К задаче
Задание 1.1-А16. КПД не может быть больше 100% = 1.   К задаче
Задание 1.1-А17. При любом ударе (как упругом, так и не упругом) сохраняется импульс системы.   К задаче
Задание 1.1-А18. При движении по наклонной поверхности под гору модуль силы трения равен FTP =μN = μmgcosa, где N — модуль силы нормальной реакции опоры; тg — модуль силы тяжести; g — величина ускорения свободного падения; a — угол, который составляет наклонная плоскость с горизонтом. Модуль ускорения а автомобиля при равнозамедленном движении можно найти из второго закона Ньютона в проекции на ось, направленную вдоль наклонной плоскости вверх: а =(Fтр-mgsina)/m = g(μcosa-sina), где т —масса автомобиля. С другой стороны, при равнозамедленном движении модуль ускорения а, пройденный до остановки путь S и модуль v0 вектора начальной скорости связаны соотношением: 2aS = v20 . Решая полученную систему уравнений,
можно получить: S =v20/(2g(μcosa-sina) . Из последней формулы видно, что тормозной путь не зависит от массы тела, уменьшается при уменьшении скорости перед торможением и увеличивается при уменьшении коэффициента трения шин о дорогу. К задаче
Задание 1.1-А19. При движении парашютиста вертикально вниз с постоянной скоростью его кинетическая энергия не изменяется, а потенциальная энергия уменьшается. При этом она превращается во внутреннюю энергию системы «парашютист — воздух».   К задаче
Задание 1.1-А20. Воспользоваться уравнением равновесия рычага: М1 = М2, где М1 — момент первой силы, а М2 — момент второй силы. Воспользоваться определением момента силы: М = Fl, где F — модуль силы; l — плечо силы. К задаче
Задание 1.1-А21. Применить формулу для расчета архимедовой (выталкивающей) силы: Fa = pgVпогр, где ρ=1000 кг/м2 — плотность жидкости; g = 10 м/с2 — модуль ускорения свободного падения; Vпогр =0,5V= — объем тела, погруженного в жидкость   К задаче
Задание 1.1-А23. Воспользоваться формулой координаты при гармонических колебаний: X = Acos(ωt + φ0), где А — амплитуда колебаний; ω — циклическая частота колебаний; φ0 — начальная фаза. Путем сравнения с законом, заданным в условии задачи, определить величину ω =π рад/с. Применить формулу, связывающую циклическую частоту и период колебаний: Т=2π/ω   К задаче
Задание 1. 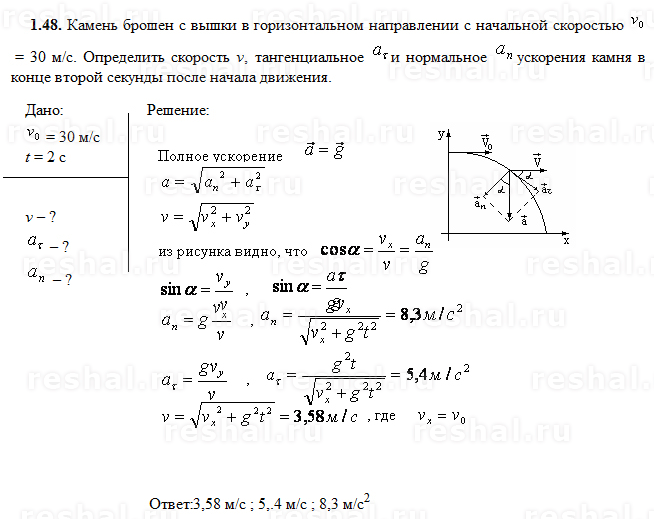1-А24. Применить формулу для периода колебаний пружинного маятника: Т = 2π√(m/k)—, где m — масса груза; k — жесткость пружины.   К задаче
Задание 1.1-А26. Написать уравнение проекции скорости при равнопеременном движении vx = vох + axt, где vох — проекция начальной скорости; ах — проекция ускорения. Путем сравнения с формулой проекции скорости, заданной в условии задания, получаем vox = 2 м/с, ах = 3 м/с2. Написать общее уравнение проекции перемещения и подставить полученные числовые значения: r=voxt+axt2/2=2t+1,5t2(м).    К задаче
Задание 1.1-А27. Из рисунка определить, что шарик пролетает расстояние h = 44 см = 0,44 м. Применить формулу пройденного пути при свободном падении тела:
h =gt2/2, где t = 0,31 с — время свободного падения тела.   К задаче
Задание 1. 1-А28. Применить формулу для модуля центростремительного ускорения при движении тела по криволинейной траектории: ацс =v2/2, где v — модуль вектора скорости; R — радиус кривизны траектории в данной точке. Так как модуль скорости точки постоянен, то центростремительное ускорение максимально в точке, в которой радиус кривизны траектории минимален.   К задаче
Задание 1.1-А29. Если к пружине динамометра и к его корпусу приложить равные по модулю и противоположные по направлению силы, то он останется в положении равновесия, и показание динамометра будет равно модулю приложенных сил. К задаче
Задание 1.1-А30. По графику определить, что для участка графика, содержащего момент времени t = 3 с, за промежуток времени Δt = 4-2 = 2с изменение скорости равно Δv = 4 — 2 = 2 м/с. Рассчитать величину ускорения по формуле а = Δv/Δt. Определить модуль равнодействующей силы по второму закону Ньютона: F = та, где т = 500 кг — масса тела.    К задаче
   
В начало     

2009 год

Кинематика

1. Лодка должна попасть на противоположный берег по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки и, а скорость лодки относительно воды υ. Moдуль скорости лодки относительно берега должен быть равен 1)υ+ и 2)υ— u 3)√ υ2+ и2 4)√ υ2— и2

2. Решаются две задачи: а) рассчитывается маневр стыковки двух космических кораблей; б) рассчитывается период обращения космических кораблей вокруг Земли. В каком случае космические корабли можно рассматривать как материальные точки? 1)только в первом случае 2)только во втором случае 3)в обоих случаях 4) ни в первом, ни во втором случае

3. Чему равно перемещение материальной точки за 5с, движение которой вдоль оси ОХ описывается уравнением: х = 6-4t +t2? 1)5м 2)11м 3)13м 4)18м

4. По графику зависимости модуля скорости от времени (см. рис1) определите путь, пройденный телом за 2 с. 1)6м 2)8м 3)5м 4)4м

5. На рисунке 2 представлен график зависимости координаты тела, движущегося вдоль оси ОХ, от времени. Сравните скорости υl, υ 2 и υ3 тела в моменты времени t1, t2, t3. 1) υ1 > υ 2 = υ 3 2) υ1> υ 2> υ 3 3) υl = υ 2< υ 3 4) υ 1 = v2>v3

6. Лестница, приставленная к вертикальной стене, падает в результате скольжения ее основания по полу. Каково отношение модулей скоростей

υ А и υB (см. рис3) в тот момент, когда угол между лестницей и стеной равен α l) sin α 2) cos α 3) tg α 4) ctg α

7. По графику зависимости модуля скорости от времени, представленному на рис4, определите ускорение прямоли­нейно движущегося тела в момент времени t=2с. 1)2м/с2 2)3м/с2 3)9м/с2 4)27м/с2

8. Уравнение зависимости проекции скорости движу­щегося тела от времени: vx = 2 + 3t (м/с). Каково соответствующее уравнение проекции перемещения тела? 1)Sx=2t+3t2 3)Sx=2t+l,5t2 2)Sx=1,5t2 4)Sx=3t+t2

9. При свободном падении тел разной массы в трубке, из которой откачан воздух, тела движутся с одинаковым ускорени­ем. Это объясняется тем, что сила тяжести: 1) на тела в вакууме не действует 2) пропорциональна массе тел

3) не зависит от массы тела 4) уравновешивается весом тел

10. Специальный фотоаппарат зафиксиро­вал два положения падающего в воздухе из состояния покоя шарика: в начале падения и через 0,31 с (см. рис5). Ускорение свободного падения по результатам такого опыта приблизительно равно…

1)10,0м/с2 2)10,5м/с2 3)9,2м/с2 4)11,0м/с2

11. Материальная точка, двигаясь равномерно по окружности против часовой стрелки, через 3 секунды первый раз попала из точки А в точку В (рис6). Частота обращения точки равна… 1)1/12c-1 2) 1/4c-1 3) 1/3c-1 4)1/2c-1

12. Автомобиль движется с постоянной по модулю ско­ростью по траектории, представленной на рис7. В каши из ука­занных точек траектории центростремительное ускорение макси­мально?

1)1 2)2 3)3 4)Во всех точках одинаково

13.На кольцевой гонке два автомобиля движутся так, что все время были расположены на одной прямой, соединяющей их положение с центром окружности (рис8) Отношение скоростей υ1/υ2 равно1)1/2 2)2 3)√2 4)4

Показ науки: наблюдайте за объектами в свободном падении

Ключевые понятия
Физика
Свободное падение
Сил
Гравитация
Масса
Инерция

Введение
Вы когда-нибудь задумывались, с какой скоростью падает тяжелый предмет по сравнению с более легким? Представьте, если бы вы бросили их обоих одновременно. Кто первым упадет на землю? Будет ли он тяжелее, потому что весит больше? Или они упадут на землю одновременно? В конце 1500-х годов в Италии известный ученый Галилей задавал некоторые из этих вопросов. И он провел несколько экспериментов, чтобы ответить на них. В этом упражнении вы выполните несколько собственных тестов, чтобы определить, падают ли более тяжелые предметы быстрее, чем более легкие.

Фон
В четвертом веке до н.э. Греческий философ Аристотель предположил, что скорость падения объекта, вероятно, зависит от его массы. Другими словами, если два объекта одинакового размера, но один из них тяжелее, то более тяжелый объект имеет большую плотность, чем более легкий. Следовательно, когда оба предмета падают с одинаковой высоты и в одно и то же время, более тяжелый предмет должен удариться о землю раньше, чем более легкий. Это правда?

Примерно 1800 лет спустя, в конце XVI века в Италии, молодой ученый и математик Галилео Галилей подверг сомнению теории Аристотеля о падающих предметах. Он даже провел несколько экспериментов для проверки теорий Аристотеля. По легенде, в 1589 г.Галилей стоял на балконе возле вершины Пизанской башни и бросал два шара одинакового размера, но разной плотности. Хотя ведутся споры о том, произошло ли это на самом деле, история подчеркивает важность использования экспериментов для проверки научных теорий, даже тех, которые были приняты в течение почти 2000 лет.

Материалы
• Два мяча одинакового размера, но разной массы. Например, вы можете использовать металлический и резиновый мяч или деревянный и пластиковый мяч, если эти два мяча примерно одинакового размера. Если два таких сферических шара недоступны, вы можете попробовать что-то вроде яблока и круглого камня такого же размера.
• Лестница или стремянка 
• Видеокамера и помощник (по желанию)

Подготовка
• Вы будете одновременно сбрасывать два мяча с одной высоты. Установите лестницу или стремянку, где вы будете проводить тест. Если вы используете тяжелый мяч, обязательно найдите тестовую площадку, где мяч не повредит пол или землю, когда приземлится.
• Если вы используете видеокамеру для записи эксперимента, установите ее сейчас и попросите помощника подготовиться к записи.
• Будьте осторожны при использовании стремянки или лестницы.

Процедура
• Осторожно поднимитесь по лестнице или стремянке с двумя шариками.
• Бросьте оба мяча одновременно с одинаковой высоты. Если вы используете видеокамеру, обязательно попросите помощника записать, как шары падают и падают на землю.
• Один мяч ударился о землю раньше другого или оба мяча ударились о землю одновременно?
• Повторите эксперимент еще как минимум два раза. Последовательны ли ваши результаты? Один мяч постоянно падает на землю раньше другого или оба мяча всегда падают на землю одновременно?
• Если вы снимали свои эксперименты на видео, вы можете просмотреть записи, чтобы проверить свои результаты.
• Можете ли вы объяснить свои результаты?
• Extra: Попробуйте повторить этот эксперимент, но на этот раз используйте шары одинаковой массы, но разных размеров. Один мяч ударяется о землю раньше другого или они ударяются о землю одновременно?
• Дополнительно: Попробуйте протестировать два объекта одинаковой массы, но разной формы. Например, вы можете попробовать большое перо и очень маленький мячик. Один предмет падает на землю раньше другого или они падают одновременно?
• Extra: Вы можете повторить этот эксперимент, но запишите его с помощью камеры, которая позволяет воспроизводить запись в замедленном темпе. Если вы посмотрите, как шары падают в замедленной съемке, что вы заметите в том, как они падают с течением времени? Оба объекта всегда падают с одинаковой скоростью или один падает быстрее другого в определенные моменты времени?

Наблюдения и результаты
Оба мяча упали на землю одновременно?

Вы должны были обнаружить, что оба мяча упали на землю примерно в одно и то же время. Согласно легенде, это то, что Галилей показал в 1589 году из своего эксперимента с Пизанской башней, но, опять же, обсуждается, произошло ли это на самом деле. Если пренебречь сопротивлением воздуха, объекты, падающие вблизи поверхности Земли, падают с тем же приблизительным ускорением 9,8 метра в секунду в квадрате (90,8 м/с 2 или г ) из-за силы тяжести Земли. Таким образом, ускорение тел одинаково, и, следовательно, их скорость также увеличивается с постоянной скоростью. Поскольку сила, действующая на объект, равна его массе, умноженной на г , более тяжелые объекты имеют большую нисходящую силу. Однако более тяжелые объекты также обладают большей инерцией, что означает, что они сопротивляются движению больше, чем более легкие объекты, и поэтому более тяжелым объектам требуется больше силы, чтобы заставить их двигаться с той же скоростью.

Еще для изучения
Слон и перо — свободное падение, из Класса физики
Двигатели нашей изобретательности: № 166: эксперимент Галилея, из Джона Х. Х. Линхарда, Университет Хьюстона Матиас Липе, Корнельский университет,
Что происходит, то должно падать: проведите знаменитый эксперимент Галилея с падающими объектами, от Science Buddies

Это задание было предложено вам в сотрудничестве с Science Buddies 9.0092

ОБ АВТОРАХ

Астрономы Корнелла сообщают о том, как камеры марсохода Spirit обнаружили изменения в марсианском грунте, в журнале Science special

ИТАКА, штат Нью-Йорк. — Глаза на борту марсохода Spirit показывают наземную правду.

После более чем шести месяцев изучения фотографических и спектральных данных с марсохода ученые марсианской миссии подтверждают, что альбедо — процент солнечного света, отражаемого пыльной поверхностью красной планеты, — указывает на важные различия в минеральном и пылевом составе. .

«Дух приземлился в области средней яркости кратера Гусева и в ходе этой миссии пересекал более яркие и более темные области, путешествуя к кратеру Бонневиль и дальше», — говорит Джим Белл, доцент астрономии Корнельского университета и ведущий научный сотрудник цветные панорамные стереокамеры с высоким разрешением, известные как Pancams, установленные на Spirit и его марсоходе-близнеце Opportunity. Белл говорит: «Изменения альбедо, которые мы заметили с помощью Pancam, коррелируют с изменениями, наблюдаемыми выше с орбитальных аппаратов Марса. Это правдивая информация». (Бонневиль был первым кратером, который марсоход исследовал после приземления.)

Данные об альбедо подробно описаны в исследовательской статье, которая вместе с 10 другими статьями, полученными в результате путешествия Spirit по марсианской поверхности, опубликована на этой неделе в специальном выпуске журнала Science (6 августа 2004 г.). В выпуске, в котором принимают участие 120 авторов, в том числе несколько из Корнелла, есть плакат длиной 2 фута, сложенный в восемь раз, на котором изображены виды Pancam на место посадки Spirit в кратере Гусева.

Наиболее известным автором номера является Стив Сквайрс, профессор астрономии Корнелльского университета и руководитель научной группы марсохода-близнеца. В своей обзорной статье Сквайрес отмечает, что за первые три месяца разведки Spirit не удалось найти «озерные» (связанные с озером) месторождения. На сегодняшний день «мы не нашли доказательств озерных отложений на месте посадки Spirit», — пишет Сквайрс в своем обзоре. Однако с момента приземления Spirit пролетел почти 2 мили или 3 километра в холмистой местности, получившей название Columbia Hills, где вероятность обнаружения материалов, связанных с водой, может быть выше. «Я думаю, что в Columbia Hills есть потенциал для гораздо большего», — говорит Сквайрс.

На пути к Колумбийским холмам Spirit использовал 13 различных спектральных фильтров на Pancams, что позволило ученым миссии получить спектры ультрафиолетовых и инфракрасных свойств почв и горных пород.

Белл и его коллеги используют панорамные камеры для идентификации участков горных пород и почвы для подходящего анализа. «Мы посмотрели, насколько пыльными или чистыми были камни», — отмечает Белл. Используя фотографические фильтры Pancam в видимом и инфракрасном спектре, ученые могут установить, стоит ли исследовать камень. «Мы используем эту информацию о форме, размере и цвете горных пород, чтобы определить, какие виды железосодержащих минералов присутствуют, и определить породы-кандидаты для дальнейшего изучения с помощью ручных инструментов», — говорит он.

Разрешение изображения с установленных на мачте камер Pancam обеспечивает вид 20/20, аналогичный тому, что увидел бы человек на поверхности Марса. Это разрешение в три раза превышает разрешение, зафиксированное камерами миссии Mars Pathfinder в 1997 году или спускаемых аппаратов Viking в середине 1970-х годов. С расстояния 3 метра (10 футов) Pancam имеет разрешение 1 миллиметр на пиксель.

Панкамы Spirit не только смотрели в землю, но и смотрели вверх. Ученые ежедневно пытались наводить свои камеры на солнце и в начале миссии обнаружили относительно непрозрачную атмосферу, связанную с глобальной пыльной бурей в конце 2003 года. К 85 солу (сол или марсианский день равен 24 часам). , 39минут 35 секунд на Земле) пыль начала рассеиваться, уменьшая непрозрачность марсианского неба. Это прояснение марсианской атмосферы в кратере Гусева позволило исследователям наблюдать сумеречное развитие образования водяно-ледяных облаков.

На прошлой неделе Spirit преодолел отметку в 200 сол и ехал вверх по Колумбийским холмам в поисках коренных пород, которые могли бы свидетельствовать о том, что они были сформированы в жидкой воде или изменены ею.