Параллелограмм. Прямоугольник.Ромб. Квадрат. Вариант 1.
Сделайте свои уроки ещё лучше с инструментами учителя для работы в классе и удалённо! Подробнее…
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Выбрать материалы
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Задания теста направлены на проверку основных умений: изображать параллелограмм, прямоугольник, ромб, квадрат и их элементы; применять определения, свойства и признаки параллелограмма, прямоугольника, ромба и квадрата.
Вопрос 1
В ромбе ABCD проведена большая диагональ AC. Определите вид треугольника ABC.
Варианты ответов
- остроугольный
- прямоугольный
- тупоугольный
- определить невозможно
Вопрос 2
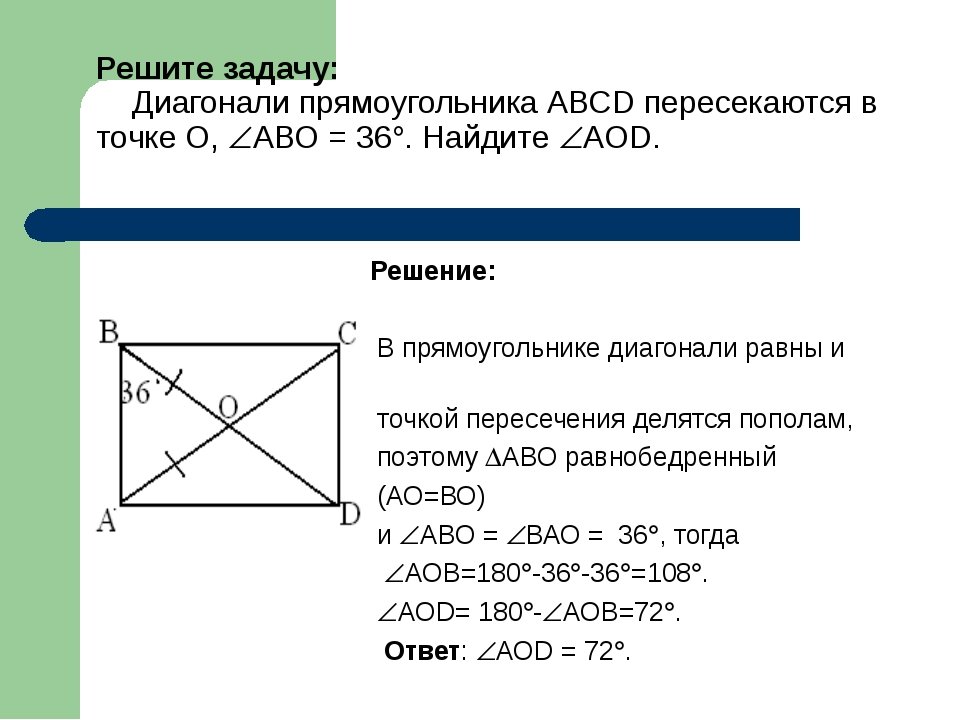
Диагонали прямоугольника ABCD пересекаются в точке О. Определите вид треугольника AOD.
Варианты ответов
- разносторонний
- равносторонний
- определить невозможно
Вопрос 3
В параллелограмме ABCD из вершины тупого угла B проведена высота BM к стороне CD, а из вершины острого угла A прведена высота AN к стороне BC.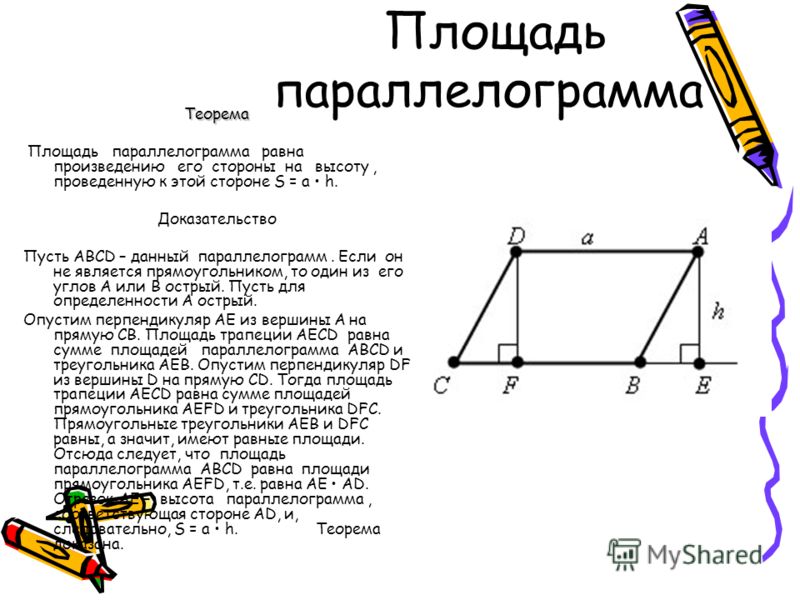 Определите взаимное расположение прямых BM и AN.
Определите взаимное расположение прямых BM и AN.
Варианты ответов
- перпендикулярны
- пересекаются, но не перпендикулярны
- параллельны
- определить невозможно
Вопрос 4
В параллелограмме ABCD углы BAC и CDB равны. Определите вид параллелограмма ABCD.
Варианты ответов
- прямоугольник, отличный от квадрата
- ромб, отличный от квадрата
- квадрат
- определить невозможно
Вопрос 5
В параллелограмме ABCD высота BH в два раза меньше стороны CD. Найдите градусную меру угла ABC.
Найдите градусную меру угла ABC.
Варианты ответов
- 30
- 150
- 120
- 45
Пройти тест
Сохранить у себя:
© 2019, Горбунова Людмила Михайловна 432
Геометрия 7-9 класс. Признаки подобия треугольников — math200.ru
Skip to contentГеометрия 7-9 класс. Признаки подобия треугольниковadmin2022-12-23T09:29:10+03:00
Скачать файл в формате pdf.
Геометрия 7-9 класс. Признаки подобия треугольников
Признаки подобия треугольников
- Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.

- Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключённые между этими сторонами, равны, то треугольники подобны.
- Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого, то треугольники подобны.
Признаки подобия прямоугольных треугольников
- Они имеют по равному острому углу.
- Катеты одного треугольника пропорциональны катетам другого треугольника.
- Гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого треугольника.
Площади подобных треугольников: отношение площадей подобных треугольников равно квадрату коэффициента подобия. Отношение сторон подобных треугольников равно отношению любых соответствующих линейных размеров.
| Задача 1. По данным на рисунке найдите SK, если \(ST\parallel KL.\) Ответ ОТВЕТ: 2,5. | |
| Задача 2. По данным на рисунке найдите ВЕ, если \(DE\parallel AC.\) Ответ ОТВЕТ: 13. | |
| Задача 3. По данным на рисунке найдите СВ – AF. Ответ ОТВЕТ: 7. | |
| Задача 4. По данным на рисунке найдите СВ – МЕ. Ответ ОТВЕТ: 24. | |
| Задача 5. По данным на рисунке найдите площадь треугольника RKO. Ответ ОТВЕТ: 216. | |
| Задача 6. По данным на рисунке найдите TF, если STFE – трапеция. Ответ ОТВЕТ: 20. | |
Задача 7. По данным на рисунке найдите периметр треугольника EFM, если MPKN параллелограмм. Ответ ОТВЕТ: 44. | |
| Задача 8. По данным на рисунке найдите CF, если ABCD параллелограмм и АВ = 14. Ответ ОТВЕТ: 10. | |
| Задача 9. По данным на рисунке найдите RE, если RT = 20. Ответ ОТВЕТ: 5. | |
| Задача 10. По данным на рисунке найдите AD, если ВС = 24. Ответ ОТВЕТ: 4. | |
| Задача 11. По данным на рисунке найдите ОС, если ABCD трапеция и АС = 14. Ответ ОТВЕТ: 10. | |
| Задача 12. По данным на рисунке найдите BO, если ABCD трапеция и BD = 21. Ответ ОТВЕТ: 6,3. | |
Задача 13.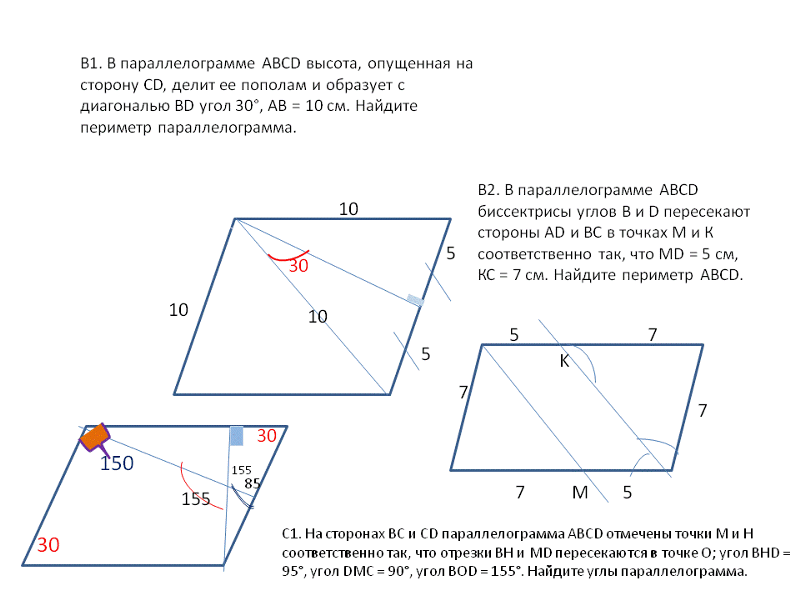 По данным на рисунке найдите TL, если MNPT параллелограмм, NK = MT, По данным на рисунке найдите TL, если MNPT параллелограмм, NK = MT, Ответ ОТВЕТ: 16. | |
| Задача 14. По данным на рисунке найдите МN, если RKLN параллелограмм и KQ = 15. Ответ ОТВЕТ: 8. | |
| Задача 15. В остроугольном треугольнике АВС высоты АК и BH пересекаются в точке О. Найдите ОН, если ВО = 3, ОК = 2 и АО = 6. Ответ ОТВЕТ: 4. | |
| Задача 16. В остроугольном треугольнике АВС высоты СК и BH пересекаются в точке Ответ ОТВЕТ: 2,4. | |
Задача 17. В трапеции ABCD с основаниями AD и BC = 4 известно, что АС = 8 и \(\angle \,BAC = \angle \,ADC.\) Найдите длину основания AD. В трапеции ABCD с основаниями AD и BC = 4 известно, что АС = 8 и \(\angle \,BAC = \angle \,ADC.\) Найдите длину основания AD.Ответ ОТВЕТ: 16. | |
| Задача 18. В трапеции ABCD с основаниями AD = 25 и BC = 4 известно, что \(\angle \,ABD = \angle \,BCD.\) Найдите длину диагонали Ответ ОТВЕТ: 10. | |
| Задача 19. В трапеции ABCD с основаниями AD и BC диагонали AC и BD пересекаются в точке О, \({P_{\Delta \,AOD}}:{P_{\Delta \,BOC}} = 5:2.\) Найдите АО, если АС = 14. Ответ ОТВЕТ: 10. | |
Задача 20. В трапеции ABCD с основаниями AD и BC диагонали AC и BD пересекаются в точке О, \({S_{\Delta \,AOD}}:{S_{\Delta \,BOC}} = 9:1.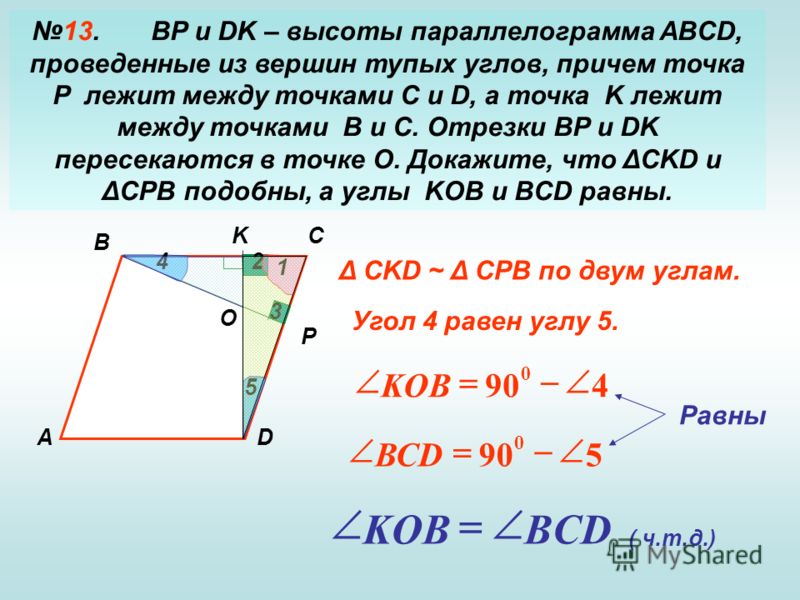 \) Найдите АО, если \) Найдите АО, если Ответ ОТВЕТ: 12. | |
| Задача 21. По данным на рисунке найдите сторону АВ, если \(\angle \,CBA = 2\,\angle \,BAC.\) Ответ ОТВЕТ: \(12\sqrt 3 .\) | |
| Задача 22. По данным на рисунке найдите периметр треугольника NML. Ответ ОТВЕТ: 34. | |
| Задача 23. В остроугольном треугольнике АВС проведены высоты АК и СМ. Докажите подобие треугольников АВС и МВК. | |
| Задача 24. В остроугольном треугольнике АВС проведены высоты АК и СМ. Найдите КС, если МВ = 3, ВК = 4 и АМ = 9. Ответ ОТВЕТ: 5. | |
Задача 25. В трапеции АВСD с основаниями AD и ВС = 5 диагонали пересекаются в точке О.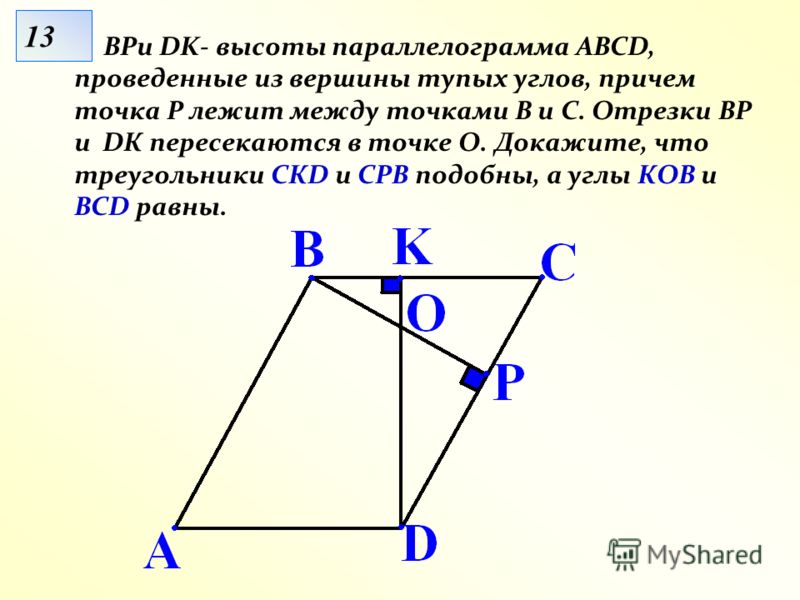 Через точку О проведена прямая параллельно основаниям, пересекающая боковые стороны трапеции в точках Е и F. Найдите длину основания AD, если EF = 8. Через точку О проведена прямая параллельно основаниям, пересекающая боковые стороны трапеции в точках Е и F. Найдите длину основания AD, если EF = 8.Ответ ОТВЕТ: 20. | |
| Задача 26. В трапеции АВСD с основаниями AD = 20 и ВС = 5 диагонали пересекаются в точке О. Через точку О проведена прямая параллельно основаниям, пересекающая боковые стороны трапеции в точках Е и F. Найдите длину отрезка EF. Ответ ОТВЕТ: 8. | |
Задача 27. В треугольнике АВС точки N, M и D принадлежат сторонам АВ, ВС и AС соответственно, причем \(MN\parallel AC\), а прямые MN и BD пересекаются в точке К. Известно, что площадь треугольника NBK равна 18, площадь трапеции ANKD равна 14 и КМ = 9.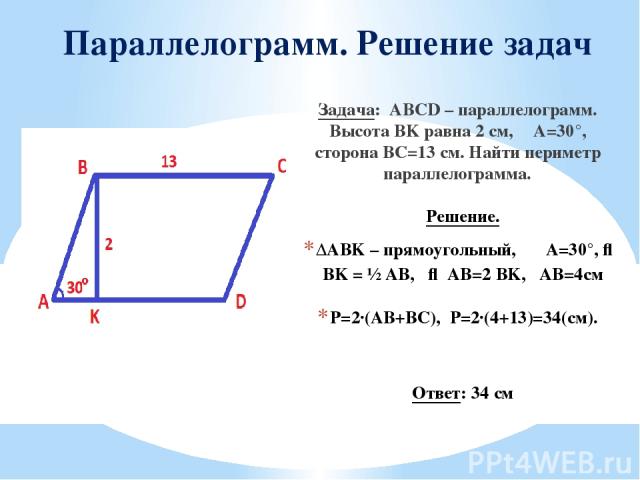 Найдите длину отрезка DC. Найдите длину отрезка DC.Ответ ОТВЕТ: 12. | |
| Задача 28. В прямоугольном треугольнике АВС проведена высота СК к гипотенузе АВ. При этом площади треугольников АКС и ВСК равны соответственно 4 и 16. Найдите длину гипотенузы АВ. Ответ ОТВЕТ: 10. | |
| Задача 29. В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О. Площади треугольников ВОС и AOD равны соответственно 2 и 50. Найдите площадь трапеции. Ответ ОТВЕТ: 72. | |
| Задача 30. В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О. Площади треугольников ВОС и СOD равны соответственно 4 и 16. Найдите площадь трапеции. Ответ ОТВЕТ: 100. | |
Задача 31. В параллелограмме ABCD точка М принадлежит стороне ВС. Отрезки АС и DM пересекаются в точке К. Площади треугольников МСК и CKD равны соответственно 8 и 12. Найдите площадь параллелограмма. В параллелограмме ABCD точка М принадлежит стороне ВС. Отрезки АС и DM пересекаются в точке К. Площади треугольников МСК и CKD равны соответственно 8 и 12. Найдите площадь параллелограмма.Ответ ОТВЕТ: 60. | |
| Задача 32. В треугольнике АВС точки М, N и K принадлежат сторонам АВ, ВС и AС соответственно, причем четырёхугольник AMNK является параллелограммом. Найдите площадь треугольника АВС, если площади треугольников MNB и KNC равны соответственно 16 и 25. Ответ ОТВЕТ: 81. | |
Задача 33. В параллелограмме ABCD F – середина стороны ВС, AF пересекает BD в точке Е, СЕ пересекает АВ в точке К, КВ = 8, AD = 18, \(\angle \,ABC = {150^ \circ }.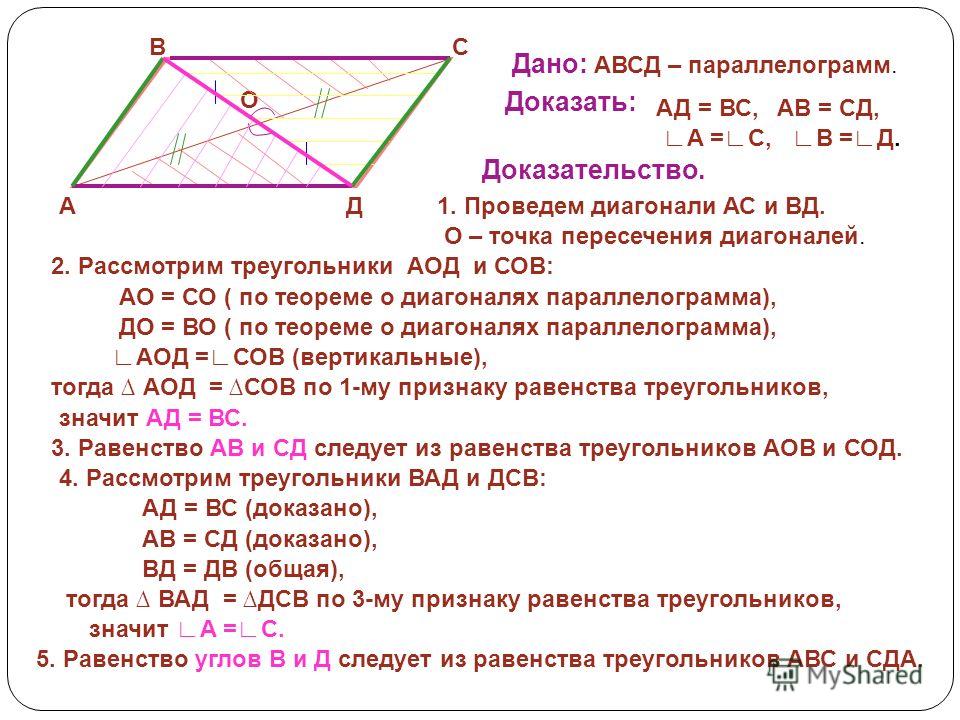 \) Найдите площадь параллелограмма. \) Найдите площадь параллелограмма.Ответ ОТВЕТ: 144. | |
Реклама
Мы Вконтакте
Поддержать нас
Доказательство площади параллелограмма
Начните доказательство площади параллелограмма с построения параллелограмма ABCD.
Затем проведите высоты от вершин D и C до отрезка AB. Возможно, вам придется удлинить отрезок AB, поскольку вы рисуете высоту из C.
Назовите прямоугольник, образованный путем рисования высот из вершин D и C, EDCF.
Доказательство не сложное. Мы уже знаем, что площадь прямоугольника равна произведению основания на высоту.
Следовательно, если мы сможем показать, что можем играть с параллелограммом ABCD, чтобы получить прямоугольник EDCF, то мы закончили.
В этом случае площадь параллелограмма ABCD должна быть равна площади прямоугольника EDCF.
То, что мы пытаемся сделать, показано ниже:
Еще раз внимательно посмотрите на рисунок. Считаете ли вы, что треугольник ADE равен треугольнику FCB? Может быть, но нам нужно это доказать.
Если треугольник ADE совпадает с треугольником FCB, вы можете просто разрезать треугольник ADE и поместить его над треугольником FCB, пока они не совпадут, и поехали!
Вы только что сделали прямоугольник, вырезав треугольник ADE из параллелограмма ABCD.
И снова, если вы можете это сделать, и параллелограмм, и прямоугольник должны иметь одинаковую площадь.
Все, что нам нужно сделать сейчас, это показать, что треугольник ADE совпадает с треугольником FCB, и все готово!
Другими словами, мы пытаемся показать, что треугольник ADE и треугольник FCB конгруэнтны.
Мы можем использовать постулат SSS, чтобы показать, что треугольники ADE и треугольники FCB конгруэнтны.
Оба треугольника прямоугольные. Если мы сможем показать, что две стороны одинаковы, последняя сторона треугольников будет одинаковой после того, как мы воспользуемся теоремой Пифагора, чтобы найти ее. Следовательно, оба треугольника будут одинаковыми.
Если мы сможем показать, что две стороны одинаковы, последняя сторона треугольников будет одинаковой после того, как мы воспользуемся теоремой Пифагора, чтобы найти ее. Следовательно, оба треугольника будут одинаковыми.
В параллелограмме ABCD отрезок AD = отрезку BC, так как в параллелограмме противоположные стороны равны
В прямоугольнике EDCF отрезок ED = отрезку FC, так как в прямоугольнике противоположные стороны равны
Мы нашли две равные стороны! Мы закончили с полным доказательством.
Вот краткое изложение шагов, которые мы выполнили, чтобы показать доказательство площади параллелограмма.
- Нарисуйте параллелограмм.
- Вырежьте из параллелограмма прямоугольный треугольник.
- Используйте прямоугольный треугольник, чтобы превратить параллелограмм в прямоугольник.
- Параллелограмм будет иметь ту же площадь, что и созданный вами прямоугольник, т. е. b × h
30-60-90 Треугольник
03 апр, 23 17:08
Что такое треугольник 30-60-90? Определение, доказательство, площадь и простые примеры из реальной жизни.

Подробнее
Расчет условной вероятности с помощью таблицы непредвиденных обстоятельств
29, 23 марта 10:19
Научитесь рассчитывать условную вероятность с помощью таблицы непредвиденных обстоятельств. Эта таблица непредвиденных обстоятельств может помочь вам разобраться быстро и безболезненно.
Подробнее
Площади параллелограммов и треугольников
Хотя вначале вы можете не заметить сходства между
параллелограммами и
треугольниками, мы увидим, что на самом деле они довольно
связаны, когда дело доходит до площади.
Но насколько они могут быть похожи, если один представляет собой трехсторонний многоугольник, а другой
представляет собой определенный тип четырехугольника? Давайте начнем рисовать некоторые связи между параллелограммами
и треугольниками, выяснив, как сначала измерить площади параллелограммов
.
Площади параллелограммов
Напомним, что параллелограммы — это особый тип четырехугольника
, у которого противоположные стороны не пересекаются. Параллелограммы бывают
Параллелограммы бывают
в виде
прямоугольников, ромбов и квадратов. При попытке определить площадь
параллелограмма необходимо будет идентифицировать два основных компонента: основание
и высота параллелограмма. Основание параллелограмма может быть на
любая сторона фигуры. Высота параллелограмма равна расстоянию
по перпендикуляру между любыми двумя параллельными основаниями. Давайте посмотрим на эти разные части на рисунке
ниже.
Мы могли бы также выбрать в качестве оснований левую и правую стороны параллелограмма.
В этом случае высота будет идти горизонтально.
Площадь параллелограмма определяется произведением основания на высоту.
То есть площади параллелограммов можно выразить как
где A представляет площадь, b — основание, а h
— высоту.
Давайте попрактикуемся в использовании этой формулы, выполнив упражнение ниже.
Упражнение 1
Найдите площадь параллелограмма ABCD .
Ответ:
Во-первых, мы хотим выбрать сторону в качестве основания нашего параллелограмма. В этом случае
мы можем выбрать сторону с маркировкой 12 дюймов в качестве нашей базы.
Высота нашего параллелограмма — это отрезок, перпендикулярный выбранному нами основанию.
На схеме мы видим, что на пересечении DC
и пунктирной синей линии длиной 9 есть прямой угол.0098 8 дюймов . Теперь, когда
у нас есть размеры нашего основания и высоты, мы можем подставить эти значения непосредственно в
нашу формулу площади. Итак, у нас есть
Площадь параллелограмма ABCD равна 96 квадратных дюймов .
Это означает, что мы можем идеально подогнать 96 квадраты размером один дюйм на один дюйм
в параллелограмм.
Давайте попробуем еще один пример, чтобы убедиться, что мы понимаем, как использовать формулу площади
для параллелограммов.
Упражнение 2
Если площадь параллелограмма EFGH равна 112 квадратных метров, то каким должно быть значение
x ?
Ответ:
Мы не можем просто «включи и пыхни» для этого упражнения, как в первом примере.
В этом упражнении нам дана площадь параллелограмма, и мы должны работать в обратном направлении.
Нам дано, что высота параллелограмма х метров. Это
и есть переменная, для которой мы будем решать. Нам также известно, что основание нашего параллелограмма
HG разделено на две меньшие длины: одна имеет длину 11
метров , а другая
2 5 90999 метров.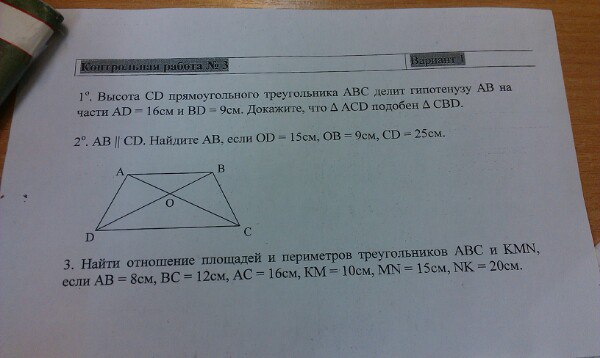 0099 метров в длину. Давайте
0099 метров в длину. Давайте
объединим их, чтобы узнать, что такое наша база:
Итак, мы обнаружили, что наша база b имеет длину 16 метров .
Давайте подставим то, что мы знаем, в нашу формулу площади и найдем x .
Таким образом, высота параллелограмма EFGH это 7 метров .
(Обратите внимание, что мы не сказали, что высота равна 7 метров в квадрате , потому что
мы говорим не о площади, а о высоте.)
Теперь давайте рассмотрим свойства площадей треугольников, чтобы установить связи, которые они имеют с параллелограммами.
Площади треугольников
Как и в параллелограмме, основными компонентами площади треугольника являются основание 9.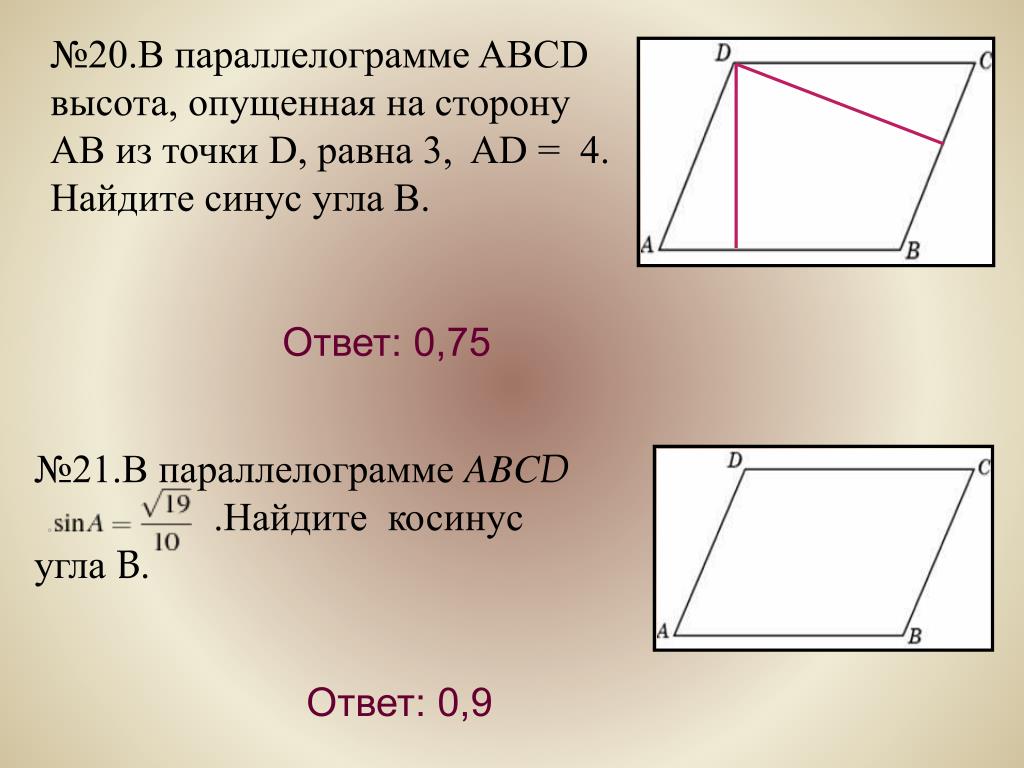 0037 и высота треугольника. Основанием треугольника может быть любая сторона. Высота
0037 и высота треугольника. Основанием треугольника может быть любая сторона. Высота
треугольника равна длине высоты треугольника , проведенной к выбранному основанию.
Высота треугольника — это прямая a, проходящая через вершину, перпендикулярную
к противоположной стороне треугольника. Давайте рассмотрим эти части в треугольнике
ниже.
Площадь треугольника равна половине произведения основания и соответствующих ему
высота. Таким образом, формула
Давайте попрактикуемся в использовании этой формулы, выполнив следующие упражнения.
Упражнение 3
Найдите площадь ?KLM .
Ответ:
Основание треугольника, представляющее собой отрезок ML , имеет длину 24
сантиметров . Поэтому мы сможем подставить 24 вместо
Поэтому мы сможем подставить 24 вместо
b , когда захотим использовать нашу формулу площади. Длина высоты,
или высота, также дана. Мы видим, что здесь высота равна 7 сантиметров ,
, поэтому мы можем подставить 7 вместо h . У нас есть оба компонента
нашей формулы, поэтому мы можем подставить эти числа, чтобы найти площадь.
Итак, площадь треугольника KLM равна 84 квадратных сантиметров .
Давайте попробуем еще один пример.
Упражнение 4
Найдите площадь ?NPQ .
Ответ:
Как мы заметили в предыдущем упражнении, площадь треугольника равна 9.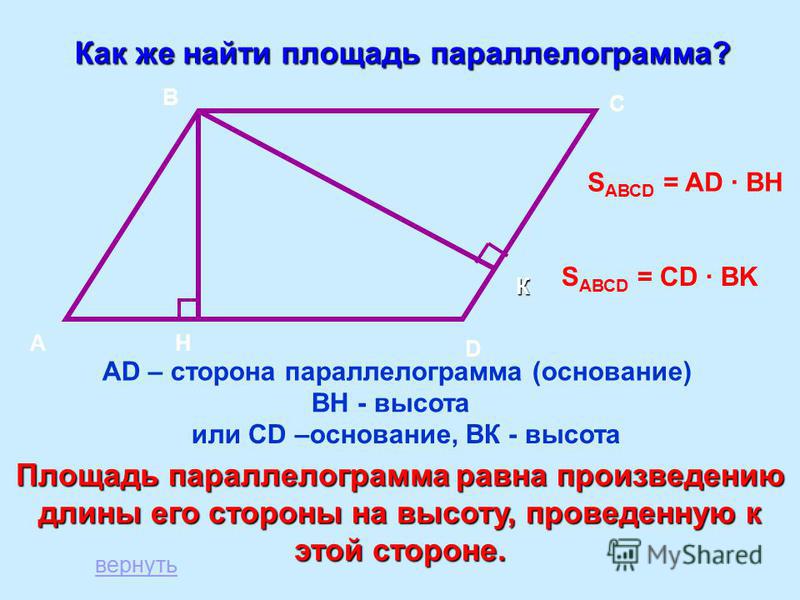 0037 просто как найти длины основания и высоты. Однако в этом упражнении
0037 просто как найти длины основания и высоты. Однако в этом упражнении
нам нужно быть осторожными, чтобы не перепутать значения нашего основания и высоты.
Давайте сначала найдем нашу базу. Отрезок NQ является нашей базой длиной
из 10 футов . Однако мы видим, что есть пунктирная линия, идущая
от Q в направлении точки R . Эта строка не
часть нашего треугольника. Единственная цель, которую он выполняет, это помочь нам найти высоту
нашего треугольника, как мы увидим.
В этом случае наша высота (и высота) лежит на внешней стороне нашего треугольника. Напомним
, что по определению высота — это отрезок, перпендикулярный основанию треугольника
, который проходит через противоположную точку. Так как NQ был выбран в качестве нашей базы
, нам нужно было расширить этот сегмент до точки R для того, чтобы для
была возможность иметь линию, перпендикулярную NQ , которая проходит через P . Мы видим, что высота ?NPQ равна
Мы видим, что высота ?NPQ равна
6 футов . Теперь мы готовы подставить значения нашего основания и высоты
в формулу площади для треугольников.
Итак, площадь ?NPQ равна 30 квадратных футов .
Теперь, когда мы знакомы с формулами площади параллелограмма и треугольника,
давайте разберемся, какая между ними связь.
Связь между параллелограммами и треугольниками
Присмотревшись строго к их формулам, мы замечаем, что формула для треугольника имеет
дополнительных множителей, равных половине, тогда как формула площади для параллелограмма равна всего 9.0037 основание умножить на высоту. Давайте выясним, как этот дополнительный множитель, равный половине
, вступает в игру.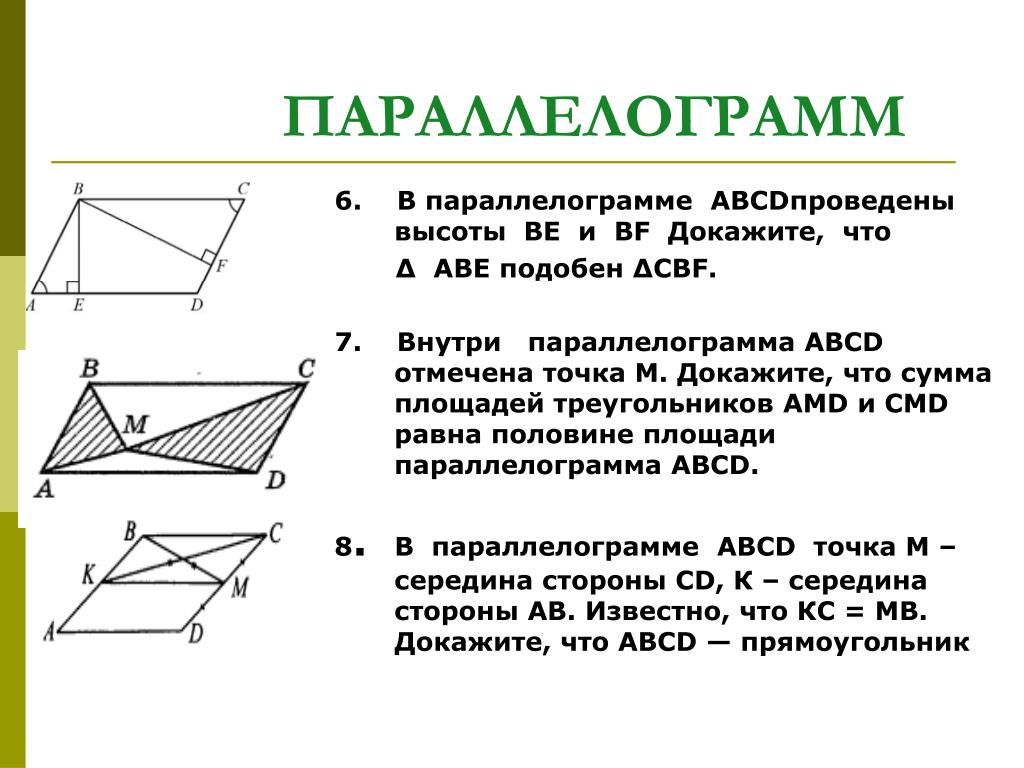
Треугольники — это самый основной тип многоугольника, из которого состоят все другие типы многоугольников.
Другими словами, мы можем поместить определенное количество конгруэнтных треугольников в любой
многоугольник. В частности, мы узнали, что (n-2) треугольников могут
вписаться в n -угольник (см.
полигонов). Таким образом, когда мы работаем с параллелограммами типа
четырехугольника, мы знаем, что мы можем поместить (4-2)=2 равных треугольников
в параллелограмм.
Параллелограмм ABCD можно разбить на два равных треугольника: ?ABD
и ?CDB.
Следовательно, если у нас есть параллелограмм с тем же основанием и высотой, что и у треугольника,
мы знаем, что можем сложить два таких треугольника вместе, чтобы создать параллелограмм.
Давайте посмотрим на это с помощью приведенных ниже диаграмм.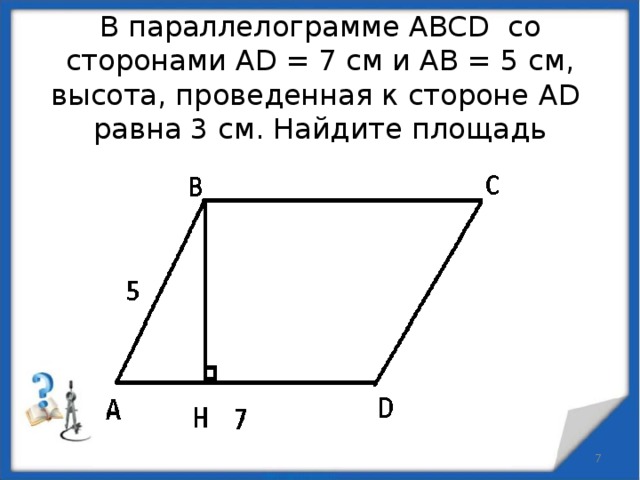


Leave A Comment