Атомная физика
Одним из явлений, подтверждающих гипотезу фотонов, является фотоэлектрический эффект.
|
Внешний фотоэффект или фотоэлектронная эмиссия — испускание электронов веществом под действием электромагнитного изучения. |
Основное влияние на характер протекания фотоэффекта оказывают свойства облучаемого материала (проводник, полупроводник, диэлектрик), а также энергия фотонов, так как для каждого материала существует минимальное значение энергии фотонов, при которой фотоэффект прекращается.
Рис. 2.4. Ге́нрих Ру́дольф Герц (1857–1894)
Впервые явление фотоэффекта было замечено Г. Герцем в 1887 г. Сущность явления состоит в том, что при освещении ультрафиолетовыми лучами металлическое тело теряет электроны.
Рис. 2.5. Освещение заряженной цинковой пластинки светом электрической дуги:
1 — отрицательно заряженная пластинка; 2 — положительно заряженная пластинка
Если цинковую пластинку зарядить отрицательно, то при ее облучении электрометр быстро разряжается. Если же пластинка заряжена положительно, то при облучении ее заряд не изменяется.
Видео 2.1. Внешний фотоэффект — разрядка светом ртутной лампы цинковой и медной пластин.
Рис. 2.6. Алекса́ндр Григо́рьевич Столе́тов (1839–1896)
Рис. 2.7. Филипп Эдуард Антон фон Ленард (1862–1947)
Первые количественные исследования фотоэлектрического эффекта принадлежат русскому физику А. Г. Столетову, который установил основные законы фотоэффекта.
Г. Столетову, который установил основные законы фотоэффекта.
Рис. 2.8. Описание опыта Столетовым А.Г. «Два металлических диска («арматуры», «электроды») в 22 см диаметром были установлены вертикально и друг другу параллельно перед электрическим фонарем Дюбоска, из которого вынуты все стекла. В фонаре имелась лампа с вольтовой дугой А. Один из дисков, близлежащий к фонарю, сделан из тонкой металлической сетки, латунной или железной, иногда гальванопластически покрытой другим металлом, которая была натянута в круглом кольце; другой диск сплошной (металлическая пластинка)» [Столетов А. Г. Избранные сочинения / Под ред. А. К. Тимирязева.— М.; Л.: Гос. изд. техн.-теор. лит., 1950. — 660 с.]. Измерения производились зеркальным гальванометром G, источником тока В служили гальванические батареи из разного числа элементов.
Позже установка Столетова была усовершенствована Ф.Э.А. Ленардом (Нобелевская премия в 1905 г. за исследование катодных лучей) и другими исследователями (рис.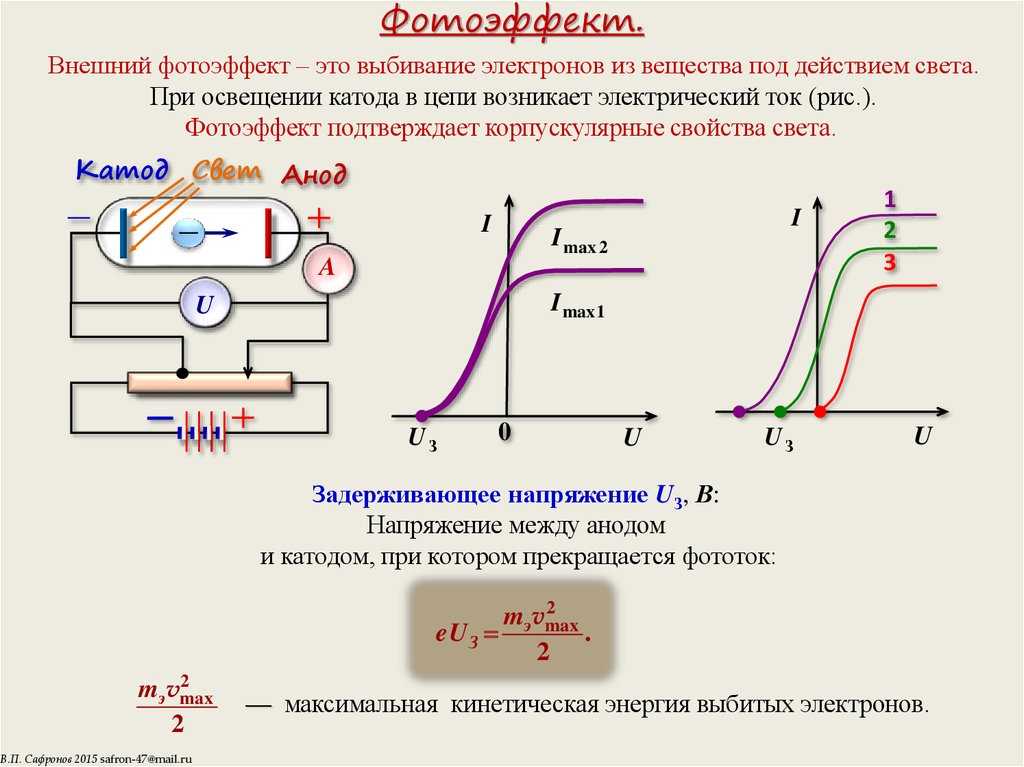
Рис. 2.9. Схема опытов по изучению внешнего фотоэффекта
Свет, проникающий через кварцевое окно КВ (кварц пропускает ультрафиолетовые лучи), освещает катод К, изготовленный из исследуемого материала. Электроны, испущенные вследствие фотоэффекта, перемещаются под действием электрического поля к аноду А. В цепи возникает фототок, измеряемый миллиамперметром. С помощью потенциометра П
Исследования привели к установлению следующих основных закономерностей фотоэффекта:
|
1. Испускаемые под действием света заряды имеют отрицательный знак. 2. Величина испускаемого телом заряда пропорциональна поглощенной им световой энергии. 3. 4. Фотоэффект протекает безынерционно, то есть фототок появляется практически одновременно с освещением катода (задержка ). |
Проанализируем вольт-амперную характеристику (то есть зависимость фототока I от напряжения между электродами U), которая получается в результате фотоэлектрического эффекта. Из кривой на рис. 2.10 видно, что при некотором напряжении фототок достигает насыщения — все электроны, испущенные катодом, попадают на анод.
Рис. 2.10. Вольт-амперная характеристика фотоэффекта
Следовательно, сила тока насыщения определяется количеством электронов, испускаемых катодом в единицу времени под действием света. Поэтому сила фототока насыщения прямо пропорциональна световому потоку
Поэтому сила фототока насыщения прямо пропорциональна световому потоку
|
|
(2.5) |
где k — коэффициент пропорциональности, характеризующий «чувствительность» данного вещества к свету.
Рис. 2.11. Зависимость силы фототока насыщения от светового потока
Анализ кривой показывает, что электроны вылетают из катода с различными по величине скоростями. Часть электронов обладает достаточными скоростями, чтобы при U =0 долететь до анода «самостоятельно» и создать фототок без помощи ускоряющего поля. Для обращения фототока в нуль необходимо приложить некоторое задерживающее напряжение .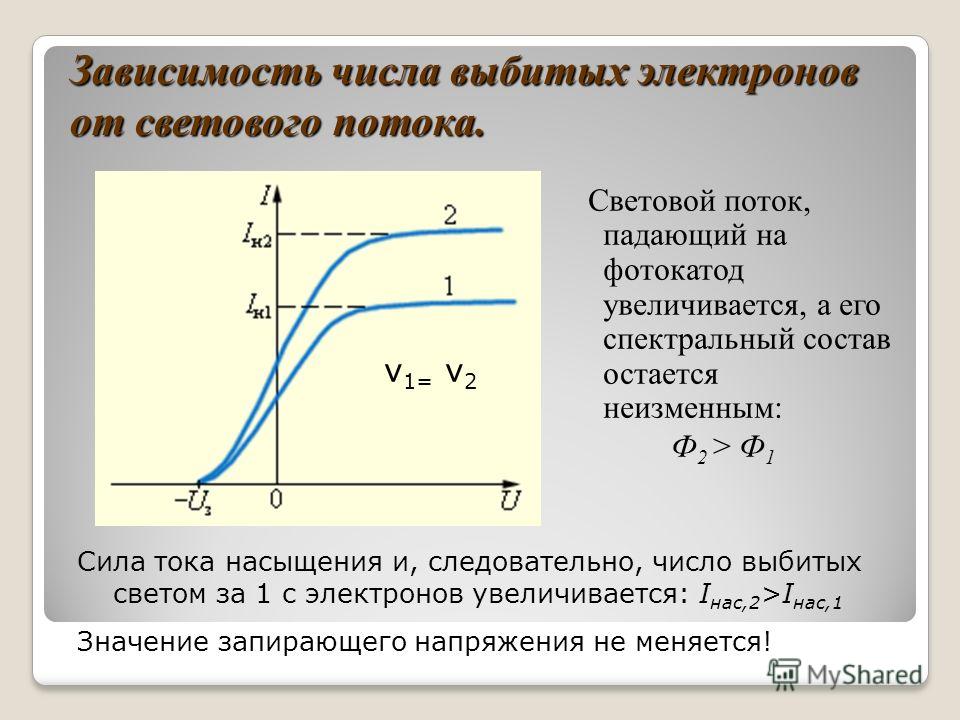 По величине тормозящей разности потенциалов
По величине тормозящей разности потенциалов
|
(2.6) |
где — масса, величина заряда (e>0) и максимальная скорость этих электронов. Экспериментально было установлено, что максимальная скорость фотоэлектронов не зависит от интенсивности света, а зависит только от частоты облучения . Растущая линейная зависимость на рис. 2.4 указывает на то, что увеличение частоты приводит к возрастанию максимальной скорости фотоэлектронов.
Рис. 2.4. Зависимость задерживающего напряжения от частоты
Эта экспериментальная зависимость не укладывается в рамки классической электродинамики, так как скорость фотоэлектронов по классическим понятиям должна зависеть от интенсивности электромагнитной волны, а не от ее частоты.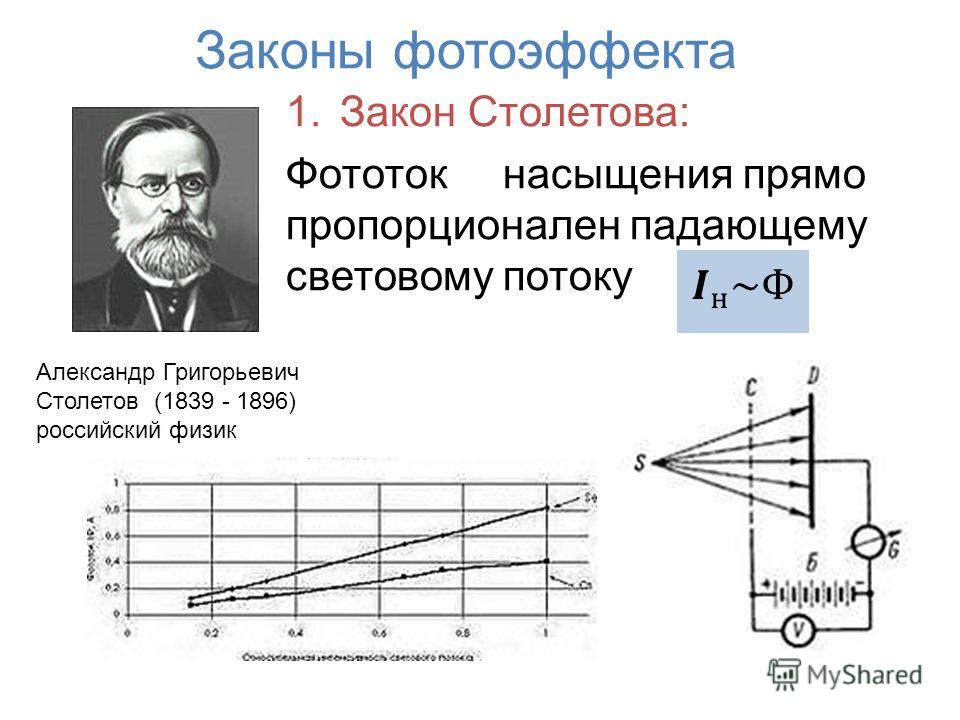
В 1905 г. А. Эйнштейн показал, что все закономерности фотоэффекта легко объясняются, если предположить, что свет распространяется и поглощается такими же порциями (квантами)
Рис. 2.13. Схема возникновения фотоэффекта в металле под действием падающих фотонов
Энергия, полученная электроном, доставляется ему в виде кванта . Часть этой энергии электрон тратит на то, чтобы «вырваться» из металла. Для каждого материала имеется своя
|
Работа выхода — это наименьшая энергия, которую необходимо сообщить электрону, чтобы удалить его из вещества в вакуум. |
Остаток энергии фотона превращается в кинетическую энергию К электрона. Кинетическая энергия максимальна, если электрон образуется вблизи поверхности вещества и не расходует энергию при случайных столкновениях в веществе. В этом случае будет выполняться
|
|
(2.7) |
Нобелевская премия по физике за 1921 г. была присуждена Эйнштейну за его «важные физико-математические исследования и особенно за открытие законов фотоэлектрического эффекта». (Знаменитая теория относительности даже не упомянута в приведенной формулировке).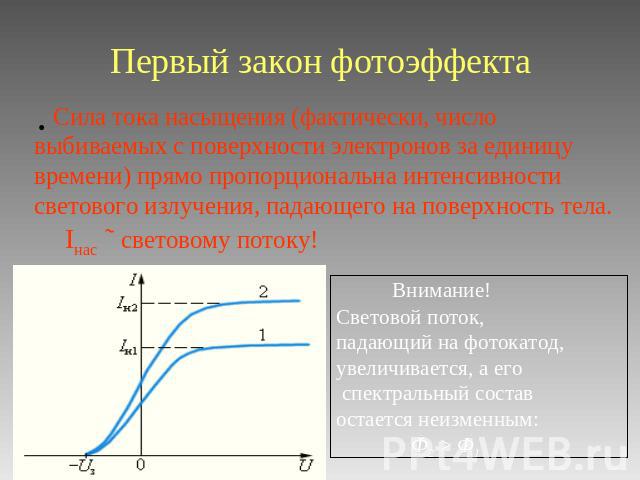 Уравнение Эйнштейна позволяет объяснить законы фотоэффекта. Действительно, из соотношения Эйнштейна непосредственно следует, что максимальная кинетическая энергия фотоэлектрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности. Так как с уменьшением частоты падающего света кинетическая энергия фотоэлектронов уменьшается (для данного вещества катода АВЫХ постоянна), то при достижении некоторой критической частоты кинетическая энергия фотоэлектронов станет равной нулю и фотоэффект прекратится.
Уравнение Эйнштейна позволяет объяснить законы фотоэффекта. Действительно, из соотношения Эйнштейна непосредственно следует, что максимальная кинетическая энергия фотоэлектрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности. Так как с уменьшением частоты падающего света кинетическая энергия фотоэлектронов уменьшается (для данного вещества катода АВЫХ постоянна), то при достижении некоторой критической частоты кинетическая энергия фотоэлектронов станет равной нулю и фотоэффект прекратится.
Согласно Эйнштейну, частота
|
|
(2.8) |
представляет красную границу фотоэффекта для данного вещества. Она зависит лишь от работы выхода электронов, то есть от химической природы вещества и состояния его поверхности.
Она зависит лишь от работы выхода электронов, то есть от химической природы вещества и состояния его поверхности.
Используя выражение (2.8) для красной границы и соотношение (2.6), перепишем уравнение Эйнштейна в виде
|
|
(2.9) |
которое объясняет экспериментальную линейную зависимость (см. рис. 2.4) задерживающего потенциала от частоты падающего электромагнитного излучения.
Таким образом, согласно Эйнштейну, свет с частотой w не только испускается, как это предполагал Планк, но и распространяется в пространстве и поглощается веществом отдельными порциями (квантами), энергия которых
В 1914 г. были проведены модифицированные опыты по фотоэффекту: лучи направлялись на металлическую пыль, помещенную в конденсаторе.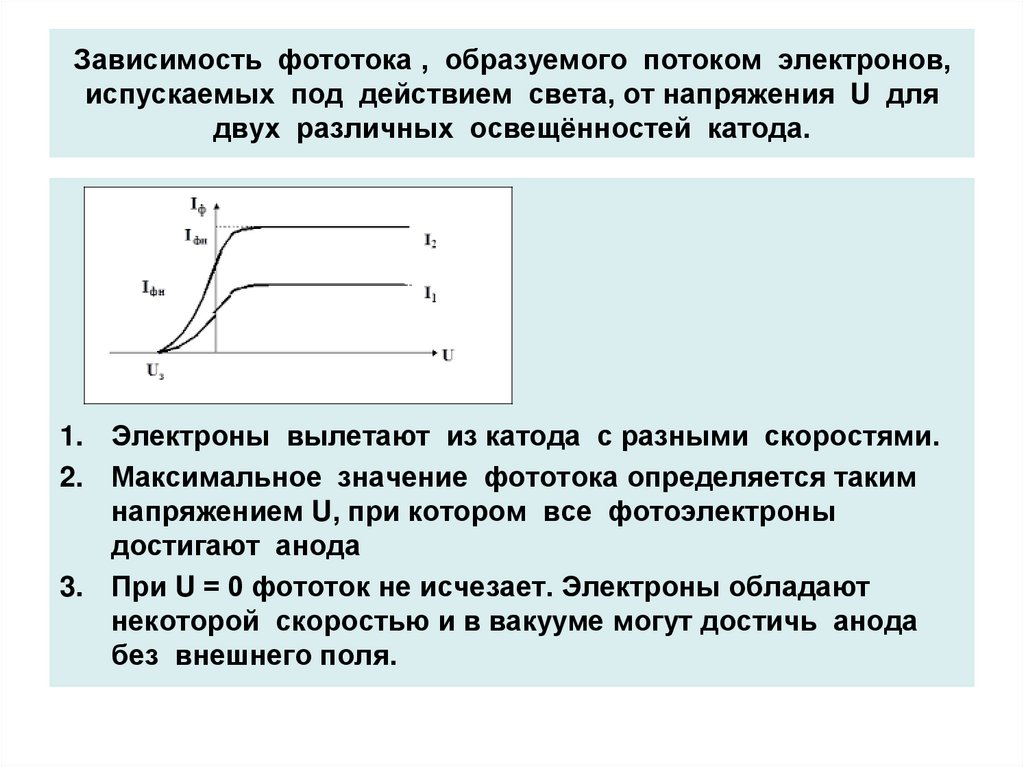 Фотоэффект практически мгновенен: при соударении пылинки с фотонами из нее выбиваются электроны, пылинка приобретает заряд и начинает двигаться в поле конденсатора. Движение пылинок наблюдалось сразу после включения источника излучения. Если бы излучение было классической электромагнитной волной, то волне потребовалось бы вполне заметное в эксперименте время для того, чтобы раскачать электроны, сообщить им энергию, равную работе выхода и, тем самым, вырвать их из пылинки. Отсутствие такого запаздывания наглядно продемонстрировало корпускулярную природу фотоэффекта.
Фотоэффект практически мгновенен: при соударении пылинки с фотонами из нее выбиваются электроны, пылинка приобретает заряд и начинает двигаться в поле конденсатора. Движение пылинок наблюдалось сразу после включения источника излучения. Если бы излучение было классической электромагнитной волной, то волне потребовалось бы вполне заметное в эксперименте время для того, чтобы раскачать электроны, сообщить им энергию, равную работе выхода и, тем самым, вырвать их из пылинки. Отсутствие такого запаздывания наглядно продемонстрировало корпускулярную природу фотоэффекта.
На явлении фотоэффекта основано действие приборов, называемых фотоэлементами. На рис. 2.14 показано устройство вакуумного фотоэлемента.
Рис. 2.14. Устройство вакуумного фотоэлемента
На внутреннюю поверхность металлического баллона наносится светочувствительный слой, служащий катодом. Он соединен с отрицательным полюсом источника тока. В центре баллона помещается проволочное кольцо, служащее анодом. Анод соединяется с положительным полюсом источника тока. Через прозрачное окно в передней стенке баллона свет проникает внутрь и, пройдя сквозь проволочное кольцо, выбивает фотоэлектроны из катода. Фотоэлектроны под действием электрического поля движутся в сторону анода, цепь замыкается и по ней начинает течь ток IФ. Если на пути световых лучей появится непрозрачная преграда, то свет перестанет поступать на катод, фотоэлектронная эмиссия прекратится, и ток в цепи прервется. При этом сработает то или иное реле, связанное с регистрирующим устройством.
В центре баллона помещается проволочное кольцо, служащее анодом. Анод соединяется с положительным полюсом источника тока. Через прозрачное окно в передней стенке баллона свет проникает внутрь и, пройдя сквозь проволочное кольцо, выбивает фотоэлектроны из катода. Фотоэлектроны под действием электрического поля движутся в сторону анода, цепь замыкается и по ней начинает течь ток IФ. Если на пути световых лучей появится непрозрачная преграда, то свет перестанет поступать на катод, фотоэлектронная эмиссия прекратится, и ток в цепи прервется. При этом сработает то или иное реле, связанное с регистрирующим устройством.
Рис. 2.15. Солнечные батареи на международной космической станции. При освещении области контакта различных полупроводников возникает фотоэдс, что позволяет преобразовывать световую энергию в электрическую.
Фотоэлементы являются основной частью всевозможных фотореле, нашедших широкое применение в промышленности.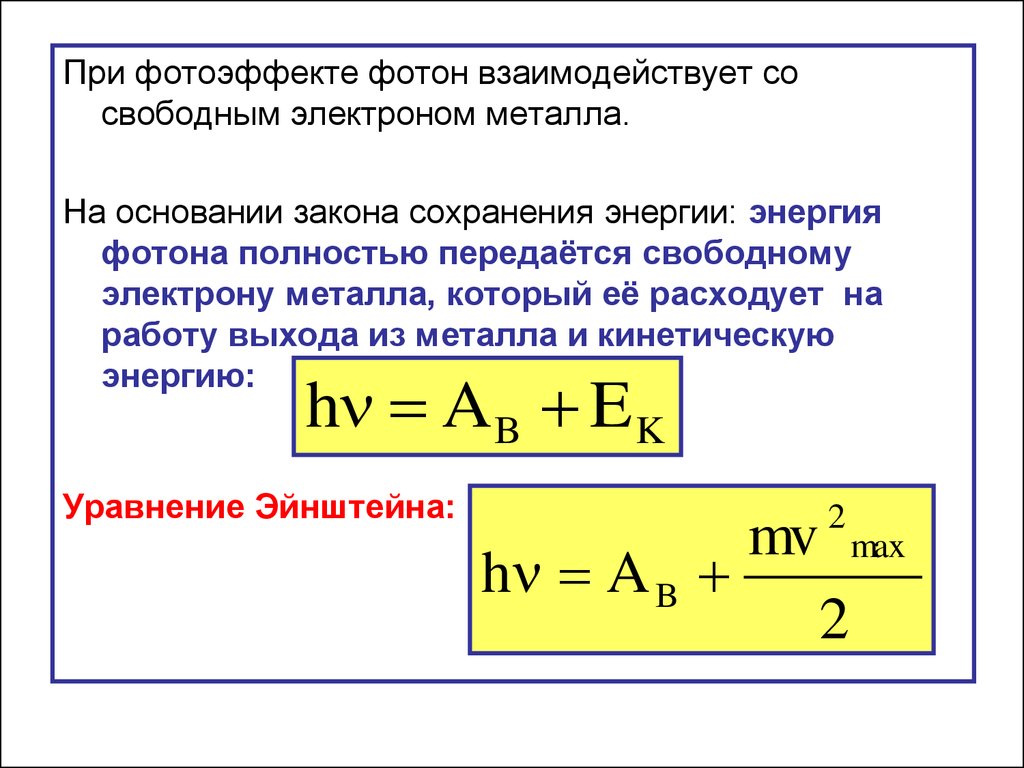 С помощью фотореле можно осуществлять управление различными приборами и установками, включая и выключая их автоматически при освещении светом фотоэлемента, либо, наоборот, при его выключении.
С помощью фотореле можно осуществлять управление различными приборами и установками, включая и выключая их автоматически при освещении светом фотоэлемента, либо, наоборот, при его выключении.
Видео 2.2. Внутренний фотоэффект. Фоторезистор: «А каковы Ваши намерения?»
Пример 1. На поверхность лития падает монохроматический свет с длиной волны . Чтобы прекратить эмиссию электронов, нужно приложить задерживающую разность потенциалов не менее . Определим работу выхода .
Энергия фотона равна
Максимальная кинетическая энергия электронов равна произведению . Отсюда находим работу выхода
В дальнейшем мы обсудим подробнее уже упоминавшуюся внесистемную единицу энергии — электрон-вольт .
Пример 2. Определить максимальную скорость электронов, вылетающих из металла под действием квантов с длиной волны .
Энергия квантов
существенно превышает работу выхода электронов из любого металла (не больше нескольких эВэВ). Поэтому в уравнении Эйнштейна (2.7) работой выхода АВЫХможно пренебречь. Учитывая, что энергия покоя электрона равна примерно , то есть близка к его кинетической энергии , для расчета скорости электронов в данном случае необходимо воспользоваться релятивистскими формулами, а именно: кинетическая энергия К равна
Поэтому в уравнении Эйнштейна (2.7) работой выхода АВЫХможно пренебречь. Учитывая, что энергия покоя электрона равна примерно , то есть близка к его кинетической энергии , для расчета скорости электронов в данном случае необходимо воспользоваться релятивистскими формулами, а именно: кинетическая энергия К равна
где — максимальная скорость электронов, с — скорость света в вакууме.
Тогда уравнение Эйнштейна приобретает вид
где
Решая его, находим скорость электронов
которая действительно оказывается близка к скорости света в вакууме .
Сила тока насыщения , возникающая при освещенности монохроматическим светом, пропорциональна световому потоку, падающему на катод: .
Скорость фотоэлектронов увеличивается с ростом частоты (с уменьшением длины волны) падающего света и не зависит от интенсивности светового потока.

Независимо от интенсивности светового потока, фотоэффект начинается только при определенной, для данного материала, минимальной частоте (максимальной длине волны) света, называемой красной границей фотоэффекта.
Коэффициент пропорциональности k, соответствующий силе фототока (выраженной в мкА) при освещенности катода световым потоком в 1 лм, называют фоточувствительностью освещаемой пластинки. Он выражается в мкА/лм.
Волновая
теория света оказалась в состоянии
объяснить лишь первый из этих законов.
Согласно этой теории, свет, представляющий
собой электромагнитные волны, приводит
электроны, находящиеся вблизи поверхности
металла, в колебательное движение с
амплитудой, зависящей от напряженности
поля, и, следовательно, от интенсивности
падающего света. В результате электрон
приобретает кинетическую энергию,
достаточную для преодоления силы
притяжения положительных ионов и вылета
его из металла. Чем больше интенсивность
падающего света, тем больше электронов
может покинуть металл, и тем больше
будет фототок. Но из этого же рассуждения
следует, что кинетическая энергия
вылетающих электронов также должна
быть пропорциональна интенсивности
падающего на пластинку света, а это
противоречит второму закону фотоэффекта.
Точно так же непонятным, с точки зрения
волновой теории, является и существование
красной границы фотоэффекта.
Чем больше интенсивность
падающего света, тем больше электронов
может покинуть металл, и тем больше
будет фототок. Но из этого же рассуждения
следует, что кинетическая энергия
вылетающих электронов также должна
быть пропорциональна интенсивности
падающего на пластинку света, а это
противоречит второму закону фотоэффекта.
Точно так же непонятным, с точки зрения
волновой теории, является и существование
красной границы фотоэффекта.
Чтобы объяснить эти загадочные закономерности фотоэффекта, Эйнштейн использовал гипотезу Планка, говорящую о том, что электромагнитное излучение представляет собой не непрерывную волну, а поток отдельных частиц – фотонов.
Эйнштейн предположил, что явление
фотоэлектрического эффекта является
подтверждением дискретности света.
Ведь если дискретность природы света
проявляется при его поглощении и
испускании, то она должна сохранятся
и когда излучение распространяется в
пространстве. Эйнштейн также показал,
что любое монохроматическое излучение
представляет собой совокупность
квантов, энергия которых пропорциональна
частоте. Коэффициентом пропорциональности
является постоянная Планка. Это
предположение дало возможность объяснить
фотоэффект. Энергия кванта
,
падающего на вещество, расходуется на
работу А вырывания электрона из
вещества и на сообщение ему кинетической
энергии. Электрон, находящейся внутри
вещества, поглотив квант света, либо
покинет вещество, либо останется внутри
него. Это зависит от того, что больше:
энергия поглощенного кванта света или
работа выхода электрона. Если энергия
поглощенного кванта больше работы
выхода, то кинетическая энергия
фотоэлектрона равна разности энергии
поглощенного фотона и работы выхода:
Коэффициентом пропорциональности
является постоянная Планка. Это
предположение дало возможность объяснить
фотоэффект. Энергия кванта
,
падающего на вещество, расходуется на
работу А вырывания электрона из
вещества и на сообщение ему кинетической
энергии. Электрон, находящейся внутри
вещества, поглотив квант света, либо
покинет вещество, либо останется внутри
него. Это зависит от того, что больше:
энергия поглощенного кванта света или
работа выхода электрона. Если энергия
поглощенного кванта больше работы
выхода, то кинетическая энергия
фотоэлектрона равна разности энергии
поглощенного фотона и работы выхода:
;
. (5.13)
Выражение (5.13) носит название уравнения Эйнштейна для внешнего фотоэффекта.
Уравнение Эйнштейна является частным
случаем закона сохранения и превращения
энергии применительно к явлению
фотоэффекта. Работа выхода зависит от
природы вещества и может быть найдена
в соответствующем справочном материале.
С уменьшением частоты падающего света (увеличением длины волны) энергия падающих квантов (фотонов) при некоторой частоте (или длине волны ) может стать равной работе выхода, т.е. или , откуда
, или . (5.14)
Граничная длина волны падающего света, при котором возникает фотоэффект, носит название красной границы фотоэффекта.
Почему ток насыщения при фотоэффекте не зависит от частоты света, поглощаемого металлическим излучателем?
спросил
Изменено 4 месяца назад
Просмотрено 6к раз
$\begingroup$
Если ток $I$ определяется выражением $I = nAev$, где $n$ – число электронов в единице объема, $A$ – площадь, $e$ – заряд электрона, а $v$ – скорости электрона, это должно означать, что ток увеличивается с увеличением скорости электрона, которая увеличивается с частотой света, падающего на металлический эмиттер.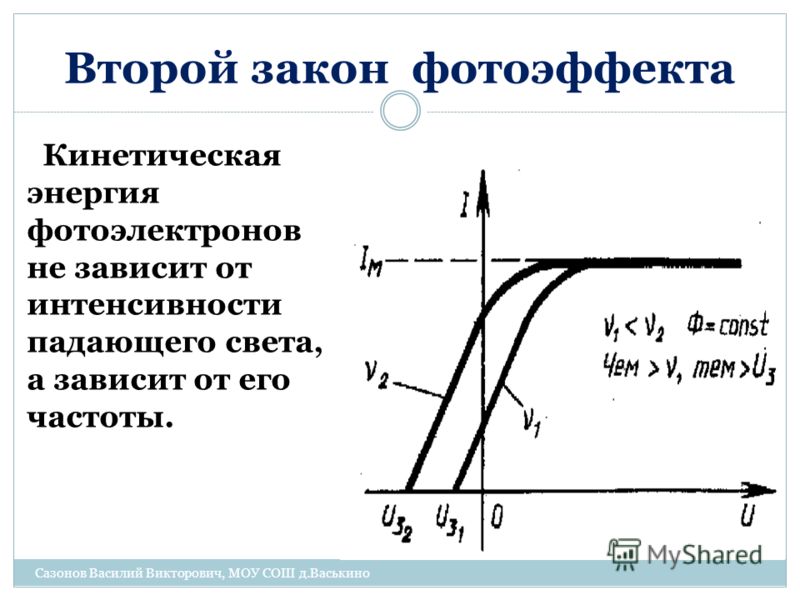 Почему тогда ток насыщения не увеличивается с увеличением частоты?
Почему тогда ток насыщения не увеличивается с увеличением частоты?
- электрический ток
- частота
- фотоэффект
$\endgroup$
$\begingroup$
В контексте фотоэффекта, возможно, не стоит использовать уравнение $ I = nAev$, поскольку скорость электронов не постоянна в промежутке.
Лучше использовать $I=Ne$, где $N$ — число фотоэлектронов, собираемых в секунду пластиной, удаленной от пластины, испускающей фотоэлектроны, а $I$ — ток.
Ток насыщения возникает, когда собираются все испускаемые фотоэлектроны.
Ток насыщения может изменяться при изменении частоты, поэтому многие графики в учебниках неверны.
Интенсивность света пропорциональна количеству фотонов, поступающих в секунду, умноженному на частоту фотона.
Если увеличить частоту света, сохраняя интенсивность неизменной, то количество фотонов, падающих на поверхность в секунду, уменьшится, что вполне может повлиять на количество фотоэлектронов, собираемых в секунду (фотоэлектрический ток).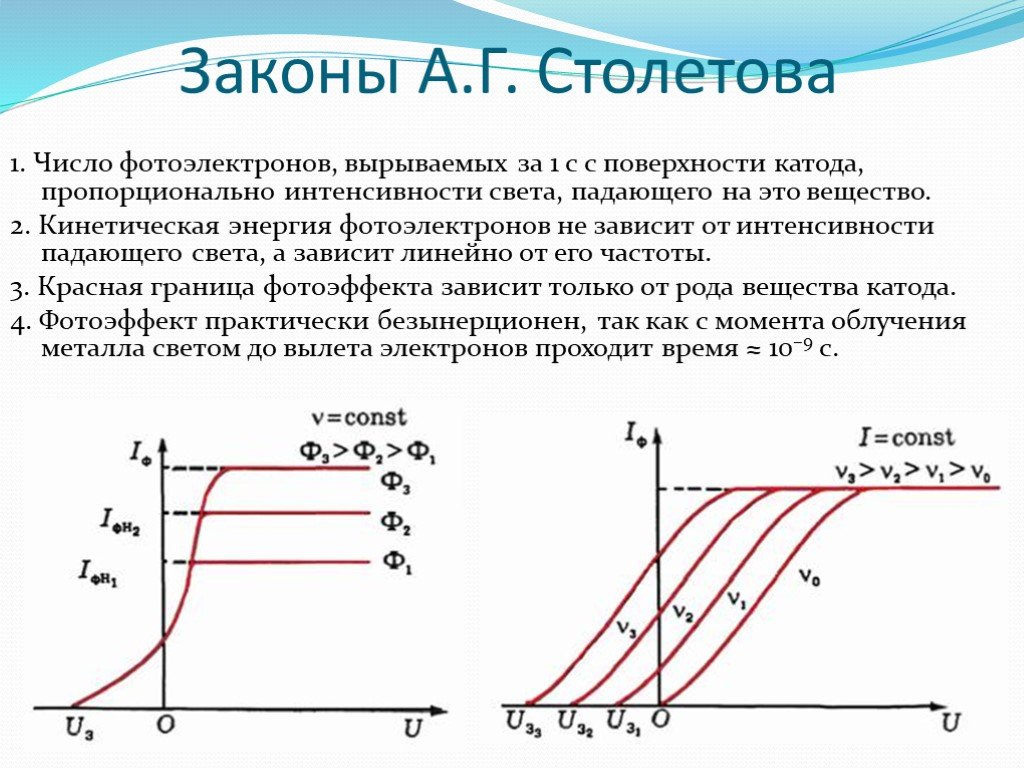
Если у вас есть все поступающие фотоны с достаточно высокой энергией, чтобы каждый из них высвободил фотоэлектрон, а затем увеличили частоту, сохраняя при этом ту же интенсивность, то ток насыщения уменьшится.
Для демонстрации такого поведения можно использовать моделирование фотоэлектрической эмиссии Phet.
Если частоту поддерживать постоянной, то ток насыщения действительно увеличивается с увеличением интенсивности.
$\endgroup$
3
$\begingroup$
В соотношении $I=neV_dA$ скорость представляет собой дрейфовую скорость электронов внутри проводящего материала.
Ток насыщения зависит от интенсивности света для данной частоты. Больше фотонов соответствует большему количеству электронов. Один фотон выбивает один электрон, и если вы увеличиваете количество фотонов (или увеличиваете интенсивность), вы увеличиваете ток.
Если вы увеличиваете частоту фотона, вы увеличиваете кинетическую энергию электрона вне поверхности. Когда вы увеличиваете частоту, вы увеличиваете тормозной потенциал, но ток насыщения остается неизменным для заданной интенсивности.
При нулевом потенциале значение фототока выше для фотона, частота которого больше, чем другая частота других фотонов. Но ток насыщения не зависит от частоты. Когда фотоэлектроны сталкиваются с анодной пластиной, они теряют часть своей кинетической энергии. Больше энергии означает потерю большего количества энергии.
$\endgroup$
$\begingroup$
При фотоэффекте электроны выбрасываются, когда падает свет достаточной частоты. Ток насыщения будет зависеть от количества фотоэлектронов, испускаемых в секунду. По мере увеличения частоты энергия в квантовых пакетах увеличивается, но количество фотоэлектронов увеличивается. Количество фотонов, которые должны попасть на катодную пластину, останется прежним. Может быть, кинетическая энергия электрона в этом случае больше, но в целом нет. количество электронов, которые должны поразить анод, остаются прежними. Это зависит только от интенсивности света. Таким образом, при увеличении частоты вероятность удара по аноду будет увеличиваться (по мере увеличения кинетической энергии), но этот эффект может быть незначительным.
Может быть, кинетическая энергия электрона в этом случае больше, но в целом нет. количество электронов, которые должны поразить анод, остаются прежними. Это зависит только от интенсивности света. Таким образом, при увеличении частоты вероятность удара по аноду будет увеличиваться (по мере увеличения кинетической энергии), но этот эффект может быть незначительным.
Таким образом, в целом из этого обсуждения мы можем сделать вывод, что ток насыщения зависит только от интенсивности, но не от частоты.
Надеюсь, это поможет 😄
$\endgroup$
$\begingroup$
Я не думаю, что важна скорость электрона, и причина этого в том, что электрон столкнется с отталкиванием электронов на поверхности анода, поэтому важно количество электронов, которые прилетят, потому что они почти остановился
$\endgroup$
$\begingroup$
Итак, в уравнении $I=neAV$ с ростом $V$ $I$ увеличивается только в том случае, если n, e, A не уменьшаются .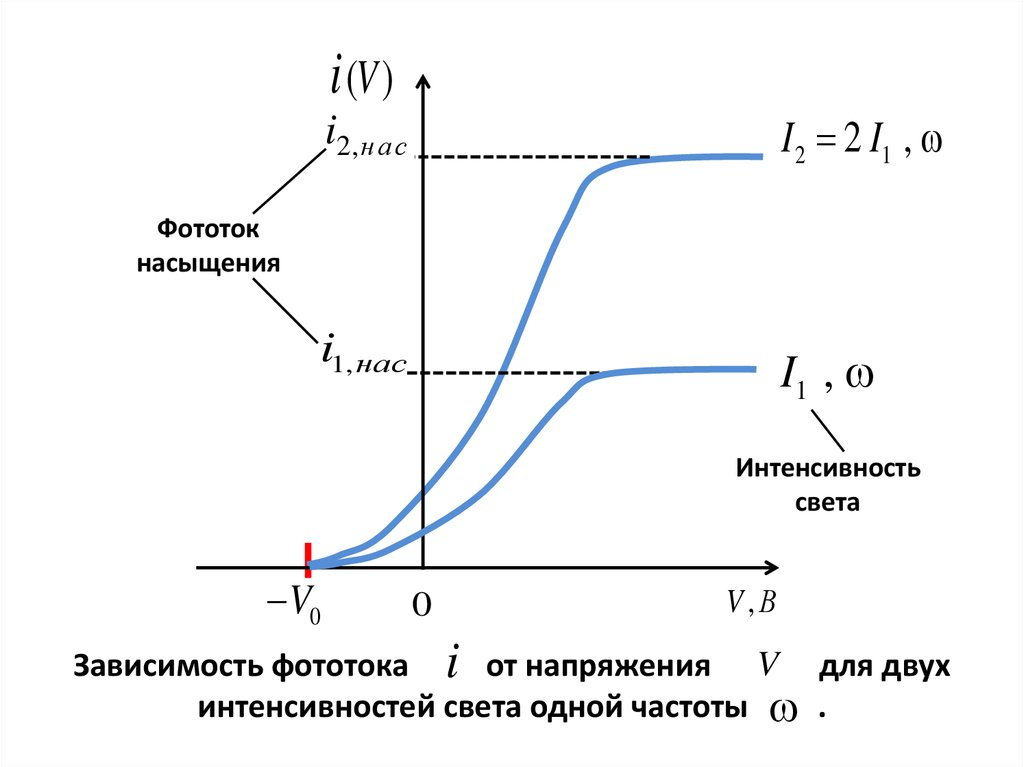 Теперь просто подумайте, если вы увеличите дрейфовую скорость электрона, тогда они сместятся со своего места, и число электронов на единицу объема (n) должно уменьшиться. Таким образом, результирующий эффект заключается в том, что I не меняется.
Теперь просто подумайте, если вы увеличите дрейфовую скорость электрона, тогда они сместятся со своего места, и число электронов на единицу объема (n) должно уменьшиться. Таким образом, результирующий эффект заключается в том, что I не меняется.
Также вы хотите увеличить скорость электрона, сохраняя $n$ постоянным, чтобы электроны двигались случайным образом только в заданной области и, следовательно, их вклад в суммарный ток был равен нулю.
$\endgroup$
$\begingroup$
Увеличение интенсивности означает увеличение количества лучей света, поэтому они будут поражать большее количество электронов, но не придадут электронам достаточной скорости. Увеличение частоты означает увеличение энергии фотона. Таким образом, электроны будут двигаться быстрее, и потребуется больше потенциала, то есть тормозной потенциал увеличится.
Электрический ток представляет собой поток количества зарядов в единицу времени, а не скорость зарядов в единицу времени.
Следовательно, интенсивность увеличивает количество электронов, частота увеличивает скорость электронов. Так что ток насыщения не зависит от частоты света.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Ток насыщения при фотоэффекте
спросил
Изменено 2 года, 11 месяцев назад
Просмотрено 38 тысяч раз
$\begingroup$
Во время изучения фотоэлектрики в моей школе мой учитель нарисовал график зависимости тока от разности потенциалов на двух электродах:
Я не могу понять, почему мы получаем ток насыщения. Я знаю, что при токе насыщения все электроны, испускаемые с поверхности металла, могут достичь другого электрода. Мой вопрос заключается в следующем: предположим, мы еще больше увеличим разность потенциалов между двумя электродами. Я думаю, что должно произойти одно из следующих двух событий:
Я знаю, что при токе насыщения все электроны, испускаемые с поверхности металла, могут достичь другого электрода. Мой вопрос заключается в следующем: предположим, мы еще больше увеличим разность потенциалов между двумя электродами. Я думаю, что должно произойти одно из следующих двух событий:
ток может увеличиться, так как теперь электроны в проводе будут находиться под большей разностью потенциалов, что сократит время, за которое электроны совершают один оборот, чтобы снова достичь той же точки, и, следовательно, увеличится ток. ($V=IR$)
ток не может быть непрерывным (установившийся ток может не достигаться), так как время, необходимое фотоэлектронам для достижения положительного электрода, может быть больше, чем время, необходимое электронам внутри провода, чтобы пройти от конца провода ближе к положительный электрод к другому концу.
Так что ни в коем случае мы не должны получить график, как показано в ссылке.
Возможно, я не до конца понял фотоэффект.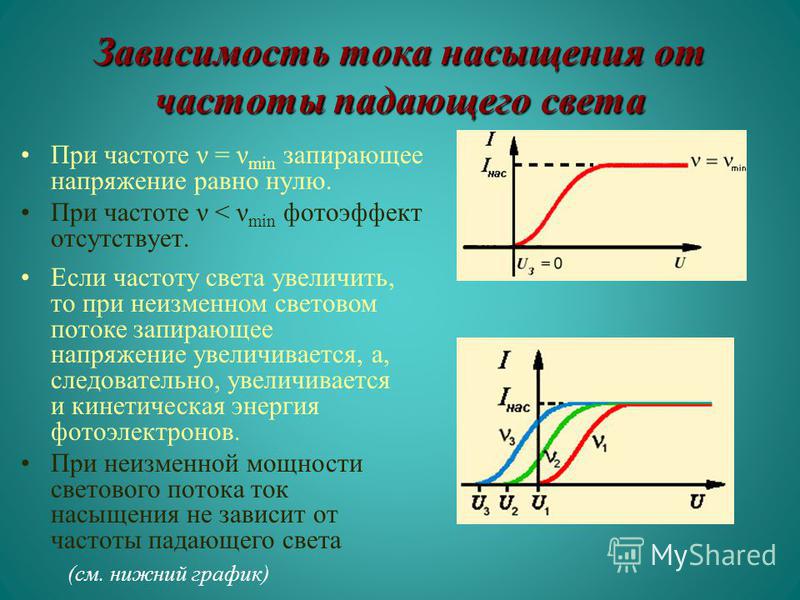 Если это так, подскажите, где я не прав?
Если это так, подскажите, где я не прав?
- фотоэффект
$\endgroup$
1
$\begingroup$
При фотоэффекте фотоны, падающие на катод, вызывают испускание электронов. Если предположить, что электрическое поле достаточно, эти электроны пробьются к аноду, внося свой вклад в ток.
Для простоты предположим, что каждый фотон порождает фотоэлектрон. Тогда, если на катод попадет $N$ фотонов в секунду, ток будет переноситься всего $N$ электронами в секунду. Мы всегда предполагаем, что есть «бесконечно много» электронов, ожидающих своей очереди, и вещь, ограничивающая ток, заключается в том, сколько электронов «вырывается» из катода (то есть, сколько фотонов попадает на катод).
Ток рассчитывается в единицу времени. Если электрон имеет заряд $q_e$, то $N$ электронов в секунду переносят ток
$$I = N\; q_e$$
Здесь ничего не говорится о скорости электронов. .. не о времени, которое требуется им, чтобы пересечь щель. Если бы они двигались в 100 раз быстрее, это не изменило бы количество электронов, пересекающих промежуток в секунду. Это число определяется тем, «сколько людей отправляются в путь в секунду» и «сколько не успевают». Второй из них объясняет, что кривая начинается не совсем ровно: очень медленные электроны могут не долететь, особенно при малом тормозящем потенциале. Но как только они двигаются достаточно быстро, чтобы полностью сбежать, их конечная скорость уже не имеет значения. И время прохождения в проводе тоже.
.. не о времени, которое требуется им, чтобы пересечь щель. Если бы они двигались в 100 раз быстрее, это не изменило бы количество электронов, пересекающих промежуток в секунду. Это число определяется тем, «сколько людей отправляются в путь в секунду» и «сколько не успевают». Второй из них объясняет, что кривая начинается не совсем ровно: очень медленные электроны могут не долететь, особенно при малом тормозящем потенциале. Но как только они двигаются достаточно быстро, чтобы полностью сбежать, их конечная скорость уже не имеет значения. И время прохождения в проводе тоже.
Вы когда-нибудь вычисляли, насколько медленно электроны движутся в проводнике с током (например, в медном проводе)? В то время как электрический сигнал очень быстрый, дрейфовая скорость самих электронов очень-очень низкая… потому что в единице объема так много электронов. Но здесь это имеет лишь косвенное значение.
$\endgroup$
1
$\begingroup$
Я хочу добавить к ответу Флориса, который правильно объясняет явление. Спросите себя, что означают потенциал остановки и ток насыщения .
Спросите себя, что означают потенциал остановки и ток насыщения .
Тормозной потенциал определяется энергией фотонов минус работа выхода рассматриваемого материала . Идеализируем ситуацию: Например, работа выхода меди равна 4,7 эВ. Скажем, если у вас есть источник света и вы освещаете медь светом с энергией 5,7 эВ, то тормозной потенциал будет примерно -1 В. Это потому, что фотон с энергией 5,7 эВ сталкивается с электроном, электрон использует 4,7 эВ, чтобы освободиться от металлической меди, и получает 1 эВ в качестве кинетической энергии. Но он никогда не сможет добраться до другого электрода, потому что его останавливает напряжение. Увеличьте потенциал (то есть приближайтесь к 0 и положительным значениям), тогда электрон может добраться до другого электрода, и вы получите ток.
В действительности, однако, некоторые электроны теряют свою кинетическую энергию еще до того, как они успевают покинуть медь.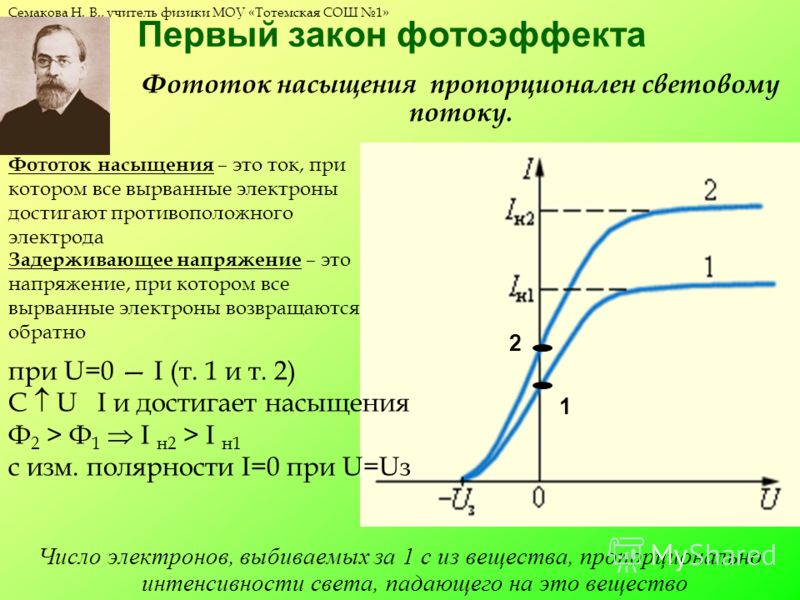 То есть они в конечном итоге имеют кинетическую энергию менее 1 эВ, и поэтому им нужен «толчок», чтобы добраться до другого электрода.
Когда вы увеличиваете напряжение, вы даете толчок этим бедным электронам и заставляете их достигать электрода и, следовательно, увеличиваете ток.
То есть они в конечном итоге имеют кинетическую энергию менее 1 эВ, и поэтому им нужен «толчок», чтобы добраться до другого электрода.
Когда вы увеличиваете напряжение, вы даете толчок этим бедным электронам и заставляете их достигать электрода и, следовательно, увеличиваете ток.
Однако в какой-то момент электроны, которые могут добраться до другого электрода, насыщаются, потому что источник света может производить определенное количество фотонов и, следовательно, определенное количество фотоэлектронов. Научный термин «количество фотонов» — 9.0182 интенсивность источника света . Если у вас есть еще один эквивалентный источник света и вы зажгли его, то вы получите ток насыщения примерно вдвое.
$\endgroup$
$\begingroup$
Нечего добавить к красиво написанным ответам выше.
В основном количество испускаемых фотоэлектронов зависит от интенсивности падающего излучения, а максимальная кинетическая энергия, которой может обладать испускаемый фотоэлектрон, зависит от потенциала пластин коллектора. Кроме того, очевидно, что максимальное количество фотоэлектронов, которые могут достичь коллекторной пластины, зависит от интенсивности, поэтому при заданной интенсивности (т.е. при заданном максимальном количестве испускаемых фотоэлектронов) достигают ли они коллектора (преодоление отталкивания объемным зарядом) зависит от потенциала.
Кроме того, очевидно, что максимальное количество фотоэлектронов, которые могут достичь коллекторной пластины, зависит от интенсивности, поэтому при заданной интенсивности (т.е. при заданном максимальном количестве испускаемых фотоэлектронов) достигают ли они коллектора (преодоление отталкивания объемным зарядом) зависит от потенциала.
Таким образом, количество фотоэлектронов, достигающих коллекторной пластины, достигает уникального постоянного значения (равного максимальному количеству фотоэлектронов, исходя из интенсивности падающего излучения).
$\endgroup$
$\begingroup$
Количество фотоэлектронов, испускаемых с поверхности металла, будет зависеть от энергии световой волны, падающей на поверхность металла. Теперь пусть максимум нет. Из электронов, которые могут быть испущены данной световой волной, будет «x» или пусть это будет целое число, например. Испускается 100 электронов, теперь только эти 100 электронов отвечают за перенос тока.
Теперь самое главное, так что читайте внимательно.
максимальная кинетическая энергия электрона k°
не все выбитые электроны смогут достичь другой пластины, это связано с тем, что немногие электроны испытают столкновение с другими электронами или испытают столкновение с молекулами газа (в основном берется атмосфера инертного газа, для которой инертные газы, такие как гелий или берется аргон).
Из-за столкновения несколько электронов не смогут достичь другой пластины. А для нескольких электронов минимум К.Э. для достижения другой пластины будет меньше, чем требуется.
пусть 60 электронов не достигают другой пластины. Теперь мы применяем разность потенциалов в цепи, чтобы электроны теперь могли легко добраться до другой пластины.
Пусть 10В будет потенциометром. Дифф. Применили, теперь пусть еще 10 электронов достигнут другой пластины в флюенсе горшка. Дифф.
Дальнейшее увеличение банка.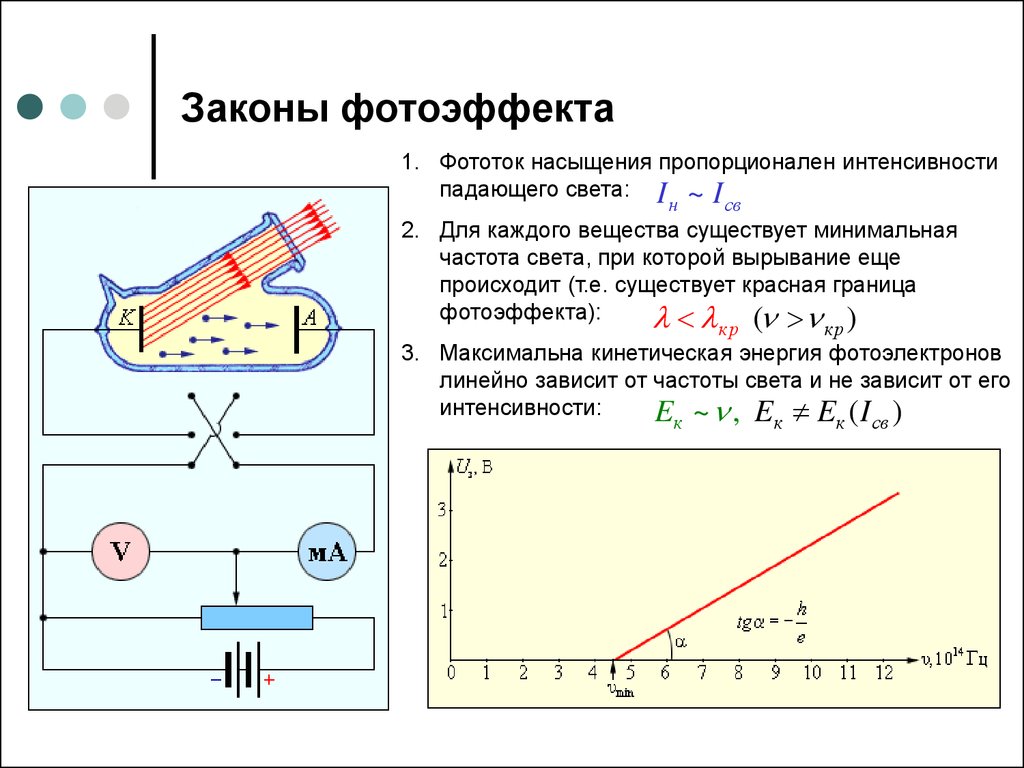 Разница в 20 В позволила еще 10 электронам достичь другой пластины, теперь оставшихся электронов 40
Разница в 20 В позволила еще 10 электронам достичь другой пластины, теперь оставшихся электронов 40
Теперь, таким образом, увеличивая por diff. Так что все 100 электронов могут достичь другой пластины, теперь оставшиеся электроны, которые не могут достичь другой пластины, будут равны нулю. Поскольку все электроны теперь могут достичь другой пластины, теперь ток, который прямо пропорционален приложенному потенциалу, достигает своего максимального значения, и после достижения этого максимального значения при дальнейшем увеличении разности потенциалов ток также должен был увеличиться (гипотетически), но дело в том, что количество фотоэлектронов, достигающих другой пластины, теперь равно 100, что означает, что все выбитые фотоэлектроны теперь могут достичь другой пластины. При дальнейшем увеличении банка. Дифф. Не увеличил бы нет. Фотоэлектронов, которые достигают другой пластины (т.е. носителей тока), нет. Количество фотоэлектронов, достигающих теперь, будет только 100, и не будет увеличиваться из-за увеличения емкости. Таким образом, дифференциальный ток после достижения своего значения насыщения не может быть увеличен.
Таким образом, дифференциальный ток после достижения своего значения насыщения не может быть увеличен.
Что касается второго пункта, Протекающий ток зависит от интенсивности света. Электроны в области между пластинами текут почти с той же скоростью, что и в проводе.
$\endgroup$
1
$\begingroup$
Что такое ток? Ток представляет собой поток электронов в заданное время, т.е. если интенсивность света постоянна, то фотоны, падающие на катод (выталкивающую пластину), также постоянны. Поскольку мы знаем, что минимальный К.Э, который может иметь фотоэлектрон, равен 0, а макс. энергия фотонов минус работа выхода материала . А ток насыщения означает, что поток электронов в данный момент времени постоянен, т.е. нет. количество электронов, вылетающих из катода, постоянно, как нет.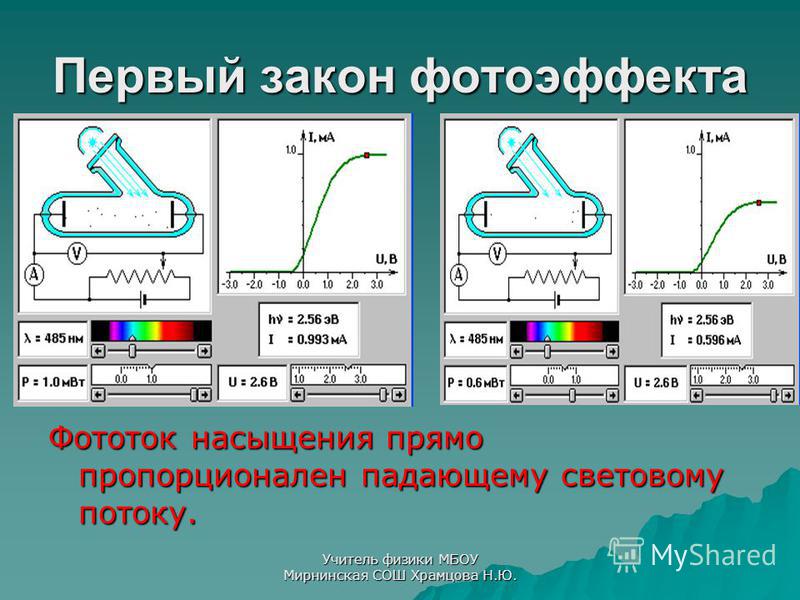

 Наибольшее действие оказывают ультрафиолетовые лучи. Максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего света, а определяется при прочих равных условиях лишь частотой падающего монохроматического света и растет с увеличением частоты.
Наибольшее действие оказывают ультрафиолетовые лучи. Максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего света, а определяется при прочих равных условиях лишь частотой падающего монохроматического света и растет с увеличением частоты.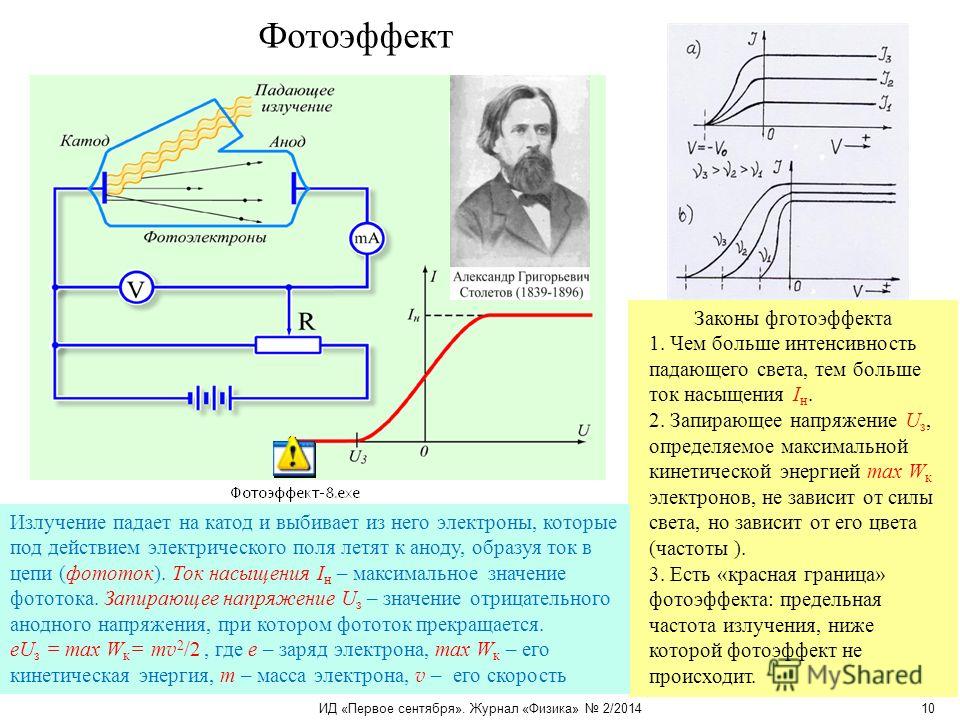

Leave A Comment