Как найти угол по клеткам – Угол на клетчатой бумаге

На клетчатой бумаге изображён вписанный угол

     Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных  заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге «Угол вписанный в окружность. Часть 1!» и про вписанный четырёхугольник, либо соответствующий раздел в учебной литературе.

Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна  особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?

Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?

Начнём с самого простого. Чему равен данный угол?

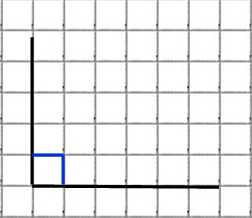
Конечно же, 90 градусам.

Чему равен этот угол?

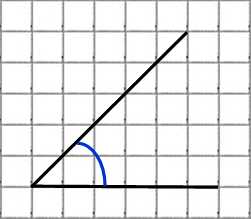
Понятно, что 45 градусам.

А этот?

Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).

А такой?

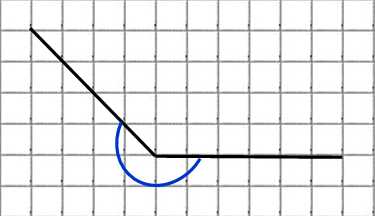
225 градусов (180 + 45    или    360 – 135).

Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.

Ещё раз напомню основное свойство вписанного угла.

«Вписанный угол равен половине центрального,

опирающегося на ту же дугу»

 

 

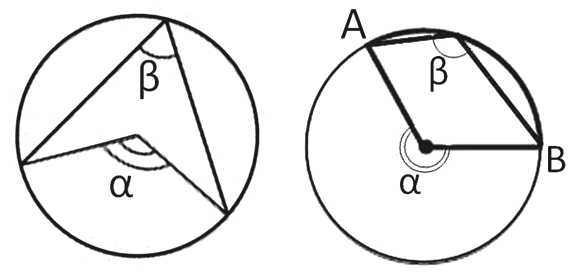
27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC. Ответ дайте в градусах.

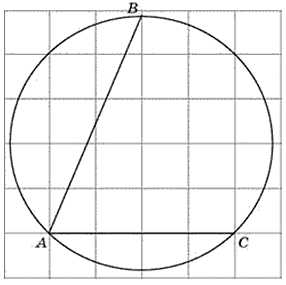
Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.

Построим центральный угол соответствующий дуге ВС:

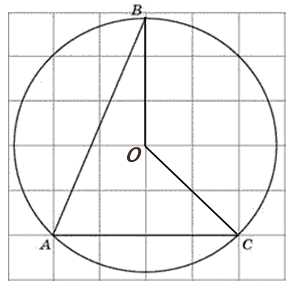
Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол  ВОС:

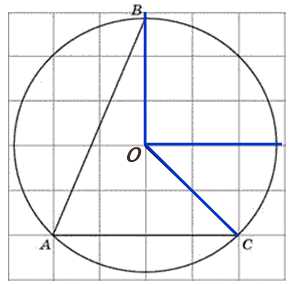
По клеткам видно, что угол ВОС равен 90⁰ + 45⁰ = 135⁰ (ОС проходит по диагонали клеток).

Ответ: 135

 

27887. Найдите величину угла ABC. Ответ дайте  в  градусах.

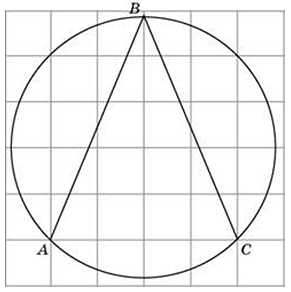
Посмотреть решение

 

27888. Найдите величину угла ABC. Ответ дайте в градусах.

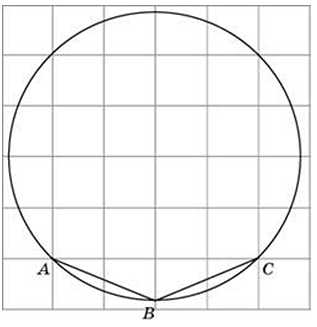
Посмотреть решение

 

27889. Найдите величину угла ABC. Ответ дайте в градусах.

Посмотреть решение

27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC. Ответ дайте в градусах.

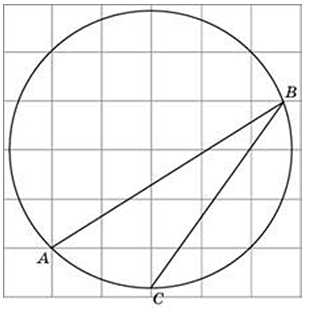
Посмотреть решение

Небольшой итог!

Нужно знать свойство вписанного угла (обязательно).

Для решения подобных задач достаточно построить центральный угол и далее использовать  указанное свойство.

На этом всё. Успеха Вам!

С уважением, Александр Крутицких

Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Подготовка к ОГЭ. «Углы на клетках»

Углы на клетках

-1-

Как построить прямой угол по клеткам? Очень просто! – скажете вы. – Отметим точку, вершину угла, от неё чертим вправо или влево луч, затем ещё один луч вверх или вниз. Угол между горизонталью и вертикалью – прямой. А можно и по диагоналям соседних клеток.

Всё верно. А если один из лучей уже построен и он не горизонтальный, не вертикальный и не проходит по диагоналям клеток? Как начертить второй луч, чтобы угол между ними был прямым?

Найдём узел сетки, через который проходит начерченный луч. На нашем рисунке до такого узла от начала луча нужно пройти 3 клетки ВЛЕВО и 1 клетку ВНИЗ. Поэтому чтобы получился прямой угол, надо от начала луча отсчитать 1 клетку ВЛЕВО и 3 клетки ВВЕРХ. Почему? Обозначим упомянутые нами точки – А, В и О. Построим векторы ОА и ОВ. Координаты вектора ОА равны (-3; -1), вектора ОВ (-1; 3). Их скалярное произведение равно 0, поэтому они перпендикулярны.

Можно отсчитывать клетки и так: 1 клетку ВПРАВО и 3 клетки ВНИЗ. Тогда вектор ОВ имеет координаты (1; -3), при этом скалярное произведение векторов ОА и ОВ также равно 0.

Вывод. Векторы с координатами (a; b) и (-b; a), или (a; b) и (b; -a), — перпендикулярны.

Рассмотрим несколько задач, связанных с умением находить прямой угол на рисунке.

№ 1. Найти угол АВС на рисунке.

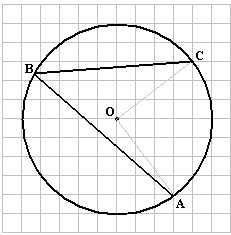
Решение. На первом рисунке угол АОС построен на диагоналях соседних клеток. На втором рисунке векторы ОА и ОС имеют координаты соответственно (3; -4) и (4; 3). Поэтому на первом и втором рисунках центральный угол АОС – прямой, а вписанный угол АВС, опирающийся на ту же дугу, равен его половине, то есть 45°. На третьем рисунке угол АОС – половина прямого, то есть 45°, а угол АВС соответственно равен 22,5°.

№ 2. Три квадрата расположены так, как показано на рисунке. Чему равен угол между прямыми АС и ВD?

Решение. Отрезок ВD переместим параллельно вниз на одну клетку. Появляется отрезок АМ, равный ВD. Угол между прямыми АС и ВD равен углу между АС и АМ на втором рисунке. Соединим отрезком точки С и М. Получается, что угол АМС – прямой и АМ = МС. Треугольник АСМ прямоугольный равнобедренный, поэтому искомый угол равен 45°.

№ 3. Найти тангенс угла, изображенного на рисунке.

Решение. Выделим на этом рисунке узлы сетки – точки А и С. Рассмотрим треугольник АВС. Заметим, что он является прямоугольным, к тому же катет ВС в 2 раза больше катета АС. Отсюда следует, что тангенс угла В равен 1:2 = 0,5.

-2-

Правильный треугольник и описанная около неё окружность, построенные на клетках, несут в себе много интересных свойств. Известно, что радиус окружности, описанной около равностороннего треугольника со стороной а, равен , а радиус вписанной в него окружности — , то есть в два раза меньше. Отсюда следует, что хорда, перпендикулярная радиусу окружности и проходящая через его середину, является стороной правильного треугольника. Другими словами,

острый вписанный угол, опирающийся на хорду, перпендикулярную радиусу и проходящую через его середину, равен 60°, а центральный угол и тупой вписанный угол, опирающиеся на эту хорду, — 120°.

Рассмотрим несколько примеров задач, решаемых на основе этого свойства.

1. Угол АВС на рисунке равен 60°, так как хорда АС проходит через середину радиуса и перпендикулярна ему.

2. Угол АВС на рисунке является половиной угла в 60° из предыдущей задачи и равен 30°.

3. Угол АВС на следующем рисунке равен 120°. При этом четырёхугольник АВСО является ромбом и его острый угол равен 60°.

-3-

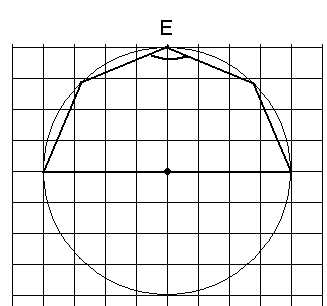
Полезным при решении задач на клетках является знание углов правильных многоугольников. Рассмотрим правильный шестиугольник и правильный восьмиугольник. Около них описаны окружности. Каждый внутренний угол правильного шестиугольника равен 120°, угол между диагоналями-диаметрами равен 60°, угол между двумя соседними диагоналями, исходящими из одной вершины, равен 30°, меньшая диагональ правильного шестиугольника перпендикулярна его стороне, а с другими соседними сторонами — угол 30°. Каждый угол правильного восьмиугольника равен 135°, угол между соседними диагоналями-диаметрами равен 45°.

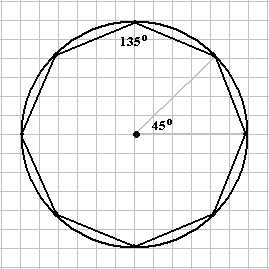
Найдите на следующих рисунках градусные меры отмеченных углов.

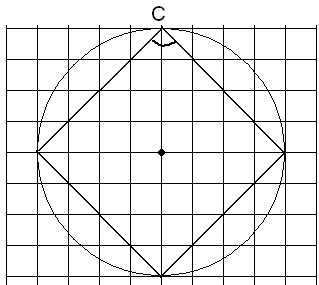
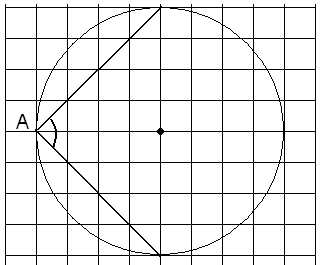
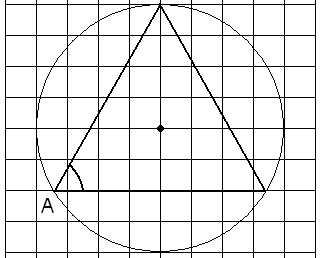
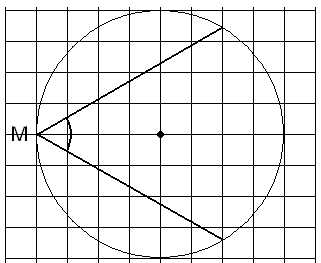
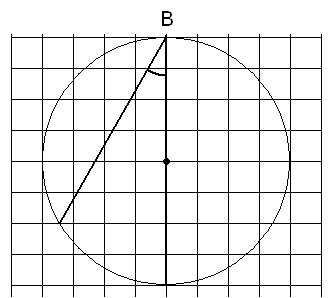
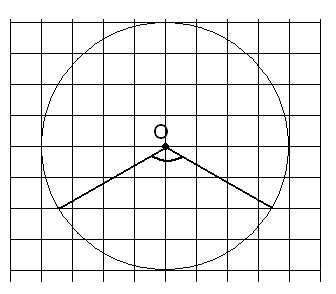
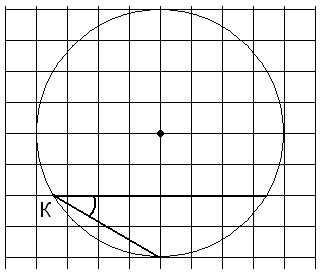
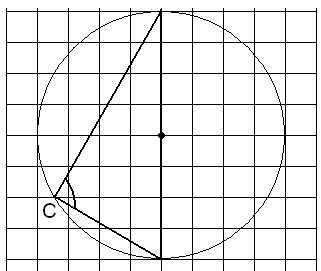
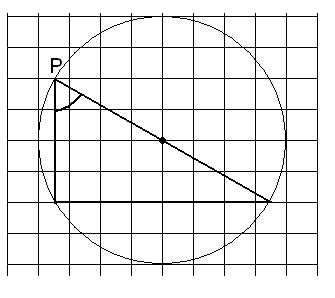
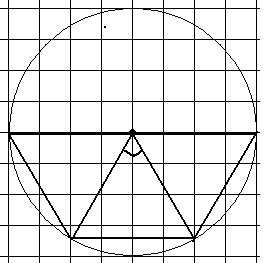
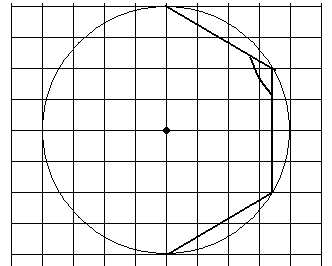
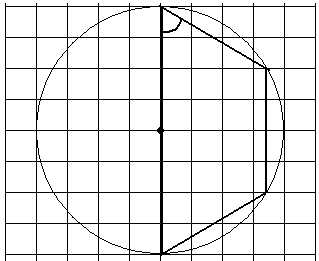
Мясникова Т.Ф.

infourok.ru

Как определить угол без транспортира на листе в клетку?

90 градусов это прямая горизонтальная и прямая вертикальная. . абсолютно перпендикулярные.. . следовательно пополам это 45….разделить чертой ну а там смареть к какой черте ближе и плюсовать или вычетать градусы. . ну и делить пополам полученный угол пока не дойдешь до своего угла

БУДЬТЕ ЛЮБЕЗНЫ ИСПРАВИТЬ СВОИ ОШИБКИ)))) ну а там смареть к

Сразу надо сказать что этим способом мерить можно только острые углы (без транспортира). Лично я не могу найти транспортир, я беру лист бумаги, прикладываю к одной из сторон угла и мыслено намечаю линию (где бы она была если бы это был прямой угол) по клеточкам (в тетради) высчитываю сколько мм от линии к которой не прикладывал до мыслено намеченной линии. Дело в том, что эти мм мы можем заменить градусами (пример: 10 мм=10 градусов) и из прямого угла ( 180 градусов ) вычетаем полученные (пример: 180-10=170градусов). Вот и ответ.

Попробуй воспользоваться рукой, растопырь пальцы и приложи к нужному углу. Более подробная инструкция <a rel=»nofollow» href=»http://life-hacki.ru/как-определить-угол-без-транспортира/» target=»_blank»>http://life-hacki.ru/как-определить-угол-без-транспортира/</a>

touch.otvet.mail.ru

Построение острых углов на клетчатой бумаге

Геометрия – часть математики, изучающая пространственные отношения и формы, а также другие отношения и формы, сходные с пространственными по своей структуре. Происхождение термина «геометрия» с греческого означает «землемерие» [гео– «земля» и метрео – «измеряю»].

Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки. Углы измеряются в градусах и радианах. Угол, образованный продолжением сторон данного угла, называется вертикальным к данному. Угол, образованный одной из сторон данного угла и продолжением другой стороны, называется смежным с ним. Приспособление для построения углов на чертежах, называется транспортир.

Значение геометрии в развитии математике

Применение евклидовой геометрии представляет самое обычное явление всюду, где определяются площади, объемы и т. п. Геометрия изучает пространственную непрерывность. Общая роль геометрии в математике состоит также в том, что с нею связано идущее от пространственных представлений точное синтетическое мышление, часто позволяющее охватить в целом то, что достигается анализом и выкладками лишь через длинную цепь шагов. Геометрия характеризуется не только своим предметом, но и методом, идущим от наглядных представлений и оказывающимся плодотворным в решении многих проблем других областей математики. Геометрия имела решающее значение в возникновении и развитии анализа. Интегрирование происходит от нахождения площадей и объемов. Графическое представление функций сыграло важную роль в выработке понятий анализа и сохраняет свое значение. Геометрия оказывает влияние на алгебру, и даже на арифметику – теорию чисел, поэтому роль геометрии в развитии математике очень велика.

Цель работы: найти способ построения углов без транспортира.

Гипотеза: Любой острый угол можно построить без транспортира по узлам клетки.

Задачи:

• рассмотреть углы и найти их связь с узлами клеток.

Построим с помощью транспортира углы от 10° до 80° со стороной, идущей по горизонтальной линии сетки.

Отметим у каждого угла ближайший узел сетки, через который прошла другая сторона каждого угла.

Определим «путь» из вершины угла в отмеченную точку и занесем данные в таблицу:

Величина угла Клеток → Клеток ↑

10° 6 1

20° 8 3

30° 7 4

40° 6 5

50° 5 6

60° 4 7

70° 3 8

80° 1 6

Если сравнить данные таблицы для углов 10° и 80°, 20° и 70°, 30° и 60°, 40° и 50°, то можно заметить, что количество клеток вправо и количество клеток вверх меняются местами.

Используя данные таблицы, можно приближенно построить любой острый угол без транспортира.

Заключение

Таким образом, обычный лист бумаги в клетку может выполнять функцию своеобразного инструмента для построения геометрических фигур. В 7 классе мы начинаем изучать геометрию и, полученными результатами, можно будет пользоваться при изучении курса планиметрии для построения схематических чертежей, точнее соответствующих условию задач.

Также, выполняя презентацию работы, я совершенствовала свои навыки работы на компьютере.

www.hintfox.com

Косинус угла между прямыми по клеточкам.

Натолкнулась в Открытом банке заданий по математике на задачу, которую в прошлом году не встречала:

Задание B7 (№ 27458)  из  Открытого банка заданий для подготовки к ЕГЭ  по математике:

Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на :

Давайте сделаем дополнительное построение:

 

Величина угла АОВ равна сумме углов и :

Примем размер клетки равным 1, и  найдем длину ОВ из треугольника ОВС и длину АО из треугольника АОС:

:

 

По формуле для косинуса суммы имеем:

Вспомним соотношения для сторон и углов в прямоугольном треугольнике:

косинус угла равен отношению прилежащего катета к гипотенузе;

синус угла равен отношению противолежащего катета к гипотенузе.

Тогда из треугольника ВОС:

Из треугольника АОС:

Подставим эти значения в формулу для косинуса суммы:

В ответе запишем значение косинуса, умноженное на :

Ответ: -2

И.В. Фельдман, репетитор по математике.

Купить видеокурс «ВСЯ ГЕОМЕТРИЯ. Часть В»

 

ege-ok.ru

Помогите пожалуйста нужно найти тангенс угла по клеткам.

Можно так. Поверни рисунок на 90 градусов и введи систему координат По определению тангенса tga=у/х = 3/(-1) = -3. <img src=»//otvet.imgsmail.ru/download/231438889_60e79a82013a97e9480ec3cc71c62153_800.png» alt=»» data-lsrc=»//otvet.imgsmail.ru/download/231438889_60e79a82013a97e9480ec3cc71c62153_120x120.png» data-big=»1″>

Загрузите свое задание на сайт: <a rel=»nofollow» href=»http://umal.me/0pk» target=»_blank» >Сервис по решению задач</a> Или пришлите мне на мейл: [email protected] Мы уже решили 5096 задач!

Здравствуйте. Пришлите мне свое задание на почту: [email protected] А то здесь писать не очень удобно. Нами уже приблизительно 2373 задач сделано!

Данный тупой угол можно записать через сумму углов: (90+а). По формуле приведения tg x = tg(90+a) = -ctga . По определению котангенс равен отношению катета прилежащего к катету противолежащему: tgx = tg(90+a) = -ctga = -3/1 = -3

touch.otvet.mail.ru