Одна из сторон параллелограмма равна 13, другая равна 20, а один из углов 45 градусов. Найдите площадь параллелограмма, умноженную на [tex] \sqrt{2} [/tex]
Ответы 1
S=a*b*sinα
a=13, b=20, α=45°
S=13*20*sin45°=360*(√2/2)=180√2
S*√2=(180√2)*√2=180*(√2)²=180*2=360
ответ: 360
Знаешь ответ? Добавь его сюда!
Последние вопросы
Физика
20 минут назад
Помогите рассчитать напряжение люстрыГеография
20 минут назад
Помогите пж с крХимия
40 минут назад
Помогите осуществить превращение пожалуйстаБиология
45 минут назад
Правда ли,что сова и филин — разные виды птиц? В детских книгах иногда пишут,что они отличаются полом,как курица и петухРусский язык
50 минут назад
Русский язык домашняя работа срочноРусский язык
1 час назад
Русский язык домашняя работаРусский язык
Алгебра
1 час назад
Винеровский процесс на конечномерном унитарном представлении компактной группы ЛиАлгебра
2 часа назад
Помогите представить виде логарифмаИстория
2 часа назад
Какой американский самолёт-разведчик был сбит в 1960 году над территорией СССР?Литература
2 часа назад
Барыня, это женщина,которая любит ходить по барам?Физика
3 часа назад
Наверное, самый простой (но симпатичный) вопрос про связь электротехники с неравновесной термодинамикой.
3 часа назад
Помогите пожалуйста подробно решить уравнениеДругие предметы
4 часа назад
СНОВА НУЖНА ПОМОЩЬ(( может у нейросетки кто узнает, просто доклад нужно подготовитьОбществознание
4 часа назад
Обществознание , закон
How much to ban the user?
1 hour 1 day 100 years
Задания для подготовке к ОГЭ по теме: «Площадь параллелограмма»
Материал опубликовал
0
#8 класс #9 класс #Геометрия #ФГОС #Учебно-дидактические материалы #Контрольные / проверочные работы #Учитель-предметник #Школьное образование #УМК любой
Задания для подготовке к ОГЭ 8 класс Тема: Параллелограмм. Вариант 1 | Тема: Параллелограмм. Площадь.. Вариант 2 |
1) Площадь параллелограмма равна 40, а две его стороны равны 5 и 10. Найдите его высоты. В ответе укажите большую высоту. 2) Площадь параллелограмма ABCD равна 60. Точка E — середина стороны AB. Найдите площадь трапеции DAEC. 3) Найдите площадь параллелограмма, изображённого на рисунке. 4) На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь. 5) Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на . 6) Одна из сторон параллелограмма равна 50, другая равна 1, а косинус одного из углов равен. 7) Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 4 и HD = 65. Диагональ параллелограмма BD равна 97. Найдите площадь параллелограмма. 8) Стороны параллелограмма равны 44 и 88. Высота, опущенная на первую сторону, равна 66. Найдите высоту, опущенную на вторую сторону параллелограмма. | 1) Площадь параллелограмма равна 36, а две его стороны равны 6 и 12. Найдите его высоты. В ответе укажите большую высоту. 2) Площадь параллелограмма ABCD равна 68. Точка E — середина стороны AB. Найдите площадь треугольника CBE. 3) Найдите площадь параллелограмма, изображённого на рисунке. 4) На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь. 5) Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 60°. 6) Одна из сторон параллелограмма равна 4, другая равна 14, а косинус одного из углов равен. Найдите площадь параллелограмма. 7) Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 5 и HD = 15. Диагональ параллелограмма BD равна 17. Найдите площадь параллелограмма. 8) Стороны параллелограмма равны 5 и 10. Высота, опущенная на первую сторону, равна 3. Найдите высоту, опущенную на вторую сторону параллелограмма. |
Тема: Параллелограмм. Площадь.. Вариант 3 | Задания для подготовке к ОГЭ 8 класс Тема: Параллелограмм. Площадь.. Вариант 4 |
1) Площадь параллелограмма равна 48, а две его стороны равны 8 и 16. 2) Площадь параллелограмма ABCD равна 84. Точка E — середина стороны AB. Найдите площадь треугольника CBE. 3) Найдите площадь параллелограмма, изображённого на рисунке. 4) На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь. 5) Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен . Найдите площадь параллелограмма. 6) Одна из сторон параллелограмма равна 15, другая равна 6, а тангенс одного из углов равен. Найдите площадь параллелограмма. 7) Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 2 и HD = 12. Диагональ параллелограмма BD равна 13. Найдите площадь параллелограмма. 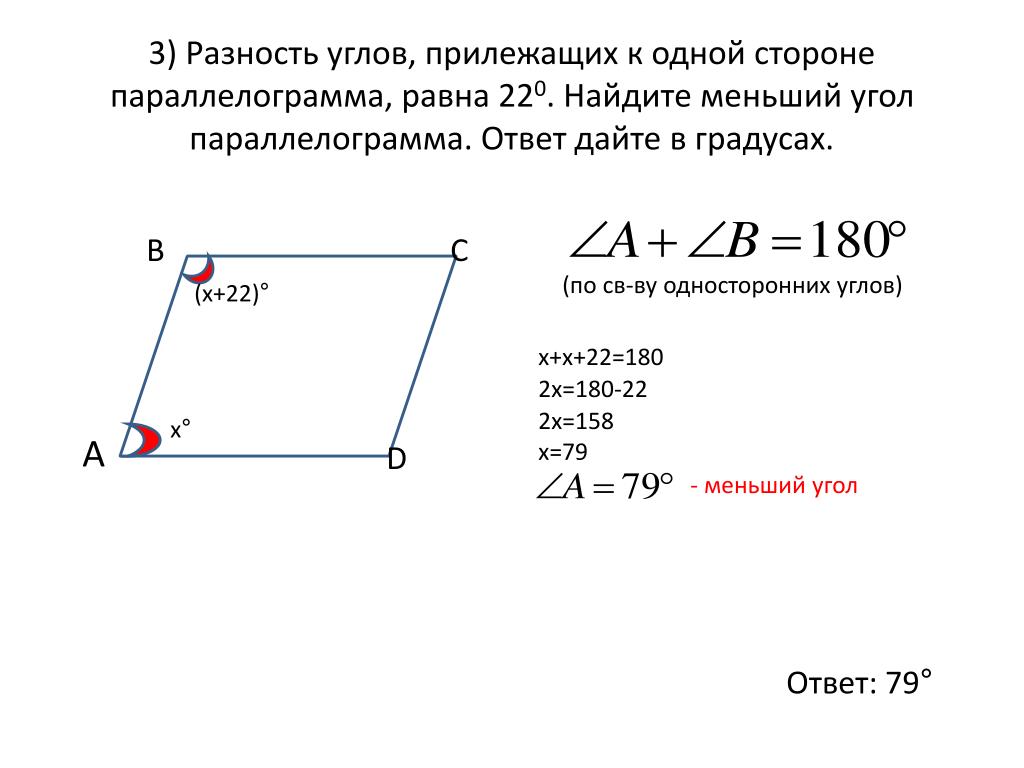 Найдите высоту, опущенную на вторую сторону параллелограмма. Найдите высоту, опущенную на вторую сторону параллелограмма. | 1) Площадь параллелограмма равна 54, а две его стороны равны 9 и 18. Найдите его высоты. В ответе укажите меньшую высоту. 2) Площадь параллелограмма ABCD равна 76. Точка E — середина стороны AB. Найдите площадь трапеции DAEC. 3) Найдите площадь параллелограмма, изображённого на рисунке. 4) На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь. 5) Одна из сторон параллелограмма равна 18, другая равна 25, а синус одного из углов равен . Найдите площадь параллелограмма. 6) Одна из сторон параллелограмма равна 8, другая равна 18, а тангенс одного из углов равен. Найдите площадь параллелограмма. 7) Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 7 и HD = 24. Диагональ параллелограмма BD равна 51. 8) Стороны параллелограмма равны 32 и 64. Высота, опущенная на первую сторону, равна 48. Найдите высоту, опущенную на вторую сторону параллелограмма. |
Задания для подготовки:
1) Площадь параллелограмма равна 32, а две его стороны равны 8 и 16. Найдите его высоты. В ответе укажите большую высоту.
2) Площадь параллелограмма равна 56, а две его стороны равны 7 и 28. Найдите его высоты. В ответе укажите меньшую высоту.
3) Площадь параллелограмма ABCD равна 180. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
4) Площадь параллелограмма ABCD равна 132. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
5) Найдите площадь параллелограмма, изображённого на рисунке.
6) На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
7) Одна из сторон параллелограмма равна 24, другая равна 20, а синус одного из углов равен . Найдите площадь параллелограмма.
8) Одна из сторон параллелограмма равна 12, другая равна 5, а косинус одного из углов равен . Найдите площадь параллелограмма.
9) Одна из сторон параллелограмма равна 20, другая равна 29, а тангенс одного из углов равен. Найдите площадь параллелограмма.
10) Одна из сторон параллелограмма равна 21, другая равна 15, а косинус одного из углов равен. Найдите площадь параллелограмма.
11) Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
12) Стороны параллелограмма равны 10 и 85. Высота, опущенная на первую сторону, равна 51. Найдите высоту, опущенную на вторую сторону параллелограмма.
ОТВЕТЫ:
Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | |
1 | 8 | 6 | 3 | 3 |
2 | 45 | 51 | 63 | 57 |
3 | 40 | 28 | 20 | 44 |
4 | 10 | 20 | 28 | 36 |
5 | 30 | 30 | 20 | 200 |
6 | 5 | 14 | 30 | 18 |
7 | 4968 | 160 | 70 | 1395 |
8 | 33 | 1,5 | 6 | 24 |
Опубликовано
Чтобы написать комментарий необходимо авторизоваться.
Диагональ параллелограмма – формула, свойства, примеры
Диагональ параллелограмма – это отрезок, соединяющий его несмежные вершины. У параллелограмма 2 диагонали и длину диагоналей параллелограмма можно найти по различным формулам в зависимости от заданных параметров и размеров. Давайте узнаем больше о диагоналях параллелограмма в этой статье.
| 1. | Что такое диагональ параллелограмма? |
| 2. | Диагональ формулы параллелограмма |
| 3. | Часто задаваемые вопросы о диагонали параллелограмма |
Что такое диагональ параллелограмма?
Диагонали параллелограмма можно провести, соединив две несмежные вершины параллелограмма. Следует отметить, что две диагонали параллелограмма делят друг друга пополам и делят параллелограмм на конгруэнтные треугольники.
Диагональ формулы параллелограмма
Формула диагоналей параллелограмма используется для вычисления длины диагоналей данного параллелограмма. Существуют разные формулы для разных видов параллелограммов. Обратите внимание на приведенный ниже рисунок, на котором показан параллелограмм вместе с его диагоналями. Здесь «p» и «q» — диагонали, а «x» и «y» — две стороны параллелограмма.
Ниже приведена простая формула для нахождения длины диагоналей параллелограмма. Для этой формулы нам понадобится длина сторон и любой из известных углов. Если мы будем следовать рисунку, приведенному выше, мы можем заметить, что: 92 — 2xy \cos B} \)
Формула 2: Другая формула, которая выражает отношение между длинами диагоналей и сторон параллелограмма:
p 2 + q 2 = 2( x 2 + y 2 )
Где
- p и q — диагонали соответственно.
- х и у — стороны параллелограмма.

Следует отметить, что квадрат, прямоугольник и ромб относятся к категории параллелограммов. А так как свойства у них разные, то и формула для нахождения их диагоналей тоже разная. Например, диагональ квадрата (d) = a√2; где «d» — диагональ, а «а» — сторона квадрата. Диагональ прямоугольника (d) = √( l 2 + w 2 ), где l = длина прямоугольника, а w = ширина прямоугольника. Поэтому формула диагонали параллелограмма различается для разных видов параллелограммов.
Свойства диагоналей параллелограмма
Следующие пункты показывают свойства диагоналей параллелограмма. Так как параллелограмм включает в себя квадрат, прямоугольник, ромб, диагонали этих фигур имеют несколько общих свойств и несколько различных.
- Диагонали параллелограмма всегда делят друг друга пополам.
- В квадрате диагонали равны и делят друг друга пополам под прямым углом.
- В прямоугольнике диагонали равны и делят друг друга пополам, но не под прямым углом.

- В ромбе диагонали могут быть не обязательно равными, но они перпендикулярны друг другу.
☛ Статьи по теме
- Диагональ квадрата
- Диагональ прямоугольника
- Диагональ куба Формула
- Диагональ ромба
Примеры использования формулы диагонали параллелограмма
Пример 1: Найдите длину диагоналей ромба со стороной 4 дюйма, если внутренние углы равны 120° и 60°.
Решение:
Дано, внутренний угол A = 120°, а угол B = 60°.
х = 4, у = 4 92 + (2 \times 4 \times 4 \times \cos 60)} \\ &= \sqrt{32 + 16} \\ p &= \sqrt {48} \\ p &= 6.92 \end{align}\ )Ответ: Длина диагоналей 4 дюйма и 6,92 дюйма.
Пример 2: Для параллелограмма ABCD, если длины смежных сторон 35 футов и 82 фута. Если один из внутренних углов равен 37°. Найдите длину любой диагонали.

Решение:
Дано, внутренний угол A = 37° 92 — (2 \times 35 \times 82 \times \cos 37)} \\ &= \sqrt{3365} \\ p &= 58 \end{align}\)
Ответ: Длина диагонали 58 футов
Пример 3: Вычислите длину диагонали параллелограмма со сторонами 4 звена, 6 звеньями и внутренним углом А, равным 60 градусам.
Решение:
Дано, a = 4 единицы, b = 6 единиц, угол A = 60°
Используя диагональ формулы параллелограмма, 92 — 24}\)= \(\sqrt28\) = 5,291
Ответ: Диагональ параллелограмма = 5,291 ед.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
Практические вопросы по диагонали параллелограмма
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о диагонали параллелограмма
Что такое диагональ параллелограмма?
Диагональ параллелограмма — это отрезок, соединяющий две несмежные вершины параллелограмма. 2 — 2xy \cos B} \), где p и q — длины диагоналей, угол A и угол B — заданные внутренние углы, а x и y — стороны параллелограмма. 92 — 2xy \cos B} \).
2 — 2xy \cos B} \), где p и q — длины диагоналей, угол A и угол B — заданные внутренние углы, а x и y — стороны параллелограмма. 92 — 2xy \cos B} \).
Какие компоненты формулы диагонали параллелограмма?
Формула диагонали параллелограмма помогает найти длину диагоналей, используя длину сторон и любой из известных углов. Таким образом, его составляющие включают в себя стороны параллелограмма и соответствующие им углы.
Делят ли диагонали параллелограмма пополам?
Да, диагонали параллелограмма делят друг друга пополам. Это означает, что диагонали параллелограмма делят друг друга на 2 равные части.
Равны ли диагонали параллелограмма?
Параллелограмм состоит из квадрата, прямоугольника и ромба. В то время как диагонали квадрата и прямоугольника равны, диагонали ромба не обязательно равны.
Как найти диагонали параллелограмма без углов?
Длину диагоналей параллелограмма можно вычислить, даже если не известны внутренние углы. Например, если параллелограмм является прямоугольником, мы знаем, что диагонали прямоугольника образуют прямоугольный треугольник. Итак, в этом случае, если стороны прямоугольника известны, длину диагонали можно вычислить по теореме Пифагора, потому что диагональ становится гипотенузой. Этот метод можно применять и в том случае, если заданный параллелограмм является квадратом.
Например, если параллелограмм является прямоугольником, мы знаем, что диагонали прямоугольника образуют прямоугольный треугольник. Итак, в этом случае, если стороны прямоугольника известны, длину диагонали можно вычислить по теореме Пифагора, потому что диагональ становится гипотенузой. Этот метод можно применять и в том случае, если заданный параллелограмм является квадратом.
Наклонные треугольники
Наклонные треугольникиНаклонный треугольник — это любой треугольник, не являющийся прямоугольным. Это может быть остроугольный треугольник (все три угла треугольника меньше прямых) или тупоугольный треугольник (один из трех углов больше прямого). На самом деле, для целей тригонометрии класс «косоугольных треугольников» может с тем же успехом включать и прямоугольные треугольники. Тогда изучение косоугольных треугольников на самом деле является изучением всех треугольников.
Примем соглашение о обозначении частей косоугольных треугольников, обобщающее правило для прямоугольных треугольников. Пусть углы обозначены А, В, и С, , а противоположные стороны обозначены а, b, и с, соответственно.
Пусть углы обозначены А, В, и С, , а противоположные стороны обозначены а, b, и с, соответственно.
Решение косоугольных треугольников
Тригонометрия косоугольных треугольников не так проста, как прямоугольных треугольников, но есть две теоремы геометрии, которые дают полезные законы тригонометрии. Они называются «законом косинусов» и «законом синусов». Есть и другие «законы», которые использовались раньше, но с момента повсеместного использования калькуляторов этих двух законов достаточно.Закон косинусов
Это просто сформулированное уравнение:Это похоже на теорему Пифагора, за исключением последнего члена, и если C — прямой угол, последний член исчезает (поскольку косинус 90° равен 0), так что закон косинусов на самом деле является обобщением закона косинусов. Теорема Пифагора.
Обратите внимание, что каждый треугольник дает три уравнения закона косинусов, так как вы можете переставлять буквы по своему усмотрению. Затем две другие версии a 2 = b 2 + c 2 – 2 bc cos A, и b 2 = c 2 + a 2 – 2 ca cos B.
Затем две другие версии a 2 = b 2 + c 2 – 2 bc cos A, и b 2 = c 2 + a 2 – 2 ca cos B.
Закон косинусов связывает три стороны треугольника с одним из углов. Вы можете использовать его несколькими способами.
Во-первых, если известен один угол и две смежные стороны, то можно определить и противоположную сторону. Например, если угол C = 60°, сторона a = 5 и сторона b = 8, то закон косинусов гласит Поскольку косинус угла 60° равен 1/2, это уравнение упрощается до c 2 = 49, поэтому c = 7.
Во-вторых, если вы знаете все три стороны треугольника, то можете использовать их для нахождения любого угла. Например, если три стороны равны a = 5, b = 6 и c = 7, то по закону косинусов 49= 25 + 36 – 60 cos C, so cos C = 12/60 = 0,2, а с помощью калькулятора C = 1,3734 радиана = 78,69°.
Примечание: Когда треугольник тупоугольный, cos C отрицателен. Предположим, что три стороны равны a = 5, b = 6 и c = 10. Тогда закон косинусов гласит: /60 = — 0,81667. Как видно из графиков на предыдущей странице, косинус тупого угла отрицателен. Это нормально, и ваш калькулятор правильно вычислит арккосинус. Вы получите C = 2,2556 радиан = 129,237°.
Закон синусов
Закон синусов также представляет собой просто сформулированное уравнениеОбратите внимание, что закон синусов гласит, что три отношения равны. Как и закон косинусов, вы можете использовать закон синусов двумя способами.
Во-первых, если известны два угла и сторона, противолежащая одному из них, то можно определить сторону, противолежащую другому из них. Например, если угол A = 30°, угол B = 45°, а сторона a = 16, то по закону синусов (sin 30°)/16 = (sin 45°)/ b. Решение для b дает b = 16(sin 45°)/(sin 30°) = 22,6274.
Во-вторых, если вы знаете две стороны и угол, противолежащий одной из них, то вы можете почти определить угол, противолежащий другой из них. Например, если сторона a = 25, сторона b = 15, а угол A = 40°, то по закону синусов (sin 40°)/25 = (sin В )/15. Нахождение sin B дает sin B = 15 (sin 40°)/25 = 0,38567. Теперь арксинус 0,38567 = 22,686°.
Предупреждение: возможно, у вас нет правильного ответа. Есть два угла между 0 и 180 ° с данным синусоидальным; второй является дополнением первого. Таким образом, в данном случае вторым является тупой угол 180 – 22,686 = 157,314°. Эта ситуация неопределенная. Зная две стороны и угол, противолежащий одной из них, не всегда достаточно для определения треугольника. В геометрии не существует детерминистской теоремы о конгруэнтности «бок-бок-угол».
Проблемы
553. AB — линия длиной 652 фута на одном берегу ручья, а C — точка на противоположном берегу. A = 53° 18′ и B = 48° 36′. Найдите ширину потока от С до АВ.
A = 53° 18′ и B = 48° 36′. Найдите ширину потока от С до АВ.
557. В треугольнике ABC, a = 700 футов, B = 73° 48′, и C = 37° 21′. Если M это середина BC найти длины AM, и углы BAM и MAC.
561. Три окружности радиусов 3, 4 и 5 касаются друг друга снаружи. Найдите углы треугольника, образованного соединением их центров.
563. A и B — точки на противоположных берегах реки. На одном берегу линия AC измеряется 650 футов. Угол А = 73° 40′ и С = 52° 38′. Найдите АБ.
570. P и Q две недоступные точки. Чтобы найти расстояние между ними, берется точка A в произведенном QP и измеряется линия AB длиной 1200 футов, образующая угол PAB = 26° 35′. Угол ABP = 48° 12′ и ABQ = 106° 42′. Как долго PQ ?
Как долго PQ ?
579. Стороны параллелограмма равны AB = 209,16 и AD = 347,25, а диагональ AC = 351,47. Найдите углы и другую диагональ.
580. В параллелограмме ABCD, диагональ AC = 521,16, угол ABC = 110° 48′ 12″, а BAC 3’9 1 = 1″. Найдите длины сторон и другой диагонали.
586. Диагонали параллелограмма равны 374,14 и 427,21, а угол между ними равен 70° 12′ 38″. Найдите стороны.
590. Стороны четырехугольника по порядку равны 763,83, 721,75, 547,12 и 593,21, а угол между первыми двумя сторонами равен 53° 13′ 12″. Найдите остальные три угла.
593. A и B — это две точки на противоположных сторонах водоема, измерения должны производиться по линии AB в точках одна четверть, половина и три четверти расстояния от A до B. На берегу измеряется линия AC длиной 1200 футов и углы BAC = 63° 19′ и ACB = 78° 43′. Какие углы нужно отклонить от СА на С , чтобы выровнять лодку, с которой производятся замеры, по нужным точкам на АВ ?
Какие углы нужно отклонить от СА на С , чтобы выровнять лодку, с которой производятся замеры, по нужным точкам на АВ ?
608. По одну сторону от ручья PA = 586,3 фута, PB = 751,6 фута являются мерами, угол APB равен 167° 36′. Q — точка на противоположной стороне потока. Угол PAQ = 63° 18′ и PBQ = 49° 24′. Найдите PQ.
612. Чтобы найти расстояние между двумя недоступными точками P и Q, линия AB длиной 763,4 фута отложена так, что AB произвел пересечение PQ снаружи [то есть два отрезка AB и PQ не пересекаются]. Углы PAB = 98° 47′, QAB = 41° 36′, PBA = 37° 16′ и QBA = 94° 12′. Найдите длину PQ.
Советы
553. Вы можете использовать закон синусов, чтобы определить любую из длин AB или BC. Задача состоит в том, чтобы найти расстояние от C — AB. Это означает, что вы опускаете перпендикуляр из точки C на эту линию и определяете ее длину. Вы можете использовать угол A и линию AC , чтобы найти его, или вы можете использовать угол B и линию BC , чтобы найти его.
Это означает, что вы опускаете перпендикуляр из точки C на эту линию и определяете ее длину. Вы можете использовать угол A и линию AC , чтобы найти его, или вы можете использовать угол B и линию BC , чтобы найти его.
557. Тот же намек, что и 553.
561. Окружности касаются друг друга, поэтому линия, проведенная из одного центра в другой, представляет собой сумму радиусов одной окружности и другой. У вас есть треугольник со сторонами 7, 8 и 9.. Вы можете использовать закон косинусов, чтобы найти углы.
563. Здесь хорошо работает закон синусов.
570. Нарисуй фигуру. Чтобы найти PQ, сначала найдите AP и AQ. Вы можете найти AP , используя закон синусов треугольника ABP, , и вы можете найти AQ , используя закон синусов треугольника ABQ.
579. Вы знаете стороны треугольников ABC и ADC, чтобы можно было определить их углы. В треугольнике ABD вы знаете угол и две смежные стороны, поэтому вы можете найти противоположную сторону BD.
В треугольнике ABD вы знаете угол и две смежные стороны, поэтому вы можете найти противоположную сторону BD.
580. Сначала решите треугольник ABC. Далее в треугольнике ABD вы знаете две стороны и легко можете определить угол BAD.
586. «Включенный угол» — это один из двух углов между двумя диагоналями. Другой прилежащий угол является его дополнением 180° – 70° 12′ 38″. Пусть P — точка пересечения двух диагоналей. Это середина каждой диагонали, так что вы знаете расстояние между P и любой вершиной. Примените закон косинусов к двум треугольникам с вершинами P и двум вершинам параллелограмма.
590. Вы знаете стороны четырехугольника ABCD и угол при B. Вы можете решить треугольник ABC. Тогда вы знаете все стороны треугольника ACD, , чтобы можно было найти его углы.
593. Сначала определите расстояние AB по закону синусов. Тогда для каждого из правильных положений лодки P, известны две стороны и угол между ними треугольника PAC, , так что по закону косинусов можно определить нужный угол.
Тогда для каждого из правильных положений лодки P, известны две стороны и угол между ними треугольника PAC, , так что по закону косинусов можно определить нужный угол.
608. Сначала решите треугольник APB. Тогда у вас будет достаточно информации, чтобы решить треугольник АКВ.
612. Есть несколько способов решить эту проблему. Вот один из способов. Определить PA по закону синусов для треугольника PAB, и определить QA по закону синусов для треугольника QAB. Тогда используйте закон косинусов для треугольника PAQ.
Ответы
553. 345,43 футов.
557. 490,83 фута.
561. 48° 11′ 24″, 58° 24′ 42″, 73° 23′ 54″.
563. 640 футов 10 дюймов.
570. 651,9 футов.
579. 106° 18′ 46″, 73° 41′ 14″, 452,92.
580. 255,93, 372,11, 369,22.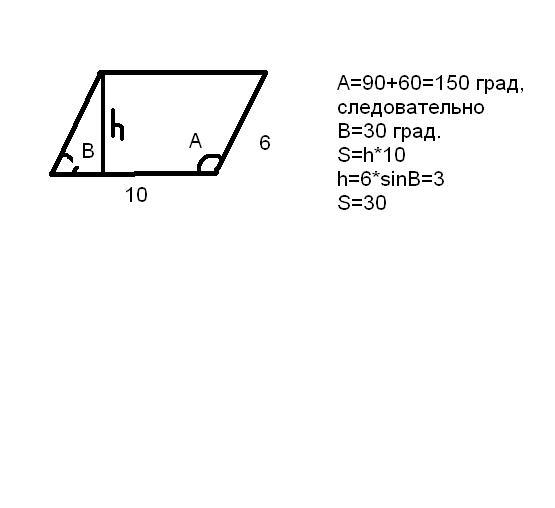


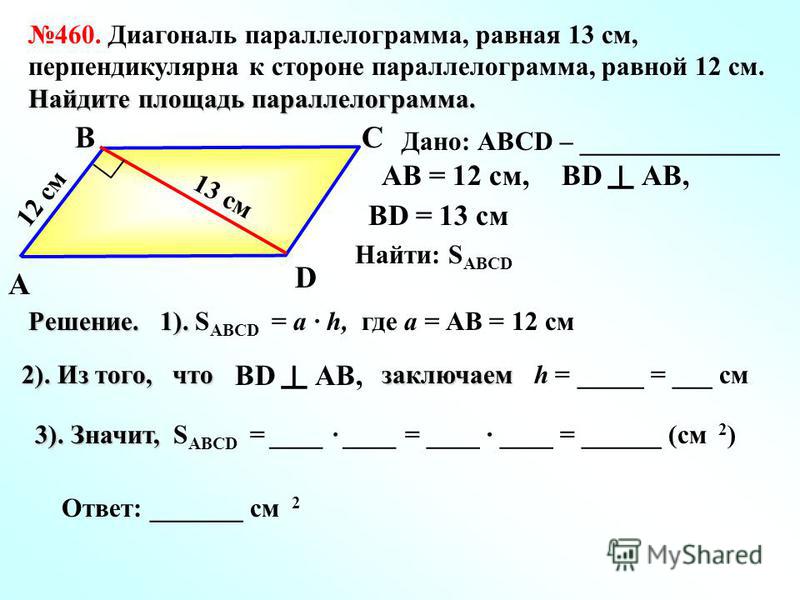 Площадь.
Площадь.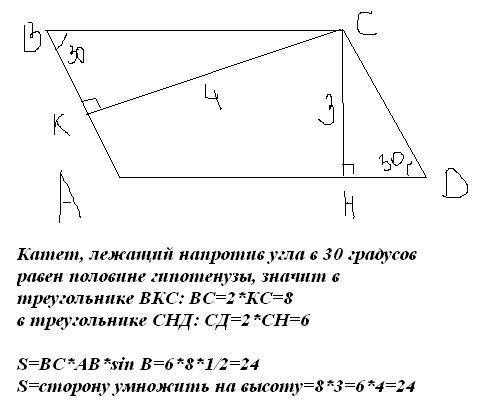 Найдите площадь параллелограмма.
Найдите площадь параллелограмма.
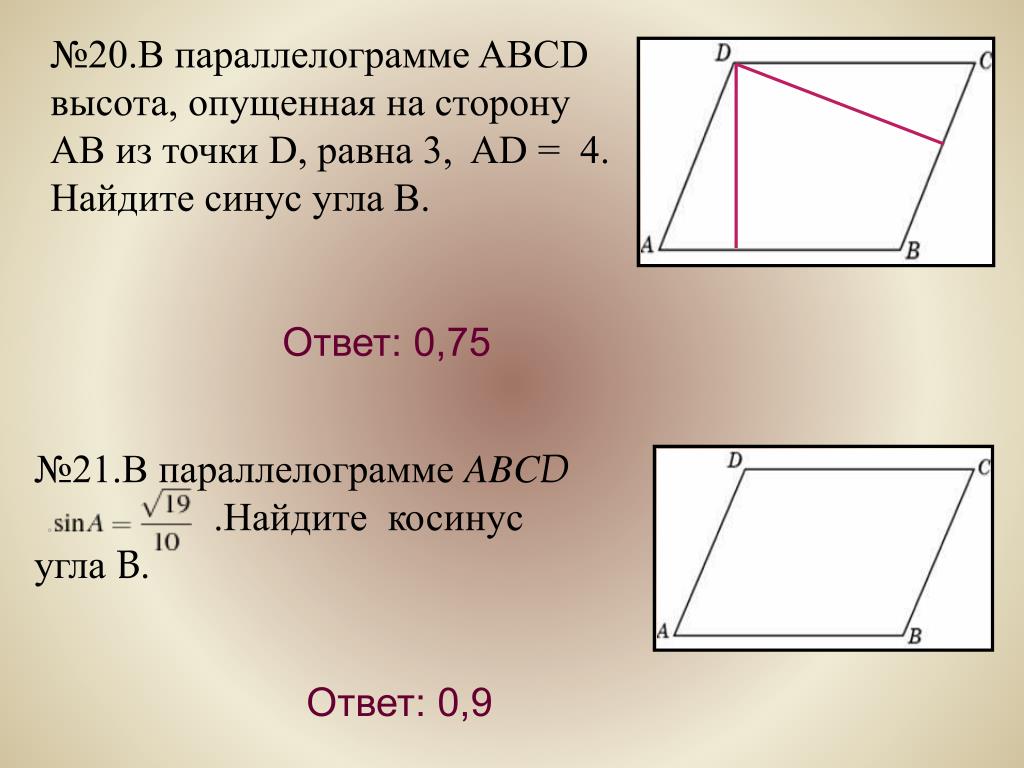 Найдите его высоты. В ответе укажите меньшую высоту.
Найдите его высоты. В ответе укажите меньшую высоту. Найдите площадь параллелограмма.
Найдите площадь параллелограмма.


Leave A Comment