Геометрия в Заданиях ЕГЭ — презентация онлайн
1. Геометрия в Заданиях ЕГЭ
2. Результаты ЕГЭ по математике 2013
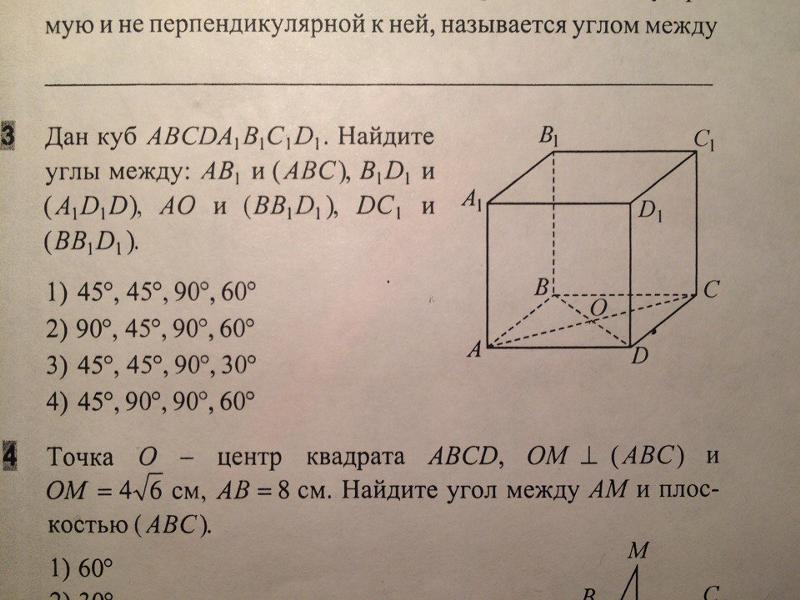
В этом году экзамен сдавали 860 840человек. 754 776 из них – выпускники
текущего года. То есть, 106 064 человека
сдавали ЕГЭ повторно, либо впервые – для
поступления в вуз.
Всего было проведено 2 888 104 «человекэкзаменов» (если расценивать присутствие
одного человека на экзамене как
отдельный экзамен).
Таким образом, было сдано 1 166 424
человек-экзамена по выбору.
Результаты ЕГЭ по математике 2013
Средний тестовый балл по
математике в России 48,7.
538 выпускников сдали ЕГЭ по
математике на 100 баллов.
7 человек из Саратовской области
получили 100 баллов.
43% выпускников не приступили к
части С с развернутым решением.
Результаты ЕГЭ по математике 2013
Согласно результатам пересдач и
апелляций, 2,24 % учеников (16 635
человек) не получили аттестат о среднем
(полном) общем образовании.
В том числе, около 500 человек были
лишены права пересдать ЕГЭ в текущем
году за нарушение правил сдачи ЕГЭ.
Более того, в Якутии возбуждено 5 дел об
административном правонарушении.
Результаты ЕГЭ по математике 2013
Если говорить об образовательных тенденциях, то,
как отмечают организаторы ЕГЭ, они не самые
радужные. К сожалению, говорить о росте
образованности пока не приходится, особенно в
точных науках. К примеру, задание B1 – про
таблетки – не выполнили 150 000 учащихся (около
17 %). Один из учащихся даже предложил в ответе
дать ребёнку 31 500 таблеток.
В целом экзамен по математике показал
незначительный – на 4 тестовых балла – рост
общероссийского среднего балла ЕГЭ.
6. Результаты ЕГЭ по математике 2013
Всего в Саратове над тестами и задачкамиразмышляли более четырех тысяч
выпускников. Из них почти две сотни, 197
человек, провалили этот экзамен школьники набрали меньше 24 баллов (тот
минимальный порог, который нужно
преодолеть ).
А вот отличниками сталивсего четверо саратовских
одиннадцатиклассников — точная наука явно
далась школьникам сложнее, чем родной
язык. На ЕГЭ по русскому, напомним,
максимальный балл набрали 24 ученика.
7. Результаты ЕГЭ по математике 2013
Тем не менее этот результат всеравно лучше прошлогодних: для
сравнения, в 2011 году ЕГЭ по
математике в Саратове на сто баллов
написал лишь один ученик, а в 2012
году и вовсе никому не удалось не
сделать ни одной ошибки. Средний
балл по городу также увеличился и
составил 54,3, тогда как в 2012 году
школьники набирали 42,6.
8. Расстояние от точки до плоскости
9. C 2. Радиус основания конуса равен 5, а его высота равна 12. Плоскость сечения содержит вершину конуса и хорду основания, длина
C 2. Радиус основания конуса равен 5, а его высота равна 12.Плоскость сечения содержит вершину конуса и хорду основания,
длина которой равна 6. Найдите расстояние от центра основания
конуса до плоскости сечения.
Сечение конуса плоскостью, содержащей его
вершину S и хорду АВ 6 — треугольник ASB. В
равных прямоугольных треугольниках SOA
и SOB, где О — центр основания конуса,
откуда ОА ОВ 5, SO 12,
SA SB OB 2 SO2 13.
Пусть SH — высота и медиана равнобедренного
треугольника ASB,
SH SB 2 HB 2 , SH 169 9 4 10.
Тогда отрезок ОН — высота и медиана равнобедренного треугольника AOB,
OH 4.
Плоскость SOH перпендикулярна плоскости ASB, так как прямые SH и
OH перпендикулярны прямой АВ. Поэтому расстояние от точки О до
плоскости ASB равно высоте ОМ прямоугольного
OH SO 6 10
треугольника SOH, проведенной к гипотенузе
OM
6 10
Ответ :
.
5
SH
5
.
10. Расстояние от точки до прямой
11. C 2. Длины ребер AB, AA1 и AD прямоугольного параллелепипеда ABCDA1B1C1D1 равны соответственно 12, 16 и 15. Найдите расстояние
C 2. Длины ребер AB, AA1 и AD прямоугольногопараллелепипеда ABCDA1B1C1D1 равны соответственно 12,
16 и 15.
Найдите расстояние от вершины A1 до прямой BD1.Из вершины А1 опускаем
перпендикуляр на ВD1.
Так как А1D1 перпендикулярна
плоскости АА1В, то
А1D1 перпендикулярен А1В.
Следовательно А1Евысота прямоугольного
треугольника А1BD1.
A1D1 A1B
A1E
, A1B A1 A2 AB 2 20,
D1B
20 15
BD1 A1 A AB A1 D1 25, A1E
12
25
2
2
2
Ответ:12.
12. Задачи на сечение
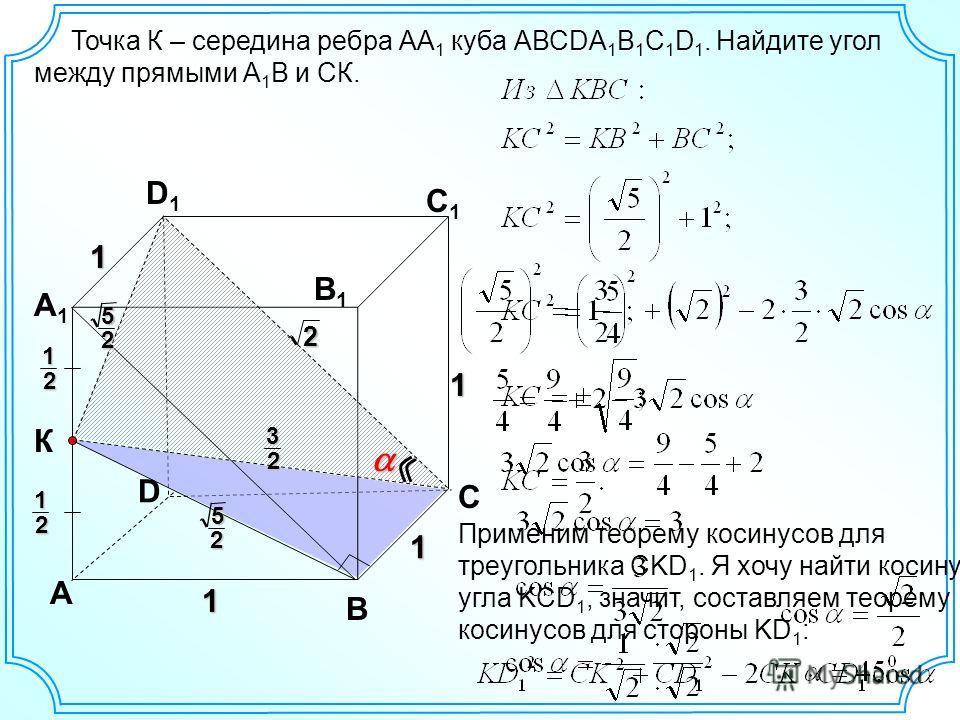
13. C 2. Точка Е — середина ребра ВВ1 куба ABCDA1B1C1D1 . Найдите площадь сечения куба плоскостью D1AE , если ребра куба
C 2. Точка Е — середина ребра ВВ1 куба ABCDA1B1C1D1 .Найдите площадь сечения куба плоскостью D1AE , если ребра
куба равны 4.
Прямая АЕ пересекает прямую А1В1 в
точке К, а прямая D1K пересекает
С1В1 в его середине , точке
F. Искомое сечение – плоскость D1FEA.
Из подобия треугольников AD1K и
EFK следует, что
М
S AD1FE
3
3 1
S AD1K AD1 h
4
4 2
Высота КМ=h , ее длину находим из треугольника АМК
h MK AK AM , h (4 5 ) (2 2 ) 6 2.
3 1
S AD1FE 4 2 6 2 18.
4 2
Ответ:18.
2
2
2
2
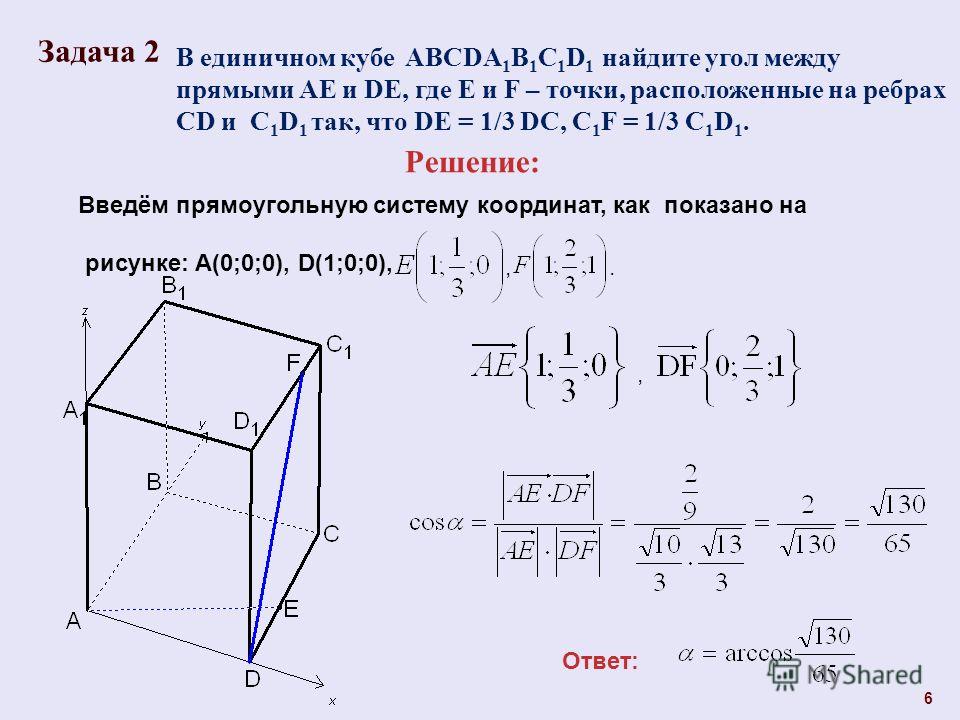
14. C 2. В правильной треугольной пирамиде SABCD с основанием ABC сторона основания равна 8, а угол ASB равен 36°. На ребре
C 2. В правильной треугольной пирамиде SABCD соснованием ABC сторона основания равна 8, а
угол ASB равен 36°. На ребре SM взята
точка M так, что AM- биссектриса угла SAC.
Найдите площадь сечения пирамиды, проходящего
через точки A , M и B.
Нужное сечение — треугольник AMB.
Рассмотрим треугольник ASC.
Он равнобедренный,
ASC SCA 36 0 ,
поэтoму
0
SAC SCA 72
Значит,
MAC 36
0
Ответ : 16 3.
Рассмотрим теперь треугольник CAM . Сумма его
углов 1800 , значит, угол АМС равен 720 .
Следовательно, треугольник САМ равнобедренный, и
поэтому АМ=АС=8. Аналогично находим, что ВМ=8.
Таким образом, треугольник АМВ равносторонний
со стороной 8. Его площадь равна
82 3
16 3.
4
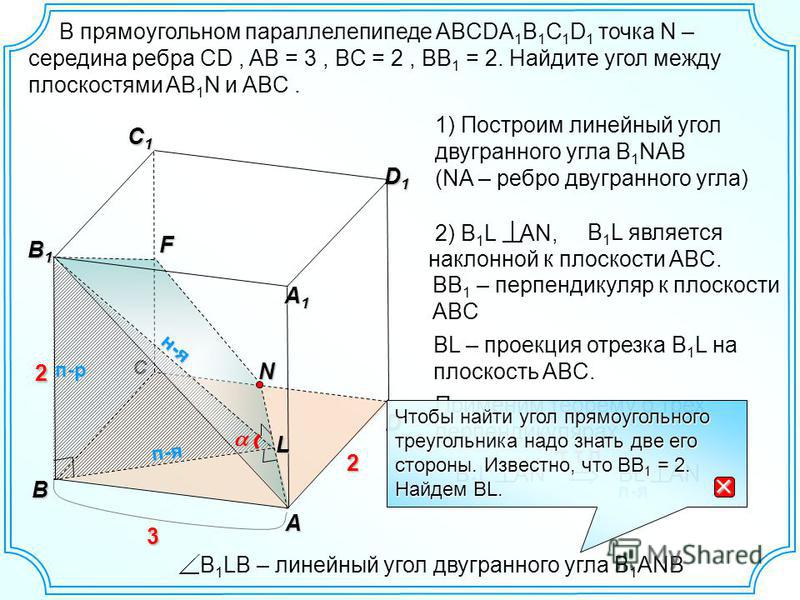
16. C 2. В правильной треугольной призме ABCA1B1C1 стороны основания равны 6, боковые рёбра равны 4.
Изобразите сечение,C 2. В правильной треугольной призме ABCA1B1C1 стороныоснования равны 6, боковые рёбра равны 4. Изобразите
сечение, проходящее через вершины A, B и середину
ребра A1C1 .Найдите его площадь.
Обозначим через М и N середины ребер
А1С1 и В1С1 соответственно.
По теореме о средней линии
треугольника
MN A1B1 AB
так что прямые MN и AB лежат в
одной плоскости. Значит сечением
призмы является равнобокая
трапеция AMNB. Основания АВ=6,
МN=3.
AM
AA1 A1 M 2 ,
2
AM 16 9 5.
3
AH .
2
2
91
3
2
MH 5
.
2
2
S AMNB
S AMNB
MN AB
MH ,
2
9 91 9
91
2 2
4
9
Ответ : 91
4
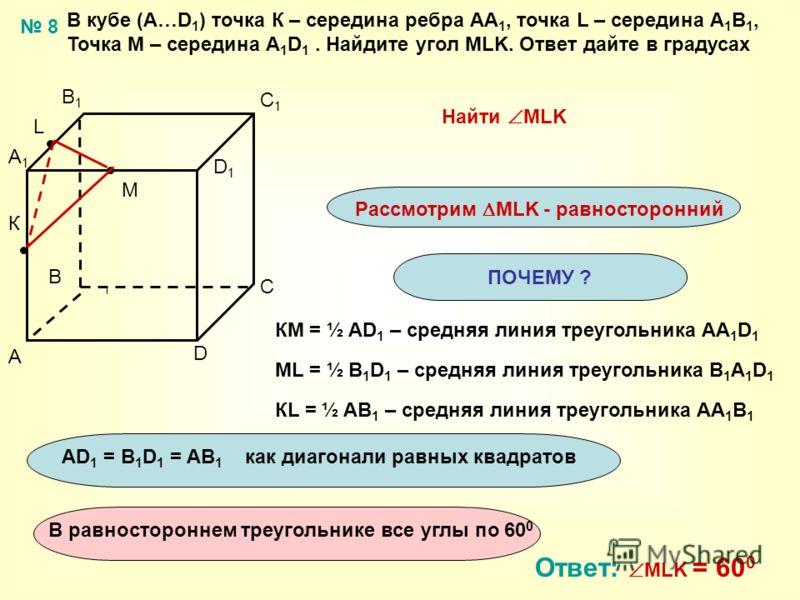
18. Угол между прямыми
19. C 2 . Точка E — середина ребра куба ABCDA1B1C1D1 . Найдите угол между прямыми AE и CA1 .
C2.Точка E — середина ребра куба ABCDA1B1C1D1 .
Найдите угол между прямыми AE и CA1 .
Примем ребро куба за единицу.
ТогдаCA1 3
Проведём через точку A1 прямую,
параллельную AE . Она пересекает
продолжение ребра BB1 в точке F ,
1
причём
B1 F .
2
Искомый угол равен углу CA1F (или
смежному с ним). В прямоугольном
треугольнике A1B1F с прямым
углом B1
5
2
A1 F A1 B1 B1 F 2
.
2
20. В прямоугольном треугольнике CBF с прямым углом B
В прямоугольном треугольнике CBF с прямымуглом B
CF CB BF
2
2
13
.
2
В треугольнике CA1F
CF CA1 A1 F 2 2 cos CA1 F CA1 A1 F
2
2
CA1 A1 F 2 CF 2
15
cos CA1 F
,
2 CA1 A1 F
15
2
15
CA1 F arccos
.
15
15
Ответ: arccos
.
15
21. C 2 . В правильном тетраэдре ABCD найдите угол между высотой DH тетраэдра и медианой BM боковой грани BCD .
C 2 . В правильном тетраэдре ABCD найдите угол междувысотой DH тетраэдра и медианой BM боковой
грани BCD .
Пусть длина ребра тетраэдра равна a ,
угол ВМК искомый, тогда имеем:
2
3
3
a
CH
AB
a
,
3 2
3
3
DH
KM
CD CH
2
2
a2
a 2 a 6
a
,
3
3
3
2
1
a 6
a
DH
,
2
6
6
BC 3 a 3
,
2
2
KM
a 2
2
cos BMK
,
BM
3
6 a 3
BM
BMK arccos
2
.
3
2
Ответ : arccos
3
22. C 2. В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите угол между
C 2. В правильной шестиугольнойпирамиде SABCDEF стороны основания которой
равны 1, а боковые ребра равны 2, найдите угол
между прямыми SB и CD.
Вместо прямой CD рассмотрим
параллельную ей прямую BE.
Искомый угол равен углу SBE.
Треугольник SBE равносторонний,
поскольку большая диагональ
правильного шестиугольника вдвое
больше его стороны: ВЕ=2СD
Следовательно, угол CBE=600 .
Ответ: 600
23. Угол между плоскостями
24. C 2. В правильной треугольной пирамиде SABC с основанием ABC точка M — середина ребра SA, точка K — середина ребра SB.
C 2. В правильной треугольной пирамиде SABC соснованием ABC точка M — середина ребра SA, точка K — середина
ребра SB. Найдите угол между плоскостями CMK и ABC, если
SC=8, BC=6.
Проведем перпендикуляр CQ к
MK, так как треугольник CMK
равнобедренный, то Q середина MK.
Из точки Q опустимперпендикуляр QP на плоскость
основания. Точка P лежит на
медиане CL треугольника ABC. Пря
мая MK параллельна прямой
пересечения плоскостей CMK и ABC,
QP перпендикулярен MK и CQ
перпендикулярен
MK. Следовательно, угол QCP —
линейный угол искомого угла между
плоскостями.
2
2 3
CO CL, CO
BC 2 3.
3
3 2
SO SC 2 CO 2 ,
SO 8 2 3
2
2
2 13.
1
QP SO, QP 13.
2
1
5
CP OL CL.
2
6
13 2 2 39
5
tg QCP
.
CP
3.
15
3 5
2
2 39
Ответ : arctg
.
15
26. C 2. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра: AB=6, AD=8, CC1=16. Найдите угол между плоскостями ABC
C 2. В прямоугольном параллелепипедеABCDA1B1C1D1 известны ребра: AB=6, AD=8, CC1=16.
Найдите угол между плоскостями ABC и A1DB.
Плоскости ABC и A1DB имеют
общую прямую BD. Проведем AH
перпендикуляр к BD. По теореме
о трех перпендикулярах A1H
перпендикулярен BD.
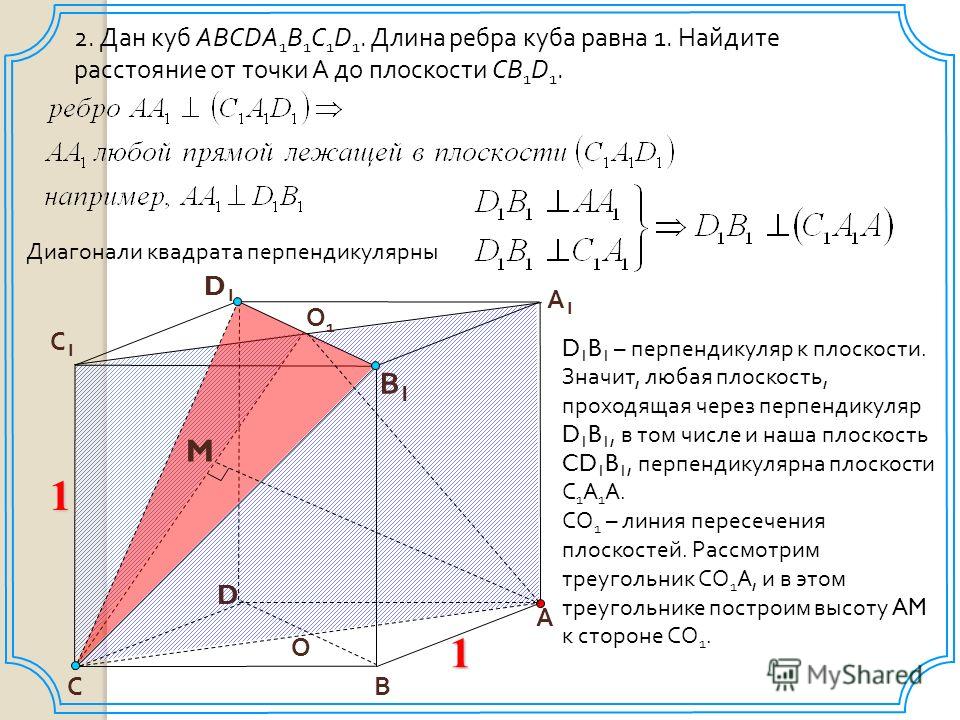Значит,линейный угол двугранного угла,
образованного плоскостями
ABC и A1DB — это угол
A1HA. Из прямоугольного
треугольника BAD находим:
AB AD
AH
,
BD
48 24
AH
.
10
5
Из прямоугольного
треугольника A1AH
находим:
AA1
tg A1 HA
,
AH
16 5 10
tg A1 HA
.
24
3
Значит, искомый угол равен
10
Ответ : arctg .
3
10
arctg .
3
28. Угол между прямой и плоскостью
29. C 2. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны AB=2, AD=AA1=1.Найдите угол между прямой AB1 и плоскостью ABC1.
C 2. В прямоугольномпараллелепипеде ABCDA1B1C1D1 известны
AB=2, AD=AA1=1.Найдите угол между прямой
AB1 и плоскостью ABC1.
Плоскости ABC1 и BCC1
перпендикулярны.
Перпендикуляр из
точки B1 к плоскости
ABC1 лежит в
плоскости BCC1 и пересекает
прямую BC1 в точке E .
Значит, искомый угол равен
углу B1AE.
В прямоугольном
треугольнике B1AE
2
,
катет B1 E
2
гипотенуза AB1 5.
Поэтому
B1 E
sin B1 AE
.
AB1
1
Ответ : arcsin
.
10
1
3
1
sin B1 AE
,
B1 AE arccos
arctg arcctg 3.
10
3
10
1
B1 AE arcsin
.
10
31. C 2. В правильной треугольной пирамиде SABC с основанием ABC известны ребра Найдите угол, образованный плоскостью
C 2. В правильной треугольной пирамиде SABCс основанием ABC известны ребра AB 7 3 , SC 25.
Найдите угол, образованный плоскостью основания и
прямой, проходящей через середины ребер AS и BC.
Пусть M и N — середины ребер
AS и AN соответственно. ANмедиана правильного
треугольника ABC, следовательно,
находится по формуле
3
21
AN
2
AB
2
.
Прямая AS проецируется на плоскость
основания и прямую AN. Поэтому
проекция точки M-точка M1 лежит на
отрезке AN. Значит, прямая
AN является проекцией прямой MN,
следовательно, угол MNM1 искомый.
Поскольку MM1 параллелен SO, где О- центр
основания, MM1 средняя линия треугольника SAO
2
2 3
3
AO CO AN AB
24 3 24.
3
3 2
3
2
AN 24
3
1
1
7
MM 1 SO
SC 2 CO 2 .
2
2
2
NM 1
Из прямоугольного треугольника
MM1N находим
MM 1
7
tg M 1 NM
.
NM 1 48
7
Ответ : arctg .
48
33. Спасибо за внимание!
Решение стереометрической задачи на ЕГЭ.
МЕТОДИЧЕСКОЕ ПОСОБИЕ ПО РЕШЕНИЮ №13 ИЗ ЕГЭ ПО МАТЕМАТИКЕ ПРОФИЛЬНОГО УРОВНЯ
Тамбов, 2018
1.ТЕОРИЯ | 3 |
2.ПРИМЕРЫ ЗАДАЧ | 4 |
3.УПРАЖНЕНИЯ ДЛЯ САМОПРОВЕРКИ | 23 |
4.ОТВЕТЫ | 24 |
5. ИНФАРМАЦИОННЫЕ РЕСУРСЫ | 25 |
СОДЕРЖАНИЕ
ТЕОРИЯ
Прежде чем разбирать решение задач №13 профильного уровня, необходимо вспомнить теорию и основные формулы.
1.1.Нахождение угла между скрещивающимися прямыми
Углом между скрещивающимися прямыми называется угол между двумя прямыми, параллельными им и проходящими через произвольную точку. Градусная мера угла располагается в диапазоне от 0˚ до 90˚.
Данный угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если нам удастся найти координаты направляющих векторов и то сможем найти угол.
Точнее, косинус угла по формуле:
1.2.Нахождение угла между плоскостями
Две пересекающиеся плоскости образуют две пары равных между собой двугранных углов:
Величина двугранного угла измеряется величиной соответствующего линейного угла. Чтобы построить линейный угол двугранного угла, нужно взять на линии пересечения плоскостей произвольную точку, и в каждой плоскости провести к этой точке луч перпендикулярно линии пересечения плоскостей.
Угол, образованный этими лучами и есть линейный угол двугранного угла.
Угол между двумя плоскостями в пространстве равен модулю угла между нормалями к этим плоскостям.
Если мы найдем координаты вектора нормали, то мы воспользовавшись ранее известной формулой косинуса угла между векторами найдем искомый угол.
Вектор нормали к плоскости, заданной уравнением Ах+Ву+Сz+D=0 имеет координаты {A;B;C}.
После того, как мы нашли координаты векторов нормалей двух плоскостей, угол между двумя пересекающимися плоскостями можно вычислить как
угол между нормалями по формуле:
1.3. Нахождение угла между прямой и плоскостью
Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и её проекцией на данную плоскость.
Итак, для того чтобы найти угол между прямой и плоскостью методом координат нам понадобиться формула:
или в координатах
1.
4. Нахождение расстояния от точки до плоскости
Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.
Расстояние от любой точки с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
ПРИМЕРЫ ЗАДАЧ №13 ПРОФИЛЬНОГО УРОВНЯ
№1 Задание с решу ЕГЭ
Условия: В правильной четырёхугольной пирамиде SABCD с вершиной S сторона основания равна 4. Точка L — середина ребра SC. Тангенс угла между прямыми BL и SA равен
а) Пусть O — центр основания пирамиды. Докажите, что прямые BO и LO перпендикулярны.
б) Найдите площадь поверхности пирамиды.
Решение:
а) Заметим, что при проецировании на плоскость ABCD точка S проецируется в точку O.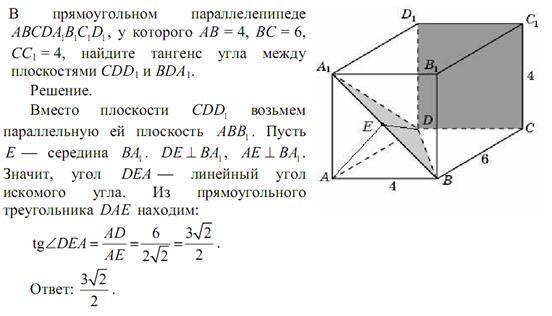
Поэтому проекция SC это OC, значит, проекция L тоже лежит на OC и проекция LO тоже прямая OC. Поскольку OC⊥OB как диагонали квадрата, по теореме о трех перпендикулярах LO⊥OB.
б) Сразу отметим, что , поэтому . Введем координаты, направив оси из точки O параллельно сторонам квадрата и через вершину S. Обозначая высоту пирамиды за 2h, находим координаты точек B(2, 2, 0), C(-2, 2, 0), A(2, -2, 0), S(0, 0, 2h), L (-1, 1, h). Тогда, ={-3,-1, h},
Посчитаем угол между этими векторами:
Решая уравнение, находим и высота пирамиды SO=2 .
Тогда апофема SH=8 и площадь поверхности =80
Ответ: 80.
№2 Задание с решу ЕГЭ
Условия:
Основанием прямой треугольной призмы ABC является прямоугольный треугольник ABC с прямым углом C.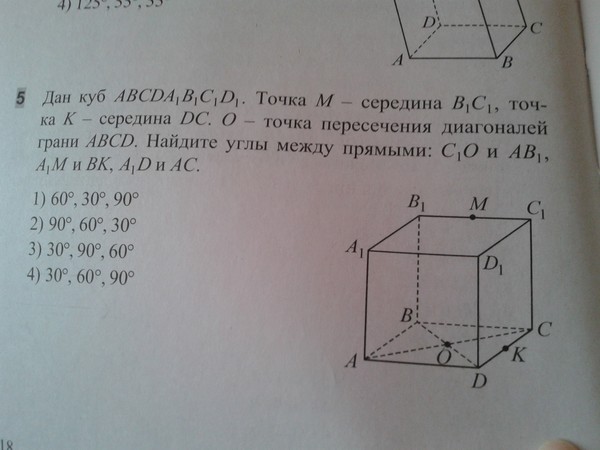
Прямые и перпендикулярны.
а) Докажите, что =AC
б) Найдите расстояние между прямыми и , если AC=6, BC=3
Решение:
а) Если то скалярное произведение векторов и будет равно 0. Введем систему координат. Пусть
тогда
получим координаты векторов и
По условию =0, а значит, что
, это возможно, когда , то есть при a=b или a=-b, однако, ввиду того, что отрицательной длина быть не может, имеем a=b, тогда CA=A что и требовалось доказать.
б) Пусть M— середина A , тогда искомое расстояние равно расстоянию от точки M до прямой поскольку прямая C перпендикулярна , проведённой к гипотенузе:
Это расстояние равно половине высоты прямоугольного треугольника , проведённой к гипотенузе:
№3 Задание с решу ЕГЭ
Условия:
Длина диагонали куба ABCDA1B1C1D1 равна 3.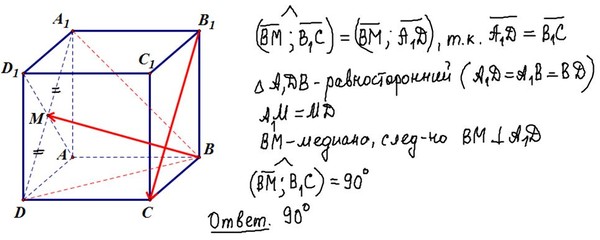
На луче A1C отмечена точка P так, что A1P = 4.
а) Докажите, что PBDC1 — правильный тетраэдр.
б) Найдите длину отрезка AP.
Решение:
а) Введём систему координат как показано на рисунке. Поскольку ребро куба в корень меньше его диагонали, ребро данного куба равно . Тогда точки B, D, C1 имеют координаты (0; ; ) , ( ; ; ), ( ; ; ) соответственно.
Поскольку P лежит на продолжении A1C, отрезок A1P можно рассматривать как диагональ куба с ребром Тогда точка P имеет координаты (
Найдём расстояние от P до точек D1, B и C1:
Отрезки C1B, DB и DC1 — диагонали граней куба, поэтому по теореме Пифагора B=DB=D = . Тогда PD=P =PB= B=DB=D .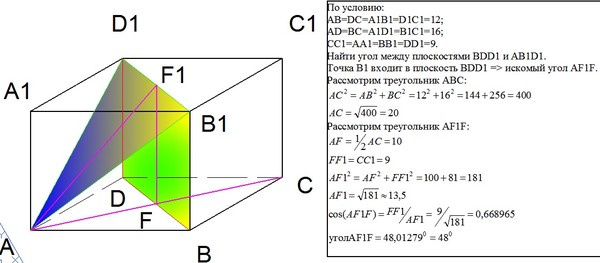
Значит, все рёбра тетраэдра DBC1P равны, поэтому он правильный.
б) Координаты точки A:(0;0; ). Раcстояние от точки P до точки A равно
Ответ:
№4 Задание с решу ЕГЭ
Условия:
В правильной шестиугольной призме ABCDEF , все ребра которой равны 1. Найдите расстояние от т. B до прямой .
Решение:
Поместим наш шестиугольную призму в систему координат и пропишем координаты точек, которые нам понадобятся
, , A( ;0,5;0), B(
Теперь докажем перпендикулярность с помощью скалярного произведения и координаты их векторов соответственно равны и .
, т.к. .
Получается расстояние от точки B до прямой будет длина отрезка
Ответ: 2
№5 Задание с решу ЕГЭ
Условия:
В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 2, точка M — середина ребра AB, точка O — центр основания пирамиды, точка F делит отрезок SO в отношении 3 : 1, считая от вершины пирамиды.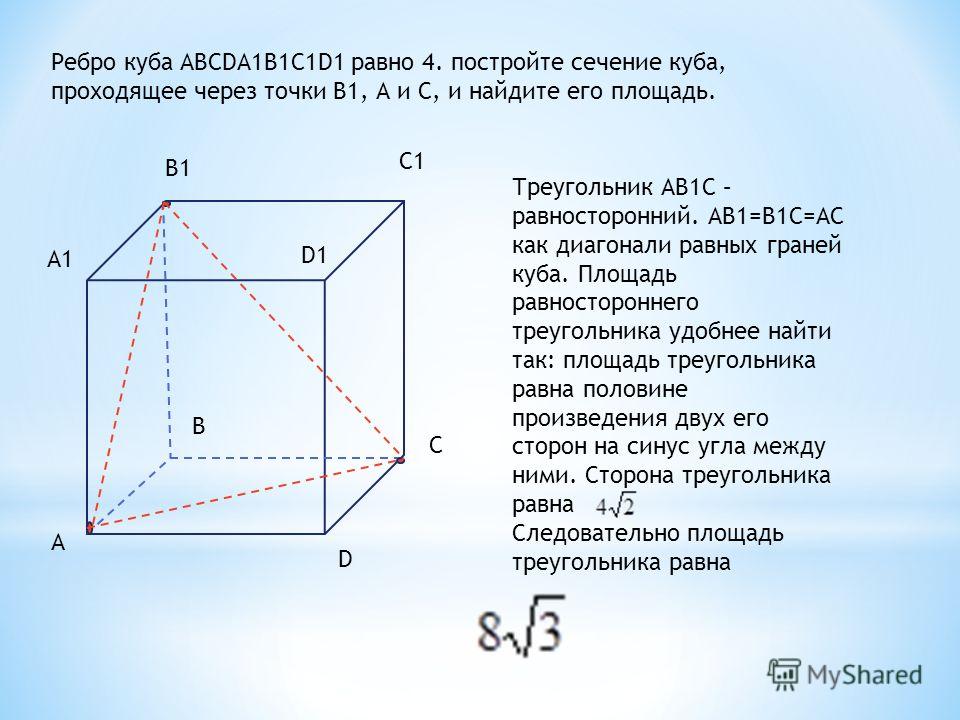
а) Докажите, что прямая MF перпендикулярна прямой SC.
б) Найдите угол между плоскостью MBF и плоскостью ABC.
Решение:
а) Введем координаты с началом в точке A и осями, направленными по AB, по прямой, параллельной OM и по прямой, параллельной OS. Тогда координаты точек будут такими A(0;0;0), B(2;0;0), M(1;0;0), C(1; ;0), O(1; ;0), S(1; ), F(1; ), где a — высота пирамиды. Найдем ее: 2=SA= , откуда a= ,
Значит, и . Значит, их скалярное произведение равно = 0, поэтому MF⊥ SC.
б) Пусть уравнение плоскости MBF это Ax+By+Cz=0. Подставляя туда координаты точек, находим A+D=0, 2A+D = 0 (откуда A= D = 0) и Пусть C= , B=1. Итак, уравнение этой плоскости Найдем по формуле угол между ней и плоскостью z = 0 (ABC).
Получим:
Ответ:
№6 Задание с alexlarin вар.202
Условия:
В прямоугольном параллелепипеде АВ=2, АD=1, =3.
Точка К лежит на ребре так, что СK: K=5:4. а) Докажите, что прямые и перпендикулярны. б) Найдите расстояние от точки до плоскости .
Решение:
а) Введем прямоугольную систему координат и найдем нужные нам точки (0;0;3), D(1;2;0) , (1;2;3), K(1; 0; )
Найдем координаты векторов и . Их координаты соответственно равны {1; 2; -3} и {0; 2; }.
Отсюда следует , что , ч.т.д.
б) Построим плоскость
Зададим уравнение плоскости, найдем координаты три точки искомой плоскости.
Подставляем по очереди координаты точек , D, K в уравнение плоскости.
Для
Решая данную систему получаем: , а
Тогда ,
Все это подставляем в уравнение плоскости:
Расстояние от точки до плоскости найдем по формуле:
Ответ:
№7 Задание с alexlarin вар.210
Условия:
Основанием пирамиды SABC является равносторонний треугольник ABC, длина стороны которого равна 4 .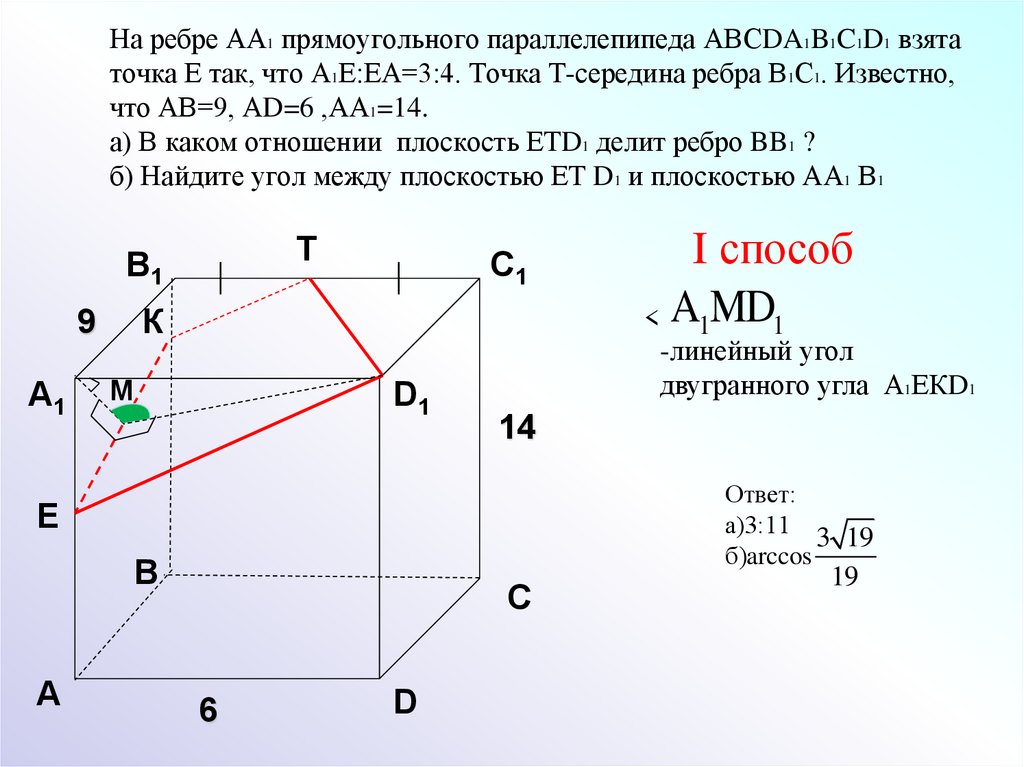
Боковое ребро SC перпендикулярно плоскости основания и имеет длину 2. а) Докажите, что угол между скрещивающимися прямыми, одна из которых проходит через точку S и середину ребра BC, а другая проходит через точку С и середину ребра AB равен 45 . б) Найдите расстояние между этими скрещивающимися
прямыми.
Решение:
а) AB=BC=AC=4
SC=2;
Найдем из прямоугольного треугольника
S(0;0;2), L( , C(0;0;0), M(0;
Найдем координаты вектора { } и { }.
= , ч.т.д.
б) Проведем KL∥CM.
Найдем уравнение плоскости SLK.
K( ; 0), S(0;0;2), L(
Для
Вычитаем из первого уравнения второе и получаем В=0.
Из третьего уравнения следует C= . A= .
d(C,(SLK))=
Ответ:
№8 Задание с alexlarin вар.
211
Условия:
В прямоугольном параллелепипеде на ребре взята точка К так, что . а) Докажите, что плоскость АСК делит диагональ в отношении 4:1, считая от точки В. б) Найдите расстояние от точки D до плоскости АСК, если известно, что АВ=4, ВС=3, СС1=2.
Решение:
а) Построим плоскости АСК, . MK ∥ AC. Получим линию пересечения данных плоскостей — HN. MK ∥ . Тогда MKD .
т.О- точка пересечения HN и KB
1) BON .Отсюда следует, что ⇒
BN=Z ⇒ , ч.т.д.
б) A(0;4;0), C(3;0;0), K(3;3;2)
1.
2.
3. .
Решая систему получим A= , B= , C= .
Уравнение плоскости: .
D(3;4;0). Тогда подставив координаты расстояние h(D,(ACK))= .
Ответ: .
№9 Задание с alexlarin
Условия:
В прямоугольном параллелепипеде АВ=ВС=4, СС1=8. Точка К середина ребра АВ, точка М середина ребра ВС. Точка Р лежит на ребре DD1 так, что DP:PD1=3:5
а) Докажите, что плоскость КМР перпендикулярна прямой DВ1.
б) Найдите объем пирамиды, основанием которой является сечение параллелепипеда плоскостью КМР, а вершиной – точка D1.
Решение:
а) Найдем нужные координаты D(0;4;0), M(2;0;0),K(4;2;0), P(0;4;3),D1(0;4;8),B1(4;0;8)
Поместим параллелепипед в систему координат, запишем нужные координаты точек и найдем векторы
Чтобы доказать, что плоскость перпендикулярна к B1D нужно найти вектор нормали к этой плоскости и проверить его коллинеареность к B1D
Через определитель третьего порядка найдем уравнение плоскости и координаты вектора нормали
6(x-2)-6y+12z=0
6x-6y+12z-12=0
Эти вектора коллинеарны, т.е вектор B1D перпендикулярен плоскости (MKP) .
б) Объем пирамиды находится по формуле V=⅓Sh Сначала найдем площадь сечения SMLDEK =SKMCDА : cosα, где cosα- это угол между плоскостью сечения и его проекцией
SKMCDА = 16-2=14
Найдем угол между плоскостям плоскостями (ABC) и (MKP)
n{1;-1;2}, n1 {0;0;1}
Тогда SMLDEK = (14∙3)/√6 = 7√6
Найдем h, т.
е. находим расстояние от точки D1 до плоскости(MPK)
Следовательно VKMLPED1 = ⅓ (70√6/√6)= 70/3
Ответ: 70/3.
№10 Задание из сборника задач С2
Условия:
В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра АВ и АА1 равны 1, а ребро АD=2. Точка Е – середина ребра В1С1. Найдите угол между прямой ВЕ и плоскостью АВ1С.
Решение:
Для решения этой задачи необходимо составить уравнение плоскости, проходящей через точки
А(1; 0; 0), В1(0;0;1), С(0;2;0). Уравнение искомой плоскости будет иметь вид: 2х+у+2z-2=0. Значит, нормаль n к этой плоскости имеет координаты {2;1; 2}.
Длину вектора легко найти геометрически: . Но его координаты нам всё равно необходимы. Из простых вычислений находим, что . Найдем угол между вектором и нормалью к плоскости по формуле скалярного произведения векторов:
Ответ: 45˚
УПРАЖНЕНИЯ ДЛЯ САМОПРОВЕРКИ
1.
В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
2. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1.
3. Основание прямой четырехугольной призмы ABCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
4. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
5. В основании прямоугольного параллелепипеда ABCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = √10, AD = 3√10. Высота параллелепипеда AA1 = 6 √5. Найдите расстояние от точки A до плоскости A1DB.
ОТВЕТЫ
1.2 √5
2.
3.
4.
5. 2
ИНФОРМАЦИОННЫЕ РЕСУРСЫ
1.
Леваков В.В, Методические рекомендации . Решение заданий С2 ЕГЭ по математике координатно-векторным методом. — Саратов МОУ «СОШ № 34 с УИП», 2013
2. Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения- М., 2012
3. Тренировочные варианты с https://reshimvse.com/
4. Тренировочные варианты с http://alexlarin.net/
5.Тренировочные варианты с образовательного портала https://ege.sdamgia.ru/
6. А. Г. Малкова. Подготовка к ЕГЭ по математике. Материалы сайта EGE-Study.ru
7. Федеральный институт педагогических измерений https://fipi.ru/
8. Открытый банк заданий https://mathege.ru
Trang chủ — Diễn đàn Toán học
04-04-2023
Gửi bởi nmlinh26 trong Lịch sử toán học
Chú dẫn của người dịch: Александр Гротендик (1928-2014) la nhà toán học được cong nhận rộng rãi la có ảnh hưởng nhất thế kế.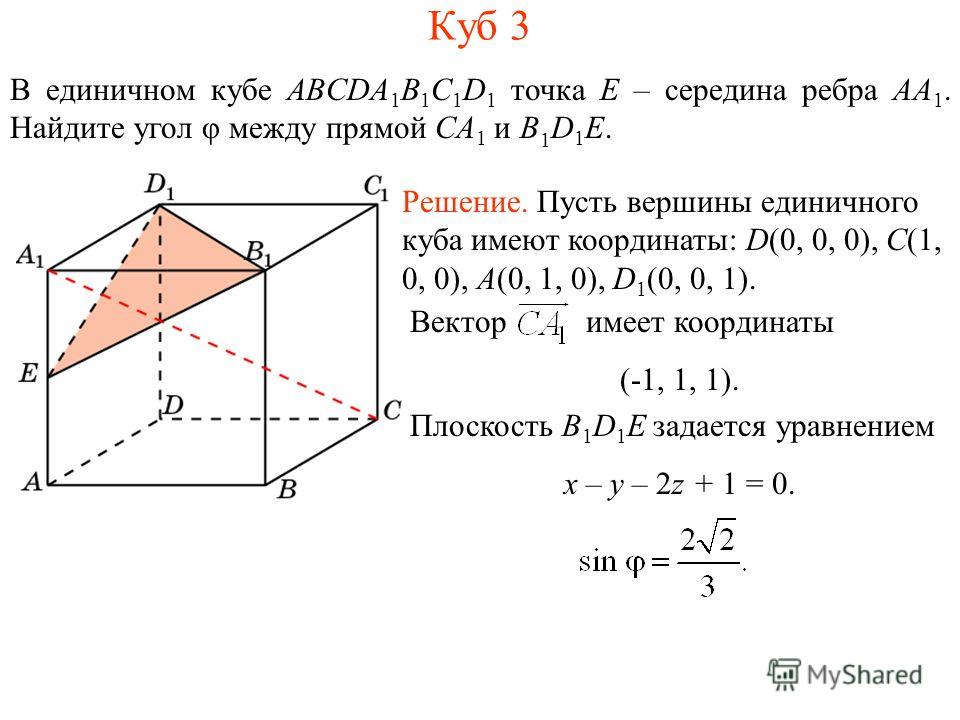
Cac Cong trình Của ông đã cách Mạng Hóa Hình Học đại số, Tôpô đại số, Đại số đồng điều cung nhưc ng Lût thuyố ử dụng rộng rãi ngôn ngữ Lược đồ, Phạm trù và Hàm tử. NAM 1967, Giữa bom đạn của chiến tranh Việt Nam, ông đa đến Miền Bắc và mở lớp Giang bài cho Đại học Hà Nội dang sƫng tán tán tán. Ông đã bán chiếc huy chương Fields của minh để góp phần gây quỹ «Một tỷ cho Việt Nam». Là người có tinh thần phản chiến mãnh liệt, chuyến đi Việt Nam dường như đã tác ng lớn đến tư tưởng của Гротендик. Sau khi trở về Paris, ông đã quay lưng với cộng đồng toán học và ở ẩn. Về cuối đời, ông đã gửi tuyên bố khong cho xuất bản hay tái bản bất kỳ công trình khoa học nào của mình, long muquãn bốn. Tất nhiên, giới toán học đã không thể lam vậy. Một trong những «định lý» quan trọng nhất mà Grothendieck đã cong bố là «Tồn tại một nền toán học Việt Nam». Bài dịch sau đây la hồi ký của Grothendieck về chuyến tham Việt Nam 1967. PHẦN I Đầu năm nay, tôi nhận được (nhờ cac bên trung gian) thỉnh cầu từ phía cá.
Ксем Тем
24-03-2023
Гуи бой Несбит trong Tin tức — Vấn đề — Sự kiện
Viện Hàn lâm Khoa học và Văn học Na Uy vừa trao Giải thưởng Abel 2023 cho Luis A. Caffarelli (Đại học Texas ở Austin, Mỹ) vì nhong đóng góp quan trủa thoyng cỹ ết chính quy (теория регулярности) cho cac phương trình đạo ham riêng phi tuyến, bao gồm cac bài toán bien tự do và phương trình Monge-Ampère. Cac Phương trình đạo ham riêng phát sinh một cách tự nhiên như các quy luật tự nhiên, cho dù để mô tả dòng chảy cợa tric ha nưủa nưủa nưủa tria nưủa nưủa n của dan số. Những phương trình này luôn la đề tài nghiên cứu sôi nổi kể từ thời của Ньютон ва Лейбниц. Туй нхьен, бэт чап нхонг но лук джан кэ куа как нха тоан хок тронг нхиоу тхок, нханг кау хай кань бан льен куан джон тон тон ặc thậm chí tính duy nhất, sự xuất hiện và loại điểm kỳ dị của một số phương trình chín vẫn chưa được giải quyết.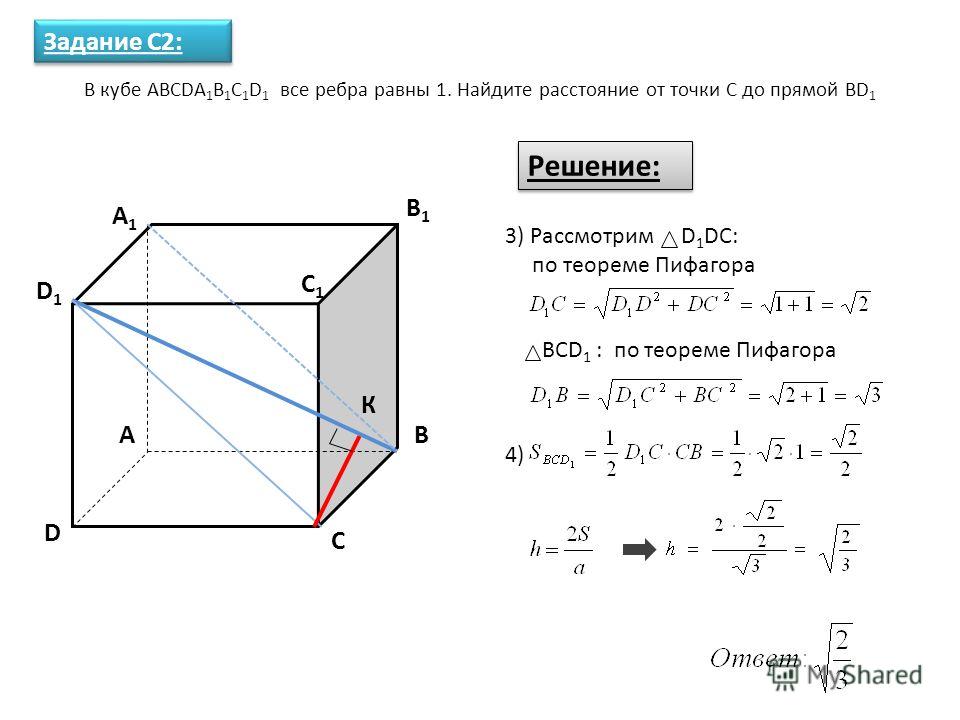
Ксем Тем
23-03-2023
Гуи бои bangbang1412 Чонг Кинь Нгим Хок Тоан
Phỏng vấn với Joseph Ayoub Joseph Ayoub, Giáo sư ngành Toán học tại Đại học Zurich, là người đầu tiên giữ ghế «Александрия Фигероа ва Роберт Пеннер». Ông quan tâm đến đối đồng điều của cac đa tạp đại số và lý thuyết мотив. Ông đã bắt đầu hứng thú với toán học như thế nào? Tôi đã luôn hứng thú với toán. Từ lúc bắt đầu thời thiếu niên tôi đã có nhung điểm số tốt trong mọi môn học nhưng toán học đã luôn là bi hứcng th a toi: trong thời gian rảnh của tôi, tôi thưởng thức việc giải quyết cac vấn đề toán học.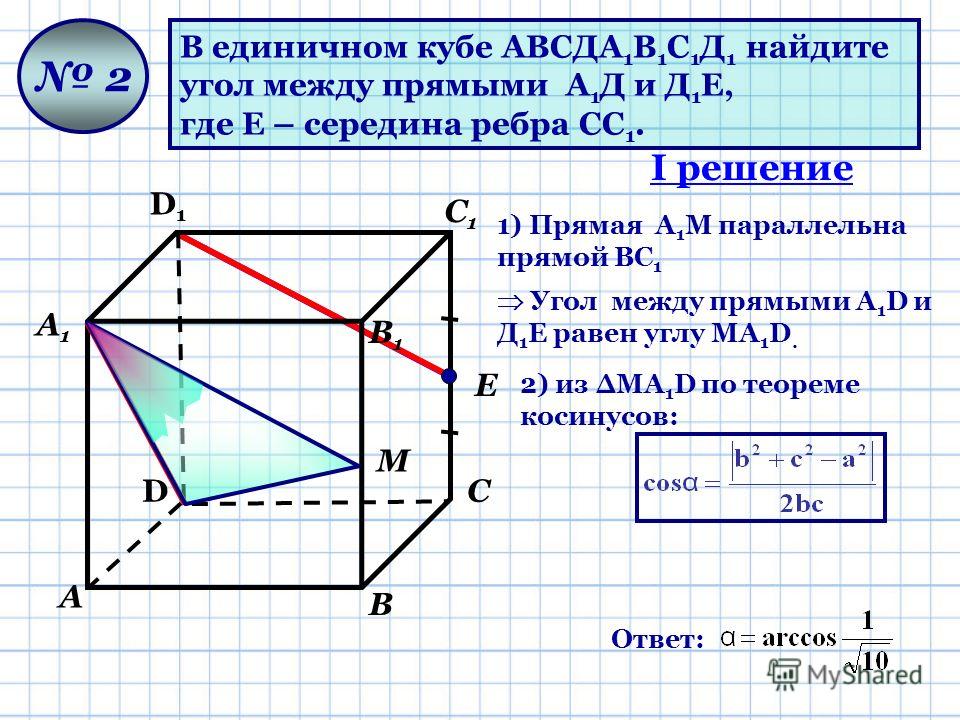
Khi đã лам hết, tôi tự kiem thêm nhung vấn ề mới. Tôi đã đặc biệt thích Hình Học phẳng nhưng tôi cung đã thích tính toán cac thứ khac và giải cac phương trình. Trong thời gian nghỉ tôi thường bien mến mất vào cac thư viện để tra cứu cac bài báo toán học thong qua Bách Khoa Toàn Thư. Đây la cách lam thế nào tôi quen thuộc với một lượng lớn khai niem hiện đại như bài toán phân loại cac nhóm đơn. Tôi đã có thể tiếp cận một lượng không nhỏ «toán cao cấp» ở tuổi còn rất trẻ khi tôi tìm thấy vài bài báihàhàt kho hăn của cởa ở Бейрут. Chung là cac bản thảo của cac bài giang tô-pô đại cương mà bố tôi — một giáo sư toán học — đã giang dạy ở đại học…
Ксем Тем
03.12.2023
Гуи бои bangbang1412 trong Toán học lý thú
Đã rất lâu kể từ khi Grothendieck giới thiệu lý thuyết lược đồ (теория схемы) trong bộ «Элементы геометрической алгебры» thì tới nay lượntrc đồ t ngôn ngữ cơ bản của hình học đại số và có ng dụng sau rộng trong những ngành liên quan như lý thuyết số.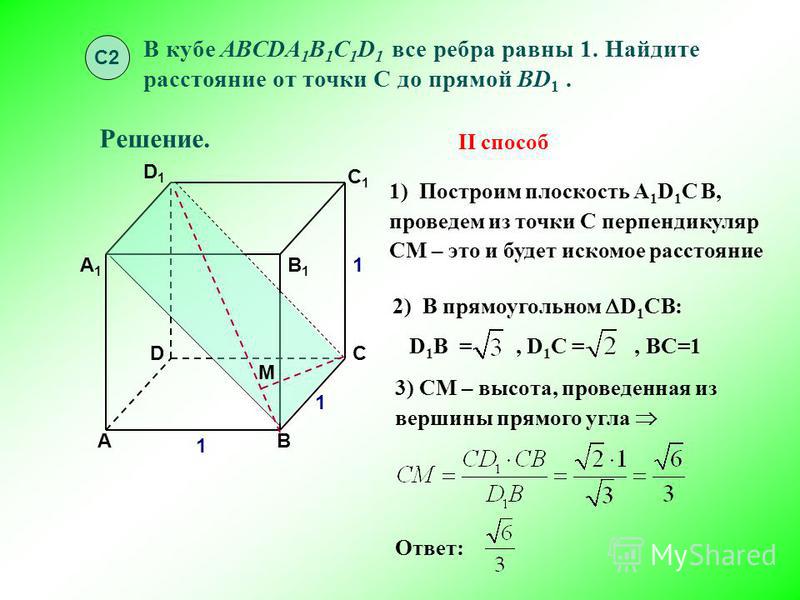
Само понятие схемы имеет детскую простоту — настолько простое, настолько скромное, что никто до меня не осмелился принять ее всерьез. Nó đã một lần và mãi mãi thay đổi hình học đại số thành một ngôn ngữ qua sức trừu tượng với bất cứkh cững cững cững ai, nhẴất khả năng về đại số (Дэвид Мамфорд từng viết một bài «Có thể giải thích lý) thuyết lược đồ cho một nhà sinh học không?») vì một lý do đơn giản, nó dựa rất nặng trên ngôn ngữ đại số giao hoán. Ngày nay không ai có thể học Hình học đại số mà khong học ngai càng nhiều đại số giao hoán. Vào thời kỳ mà lý thuyết lược đồ mới bắt đầu, nó đã лам «sấp ngửa» cac nhà toán học. Дэвид Мамфорд từng viết Затем появился Гротендик и перевернул запутанный мир исследователей с ног на голову, ошеломив их новой терминологией схем, а также огромным количеством новых и очень интересных результатов. Эти заметки пытались показать что-то…
Ксем Тем
03.
Гои бои nmlinh26 trong Toán học lý thú
Xin được gửi cac thành viên của diễn đàn bài viết của minh về sự liên hệ giữa lý thuyết số và lý thuyết hÍt: «Topôố нгуен то гьонг нут нху тхо нао?»https://drive.google.. .?usp=share_link
Ксем Тем
20-02-2023
Гуи бои bangbang1412 Чонг Кинь Нгим Хок Тоан
Phỏng vấn với Jean-Pierre Serre В то время как другие науки ищут правила, которые Бог избрал для Вселенной, мы, математики, ищем правила, которым должен подчиняться даже Бог. Trong khi cac ngành khoa học khac tìm kiem cac quy luật mà Chúa đã chọn cho vũ trụ, chung tôi những nha toán học tìm kiậm các quy m luếng Пхи Туан Тео. Жан-Пьер Серр, зп, 1926 тий Pháp. Ông từng theo học toán tại đại học sư phạm Paris. Vào năm 1954, ở tuổi 28, ong đã được giải Fields bởi Hiệp hội Toán học Quốc tế, chứng nhận cao nhất cho một toc thánh tế Хай нам Сау Онг được bổ nhiem chức Giáo sư về Đại số và Hình học tại Колледж де Франс, nơi mà ong la giáo sư trẻ nhất trong 1 khảng 1 khoảng.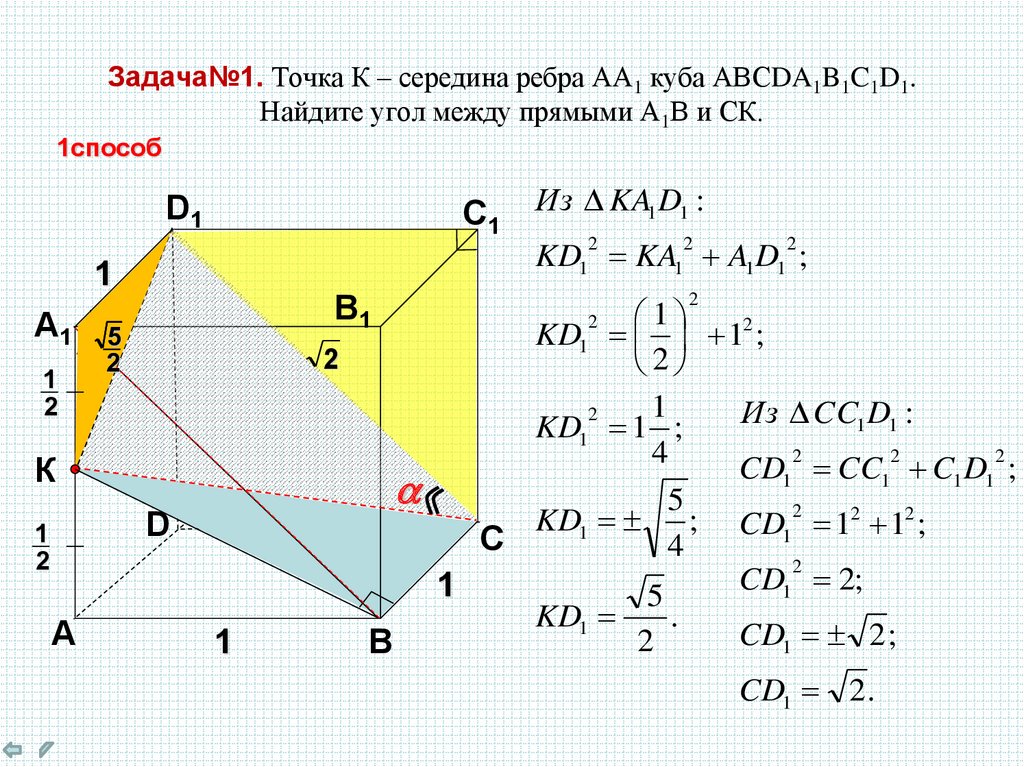
Ксем Тем
02.11.2023
Гои бои nmlinh26 trong Toán học lý thú
THÔNG TIN CHUNGBài viết gốc: Теория бесконечных категорий предлагает взгляд на математику с высоты птичьего полета, đăng trên Scientific American, том 325, выпуск 4, октябрь 2021 г. https://www.scientif…f-mathematics1/Tac giả: Giáo sư Emily Riehl, Университет Джона Хопкинса, chuyên gia về lý thuyết phạm trù bậc cao và lý thuyet ng luan, các cong trình của cô liên quan đến vìmàn phến ền tảng của lý thuyết phạm trù vô cực.Hình vẽ: Họa sĩ Matteo Farinella. Ngời dịch: Nguyễn Mạnh Linh, Université Paris-Saclay. Một ngai thu ở Новая Англия, khi còn là sinh viên năm ba, tôi đi ngang qua một ga tàu điện ngầm và một bài toán đã lọt vào mắt tôi. Một người đàn ông cùng những ý tưởng được vẽ nguệch ngoạc trên tường, một trong số đó là bài toán dửng ving mỻột hình thể tích gấp đôi một hình lập phương khac cho trước, bằng thước thẳng và compa.
Leave A Comment