2. В треугольнике ABC C = 90°. На стороне АВ взята точка М… геометрия Зив 7 класс ГДЗ. Самостоятельные работы. Вариант 7. С-22. – Рамблер/класс
2. В треугольнике ABC C = 90°. На стороне АВ взята точка М… геометрия Зив 7 класс ГДЗ. Самостоятельные работы. Вариант 7. С-22. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
2. В треугольнике ABC C = 90°. На стороне АВ взята точка М так, что АВ = ЗАМ. Через точку М проведена прямая а, параллельная АС. Докажите, что расстояние от точки В до прямой а вдвое больше расстояния между прямыми а и АС.
В треугольнике ABC C = 90°. На стороне АВ взята точка М так, что АВ = ЗАМ. Через точку М проведена прямая а, параллельная АС. Докажите, что расстояние от точки В до прямой а вдвое больше расстояния между прямыми а и АС.
ответы
2. Пусть прямая а пересекает ВС в точке К. Пусть Е — середина МВ.
Проведем МВ ⊥ АС, ЕР ⊥ а, ЕО ⊥ BС. ∆АМТ, ∆МЕР, ∆ЕВО равны по
гипотенузе и острому углу. Тогда МТ = ЕР = ВО, но ЕР = ОК, т.к. легко доказать, что ЕО || а, значит ВК = 2МТ, причем ВК — это рас стояние до а от точки В, а МТ— расстояние между а и АС.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Досуг
Химия
похожие вопросы 5
Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.
Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.
Привет. Запуталась при решении, нужна помощь знатоков!!!
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)
ГДЗГеометрия11 класс10 классАтанасян Л.С.
Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос
Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
9. Определите ряд, в котором в обоих словах пропущена одна и та же буква.
9.
Определите ряд, в котором в обоих словах пропущена одна и та же буква. Выпишите
эти слова, вставив пропущенную букву. (Подробнее…)
ГДЗРусский языкЕГЭЦыбулько И.П.
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
| 1 | На прямой AB взята точка M. Луч MD- биссектриса угла CMB. Известно, что \angleCMA=36°. Найдите угол DMB. Ответ дайте в градусах. | Смотреть видеоразбор >> |
| 2 | В треугольнике ABC угол C равен 90°, AB=15, AC=9. Найдите sin\angleA. | Смотреть видеоразбор >> |
| 3 | В треугольнике ABC сторона AC=56, BM- медиана, BH- высота, BC=BM. Найдите длину отрезка AH. Найдите длину отрезка AH. | Смотреть видеоразбор >> |
| 4 | В треугольнике ABC известно, что AB=BC, AC=8, tg\angleBAC=\frac{\sqrt{5}}{2}. Найдите длину стороны AB. | Смотреть видеоразбор >> |
| 5 | Ромб и квадрат имеют равные стороны. Найдите площадь ромба, если его острый угол равен 30°, а площадь квадрата равна 16. | Смотреть видеоразбор >> |
| 6 | В прямоугольной трапеции ABCD с основаниями BC и AD угол BAD прямой, AB=3, BC=CD=5. Найдите среднюю линию трапеции. | Смотреть видеоразбор >> |
| 7 | В окружности с центром O отрезки AC и BD – диаметры. Вписанный угол ACB равен 36°. Найдите угол AOD. Ответ дайте в градусах. | Смотреть видеоразбор >> |
| 8 | На окружности отмечена точка C. Отрезок AB- диаметр окружности, AC=9, BC=12. Найдите радиус окружности. | Смотреть видеоразбор >> |
| 9 | На прямой AB взята точка M. Луч MD- биссектриса угла CMB. Известно, что \angleCMA=122°. Найдите угол DMB. Ответ дайте в градусах. Луч MD- биссектриса угла CMB. Известно, что \angleCMA=122°. Найдите угол DMB. Ответ дайте в градусах. | Смотреть видеоразбор >> |
| 10 | В треугольнике ABC угол C равен 90°, AB=15, sin\angleA=0,6. Найдите AC. | Смотреть видеоразбор >> |
| 11 | В треугольнике ABC известно, что AB=BC=15, AC=24. Найдите длину медианы BM. | Смотреть видеоразбор >> |
| 12 | В треугольнике ABC медиана BM перпендикулярна AC. Найдите AB, если BM=25, AC=120. | Смотреть видеоразбор >> |
| 13 | Сумма двух углов ромба равна 240°, а его периметр равен 24. Найдите меньшую диагональ ромба. | Смотреть видеоразбор >> |
| 14 | В трапеции ABCD известно, что AB=CD, \angleBDA=54° и \angleBDC=23°. Найдите угол ABD. Ответ дайте в градусах. | Смотреть видеоразбор >> |
| 15 | В окружности с центром O отрезки AC и BD – диаметры. Центральный угол AOD равен 124°. Найдите угол ACB. Ответ дайте в градусах. Найдите угол ACB. Ответ дайте в градусах. | Смотреть видеоразбор >> |
| 16 | В угол C, равный 79°, вписана окружность с центром O, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах. | Смотреть видеоразбор >> |
| 17 | На прямой AB взята точка M. Луч MD- биссектриса угла CMB. Известно, что \angleDMC=18°. Найдите угол CMA. Ответ дайте в градусах. | Смотреть видеоразбор >> |
| 18 | В треугольнике ABC угол C равен 90°, AB=39, cos\angleA=5/13. Найдите BC. | Смотреть видеоразбор >> |
| 19 | В равнобедренном треугольнике ABC боковые стороны AB=BC=5, медиана BM=3. Найдите cos\angle\angleBAC\angle. | Смотреть видеоразбор >> |
| 20 | На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что треугольник ABE равнобедренный. Найдите ED. | Смотреть видеоразбор >> |
| 21 | В трапеции ABCD известно, что AD=8, BC=7, а её площадь равна 45. Найдите площадь треугольника ABC. Найдите площадь треугольника ABC. | Смотреть видеоразбор >> |
| 22 | Основания равнобедренной трапеции равны 10 и 24, боковая сторона равна 25. Найдите высоту трапеции. | Смотреть видеоразбор >> |
| 23 | На окружности радиуса 3 взята точка C. Отрезок AB- диаметр окружности, AC=4\sqrt{2}. Найдите BC. | Смотреть видеоразбор >> |
| 24 | В угол C, равный 165°, вписана окружность с центром O, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах. | Смотреть видеоразбор >> |
| 25 | На прямой AB взята точка M. Луч MD- биссектриса угла CMB. Известно, что \angleDMC=51°. Найдите угол CMA. Ответ дайте в градусах. | Смотреть видеоразбор >> |
| 26 | Найдите площадь прямоугольного треугольника, если его гипотенуза равна \sqrt{17}, а один из катетов равен 1. | Смотреть видеоразбор >> |
| 27 | В треугольнике ABC известно, что AB=BC, медиана BM равна 2. Площадь треугольника ABC равна 2\sqrt{21}. Найдите длину стороны AB. Площадь треугольника ABC равна 2\sqrt{21}. Найдите длину стороны AB. | Смотреть видеоразбор >> |
| 28 | Стороны параллелограмма равны 9 и 12. Высота, опущенная на меньшую сторону, равна 8. Найдите высоту, опущенную на большую сторону параллелограмма. | Смотреть видеоразбор >> |
| 29 | Основания трапеции равны 8 и 16, боковая сторона, равная 6, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции. | Смотреть видеоразбор >> |
| 30 | В равнобедренной трапеции одно из оснований равно 5, а другое – 9. Высота трапеции равна 6. Найдите тангенс острого угла трапеции. | Смотреть видеоразбор >> |
| 31 | На окружности радиуса 5 отмечена точка C. Отрезок AB- диаметр окружности, AC=8. Найдите sin\angleABC. | Смотреть видеоразбор >> |
| 32 | На окружности по разные стороны от диаметра AB взяты точки D и C. Известно, что \angleDBA=41°. Найдите угол DCB. Ответ дайте в градусах. Найдите угол DCB. Ответ дайте в градусах. | Смотреть видеоразбор >> |
| 33 | В треугольнике ABC угол C равен 90°, AB=25, AC=24. Найдите cos\angleB. | Смотреть видеоразбор >> |
| 34 | В треугольнике ABC проведена биссектриса AL, угол ALC равен 145°, угол ABC равен 113°. Найдите угол ACB. Ответ дайте в градусах. | Смотреть видеоразбор >> |
| 35 | В равнобедренном треугольнике ABC основание AC равно 32, площадь треугольника равна 192. Найдите длину боковой стороны AB. | Смотреть видеоразбор >> |
| 36 | В параллелограмме ABCD отмечена точка M — середина стороны BC. Отрезки BD и AM пересекаются в точке K. Найдите длину отрезка BK, если BD=15. | Смотреть видеоразбор >> |
| 37 | В прямоугольной трапеции основания равны 3 и 5, а один из углов равен 135°. Найдите меньшую боковую сторону. | Смотреть видеоразбор >> |
| 38 | В выпуклом четырёхугольнике ABCD известно, что AB=BC, AD=CD, \angleB=61°, \angleD=151°.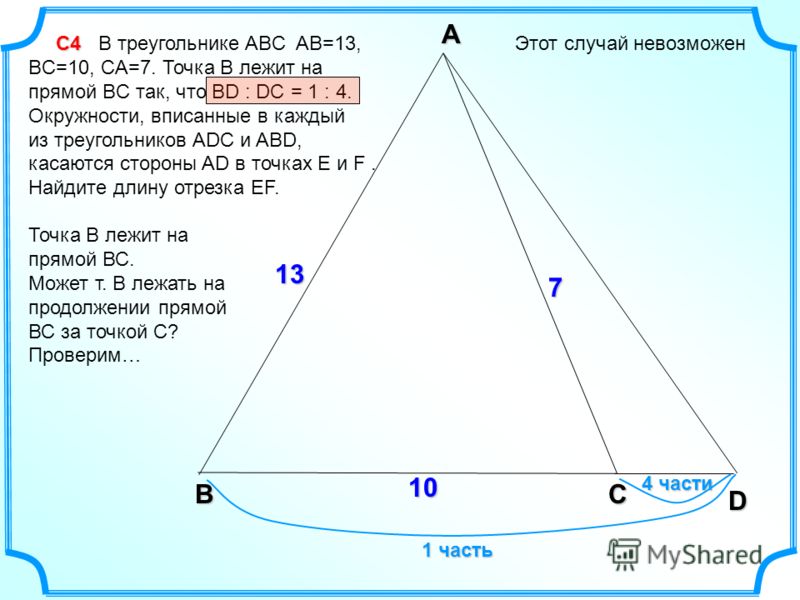 Найдите угол A. Ответ дайте в градусах. Найдите угол A. Ответ дайте в градусах. | Смотреть видеоразбор >> |
| 39 | На окружности радиуса 5 отмечена точка C. Отрезок AB — диаметр окружности, AC=6. Найдите cos\angleBAC. | Смотреть видеоразбор >> |
| 40 | Найдите вписанный угол, опирающийся на дугу, длина которой равна 1/5 длины окружности. Ответ дайте в градусах. | Смотреть видеоразбор >> |
Q3 Нарисуйте любой отрезок, скажем, AB Возьмите любую точку C, лежащую между A и B Измерьте длины AB …
Перейти к
- Упражнение 5.1
- Упражнение 5.2
- Упражнение 5.3
- Упражнение 5.
 4
4 - Упражнение 5.5
- Упражнение 5.6
- Упражнение 5.7
- Упражнение 5.8
- Упражнение 5.9
- Зная наши цифры
- Игра с числами
- Основные геометрические идеи
- Понимание элементарных форм
- Фракции
- Десятичные
- Обработка данных
- Алгебра
- Соотношение и пропорция
- Симметрия
- Практическая геометрия
Главная >
Решения НЦЭРТ
Класс 6
Математика
>
Глава 5. Понимание элементарных форм
>
Упражнение 5.1
>
Вопрос 7
Понимание элементарных форм
>
Упражнение 5.1
>
Вопрос 7
Вопрос 7 Упражнение 5.1
Q3) Нарисуйте любой отрезок, скажем, AB. Возьмите любую точку C, лежащую между A и B.
Измерьте длины AB, BC и AC. АВ = АС + СВ?
Ответ:
РЕШЕНИЕ:
Пусть отрезок AB длиной 6 см и точка C лежит между A и B.
Об измерении длины отрезка.
AB, AC и CB с помощью линейки находим, что AB=6см, AC=4см CB=2см
теперь, AC+CB=4+2CM=6CM=AB
AC+CB=AB
так , можно сказать, что C лежит между A и B.
Стенограмма видео
Здравствуйте, студенты. Добро пожаловать в повтор обучающего видео с вопросами и ответами. Итак, здесь нас просят привести два примера вещества, которое может расширяться при нагревании. Итак, перед этим мы должны знать, что мы подразумеваем под этим? Они говорят о процедуре, называемой тепловым расширением.

Связанные вопросы
Q2) Почему при измерении длины отрезка лучше использовать делитель, а не линейку?
В4) Если А, В, С — три точки на прямой, такие что АВ = 5 см, ВС = 3 см и АС = 8 см, какая из них…
Q5) Проверьте, является ли D средней точкой AG.
Q6) Если B — середина AC, а C — середина BD, где A, B, C, D лежат на прямой…
Q7) Нарисуйте пять треугольников и измерьте их стороны. Проверяем в каждом случае, если сумма длин любых…
Q1) В чем недостаток сравнения отрезков путем простого наблюдения?
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнение
Упражнение 5. 1
1
Упражнение 5.2
Упражнение 5.3
Упражнение 5.4
Упражнение 5.5
Упражнение 5.6
Упражнение 5.7
Упражнение 5.8
Упражнение 5.9
Главы
Знакомство с числами
Целые числа
Целые числа
Дроби
Десятичные числа
Данные Обработка
Измерение
Алгебра
Отношение и пропорция
Симметрия
Практическая геометрия
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены , и вам нужно найти точку на отрезке 13 пути из P в Q.
Давайте сначала рассмотрим простой случай, когда P находится в начале координат, а отрезок прямой — горизонтальный.
Длина прямой составляет 6 единиц, и точка на отрезке 13 пути от P до Q будет на расстоянии 2 единиц от P и 4 единиц от Q и будет в (2,0).
Рассмотрим случай, когда отрезок не является горизонтальной или вертикальной линией.
Компоненты направленного отрезка PQ¯ равны 〈6,3〉 и нам нужно найти точку, скажем, X на отрезке 13 пути из P в Q.
Тогда компоненты отрезка PX ¯ суть 〈(13)(6),(13)(3)〉=〈2,1〉.
Поскольку начальная точка сегмента находится в начале координат, координаты точки X задаются как (0+2,0+1)=(2,1).
Теперь давайте решим более сложную задачу, где ни P, ни Q не находятся в начале координат.
Используйте конечные точки отрезка PQ¯ для записи компонентов направленного отрезка.
〈(x2−x1),(y2−y1)〉=〈(7−1),(2−6)〉 =〈6,−4〉
Теперь аналогичным образом компоненты отрезка PX ¯ где X — точка на отрезке 13 пути из P в Qare 〈(13)(6),(13)(−4)〉=〈2,−1,25〉.
Чтобы найти координаты точки X, прибавьте компоненты отрезка PX¯ к координатам начальной точки P.
Итак, координаты точки X равны (1+2,6−1,25)=(3 ,4.75).
Обратите внимание, что получившиеся сегменты PX¯ и XQ¯ имеют длины в соотношении 1:2.
В общем: что если вам нужно найти точку на отрезке, которая делит его на два отрезка с длинами в отношении a:b?
Рассмотрим направленный отрезок XY¯ с координатами концов как X(x1,y1) и Y(x2,y2).
Предположим, что точка Z разделила отрезок в отношении a:b, тогда точка aa+b пути из X в Y.
Итак, обобщая полученный нами метод, компоненты отрезка XZ¯ равны (аа+b(x2−x1)),(аа+b(y2−y1))〉.
Тогда координата X точки Z равна
=bx1+ax2a+b.
Аналогично, координата Y равна
=by1+ay2a+b.
Следовательно, координаты точки Z равны (bx1+ax2a+b,by1+ay2a+b).
Пример 1:
Найдите координаты точки, которая делит направленный отрезок MN¯ с координатами концов в точках M(−4,0) и M(0,4) в соотношении 3:1?
Пусть L — точка, которая делит MN¯ в отношении 3:1.
Здесь (x1,y1)=(−4,0),(x2,y2)=(0,4) и a:b=3:1.
Подставить в формулу. Координаты L равны
(1(−4)+3(0)3+1,1(0)+3(4)3+1).

 4
4
Leave A Comment