Проверка опытом законов падения . О движении [Из истории механики]
Как же можно было проверить законы Галилея на опыте? Нельзя же заметить, какое расстояние пролетает свободно падающее тело в первую, вторую, третью и так далее секунду. С большим трудом, и не очень точно, можно было, пожалуй, лишь установить время, в течение которого падающее тело проходит расстояние от вершины башни до земли.
Галилей избрал, однако, другой путь для проверки теоретически найденных им законов. Он прибег к помощи наклонной плоскости.
Шарик скатывается по наклонной плоскости под действием силы тяжести. Значит, свободное скатывание шарика по наклонной плоскости должно происходить по тем же законам, как и свободное падение. Скорость же скатывания можно сколько угодно уменьшить, изменяя угол наклона плоскости.
Пуская шарик по наклонной плоскости, можно было измерить время, необходимое шарику, чтобы скатиться до ее основания. Длина наклонной плоскости известна. Значит, можно было вычислить, каково ускорение скатывания по наклонной плоскости.
Значит, можно было вычислить, каково ускорение скатывания по наклонной плоскости.
Для опытов Галилей взял доску длиной двенадцать локтей, конец которой был приподнят только на один-два локтя. Посередине доски был простроган узкий желоб, выстланный очень гладким пергаментом для уменьшения трения. По желобу скатывались бронзовые шарики, пускавшиеся Галилеем. Время измерялось водяными часами, то-есть по количеству воды, успевавшей вытечь из верхнего сосуда в нижний.
Сперва шарик был пущен с верхнего конца желоба. Когда он докатился вниз, Галилей заметил по водяным часам, сколько понадобилось ему на это времени.
По закону, выведенному теоретически Галилеем, расстояние, пройденное свободно падающим телом, увеличивается пропорционально квадрату времени. Следовательно, в четыре раза более короткий путь шарик должен пройти во вдвое более короткий промежуток времени. Пустив шарик с верхнего конца четвертой части длины желоба, Галилей убедился, что для этого расстояния шарику действительно понадобилось только вдвое меньше времени.
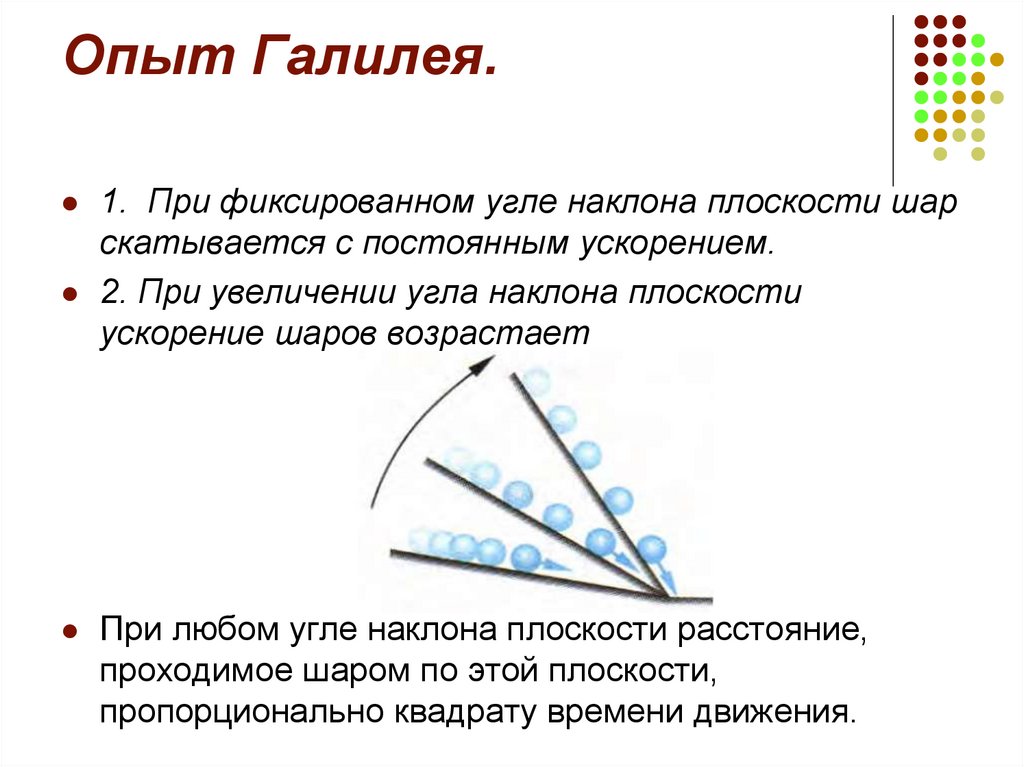
Опыт Галилея со скатыванием шариков по наклонной плоскости.
Так было доказано, что скатывание по наклонной плоскости подчиняется закону, выведенному для свободного падения. Значит, предположение Галилея, что ускорение свободного падения постоянно, справедливо.
Пользуясь наклонной плоскостью, можно было определить ускорение скатывания по ней. Для этого достаточно только заметить время, в течение которого шарик проходит всю ее длину.
Галилей хотел из этого опыта определить ускорение свободного падения. Он не знал, что вращение шарика очень усложняет эту задачу, которая могла быть решена таким путем только после открытия законов вращения тел.
Вот если бы можно было осуществить опыт скольжения тела без трения по наклонной плоскости, то такая задача не представила бы затруднений.
Допустим, что тело, скользящее по наклонной плоскости, прошло длину ее

Из закона наклонной плоскости следует, что сила, действующая вдоль нее, во столько раз меньше силы тяжести, во сколько высота ее меньше длины. Поэтому ускорение свободного падения легко было бы определить, зная ускорение скользящего тела.
Галилей изучал движение падающего тела кинематически, то-есть только с геометрической стороны. Он не принимал во внимание силы тяжести, сообщающей телам движение. Самое понятие о силе еще было неясным. Галилей часто называл причину, вызывающую движение, «импульсом» — слово, обозначающее в современной механике произведение силы на время (равное количеству движения). Но открытие кинематических законов движения падающих тел все-таки позволило Галилею решать практические задачи техники, например баллистики — науки о движении пушечных ядер.
Привет! Какой путь он пройдет шарик? № 61. ГДЗ Физика 10 класс Рымкевич.
 – Рамблер/класс Привет! Какой путь он пройдет шарик? № 61. ГДЗ Физика 10 класс Рымкевич. – Рамблер/класс
– Рамблер/класс Привет! Какой путь он пройдет шарик? № 61. ГДЗ Физика 10 класс Рымкевич. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Шарик, скатываясь с наклонного желоба из состояния покоя, за первую секунду прошел путь 10 см.
ответы
При равноускоренном движении
s = v0t + at2/2,
где v0 = 0.
Пусть за первую секунду
откуда
а = 20 см/с2 = 0,2 м/с2.
За три секунды шарик пройдет путь
Ответ: s2 = 0,9 м = 90 см.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Досуг
Химия
похожие вопросы 5
ГДЗ по Физике Громов 10 класс, вопросы. Гл.4§22№4. . На чем основа- на гравиметрическая разведка?
Помогите ответить на вопрос Гл.4§22№4.
На чем основана гравиметрическая разведка?
ГДЗ10 классГромов С.В.Физика
ГДЗ.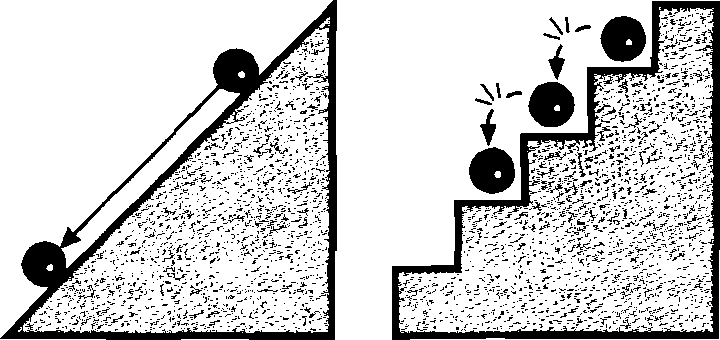 Физика 11. класс.Рымкевич.Глава 10.Электрический ток в различных средах..Задание 859.Найти приблизительно температуру накала вольфрамовой нити.
Физика 11. класс.Рымкевич.Глава 10.Электрический ток в различных средах..Задание 859.Найти приблизительно температуру накала вольфрамовой нити.
Решите пожалуйста:
100 Вт. Для измерения сопротивления нити накала (Подробнее…)
ГДЗФизика11 классРымкевич А.П.
ГДЗ по Физике 10 класс Громов, вопросы. Гл.5§31№1. Чему равна полная механическая энергия?
Как ответить на вопрос Гл.5§31№1.
Чему равна полная механическая энергия?
ГДЗФизика10 классГромов С.В.
Выполните деление. ГДЗ Математика 6 класс Чесноков. Дидактические материалы по математике для 6 класса. Вар.1 Вопр.161
Кто сможет? Выполните деление:
(Подробнее…)
ГДЗМатематика6 классЧесноков А.С.
ГДЗ. Математика. Базовый уровень ЕГЭ — 2017. Вар.№45. Зад.№1.Под руководством Ященко. Помогите найти значение выражения.
Здравствуйте! Помогите найти значение выражения: (Подробнее. ..)
..)
ГДЗЭкзаменыМатематикаЯщенко И.В.
Мяч катится по наклонной плоскости
Эта демонстрация показывает постоянное ускорение под действием силы тяжести, воспроизводя знаменитый эксперимент Галилея. Его также можно использовать в динамике вращения [для обсуждения динамики вращения нажмите здесь], чтобы показать и рассчитать момент инерции, угловую скорость, угловое ускорение и угловой момент.
Эту демонстрацию также можно использовать, чтобы показать коэффициенты статического трения различных материалов и то, как сила, действующая на объект, будет увеличиваться по мере увеличения угла поверхности, на которой он лежит.
Список деталей:
- Деревянная рампа, окрашенная в черный цвет
- Лабораторный домкрат
- Два мешка с песком
- Стальной шарик диаметром 50,8 мм, масса 534,6 г
- Два секундомера
Дополнительно (для отображения угла плоскости и связанных с ним эффектов трения)
- Гигантский транспортир
- 2 небольших зажима для крепления транспортира к уклону
- Пухлый боб/нитка (тонкая леска и грузик 20 г, можно найти в механике классной доски)
Объяснение:
Постоянное ускорение:
Чтобы продемонстрировать постоянное ускорение в этой демонстрации, полезно отметить расстояния на пандусе, а затем попросить учащихся определить, сколько времени требуется мячу, чтобы катиться между отметками. Они могут использовать время, которое требуется мячу, чтобы катиться между отметками, и исходя из этого вычислить ускорение в разных точках на рампе, что должно дать один и тот же результат (это означает, что ускорение не меняется во времени).
Они могут использовать время, которое требуется мячу, чтобы катиться между отметками, и исходя из этого вычислить ускорение в разных точках на рампе, что должно дать один и тот же результат (это означает, что ускорение не меняется во времени).
Для расчета ускорения мяча можно использовать уравнение a = (V 1 – V 2 )/t *. Вам нужно будет провести восемь различных измерений времени и рассчитать четыре скорости и два ускорения. Затем вы можете сравнить рассчитанные вами ускорения, чтобы увидеть, остается ли ускорение на рампе постоянным (что и должно быть). Для этого вам нужно отметить восемь равномерно расположенных меток на рампе и отметить время, когда мяч пересекает каждую метку (изображение того, как должна выглядеть рампа ниже)
Как должна выглядеть рампа, если она отмечена для демонстрации постоянного ускорения, где изменение x должно быть одинаковым на всех четырех расстояниях.
Вы можете рассчитать Δt для каждого из четырех сегментов рампы по уравнению: 47 3
И аналогично для Δt 3 и Δt 4
Δx — расстояние между отмеченными точками. Вы не хотите, чтобы они были слишком длинными, потому что вы хотите оставить время для ускорения мяча между тем, где вы рассчитываете скорости, поэтому они должны быть между 10 и 15 см каждая. Расстояние между наборами отметок не влияет на окончательные расчеты.
Вы не хотите, чтобы они были слишком длинными, потому что вы хотите оставить время для ускорения мяча между тем, где вы рассчитываете скорости, поэтому они должны быть между 10 и 15 см каждая. Расстояние между наборами отметок не влияет на окончательные расчеты.
Поскольку мы знаем, что V = Δt/Δx, мы можем вычислить скорости на каждом расстоянии Δx. Это даст V 1 , V 2 , V 3 , V 4 , которые мы можем использовать, чтобы найти два ускорения: 1 и 2 . для нахождения ускорений используем уравнение:
a 1 = (V 1 – V 2 )/ t
, где t 47 1 , 2 т 4 и т 8 соответственно.
Из этих вычислений мы должны найти, что 1 и 2 равны (или почти равны).
Трение:
Эта демонстрация также может быть использована для демонстрации относительных коэффициентов статического трения различных материалов по дереву. Эта демонстрация похожа на демонстрацию статического и кинетического трения, но вместо изменения веса, необходимого для перемещения блока, мы можем изменить угол плоскости. В то время как сила тяжести, действующая на блок, не меняется в зависимости от угла наклона доски, более крутой наклон дает большую составляющую силы, толкающую блок вниз по пандусу. Это видно на изображениях ниже:
Эта демонстрация похожа на демонстрацию статического и кинетического трения, но вместо изменения веса, необходимого для перемещения блока, мы можем изменить угол плоскости. В то время как сила тяжести, действующая на блок, не меняется в зависимости от угла наклона доски, более крутой наклон дает большую составляющую силы, толкающую блок вниз по пандусу. Это видно на изображениях ниже:
Как видно выше, рампа с большим θ (угол наклона) будет иметь большую составляющую вектора силы, толкающую ее вниз по рампе (F 2 ), и меньшую составляющую вектора силы, толкающую ее непосредственно в пандус (F 1 ). Поскольку существует большая сила, тянущая блок вниз по плоскости, более крутой уклон приведет к тому, что блок начнет опускаться, когда он может не иметь более пологого уклона. Здесь важно отметить, что угол наклонной плоскости будет таким же, как угол между силой тяжести и силой, перпендикулярной плоскости. Именно под этим углом мы измеряем составляющие силы, F 1 и F 2 .
Коэффициент статического трения (μ) блока о рампу изменит величину силы (F 2 ), необходимой для начала скольжения блока. Большее μ потребует большей силы (и, следовательно, более крутого наклона), чтобы начать движение, чем меньшее μ. [Для более подробного обсуждения того, как коэффициент трения изменяет силу, необходимую для начала движения объекта, см. демонстрацию статического и кинетического трения здесь.]
Большую силу, действующую на блок, можно создать, увеличив угол (θ) рампы. Это связано с тем, что sin(θ) [когда он находится между значениями 0 и (π/2)] будет увеличиваться с увеличением θ. Таким образом, мы можем легко видеть, что
Если θ 1 > θ 2 , то
F g sinθ 1 > F g sinθ 2 F
As 900 8 увеличивается с увеличением θ, это позволит блокировать с большими коэффициентами статического трения, чтобы начать скользить вниз.
Примечания:
- Сделайте разницу в высоте примерно 10 см между концами пандуса.

- Рекомендуется, чтобы два ученика измерили время в пути между отметками на рампе, чтобы рассчитать ускорение.
*Это потребует времени и координации, поэтому может оказаться невозможным на большом вводном уроке физики, но может хорошо подойти для практической демонстрации в местной старшей или средней школе.
Автор Sophia Sholtz
Ньютоновская механика — Силы, возникающие при скатывании мяча по наклонной плоскости
спросил
Изменено 6 лет, 3 месяца назад
Просмотрено 1к раз
$\begingroup$
Прошу прощения, если это кажется тривиальным, но у меня возникли проблемы с пониманием решения следующей задачи:
Во-первых, существует нормальная сила, с которой плоскость действует на мяч, и составляющая веса мяча то есть параллельно плоскости. Но разве трение не действует и в направлении качения шарика? Поскольку мяч катится/вращается в направлении, противоположном его общему движению, разве трение на самом деле не помогает мячу двигаться вниз по склону? Вот что я подумал и понял, что общая сила, параллельная наклону, равна силе трения плюс параллельная составляющая веса мяча. Так не должен ли правильный ответ на вопрос быть вниз и вправо?
Но разве трение не действует и в направлении качения шарика? Поскольку мяч катится/вращается в направлении, противоположном его общему движению, разве трение на самом деле не помогает мячу двигаться вниз по склону? Вот что я подумал и понял, что общая сила, параллельная наклону, равна силе трения плюс параллельная составляющая веса мяча. Так не должен ли правильный ответ на вопрос быть вниз и вправо?
Спасибо
- ньютоновская механика
- вращение
$\endgroup$
1
$\begingroup$
Вопрос ограничивает наше рассмотрение силой, действующей на плоскость на шар. У этой силы есть только две составляющие: (1) нормальная сила, действующая на плоскость со стороны шара, перпендикулярного поверхности плоскости, и (2) сила трения, действующая на плоскость со стороны шарика, направленного вниз параллельно плоскости.


Leave A Comment