Изобразите пройденный путь за время t на графике скорости: Изобразите № 1470 ГДЗ Физика 7-9 класс Перышкин А.В. – Рамблер/класс

Изобразите № 1470 ГДЗ Физика 7-9 класс Перышкин А.В. – Рамблер/класс

Изобразите № 1470 ГДЗ Физика 7-9 класс Перышкин А.В. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Изобразите пройденный путь за время t на гра­фике скорости равнозамедленного движения.

Принять υ0=10 м/с, а  = 2 м/с².

ответы

Изобразила:

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Досуг

Химия

похожие вопросы 5

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?

Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло. В обоих (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости.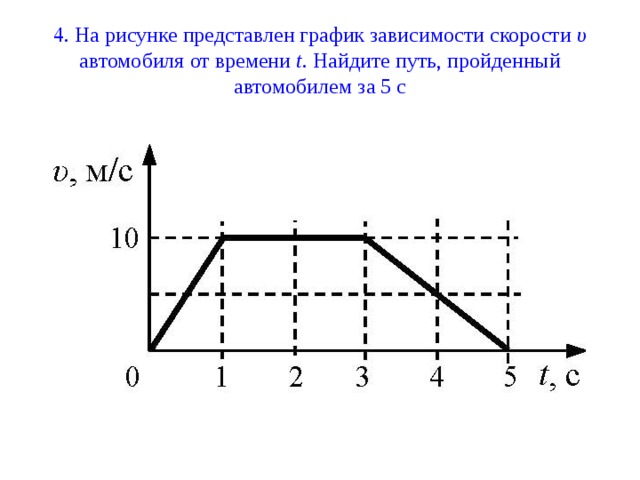 (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Ребята нужны ответы на пересдачу по математике 9 класс 11 регион. Срочно!

ГИА9 класс

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 12. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

§6. Примеры движения тела. Методы решения задач. — ЗФТШ, МФТИ

Рассмотрим некоторые характерные примеры движения тела, знание которых будет полезно при дальнейшем изучении физики.

1.Равномерное прямолинейное движение тела.

При равномерном прямолинейном движении тело совершает равные перемещения `Delta vecr`  за одинаковые промежутки времени  `Delta t`. Иными словами, скорость  `vec v` тела не зависит от времени и остаётся постоянной в процессе движения:

При этом зависимость `vec r(t)` имеет вид:

где  `vec r_0`  —  радиус-вектор тела в начальный момент времени  $$ t=0$$ . В этой связи вспомним замечание о начальных условиях,

сделанное в §4.  Вектор  $$ {\overrightarrow{r}}_{0}$$  здесь является тем начальным условием, которое позволяет однозначно определить радиус-вектор $$ \overrightarrow{r}$$ тела в любой момент времени в процессе движения.

Векторное уравнение (7) равносильно системе двух скалярных уравнений, выражающих зависимость от времени $$ t $$ координат $$ x$$ и $$ y$$ движущегося тела:

где $$ {x}_{0}$$ и $$ {y}_{0}$$ — начальные координаты тела в момент времени $$ t=0$$, а $$ {v}_{x}$$ и $$ {v}_{y}$$ -проекции вектора скорости `vecv` на координатные оси $$ Ox$$ и $$ Oy$$ соответственно.

 

Траектория равномерного прямолинейного движения тела графически представляет собой отрезок прямой линии (рис. 9), тангенс угла наклона которой к оси абсцисс равен отношению проекций скорости на оси координат: $$ \mathrm{tg}\alpha ={v}_{y}/{v}_{x}$$. Аналитическое уравнение траектории, т. е. зависимость $$ y\left(x\right)$$, легко получить, исключив параметр $$ t$$ из системы уравнений (8):

2. Неравномерное движение тела.

Для неравномерного движения характерно то, что с течением времени изменяется скорость движущегося тела, а в общем случае и его ускорение. В качестве примера может служить движение, при котором тело проходит различные участки своего пути с разной скоростью. Такое движение принято характеризовать, прежде всего, средней путевой скоростью. Причём прилагательное «путевая» в условиях задач часто опускается.

Другим характерным примером неравномерного движения служит так называемое равнопеременное движение, которое целесообразно рассмотреть подробно, не выходя при этом за рамки школьной программы.

3. Равнопеременное движение.

Равнопеременным называется такое неравномерное движение, при котором скорость

`vec v` за любые равные промежутки   времени   `Delta t`  изменяется  на  одинаковую  величину   `Deltavecv`. В этом случае ускорение `veca` тела не зависит от времени и остаётся постоянным в процессе движения:

(при этом `vec v != «const»`, и траектория движения не обязательно прямолинейная).
При равнопеременном движении скорость $$ \overrightarrow{v}$$ тела изменяется с течением времени по закону

где `vecv_0` — скорость тела в начальный момент времени `t=0`.
В свою очередь, зависимость `vecr(t)` имеет вид:

где `vecr_0` — начальный радиус-вектор тела при `t=0`. Вновь заметим, что величины `vecv_0` и `vecr_0` представляют собой начальные условия, позволяющие в любой момент времени однозначно определить векторы `vecv` и `vecr`.

При координатном способе описания равнопеременного движения векторным уравнениям (11) и (12), равносильны следующие системы уравнений для проекций скорости и радиус-вектора тела на оси выбранной системы отсчёта. 2)/(2a_x)`.

Удобство этой формулы заключается в том, что она не содержит времени $$ t$$ в явном виде. Вместе с тем надо помнить, что формула получена в предположении о неизменности направления движения тела.

Одним из наиболее наглядных примеров равнопеременного движения является движение тела в поле тяжести Земли, которое мы имеем возможность наблюдать повседневно. Для решения задач в этом случае надо заменить в приведённых выше формулах вектор $$ \overrightarrow{a}$$ на ускорение свободного падения $$ \overrightarrow{g}$$, сообщаемое силой гравитационного притяжения всякому телу, движущемуся в поле тяжести Земли. Рассмотрим три конкретных случая такого движения.

Движение тела, брошенного вертикально.
Тело бросили с поверхности земли, сообщив ему начальную скорость $$ {\overrightarrow{v}}_{0}$$ направленную вертикально вверх. Пренебрегая сопротивлением воздуха, определите время $$ \tau $$ полёта тела до момента падения на землю; скорость тела в момент падения; максимальную высоту $$ H$$ подъёма тела над землёй; время $$ {\tau }_{1}$$ подъёма тела на максимальную высоту; путь `S`, пройденный телом за время полёта и перемещение тела.

{2}+\mathrm{tg}\alpha x$$. 

График траектории тела представляетсобой участок параболы, ветви которой направлены вниз.

 

Счет, математика и статистика — Комплект академических навыков

Графики скорость-время и расстояние-время (механика)

Главное меню ContentsToggle 1 Графики скорость-время 2 Рабочий пример: Графики скорость-время и графики ускорение-время 3 Проверьте себя

Графики скорость-время

На графике скорость-время скорость всегда откладывается по вертикальной оси, а время всегда откладывается по горизонтальной. Это представляет собой движение частицы, ускоряющейся от скорости в момент времени $0$, $u$, до скорости $v$ в момент времени $t$.

Градиент линии графика скорость-время есть ускорение частицы (для прямых ускорение постоянно). \begin{align} \text{Градиент линии} & = \frac{\text{изменение скорости} }{\text{время}}, \\ & = \frac{v — u}{t}, \\ &= а.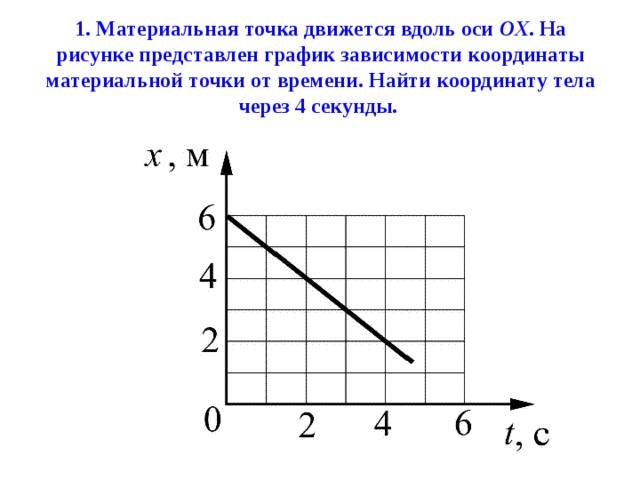 \end{align} Площадь под графиком скорость-время — это расстояние, которое проходит частица. \begin{align} \text{Заштрихованная область} & = \left( \frac{u + v}{2} \right)t, \\ & = s. \end{выравнивание}

Графики «расстояние-время» и Графики «ускорение-время»

также могут быть построены для движения частицы, где время всегда откладывается по горизонтальной оси.

Прямая линия на графике расстояние-время показывает, что частица имеет постоянную скорость . Кривизна предполагает, что частица ускоряется или замедляется .

Рабочий пример: графики скорость-время и ускорение-время

Пример с автомобилем на прямой дороге 9{-1} }$ за $2T \mathrm{seconds}$. Затем он движется с постоянной скоростью в течение $1 \mathrm{минуты}$. Затем автомобиль равномерно замедляется до состояния покоя еще за $8T \mathrm{seconds}$. Нарисуйте график зависимости скорости от времени, иллюстрирующий движение автомобиля.

{-2} }. \end{align} Здесь за последние 32 секунды координата $v$ уменьшается на 10, а координата $t$ увеличивается на 32. Это дает отрицательный ответ.

Проверь себя

Попробуйте наш тест Numbas на Линейное измерение — расстояние и длина.

Попробуйте наш тест Numbas на скорость.

Пояснение к уроку: расчет скорости по графикам расстояние-время

В этом пояснении мы научимся определять скорость по графики расстояние-время.

Напомним, что на графике расстояние-время линия, проходящая через набор точек нанесенный на график представляет собой скорость.

На следующем рисунке показана диаграмма расстояние-время. На графике показаны две линии.

Мы видим, что пунктирная линия представляет большую скорость, чем пунктирная.

Для пунктирной линии произошло большее изменение расстояния, чем для синей линия. Обе строки начинаются с одного и того же значения времени и заканчиваются в одно и то же время.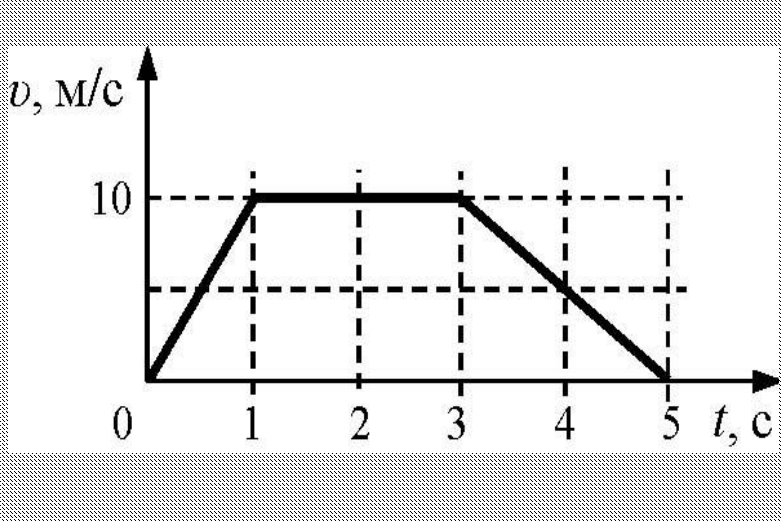 ценить.

На оси расстояния или времени графика не отображаются числа. Это значит, что нет способа узнать, какое значение скорости для любой линии. Мы можем только сказать что скорость пунктирной линии должна быть больше скорости синей линии.

Теперь рассмотрим график расстояние-время с числами на осях. Мы называем это масштабированным графиком. Пример показан на следующем рисунке.

Поскольку график масштабируется, теперь можно подсчитывать пройденное расстояние и время принято преодолевать эти расстояния.

Сначала рассмотрим пунктирную линию.

Пунктирная линия имеет начальную и конечную точки. Они показаны в следующий рисунок.

Во-первых, давайте рассмотрим, что начальная и конечная точки показывают нам о пройденный путь.

Начальная и конечная точки соответствуют числам на оси расстояния график. Это показано на следующем рисунке.

Мы видим, что начальная точка соответствует расстоянию 0 метров и конечная точка соответствует расстоянию 5 метров.

Мы называем 0 метров начальное расстояние и называем 5 метров конечная дистанция.

Теперь мы сравним конечное расстояние и начальное расстояние, чтобы увидеть, насколько меняется дистанция. Это показано на следующем рисунке.

Мы видим, что конечное расстояние равно на 5 метров больше, чем начальное расстояние. Изменение расстояния равно 5 метров.

Мы можем записать это как Δ𝑑=5−0=5, ммм где Δ𝑑 — изменение расстояния.

Чтобы узнать скорость, мы должны также знать время, за которое изменился на 5 метров.

Давайте снова посмотрим на начальную и конечную точки линии, показанные на следующий рисунок.

То, что мы только что сделали для изменения расстояния, мы можем сделать и для изменения времени. Это показать на следующем рисунке.

Из начального и конечного времени мы можем найти изменение во времени. Это показано на следующем рисунке.

Мы видим, что последнее время 5 секунд больше, чем начальное время.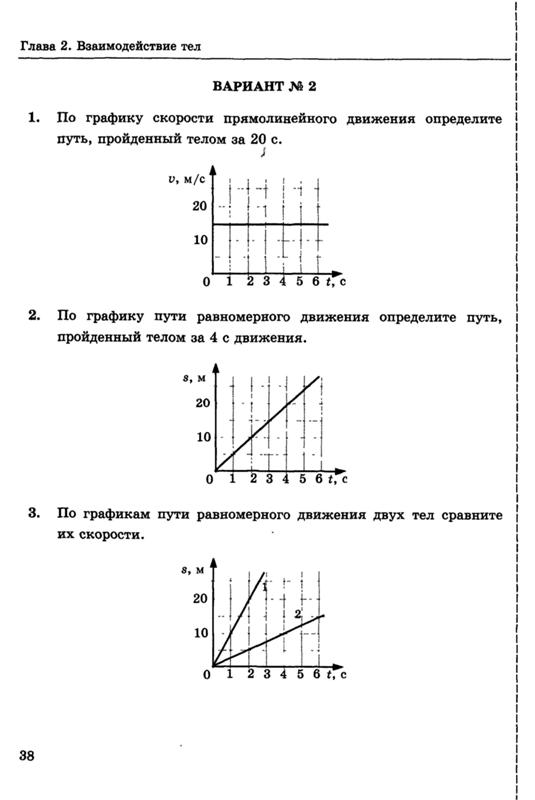 Изменение во времени есть 5 секунд.

Мы можем записать это как Δ𝑡=5−0=5,сс где Δ𝑡 — изменение во времени.

Теперь у нас есть вся информация, необходимая для определения значения скорости. представлен пунктирной линией.

Мы можем вспомнить, что средняя скорость объекта, 𝑣, определяется формулой 𝑣=Δ𝑑Δ𝑡.

Мы только что нашли значения Δ𝑑 и Δ𝑡 для пунктирной линии. Используя эти значения, мы находим, что 𝑣=55.ms

Мы видим, что 55=1.

Значение скорости равно 1.

Также необходимо определить единицу измерения скорости. Единицей скорости является единицы =.

Единица измерения м/с. На словах это записывается как «метры в секунду».

Скорость 1 метр в секунду, или 1 м/с.

Эта скорость показана на следующем рисунке.

Теперь повторим все эти шаги для пунктирной линии. Это показано в следующий рисунок.

Мы видим, что Δ𝑑=1−0=1ммм и что Δ𝑡=5−0=5. sss

Мы можем использовать формулу 𝑣=Δ𝑑Δ𝑡 с этими значениями. Это дает нам 𝑣=15 𝑣=0,2/.msms

Эта скорость показана на следующем рисунке.

Мы видим, что значение скорости пунктирной линии меньше, чем пунктирной линии. Это показано на следующем рисунке.

Изменение расстояния, деленное на изменение времени для расстояния-времени график является градиентом графика.

Это означает, что градиент графика расстояние-время равен скорости объект, движение которого представлено линией, показывающей изменение расстояние со временем.

Теперь потренируемся на нескольких примерах определения скорости с помощью расстояния-времени. графики.

Пример 1. Определение расстояния, пройденного с постоянной скоростью, с помощью График расстояние-время

На графике расстояние-время показан объект, движущийся с постоянной скоростью.

1. На какое расстояние перемещается объект между 0 секунд и 1 секунда?
2. На какое расстояние перемещается объект между 4 секунды и 5 секунд?

Ответ

Часть 1

В момент времени 0 секунд, пройденное расстояние равно 0 метров.

За 1 секунду пройденное расстояние равно 1 метр.

Расстояние, пройденное между 0 секунд и 1 секунда дается Δ𝑑=1−0,мм

Расстояние изменяется на 1 метр.

Часть 2

Во время 4 секунды, пройденное расстояние равно 4 метра.

Во время 5 секунд, пройденное расстояние равно 5 метров.

Расстояние, пройденное между 4 секунды и 5 секунд дан кем-то Δ𝑑=5−4,мм

Расстояние изменяется на 1 метр.

Это такое же изменение расстояния, как между 0 секунд и 1 секунда. Следует ожидать равных изменений во времени. Изменение во времени между 4 секунды и 5 секунд равно изменению времени между 0 секунд и 1 секунда. В каждом случае время увеличивается на 1 секунда.

Объект имеет постоянную скорость и поэтому должен иметь одинаковые изменения расстояния при одинаковых изменениях во времени на всем протяжении его движения.

В объяснениях, приведенных в эксплейнере, график разбит на квадраты.

Вертикальная длина квадрата представляет собой изменение расстояния 1 метр.

Горизонтальная длина квадрата представляет изменение во времени 1 секунда.

Это не обязательно значения, используемые для масштабирования осей график расстояние-время.

Теперь рассмотрим пример, где масштаб по осям графика не 1 метр на квадрат на оси расстояний ни 1 секунда на квадрат на оси времени.

Пример 2. Определение скорости с помощью графика «расстояние-время»

График «расстояние-время» показывает объект, движущийся с постоянной скоростью. Какова скорость объекта?

Ответ

Скорость объекта находится путем деления пути, пройденного объектом за время, необходимое для перемещения на это расстояние.

Из графика видно, что линия, представляющая скорость, проходит через углы набора квадратов на графике, которые показаны на следующем фигура.

Глядя на ось расстояний, мы видим, что первый квадрат начинается с 0 метров, второй квадрат начинается с 10 метров, третий квадрат начинается с 20 метров, и так далее.

Расстояние увеличивается на по 10 метров на каждого квадрат.

Глядя на ось времени, мы видим, что первый квадрат начинается с 0 секунд, второй квадрат начинается с 10 секунд, третий квадрат начинается с 20 секунд, и так далее.

Время увеличивается на 10 секунд для каждого квадрата.

Это показывает нам, что каждый 10-метровый увеличение расстояния соответствует 10 секунд увеличение во времени.

Скорость объекта определяется как изменение расстояния, деленное на изменение во времени. Это дается скорость = 1010.

Скорость имеет значение и единицу измерения. Значение скорости определяется значениезначение=1010=1.

Единица измерения скорости: единицы =.

Скорость 1 м/с.

Давайте теперь рассмотрим пример, когда изменения расстояния пройденное и пройденное время не одинаково масштабированы по осям график.

Пример 3. Определение скорости с помощью графика «расстояние-время»

На графике «расстояние-время» показано движение объекта с постоянной скоростью. скорость. Какова скорость объекта?

Ответ

Скорость объекта находится путем деления расстояния, пройденного объектом за время, необходимое для перемещения на это расстояние.

Из графика видно, что линия, представляющая скорость, проходит через углы набора квадратов на графике, которые показаны на следующем фигура.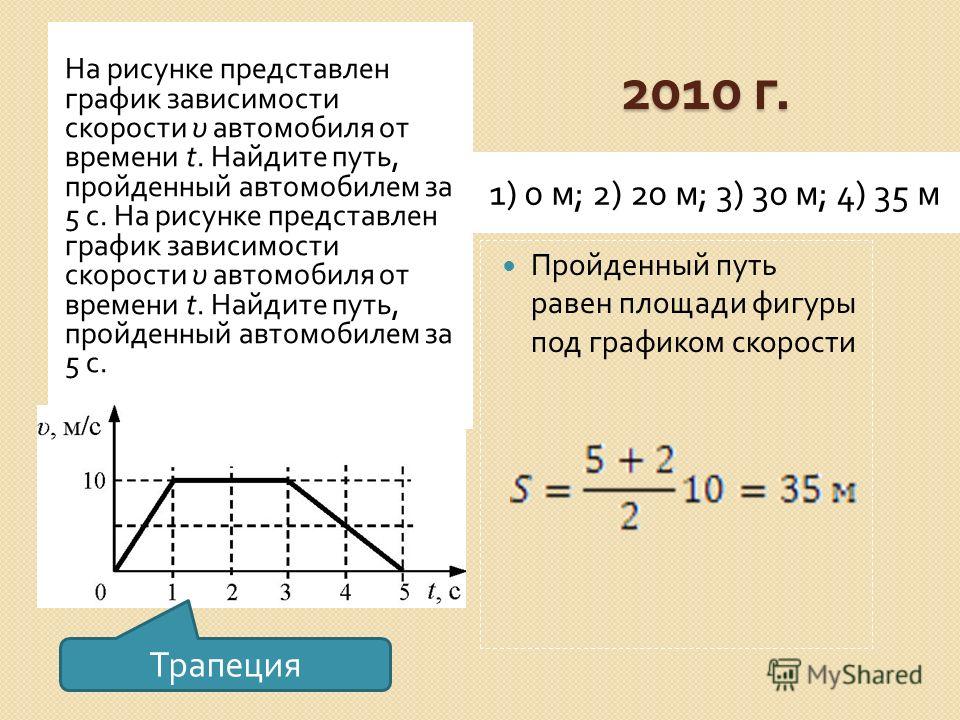

Глядя на ось расстояний, мы видим, что первый квадрат начинается с 0 метров, второй квадрат начинается с 2 метра, третий квадрат начинается с 4 метра, и так далее.

Расстояние увеличивается на 2 метра для каждого квадрата.

Глядя на ось времени, мы видим, что первый квадрат начинается с 0 секунд, второй квадрат начинается с 1 секунда, третий квадрат начинается с 2 секунды, и так далее.

Время увеличивается на 1 секунда для каждого квадрата.

Очень важно понимать, что это означает, что хотя вертикальные стороны квадратов имеют ту же длину, что и горизонтальные стороны квадрата, вертикальная и горизонтальная стороны не представляют изменения такая же величина.

Каждый 2-метровый увеличение расстояния на этом графике соответствует только 1 секунда увеличение во времени.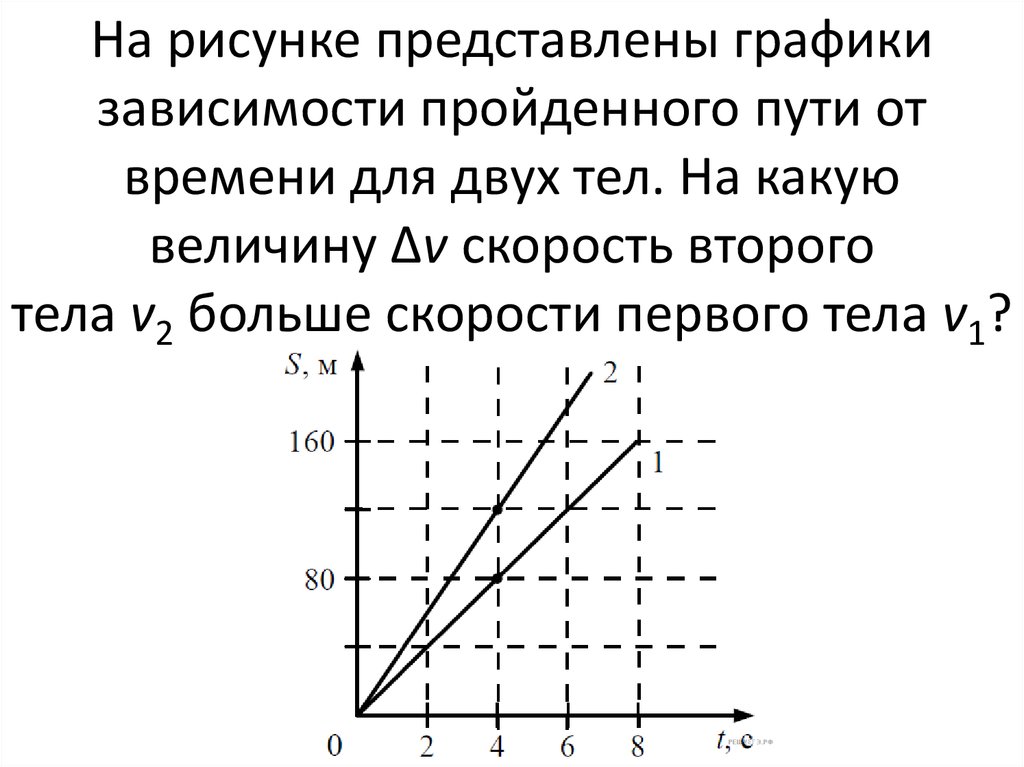

Скорость объекта определяется как изменение расстояния, деленное на изменение во времени. Это дается скорость = 21.

Скорость имеет значение и единицу измерения. Значение скорости определяется значениезначение=21=2.

Единица скорости определяется выражением единицы =.

Скорость 2 м/с.

Давайте теперь рассмотрим пример, где изменения пройденного расстояния и время, пройденное объектом, имеет разные значения.

Пример 4. Определение скорости с помощью графика «расстояние-время»

На графике «расстояние-время» показан объект, движущийся с постоянной скоростью. Какова скорость объекта?

Ответ

Скорость объекта находится путем деления пути, пройденного объектом за время, необходимое для перемещения на это расстояние.

Из графика видно, что линия, представляющая скорость, проходит через углы набора прямоугольников на графике, которые показаны на следующий рисунок.

Глядя на ось расстояний, мы видим, что первый прямоугольник начинается в 0 метров, второй прямоугольник начинается с 2 метра, третий прямоугольник начинается с 4 метра, и так далее.

Расстояние увеличивается на 2 метра для каждого прямоугольника.

Глядя на ось времени, мы видим, что первый прямоугольник начинается в 0 секунд, второй прямоугольник начинается с 1 секунда, и так далее.

Время увеличивается на 1 секунда для каждого прямоугольника.

Это показывает нам, что каждый 2 метра увеличение расстояния соответствует 1 секунда увеличение во времени.

Скорость объекта определяется как изменение расстояния, деленное на изменение во времени. Это дается скорость = 21.

Скорость имеет значение и единицу измерения.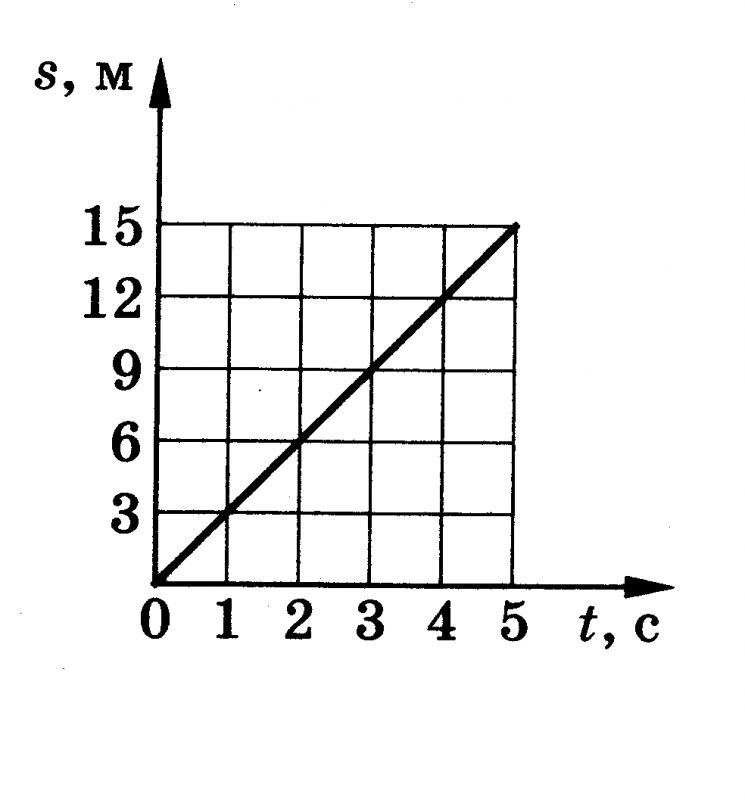 Значение скорости определяется значениезначение=21=2.

Единица скорости определяется выражением единицы =.

Скорость 2 м/с.

Давайте рассмотрим еще один такой пример.

Пример 5. Определение скорости с помощью графика «расстояние-время»

На графике «расстояние-время» показан объект, движущийся с постоянной скоростью. Какова скорость объекта?

Ответ

Скорость объекта находится путем деления пути, пройденного объектом за время, необходимое для перемещения на это расстояние.

Из графика видно, что линия, представляющая скорость, проходит через углы набора прямоугольников на графике, которые показаны на следующий рисунок.

Глядя на ось расстояний, мы видим, что первый прямоугольник начинается в 0 метров, второй прямоугольник начинается с 1 метр, третий прямоугольник начинается с 2 метра, и так далее.

Расстояние увеличивается на 1 метр для каждого прямоугольника.

Глядя на ось времени, мы видим, что первый прямоугольник начинается в 0 секунд, второй прямоугольник начинается с 2 секунды, и так далее.

Время увеличивается на 2 секунды для каждого прямоугольника.

Это показывает нам, что каждый 1 метр увеличение расстояния соответствует 2 секунды увеличение во времени.

Скорость объекта определяется как изменение расстояния, деленное на изменение во времени. Это дается скорость=12.

Скорость имеет значение и единицу измерения. Значение скорости определяется значениезначение=12=0,5.

Единица скорости определяется выражением единицы =.

Скорость 0,5 м/с.

Давайте теперь обобщим то, что было изучено в этом объяснителе.