Помогите пожалуйста!!1.шарик движется под действием постоянной по модулю и направлению силы.выберите правильное утверждение:а.скорость шарика не изменяется.б.шарик движется равномерно.в.шарик движется с постоянным ускорением.2.как движется шарик массой 500г. под действием силы 4 н?а.с ускорением 2 м/с(в квадрате) б.с постоянной скоростью 0,125м/с.в.с постоянным ускорение 8м/с(в квадрате)3.в каких приведённых ниже случаев идёт речь о движении тел по инерции?а.тело лежит на поверхности стола.б.катер после выключения двигателя продолжает двигаться по повехности водыв.спутник движется по орбите вокруг солнца. 4.а)почему первый закон ньютона называют законом инерции? б.как движется тело,если векторная сумма действующих на него сил равна нулю? в.о векторное стекло движущегося автомибиля ударился комар.сравните силы,действующие на комара и автомобиль во время удара.5.а.при каком условии тело может двигаться равномерно и прямолинейно? б.с помощью двух одинаковых воздушных шаров подминают из состояния покоя разные тела.
 по какому признаку можно заключить,у какого из этих тел болльшая масса? в.мяч ударяет в оконное стекло.на какое из тел(мяч или стекло) действует при ударе большая сила?7.а.на столе лежит брусок.какие силы дейчствуют на него?почему брусок покоится?б.с каким ускорением движется при разбеге реактивный самолёт ммассой 60 т.,ксли сила тяги двигателей 90 кн?в.теплоход при столкновении с лодкой может потопить её без всяких для себя повреждений.как это согласуется с равенством модулей сил взаимодействия?8.а.какими способами насажисают топор на рукоятку?как объяснить происхождящие при этом явления?б.какая сила сообщает телу массой 400г. ускорение 2 м/с(в квадрате)?в.двое мальчиков тянут шнур в противоположные стороны,каждый с силой 100н.разорвётся ли шнур,если он может выдержать нагрузку 150н? — Знания.site
по какому признаку можно заключить,у какого из этих тел болльшая масса? в.мяч ударяет в оконное стекло.на какое из тел(мяч или стекло) действует при ударе большая сила?7.а.на столе лежит брусок.какие силы дейчствуют на него?почему брусок покоится?б.с каким ускорением движется при разбеге реактивный самолёт ммассой 60 т.,ксли сила тяги двигателей 90 кн?в.теплоход при столкновении с лодкой может потопить её без всяких для себя повреждений.как это согласуется с равенством модулей сил взаимодействия?8.а.какими способами насажисают топор на рукоятку?как объяснить происхождящие при этом явления?б.какая сила сообщает телу массой 400г. ускорение 2 м/с(в квадрате)?в.двое мальчиков тянут шнур в противоположные стороны,каждый с силой 100н.разорвётся ли шнур,если он может выдержать нагрузку 150н? — Знания.siteПомогите пожалуйста!!
1.Шарик движется под действием постоянной по модулю и направлению силы.Выберите правильное утверждение:
А.Скорость шарика не изменяется.
Б.Шарик движется равномерно.
В.Шарик движется с постоянным ускорением.
2.КАк движется шарик массой 500г. под действием силы 4 Н?
А.С ускорением 2 м/с(в квадрате)
Б.С постоянной скоростью 0,125м/с.
В.С постоянным ускорение 8м/с(в квадрате)
3.В каких приведённых ниже случаев идёт речь о движении тел по инерции?
А.Тело лежит на поверхности стола.
Б.Катер после выключения двигателя продолжает двигаться по повехности воды
В.Спутник движется по орбите вокруг Солнца.
4.а)почему первый закон Ньютона называют законом инерции?
б.как движется тело,если векторная сумма действующих на него сил равна нулю?
в.О векторное стекло движущегося автомибиля ударился комар.Сравните силы,действующие на комара и автомобиль во время удара.
5.а.При каком условии тело может двигаться равномерно и прямолинейно?
б.С помощью двух одинаковых воздушных шаров подминают из состояния покоя разные тела.По какому признаку можно заключить,у какого из этих тел болльшая масса?
в.Мяч ударяет в оконное стекло. На какое из тел(мяч или стекло) действует при ударе большая сила?
На какое из тел(мяч или стекло) действует при ударе большая сила?
7.а.На столе лежит брусок.Какие силы дейчствуют на него?Почему брусок покоится?
б.С каким ускорением движется при разбеге реактивный самолёт ммассой 60 т.,ксли сила тяги двигателей 90 кН?
в.Теплоход при столкновении с лодкой может потопить её без всяких для себя повреждений.Как это согласуется с равенством модулей сил взаимодействия?
8.а.Какими способами насажисают топор на рукоятку?Как объяснить происхождящие при этом явления?
б.Какая сила сообщает телу массой 400г. ускорение 2 м/с(в квадрате)?
в.Двое мальчиков тянут шнур в противоположные стороны,каждый с силой 100Н.Разорвётся ли шнур,если он может выдержать нагрузку 150Н?
Законы Ньютона — простыми словами. Объяснение с примерами
Покажем, как применять знание физики в жизни
Начать учиться
167.4K
Почему при резком торможении автобуса пассажиры движутся вперед? С какой силой действует груша на боксера при ударе? На эти и другие вопросы отвечают законы Ньютона, которые лежат в основе классической механики.
С помощью законов Ньютона можно описать движение любой механической системы, будь то старушка, переходящая дорогу, или робот-пылесос. А может быть, это девятиклассница Соня, которая едет в поезде метро на занятия. При торможении электропоезда на станции Соня некоторое время продолжает по инерции двигаться вперед.
Инерция — явление сохранения постоянной скорости тела при отсутствии действия на него других тел.
- велосипед движется, если перестать крутить педали;
- бегун не может остановиться сразу после финиша, а пробегает некоторое расстояние;
- чай в кружке продолжает вращаться, если перестать его размешивать и убрать ложку;
- дверь способна сама захлопнуться после толчка.
Объяснить это явление можно с помощью первого закона Ньютона, который также называют законом инерции.
Первый закон Ньютона: формулировка
Существуют системы отсчета, называемые инерциальными (ИСО), в которых тело находится в состоянии покоя (V = 0) или движется равномерно и прямолинейно (V = const), если на тело не действуют силы (F = 0) или действие этих сил скомпенсировано (F = 0).
Инерциальные системы отсчета окружают нас повсюду. Например, равномерно спускающийся лифт или тот самый поезд метро, в котором Соня равномерно движется между станциями.
Инерциальные системы отсчета обладают следующими свойствами:
- тела в таких системах движутся равномерно или находятся в состоянии покоя;
- при одинаковых начальных условиях тела движутся одинаково;
- изменение скорости тела происходит в результате действия на него других тел.
Остановимся на последнем свойстве подробнее и рассмотрим пример.
Кот Василий неподвижно спит на батарее.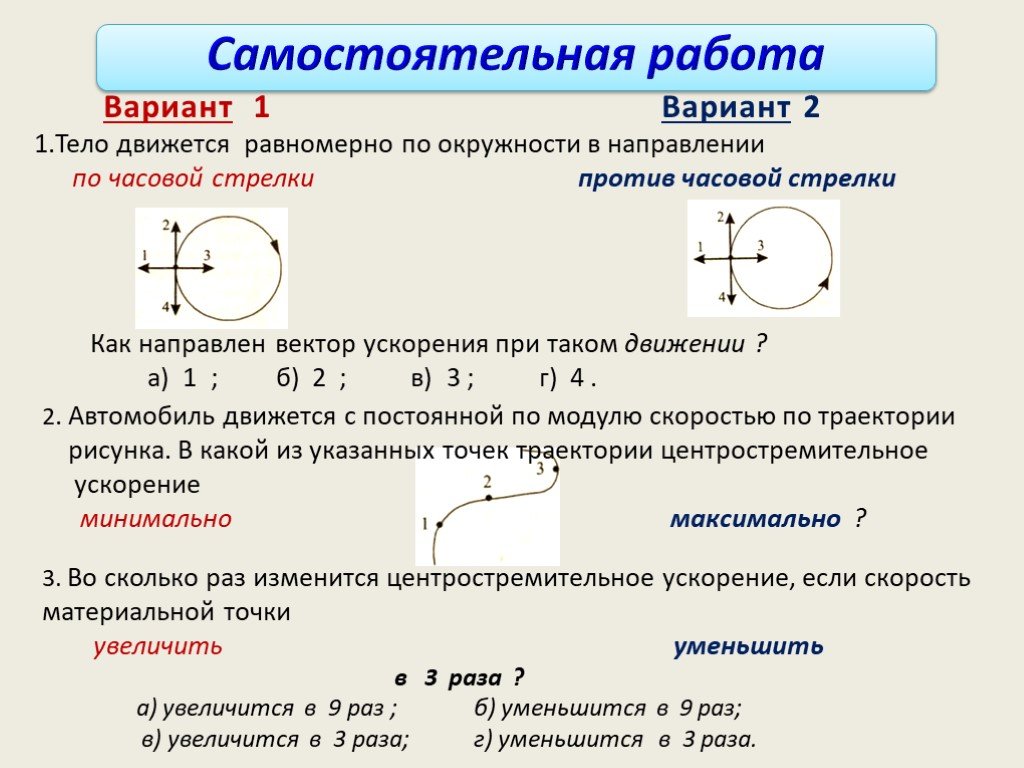 На него определенно действуют силы: со стороны Земли — сила тяжести, направленная вниз, а со стороны батареи — сила реакции опоры, направленная вертикально вверх. Однако изменения скорости Василия не происходит потому, что действие вышеупомянутых сил скомпенсировано.
На него определенно действуют силы: со стороны Земли — сила тяжести, направленная вниз, а со стороны батареи — сила реакции опоры, направленная вертикально вверх. Однако изменения скорости Василия не происходит потому, что действие вышеупомянутых сил скомпенсировано.
1-й закон Ньютона не имеет формулы, однако математически его можно описать следующим образом:
,
где — скорость тела [м/с],
— равнодействующая сила [Н].
Равнодействующая сила — векторная сумма всех сил, действующих на тело. При равномерном прямолинейном движении или в состоянии покоя равнодействующая сила равна нулю.
Вернемся к примеру с котом Василием. До тех пор, пока кота никто не трогает, он находится в состоянии покоя. Когда Соня толкнет Василия с некоторой силой, его скорость изменится. Причем чем большую силу приложит Соня, тем большее ускорение приобретет Василий. Связь между ускорением тела и приложенной силой устанавливает 2-й закон Ньютона.
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Второй закон Ньютона: формулировка
В ИСО ускорение, с которым движется тело, прямо пропорционально равнодействующей всех сил и обратно пропорционально массе этого тела.
Вспомним Соню в поезде метро. Рассмотрим участок разгона электропоезда под действием равнодействующей силы. Согласно 2-му закону Ньютона, чем больше равнодействующая сила, тем большее ускорение приобретет поезд. Под действием той же силы более легкий поезд будет двигаться с бóльшим ускорением.
Второй закон Ньютона: формула
,
где — ускорение [м/с2],
— равнодействующая сила [Н],
— масса [кг].
Важно
Сила и ускорение — величины векторные, их направления всегда совпадают.
Рассмотрим примеры решения задач с использованием второго закона Ньютона.
Задача 1
Уставший Аркаша пришел домой после школы и с силой 4,5 Н горизонтально бросил в сторону кровати рюкзак массой 6 кг. Какое ускорение приобрел рюкзак? Силой сопротивления воздуха можно пренебречь.
Решение.
Сила воздействия Аркаши на рюкзак при горизонтальном броске равна равнодействующей силе. Подставим в формулу 2-го закона Ньютона числа:
м/с2.
Ответ: рюкзак приобрел ускорение 0,75 м/с2.
Задача 2
На рисунке отмечены все силы, действующие на тело. Чему равна равнодействующая сила, если одной клетке соответствует 1 Н?
Решение.
Для определения равнодействующей силы необходимо найти векторную сумму F Согласно правилу треугольника, чтобы сложить два вектора, нужно последовательно отложить их друг от друга (т. е. начало второго вектора должно совпадать с концом первого).
Согласно правилу треугольника, чтобы сложить два вектора, нужно последовательно отложить их друг от друга (т. е. начало второго вектора должно совпадать с концом первого).
Сложим силы F2 и F3, лежащие в горизонтальной плоскости. Их сумма имеет длину 3 клетки и направлена вправо в сторону большей силы.
Затем полученную сумму сложим с силой F1
По теореме Пифагора найдем гипотенузу:
И вычислим:
Ответ: равнодействующая сила равна 34.
Хотите найти универсальный способ решения всех задач по динамике, успешно справляться с заданиями ОГЭ и даже освоить самую сложную задачу № 30 из ЕГЭ? Тогда записывайте алгоритм. Вот 7 шагов к успеху!
Вот 7 шагов к успеху!
Алгоритм решения задач с использованием 2-го закона Ньютона
Выбрать ИСО.
Отметить на рисунке все силы, действующие на тело.
Записать 2-й закон Ньютона в векторном виде.
Найти проекции сил на координатные оси.
Записать 2-й закон Ньютона в проекциях на координатные оси.
Составить и решить систему уравнений.
Выполнить расчет и записать ответ.
Попробуем применить алгоритм прямо сейчас, чтобы лучше разобраться в каждом шаге.
Задача 3
Серёжа с силой F = 12 Н, приложенной под углом 30°, тянет машинку массой 600 г по шероховатому ламинату, как показано на рисунке. С каким ускорением движется машинка? Коэффициент трения равен 0,1.
С каким ускорением движется машинка? Коэффициент трения равен 0,1.
Решение.
При решении задачи будем считать машинку материальной точкой. Выберем направления осей, как показано на рисунке, и отметим все действующие в системе силы. На машинку действуют сила тяги Серёжи F, сила тяжести m
Запишем 2-й закон Ньютона в векторном виде:
Определим проекции силы на координатные оси и запишем 2-й закон Ньютона в проекциях на эти оси.
Ox: ma = Fcosα − Fтр; (1)
Oy: 0 = N + Fsinα − mg. (2)
Запишем формулу для силы трения скольжения: Fтр = μN. (3)
Решим полученную систему из трех уравнений. Для этого подставим выражение для силы трения (3) в уравнение (1) и получим:
ma = Fcosα − μN; (1)
0 = N + Fsinα − m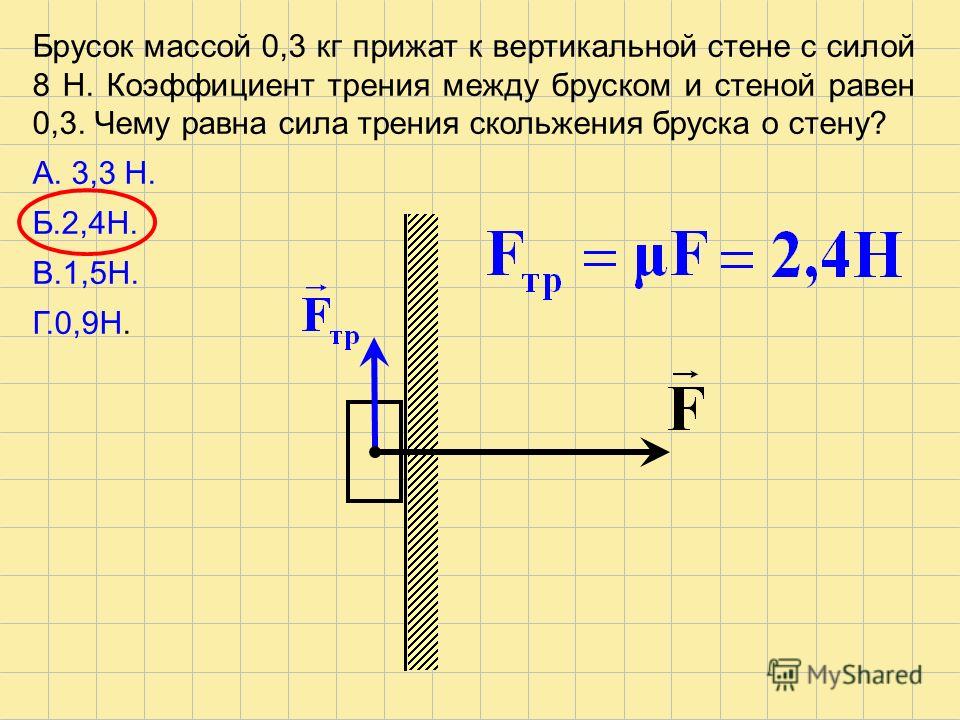 (2)
(2)
Затем выразим в уравнении (2) силу реакции опоры N = mg − Fsinα и подставим полученное выражение в уравнение (1):
ma = Fcosα − μ(mg − Fsinα).
Выразим искомое ускорение:
И вычислим:
м/с2.
Ответ: машинка движется с ускорением 17,3 м/с2.
Как мы уже заметили, тела постоянно взаимодействуют друг с другом. Именно об этом говорит 3-й закон Ньютона.
Третий закон Ньютона: формулировка
Тела действуют друг на друга с силами, направленными вдоль одной прямой, противоположными по направлению и разными по модулю.
Суть закона в том, что сила действия равна силе противодействия. Причем силы имеют одну природу, а приложены они к разным телам.
Действие и противодействие встречаются повсюду:
мы притягиваем к себе Землю с той же силой, с какой она притягивает нас;
боксер носит перчатки потому, что груша ударяет его с той же силой, что и он;
ноутбук давит на стол с той же силой, что и стол на ноутбук;
прыжок гребца из лодки непременно вызовет движение лодки в противоположную сторону;
лебедь плавает по озеру за счет взаимодействия с водой.

Третий закон Ньютона: формула
,
где — сила, с которой тело 1 действует на тело 2 [Н],
— сила, с которой тело 2 действует на тело 1 [Н].
Для решения задач часто используют комбинацию 2-го и 3-го законов Ньютона, которая имеет следующий вид:
,
где — масса тела 1 [кг],
— масса тела 2 [кг],
— ускорение тела 1 [м/с2],
— ускорение тела 2 [м/с2].
Задача 4
Во время веселых стартов две команды перетягивают канат. Команда «Чемпионы» тянет с максимальной силой 240 Н, а команда «Апельсинки» — с силой 280 Н. С какой силой команды могут натянуть канат, стоя неподвижно на одном месте?
Решение.
Поскольку сила действия равна силе противодействия, а «Чемпионы» могут действовать с силой не более 240 Н, то именно с такой силой команды могут натягивать канат, удерживая его неподвижно.
Ответ: команды могут натягивать канат, стоя неподвижно, с силой 240 Н.
Вот мы и рассмотрели три закона Ньютона. С их помощью любая задача по динамике теперь вам по плечу!
Но это еще не все. Мы подготовили подарок — готовые схемы и формулы по наиболее часто встречающимся типам задач на законы Ньютона.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи. На уроках вы изучите немало любопытных физических явлений и научитесь решать самые разнообразные задачи. Ждем вас!
Софья Ефименко
К предыдущей статье
Диффузия
К следующей статье
Влажность воздуха
Получите индивидуальный план обучения физике на бесплатном вводном уроке
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Объяснение урока: Работа, совершаемая силой, выраженная в векторном представлении действуя на тело по вектору смещения с помощью скалярного произведения.

Работу, совершаемую силой над телом, можно определить следующим образом.
Определение: работа, совершаемая силой над телом
Работа, совершаемая силой над телом, зависит от силы, действующей на тело, и расстояние, на которое тело перемещается в направлении действия этой силы по формуле 𝑊=𝐹⋅𝑑(𝜃), потому что где 𝐹 — величина силы, 𝑑 — величина перемещение тела под действием силы, а 𝜃 – угол между направлениями 𝐹 и 𝑑.
Альтернативным способом представления работы, совершаемой силой над телом, является представление сила и перемещение как векторы, а не как величины векторов.
Произведение двух векторов ⃑𝑎 и ⃑𝑏 может быть скалярным произведением векторов, которое определяется как следует.
Определение: Скалярное произведение двух векторов
Скалярное произведение двух векторов определяется как
𝜃 — угол между ⃑𝑎 и
⃑𝑏. Угол берется против часовой стрелки от
от ⃑𝑎 до ⃑𝑏, как показано
следующий рисунок.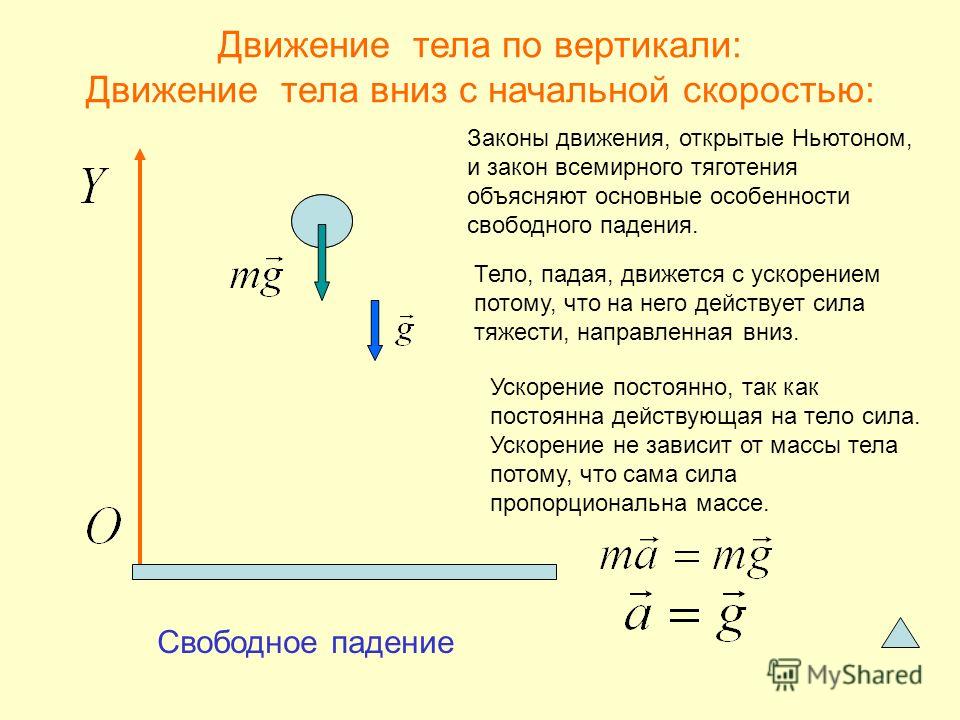
Работа, совершаемая силой с величиной 𝐹 при перемещении с величина 𝑑 равна ⃑𝐹⋅⃑𝑑⃑𝐹⋅⃑𝑑=‖‖⃑𝐹‖‖‖‖⃑𝑑‖‖(𝜃).cos
Графическое представление ⃑𝐹 и ⃑𝑑 показывает, что произведение величины ⃑𝐹 и величина компонента ⃑𝑑 в направлении ⃑𝐹 есть равно ‖‖⃑𝐹‖‖‖‖⃑𝑑‖‖(𝜃)cos.
Скалярное произведение двух векторов, выраженных в компонентной форме, может быть определено без речь идет об угле между векторами.
Предположим теперь, что векторы ⃑𝐹 и ⃑𝑑 перпендикулярны, как показано на следующем рисунке.
Произведение определяется как ⃑𝐹⋅⃑𝑑=(4,−3)⋅(3,4)⃑𝐹⋅⃑𝑑=(4×3)+(−3×4)=12−12=0.
Скалярное произведение двух перпендикулярных векторов равно нулю. На тело не действуют никакие силы направление перемещения, поэтому сила не действует на тело.
Давайте рассмотрим пример использования векторной записи для определения работы силы.
Пример 1. Расчет работы силы, действующей на частицу, где сила и положение даны в виде векторов
Частица движется в плоскости, в которой ⃑𝑖 и
⃑𝑗 — перпендикулярные единичные векторы. Сила
⃑𝐹=9⃑𝑖+⃑𝑗N действует на частицу. Частица движется из начала координат в точку
с вектором положения
−9⃑𝑖+6⃑𝑗 м. Найдите работу, совершенную силой.
Сила
⃑𝐹=9⃑𝑖+⃑𝑗N действует на частицу. Частица движется из начала координат в точку
с вектором положения
−9⃑𝑖+6⃑𝑗 м. Найдите работу, совершенную силой.
Ответ
Работа силы равна скалярному произведению вектора силы и вектора смещения частицы. Вопрос не дает вектор смещения, однако он дает вектор положения. В вопросе также указано что частица движется в указанное положение от начала координат, поэтому вектор смещения частицы определяется выражением ⃑𝑑=(−9−0)⃑𝑖+(6−0)⃑𝑗,м который равен заданному вектору положения.
Работа силы 𝑊 определяется скалярным произведением векторов что определяется как 𝑊=(9,1)⋅(−9,6)𝑊=(9×−9)+(1×6)=−81+6=−75.
Таким образом, выполненная работа определяется выражением 𝑊=−75.J
Проделанная работа отрицательна. Если энергия частицы сохраняется,
то кинетическая энергия частицы должна уменьшаться. Если энергия частицы не сохраняется,
вместо этого проделанная работа может увеличить потенциальную энергию частицы.
Теперь давайте рассмотрим пример, когда на тело действуют несколько сил, вызывающих перемещение.
Пример 2. Нахождение работы равнодействующей двух сил, действующих на тело
Тело движется в плоскости, в которой ⃑𝑖 и ⃑𝑗 — перпендикулярные единичные векторы. Две силы ⃑𝐹=9⃑𝑖−2⃑𝑗N и ⃑𝐹=9⃑𝑖−7⃑𝑗N действовать на тело. Частица движется из точки с вектором положения −6⃑𝑖+2⃑𝑗 м к точке 2⃑𝑖+3⃑𝑗 м. Найдите работу равнодействующей сил.
Ответ
На тело действуют две силы. Силы являются векторами, и равнодействующая векторов может определяется суммированием компонент векторов. 𝑥-составляющая результирующей силы определяется выражением ⃑𝐹=9⃑𝑖+9⃑𝑖=18⃑𝑖,R а 𝑦-компонента равнодействующей силы определяется выражением ⃑𝐹=−2⃑𝑗−7⃑𝑗=−9⃑𝑗.R
Следовательно, результирующая сила, действующая на тело, равна
⃑𝐹=18⃑𝑖−9⃑𝑗. RN
RN
Конечный вектор положения тела равен 2⃑𝑖+3⃑𝑗, а вектор начального положения тела равен −6⃑𝑖+2⃑𝑗.
Таким образом, вектор смещения из начального положения в конечное положение равен ⃑𝑑=2⃑𝑖+3⃑𝑗−−6⃑𝑖+2⃑𝑗⃑𝑑=2−(−6)⃑𝑖+(3−2)⃑𝑗=8⃑𝑖+⃑𝑗.mm
.mm
.mm , у нас есть это 𝑊=⃑𝐹⋅⃑𝑑,R что дает нам 𝑊=(18,−9)⋅(8,1)𝑊=(18×8)+(−9×1)=144−9=135.J
Теперь рассмотрим пример, в котором ни одна из компонент ни вектор силы, ни компоненты вектора смещения не заданы напрямую.
Пример 3. Использование векторов для нахождения работы силы с направлением и величиной, заданными отдельно
Частица переместилась из точки 𝐴(7,−3) в точку
𝐵(−9,2) по прямой под действием
силы ⃑𝐹 величины
8√10 Н
действует в том же направлении, что и вектор
⃑𝑐=−3⃑𝑖−⃑𝑗. Рассчитать работу
совершается силой, учитывая, что величина смещения
измеряется в метрах.
Ответ
Мы можем назвать вектор смещения 𝐴𝐵, ⃑𝑑. Вектор ⃑𝑑 показан с вектором ⃑𝑐 на следующем рисунке.
Вектор ⃑𝑑 задается ⃑𝑑=(−9−7)⃑𝑖+(2−(−3))⃑𝑗=−16⃑𝑖+5⃑𝑗.m
Скалярное произведение ⃑𝑑 и ⃑𝑐 не равно скалярному произведению ⃑𝑑 и ⃑𝐹.
Величина ⃑𝐹 дана, но использовать ⃑𝐹 через точку расчет продукта, необходимо определить компоненты ⃑𝑖 и ⃑𝑗 ⃑𝐹.
Поскольку ⃑𝐹 действует по линии ⃑𝑐, ⃑𝑖 компонент ⃑𝐹 должна иметь величину, которая в три раза больше величины ⃑𝑗 компонента ⃑𝐹. Эти отношения можно выразить как 𝐹=3𝐹.
𝐹 и 𝐹 две стороны прямоугольного треугольника с гипотенузой длиной 8√10. Поэтому это в случае, когда
И снова, так как 𝐹=3𝐹,𝐹=24.
Зная компоненты ⃑𝐹, можно выразить ⃑𝐹 как ⃑𝐹=−24⃑𝑖−8⃑𝑗.N
Таким образом, выполненная работа 𝑊
𝑊=(−24,−8)⋅(−16,5)𝑊=(−24×−16)+(−8×5)=384−40=344.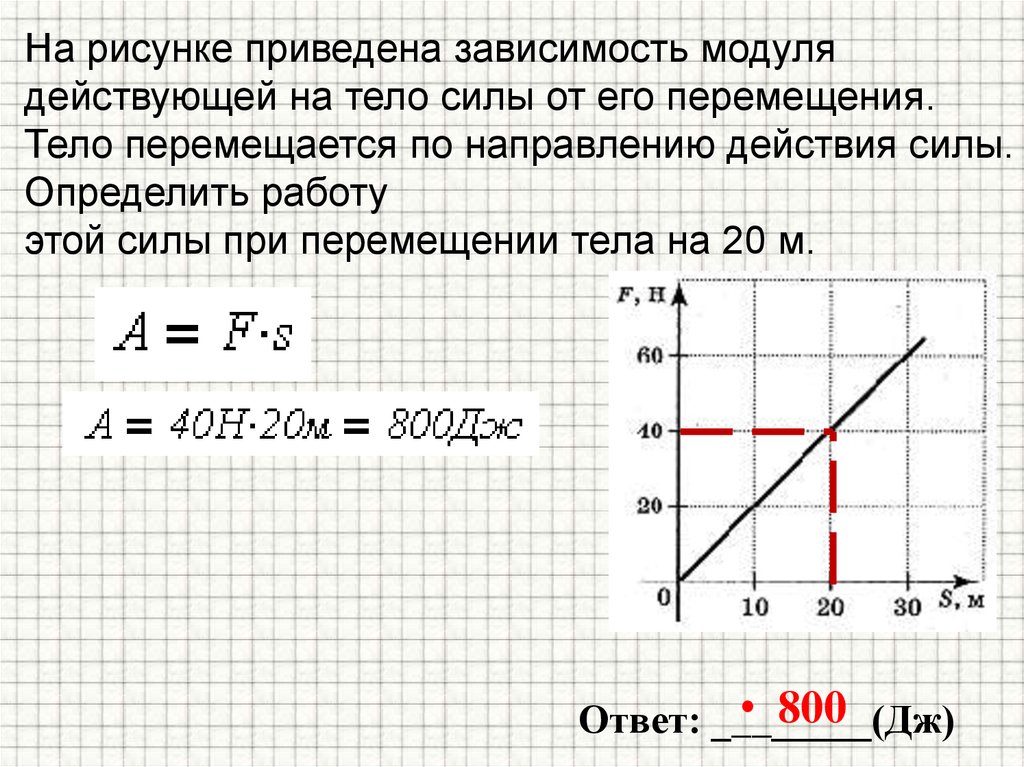 J
J
Теперь давайте рассмотрим другой пример, где ни компоненты вектора силы, ни компоненты вектора смещения не заданы напрямую.
Пример 4. Нахождение работы векторной силы, действующей на тело, движущееся между двумя точками
Частица переместилась из точки 𝐴(−2,−2) в точку 𝐵(6,10) по прямой под действием сила ⃑𝐹=𝑘⃑𝑖−6⃑𝑗 действующий в направлении, противоположном перемещению 𝐴𝐵. Найдите работу силы ⃑𝐹.
Ответ
Вектор смещения ⃑𝑑 — это вектор, хвост которого находится в точке ⃑𝐴 и его голова в ⃑𝐵. Вектор ⃑𝑑 задается выражением ⃑𝑑=(6−(−2))⃑𝑖+(10−(−2))⃑𝑗=8𝑖+12⃑𝑗.m
Направление ⃑𝑑 𝐴𝐵. Направление, в котором ⃑𝐹 действует противоположно 𝐴𝐵, поэтому ⃑𝐹 должен действовать вдоль прямой 𝐵𝐴𝐵𝐴=−8⃑𝑖−12⃑𝑗
Δ𝑦Δ𝑥=−12−8=32.
Чтобы ⃑𝐹 имел то же направление, что и
𝐵𝐴,
доля 𝑦-компоненты над
его 𝑥-компонента должна быть равна
𝐵𝐴. Следовательно, мы имеем это
Δ𝑦Δ𝑥=−6𝑘=32.
Следовательно, мы имеем это
Δ𝑦Δ𝑥=−6𝑘=32.
Перестановка, чтобы сделать 𝑘 предмет уравнения дает 3𝑘=−6×2𝑘=−4.
Теперь мы можем выразить ⃑𝐹 как ⃑𝐹=−4⃑𝑖−6⃑𝑗.N
Таким образом, выполненная работа 𝑊 равна 𝑊=(−4,−6)⋅(8,12)𝑊=(−4×8)+(−6×12)=−32−72=−104.J
Неудивительно, что проделанная работа отрицательна, поскольку сила действует в направлении, противоположном перемещению.
Когда энергия частицы, на которую действует сила, сохраняется, путь, который проходит частица, чтобы сместить ее, когда на нее действует сила, не влияет на работу, совершаемую этой силой над частицей.
Теперь рассмотрим пример, в котором рассматривается работа, совершаемая силой за интервал времени.
Пример 5. Определение работы силы при задании смещения во времени
Частица движется в плоскости, в которой ⃑𝑖 и
⃑𝑗 — перпендикулярные единичные векторы. Его водоизмещение
от источника в момент времени 𝑡 секунд
определяется выражением ⃑𝑟=2𝑡+7⃑𝑖+(𝑡+7)⃑𝑗m и на него действует
силой ⃑𝐹=6⃑𝑖+3⃑𝑗Н. Какую работу совершает сила между 𝑡=2с и
𝑡=3s?
Какую работу совершает сила между 𝑡=2с и
𝑡=3s?
Ответ
Включение в этот пример не требует, чтобы его решение сильно отличалось от предыдущих примеров, так как скалярные произведения векторов используются таким же образом. Единственная новая особенность, обнаруженная в этом примере, заключается в том, что мы должны найти перемещения, которые соответствуют двум разным временам.
Смещение частицы при 𝑡=3 с и 𝑡=2с должны быть определены. Это делается путем замены 3 и 2 как значения 𝑡, чтобы дать ⃑𝑑 и ⃑𝑑, соответственно, что дает нам ⃑𝑑=2×3+7⃑𝑖+(3+7)⃑𝑗=25⃑𝑖+10⃑𝑗,⃑𝑑=2×2+7⃑𝑖+(2+7)⃑𝑑 15⃑𝑖+9⃑𝑗.мм
Смещение частицы между 𝑡=3 с и 𝑡=2s равно ⃑𝑑 минус ⃑𝑑, заданный ⃑𝑑−⃑𝑑=Δ𝑑=25⃑𝑖+10⃑𝑗−15⃑𝑖+9⃑𝑗=10⃑𝑖+⃑𝑗.m
Скалярное произведение ⃐
и Δ𝑑 дает нам выполненную работу, 𝑊,
между 𝑡=3s и
𝑡=2с. С
⃑𝐹=6⃑𝑖+3⃑𝑗,N
это дано
𝑊=(6,3)⋅(10,1)𝑊=(6×10)+(1×3)=63. J
J
Ключевые точки
- Работа, совершаемая постоянной силой ⃑𝐹 при перемещении ⃑𝑑 равно скалярному произведению ⃑𝐹 и ⃑𝑑, 𝑊=⃑𝐹⋅⃑𝑑, или 𝑊=‖‖⃑𝐹‖‖‖‖⃑𝑑‖‖(𝜃), cos где 𝜃 — угол между ⃑𝐹 и ⃑𝑑.
- Скалярное произведение ⃑𝐹 и ⃑𝑑 можно определить без использования угла 𝜃 выражая ⃑𝐹 и ⃑𝑑 в компонентной форме.
- Если компоненты ⃑𝐹 и ⃑𝑑 находятся в перпендикулярных направлениях ⃑𝑖 и ⃑𝑗, то ⃑𝐹⋅⃑𝑑=𝐹,𝐹⋅𝑑,𝑑=(𝐹𝑑)+𝐹𝑑.
6.1: Введение — LibreTexts по физике
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 16957
- Boundless (теперь LumenLearning)
- Boundless
Введение в работу и энергию
Работа — это энергия, связанная с действием силы.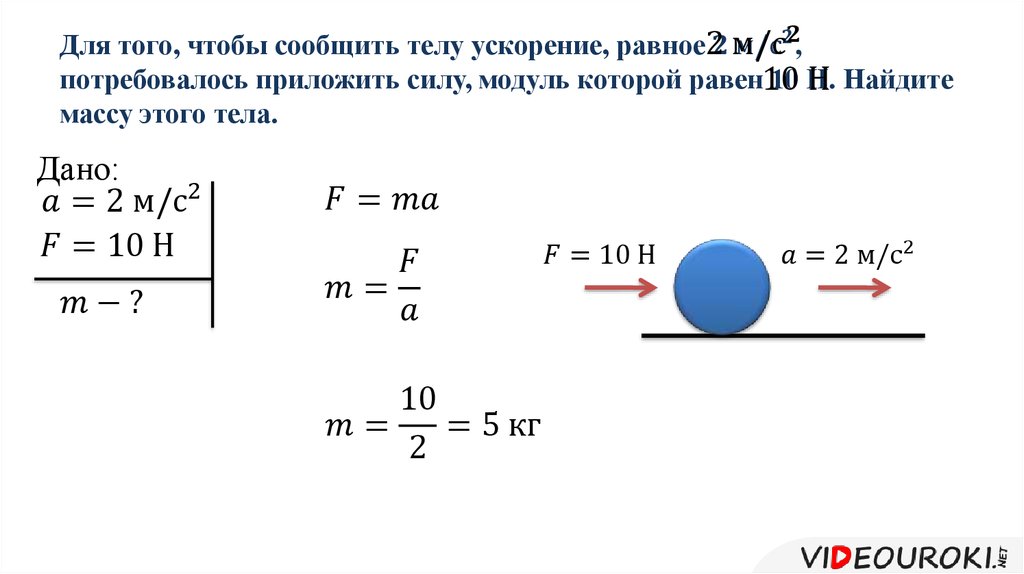
цели обучения
- Опишите взаимосвязь между работой, энергией и силой
Работа, совершаемая над системой постоянной силой, равна произведению составляющей силы, направленной в направлении движения, на расстояние, на котором действует сила. Для одностороннего движения в одном измерении это выражается в виде уравнения как \(\mathrm{W=Fd \cos θ}\), где W — работа, F — величина силы, действующей на систему, d — сила, действующая на систему. величина смещения системы, а θ — угол между вектором силы F и вектором смещения d.
Работа, сила и энергия : Биология полезна.
Возьмем этот пример работы в действии из: (A) Работа, совершаемая силой F на этой газонокосилке, равна \(\mathrm{W=Fd \cos θ}\). Обратите внимание, что \(\mathrm{W=Fd \cos θ}\) — это составляющая силы в направлении движения.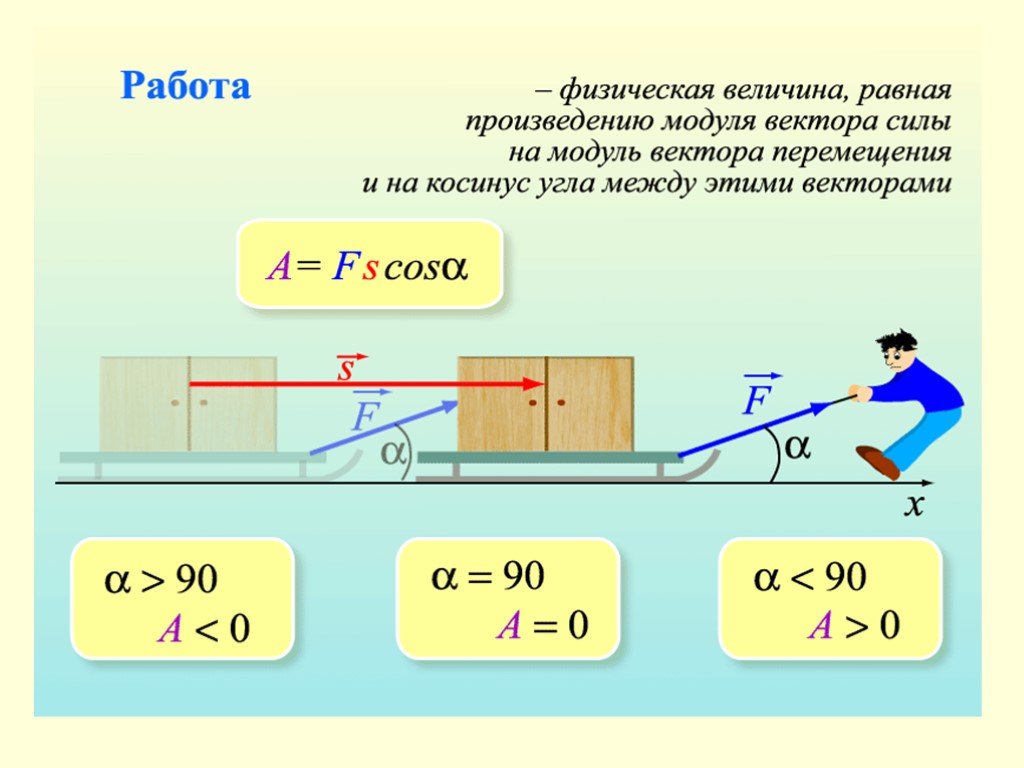 (Б) Человек, держащий портфель, не работает над ним, потому что нет движения. Никакая энергия не передается в портфель или из него. (C) Человек, перемещающий портфель горизонтально с постоянной скоростью, не совершает над ним работы и не передает ему никакой энергии. (D) Над портфелем совершается работа, когда он поднимается по лестнице с постоянной скоростью, потому что обязательно присутствует составляющая силы F в направлении движения. Энергия передается в портфель и может, в свою очередь, использоваться для выполнения работы. (E) Когда портфель опускается, энергия передается из портфеля в электрический генератор. Здесь работа, проделанная над портфелем генератором, отрицательна, удаляя энергию из портфеля, потому что F и d направлены в противоположные стороны.
(Б) Человек, держащий портфель, не работает над ним, потому что нет движения. Никакая энергия не передается в портфель или из него. (C) Человек, перемещающий портфель горизонтально с постоянной скоростью, не совершает над ним работы и не передает ему никакой энергии. (D) Над портфелем совершается работа, когда он поднимается по лестнице с постоянной скоростью, потому что обязательно присутствует составляющая силы F в направлении движения. Энергия передается в портфель и может, в свою очередь, использоваться для выполнения работы. (E) Когда портфель опускается, энергия передается из портфеля в электрический генератор. Здесь работа, проделанная над портфелем генератором, отрицательна, удаляя энергию из портфеля, потому что F и d направлены в противоположные стороны.
Примеры работы : Вот как незавершенное производство и энергия сосуществуют и работают. Работа – это энергия, связанная с действием силы.
В физике считается, что сила совершает работу, когда она действует на тело так, что точка приложения смещается, хотя и мало, в направлении действия силы.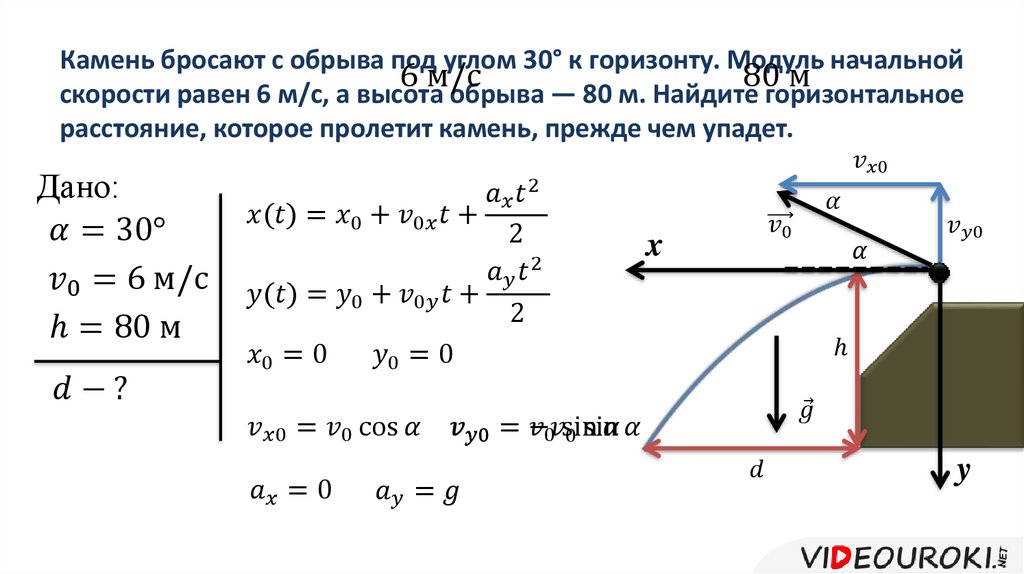 Таким образом, сила работает, когда есть движение под действием силы. Работа, совершаемая постоянной силой величины F над точкой, перемещающейся на расстояние d в направлении действия силы, равна произведению:
Таким образом, сила работает, когда есть движение под действием силы. Работа, совершаемая постоянной силой величины F над точкой, перемещающейся на расстояние d в направлении действия силы, равна произведению:
\[\mathrm{W=Fd}\]
Например, если сила в 10 ньютонов (F = 10 Н) действует вдоль точки, которая проходит два метра (d = 2 м), то она выполняет работу W = (10 Н)(2 м) = 20 Н·м = 20 Дж. Это приблизительно равно работе, выполняемой при подъеме груза массой 1 кг с земли на голову человека против силы тяжести. Обратите внимание, что работа удваивается либо при подъеме вдвое большего веса на одно и то же расстояние, либо при подъеме того же веса вдвое на большее расстояние.
Работа тесно связана с энергией. Закон сохранения энергии утверждает, что изменение полной внутренней энергии системы равно добавленному теплу за вычетом работы, выполненной системой (см. первый закон термодинамики и ):
Бейсбольный питчер : Бейсбольный питчер работает с бейсбольным мячом, бросая мяч с некоторой силой F на некоторое расстояние d, которое для среднего бейсбольного поля составляет около 60 футов.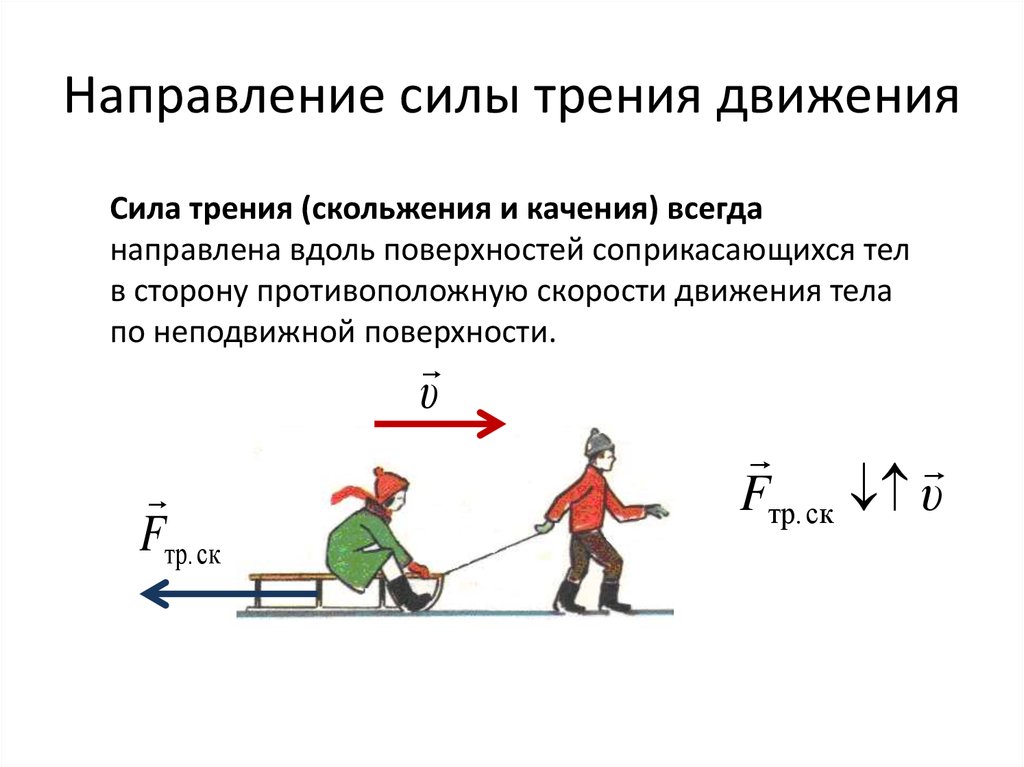
\[\mathrm{δE=δQ−δW}\]
Кроме того, из второго закона Ньютона для твердых тел можно показать, что работа над объектом равна изменению кинетической энергии этого объекта:
\[\mathrm{W=ΔKE}\]
Работа сил, создаваемых потенциальной функцией, называется потенциальной энергией, а силы называются консервативными. Поэтому работа над телом, движущимся в консервативном силовом поле, равна минус изменению потенциальной энергии тела:
\[\mathrm{W=-ΔPE}\]
Это показывает, что работа представляет собой энергию, связанную с действием силы, а также физические размеры и единицы энергии.
Ключевые моменты
- Работа — это передача энергии силой, действующей на объект при его перемещении.
- Работа, совершаемая силой, равна нулю, если перемещение либо равно нулю, либо перпендикулярно силе.
- Совершенная работа положительна, если сила и перемещение имеют одинаковое направление, а совершенная работа отрицательна, если они имеют противоположное направление.

Ключевые термины
- энергия : Величина, обозначающая способность выполнять работу и измеряемая в единицах массы × расстояние²/время² (ML²/T²) или эквивалентных единицах.
ЛИЦЕНЗИИ И АВТОРСТВО
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, ПРЕДОСТАВЛЕННОЕ РАНЕЕ
- Курирование и пересмотр. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, КОНКРЕТНОЕ АВТОРСТВО
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42146/latest/?collection=col11406/latest . Лицензия : CC BY: Attribution
- Работа (физика). Предоставлено : Википедия. Расположен по адресу : en.
 Wikipedia.org/wiki/Work_(physics)%23Work_and_energy . Лицензия : CC BY-SA: Attribution-ShareAlike
Wikipedia.org/wiki/Work_(physics)%23Work_and_energy . Лицензия : CC BY-SA: Attribution-ShareAlike - Работа (физика). Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Work_(physics)%23Work_and_energy . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42146/latest/?collection=col11406/latest . Лицензия : CC BY: Attribution
- Работа (физика). Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Work_(physics)%23Work_and_energy .
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - энергии. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/energy . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Работа: научное определение. 3 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : cnx.org/content/m42146/latest/Figure_08_02_01.jpg . Лицензия : CC BY: Attribution
- Движение подачи бейсбольного мяча, 2004 г. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/File:Baseball_pitching_motion_2004.jpg . Лицензия : CC BY-SA: Attribution-ShareAlike
- Работа, мощность и энергия.




 Wikipedia.org/wiki/Work_(physics)%23Work_and_energy . Лицензия : CC BY-SA: Attribution-ShareAlike
Wikipedia.org/wiki/Work_(physics)%23Work_and_energy . Лицензия : CC BY-SA: Attribution-ShareAlike  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike 
Leave A Comment