Алгебра 8 класс формулы: Формулы по математике 8 класс

все классы, все формулы, все темы

Дорогие школьники, студенты! На сайте вы найдете темы по математике за 5-11 класс и лекции по высшей математике. Мы не только изучаем теоретический материал, но и решаем задачи — подробно их разбираем. Уделяем внимание и разбору интересных задач ЕГЭ по математике. У нас вы найдете все формулы по математике за 5-11 класс, научитесь рассуждать и решать уравнения, неравенства, системы уравнений и неравенств, анализировать функции, брать производные и интегралы. Особое внимание мы уделили важному разделу математики — «Геометрии». Решение пространственных задач, рассуждения, схемы и многое другое ждет вас в этом разделе.
Тригонометрия — еще один важный раздел в математике, он связывает воедино и геометрию и алгебру, помогает осмыслить пространство. Подробно разобраны в этом разделе тригонометрические уравнения и неравенства. Приведены все необходимые формулы.

7 класс. Алгебра.

Решить неравенство t^2≤5t

05. 9k.26 января 2023

Больше или меньше? А если «меньше или равно»? Как решить неравенство? В этом уроке мы решим неравенство

5 класс. Математика.

Таблица умножения на 3

13.5k.23 января 2023

Сколько будет трижды три? Девять. А откуда мы это знаем? Из таблицы умножения на 3. О ней и пойдет речь

6 класс. Математика.

Решите примеры: 8 5/6+4 3/8 и 8 5/6-4 3/8

11.9k.18 января 2023

Два примера на проверку умений складывать и вычитать смешанные числа, то есть такие числа, которые содержат

5 класс. Математика.

Выполните действия: а) 3 2 /3+2 /3 б) 4 1/6 — 1 1/ 5 в) 12×5/18 г) 6: 1 1/5

01.1k.17 января 2023

Решать примеры с дробями можно легко и просто, если знать всего несколько правил — определение общего

5 класс. Математика.

Таблица умножения на 3

13.5k.

Сколько будет трижды три? Девять. А откуда мы это знаем?

5 класс. Математика.

Выполните действия: а) 3 2 /3+2 /3 б) 4 1/6 — 1 1/ 5 в) 12×5/18 г) 6: 1 1/5

01.1k.

Решать примеры с дробями можно легко и просто, если

5 класс. Математика.

Сколько всего двузначных чисел

11.9k.

Как записать, что у Маши двадцать пять карандашей

5 класс. Математика.

Сколько трёхзначных чисел

13.4k.

Подсчитаем сколько всего трехзначных чисел.

5 класс. Математика.

Таблица умножения на 2

3695

Как умножать на два? Что это вообще означает?

5 класс. Математика.

5 5 5 5 5 расставить знаки и скобки чтобы получилось 6, 7, 8, 9, 10

1795

Логическая задача. Даны числа 5 5 5 5 5, расставить

6 класс. 2

0938

Вычислите. 1) 2) 3) 4) Вычисление: 1) В первом примере

7 класс. Алгебра.

Абсолютная погрешность

1565

Не всегда получается точно измерить длину отрезка или

7 класс. Алгебра.

Формулы сокращенного умножения

01.3k.

Чтобы быстро умножить одно число на другое, придумали

7 класс. Алгебра.

Разность квадратов

12.6k.

Как быстро умножать алгебраические выражения?

7 класс. Алгебра.

Линейная функция y=kx+b и ее график

02.5k.

Если функция задана формулой , где и  — некоторые числа

8 класс. Алгебра.

Дискриминант — определение, свойства, геометрический смысл

85.9k.

Важная характеристика квадратных уравнений — их дискриминант.

8 класс. Алгебра.

Теорема Виета

23. 2

11.9k.2 декабря 2022

Правильное решение получить иногда совсем не просто, хотя под корнем кажется все прекрасно извлекается, но.

9 класс. Алгебра.

9.3.3. Определение арифметической прогрессии. Примеры

02.2k.22 декабря 2013

Числовую последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с

9 класс. Алгебра.

9.3.1. Числовая последовательность

022k.6 декабря 2013

Функция an=f (n) натурального аргумента n (n=1; 2; 3; 4;…) называется числовой последовательностью. Числа a1;

9 класс. Алгебра.

9.3.2. Арифметическая прогрессия. Теория

06.7k.25 сентября 2012

Числовую последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с

10 класс. Алгебра.

Формулы приведения

116.7k.

Формулы приведения относятся к тригонометрической функции

10 класс. Алгебра.

10.3.0. Вычисление производных

014.8k.

На этом занятии мы будем учиться применять формулы

10 класс. Алгебра.

10.2.6. Решение тригонометрических неравенств. Часть 6

03k.

На предыдущих занятиях мы решали тригонометрические

11 класс. Алгебра.

Показательные уравнения и методы решения показательных уравнений

56k.

В 10-11 классе в курсе алгебры изучаются показательные

11 класс. Алгебра.

Площадь криволинейной трапеции, ограниченной линиями

02.7k.

Как найти площадь криволинейной трапеции ограниченной прямыми?

11 класс. Алгебра.

11.1.9.2. Площадь криволинейной трапеции, прилегающей к оси Оу

02.9k.

Если криволинейная трапеция прилегает к оси Оу (рис.

11 класс. Алгебра.

11.1.9.2. Площадь криволинейной трапеции. Примеры

041k.

Площадь криволинейной трапеции, ограниченной сверху

Геометрия

Площадь трапеции

43.6k.

Формулы для вычисления площади всех видов трапеции

Геометрия

Площадь прямоугольника

214.6k.

Площадь прямоугольника очень часто требуется найти

Геометрия

Как рассчитать площадь круга — все формулы

116.7k.

Площадь круга часто требуется рассчитать в различных

5 класс. Тесты.

Тренажер таблицы умножения на 2 по возрастанию

0403

Порядок умножения на 2, в котором мы все начинаем учить

5 класс. Тесты.

Тренажер таблицы умножения на 2 (в разброс)

1272

Потренируйтесь в знании таблицы умножения на 2 на нашем

5 класс. Тесты.

Тренажер таблицы умножения на 2 с окошками для введения ответа

0304

Это интерактивный онлайн тренажер таблицы умножения на 2.

6 класс. Тесты.

Тест 6.9.2.1. Линейная функция и ее график

02.2k.

Математика. 6 класс.              Тест 9.

ГДЗ учебник по алгебре 8 класс Макарычев. 22. Формула корней квадратного уравнения Номер 534

1. Учебники
2. 8 класс
3. Алгебра 👍
4. Макарычев
5. №534

авторы: Макарычев, Миндюк, Нешков, Суворова.

издательство: «Просвещение» 2013 г

Раздел:

• Предыдущее
• Следующее

Решите уравнение:
а)

3×2−7x+4=0

;
б)

5×2−8x+3=0

;
в)

3×2−13x+14=0

;
г)

2y2−9y+10=0

;
д)

5y2−6y+1=0

;
е)

4×2+x−33=0

;
ж)

y2−10y−24=0

;
з)

p2+p−90=0

.

reshalka.com

Решение а

3×2−7x+4=0

D=72−4∗3∗4=49−48=1

x=7±12∗3

x1=7−12∗3=66=1

x2=7+12∗3=86=43=113

Ответ:

x1=1

;

x2=113

.

Решение б

5×2−8x+3=0

D=82−4∗5∗3=64−60=4

x=8±42∗5

x1=8−22∗5=610=0,6

x2=8+22∗5=1010=1

Ответ:

x1=0,6

;

x2=1

.

Решение в

3×2−13x+14=0

D=132−4∗3∗14=169−168=1

x=13±12∗3

x1=13−12∗3=126=2

x2=13+12∗3=146=73=213

Ответ:

x1=2

;

x2=213

.

Решение г

2y2−9y+10=0

D=92−4∗2∗10=81−80=1

y=9±12∗2

y1=9−12∗2=84=2

y2=9+12∗2=104=52=212

Ответ:

y1=2

;

y2=212

.

Решение д

5y2−6y+1=0

D=62−4∗5∗1=36−20=16

y=6±162∗5

y1=6−42∗5=210=0,2

y2=6+42∗5=1010=1

Ответ:

y1=0,2

;

y2=1

.

Решение е

4×2+x−33=0

D=12−4∗4∗(−33)=1+528=529

x=−1±5292∗4

x1=−1−232∗4=−248=−3

x2=−1+232∗4=228=114=234

Ответ:

x1=−3

;

x2=234

.

Решение ж

y2−10y−24=0

D=102−4∗1∗(−24)=100+96=196

y=10±1962

y1=10−142=−42=−2

y2=10+142=242=12

Ответ:

y1=−2

;

y2=12

.

Решение з

p2+p−90=0

D=12−4∗1∗(−90)=1+360=361

p=−1±3612

p1=−1−192=−202=−10

p2=−1+192=182=9

Ответ:

p1=−10

;

p2=9

.

• Предыдущее
• Следующее

Нашли ошибку?

Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом

Настройка уравнений | Алгебраические уравнения

В этой главе вы узнаете чтобы найти числа, которые делают некоторые утверждения верными. Заявление относительно неизвестного числа называется уравнением. Когда мы работаем, чтобы выяснить, какое число сделает уравнение верным, мы говорим, что мы решить уравнение. Число, которое делает уравнение верным, равно называется решением уравнения.

Настройка уравнений

Уравнение представляет собой математическое предложение, истинное для некоторых чисел, но ложное для других номеров. Ниже приведены примеры уравнения: 9х = 8\]

\(х + 3 = 11\) верно если \(х=8\), но ложно, если \(x = 3\).

Когда мы ищем число или числа, которые делают уравнение верным, мы говорим, что решим уравнение . Например, \(x = 4\) является решением уравнения \(2x + 8\), потому что оно делает \(2x +8\) истинным. (Проверьте: \(2 \times 4 = 8\)

Ищем числа, чтобы сделать утверждение верным

1. Следующие утверждения правда или ложь? Обосновать ответ. 93 = 8\), если \(х = -2\)

   ---

2. \(3x = -6\), если \(x = -3\)

   ---

3. \(3x = 1\), если \(x = 1\)

   ---

4. \(6x + 5 = 47\), если \(x = 7\)

   ---

Найдите исходное число. Показывать ваше рассуждение.

1. Число, умноженное на 10, равно 80.

   ---

2. Прибавьте к числу 83 и получите 100.

   ---

3. Разделите число на 5 и получите 4.

   ---

4. Умножьте число на 4 и получите 20.

   ---

5. Дважды число равно 100.

   ---

6. Число, возведенное в степень 5, равно 32.

   ---

7. Число, возведенное в степень 4, равно -81.

   ---

8. Пятнадцать раз число 90.

   ---

9. 93 добавлено к числу -3.

   ---

10. Половина числа равна 15.

    ---

Напишите уравнения ниже словами, используя «число» вместо буквенного символа \(Икс\). Тогда напишите, что вы думаете, что «число» есть в каждом случае.

Пример: \(4 +x = 23\). Четыре плюс число равно двадцати трем. Номер 19.

1. \(8x = 72\)

   ---

2. \( \frac{2x}{5} = 2 \)

   ---

3. \( 2x+ 5 = 21\)

   ---

4. \(12 + 9х = 30\)

   ---

5. \(30 — 2x = 40\)

   ---

6. \(5x + 4 = 3x+ 10\)

   ---

w3.org/1999/xhtml»> Решение уравнений методом проверки

Ответ на виду

1. Под таблицей приведены семь уравнений. Используйте таблицу, чтобы выяснить, для какого из заданных значений \(х\) будет верно, что левая часть уравнения равна Правая сторона.
   Вы можете прочитать решения уравнение из таблицы.

   \(х\)	-3	-2	-1	0	1	2	3	4
   \(2x + 3\)	-3	-1	1	3	5	7	9	11
   \(х + 4\)	1	2	3	4	5	6	7	8
   \(9 -х\)	12	11	10	9	8	7	6	5
   \(3x -2\)	-11	-8	-5	-2	1	4	7	10
   \(10x -7\)	-37	-27	-17	-7	3	13	23	33
   \(5x+3\)	-12	-7	-2	3	8	13	18	23
   \(10 — 3x\)	19	16	13	10	7	4	1	-2

   1. \(2x + 3 = 5x + 3\)

      ---

   2. \(5х + 3 = 9 — х\)

      ---

   3. \(2x + 3 = x+4\)

      ---

   4. \(10x -7 = 5x + 3\)

      ---

   5. \(3x -2 = x+4\)

      ---

   6. \(9 -х = 2х + 3\)

      ---

   7. \(10 -3x = 3x — 2\)

      ---

Два или более уравнений могут иметь одно и то же решение. Например, \(5x = 10\) и \(x + 2 = 4\) имеют одно и то же решение; \(x = 2\) является решением обоих уравнений.

Два уравнения называются эквивалентными , если они имеют одинаковые решение.

2. Какое из уравнений в вопрос 1 имеют те же решения? Объяснять.

   ---

3. Заполните приведенную ниже таблицу. Затем ответьте на следующие вопросы.

   Вы также можете выполнить поиск по сужение возможного решения уравнения.

   \(х\)	0	5	10	15	20	25	30	35	40
   \(2x + 3\)
   \(3x -10\)

   1. Можете ли вы найти решение для \(2x + 3 = 3x — 10\) в таблице?

      ---

   2. Что происходит со значениями из \(2x + 3\) и \(3x — 10\) при увеличении \(x\)? Делать они становятся больше или меньше?

      ---

   3. Есть ли точка, в которой значение \(3x — 10\) становится больше или меньше значения \(2x + 3\) при увеличении значения \(x\)? Если так, между какими \(x\)-значениями это происходит?

      ---

      Точка, где два выражения равны, называется безубыточностью пункт .

   4. Теперь, когда вы сузили круг поиска возможное решение может быть, попробуйте другие возможные значения для \(x\), пока не найдете для какого значения \(x\) утверждение \(2x + 3 = 3x — 10\) верно.

      ---

      «Поиск» решения уравнение с помощью таблиц или путем сужения до возможное решение называется решение от осмотр .

Другие примеры

Поиск и проверка решений

1. Какое решение для уравнения ниже?
   1. \(х — 3 = 4\)

      ---

   2. \(х + 2 = 9\)

      ---

   3. \(3x = 21\)

      ---

   4. \(3x + 1 = 22\)

      ---

Когда определенный номер решения уравнения мы говорим, что число удовлетворяет уравнению.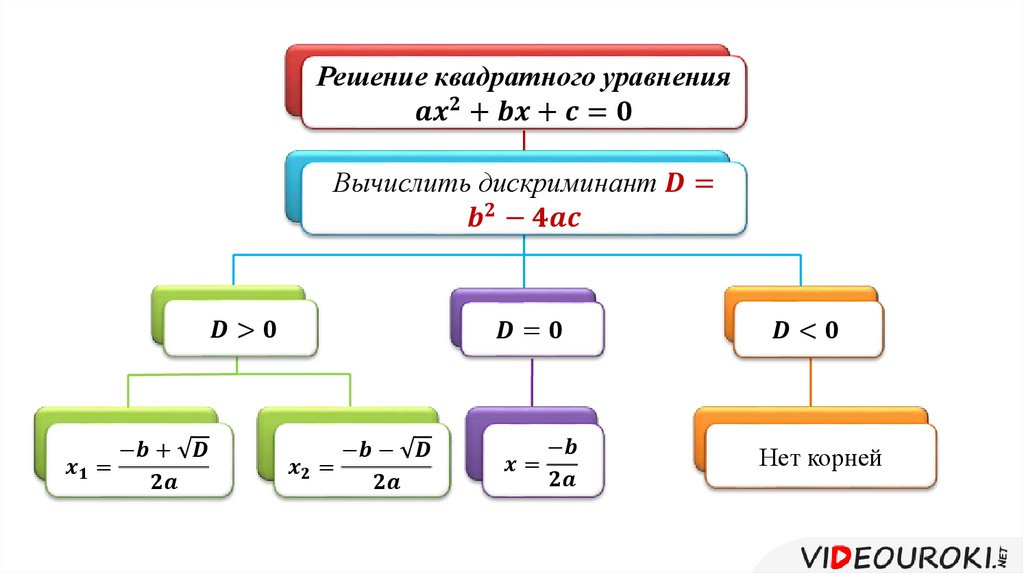 Например, \(х=4\) удовлетворяет уравнению \(3x=12\), потому что \(3 \times 4 = 12\).

2. Выберите номер в скобках, который удовлетворяет уравнению. Объяснить ваш выбор.
   1. \(12x = 84\) {5; 7; 10; 12}

      ---

   2. \( \frac{84}{x} = 12\) {-7; 0; 7; 10}

      ---

   3. \(48 = 8k + 8\) {-5; 0; 5; 10}

      ---

   4. \(19 — 8m = 3\) {-2; -1; 0; 1; 2}

      ---

   5. \(20 = 6у — 4\) {3; 4; 5; 6}

      ---

   92 = 9\) {1; 2; 3; 4}

   ---

3. Что делает следующее уравнения верны? Проверить ответы.
   1. \(м + 8 = 100\)

      ---

   2. \( 80 = х + 60 \)

      ---

   3. \(26 — к = 0 \)

      ---

   4. \(105 \умножить на 0\)

      ---

   5. \(к\умножить на 10 = 10\)

      ---

   6. \(5x = 100\)

      ---

   7. \( \frac{15}{t} = 5 \)

      ---

   8. \( 3 = \frac{t}{5} \)

      ---

4. Решите приведенные ниже уравнения с помощью осмотр. Проверить ответы.
   1. \(12х+14=50\)

      ---

   2. \(100 = 15м + 25\)

      ---

   3. \( \frac{100}{x} =20\)

      ---

   4. \( 7м + 5 = 40\)

      ---

   5. \(2x + 8 = 10\)

      ---

   6. \(3x + 10 = 31\)

      ---

   7. \(-1 + 2x = -11\)

      ---

   8. \(2 + \frac{x}{7} = 5\)

      ---

   9. \(100 = 64 + 9x\)

      ---

   10. \( \frac{2x}{6}= 4\)

       ---

Предварительная алгебра онлайн и планы уроков

Посмотрите наши демонстрации уроков!

Математика в восьмом классе обычно представляет собой курс предварительной алгебры, который помогает подготовить учащихся к алгебре в старших классах. Наша учебная программа по математике для 8-го класса может использоваться либо в качестве основной программы домашнего обучения, либо в качестве дополнения к другой учебной программе домашнего обучения или традиционной школе. Следующая информация объяснит, какие шаги вы должны предпринять, чтобы достичь целей и задач вашего ребенка по математике в 8-м классе, и как может помочь наша учебная программа по математике для 8-го класса.

Что по математике должен знать восьмиклассник?

Математическая программа для 8-го класса должна охватывать различные области математики, а не только арифметику. Основными разделами программы по математике для 8-го класса являются числовой смысл и операции, алгебра, геометрия и пространственный смысл, измерения, анализ данных и вероятность. Хотя эти математические направления могут вас удивить, все они являются важными уроками для математической программы 8-го класса.

Эти навыки улучшат беглость математики и помогут опираться на математические факты, концепции и стратегии, полученные в прошлом, что сделает будущие успехи более достижимыми. Вот некоторые темы, которые восьмиклассники уже должны знать по математике:

• Запись чисел в словесной, стандартной, расширенной и экспоненциальной записи
• Определение и использование соотношений и ставок
• Умножение и деление положительных и отрицательных рациональных чисел
• Нахождение периметра и площади двумерных фигур
• Идентификация и построение упорядоченных пар в четырех квадрантах и ​​вдоль осей
• Расчет вероятностей независимых и зависимых событий

Если вашему учащемуся необходимо повторить математические концепции 7-го класса, вы можете легко получить доступ к этим урокам благодаря нашим гибким параметрам уровня обучения, которые дают вам доступ на один уровень выше и на один ниже уровня по умолчанию для вашего ребенка.

Математические задачи для восьмого класса

Ниже приводится общий список некоторых целей обучения математике, которых должны достичь восьмиклассники:

Определите рациональные и иррациональные числа и опишите их значения.
Вычисление и аппроксимация главных квадратных корней.
Определение и преобразование фигуры на координатной плоскости.
Решение задач с двумя переменными с помощью линейных уравнений.
Дайте определение и различие между различными типами методов выборки.
Использовать технологию для определения среднего значения, медианы, режима и диапазона набора реальных данных.

Математический прицел и последовательность для восьмиклассников

 Глава 1. «Системы счисления»

 Урок 1. Экспоненциальное представление

Представление чисел от нуля до единицы в экспоненциальном представлении.

 Урок 2. Рациональные и иррациональные числа

Определите рациональные и иррациональные числа и опишите их значения.

 Урок 3. Абсолютное значение

Определите и объясните абсолютное значение.

 Глава 2. Сравнение чисел с операциями в экспоненциальном представлении

 Урок 2. Сравнение небольших чисел в экспоненциальном представлении

Сравнение небольших чисел в экспоненциальном представлении.

 Урок 3. Сложение и вычитание чисел в экспоненциальном представлении

Сложение и вычитание чисел в экспоненциальном представлении.

Урок 4: Использование научной нотации с технологией

Используйте научные нотации с технологией

Глава 3: «Реальные числа»

Урок 1: Повторяя. дроби.

 Урок 2. Корни

Вычисление и приближение главных квадратных корней.

 Урок 3. Использование корней для решения уравнений

Использование корней для решения уравнений.

 Урок 4. Сравнение и упорядочивание

Сравнивайте и упорядочивайте числа во многих формах, включая дроби, десятичные дроби, экспоненциальное представление, абсолютное значение и радикалы.

 Урок 5. Оценка

Используйте оценку для ситуаций, когда используются действительные числа.

 Урок 6. Свойства

Применение свойств для решения задач с вещественными числами.

 Урок 7. Операции с действительными числами

Упрощайте числовые выражения с помощью действительных чисел.

 Глава 4. «Теория чисел»

 Урок 1. Правила делимости

Используйте правила делимости для решения задач.

 Урок 2. Множественные представления

Представление чисел в десятичной системе счисления в других системах счисления (двойке, пятерке и восьмерке) и наоборот.

 Урок 3. Простые и составные числа

Определение чисел как взаимно простых.

 Глава 5: «Отношение, доля и процент»

 Урок 1: Скорость изменения

Опишите и используйте скорость изменения для решения проблем.

 Урок 2.

Пропорции

Используйте отношения пропорциональности, чтобы найти меры длины, веса или массы, а также вместимости или объема.

 Урок 3. Проценты

Решайте реальные задачи с процентами больше 100.

 Глава 6: «Вычисления в реальном мире»

 Урок 1: Операции

Решайте реальные задачи с рациональными числами (включая целые, десятичные дроби и дроби).

 Урок 2: Реальные задачи

Решайте реальные задачи с отношениями, коэффициентами, пропорциями и процентами.

 Урок 3. Многоэтапные задачи

Решайте реальные двух- или трехэтапные задачи с целыми числами, десятичными дробями, дробями, отношениями, долями, пропорциями и процентами.

 Глава 7. Выражения и уравнения

 Урок 2. Выражения с показателями степени

Подставьте рациональные числа в выражения с показателями степени и радикалами.

 Урок 3. Выражения и уравнения

Преобразование словесных выражений и уравнений в алгебраические выражения и уравнения (включая одну или несколько переменных и показателей степени).

 Урок 4. Выражения, уравнения и неравенства

Перевод словесных выражений и предложений в алгебраические неравенства и наоборот.

 Урок 5. Выражения в реальном мире

Используйте переменные для представления неизвестных величин в реальных ситуациях.

 Урок 6. Упрощение

Объединяйте и упрощайте алгебраические выражения максимум с двумя переменными.

 Урок 7. Подстановка

Вычисляйте алгебраические выражения и уравнения, подставляя целые значения вместо переменных и упрощая.

 Урок 8. Неравенства

Алгебраически решать линейные неравенства с одной переменной.

 Глава 8. «Нахождение решений и решение уравнений»

 Урок 1. Определение количества решений линейного уравнения

Определение количества решений линейного уравнения.

 Урок 2. Решение уравнений с переменными в обеих частях

Решите уравнения с переменными в обеих частях.

 Урок 3. Решение уравнений, требующих распределительного свойства

Решите уравнения, требующие распределительного свойства.

 Урок 4. Решение уравнений, требующих объединения одинаковых членов

Решайте уравнения, требующие объединения одинаковых членов.

 Глава 9: «Системы уравнений»

 Урок 1: Анализ систем уравнений

Анализ систем уравнений.

 Урок 2. Определение количества решений линейного уравнения

Определение количества решений линейного уравнения.

 Глава 10. «Плоская геометрия»

 Урок 1. Геометрические свойства

Используйте свойства параллельности, перпендикулярности и симметрии для решения реальных задач.

 Урок 2. Многоугольники

Сравните и опишите свойства выпуклых и вогнутых многоугольников.

 Урок 3. Теорема Пифагора

Примените теорему Пифагора для решения реальных задач.

 Урок 4. Соответствие и сходство

Определите соответствие и сходство в реальных ситуациях и обосновайте.

 Урок 5. Преобразования

Определение и выполнение преобразований (отражение, перемещение, вращение и расширение) фигуры на координатной плоскости.

 Урок 6. Отношения пропорциональности

Определите, как изменения размеров влияют на площадь и периметр.

 Глава 11. «Расширенные преобразования»

 Урок 1. Преобразование линий и сегментов линий

Преобразование линий и сегментов линий.

 Урок 2. Преобразование углов

Преобразование углов.

 Урок 3. Преобразование параллельных линий

Преобразование параллельных линий.

 Урок 4. Понимание конгруэнтности

Понимание конгруэнтности.

 Урок 5. Использование последовательности преобразований

Использование последовательности преобразований.

 Урок 6. Понимание похожих фигур

Понимание похожих фигур.

 Урок 7. Описание последовательностей трансформаций, демонстрирующих сходство

Опишите последовательности трансформаций, которые показывают сходство.

 Глава 12. «Треугольники»

 Урок 1. Неформальное доказательство теорем о треугольниках

Неформальное доказательство теорем о треугольниках.

 Урок 2. Понимание углов, образующихся при пересечении параллельных прямых секущей

Понимание углов, образующихся при пересечении параллельных прямых секущей.

 Урок 3. Изучение подобия углов

Исследуйте сходство углов.

 Глава 13. «Расширенная теорема Пифагора»

 Урок 1. Использование обратной теоремы Пифагора

Используйте обратную теорему Пифагора.

 Урок 2. Применение теоремы Пифагора в трех измерениях

Применение теоремы Пифагора в трех измерениях.

 Урок 3. Применение теоремы Пифагора в координатной плоскости

Примените теорему Пифагора в координатной плоскости.

 Глава 14. «Трехмерная геометрия»

 Урок 1. Объем

Найдите объем пирамид, призм и конусов.

 Урок 2. Применение формул объема

Применение формул объема.

 Урок 3. Площадь поверхности

Найдите площадь поверхности пирамид, призм и конусов.

 Урок 4. Правильные и неправильные многоугольники

Сравните правильные и неправильные многоугольники.

 Урок 5. Измерение угла

Нахождение меры угла в двумерных фигурах и двухмерных сторонах трехмерных фигур на основе геометрических соотношений.

 Урок 6. Соотношения пропорциональности

Определите взаимосвязь между объемом или площадью поверхности и размером.

 Глава 15. «Измерение»

 Урок 1.

Шкала

Интерпретация и применение различных шкал, включая числовые линии, графики, модели и карты.

 Урок 2: Оценка

Выбрать инструменты для измерения величин и размеров с заданной степенью точности и определить максимально возможную погрешность измерения.

 Урок 3. Значащие цифры

Определите количество значащих цифр по отношению к наименее точной единице измерения и примените их к реальному миру.

Глава 16. «Построение графиков»

 Урок 1. Таблицы и упорядоченные пары

 Урок 2. Уравнения для линий

Графики линейных уравнений в стандартной форме.

 Урок 3. Линейные неравенства

Определение и графическое отображение неравенств на числовой прямой.

 Урок 4. Неравенства

Определение и графическое отображение неравенств в координатной плоскости.

 Урок 5. Применение линейных неравенств

Решение задач с двумя переменными с помощью линейных неравенств. Глава 17. «Линейные отношения»

 Урок 2. Наклон линии

По графику линии определите наклон.

 Урок 3. Написание уравнений в форме наклона и пересечения

Зная наклон и пересечение по оси Y, напишите уравнение.

 Урок 4. Поиск правила функции

Найдите правило функции для описания линейной зависимости с помощью таблиц связанных переменных ввода-вывода.

 Урок 5. Определение линейности функции

Используя информацию из таблицы, графика или правила, определите, является ли функция линейной, и выровняйте ее.

 Глава 18. «Понимание, использование и интерпретация уклона»

 Урок 1. Отображение пропорциональных отношений и интерпретация уклона

Графики пропорциональных отношений и интерпретация уклона.

 Урок 2. Использование похожих треугольников для определения уклона

Использование подобных треугольников для определения уклона.

 Урок 3. Использование формы пересечения наклона

Используйте форму пересечения наклона.

 Урок 4. Интерпретация y = mx + b как линейной функции

Интерпретация y = mx + b как линейной функции.

 Глава 19. «Функции»

 Урок 1. Распознавание функций

Распознавание функций.

 Урок 2. Сравнение функций, представленных в разных формах

Сравните функции, представленные в разных формах.

 Урок 3. Интерпретация y = mx + b как линейной функции

Интерпретируйте y = mx + b как линейную функцию.

 Урок 4. Построение линейных функций

Построение линейных функций.

 Урок 5. Описание функциональной связи с помощью анализа графика

Описание функциональной связи с помощью анализа графика.

 Урок 6. Набросок графиков функций

Набросок графиков функций.

 Глава 20: «Вероятность»

 Урок 1: Условная вероятность

Расчет условных вероятностей и вероятностей зависимых событий.

 Урок 2. Методы выборочного контроля

Дайте определение и различие между различными типами методов выборочного контроля.

 Урок 3. Применение выборки

Используйте различные методы выборки для сбора данных.

 Урок 4. Выборочная погрешность

Определите, является ли выборка необъективной.

 Глава 21. «Данные и статистика»

 Урок 1. Представление данных проявления приводят к различным интерпретациям.

 Урок 2. Статистика

Определите и объясните, как статистика и графики могут быть использованы для введения в заблуждение.

 Урок 3. Среднее значение, медиана и мода

Определите соответствующие меры центральной тенденции для данной ситуации или набора данных.

 Урок 4. Технология

Используйте технологию для определения среднего значения, медианы, режима и диапазона набора реальных данных.

Почему стоит выбрать Time4Learning Учебная программа по математике для восьмого класса на дому

Наш онлайн-учебный план по математике для 8-го класса можно использовать в качестве основной программы домашнего обучения или в дополнение к другим учебным планам или школьным программам.