Решение задания В15 (системы логических уравнений)

1. Решение задания В15 (системы логических уравнений)

Вишневская М.П., МАОУ «Гимназия №3»
18 ноября 2013 г., г. Саратов

2. Задание В15 — одно из самых сложных в ЕГЭ по информатике!!!

Проверяются умения:
• преобразовывать выражения, содержащие логические
переменные;
• описывать на естественном языке множество значений
логических переменных, при которых заданный набор
логических переменных истинен;
• подсчитывать число двоичных наборов, удовлетворяющих
заданным условиям.
Самое сложное, т.к. нет формальных правил, как это сделать,
требуется догадка.

3. Без чего не обойтись!

4. Без чего не обойтись!

5. Условные обозначения

• конъюнкция :A /\ B , A B, AB, А&B, A and B
• дизъюнкция: A \/ B , A+ B, A | B, А or B
• отрицание: A , А, not A
• эквиваленция: A В, A B, A B
• исключающее «или»: A B , A xor B

6. Метод замены переменных

Сколько существует различных наборов значений логических
переменных х1, х2, …, х9, х10, которые удовлетворяют всем
перечисленным ниже условиям:
((x1 ≡ x2) \/ (x3 ≡ x4)) /\ (¬(x1 ≡ x2) \/ ¬(x3 ≡ x4)) =1
((x3 ≡ x4) \/ (x5 ≡ x6)) /\ (¬(x3 ≡ x4) \/ ¬(x5 ≡ x6)) =1
((x5 ≡ x6) \/ (x7 ≡ x8)) /\ (¬(x5 ≡ x7) \/ ¬(x7 ≡ x8)) =1
((x7 ≡ x8) \/ (x9 ≡ x10)) /\ (¬(x7 ≡ x8) \/ ¬(x9 ≡ x10)) =1
В ответе не нужно перечислять все различные наборы х1, х2,
…, х9, х10, при которых выполняется данная система
равенств. В качестве ответа необходимо указать количество
таких наборов (демо-версия 2012 г.)

7. Решение Шаг 1. Упрощаем, выполнив замену переменных

t1 =
t2 =
t3 =
t4 =
t5 =
x1 x2
x3 x4
x5 x6
x7 x8
x9 x10
¬(t1 ≡ t2 ) =1
¬(t2 ≡ t3 ) =1
¬(t3 ≡ t4 ) =1
¬(t4 ≡ t5 ) =1
После упрощения:
(t1 \/ t2) /\ (¬t1 \/ ¬ t2 ) =1
(t2 \/ t3) /\ (¬t2 \/ ¬ t3 ) =1
(t3 \/ t4) /\ (¬t3 \/ ¬ t4 ) =1
(t4 \/ t5) /\ (¬t4 \/ ¬ t5 ) =1
Рассмотрим одно из уравнений:
(t1 \/ t2) /\ (¬t1 \/ ¬ t2 ) =1
Очевидно, оно =1 только если одна из
переменных равна 0, а другая – 1.
Воспользуемся формулой для выражения
операции XOR через конъюнкцию и
дизъюнкцию:
(t1 \/ t2) /\ (¬t1 \/ ¬ t2 ) = t1 t2 = ¬(t1 ≡ t2 ) =1

8. Шаг2. Анализ системы

¬(t1 ≡ t2 ) =1
¬(t2 ≡ t3 ) =1
¬(t3 ≡ t4 ) =1
¬(t4 ≡ t5 ) =1
t1
t2
t3
t4
t5
0
1
0
1
0
1
0
1
0
1
Т.к. tk = x2k-1 ≡ x2k (t1 = x1 x2,…. ), то каждому значению tk
соответствует две пары значений x2k-1 и x2k ,
например:
tk=0 соответствуют две пары — (0,1) и (1,0) ,
а tk=1 – пары (0,0) и (1,1).

9. Шаг3. Подсчет числа решений.

Каждое t имеет 2 решения, количество t – 5. Т.о. для
переменных t существует 25 = 32 решения.
Но каждому t соответствует пара решений х, т.е. исходная
система имеет 2*32 = 64 решения.
Ответ: 64

10. Метод исключения части решений

Сколько существует различных наборов значений
логических переменных х1, х2, …, х5, y1,y2,…, y5, которые
удовлетворяют всем перечисленным ниже условиям:
(x1→ x2)∧(x2→ x3)∧(x3→ x4)∧(x4→ x5) =1;
( y1→ y2)∧( y2→ y3)∧( y3→ y4)∧( y4→ y5) =1;
y5→ x5 =1.
В ответе не нужно перечислять все различные наборы х1,
х2, …, х5, y1,y2,…, y5, при которых выполняется данная
система равенств. В качестве ответа необходимо указать
количество таких наборов.

11. Решение. Шаг1. Последовательное решение уравнений

Первое уравнение – конъюнкция нескольких операций
импликации, равна 1, т. е. каждая из импликаций истинна.
Импликация ложна только в одном случае, когда 1 0, во всех
других случаях (0 0, 0 1, 1 1) операция возвращает 1.
Запишем это в виде таблицы:
х1 1
х2 1
х3 1
х4 1
х5 1
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1

12. Шаг1. Последовательное решение уравнений

Т.о. получено 6 наборов решений для х1,х2,х3,х4,х5:
(00000), (00001), (00011), (00111), (01111), (11111).
Рассуждая аналогично, приходим к выводу, что для y1, y2, y3,
y4, y5 существует такой же набор решений.
Т.к. уравнения эти независимы, т.е. в них нет общих
переменных, то решением этой системы уравнений (без учета
третьего уравнения) будет 6*6=36 пар «иксов» и «игреков».
Рассмотрим третье уравнение:
y5→ x5 =1
Решением являются пары:
Не является решением пара:
0
0
1
1
0
1
1
0

13. Сопоставим полученные решения

Там, где y5=1, не подходят x5=0. таких пар 5.
Количество решений системы : 36-5=31.
Ответ: 31
Понадобилась комбинаторика!!!

14. Метод динамического программирования

Сколько различных решений имеет логическое уравнение
x1 → x2 → x3 → x4 → x5 → x6 = 1,
где x1, x2, …, x6 – логические переменные? В ответе не
нужно перечислять все различные наборы значений
переменных, при которых выполнено данное равенство. В
качестве ответа нужно указать количество таких наборов.

15. Решение Шаг1. Анализ условия

1. Слева в уравнении последовательно записаны операции
импликации, приоритет одинаков.
2. Перепишем:
((((X1 → X2) → X3) → X4) → X5) → X6 = 1
NB! Каждая следующая переменная зависит не
от предыдущей, а от результата предыдущей
импликации!

16. Шаг2. Выявление закономерности

Рассмотрим первую импликацию, X1 → X2. Таблица
истинности:
X1
X2
X1 →X2
0
0
1
0
1
1
1
0
0
1
1
1
Из одного 0 получили 2 единицы, а из 1 получили один
0 и одну 1. Всего один 0 и три 1, это результат первой
операции.

17. Шаг2. Выявление закономерности

Подключив к результату первой операции x3 , получим:
F(x1,x2)
x3
F(x1,x2) x3
0
0
0
1
1
1
1
1
1
0
1
0
0
1
0
1
1
1
1
1
0
1
0
1
Из двух 0 – две
1, из каждой 1
(их 3) по
одному 0 и 1
(3+3)

18. Шаг 3. Вывод формулы

,
Шаг 3. Вывод формулы
Т.о. можно составить формулы для вычисления количества
нулей Ni и количества единиц Ei для уравнения с i
переменными:
Ni Ei 1
Ei 2 Ni 1 Ei 1
N1 E1 1

19. Шаг 4. Заполнение таблицы

:
Шаг 4. Заполнение таблицы
Заполним слева направо таблицу для i=6, вычисляя число
нулей и единиц по приведенным выше формулам; в таблице
показано, как строится следующий столбец по предыдущему:
число
переменных
Число нулей
Ni
Число
единиц Ei
Ответ: 43
1
2
3
4
5
6
1
1
3
5
11
21
1
2*1+1
=3
2*1+3=
5
11
21
43

20.

Метод с использованием упрощений логических выраженийСколько различных решений имеет уравнение
((J → K) →(M N L)) ((M N L) → (¬J K)) (M → J) = 1
где J, K, L, M, N – логические переменные? В ответе не нужно
перечислять все различные наборы значений J, K, L, M и N, при
которых выполнено данное равенство. В качестве ответа Вам
нужно указать количество таких наборов.

21. Решение

1. Заметим, что J → K = ¬J K
2. Введем замену переменных:
J → K=А, M N L =В
3. Перепишем уравнение с учетом замены:
(A → B) (B → A) (M → J)=1
4.
(A B) (M → J)=1
5. Очевидно, что A B при одинаковых значениях А и В
6. Рассмотрим последнюю импликацию M → J=1
Это возможно, если:
a) M=J=0
b) M=0, J=1
c) M=J=1

22. Решение

7. Т.к. A B, то ¬J K= M N L
8. При M=J=0 получаем 1 + К=0. Нет решений.
9. При M=0, J=1 получаем 0 + К=0, К=0, а N и L — любые ,
4 решения:
K N L
0
0
0
0
0
1
0
1
0
0
1
1

23.

Решение10. При M=J=1 получаем 0+К=1*N*L, или K=N*L,
4 решения:
K N L
0 0 0
0 0 1
0 1 0
1 1 1
11. Итого имеет 4+4=8 решений
Ответ: 8

24. Источники информации:

• О.Б. Богомолова, Д.Ю. Усенков. В15: новые задачи и новое
решение // Информатика, № 6, 2012, с. 35 – 39.
• К.Ю. Поляков. Логические уравнения // Информатика, № 14,
2011, с. 30-35.
• http://ege-go.ru/zadania/grb/b15/, [Электронный ресурс].
• http://kpolyakov.narod.ru/school/ege.htm, [Электронный
ресурс].

Дистанционные мероприятия

      ДИСТАНТ-МЕРОПРИЯТИЯ

      семинары, мастер-классы, практикумы, лекции

       Информатика:

  1. Использование онлайн-компиляторов для решения задач ЕГЭ по Информатике.
  2. Исследование биометрических шаблонов и оценка их объема.
  3. Компьютерный ЕГЭ по информатике: решаем новые и старые задачи ЕГЭ с помощью компьютер.
  4. Метод прогноза рекламных бюджетов.
  5. Моделирование закона сохранения импульса в условиях гравитации с помощью графики на языке C# (Си-шарп).
  6. Основы автоматизированного проектирования и компьютерного моделирования.
  7. Особенности циклов с параметром в разных языках программирования.
  8. Построение программ, моделирующих движение летательных аппаратов, на языке С++.
  9. Применение LabView для физических расчетов визуализации данных.
  10. Разработка новостного модуля на языке С++
  11. Сегментация клиентской базы с использованием средств Excel.
  12. Создание управляющей программы для станка с числовым программным управлением.
  13. Цифровая схемотехника и алгебра логики: создание цифровых устройств в онлайн-симуляторе.

     

       Физика:

  1. Измерение параметров взрыва газовоздушной смеси в воздухе.
  2. Изучение движения снаряда, управляемого с помощью импульсной коррекции.
  3. Изучение движения тела, брошенного под углом к горизонту.
  4. Изучение явлений дифракции и интерференции на примере фотонных кристаллов.
  5. Использование явления наведения ЭДС для измерения твердости материалов с использованием твердомера.
  6. Исследование влияния атмосферного сопротивления на полёт тела, брошенного под углом к горизонту.
  7. Исследование эффекта Доплера при передаче электромагнитных волн на примере приёма информации со спутника.
  8. Определение скорости пули и её максимальной кинетической энергии.
  9. Определение температурного коэффициента сопротивления металла.
  10. Орбиты и простейшие манёвры искусственных спутников земли.
  11. Основы биометрии и биометрические сканеры.
  12. Особенности решения многоуровневых заданий с развернутым ответом по электродинамике.
  13. Особенности решения многоуровневых заданий с развернутым ответом по молекулярной физике и термодинамике.
  14. Особенности решения многоуровневых заданий с теоретическим обоснованием по механике.
  15. Ток в различных средах. Свойства полупроводников.
  16. Упругая деформация как параметр настройки технических устройств.
  17. Физические принципы регистрации отпечатков пальцев
  18. Экспериментальное изучение процесса работы теплового двигателя.
  19. Экспериментальное изучение теплофизических свойств материалов.

     

      Математика:

  1. Выбор эмпирической формулы и нахождение ее параметров (восстановление функции по заданному набору ее значений).
  2. Методы теории чисел и алгебры в примерах и практических задачах.
  3. Нахождение экстремальных значений функций при решении практических инженерных задач.
  4. Орбиты и простейшие манёвры искусственных спутников Земли.
  5. Особенности решения многоуровневых заданий с развернутым ответом по геометрической оптике.
  6. Построение идеальной трассы самолёта над поверхностью Земли с применением основ сферической тригонометрии.
  7. Построение разверток и сечений многогранников.
  8. Приближенное решение уравнений с одним неизвестным методами половинного деления, хорд и касательных и т. д.
  9. Применение производной в приближённых вычислениях с использованием формулы Эйлера и рядов Тейлора.
  10. Применение производных при решении задач ЕГЭ.
  11. Применение теорем косинусов и синусов в задаче приближённого расчёта торпедной атаки.
  12. Решение параметрических уравнений, неравенств и их систем.
  13. Решение систем линейных уравнений и неравенств в задачах оптимизации.

 

Занятия проводят ведущие учёные и специалисты МГТУ им. Н. Э. Баумана, участие бесплатное, регистрация обязательна

Периоды обучения: октябрь – декабрь; февраль – май

 

Актуальное расписание занятий

 

 

CS по алгебре | Code.org

Работает на Bootstrap, предпочтительный поставщик для профессионального развития

Code.org сотрудничает с Bootstrap для разработки учебной программы, которая обучает алгебраическим и геометрическим понятиям с помощью компьютерного программирования. Два десятичасовых курса от Code.org посвящены таким понятиям, как порядок операций, декартова плоскость, композиция и определение функций, а также решение текстовых задач. Или посетите Bootstrap, чтобы изучить их более длинные курсы Bootstrap:1 и Bootstrap:2, которые преподают больше математических концепций и программирования. Смещая классную работу с абстрактных задач с карандашом и бумагой на серию соответствующих задач программирования, CS в алгебре Code. org демонстрирует, как алгебра применяется в реальном мире, используя захватывающий практический подход для создания чего-то классного.

Два курса

CS по алгебре, курс A

Первые 10 часов курса дают учащимся базовые навыки и знания, необходимые для начала использования компьютерного программирования в качестве инструмента для изучения и разработки алгебраических функций. Студенты познакомятся с графическим языком программирования, разработанным для обучения алгебре, благодаря которому они получат более глубокое понимание порядка операций, создадут изображения с алгебраическими выражениями и изучат технику создания функций, называемую «Рецепт проектирования». К концу курса А учащиеся будут иметь инструменты, необходимые для превращения текстовых задач из собственного класса алгебры в функции, которые можно использовать в качестве мини-приложений.

CS по алгебре, курс B

Для тех, кто хочет пойти дальше, второй 10-часовой курс строится на навыках, которые учащиеся развили на курсе A посредством разработки простой видеоигры. Учащиеся углубятся в пересечение математики и компьютерных наук, изучая такие темы, как логическая логика, кусочные функции и обнаружение столкновений с помощью теоремы Пифагора, используя эти концепции для построения вспомогательных функций, которые в конечном итоге будут управлять логикой в ​​их кульминационной игре.

Согласовано со стандартами

Оба курса CS in Algebra приведены в соответствие с Common Core Standards for Mathematics, что позволяет плавно интегрировать нашу учебную программу в учебный процесс. CS in Algebra также является моделью реализации Common Core Standards for Mathematical Practice, предлагающей четкие педагогические рекомендации по всем восьми практическим стандартам. Наша учебная программа также соответствует нескольким стандартам CSTA (Ассоциации учителей информатики) для уровней 1 (классы K-6) и 2 (классы 6-9).). Для получения дополнительной информации вы можете просмотреть наше полное соответствие стандартам.

В чем разница между CS в алгебре и Bootstrap?

Курс CS по алгебре Code. org — это адаптация учебного плана Bootstrap. Основная цель нашей модификации состояла в том, чтобы объединить содержание и педагогику Bootstrap с нашим блочным языком, системой онлайн-обучения и парадигмой обучения на основе строительных лесов. Кроме того, мы разделили исходный контент из Bootstrap на два отдельных курса, чтобы упростить внедрение для учителей, которые обеспокоены тем, что им не хватает времени на полные 20 часов. И, начиная с 2016-2017 годов, личное профессиональное развитие Code.org будет сосредоточено на курсе A. Для школ, которые хотят больше инвестировать в CS, Bootstrap предлагает более глубокую учебную программу, которая дает классу гибкость, позволяющую выходить за рамки 20 часов и дольше. семинар по профессиональному развитию человека, охватывающий 20 часов материала. В зависимости от потребностей вашей школы или класса каждая учебная программа предлагает различное сочетание педагогики, содержания и учебного плана:

Code.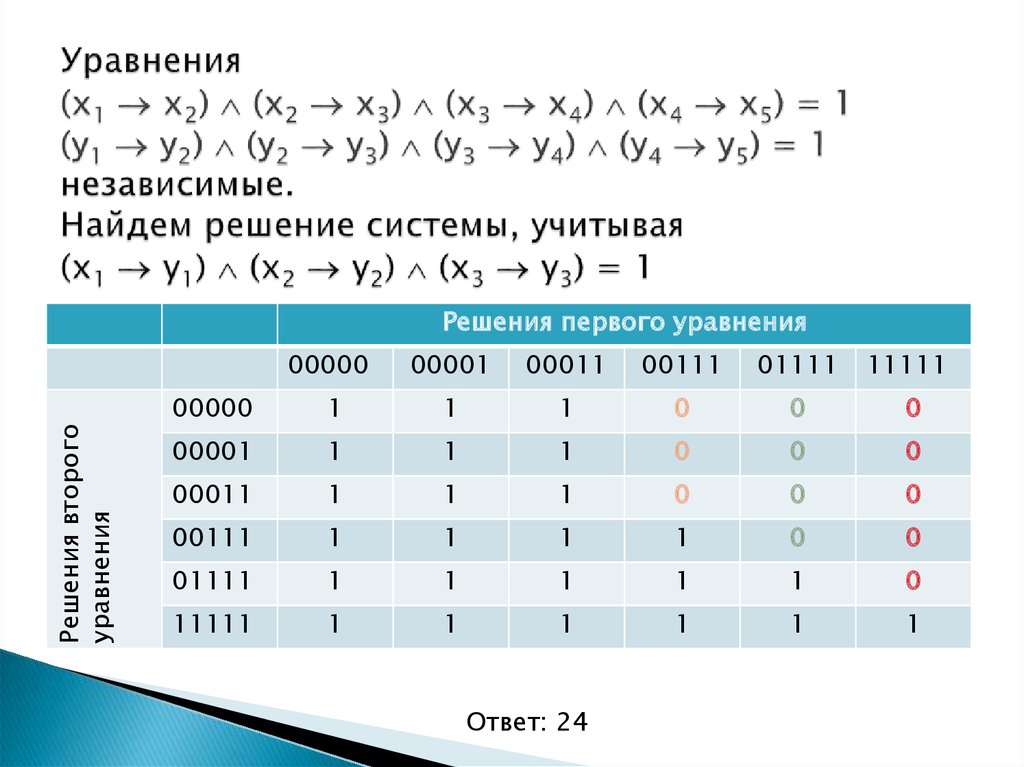 org CS по алгебре Бутстрап
Язык программирования Блочный
Текстовый
Учебные леса Леса на основе головоломок для всех уроков программирования в сочетании с упражнениями с карандашом и бумагой на основе псевдокода.
Работа с карандашом и бумагой в рабочей тетради с использованием того же текстового языка, который учащиеся будут использовать в Интернете.
Фокус деятельности Комбинация структурированных головоломок и открытых задач Решение открытых задач
Требуется компьютер Для решения головоломок по программированию требуется компьютер. Уроки без подключения к сети полностью автономны, а некоторые действия по программированию включают дополнительные страницы рабочей тетради. Все действия Bootstrap поддерживаются страницей рабочей книги, которую можно выполнять без компьютера.
Поддерживающие инструменты Создание студенческой учетной записи и управление ею
Монитор прогресса класса
Средство просмотра решений		 Вход в гугл
Средство просмотра решений
Дополнительные материалы Слайды для уроков
Действия по вызову
Рубрики
Ученик и учитель смотрят видео		 Слайды для уроков
Действия по вызову
Рубрики
Домашнее задание
Разминка
Выходные листы
оценок
Дополнительные уроки
Путь для продолжающих обучение CS по алгебре, курс B
Начальная загрузка: 1		 Начальная загрузка: 2
Программы обработки изображений
Как разрабатывать программы
Оценка и публикация Проходит независимую оценку Независимая оценка с опубликованными результатами передачи
Повышение квалификации нет Очные семинары, охватывающие весь курс
Учебная программа Курс А
Порядок операций и круги оценки
Типы данных (числа, строки и изображения)
Переменные
Контракты — домен и диапазон
Определение линейных функций
Рецепт дизайна

Курс В
Видеоигры и координатные плоскости
функций для анимации
Логические значения и обнаружение границ
Условные операторы и кусочные функции
Обнаружение столкновений и теорема Пифагора

 Видеоигры и координатные плоскости
Порядок операций и круги оценки
Типы данных (числа, строки и изображения)
Переменные
Контракты — домен и диапазон
Определение линейных функций
Рецепт дизайна
Функции для анимации
Логические значения и обнаружение границ
Условные операторы и кусочные функции
Обнаружение столкновений и теорема Пифагора

Я преподавал информатику по алгебре в 2015-2016 гг.

, чем это отличается?

Ни один из уроков из исходной версии CS in Algebra не был удален, но в ответ на отзывы учителей мы изменили структуру курса, чтобы упростить интеграцию в ваш класс только блоков оценки и элементов рецепта дизайна. Курс A и курс B вместе составляют одни и те же оригинальные 20 уроков, но если вы хотите использовать оригинальные материалы, они все еще доступны здесь

Дополнительные вспомогательные документы

Руководство учителя
Рабочая тетрадь для учащихся
Обзор курса
Структура курса
Согласование стандартов

Видео

1. Почему алгебра такая сложная?

Скачать видео

2. Моделирование и координаты

Скачать видео

3. Порядок работы

Скачать видео

4. Домен и диапазон

Скачать видео

Попробуйте учебный курс Bootstrap Hour of Code

Курс «Информатика в алгебре» был вдохновлен и разработан в сотрудничестве с Bootstrap. Если вам понравился CS в алгебре и вы хотите пойти дальше со своими учениками, Bootstrap использует WeScheme вместо блочного программирования и позволяет вам и вашим ученикам изучать более сложные приложения, игры или алгебраические концепции, такие как рекурсия. Если вы хотите попробовать WeScheme или ищете учебник «Час кода» для класса алгебры, мы рекомендуем этот короткий одночасовой учебник, предназначенный для начинающих.

Онлайн-калькулятор: Балансировщик химических уравнений

Учеба Химия

Этот онлайн-калькулятор балансирует уравнения химических реакций алгебраическим методом.

Существует несколько методов уравновешивания химических уравнений:

  1. Метод проверки или метод «проб и ошибок»
  2. Алгебраический метод
  3. Метод, предложенный Арсезио Гарсия
  4. Метод изменения степени окисления
  5. Ионно-электронный метод или метод полуреакции

Последние два используются для окислительно-восстановительных реакций.

Этот балансировщик химических уравнений использует алгебраический метод, который обычно довольно сложен для ручных вычислений, однако он идеально подходит для компьютерной программы.

Алгебраический метод основан на Законе Сохранения Массы – материя не может быть ни создана, ни уничтожена. Следовательно, количество атомов каждого типа в каждой части химического уравнения должно быть одинаковым. Уравновешивание химических уравнений — это процесс обеспечения сохранения материи. Итак, вам просто нужно создать набор алгебраических уравнений, выражающих количество атомов каждого элемента, участвующих в реакции, и решить его. Поэтому этот метод можно использовать для любого типа химической реакции (включая окислительно-восстановительные реакции).

Позвольте мне проиллюстрировать этот метод на примере.

Рассмотрим реакцию:

Начнем с введения неизвестных коэффициентов:

Затем запишем уравнения баланса для каждого элемента через неизвестные:
Для Fe:
Для Cl:
Для Na:
Для P:
Для O:

Они составят систему линейных уравнений:

Здесь у нас пять уравнений для четырех неизвестных, однако последнее зависит от четвертого, поэтому его можно опустить.

Теперь мы можем переписать эту систему в матричной форме:

Эту систему можно решить методом исключения Гаусса. Конечно, нельзя было ожидать, что количество неизвестных всегда будет равно количеству уравнений. Однако метод исключения Гаусса на самом деле мог найти решение для любого количества уравнений и неизвестных. Я создал специальный калькулятор, реализующий метод исключения Гаусса — Общее решение системы линейных уравнений с помощью исключения Гаусса — в форме, пригодной для химических реакций. Короче говоря, он просто сохраняет все дроби и в конце получает целочисленное решение.

Таким образом, приведенный ниже калькулятор просто анализирует химическую реакцию, создает систему линейных уравнений и передает ее в упомянутый выше калькулятор исключения Гаусса. Затем возвращенное решение используется для отображения сбалансированного уравнения.

Примечание. Всегда используйте верхний регистр для первого символа в имени элемента и нижний регистр для второго символа, как в периодической таблице.