Определение:
Функцию, заданную формулой , называют степенной функцией с натуральным показателем, где x — независимая переменная, а n - натуральное число.
Например:
Существуют два случая степенной функции: с чётным показателем и с нечётным показателем.
Рассмотрим пример: найти на рисунке степенные функции с чётным показателем и с нечётным показателем.
С чётным показателем:
С нечётным показателем:
Определение:
Областью определения любой степенной функции с натуральным показателем является множество всех действительных чисел.
Рассмотрим случай, когда n - чётное число. График выглядит так:
Опишем свойства этой функции:
1. Если x=0, то y=0.
2. Если x≠0, то
 к. чётная степень как положительного, так и
к. чётная степень как положительного, так иотрицательного числа положительна.
3. Противоположным значениям аргумента соответствуют равные значения функции.
4. Функция возрастает и убывает на промежутке:
5. При любых значения аргумента функция принимает неотрицательные значения. Областью значений является:
Рассмотрим случай, когда n - нечётное число (n>1).
График выглядит так:
Опишем свойства этой функции:
1. Если x=0, то y=0. Ноль в любой степени равен нулю.
Если x>0, то y>0.
Если x<0, то y<0.
2. Нечётная степень отрицательного числа отрицательна.
3. Противоположным значениям аргумента соответствуют противоположные значения функции.
4. Функция возрастает на всей области определения, принимая любые значения.
5. Областью
значений является:
Областью
значений является:
Рассмотрим пример: сравнить значения выражений:
Показатель степени у обоих выражений одинаковые. Рассмотрим график степенной функции с нечётным показателем:
На рисунке изображен график степенной функции с нечётным показателем, функция возрастает на всей области определения. В данном случае при любых значениях аргумента из множества всех действительных чисел, т.е. большему значению аргумента соответствует большее значение функции.
Рассмотрим пример: сравнить значения выражений:
Показатель степени у обоих выражений нечётный, т.е большему значению аргумента соответствует большее значение функции.
Рассмотрим пример: сравнить значения выражений:
Рассмотрим график:
Показатель степени у обоих выражений чётный, т.е. большему значению аргумента соответствует меньшее значение функции.
Пример.
Сравнить значения выражений:
Данные значения принадлежат промежутку возрастания, то есть большему значению аргумента соответствует большее значение функции.
Пример.
Определить, принадлежат ли графику функции точки А(2,16), В(3,9), С(-1,1).
Точка А.
Значит, точка А принадлежит графику функции.
Точка Б.
Значит, точка Б не принадлежит графику функции.
Точка С.
Значит, точка С принадлежит графику функции.
Предыдущий урок 8 Построение графика квадратичной функции
Следующий урок 10 Корень n-й степени
Получите полный комплект видеоуроков, тестов и презентаций Алгебра 9 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Степенные или показательные уравнения.

Для начала вспомним основные формулы степеней и их свойства.
Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a•a•…•a=an
1. a0 = 1 (a ≠ 0)
2. a1 = a
3. an • am = an + m
4. (an)m = anm
5. anbn = (ab)n
6. a-n= 1/an
7. an/am= an — m
Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.
Примеры показательных уравнений:
6x=36
В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.
Приведем еще примеры показательных уравнений.
2x*5=10
16x — 4x — 6=0
Теперь разберем как решаются показательные уравнения?
Возьмем простое уравнение:
2х = 23
Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:
2х = 23
х = 3
Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.
Теперь подведем итоги нашего решения.
Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.
Теперь прорешаем несколько примеров:
Начнем с простого.
2х+2 = 24
Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.
x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2
В следующем примере видно, что основания разные это 3 и 9.
33х — 9х+8 = 0
Для начала переносим девятку в правую сторону, получаем:
33х = 9х+8
Теперь нужно сделать одинаковые основания. Мы знаем что 9=32 . Воспользуемся формулой степеней (an)m = anm.
33х = (32)х+8
Получим 9х+8 =(32)х+8 =3 2х+16
33х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.
3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.
Смотрим следующий пример:
22х+4 — 10•4х = 24
В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (an)m = anm.
А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (an)m = anm.
4х = (22)х = 22х
И еще используем одну формулу an • am = an + m:
22х+4 = 22х•24
Добавляем в уравнение:
22х•24 — 10•22х = 24
Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 22х ,вот и ответ — 22х мы можем вынести за скобки:
22х(24 — 10) = 24
Посчитаем выражение в скобках:
24 — 10 = 16 — 10 = 6
6•22х = 24
Все уравнение делим на 6:
22х = 4
Представим 4=22:
22х = 22 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение.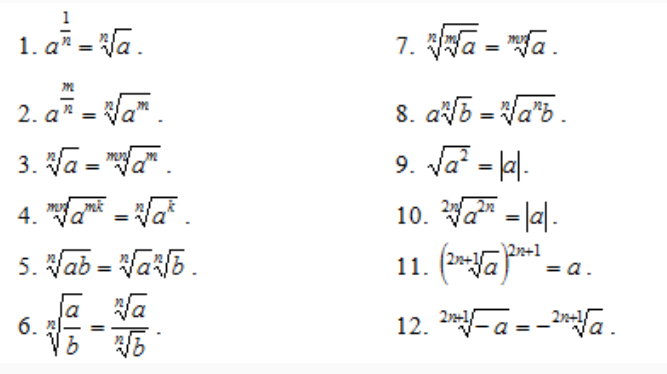 Делим его на 2 получаем
Делим его на 2 получаем
х = 1
Ответ: х = 1.
Решим уравнение:
9х – 12*3х +27= 0
Преобразуем:
9х = (32)х = 32х
Получаем уравнение:
32х — 12•3х +27 = 0
Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены. Число с наименьшей степенью заменяем:
3х = t
Тогда 32х = (3х)2 = t2
Заменяем в уравнении все степени с иксами на t:
t2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t1 = 9
t2 = 3
Возвращаемся к переменной x.
Берем t1:
t1 = 9 = 3х
Стало быть,
3х = 9
3х = 32
х1 = 2
Один корень нашли. Ищем второй, из t2:
Ищем второй, из t2:
t2 = 3 = 3х
3х = 31
х2 = 1
Ответ: х1 = 2; х2 = 1.
На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.
Вступайте в группу ВКОНТАКТЕ
Законы экспонентов
Экспоненты также называются Степени или Индексы
В этом примере: 8 2 = 8 × 8 = 64
Прописью: 8 2 можно назвать «8 во второй степени», «8 во второй степени» или просто «8 в квадрате»
Попробуйте сами:
изображения/экспонента-calc.js
Таким образом, экспонента избавляет нас от записи большого количества умножений!
Пример: a
7a 7 = a × a × a × a × a × a × a = aaaaaaa
Обратите внимание, как мы написали буквы вместе, чтобы означать умножение? Мы будем делать это много здесь.
Пример: x
6 = xxxxxxКлюч к законам
Написание всех букв — ключ к пониманию Законов
Пример: x
2 x 3 = (xx)(xxx) = xxxxx = x 5 Что показывает, что x 2 x 3 = x9 5, но больше, что 9 на9 = x 9 5 позже! Итак, если вы сомневаетесь, просто не забудьте записать все буквы (столько, сколько вам говорит показатель степени) и посмотреть, сможете ли вы понять это. «Законы экспонентов» (также называемые «Правилами экспонентов») исходят из три идеи : Если вы их понимаете, то понимаете и экспоненты! И все законы ниже основаны на этих идеях. Вот законы
(пояснения следуют): Все, что вам нужно знать…
Показатель степени говорит сколько раз использовать число в умножении . Отрицательный показатель степени означает, что делят , потому что деление противоположно умножению.
Дробная экспонента, такая как 1/n , означает, что извлекает корень n-й степени : х ( 1 п ) =
п√х Законы экспонентов
Право Пример х 1 = х 6 1 = 6 х 0 = 1 7 0 = 1 х -1 = 1/х 4 -1 = 1/4 х м х п = х м+п х 2 х 3 = х 2+3 = х 5 x м /x n = x м-n x 6 /x 2 = x 6-2 = x 4 (х м ) н = х мн (х 2 ) 3 = х 2×3 = х 6 (ху) н = х н у н (ху) 3 = х (x/y) n = x n /y n (х/у) 2 = х 2 / у 2 x -n = 1/x n х -3 = 1/х 3 И закон о дробных показателях: х м/н =
n√x м
=
(n√x) м х 2/3 =
3√х 2
=
(3√x) 2
Объяснение законов
Первые три вышеприведенных закона (x 1 = x, x 0 = 1 и x -1 = 1/x) являются лишь частью естественной последовательности показателей степени.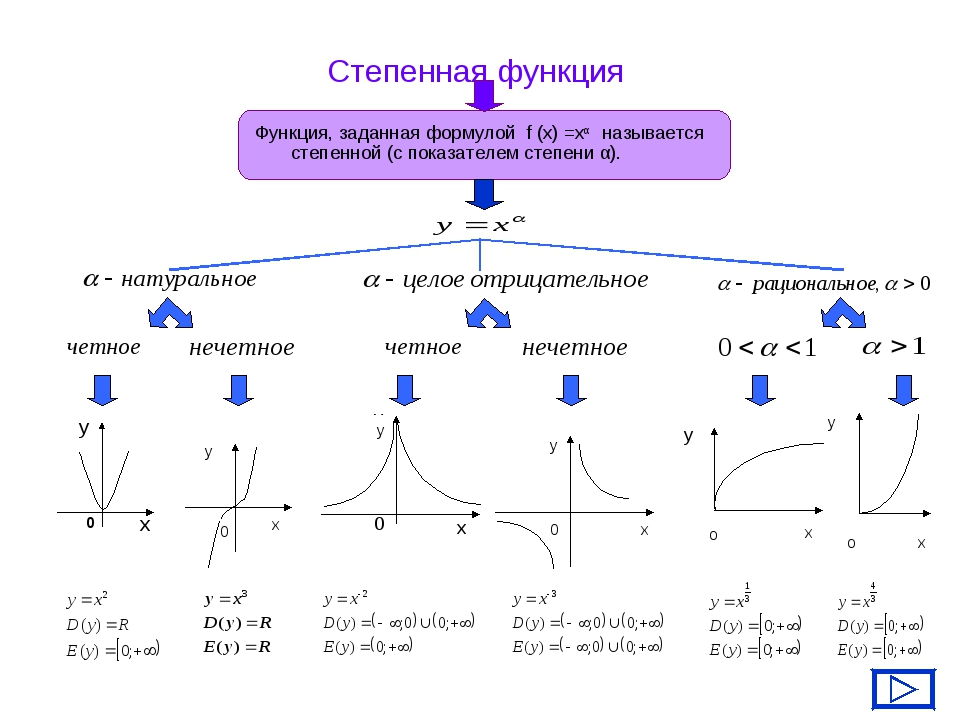 Взгляните на это:
Взгляните на это:
| Пример: Степени числа 5 | |||
|---|---|---|---|
| .. и т.д.. | |||
| 5 2 | 1 × 5 × 5 | 25 | |
| 5 1 | 1 × 5 | 5 | |
| 5 0 | 1 | 1 | |
| 5 -1 | 1 ÷ 5 | 0,2 | |
| 5 -2 | 1 ÷ 5 ÷ 5 | 0,04 | |
| .. и т.д.. | |||
Некоторое время посмотрите на эту таблицу. .. обратите внимание, что положительные, нулевые или отрицательные показатели степени на самом деле являются частью одного и того же шаблона, то есть в 5 раз больше (или в 5 раз меньше) в зависимости от того, увеличивается (или уменьшается) показатель степени.
.. обратите внимание, что положительные, нулевые или отрицательные показатели степени на самом деле являются частью одного и того же шаблона, то есть в 5 раз больше (или в 5 раз меньше) в зависимости от того, увеличивается (или уменьшается) показатель степени.
Закон о том, что x
m x n = x m+nС x m x n , сколько раз мы в итоге умножаем «x»? Ответ: сначала «m» раз, затем еще «n» раз, всего «m+n» раз.
Пример: x
2 x 3 = (xx)(xxx) = xxxxx = x 5Итак, x 2 x 3 = x = x (2+19) 900
Закон, который х
м /х н = х м-нКак и в предыдущем примере, сколько раз нам нужно умножить «x»? Ответ: «m» раз, тогда уменьшите это в «n» раз (потому что мы делим), итого в «m-n» раз.
Пример: х
4 /х 2 = (хххх) / (хх) = хх = х 2Итак, х 4 /х 2 = х 9 (01-2) х 2
(Помните, что х / x = 1, так что каждый раз, когда вы видите x «над чертой» и одну «ниже черты», вы можете отменить их. )
)
Этот закон также может показать вам, почему x 0 = 1 :
Пример: x
2 /x 2 = x 2-2 = x 0 =1 7 7 7Закон того, что (x
m ) n = x mnСначала вы умножаете «m» раз. Тогда у вас есть сделать это «n» раз , всего m×n раз.
Пример: (x
3 ) 4 = (xxx) 4 = (xxx)(xxx)(xxx)(xxx) = xxxxxxxxxxxx = x 12Итак, (x 3 ) 9 = х 3×4 = х 12
Закон того, что (xy)
n = x n y nЧтобы показать, как это работает, просто подумайте о перестановке всех «x» и «y», как в этом примере:
Пример: (ху)
3 = (xy)(xy)(xy) = xyxyxy = xxxyyy = (xxx)(yyy) = x 3 y 3Закон о том, что (x/y)
n = x n /y nАналогично предыдущему примеру, просто переставьте «x» и «y»
Пример: (x/y)
3 = (x/y)(x/y)(x/y) = (xxx)/(yyy) = x 3 /y 3Закон, который х
м/н = п√х м «=» (п√х) мХорошо, это немного сложнее!
Я предлагаю вам сначала прочитать дробные экспоненты, так это имеет больше смысла.
В любом случае, важная идея заключается в том, что:
x 1/ n = n--й корень из x
Таким образом, дробная экспонента, такая как 4 3/2 , на самом деле говорит о том, что нужно сделать куб (3) и квадратный корень из (1/2) в любом порядке.
Просто запомните из дробей, что м/н = м × (1/н) :
Пример: x
( м n ) = x (м × 1 n ) = (x м ) 1/n = n√x мПорядок не имеет значения, поэтому он работает и для m/n = (1/n) × m :
Пример: x
( м n ) = х ( 1 п × м) = (x 1/n ) м = (n√x) мЭкспоненты экспонентов .
 ..
..Что насчет этого примера?
4 3 2
Мы делаем показатель степени в top first , поэтому мы вычисляем его следующим образом:
| Начните с: | 4 3 2 | |
| 3 2 = 3×3: | 4 9 | |
| 4 9 = 4×4×4×4×4×4×4×4×4: | 262144 |
Вот и все!
Если вам сложно запомнить все эти правила, то запомните это:
, вы сможете понять их, когда поймете
три идеи в верхней части этой страницы:
- Показатель степени говорит сколько раз использовать число при умножении
- A отрицательный показатель степени означает деление
- Дробная экспонента, такая как 1/n , означает, что берет корень n-й степени : х ( 1 п ) = п√х
О, еще кое-что.
 .. Что, если x = 0?
.. Что, если x = 0?| Положительный показатель степени (n>0) | 0 п = 0 | |
| Отрицательная экспонента (n<0) | 0 -n равно undefined (поскольку деление на 0 не определено) | |
| Показатель степени = 0 | 0 0 … ммм … см. ниже! |
Странная история 0
0Существуют разные аргументы в пользу правильного значения 0 0
0 0 может быть 1 или, возможно, 0, поэтому некоторые люди говорят, что это действительно «неопределенно»:
| х 0 = 1, значит… | 0 0 = 1 |
0 n = 0, значит. .. .. | 0 0 = 0 |
| Если есть сомнения… | 0 0 = «неопределенный» |
323, 2215, 2306, 324, 2216, 2307, 371, 2217, 2308, 2309
Формула экспонентов– Что такое формула экспонентов? Примеры
Показатель степени числа означает, сколько раз любое число умножается само на себя. Существуют различные формулы показателей степени, используемые для решения уравнений. Показатели важны, потому что они помогают в представлении продуктов, где число повторяется само по себе много раз. Давайте узнаем о формулах экспонент с несколькими решенными примерами в конце.
Что такое формулы экспоненты?
Формулы экспоненты относятся к формулам, помогающим вычислять экспоненты. Показатель степени числа представлен в виде: x n , что означает, что x умножается сам на себя n раз. Здесь
- x называется «основой» .
- n называется «показатель степени» или «степень»
- x n читается как «x в степени n» (или) «x возводится в n»

Экспоненты Формулы
Формулы экспоненты выражаются следующим образом:
- a 0 = 1
- а 1 = а
- a м × a n = a m+n
- a m / a n = a m−n
- а − м = 1/а м
- (a м ) n = a mn
- (ab) м = a м b м
- (a/b) м = a м /b м
Давайте лучше разберемся в формулах экспонент на нескольких решенных примерах.
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.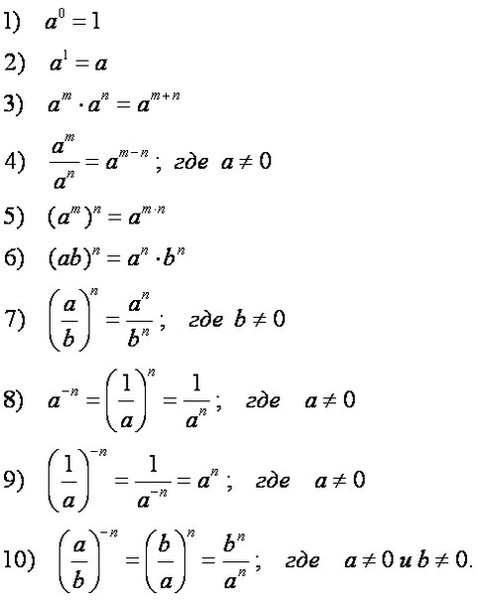
Запишитесь на бесплатный пробный урок
Примеры с использованием экспонентных формул
Пример 1: В лесу у каждого дерева около 5 7 листья и в лесу около 5 3 деревьев. Используя формулу показателей, найдите общее количество листьев.
Решение:
Найти: Общее количество листьев.
Количество деревьев в лесу = 5 3
Количество листьев на каждом дереве = 5 7 (дано)
Используя формулу показателей, x+y
Ввод значений,
5 3 x 5 7 = 5 3+7
5 3 x 5 7 = 5 10
Ответ: Общее количество листьев 5 .
Пример 2: Размеры шкафа: x 5 дюймов, y 3 дюймов и x 8 дюймов. Найдите его объем.
Решение:
Найти: объем гардероба.
Размеры шкафа: длина (д) = x 5 дюймов, ширина (ш) = y 3 дюймов, высота (h) = x 8 дюймов (дано)
Используя формулу экспонент, +y
Putting the values,
Volume = x 5 × x 8 × y 3 = x 13 × y 3
Volume = x 13 × y 3
Ответ: Объем шкафа x 13 × y 3 .
Пример 3: Определить значение x -5/2 при x = 3.
Решение:
Найти: значение x 7 x 0 7 0 0 900 9001 = 3
Используя формулу экспонент,
x -5/2 = (3) -5/2
= (1/3) 5/2
= (1/3 × 1 /3 × 1/3 × 1/3 × 1/3) 1/2
= (1/243) 1/2
= √(1/243) = 1/9√3.
Ответ: Значение x -5/2 при x = 3 равно 1/9√3.
Часто задаваемые вопросы о формулах экспоненты
Что такое формулы экспоненты в математике?
Мы знаем, что показатель степени числа представлен в виде: x n (n — показатель степени). Другими словами, вы можете сказать, что показатели степени — это надстрочные числа. Формулы экспонент – это формулы, которые помогают решать задачи, связанные с экспонентами. Некоторые важные формулы показателей приведены как
Другими словами, вы можете сказать, что показатели степени — это надстрочные числа. Формулы экспонент – это формулы, которые помогают решать задачи, связанные с экспонентами. Некоторые важные формулы показателей приведены как
- .
- a 0 = 1
- а 1 = а
- a м × a n = a m+n
- a m / a n = a m−n
- а − м = 1/а м
- (a м ) n = a mn
- (ab) м = a м b м
- (a/b) м = a м /b м
Каковы применения формул экспоненты?
Формулы экспонентов имеют широкий спектр применения:
- научные шкалы, такие как шкала pH или шкала Рихтера.
- расчет площади, объема и другие подобные задачи.
- сокращает то, что в противном случае было бы очень утомительно писать.


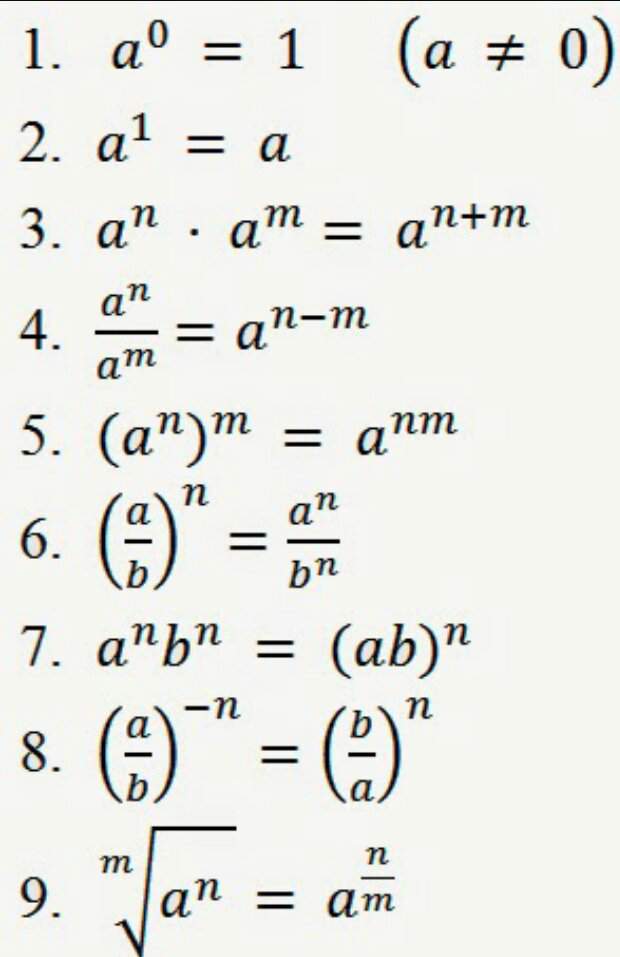
Leave A Comment