Все ли углы ромба равны: Какие из следующих утверждений верны? 1. Все углы ромба равны. 2. Если стороны одного четырёхугольника…

Что не обязательно является ромбом? – Обзоры Вики

Одной из двух характеристик, которые делают ромб уникальным, является то, что его четыре стороны равны по длине или конгруэнтны. … Если у вас есть четырехугольник с двумя парами параллельных сторон, у вас не обязательно ромб; у вас может быть параллелограмм или ромб, если все четыре стороны имеют одинаковую длину.

Следовательно, все ли четырехугольники ромбы? Четырехугольник: замкнутая фигура с четырьмя сторонами. Например, воздушные змеи, параллелограммы, прямоугольники, ромбы, квадраты и трапеции. все четырехугольники. …Ромб: Параллелограмм с четырьмя сторонами одинаковой длины.

Почему ромб не квадрат? Ромб – это четырехугольник, у которого все стороны равны по длине. Квадрат – это четырехугольник, у которого все стороны равны по длине, а все внутренние углы прямые. Значит ромб не квадрат если все углы прямые.. … Квадрат, однако, является ромбом, поскольку все четыре его стороны имеют одинаковую длину.

Дополнительно Почему все квадраты ромбы? Квадрат — это ромб, потому что ромб: все стороны квадрата равны по длине. Даже диагонали квадрата и ромба перпендикулярны друг другу и делят пополам противоположные углы. Поэтому можно сказать, что квадрат — это ромб.

Квадрат это ромб да или нет? Так как ромбы – это четырехугольники, у которых 4 равные стороны, квадраты по определению также являются ромбами. 5. Параллелограмм – это прямоугольник.

Чем четырехугольник отличается от ромба?

Четырехугольник имеет четыре стороны, четыре вершины и четыре угла. Существуют различные типы четырехугольников, такие как квадрат, прямоугольник, трапеция, воздушный змей, ромб, параллелограмм и т. Д. … Ромб – это четырехугольник, у которого все четыре стороны равны по длине. Ромб также называют наклонным квадратом.

Почему все воздушные змеи ромбовидные? Все воздушные змеи являются ромбами. Ромб имеет все стороны одинаковой длины тогда как у воздушного змея не все стороны одинаковой длины.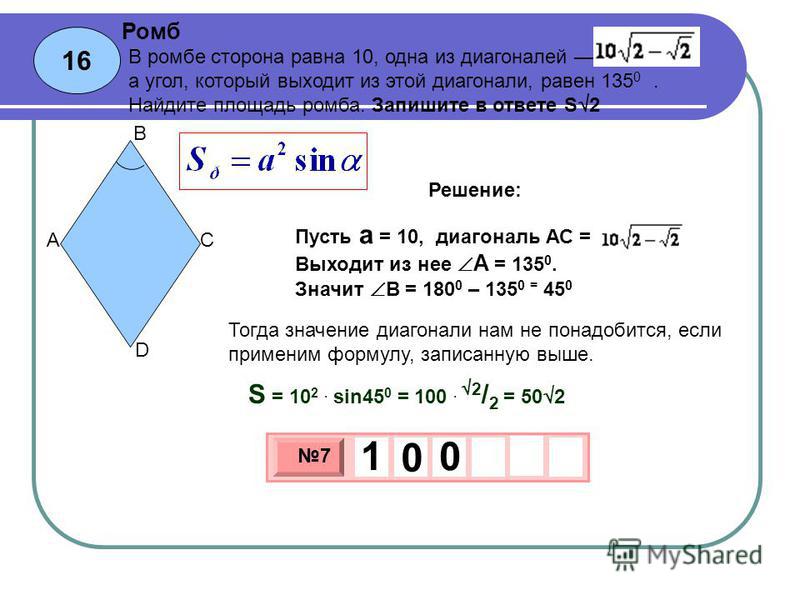 Все ромбы — воздушные змеи. Так как все ромбы имеют равные стороны и диагонали делят друг друга пополам.

Каковы два различия между ромбом и квадратом? Стороны квадрата перпендикулярны друг другу и его диагонали имеют одинаковую длину. Ромб – это четырехугольник, у которого противоположные стороны параллельны, а противолежащие углы равны.
…
Разница между квадратом и ромбом.

ПЛОЩАДЬ	РОМБ
У квадрата четыре линии симметрии.	У ромба две линии симметрии.

Каковы 8 свойства ромба?

Свойства ромба

• Все стороны ромба равны.
• Противоположные стороны ромба параллельны.
• Противоположные углы ромба равны.
• В ромбе диагонали пересекают друг друга под прямым углом.
• Диагонали делят углы ромба пополам.
• Сумма двух смежных углов равна 180 градусам.

Также каждый квадрат является ромбом, правда или ложь? Ромб — это особый вид параллелограмма, у которого противоположные стороны параллельны и все стороны равны по длине.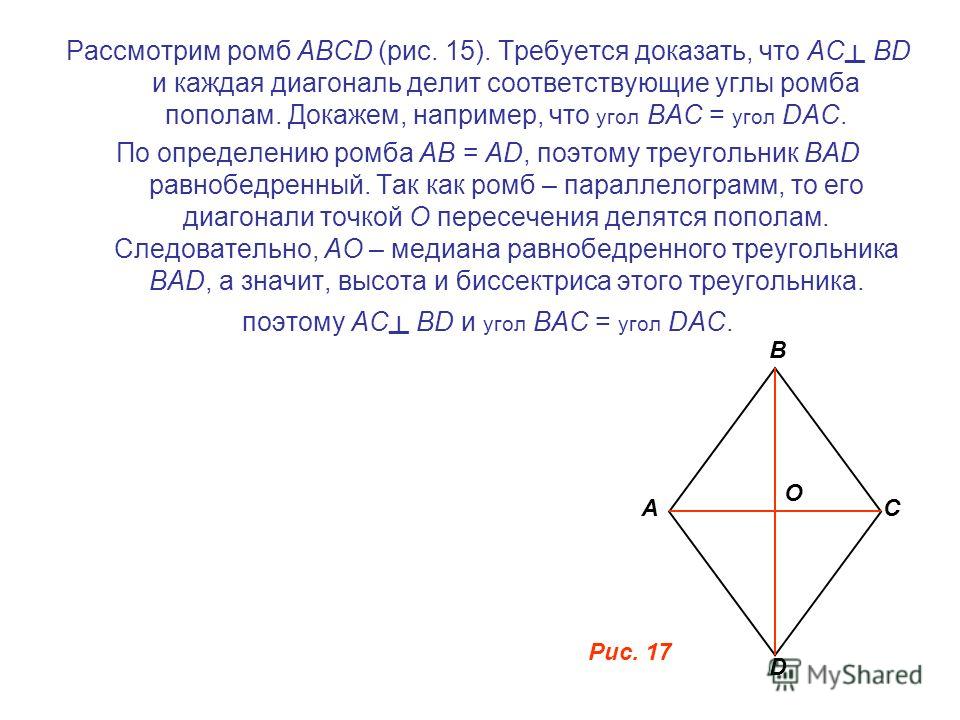 Каждый квадрат — ромб. Верно — определение ромба гласит, что все стороны имеют одинаковую длину. Квадрат — это особый тип ромба, потому что у него все стороны одинаковой длины и 4 прямых угла.

Чем ромб отличается от квадрата?

Квадрат и ромб имеют равные длины сторон. Но у квадрата все углы равны 90 градусам, но у ромба равны только противоположные углы.

Чем ромб отличается от прямоугольника? У ромба четыре стороны равны, а у прямоугольника противоположные стороны равны. Диагонали ромба делят друг друга пополам под углом 90°, а диагонали прямоугольника делят друг друга пополам под разными углами. У ромба противоположные углы равны, а у прямоугольника все углы равны 90°.

Являются ли воздушные змеи параллелограммами?

Воздушные змеи — это особый тип четырехугольника с двумя различными парами последовательных сторон одинаковой длины. …Каждый воздушный змей не является ромбом, потому что все стороны воздушного змея не равны. Так же, каждый воздушный змей не является параллелограммом, потому что противоположные стороны воздушного змея не обязательно параллельны.

Ромб параллелограмм или нет?

Параллелограмм и ромб — четырехсторонние многоугольники, также известные как четырехугольники, имеющие четыре стороны и четыре угла.
…

Параллелограмм	Ромб
Каждый параллелограмм не является ромбом.	Каждый ромб является параллелограммом.

Ромб это алмаз? Ромб — это двумерная фигура, известная как параллелограмм с четырьмя прямыми равными сторонами. Этот форма похожа на ромб и это форма, которую вы ожидаете увидеть в игральных картах, представляющая бубновую масть. Ромбы можно увидеть в быту по-разному.

Воздушный змей и ромб — это одно и то же? Основное отличие воздушного змея от ромба в том, что у ромба все стороны равны тогда как воздушный змей имеет две пары смежных равных сторон. Мы можем сказать, что ромб — это воздушный змей, но воздушный змей может быть ромбом, а может и не быть.

Воздушный змей — это ромб, да или нет?

Воздушный змей — это четырехугольник (четырехугольная форма), в котором четыре стороны могут быть сгруппированы в две пары смежных (соседних / соединенных) сторон равной длины. Итак, если все стороны равны, у нас есть ромб. … Воздушный змей — не всегда ромб. Ромб — это не всегда квадрат.

Всякий ли ромб — воздушный змей, правда или ложь? Каждый ромб — воздушный змей, а любой четырехугольник, который одновременно является воздушным змеем и параллелограммом, является ромбом.

Все ли ромбы подобны Объясните свой ответ?

Все ли ромбы подобны? У ромба все стороны равны. … Итак, очень может случиться так, что два ромба имеют разные углы. Следовательно, все ромбы не похожи.

Можете ли вы сказать, что квадрат и ромб подобны, чтобы обосновать свой ответ? Нет. Потому что у ромба все стороны равны по длине, а у квадрата все стороны равны по длине, а также все внутренние углы прямые. Таким образом они не похожи.

Как вы думаете, почему вместо прямоугольного треугольника или ромба используется квадрат?

Квадрат – это разновидность прямоугольник, только тот, у которого все четыре стороны имеют одинаковую длину.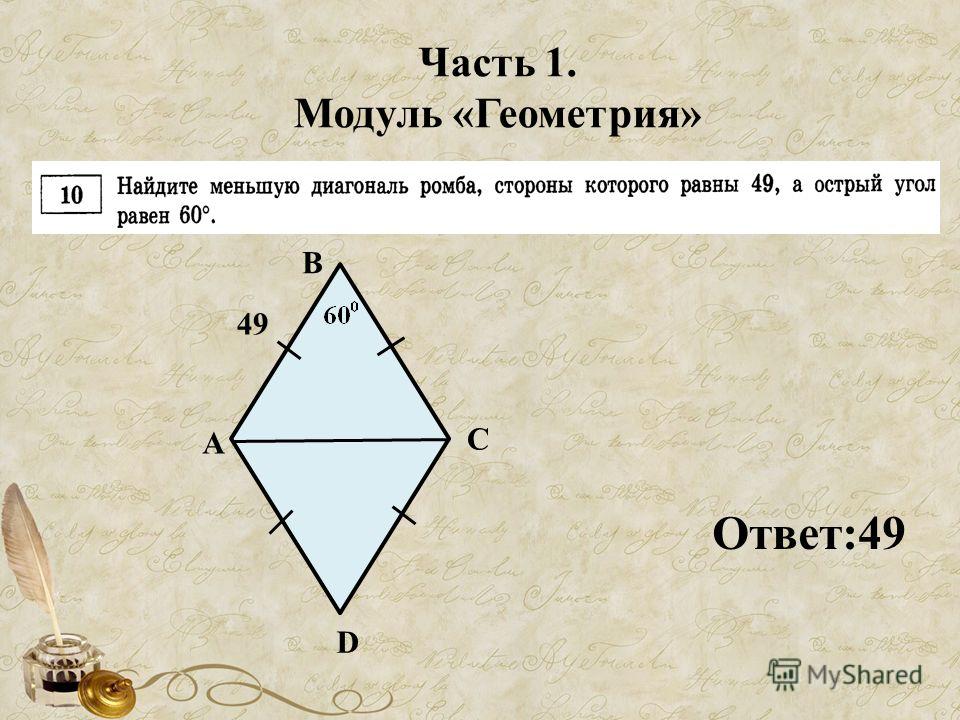 Наконец, есть ромб, который представляет собой четырехгранную фигуру со сторонами одинаковой длины. Углы могут быть 90 градусов, но это не обязательно. Итак, квадрат — это ромб, но не всякий ромб — квадрат.

Что особенного в ромбе? Ромб – это особый вид параллелограмм, у которого все стороны равны. Разница между квадратом и ромбом в том, что все углы квадрата прямые, но углы ромба не обязательно должны быть прямыми углами. Итак, ромб с прямыми углами становится квадратом.

Все ли углы ромба равны?

Ромб. Все стороны (обозначены синим цветом) имеют одинаковую длину; противоположные углы (дуга одного цвета) равны; диагонали пересекаются под прямым углом. Ромб или ромб – это четырехугольник (четырехугольник) со сторонами равной длины. … Квадрат — это частный случай ромба, у которого все четыре угла при вершине равны 90°.

Что такое ромб? Геометрические фигуры. Ромб Свойства и теоремы ромба

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

с равными сторонами. Ромб с прямыми углами является квадратом .

Ромб рассматривают как вид параллелограмма, с двумя смежными равными сторонами либо с взаимно перпендикулярными диагоналями, либо с диагоналями делящими угол на 2 равные части.

Свойства ромба.

1. Ромб — это параллелограмм, поэтому противоположные стороны имеют одинаковую длину и параллельны попарно, АВ || CD, AD || ВС.

2. Угол пересечения диагоналей ромба является прямым (AC ⊥ BD) и точкой пересечения делятся на две одинаковые части. То есть диагонали делят ромб на 4 треугольника — прямоугольных.

3. Диагонали ромба — это биссектрисы его углов (∠ DCA = ∠ BCA, ∠ ABD = ∠ CBD и т.

д.).

4. Сумма квадратов диагоналей равняется квадрату стороны, умноженному на четыре (вывод из тождества параллелограмма).

Признаки ромба.

Параллелограмм ABCD будет называться ромбом только в случае выполнения хотя бы одного из условий:

1. 2 его смежные стороны имеют одинаковую длину (то есть, все стороны ромба равны, AB=BC=CD=AD ).

2. Угол пересечения диагоналей прямой (AC ⊥ BD ).

3. 1-на из диагоналей делит углы, которые ее содержат пополам.

Пусть мы заранее не знаем, что четырёхугольник оказывается параллелограммом, однако известно, что все его стороны равны. Значит этот четырёхугольник является ромбом.

Симметрия ромба.

Ромб симметричен относительно всех своих диагоналей, зачастую его используют в орнаментах и паркетах.

Периметр ромба.

Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. У периметра та же размерность величин, что и у длины.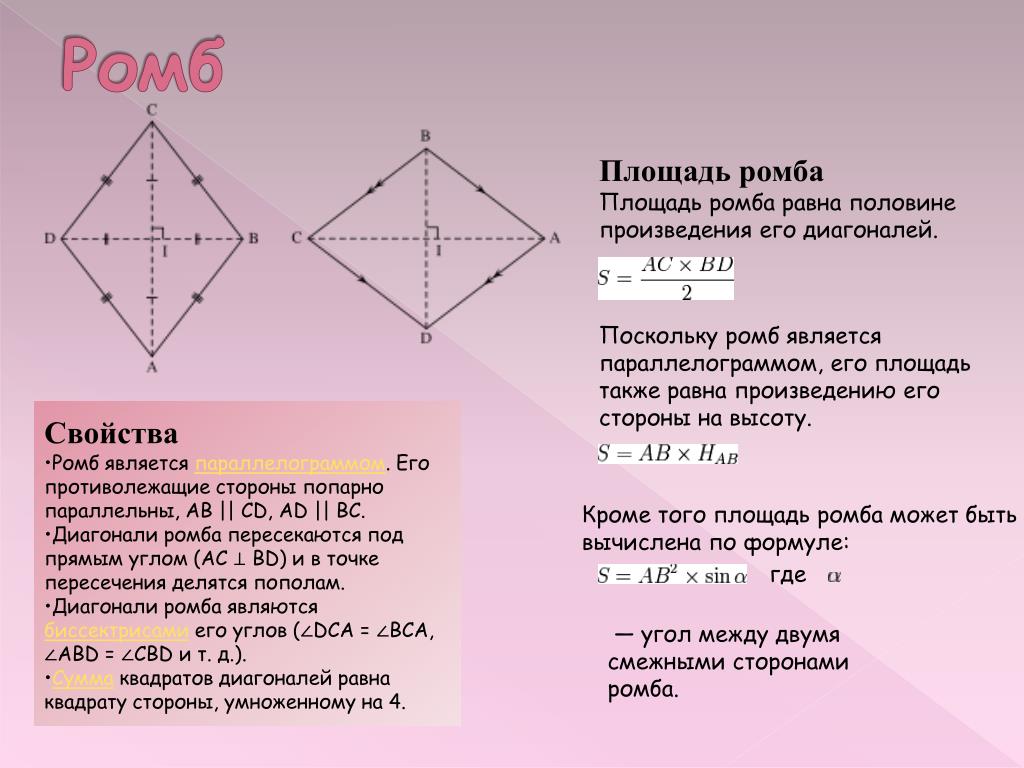

На рисунке 1 $ABCD$ — ромб, $A B=B C=C D=A D$. Так как ромб — это параллелограмм , то он обладает всеми свойствами параллелограмма, но так же есть свойства присущие только ромбу.

В любой ромб можно вписать окружность. Центр окружности, вписанной в ромб, является точкой пересечения его диагоналей. Радиус окружности равен половине высоты ромба $r=\frac{A H}{2}$ (рис.1)

Свойства ромба

1. Диагонали ромба перпендикулярны;
2. Диагонали ромба являются биссектрисами его углов.

Признаки ромба

1. Параллелограмм, диагонали которого пересекаются под прямым углом, есть ромб;
2. Параллелограмм, диагонали которого являются биссектрисами его углов, есть ромб.

Примеры решения задач

Пример

Задание. Диагонали ромба $ABCD$ равны 6 и 8 см. Найти сторону ромба.

Решение. Сделаем рисунок (рис. 1). Пусть для определенности, $A C=6$ см, $B D=8$ см. По свойству ромба его диагонали пересекаются под прямым углом.

2

Признаки ромба

1. Параллелограмм с перпендикулярными диагоналями является ромбом.

\begin{cases} AC \perp BD \\ ABCD \end{cases} — параллелограмм, \Rightarrow ABCD — ромб.

Доказательство

ABCD является параллелограммом \Rightarrow AO = CO ; BO = OD . Также указано, что AC \perp BD \Rightarrow \triangle AOB = \triangle BOC = \triangle COD = \triangle AOD — по 2-м катетам.

Получается, что AB = BC = CD = AD .

Доказано!

2. Когда в параллелограмме хотя бы одна из диагоналей разделяет оба угла (через которые она проходит) пополам, то этой фигурой будет ромб.

Доказательство

На заметку: не каждая фигура (четырехугольник) с перпендикулярными диагоналями будет ромбом.

К примеру:

Это уже не ромб, не смотря на перпендикулярность диагоналей.

Для отличия стоит запомнить, что сначала четырехугольник должен быть параллелограммом и иметь

Среди многообразия геометрических фигур заметно выделяется такой четырехугольник, как ромб. Даже само его название не типично для обозначения четырехугольников. И хотя в геометрии он встречается значительно реже, чем такие простые фигуры, как круг, треугольник, квадрат или прямоугольник, его также нельзя оставлять без внимания.

Ниже представлены определение, свойства и признаки ромбов.

Определение

Ромб — это параллелограмм, имеющий равные стороны. Ромб называется квадратом, если все его углы прямые. Наиболее ярким примером ромба является изображение бубновой масти на игральной карте. Кроме того, ромб часто изображали на различных гербах. Примером ромба в повседневной жизни может служить баскетбольное поле.

Свойства

1. Противолежащие стороны ромба лежат на параллельных прямых и имеют одинаковую длину.
2. Пересечение диагоналей ромба происходит под углом 90 о в одной точке, которая является их серединой.
3. Диагонали ромба делят угол, из вершины которого они вышли, пополам.
4. Исходя из свойств параллелограмма, можно вывести сумму квадратов диагоналей. Согласно формуле она равна стороне, возведенной в квадратичную степень и умноженной на четыре.

Признаки

Мы должны четко понимать, что любой ромб является параллелограммом, но в то же время не любой параллелограмм обладает всеми показателями ромба. Чтобы отличать эти две геометрические фигуры, нужно знать признаки ромба. Ниже перечислены характерные признаки данной геометрической фигуры:

1. Две любые стороны с общей вершиной равны.
2. Диагонали пересекаются под углом 90 о С.
3. Хотя бы одна диагональ делит углы, из точек вершин которых она выходит, пополам.

Формулы площади

Основная формула:

• S = (AC*BD)/2

Исходя из свойств параллелограмма:

• S = (AB*H AB)

Исходя из величины угла между двумя смежными сторонами ромба:

• S = AB2*sinα

Если нам известна длина радиуса окружности, вписанной в ромб:

• S = 4r 2 /(sinα), где:
  • S — площадь;
  • AB, AC, BD — обозначение сторон;
  • H — высота;
  • r — радиус окружности;
  • sinα — синус альфа.

Периметр

Чтобы вычислить периметр ромба, достаточно лишь умножить длину любой из его сторон на четыре.

Построение рисунка

У некоторых возникают трудности с построением рисунка ромба. Даже если вы уже разобрались с тем, что такое ромб, не всегда ясно, как построить его рисунок аккуратно и с соблюдением необходимых пропорций.

Есть два способа построения рисунка ромба:

1. Построить вначале одну диагональ, затем перпендикулярно к ней вторую диагональ, а потом соединить концы отрезков смежных попарно параллельных сторон ромба.
2. Отложить вначале одну сторону ромба, затем параллельно ей построить отрезок, равный по длине, и соединить концы этих отрезков также попарно параллельно.

Будьте внимательны при построении — если на рисунке сделаете длину всех сторон ромба одинаковой, вы получите не ромб, а квадрат.

Ромб — свойства, определение, формулы, примеры

Ромб — замкнутая двумерная плоская фигура.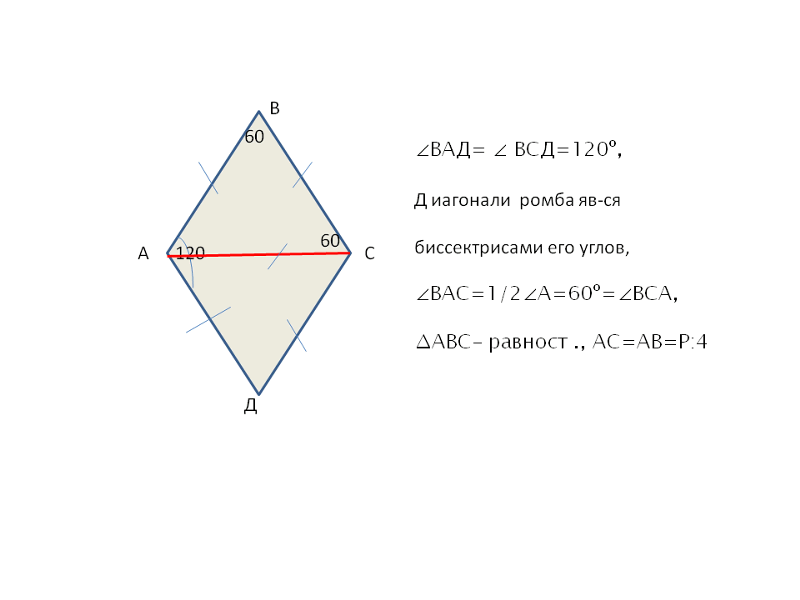 Он считается особым параллелограммом, и благодаря своим уникальным свойствам он приобретает индивидуальную идентичность четырехугольника. Ромб также называют равносторонним четырехугольником, так как все его стороны равны по длине. Термин «ромб» произошел от древнегреческого слова «ромбос», что на самом деле означает что-то вращающееся. Давайте узнаем больше о ромбе и его свойствах в этой статье.

1.	Что такое ромб?
2.	Свойства ромба
3.	Как выглядит ромб?
4.	Формулы ромба
5.	Часто задаваемые вопросы о Rhombus

Что такое ромб?

Ромб можно определить как специальный параллелограмм , поскольку он удовлетворяет требованиям параллелограмма, то есть четырехугольника с двумя парами параллельных сторон.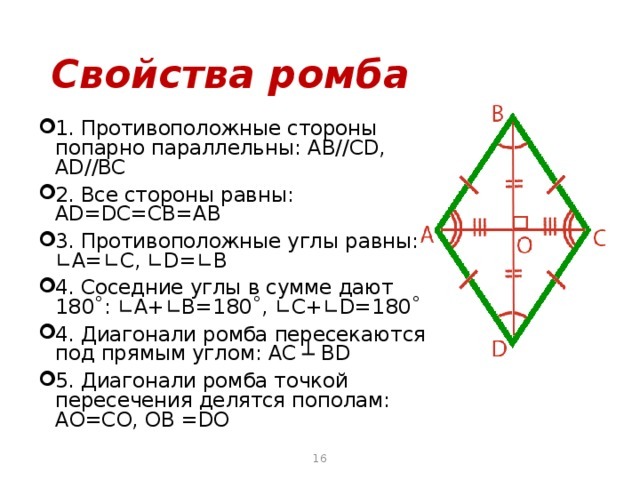 Кроме того, у ромба все четыре стороны равны, как у квадрата. Вот почему он также известен как наклонный квадрат. Посмотрите на изображение ниже, чтобы понять взаимосвязь формы ромба с параллелограммом и квадратом.

На приведенном выше рисунке мы можем заметить, что каждый ромб, который мы видим, также будет параллелограммом, но не каждый параллелограмм является ромбом. Квадрат можно рассматривать как частный случай ромба, поскольку он имеет четыре равные стороны. Все углы квадрата прямые, но углы ромба не обязательно должны быть прямыми . И, следовательно, ромб с прямыми углами можно считать квадратом. Отсюда можно сделать вывод, что:

• Все ромбы или ромбы являются параллелограммами, но не все параллелограммы являются ромбами.
• Все ромбы или ромбы не являются квадратами, но все квадраты являются ромбами.

Ромб может иметь три дополнительных имени:

• Ромб
• Пастилка
• Ромб

Свойства ромба

Ромб считается одним из особых параллелограммов, так как обладает всеми свойствами параллелограмма. Две диагонали ромба являются его двумя линиями симметрии. Ось симметрии можно рассматривать как линию, которая делит объект на две равные половины. Он создает зеркальное отражение обеих сторон объекта. Говорят, что ромб обладает симметрией отражения по обеим диагоналям. Общие свойства параллелограмма следующие:

• Противоположные углы равны или равны.
• Противоположные стороны равны и параллельны.
• Диагонали делят друг друга пополам.
• Сумма любых двух соседних или следующих друг за другом углов равна 180°.

Ромб, как и все геометрические фигуры, обладает уникальными свойствами. В таблице ниже описаны свойства ромба.

Свойства ромба	Артикул
Все стороны ромба конгруэнтны (равны).	Здесь AB = CD = DA = BC
Диагонали делят друг друга пополам под углом 90°, или мы также можем сказать, что каждая из двух диагоналей ромба является серединным перпендикуляром к другой.	Здесь диагонали DB и CA делят друг друга пополам под углом 90°
Противоположные углы равны, а противоположные стороны параллельны.	Здесь, компакт-диск || АВ и ВС || ОБЪЯВЛЕНИЕ. ∠А = ∠С и ∠D = ∠В
Смежные углы в сумме дают 180°	∠А + ∠В = 180° ∠В + ∠С = 180° ∠C + ∠D = 180° ∠А + ∠D = 180°

Одна вещь, которую мы должны помнить о диагонали ромба, заключается в том, что в дополнение к разделению пополам под углом 90 ° две диагонали, разделенные пополам, будут иметь одинаковую длину. Например: если длина диагонали равна 10 см, а другая диагональ делит ее пополам, то она делится на два отрезка по 5 см. Если знать сторону ромба и величину некоторых углов, то можно определить длину диагонали.

Как выглядит ромб?

Ромб – это четырехугольник в форме ромба, у которого все четыре стороны равны.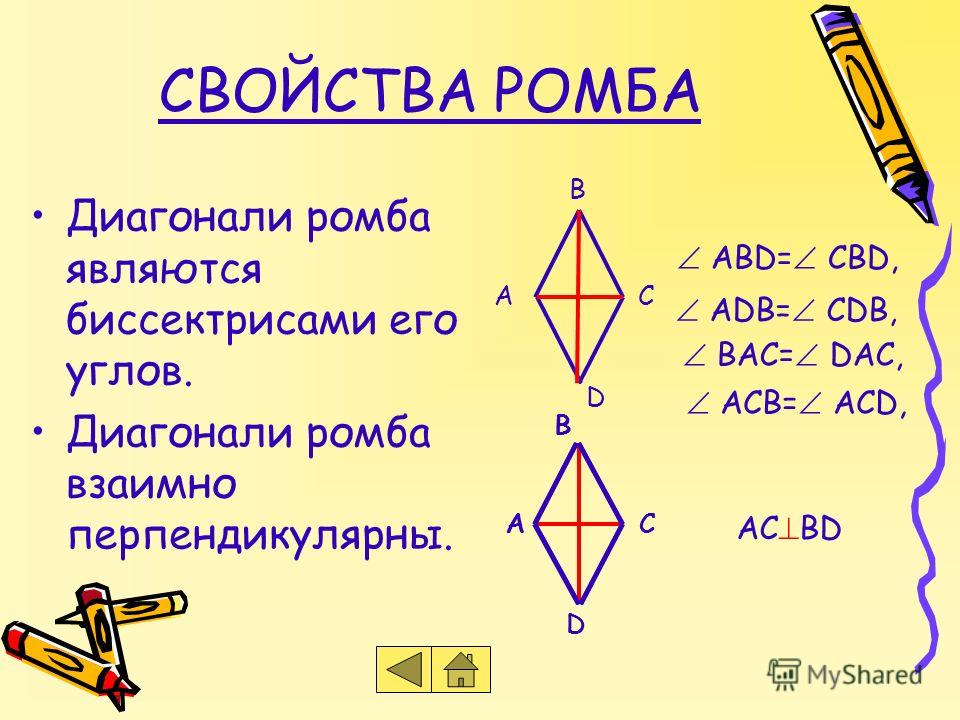 Мы можем видеть фигуры в форме ромба в нашей повседневной жизни. Некоторые из реальных примеров ромба показаны на рисунке ниже: бриллиант, воздушный змей, серьга и т. д.

Формулы ромба

Формулы для ромбов определены для двух атрибутов:

1. Площадь ромба, A = 1/2 × d ₁ × d ₂ , где d ₁ и d ₂ — диагонали ромба.
2. Периметр ромба, P = 4 × a, где a — сторона.

Площадь и периметр ромба

Площадь ромба можно определить как количество пространства, заключенного или охваченного ромбом в двухмерной плоскости. Это половина произведения длин диагоналей. Итак, A = 1/2 × d ₁ × d ₂ , где d ₁ и d ₂ — длины диагоналей.

Так же, как и у квадрата, все четыре стороны ромба равны, значит, формула периметра ромба есть произведение длины одной стороны на 4. Получаем P = (4 × a) единиц , где а — сторона ромба.

☛ Важные примечания о ромбе

Вот список нескольких моментов, которые следует помнить при изучении ромба:

• Смежные углы в ромбе смежные, в сумме они составляют 180°.
• Диагонали делят друг друга пополам под прямым углом.
• Все квадраты — ромбы, но не все ромбы — квадраты.

☛ Похожие темы:

Ознакомьтесь с этими интересными статьями, чтобы узнать больше о ромбе и связанных с ним темах.

• Калькулятор площади ромба
• Рабочие листы с ромбами
• Разница между воздушным змеем и ромбом

Cuemath — одна из ведущих мировых платформ для обучения математике, которая предлагает онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

 

Ромб Примеры

1. Пример 1: Давид начертил ромб, длины двух диагоналей d ₁ и d ₂ равны 5 единицам и 10 единицам соответственно. Он просит свою сестру Линду помочь ему найти этот район. Поможешь Линде найти ответ?

   Решение:

   Дано:

   Диагональ, d ₁ = 5 единиц, а d ₂ = 10 единиц

   A = (d 1_{0165 × d 2 )/2}

   A = (5×10)/2

   A = 25 кв. ед.

   Ответ: Площадь ромба = 25 кв. ед.

2. Пример 2: Эльзе дали площадь ромба, равную 100 квадратным единицам, и длину одной диагонали, равную 20 единицам. Поможешь Эльзе найти длину другой диагонали?

   Решение:

   Дано:

   Площадь = 100 кв. единиц и диагональ d ₁ = 20 единиц

   A = (D ₁ × D ₂ )/ 2

   100 = (20 × D ₂ )/ 2

   D ₂ = 10 UNITS

   9002 . Длина другой диагонали равна 10 единицам.

3. Пример 3: Сэм и Виктор играли в классики и заметили на детской площадке плитку в форме ромба. Длина каждой стороны плитки равнялась 15 единицам. Поможешь Сэму и Виктору найти периметр плитки?

   Решение:

   Дано:

   Длина плитки = 15 единиц.

   Поскольку все стороны ромба равны, все четыре стороны равны 15 единицам.

   Периметр = 4 × сторона = 4 × 15 = 60 единиц

   Ответ: Периметр плитки = 60 единиц.

перейти к слайдуперейти к слайдуперейти к слайду

Готовы увидеть мир глазами математика?

Математика — это жизненный навык. Помогите своему ребенку усовершенствовать это с помощью реального приложения с Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по ромбу

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о Rhombus

Что такое ромб в геометрии?

Ромб — это двумерная фигура с четырьмя сторонами, поэтому ее называют четырехугольником. Он имеет две диагонали, которые делят друг друга пополам под прямым углом. У него также параллельны противоположные стороны, а сумма всех четырех внутренних углов равна 360 градусам.

Все ли квадраты ромбы?

Да, все квадраты ромбы. Квадрат можно рассматривать как частный случай ромба, поскольку он имеет четыре стороны одинаковой длины. Все углы квадрата прямые, но углы ромба не обязательно должны быть прямыми. Следовательно, ромб с прямыми углами можно считать квадратом.

Какой формы ромб?

Ромб – четырехугольник в форме ромба. Если вы посмотрите на колоду карт и вытащите 13 ромбовидных карт, вы обнаружите, что геометрическая форма ромба — это ромб. У него все четыре стороны равны, а противоположные стороны параллельны друг другу. Он выглядит как наклонный квадрат.

Является ли ромб правильным многоугольником?

Нет, ромб не является правильным многоугольником. Правильный многоугольник должен быть равноугольным (все его углы имеют одинаковую меру) и конгруэнтным или равносторонним (все его стороны имеют одинаковую длину). Но ромб только равносторонний: все его стороны имеют одинаковую длину и только противоположные углы равны. Ромб никогда нельзя считать правильным многоугольником, так как это всего лишь равносторонний многоугольник, а не равноугольный многоугольник.

Какова площадь ромба?

Площадь ромба рассчитывается путем деления произведения диагоналей на 2. Математически это можно определить как: \(A = \frac{{d_1 d_2}}{2}\), где d ₁ d ₂ — диагонали ромба.

Каковы четыре свойства ромба?

Ромб – это четырехугольник, обладающий следующими четырьмя свойствами:

• Противоположные углы всегда равны.
• Все стороны равны, а противоположные стороны параллельны друг другу.
• Диагонали делят друг друга пополам под углом 90 градусов и имеют одинаковую длину.
• Сумма любых двух смежных углов всегда будет равна 180°.

В чем разница между ромбом и квадратом?

Основное отличие ромба от квадрата в том, что углы ромба не равны 90°, тогда как все углы квадрата равны 90°. Часто говорят, что квадрат — это ромб, но ромб — это не всегда квадрат.

В чем разница между параллелограммом и ромбом?

Отличие параллелограмма от ромба в том, что у ромба все четыре стороны равны по размеру, тогда как у параллелограмма противоположные стороны равны.

Какие основные формулы ромба?

Несколько основных формул ромба приведены ниже:

• Площадь ромба = 1/2 × d ₁ × d ₂ квадратных единиц.
• Периметр ромба = (4 × стороны) единиц.

Чему равна сумма внутренних углов ромба?

Сумма внутренних углов ромба равна 360°.

Все ли углы ромба равны 90°?

Нет, углы ромба не обязательно должны быть прямыми. Ромб, у которого все четыре внутренних угла равны 90 градусам, считается квадратом.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочий лист по ромбу

Свойства ромба: определение, формулы и примеры

Интересно, какая фигура получится, если наклонить квадрат на 45°? Тем не менее, ромб отличается от этого. Давайте узнаем больше о ромбе и его свойствах ромбов.

Ромб — форма четырехугольника в евклидовой геометрии. Это частный случай свойств параллелограмма, у которого диагонали пересекаются под углом 90 градусов. Основным атрибутом ромба является его уникальная форма. Форма ромба похожа на ромб. В результате он также известен как алмаз. В ромбе ищите линии симметрии для его правильной идентификации.

Ромб напоминает форму четырехугольника. Он имеет четыре вершины и четыре стороны, заключающие в себе четыре угла, точно так же, как и большинство других четырехугольников, таких как прямоугольники, квадраты и т. д. Однако это еще не все. Нам предстоит еще многое узнать об этой увлекательной двумерной форме, которая является важным компонентом математики.

Это также один из ключевых предметов, который следует за нами из школы в университет. Итак, давайте узнаем все, что нужно знать о ромбе, включая его качества, углы, стороны и две диагонали. Но сначала давайте разберемся с четырехугольниками.

Что вы понимаете под четырехугольником?

Как видно из названия, четверка означает четыре. Прежде чем мы перейдем к ромбу и его атрибутам, знаете ли вы, что такое четырехугольник? Это многоугольник с четырьмя сторонами и четырьмя вершинами с четырьмя углами. Сумма внутренних углов четырехугольника равна 360 градусов.

В геометрии есть шесть различных видов четырехугольников:

1. Трапеция
2. Площадь
3. Прямоугольник
4. Параллелограмм
5. Ромб
6. Воздушный змей

Что такое ромб?

Ромб – четырехсторонняя фигура (четырехугольник), являющаяся частным случаем параллелограмма. Противоположные стороны ромба параллельны, а внутренние углы равны.

Кроме того, все стороны ромба имеют одинаковую длину, а диагонали пересекаются под углами, перпендикулярными друг другу. Ромб также может называться ромбом или ромбовидным ромбом из-за его уникальной формы. Ромбы или ромбы — это множественное представление ромба.

Является ли квадрат ромбом?

У квадрата, как и у ромба, все стороны равны. Кроме того, диагонали квадрата перпендикулярны друг другу и делят противоположные углы пополам. В результате квадрат является своего рода ромбом.

Какие факты об углах ромба?

Можно спорить, является ли ромб квадратом или нет. Однако, хотя ромб не является квадратом, квадрат является разновидностью ромба. Это делает его немного отличным от квадратной формы.

Ниже приведены некоторые важные факты об углах ромба.

• В ромбе четыре внутренних угла
• Сумма всех внутренних углов ромба равна 360 градусов
• Внутренние противоположные углы равны друг другу
• В ромбе смежные углы дополняют друг друга
• Диагонали внутри ромба пересекаются перпендикулярно под прямым углом
• Диагонали делят пополам каждый угол, образованный между ними

Углы ромба

У любого ромба четыре угла, причем противоположные равны.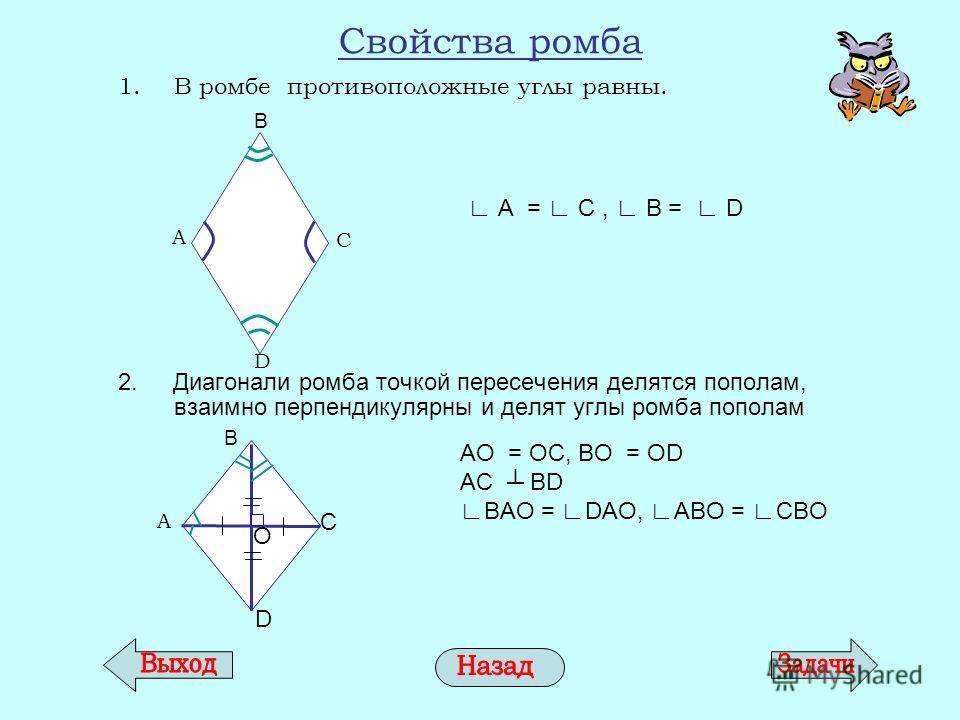 Кроме того, эта фигура состоит из диагоналей, которые пересекают друг друга под прямым углом. Иными словами, каждая диагональ ромба делит другую на две равные части, а угол, образованный в точках их пересечения, равен 90 градусов.

Ромб имеет четыре внутренних угла, и, поскольку сумма двух противоположных сторон равна 180 градусам, общая сумма четырех внутренних углов ромба составляет 360 градусов. Диагонали также делят пополам противоположные углы ромба, разделяя ромб на два отдельных треугольника, конгруэнтных друг другу.

Назовите свойства ромба

Поскольку он обладает всеми качествами параллелограмма, ромб считается одним из исключительных параллелограммов.

Симметричные линии ромба являются его двумя диагоналями. Линия, которая разделяет объект на две одинаковые половины, называется осью симметрии. Обе стороны объекта отражаются в зеркальном отражении. Говорят, что по обеим диагоналям ромб проявляет отражательную симметрию. Вот некоторые из общих качеств параллелограмма:

• Противоположные углы внутри параллелограмма равны или равны
• В параллелограмме противоположные стороны параллельны друг другу
• Противоположные стороны равны по длине
• Каждая диагональ делит другую пополам
• Сумма двух последовательных углов параллелограмма равна 180 градусов

Следует помнить о диагонали ромба, потому что, помимо того, что они делятся пополам под прямым углом, две диагонали, разделенные пополам, также будут иметь одинаковую длину.

Подобно другим геометрическим фигурам, ромб обладает особыми свойствами. Свойства ромба показаны в таблице ниже.

Свойства ромбов.	В этом случае AB = CD = DA = BC
Биссектриса каждой из двух диагоналей ромба — это диагональ, которую он делит пополам в точке 90 градусов.	Здесь диагонали DB и CA образуют друг с другом угол 90°.
Противоположные стороны параллельны, а противоположные углы равны.	CD || АВ и ВС || AD
Смежные углы в сумме составляют 180 градусов.	∠A + ∠B = 180°   ∠B + ∠C = 180°   ∠C + ∠D = 180°   ∠A + ∠D = 180°

разделен пополам другой диагональю, он разделен на две части по 6 см. Длину диагонали можно вычислить, зная сторону ромба и значения некоторых углов.

Как определить ромб?

Ромб – четырехугольник. Он имеет форму алмаза и имеет равные стороны со всех сторон. В повседневной жизни мы видим фигуры в форме ромба. Алмаз, воздушный змей и другие примеры из жизни.

Как найти Ромб в повседневной жизни?

Даже если этого не заметить, форма ромба всегда присутствует перед нашими глазами. От формы воздушного змея до формы ромба. Применение ромбической формы можно увидеть повсюду, от дизайна воздушного змея до формы ювелирных изделий.

Форма ромба настолько распространена, что ее можно найти на вывесках магазинов, дорожных знаках, цепочках для ключей, плитках, бейсбольных полях и так далее. Эту форму также можно увидеть в нескольких известных архитектурных сооружениях по всему миру.

Ромбическая форма настолько популярна, потому что она симметрична и имеет очень привлекательную и приятную форму. Поскольку все четыре стороны ромба равны, фигура также геометрически жизнеспособна.

Формулы ромба

Формула ромба имеет дело с двумя основными параметрами. Это – периметр и площадь.

• Выражение дает формулу площади ромба-

A = ½ × d1 × d2

Здесь d1 и d2 — диагонали ромба.

• Формула периметра ромба задается как-.

P = сторона + сторона + сторона + сторона

Поскольку четыре смежные стороны ромба равны,

P = 4 × сторона

Что такое периметр ромба и как его вычислить?

Периметр фигуры относится к общей длине, покрываемой всеми сторонами этой фигуры. Другими словами, его лучше определить как границу, ограничивающую фигуру и ограничивающую ее очертания.

Для ромба его периметр будет суммой всех его четырех сторон, ограничивающих его страны. Итак, периметр будет равен:

P = сторона + сторона + сторона + сторона

P = 4 × сторона

Например, как известно, у ромба все стороны равны. Итак, если одна сторона = 7 см

Тогда периметр будет:

P = 7 + 7 + 7 + 7

P = 28 см

Чему равна площадь ромба и как ее вычислить?

Площадь объекта определяется как общее пространство, занимаемое этим конкретным объектом. В этом случае площадь ромба — это все пространство, занимаемое четырьмя сторонами и всем, что между ними.

Площадь ромба определяется следующим уравнением:

A = ½ × d1 × d2

Здесь d1 и d2 относятся к диагоналям ромба.

Например: если диагонали ромба равны 12 см и 6 см. Тогда площадь будет:

A = ½ × d1 × d2

A = ½ × 12 × 6

A = 36 см²

Каковы другие свойства ромба?

Для быстрого ознакомления со свойствами ромба прочтите следующие пункты.

• Все четыре стороны имеют одинаковую длину.
• Противоположные стороны параллельны.
• Противоположные внутренние углы одинаковы.
• Под прямым углом или под углом 90 градусов диагонали делят друг друга пополам перпендикулярно.
• Диагонали ромба пересекают его противоположные углы.
• Сумма двух соседних углов, т. е. 180°, является дополнительной.
• Прямоугольник образован соединением середины сторон ромба.
• В ромб нельзя вписать окружность.
• Два конгруэнтных равносторонних треугольника образуются, когда кратчайшая диагональная сторона ромба равна одной из его сторон.

Резюме

Подводя итог, можно сказать, что форма ромба симметрична по диагоналям, а это означает, что площади по обе стороны от диагоналей равны. То есть деление ромба по одной из его диагоналей дает симметричные объекты с одинаковой площадью и периметром. Симметричность ромба в основном связана с наличием двух диагоналей, которые равны и делят друг друга пополам. Свойства ромба — важное понятие в математике и геометрии.

Примеры решенных ромбов 

Пример 1. Дэвид нарисовал ромб с двумя диагоналями, длина которых составляет соответственно 5 и 10 единиц. Он просит Линду, свою сестру, провести его к месту. Можете ли вы помочь Линде найти решение?  

Решение:  

  Дано:

 Диагональные значения d1 = 5 единиц и d2 = 10 единиц.

A = (d1 × d2)/2

A = (5×10)/2

A = 25 квадратных метров

Ромб имеет площадь поверхности 25 квадратных единиц.

Пример 2: Сэм и Виктор играли в классики, когда заметили на детской площадке плитку в форме ромба.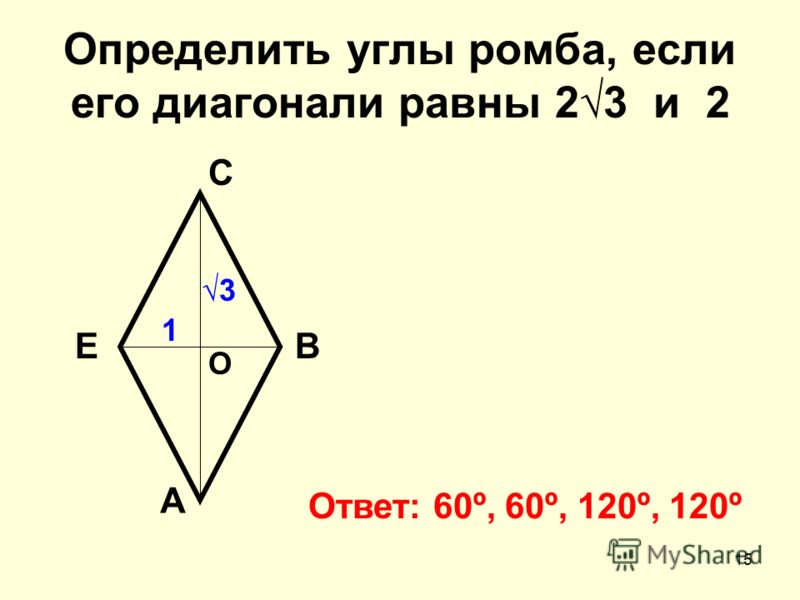 Плитка имела длину 15 единиц с каждой стороны. Поможешь Сэму и Виктору найти периметр плитки?  

Решение: 

Дано:

Плитка имеет длину 15 единиц.

Все четыре стороны ромба равны 15 единицам, так как все его стороны равны.

4 единицы по периметру, 4 единицы с каждой стороны и всего 15 единиц.

Периметр плитки равен 60 единицам, вот и ответ.

Часто задаваемые вопросы

1. Каковы качества ромба?

Ответ. У ромба четыре равные стороны, две из которых перпендикулярны двум другим.

Ромбы названы в честь их формы: ромб можно представить как алмаз, разрезанный пополам.

2. Какой реальный пример ромба?

Ответ. Ромб – это четырехгранная фигура, у которой все стороны равны по длине и все углы равны. Наиболее распространенным примером ромба является ромб. Форма алмаза — ромб, потому что все его ребра имеют одинаковую длину и все его углы равны.

3.