Правильный многоугольник. Формулы, признаки и свойства правильного многоугольника
Навигация по странице: Определение правильного многоугольника Признаки правильного многоугольника Основные свойства правильного многоугольника Правильный n-угольник — формулы — длина стороны — радиус вписанной окружности — радиус описанной окружности — площадь — периметр — угол между сторонами Правильный треугольник Правильный четырехугольник Правильный шестиугольник Правильный восьмиугольник
Определение. Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
 1 1 |
Рис.2 |
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие:
Все стороны и углы одинаковы:
a1 = a2 = a3 = … = an-1 = an
α1 = α2 = α3 = … = αn-1 = αn
Основные свойства правильного многоугольника
1. Все стороны равны:
2. Все углы равны:
3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O
4. Сумма всех углов n-угольника равна:
180° · (n — 2)
5. Сумма всех внешних углов n-угольника равна 360°:
Сумма всех внешних углов n-угольника равна 360°:
β1 + β2 + β3 + … + βn-1 + βn = 360°
6. Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:
| Dn = | n · (n — 3) |
| 2 |
7. В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:
| S = | π | a2 |
| 4 |
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O
Правильный n-угольник — формулы
Формулы длины стороны правильного n-угольника
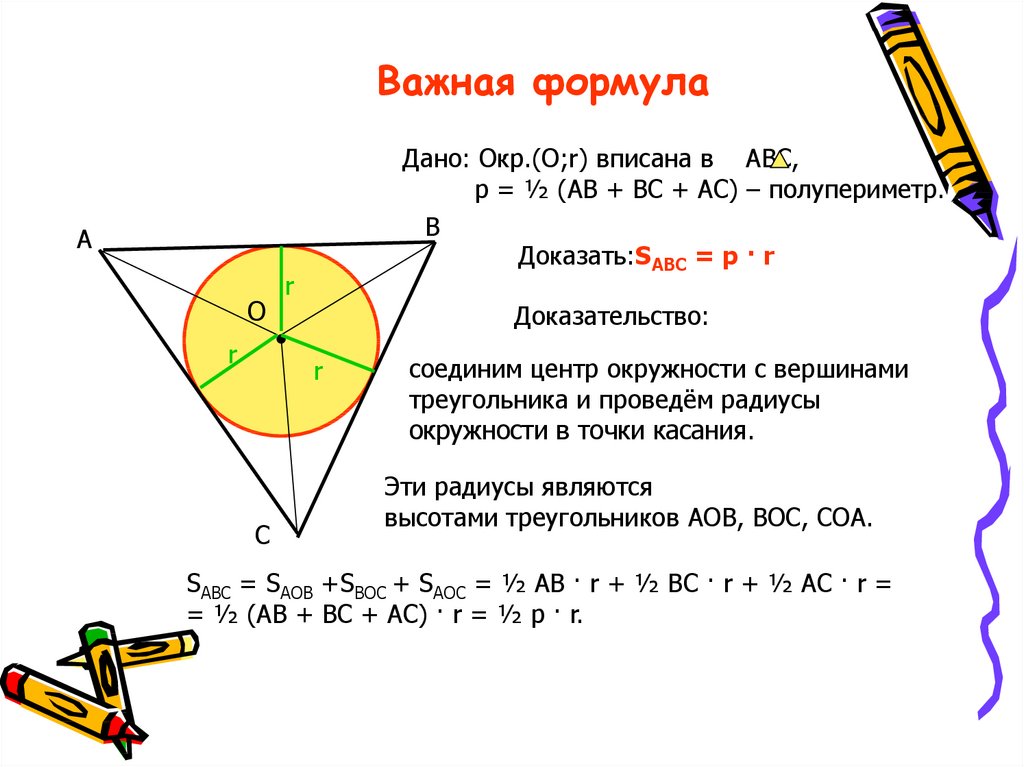
1. Формула стороны правильного n-угольника через радиус вписанной окружности:
| a = 2r · tg | 180° |
| n |
| a = 2r · tg | π |
| n |
2. Формула стороны правильного n-угольника через радиус описанной окружности:
Формула стороны правильного n-угольника через радиус описанной окружности:
| a = 2 R · sin | 180° |
| n |
| a = 2 R · sin | π |
| n |
Формула радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны:
| r = a : (2tg | 180° | ) |
| n |
| r = a : (2tg | π | ) |
| n |
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны:
| R = a : (2sin | 180° | ) |
| n |
| R = a : (2sin | π | ) |
| n |
Формулы площади правильного n-угольника
1. Формула площади n-угольника через длину стороны:
Формула площади n-угольника через длину стороны:
| S = | na2 | · ctg | 180° |
| 4 | n |
2. Формула площади n-угольника через радиус вписанной окружности:
| S = | nr2 · tg | 180° |
| n |
3. Формула площади n-угольника через радиус описанной окружности:
| S = | nR2 | · sin | 360° |
| 2 | n |
Формула периметра правильного многоугольника:
Формула периметра правильного n-угольника:
P = na
Формула определения угла между сторонами правильного многоугольника:
Формула угла между сторонами правильного n-угольника:
| αn = | n — 2 | · 180° |
| n |
Рис. 3 3 |
Правильный треугольник
Формулы правильного треугольника:
1. Формула стороны правильного треугольника через радиус вписанной окружности:
a = 2r √3
2. Формула стороны правильного треугольника через радиус описанной окружности:
a = R√3
3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:
| r = | a√3 |
| 6 |
4. Формула радиуса описанной окружности правильного треугольника через длину стороны:
| R = | a√3 |
| 3 |
5. Формула площади правильного треугольника через длину стороны:
| S = | a2√3 |
| 4 |
6. Формула площади правильного треугольника через радиус вписанной окружности:
S = r2 3√3
7.
| S = | R2 3√3 |
| 4 |
8. Угол между сторонами правильного треугольника:
α = 60°
| Рис.4 |
Правильный четырехугольник
Правильный четырехугольнику — квадрат.
Формулы правильного четырехугольника:
1. Формула стороны правильного четырехугольника через радиус вписанной окружности:
a = 2r
2. Формула стороны правильного четырехугольника через радиус описанной окружности:
a = R√2
3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:
| r = | a |
| 2 |
4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
| R = | a√2 |
| 2 |
5. Формула площади правильного четырехугольника через длину стороны:
S = a2
6. Формула площади правильного четырехугольника через радиус вписанной окружности:
S = 4 r2
7. Формула площади правильного четырехугольника через радиус описанной окружности:
S = 2 R2
8. Угол между сторонами правильного четырехугольника:
α = 90°
Смотрите также формулы и свойства квадрата
Правильный шестиугольник
Формулы правильного шестиугольника:
1. Формула стороны правильного шестиугольника через радиус вписанной окружности:
| a = | 2√3 | r |
| 3 |
2.
a = R
3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:
| r = | a√3 |
| 2 |
4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны:
R = a
5. Формула площади правильного шестиугольника через длину стороны:
| S = | a2 3√3 |
| 2 |
6. Формула площади правильного шестиугольника через радиус вписанной окружности:
S = r2 2√3
7. Формула площади правильного шестиугольника через радиус описанной окружности:
| S = | R2 3√3 |
| 2 |
8. Угол между сторонами правильного шестиугольника:
α = 120°
Правильный восьмиугольник
Формулы правильного восьмиугольника:
1.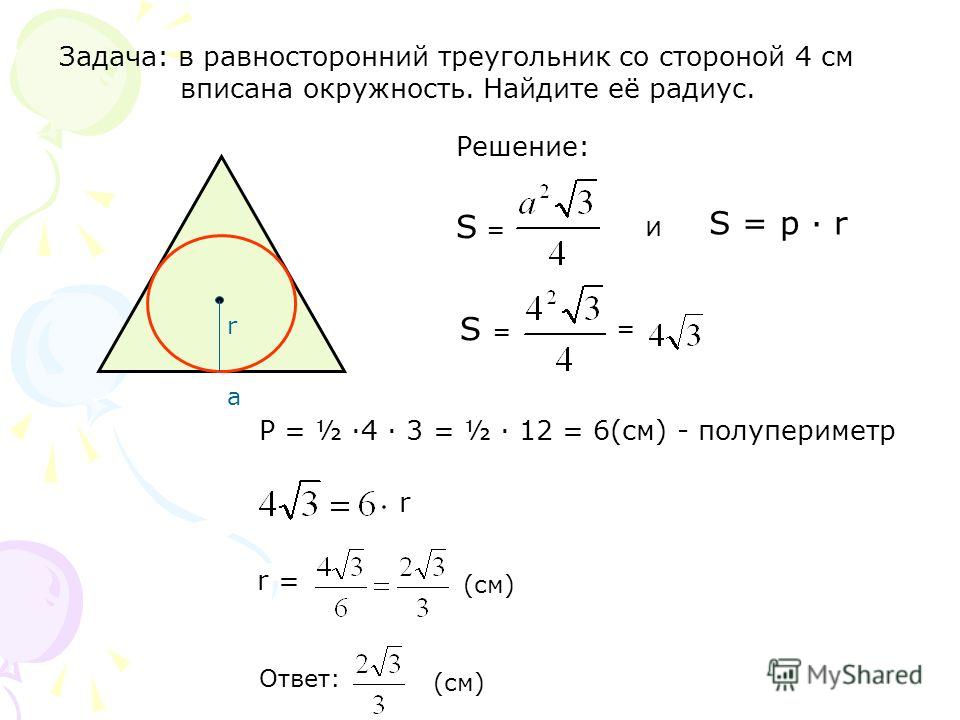 Формула стороны правильного восьмиугольника через радиус вписанной окружности:
Формула стороны правильного восьмиугольника через радиус вписанной окружности:
a = 2r · (√2 — 1)
2. Формула стороны правильного восьмиугольника через радиус описанной окружности:
a = R√2 — √2
3. Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:
| r = | a(√2 + 1) |
| 2 |
4. Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:
| R = | a√4 + 2√2 |
| 2 |
5. Формула площади правильного восьмиугольника через длину стороны:
S = a2 2(√2 + 1)
6. Формула площади правильного восьмиугольника через радиус вписанной окружности:
S = r2 8(√2 — 1)
7. Формула площади правильного восьмиугольника через радиус описанной окружности:
S = R2 2√2
8. Угол между сторонами правильного восьмиугольника:
Угол между сторонами правильного восьмиугольника:
α = 135°
Все таблицы и формулы
Правильные многоугольники и окружность описанная и
Бизнес с Oriflame — рост и РАЗВИТИЕ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2014-03-18
Правильные многоугольники и окружность. Здравствуйте, Дорогие друзья! Во многих задачах в курсе геометрии, в том числе и в составе ЕГЭ имеется много заданий связанных с понятием окружности вписанной в правильный многоугольник и описанной около него. Если конкретней, то в данном случае мы рассмотрим правильный треугольник, также квадрат и правильный шестиугольник. Именно с этими правильными многоугольниками связаны условия заданий на экзамене. Обычно в ходе решения таких задач возникает необходимость выразить:
1. Сторону правильного треугольника через радиус вписанной или описанной окружности.
2. Сторону квадрата через радиус вписанной окружности или описанной окружности.
3. Сторону правильного шестиугольника через радиус вписанной или описанной окружности.
4. Радиус вписанной в правильный многоугольник окружности через радиус описанной около него окружности и наоборот.
На сайте рассмотрены (и в будущем будут рассматриваться) задачи, в которых эти формулы используются. При решении подробно не описывается как они выводятся. Просто говорится, например, что сторона правильного треугольника соотносится с радиусом вписанной в него окружности как:
У многих возникают вопросы по этому поводу: Как? Почему? В этой статье мы выведем все указанные соотношения и в будущем при решении задач, если потребуется, просто буду давать ссылку на эту статью.
Что нужно всегда помнить и понимать?
Центр правильного многоугольника совпадает с центром вписанной о описанной около него окружности. Итак, приступим!
Правильный треугольник, вписанная и описанная окружность.
Пусть а – это его сторона, радиус описанной окружности равен R, а радиус вписанной окружности равен r.
Стороны правильного треугольника и вписанная в него окружность имеют общие точки (точки касания), эти точки делят стороны треугольника пополам. Радиус описанной окружности, проведённый к вершине треугольника является биссектрисой, то есть делит угол при этой вершине, равный 60 градусам, пополам. Рассмотрим прямоугольный треугольник (выделен жёлтым). По определению тангенса: Получаем, что: По определению косинуса: Получаем, что: Можем записать соотношение радиусов:
Радиус описанной окружности, проведённый к вершине треугольника является биссектрисой, то есть делит угол при этой вершине, равный 60 градусам, пополам. Рассмотрим прямоугольный треугольник (выделен жёлтым). По определению тангенса: Получаем, что: По определению косинуса: Получаем, что: Можем записать соотношение радиусов:
Квадрат, вписанная и описанная около него окружность.
Пусть а – это сторона квадрата, радиус описанной окружности равен R, а радиус вписанной окружности равен r.
Стороны квадрата и вписанная в него окружность имеют общие точки (точки касания), эти точки делят стороны квадрата пополам.
Радиус описанной окружности, проведённый к вершине квадрата является биссектрисой, то есть делит угол квадрата пополам.
Рассмотрим прямоугольный треугольник (выделен жёлтым). На основании вышеизложенного можно сделать вывод о том, что:
По определению косинуса: Получаем, что: *Можно было воспользоваться также теоремой Пифагора. Запишем соотношение радиусов:
Правильный шестиугольник. Вписанная и описанная окружность.
Вписанная и описанная окружность.
Стороны правильного шестиугольника и вписанная окружность имеют общие точки (точки касания), эти точки делят стороны данного шестиугольника пополам.
Радиус описанной окружности, проведённый к вершине шестиугольника является биссектрисой, то есть делит угол правильного шестиугольника равный 120 градусам пополам. Подробнее о правильном шестиугольнике и описанной около него окружности можете посмотреть информацию в этой статье.
Рассмотрим прямоугольный треугольник (выделен жёлтым). По определению тангенса: Получаем, что:
Тот факт, что сторона правильного шестиугольника равна радиусу описанной окружности известен практически всем школьникам изучившим соответствующий материал по планиметрии:
Если интересно посмотрите как это можно вывести. По определению косинуса в прямоугольном треугольнике: Получаем, что: Можем записать соотношение радиусов: Вот и всё.
Конечно же, учить и запоминать данные формулы не нужно. В ходе решения вы всегда сможете их также вывести используя свойства правильных многоугольников, определения тангенса и косинуса, теорему Пифагора.
В ходе решения вы всегда сможете их также вывести используя свойства правильных многоугольников, определения тангенса и косинуса, теорему Пифагора.
Я решил изложить это в отдельной статье только для того, чтобы у вас не возникали вопросы при решении и изучении соответствующих заданий на блоге и вы всегда могли бы посмотреть откуда взялась формула. Везде, где потребуется данная информация я буду размещать ссылку на эту статью.
Получить материал статьи в формате PDF
Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Формулы Теория | Формулы
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
геометрия — Каков радиус окружности, вписанной в треугольник ABC?
Задавать вопрос
спросил
Изменено 1 год, 6 месяцев назад
Просмотрено 305 раз
$\begingroup$
Для справки: В полуокружность диаметра $AC$ вписан треугольник $ABC$, точки которого соединены средними величинами $\overset{\LARGE{\frown}}{AB}$ и $\overset{\ LARGE{\frown}}{BC}$ с вершинами $C$ и $A$, пересекающимися в точках $E$ и $F$ со сторонами $AB$ и $BC$ соответственно. Затем проводим $EH$ и $FG$ перпендикулярно $AC$. Вычислить радиус круга
вписан в треугольник $ABC$, если $HG = 4m$.
Затем проводим $EH$ и $FG$ перпендикулярно $AC$. Вычислить радиус круга
вписан в треугольник $ABC$, если $HG = 4m$.
Мой прогресс:
Я сделал рисунок выше(без масштаба). Отношения, которые я нашел: $\треугольник ABC$ — прямоугольник. $\треугольник AJH \sim \треугольник AMI \sim \треугольник AFG$ Я думаю, что некоторые данные отсутствуют…
это правильная картинка
- геометрия
- евклидова геометрия
- треугольники
- круги
$\endgroup$
3
$\begingroup$
Если я правильно понимаю, $E$ лежит на отрезке $\overline{AB}$ и прямая $\overleftrightarrow{CE}$ пересекает дугу $\overset{\large\frown}{AB}$ в середине дуги; $F$ лежит на отрезке $\overline{BC}$, а прямая $\overleftrightarrow{AF}$ пересекает дугу $\overset{\large\frown}{BC}$ в середине дуги.
Следовательно, $\overrightarrow{CE}$ — биссектриса угла $\angle ACB$
$\overrightarrow{AF}$ — биссектриса угла $\angle BAC. {\ circ} \ right)} = \ frac {r (\ cos \ alpha+ \ sin \ alpha)} {\ cos \ alpha+ \ sin \ alpha-1} $ $
и мы видим, что что-то упущено в данном.
{\ circ} \ right)} = \ frac {r (\ cos \ alpha+ \ sin \ alpha)} {\ cos \ alpha+ \ sin \ alpha-1} $ $
и мы видим, что что-то упущено в данном.
Мы также получили $4 млн=\frac{1}{2}(AB+BC)=\frac{1}{2}(AB+BC-AC)+\frac{1}{2}AC=r +Р.$$
$\endgroup$
1
Окружность вписана в треугольник со сторонами 9, 12 и 15. Радиус окружности равен
Дата последнего обновления: 08 апреля 2023
•
Всего просмотров: 306.9k
3
сегодня: 5,79k
Ответить
Проверено
306,9 тыс.+ просмотров
Подсказка: чтобы найти радиус вписанной окружности, сначала найдите площадь треугольника по формуле $\dfrac{1}{2}\times \text{base}\times \text{height} $
Здесь мы должны найти радиус окружности, вписанной в треугольник со сторонами 9, 12, 15.
Полный пошаговый ответ:
Стороны треугольника, указанные в вопросе, равны 9, 12, 15.
Пусть AB = 9, BC = 12, CA = 15.
Теперь проверим, является ли данный треугольник прямоугольным. Для этого воспользуемся теоремой Пифагора. 9{2}} \\
& \Rightarrow 81+144=225 \\
& \Rightarrow 225=225 \\
\end{align}$
Отсюда видно, что данный треугольник удовлетворяет теореме Пифагора, поэтому данный треугольник — прямоугольный треугольник. Таким образом, соответствующая диаграмма будет выглядеть так:
Итак, пусть окружность, вписанная в треугольник ABC, имеет радиус как «r», а «O» — центр окружности.
Из рисунка видно, что радиус вписанной окружности перпендикулярен соответствующим сторонам, поэтому OD, OF, OE перпендикулярны AB, BC и AC соответственно.
Теперь из рисунка мы также можем сказать, что
Площадь треугольника ABC = площадь треугольника AOB + площадь треугольника BOC + площадь треугольника COA
Теперь мы знаем, что площадь треугольника = ½ основания, умноженного на высоту.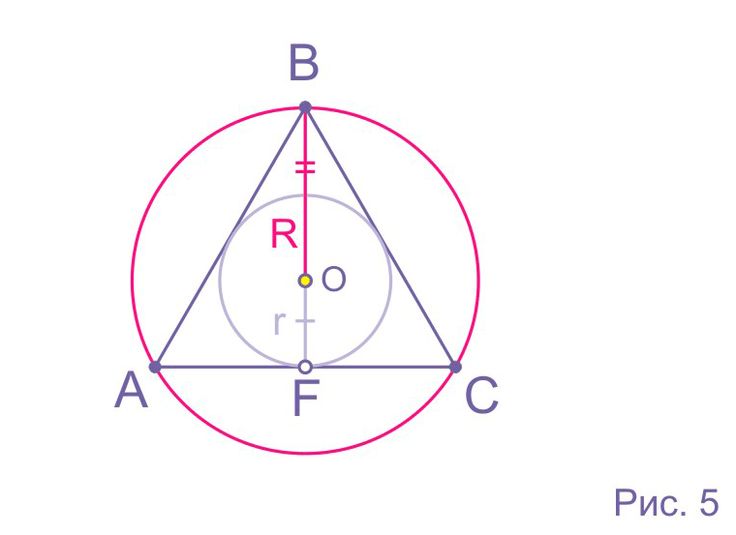 Таким образом, мы можем записать это как
Таким образом, мы можем записать это как
$\begin{align}
& \Delta ABC=\Delta AOB+\Delta BOC+\Delta COA \\
& \Rightarrow \dfrac{1}{2}\times AB\times BC= \dfrac{1}{2}\times OD\times AB+\dfrac{1}{2}\times OF\times BC+\dfrac{1}{2}\times OE\times AC \\
\end{align} $
Подставляя значения из приведенного выше рисунка, получаем
$\Rightarrow \dfrac{1}{2}\times 9\times 12=\dfrac{1}{2}\times r\times 9+\dfrac{1}{2}\times r\times 12+\ dfrac{1}{2}\times r\times 15$
Сокращая подобные члены, получаем
$\begin{align}
& \Rightarrow 108=9r+12r+15r \\
& \Rightarrow 108=36r \ \
& \Rightarrow r=\dfrac{108}{36}=3 \\
\end{align}$
Следовательно, радиус вписанной окружности равен 3.
Примечание. Другим подходом к этой задаче является использование формулы ,
$\text{радиус}=\left( \dfrac{a+b-c}{2} \right)$
Здесь a и b — стороны, а c — гипотенуза прямоугольного треугольника.
Используется, когда окружность вписана в прямоугольный треугольник.


Leave A Comment