Свободные колебания. Математический маятник
При наличии механических колебаний происходит периодическое изменение кинетической и потенциальной энергии. Обращение в ноль кинетической энергии и скорости связано с максимальным отклонением тела от положения равновесия. Энергия такого колеблющегося тела достигает максимального значения. Если груз располагается на горизонтальной пружине, то потенциальная энергия считается энергией упругих деформаций пружины. У математического маятника – это энергия в поле тяготения Земли.
Когда тело принимает положение равновесия при движении, это говорит о наличии минимальной его скорости. Тогда кинетическая энергия обладает максимальным значением, а потенциальная – минимальным. По 3-му закону Ньютона формула силы натяжения записывается как T=mg при вертикальном подвешивании тела на нити. Уменьшение потенциальной приводит к увеличению кинетической. Дальнейшее движение показывает, что происходит уменьшение кинетической и увеличение потенциальной.
Рисунок 2.4.1. Модель превращения энергии при колебаниях.
Математический и пружинный маятник
Когда колебательная система не имеет силы трения, тогда остается неизменной полная механическая энергия.
Формулы, характеризующие груз на пружине:
E=Ek+Ep=mυ22+kx22, ω02=km,(Ep)max=kxm22, (Ek)max=mυm22=mω02xm22=(Ep)max.
Выражения при малых колебаниях математического маятника записываются:
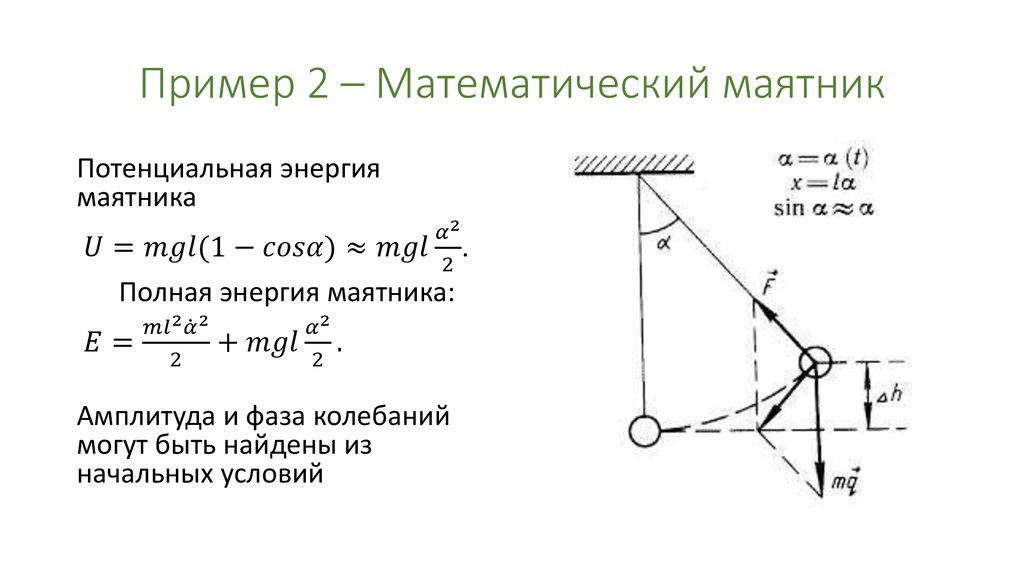
E=Ek+Ep=mυ22+mgh=mυ22+mgx22l, ω02=gl,(Ep)max=mghm=mgxm22l, (Ek)max=mυm22=mω02xm22=(Ep)max.
Значение hm является максимальной высотой подъема маятника, xm и υm=ω0xm – максимальными значениями отклонения физического маятника от положения равновесия и его скорости.
Для объяснения превращения энергии при свободных механических колебаниях без силы трения приводится иллюстрация.
Пример 1Если рассматривать колебания с грузом массой m на пружине с жесткостью k, тогда смещение груза x(t) из положения равновесия и его скорость υ(t) могут изменяться со временем согласно законам:
x(t)=xmcos (ω0t), где ω02=km,
υ(t)=-ωxmsin (ω0t).
Формулы кинетической и потенциальной энергии запишутся так:
Ep(t)=12kx2=12kxm2 cos2ω0t=14kxm2(1+cos 2ω0t),
Ek(t)=12mυ2=12kω02xm2 sin2ω0t=14kxm2(1-cos 2ω0t).
Рисунок 2.4.2 показывает два графика функций изменения Ep(t) и Ek(t). Обе энергии в период колебаний T=2πω0, достигают максимальных значений по два раза. Значение их суммы не изменяется Ep(t)+Ek(t)=E=const.
Рисунок 2.4.2. Превращения энергии при свободных колебаниях.
Определение 2Реальные условия для колебательной системы – это наличие воздействия сил трения (сопротивления).
Определение 3При переходе части механической энергии во внутреннюю энергию теплового движения атомов и молекул колебания становятся затухающими, как показано на рисунке 2.4.3.
Рисунок 2.4.3. Свободные затухающие механические колебания.
Скорость затухания колебаний зависит от величины сил трения.
Частота. Добротность. Формулы
Определение 4Промежуток времени τ с уменьшением колебаний в e≈2,7 раз называют временем затухания.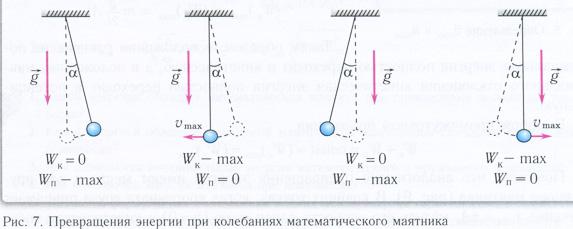
Скорость затухания зависит от частоты свободных колебаний, как видно из формулы. При увеличении действия сил трения происходит уменьшение собственной частоты. Если действия силы трения достаточно велико, то изменение частоты становятся заметными.
Определение 5Колебательная система с затухающими колебаниями характеризуется добротностью Q.
Определение параметра представляет собой произведение числа полных колебаний N за время затухания τ на значение π:
Q=πN=πτT.
Повышение Q колебательной системы происходит при медленных затуханиях свободных колебаний. На рисунке 2.4.3 показано, что Q имеет значение, приближенное к 15.
Добротность механических колебательных систем может достигать огромных значений. Для определения Q колебательной системы применяют формулу:
Q=2πЗапас энергии в колебательной системеПотеря энергии за 1 период колебаний.
То есть добротность способна характеризовать относительную убыль (затухание) энергии при наличии действия силы трения на данном промежутке времени, равняющемуся одному периоду колебаний.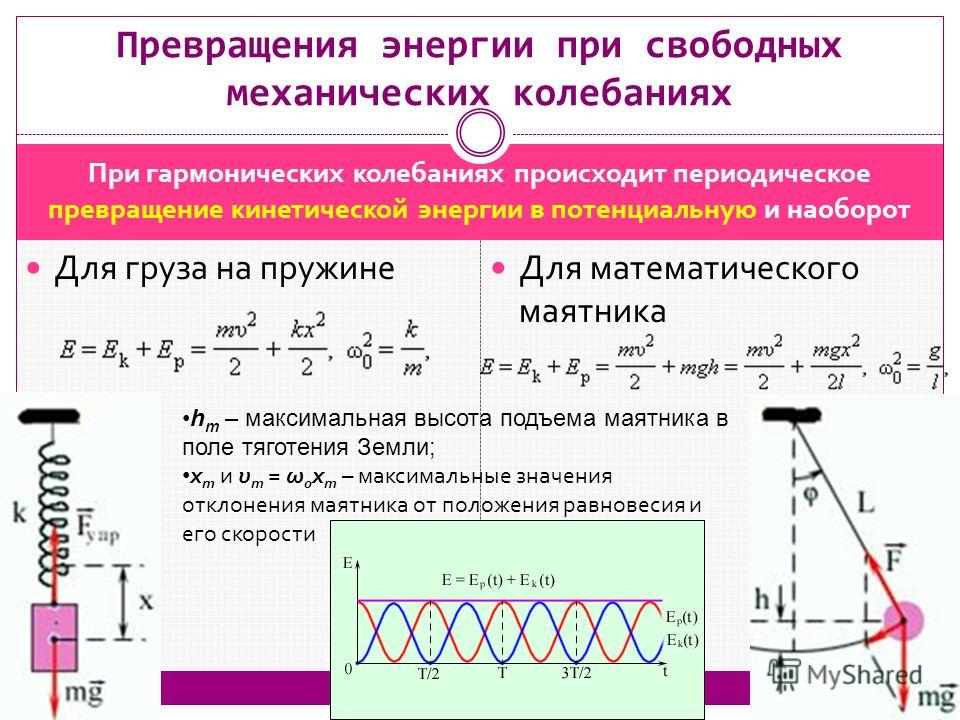
Автор: Роман Адамчук
Преподаватель физики
Превращение энергии при гармонических колебаниях. Затухающие колебания. Школьный курс физики
Главная | Физика 11 класс | Превращение энергии при гармонических колебаниях
Превращение энергии при гармонических колебаниях.
При механических колебаниях пружинного и математического маятников происходят изменения кинетической и потенциальной энергий.
Рассмотрим свободные колебания пружинного маятника (силами трения в системе пренебрежём). Оттянув груз, подвешенный на пружине, вниз, мы сообщаем грузу некоторый запас потенциальной энергии. При движении груза вверх пружина сокращается и потенциальная энергия системы уменьшается.
Рис. 5.10
После прохождения положения равновесия скорость движения груза начинает уменьшаться. Следовательно, уменьшается и его кинетическая энергия, а потенциальная энергия системы снова возрастает. В самой верхней точке она достигает максимума, а кинетическая энергия груза становится равной нулю.
Таким образом, при гармонических колебаниях периодически происходит переход потенциальной энергии в кинетическую энергию и обратно. При этом частота колебаний потенциальной и кинетической энергий в 2 раза больше частоты колебаний груза.
Полный период колебаний кинетической и потенциальной энергий вдвое меньше периода колебаний груза. Кроме того, в момент обращения в нуль одной из энергий другая энергия достигает максимального значения.
Механическая энергия при отсутствии трения в колебательной системе остаётся постоянной (см. рис. 5.10). При колебаниях груза на пружине она равна сумме кинетической и потенциальной энергий:
Кинетическая и потенциальная энергии периодически изменяются, но механическая энергия в системе без трения, согласно закону сохранения энергии, остаётся неизменной (сохраняется). Она равна либо потенциальной энергии системы в момент максимального отклонения маятника от положения равновесия, либо кинетической энергии груза в момент, когда он проходит положение равновесия.
Докажем это. Подставим в формулу для механической энергии выражения для υx и x, полученные в § 25 «Кинематика колебательного движения. Гармонические колебания»:
Заменив в первом члене последнего уравнения ω2 на ω2= k / m, получим
Если же во второй член уравнения (2) подставить k = mω2 и учесть, что ωxm = υm, то
Такие же изменения кинетической и потенциальной энергий происходят при гармонических колебаниях математического маятника.
Затухающие колебания.
В природе не существует колебательных систем, в которых бы не было трения. Силы трения совершают отрицательную работу и уменьшают механическую энергию системы. Поэтому амплитуда колебаний с каждым периодом уменьшается. В итоге после того, как запас механической энергии исчерпается, колебания прекратятся совсем. Другими словами, колебания при наличии трения являются затухающими. Только в пределах небольшого интервала времени уменьшением амплитуды колебаний можно пренебречь и считать (приближённо) колебания незатухающими.
В реальных колебательных системах обязательно происходят потери энергии. Если произвести графическую запись колебаний реальной колебательной системы, то она окажется подобной той, что изображена на рисунке 5.11.
Рис. 5.11
Эту зависимость координаты тела от времени можно заставить «вычерчивать» само колеблющееся тело, например маятник.
На рисунке 5.12 изображён маятник с песочницей.
Рис. 5.12
На равномерно движущемся листе картона он струйкой песка вычерчивает график зависимости координаты от времени. Данный метод «временной развёртки» колебаний позволяет получить представление о процессе движения. Чем быстрее движется лист картона, тем большими оказываются расстояния между соседними максимумами смещения.
C увеличением силы трения колебания затухают быстрее. При большом трении они не возникают совсем. Тело, выведенное из положения равновесия, останавливается, не переходя через положение равновесия (рис. 5.13). Всё это можно наблюдать, постепенно увеличивая трение маятника с песочницей, прикрепляя к нитям подвеса листы плотной бумаги всё большей площади поверхности (сопротивление воздуха зависит от площади листа).
Рис. 5.13
При трении механическая энергия колебательной системы будет постепенно расходоваться на нагревание окружающей среды, именно поэтому амплитуда колебаний будет убывать с течением времени. Трение приводит к торможению колебаний в системе, поэтому следует ожидать и некоторого уменьшения частоты колебаний.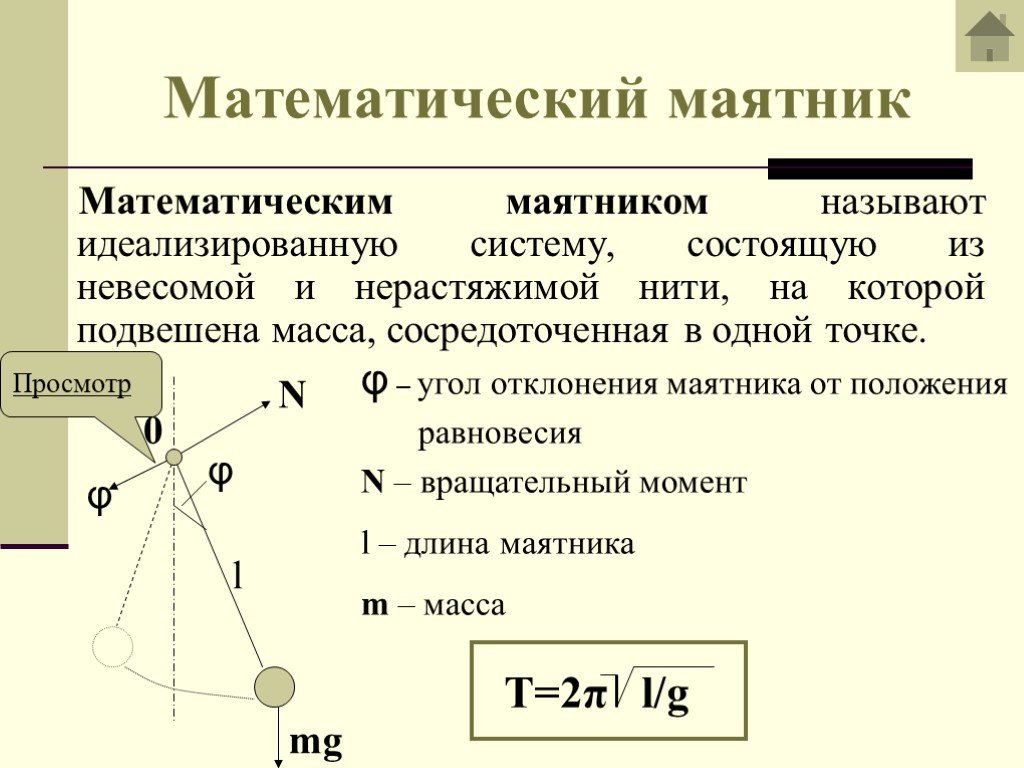 При затухающих колебаниях движение является непериодическим. Соответственно понятие периода колебаний утрачивает свой непосредственный смысл.
При затухающих колебаниях движение является непериодическим. Соответственно понятие периода колебаний утрачивает свой непосредственный смысл.
Вопросы:
1. Как изменяются с течением времени кинетическая и потенциальная энергии пружинного маятника при гармонических колебаниях?
2. Изменяется ли механическая энергия колебательной системы при гармонических колебаниях?
3. Как влияют силы трения, действующие в колебательной системе, на её механическую энергию и амплитуду колебаний?
4. Что является причиной затухания свободных колебаний в колебательной системе?
Вопросы для обсуждения:
1. Изобразите и проанализируйте графики зависимости от времени кинетической энергии, потенциальной энергии и механической энергии математического маятника, совершающего гармонические колебания.
2. Шарик, закреплённый на упругой пружине жёсткостью k, совершает свободные колебания с амплитудой, равной хm.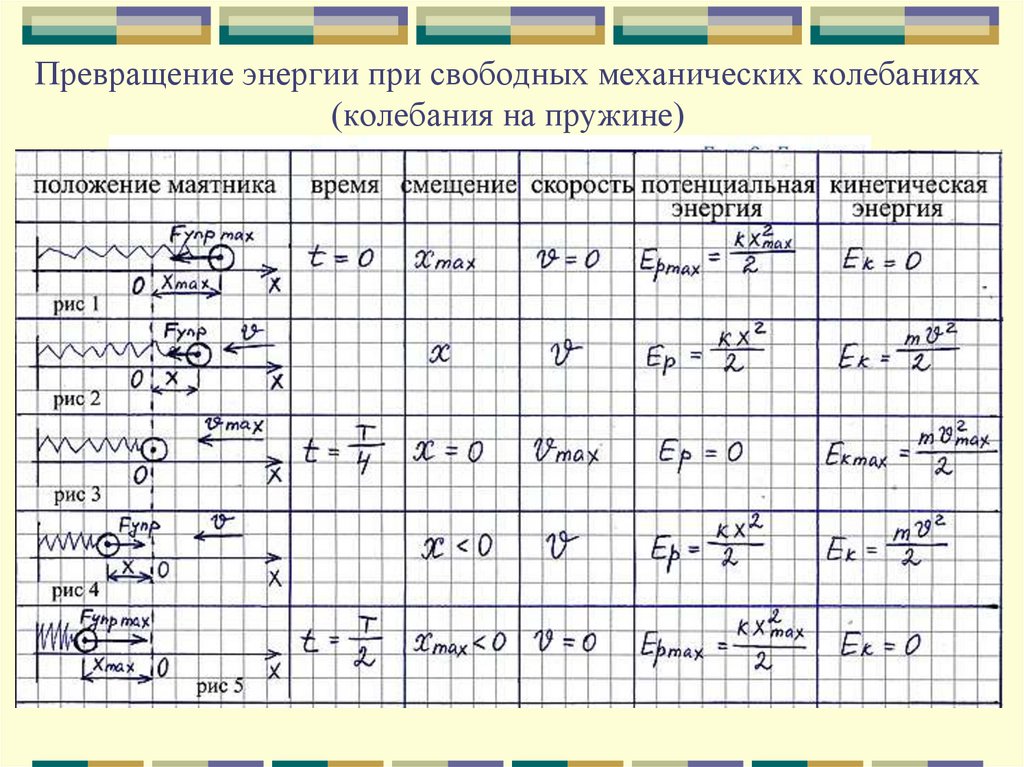 Чему равна кинетическая энергия шарика в момент прохождения им положения равновесия?
Чему равна кинетическая энергия шарика в момент прохождения им положения равновесия?
3. Шарик колеблется на пружине, подвешенной вертикально к потолку. При этом максимальное расстояние от потолка до центра шарика равно Н, минимальное расстояние — h. Какая энергия будет максимальной в точке, удалённой от потолка на расстояние Н?
Пример решения задачи
Груз массой 470 г совершает горизонтальные колебания с амплитудой 4,2 см на упругой пружине с жёсткостью, равной 56 Н/м.
Найдите:
а) механическую энергию системы;
б) потенциальную энергию системы в точке с координатой 2,1 см;
в) кинетическую энергию груза в этой точке;
г) скорость прохождения грузом этой точки.
Ответ:
E ≈ 0,049 Дж;
Ep(x2) ≈ 0,012 Дж;
Ek(x2) = 0,037 Дж;
υ2 ≈ 0,4 м/с.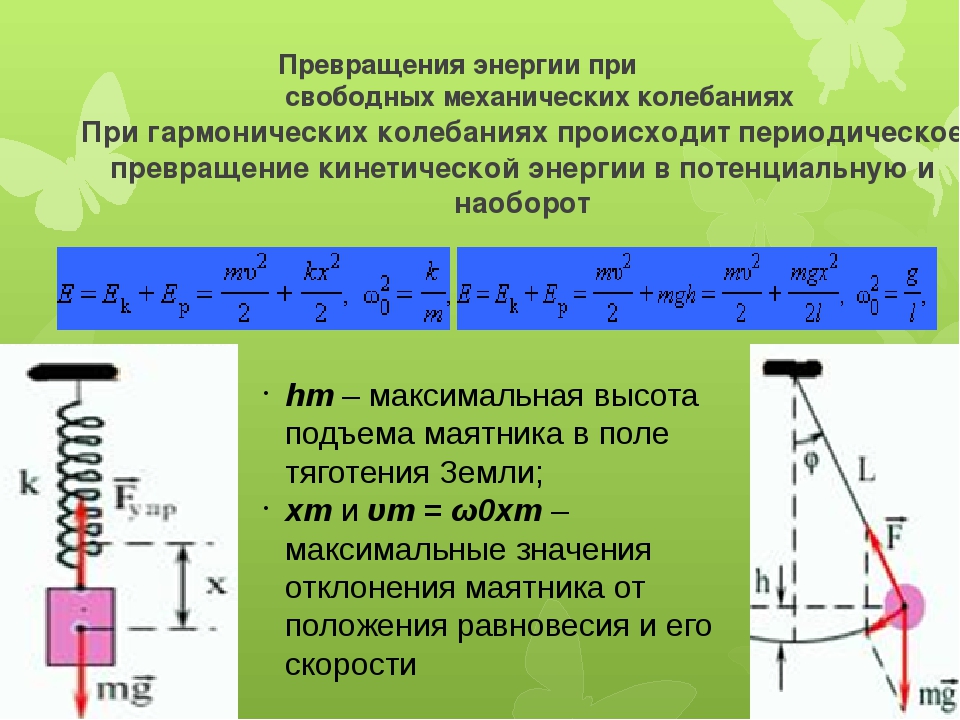
Упражнения:
1. На рисунке 5.14 представлен график зависимости потенциальной энергии математического маятника (относительно его положения равновесия) от времени. Чему будет равна кинетическая энергия маятника в момент времени t = 2 с?
Рис. 5.14
2. Груз массой 400 г совершает колебания на пружине с жёсткостью 250 Н/м. Амплитуда колебаний 15 см. Найдите полную механическую энергию и частоту колебаний груза.
3. C какой скоростью колеблющееся тело, подвешенное на пружине, проходит положение равновесия, если масса тела равна 1 кг, жёсткость пружины — 100 Н/м, а амплитуда колебаний — 0,5 м?
4. Тело массой 5 кг совершает гармонические колебания с амплитудой 10 см. Максимальная кинетическая энергия тела равна 2,5 Дж. Найдите период колебаний.
5. Чему равна масса груза, колеблющегося на пружине с жёсткостью 0,5 кН/м, если при амплитуде колебаний 6 см он имеет максимальную скорость, равную 53 м/с?
Это любопытно.
 ..
..Из истории развития физики и техники
В 1851 г. французский физик Жан Бернар Леон Фуко (1819 — 1868) провёл в здании Пантеона в Париже (усыпальница выдающихся людей Франции) опыт, который наглядно продемонстрировал факт суточного вращения Земли (рис. 5.15).
Рис. 5.15
К куполу Пантеона была прикреплена стальная проволока длиной 67 м, а к ней был подвешен массивный металлический шар. По разным источникам, масса шара составляла от 25 до 28 кг.
Проволока крепилась к куполу таким образом, чтобы получившийся маятник мог качаться в любой плоскости. При этом на груз маятника действовали сила тяжести, направленная вертикально вниз, и сила натяжения проволоки, направленная вдоль проволоки вверх. Таким образом, равнодействующая сил, действующих на маятник, лежала в вертикальной плоскости, проходящей через проволоку, т. е. в плоскости качаний маятника.
Маятник совершал колебания над круглым постаментом диаметром 6 м, по краю которого был насыпан валик из песка. При каждом качании маятника острый стержень, укреплённый на шаре снизу, оставлял на валике отметку, сметая с ограждения песок. Для того чтобы исключить влияние подвеса на маятник Фуко, применялись специальные подвесы. При запуске маятника принимались меры для устранения толчков в направлении, перпендикулярном к начальной плоскости качаний. Период колебаний маятника в опыте Фуко составлял примерно 16,4 с. По прошествии каждого периода колебаний новая отметка, наносимая остриём стержня на песке, оказывалась примерно в 3 мм от предыдущей. За первый час наблюдений плоскость качаний маятника повернулась на угол около 11° по часовой стрелке. Полный же оборот плоскость маятника совершила примерно за 32 ч, после чего вернулась в прежнее положение.
При каждом качании маятника острый стержень, укреплённый на шаре снизу, оставлял на валике отметку, сметая с ограждения песок. Для того чтобы исключить влияние подвеса на маятник Фуко, применялись специальные подвесы. При запуске маятника принимались меры для устранения толчков в направлении, перпендикулярном к начальной плоскости качаний. Период колебаний маятника в опыте Фуко составлял примерно 16,4 с. По прошествии каждого периода колебаний новая отметка, наносимая остриём стержня на песке, оказывалась примерно в 3 мм от предыдущей. За первый час наблюдений плоскость качаний маятника повернулась на угол около 11° по часовой стрелке. Полный же оборот плоскость маятника совершила примерно за 32 ч, после чего вернулась в прежнее положение.
В России маятник Фуко длиной 98 м был установлен в Исаакиевском соборе в Ленинграде (в 1986 г. маятник был демонтирован). Обычно показывался такой удивительный эксперимент — на полу устанавливался спичечный коробок чуть поодаль от плоскости вращения маятника.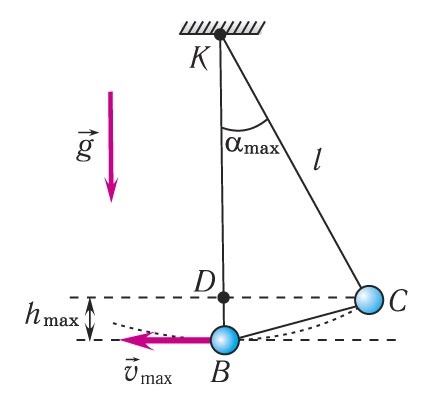 Пока гид рассказывал о маятнике, плоскость его вращения поворачивалась и стержень, укреплённый на шаре, сбивал коробок.
Пока гид рассказывал о маятнике, плоскость его вращения поворачивалась и стержень, укреплённый на шаре, сбивал коробок.
Более подробно на сайте «История техники»
Предыдущая страницаСледующая страница
Кинетическая энергия маятника Калькулятор
Скромный маятник ! Каким-то образом маятники возвращают травмирующие воспоминания. Для (бывших) студентов эти воспоминания принимают форму загадочных уравнений и классных досок, заполненных нечитаемыми знаками… Для старых домов все разрушение и снос . Давайте построим мосты понимания к , покажем, как маятники и шары-разрушители не только полны науки и могучей силы, но и могут быть забавными, как F…LYING!
Мы сняли видео о маятниках! Смотреть здесь:
Смотреть на YouTubeОсновы математического маятника
Начнем с самого начала: что такое (математический) маятник? Маятник — это просто груз , свисающий с веревки или палки , который может свободно качаться. «Математическая» версия — это приближение, в котором мы игнорируем потери на трение (с воздухом или при вращении), а также вес стержня или веревки, на которой висит груз.
«Математическая» версия — это приближение, в котором мы игнорируем потери на трение (с воздухом или при вращении), а также вес стержня или веревки, на которой висит груз.
Этих приближений достаточно для всех расчетов, кроме самых точных, и они помогают нам сосредоточиться на физике в игре без необходимости иметь дело с препятствиями реальной установки, где нет ничего идеального. Используя эти приближения, мы можем связать период маятника с его длиной с помощью этого простого уравнения :
T=2πLgT=2\pi\sqrt{\frac{L}{g}}T=2πgL
, где TTT — период, LLL — длина веревки/стержня, а ggg — ускорение свободного падения (92}в среднем 9,8 м/с2 на поверхности Земли).
Этому обычно учат как наиболее важное уравнение маятника , так как его часто преподают физики или математики. Однако, если нас интересует полезность маятника (например, в качестве шара-разрушителя), это уравнение не так уж полезно. Он ничего не говорит нам о энергии маятника, о скорости , с которой он движется, или о том, как все это соотносится, например, с его разрушительной силой.
Он ничего не говорит нам о энергии маятника, о скорости , с которой он движется, или о том, как все это соотносится, например, с его разрушительной силой.
Энергия маятника — другой способ мышления
Если мы хотим знать, как маятник будет взаимодействовать с другими объектами , нам нужно больше информации. Мы можем получить это, взглянув на калькулятор физического маятника или посмотрев, как рассчитать потенциальную энергию (энергию, связанную с высотой) и кинетическую энергию (энергию движения) и как они соотносятся друг с другом.
Оставаясь в математическом приближении, полная энергия маятника всегда постоянна , превращаясь из потенциальной энергии в кинетическую и наоборот. Чтобы вычислить эти величины в любой точке движения маятника, нам нужно знать массу маятника, а также его высоту по вертикали.
Уравнение, связывающее преобразование энергии в маятнике , выглядит следующим образом: Etotal=Ekin+Epot
и может быть расширена до:
Etotal=m⋅h⋅g+12⋅m⋅v2E_{\mathrm{total}} = m\cdot h\cdot g +\frac{ 1}{2}\cdot m \cdot v^2Etotal=m⋅h⋅g+21⋅m⋅v2
Где mmm — масса маятника, hhh — высота груза, а vvv — скорость, с которой движется груз. Полная энергия (EtotalE_{\mathrm{total}}Etotal) кажется неизвестной, но ее можно легко рассчитать, используя точку, в которой есть только кинетическая или потенциальная энергия. Например, если мы возьмем маятник в его высшей точке (h=hmaxh = h_{\mathrm{max}}h=hmax), то мы знаем, что скорость равна 0 м/с0\ \mathrm{м/с}0 м/с и, следовательно, Etotal=m⋅hmax⋅gE_{\mathrm{total}} = m \cdot h_{\mathrm{max}} \cdot gEtotal=m⋅hmax⋅g.
Полная энергия (EtotalE_{\mathrm{total}}Etotal) кажется неизвестной, но ее можно легко рассчитать, используя точку, в которой есть только кинетическая или потенциальная энергия. Например, если мы возьмем маятник в его высшей точке (h=hmaxh = h_{\mathrm{max}}h=hmax), то мы знаем, что скорость равна 0 м/с0\ \mathrm{м/с}0 м/с и, следовательно, Etotal=m⋅hmax⋅gE_{\mathrm{total}} = m \cdot h_{\mathrm{max}} \cdot gEtotal=m⋅hmax⋅g.
🙋 Чтобы узнать об остальных математических функциях маятника, посетите калькулятор периода маятника Omni и калькулятор частоты маятника.
Использование маятника (да, это форма множественного числа)
Хотя маятник очень просто построить, он предлагает удивительно широкий спектр применений. На самом деле, вы, вероятно, сталкивались со многими маятниками в своей жизни, даже не осознавая этого. Вот несколько примеров того, где их можно встретить в повседневной жизни:
- Маятниковые часы не так популярны, как раньше, но они заслуживают упоминания, учитывая, что они существуют с 17 века.
 Они используют повторяемость движения маятника для отслеживания времени — каждый раз, когда груз проходит положение равновесия, соответствующее колесо перемещается, а рука следует за ним.
Они используют повторяемость движения маятника для отслеживания времени — каждый раз, когда груз проходит положение равновесия, соответствующее колесо перемещается, а рука следует за ним. - Аналогичный механизм используется в метрономах , устройствах, используемых в основном музыкантами. Они производят звук через равные промежутки времени, чтобы помочь музыкантам играть вовремя. Они могут пригодиться, если вы изо всех сил пытаетесь сохранить ритм.
- В регионах, часто посещаемых землетрясениями, многие здания используют маятник трения в качестве сейсмоизолятора. Движение земли заставляет маятник колебаться, что снижает риск повреждения конструкции.
- Однако, если вы хотите снести здание, а не защищать его, не ищите дальше — шар-разрушитель — один из способов сделать это. По сути, это большой массивный маятник, который использует свою кинетическую энергию, чтобы приложить силу к объекту, чтобы сломать его.
 Чем он длиннее и тяжелее, тем больше энергии доступно и тем больше разрушений вы можете посеять.
Чем он длиннее и тяжелее, тем больше энергии доступно и тем больше разрушений вы можете посеять. - Многие аттракционы в парках развлечений используют маятниковый механизм; они просто немного более сложные, особенно если они также могут качаться вертикально. Типичные качели на детской площадке также могут быть примером, когда вы становитесь частью боба.
- Научные инструменты , такие как сейсмометры, которые используются для обнаружения сейсмических волн и таких явлений, как землетрясения. Другой тип прибора — гравиметр — особый вид акселерометра, используемый специально для определения ускорения свободного падения, ggg. Хотя мы обычно рассматриваем его как константу, на самом деле он меняется в зависимости от местоположения на Земле!
Есть и другие применения маятника, такие как гипноз (предположительно) или курильницы, используемые в некоторых религиозных обрядах. Как видите, есть причина, по которой они так широко изучаются — они составляют основу многих объектов и могут быть легко изучены с небольшим оборудованием!
Энергия в маятнике: кинетика и потенциал
Вы и ваши друзья весело качаетесь на веревочных качелях и прыгаете в озеро. Когда наступает ваша очередь, вы хотите отпустить качание веревки, когда ваша скорость будет максимальной. Вы помните из урока физики, что наибольшая скорость соответствует наибольшей кинетической энергии. Какое место на пути вашего раскачивания будет иметь наибольшую кинетическую энергию? Когда вы хватаетесь за веревку и начинаете раскачиваться, ваша скорость увеличивается до тех пор, пока вы не достигнете нижней части пути, где ваша скорость максимальна, после чего ваша скорость начинает уменьшаться, поскольку раскачивание снова поднимает вас в воздух. Таким образом, вы достигаете наибольшей скорости и кинетической энергии в нижней части вашего пути. Увеличение скорости, которое вы испытываете, когда раскачиваетесь на канатных качелях, является примером сохранения энергии маятника. Обсудим подробнее энергию маятников!
Когда наступает ваша очередь, вы хотите отпустить качание веревки, когда ваша скорость будет максимальной. Вы помните из урока физики, что наибольшая скорость соответствует наибольшей кинетической энергии. Какое место на пути вашего раскачивания будет иметь наибольшую кинетическую энергию? Когда вы хватаетесь за веревку и начинаете раскачиваться, ваша скорость увеличивается до тех пор, пока вы не достигнете нижней части пути, где ваша скорость максимальна, после чего ваша скорость начинает уменьшаться, поскольку раскачивание снова поднимает вас в воздух. Таким образом, вы достигаете наибольшей скорости и кинетической энергии в нижней части вашего пути. Увеличение скорости, которое вы испытываете, когда раскачиваетесь на канатных качелях, является примером сохранения энергии маятника. Обсудим подробнее энергию маятников!
Рис. 1. Человек, качающийся на канатных качелях, является примером маятника.
Простые и физические маятники
Для начала давайте рассмотрим определение маятника. Маятник представляет собой систему, в которой объект подвешен к фиксированной точке и колеблется взад и вперед под действием силы тяжести. Гравитация действует как восстанавливающая сила для маятника, поскольку она толкает массу к положению равновесия. Если предположить, что гравитация является единственной силой, действующей на маятник, маятник будет колебаться вечно, пока на него не подействует другая сила.
Маятник представляет собой систему, в которой объект подвешен к фиксированной точке и колеблется взад и вперед под действием силы тяжести. Гравитация действует как восстанавливающая сила для маятника, поскольку она толкает массу к положению равновесия. Если предположить, что гравитация является единственной силой, действующей на маятник, маятник будет колебаться вечно, пока на него не подействует другая сила.
Маятник — это система, в которой объект подвешен к фиксированной точке и колеблется взад-вперед под действием силы тяжести.
В физике изучаются два типа маятников: простой маятник и физический маятник. Физический маятник — это реальный маятник, в котором размеры колеблющегося объекта связаны с его движением. В случае физического маятника движение зависит от момента инерции маятника, силы тяжести и расстояния от точки вращения. простой маятник — это маятник, в котором мы рассматриваем висящий объект как точечную массу. Движение простого маятника не зависит от массы объекта и зависит от силы тяжести и длины струны, которую мы предполагаем безмассовой. Поскольку в этой статье мы обсуждаем сохранение энергии в маятниках, мы сосредоточимся на простых маятниках, поэтому, когда мы говорим о маятнике, мы имеем в виду простой маятник.
Движение простого маятника не зависит от массы объекта и зависит от силы тяжести и длины струны, которую мы предполагаем безмассовой. Поскольку в этой статье мы обсуждаем сохранение энергии в маятниках, мы сосредоточимся на простых маятниках, поэтому, когда мы говорим о маятнике, мы имеем в виду простой маятник.
Изменение энергии маятника
Теперь давайте обсудим энергию маятника. Механическая энергия колеблющегося маятника включает в себя кинетическую энергию \((K)\) и потенциальную энергию \((U)\). Консервативная сила, действующая на маятник и сообщающая системе потенциальную энергию, называется силой тяжести. Таким образом, типом потенциальной энергии в системе является гравитационная потенциальная энергия, которая зависит от высоты массы относительно выбранной нулевой точки. Мы позвоним положение равновесия маятника нулевая точка, так что гравитационная потенциальная энергия равна нулю в этой точке. Учтите, что груз на маятнике поднят так, что он находится в положении справа, показанном на изображении ниже.
Рис. 2. Когда маятник качается справа налево, потенциальная энергия и кинетическая энергия меняются в зависимости от положения.
Когда маятник отпускают из этого положения, потенциальная энергия уменьшается до тех пор, пока он не достигнет положения равновесия, а затем увеличивается, когда маятник качается вверх в другую сторону. С другой стороны, поскольку маятник изначально покоится, кинетическая энергия начинается с нуля и увеличивается до положения равновесия, после чего она уменьшается по мере того, как маятник качается вверх.
В большинстве случаев мы будем предполагать, что сила сопротивления воздуха на маятник незначительна. Если это так, то полная механическая энергия в системе постоянна. В тех случаях, когда им нельзя пренебречь, сопротивление воздуха вводит неконсервативную силу, что означает, что полная механическая энергия системы будет уменьшаться, поскольку часть кинетической энергии преобразуется в другие формы энергии, такие как тепловая энергия, во время колебаний. В этом случае маятник не будет колебаться вечно, а будет уменьшать амплитуду и механическую энергию до тех пор, пока колебание в конце концов не прекратится. 92.\,\]В этом уравнении \(m\) — масса маятника в килограммах, \(\mathrm{kg},\) и \(v\) — его скорость в метрах в секунду, \( \mathrm{\frac{m}{s}}.\) Как упоминалось в предыдущем разделе, кинетическая энергия увеличивается по мере движения к положению равновесия и уменьшается по мере удаления от положения равновесия. Это потому, что кинетическая энергия пропорциональна квадрату скорости маятника. Маятник начинает с покоя и увеличивает скорость, пока не достигнет равновесия, после чего маятник замедляется, пока не достигнет максимальной высоты, где его скорость на мгновение становится равной нулю.
В этом случае маятник не будет колебаться вечно, а будет уменьшать амплитуду и механическую энергию до тех пор, пока колебание в конце концов не прекратится. 92.\,\]В этом уравнении \(m\) — масса маятника в килограммах, \(\mathrm{kg},\) и \(v\) — его скорость в метрах в секунду, \( \mathrm{\frac{m}{s}}.\) Как упоминалось в предыдущем разделе, кинетическая энергия увеличивается по мере движения к положению равновесия и уменьшается по мере удаления от положения равновесия. Это потому, что кинетическая энергия пропорциональна квадрату скорости маятника. Маятник начинает с покоя и увеличивает скорость, пока не достигнет равновесия, после чего маятник замедляется, пока не достигнет максимальной высоты, где его скорость на мгновение становится равной нулю.
Максимальная и минимальная кинетическая энергия маятника
В положении равновесия маятника кинетическая энергия и линейная скорость максимальны, как показано на рисунке ниже. Поскольку скорость маятника равна нулю в положениях наибольшей амплитуды, кинетическая энергия в этих положениях также равна нулю. 2}},\) и \(h\) — наибольшая высота, достигнутая маятником в метров, \(\mathrm{m}.\) Когда маятник качается в сторону положения равновесия, потенциальная энергия уменьшается по мере уменьшения высоты. Затем потенциальная энергия увеличивается с высотой по мере того, как маятник удаляется от положения равновесия.
2}},\) и \(h\) — наибольшая высота, достигнутая маятником в метров, \(\mathrm{m}.\) Когда маятник качается в сторону положения равновесия, потенциальная энергия уменьшается по мере уменьшения высоты. Затем потенциальная энергия увеличивается с высотой по мере того, как маятник удаляется от положения равновесия.
Максимальная и минимальная потенциальная энергия маятника
Потенциальная энергия маятника имеет максимум в местах, где маятник достигает наибольшей высоты, как показано на рисунке ниже. Поскольку мы определили положение равновесия как нулевую точку, высота и, следовательно, потенциальная энергия маятника в этом месте равны нулю.
Рис. 4 — Потенциальная энергия маятника максимальна в местах наибольшей амплитуды и имеет минимум в положении равновесия, где потенциальная энергия равна нулю.
Сохранение энергии в маятнике
Если силой сопротивления воздуха маятнику можно пренебречь, полная механическая энергия в системе сохраняется. Это означает, что изменение механической энергии при перемещении маятника из одного положения в другое равно нулю, или, другими словами, механическая энергия постоянна.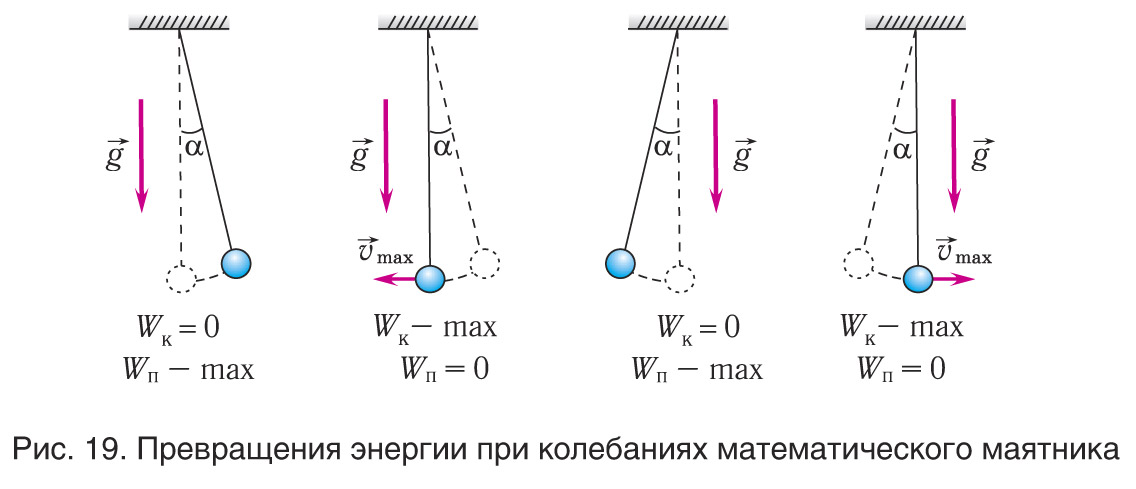 Сохранение энергии в маятнике можно описать следующим уравнением: \[\Delta E=\Delta K+\Delta U=0.\]
Сохранение энергии в маятнике можно описать следующим уравнением: \[\Delta E=\Delta K+\Delta U=0.\]
Когда на маятник действуют другие силы, такие как сопротивление воздуха, мы должны учитывать рассеянная энергия в уравнении сохранения энергии, а также. Механическая энергия уменьшается, так как часть кинетической энергии рассеивается в виде тепловой энергии. Когда это происходит, происходит изменение внутренней энергии \(IE\) системы, которое необходимо учитывать. Тогда уравнение, описывающее сохранение энергии в маятнике, имеет вид: \[\Delta E=\Delta K+\Delta U+\Delta IE=0.\] 9{\circ}\) относительно вертикали. Найдите кинетическую энергию и скорость маятника, когда он находится в положении равновесия. Не учитывать сопротивление воздуха.
Рис. 5 — Механическая энергия маятника в верхней и нижней точках постоянна.
Рассмотрим полную механическую энергию системы на максимальной высоте и в положении равновесия. На максимальной высоте механическая энергия представляет собой сумму кинетической и потенциальной энергий: \(E_1=K_1+U_1. 2,\end{align*}\]где \(v\) — скорость маятника в положении равновесия. 92&=\frac{2K_2}{m}\\[8pt]v &=\sqrt{\frac{2K_2}{m}}\\[8pt]&=\sqrt{\frac{2(0,23\,\mathrm) {J})}{0,5\,\mathrm{kg}}}\\[8pt]&=0,96\,\mathrm{\frac{m}{s}}.\end{align*}\]
2,\end{align*}\]где \(v\) — скорость маятника в положении равновесия. 92&=\frac{2K_2}{m}\\[8pt]v &=\sqrt{\frac{2K_2}{m}}\\[8pt]&=\sqrt{\frac{2(0,23\,\mathrm) {J})}{0,5\,\mathrm{kg}}}\\[8pt]&=0,96\,\mathrm{\frac{m}{s}}.\end{align*}\]
Энергия in Pendulum — Key takeaways
- Маятник — это система, в которой объект свисает с фиксированной точки и колеблется взад-вперед под действием силы тяжести.
- Если маятник колеблется только под действием силы тяжести, полная механическая энергия системы сохраняется, и маятник будет колебаться до тех пор, пока на него не подействует другая сила.
- Если колебательный маятник движется под действием силы тяжести и сопротивления воздуха, то полная механическая энергия системы не сохраняется, и колебания маятника будут уменьшаться до полной остановки.
- Кинетическая энергия маятника максимальна в положении равновесия и минимальна в положении наибольшей высоты.
- Потенциальная энергия маятника максимальна в положении наибольшей высоты и минимальна в положении равновесия.


 Они используют повторяемость движения маятника для отслеживания времени — каждый раз, когда груз проходит положение равновесия, соответствующее колесо перемещается, а рука следует за ним.
Они используют повторяемость движения маятника для отслеживания времени — каждый раз, когда груз проходит положение равновесия, соответствующее колесо перемещается, а рука следует за ним.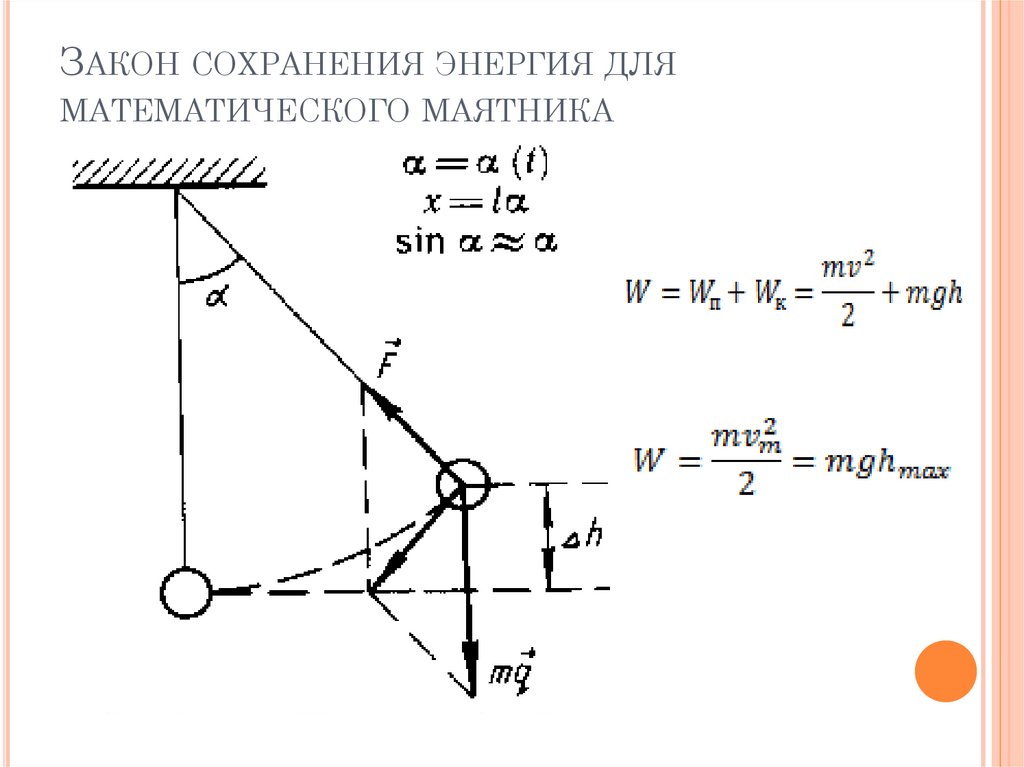 Чем он длиннее и тяжелее, тем больше энергии доступно и тем больше разрушений вы можете посеять.
Чем он длиннее и тяжелее, тем больше энергии доступно и тем больше разрушений вы можете посеять.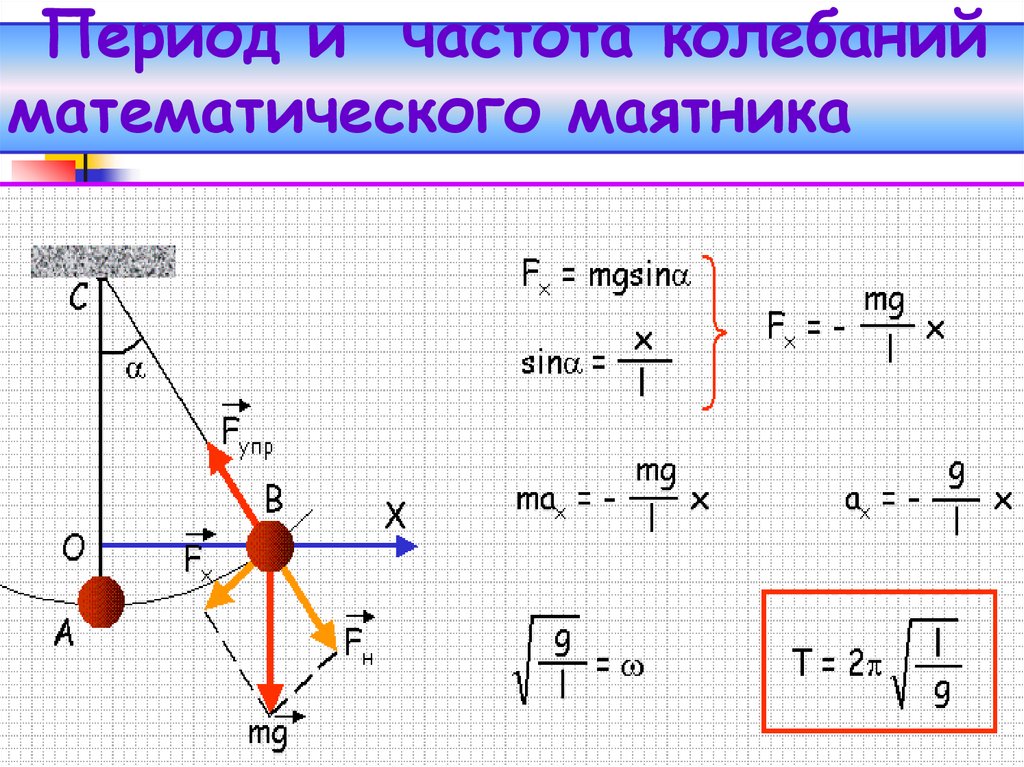
Leave A Comment