Как называются фазы каждой пространственной геометрической фигуры?
содержание
Как называются пространственные геометрические фигуры?
Особенности пространственной геометрии
- призма.
- Куб.
- брусчатка.
- пирамида.
- конус.
- цилиндр.
- мяч.
Сколько граней у пространственной фигуры?
Сколько граней у пространственной фигуры? Сколько граней у пространственной фигуры? Грани: у него 6 квадратных граней; Диагонали: внутри куба 4 диагонали; Вершины: имеет 8 вершин; Углы: 24 прямых угла.
Что такое фазы геометрической фигуры?
Грани — это многоугольники («стороны» многогранника), ребра — стороны многоугольника, а вершины — вершины многоугольника.
Какова классификация каждой из космических фигур?
Пространственные геометрические фигуры – это те, которые имеют три измерения: длину, высоту и ширину. Эти фигуры делятся на две группы: круглые тела (ограниченные какой-либо округлой поверхностью) и многогранники (поверхности, ограниченные плоскими геометрическими фигурами).
Сколько граней у пространственного треугольника?
Сколько граней у пространственного треугольника? Лица: имеет 6 граней; Вершины: имеет 8 вершин; Ребра: имеет 12 ребер.
Что такое вершины, грани и ребра?
Грани: плоские поверхности, составляющие твердое тело; Края: соответствуют линиям, полученным в результате встречи двух граней; Вершины: точки встречи ребер.
Что такое геометрические и пространственные фигуры?
ПРОСТРАНСТВЕННЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ ИЛИ ГЕОМЕТРИЧЕСКИЕ ТЕЛА ЯВЛЯЮТСЯ ТЕ, КОТОРЫЕ ПРОИСХОДЯТ В ПРОСТРАНСТВЕ, В СВЯЗИ С ИХ ТРЕХМЕРНОСТЬЮ, Т.Е. ИМЕЮТ ТРИ ИЗМЕРЕНИЯ (ВЫСОТУ, ШИРИНУ И ДЛИНУ).
Какие фигуры имеют грани, ребра и вершины?
Многогранники — это геометрические фигуры, образованные плоскостями и имеющие в качестве элементов вершины, ребра и грани.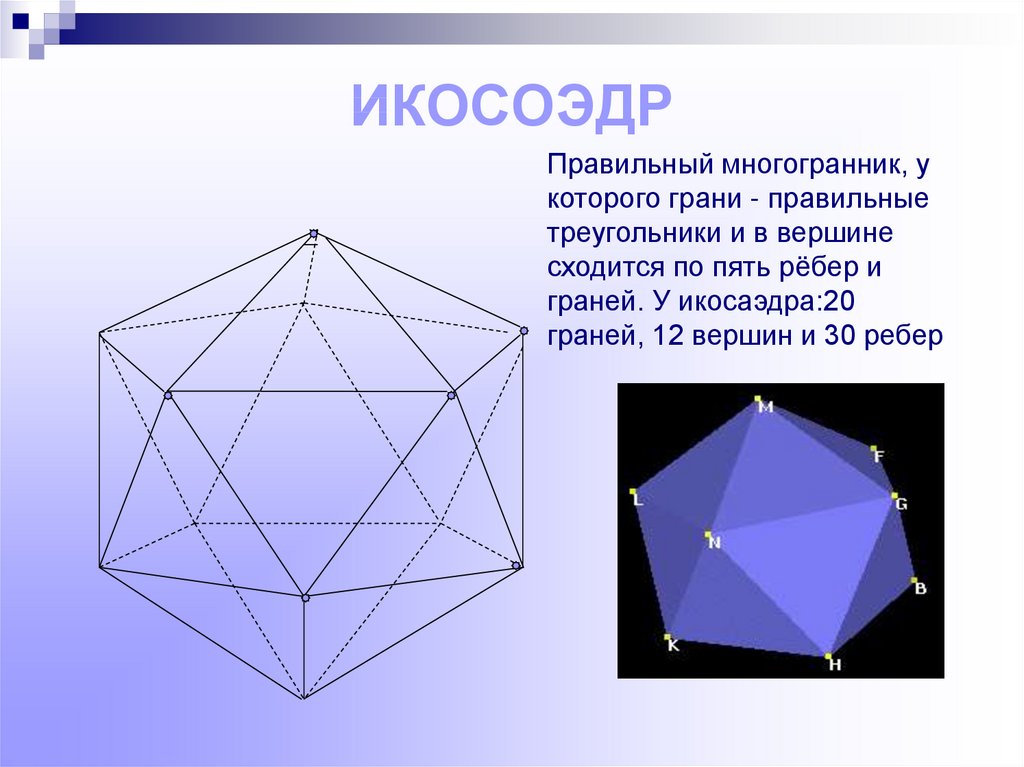
Как называется фигура, у которой 8 граней?
Согласно греческому философу Платону, октаэдр является представителем элемента воздуха. Это платоническое тело образовано 12 ребрами, 6 вершинами и 8 гранями, имеющими форму равностороннего треугольника.
Как называется фигура, имеющая 4 фазы?
Тетраэдр: геометрическое тело, образованное 4 вершинами, 4 треугольными гранями и 6 ребрами.
Сколько фаз имеет фигура призмы?
Призма: Пространственная фигура, имеющая две противоположные, параллельные и конгруэнтные многоугольные грани, называемые основаниями, разделенные расстоянием, называемым высотой. Остальные грани имеют форму параллелограмма, стороны которого являются отрезками, соединяющими соответствующие вершины двух оснований.
Сколько граней у призмы?
У него 8 вершин, 12 ребер и 6 граней, две из которых являются основаниями, а остальные прямоугольными.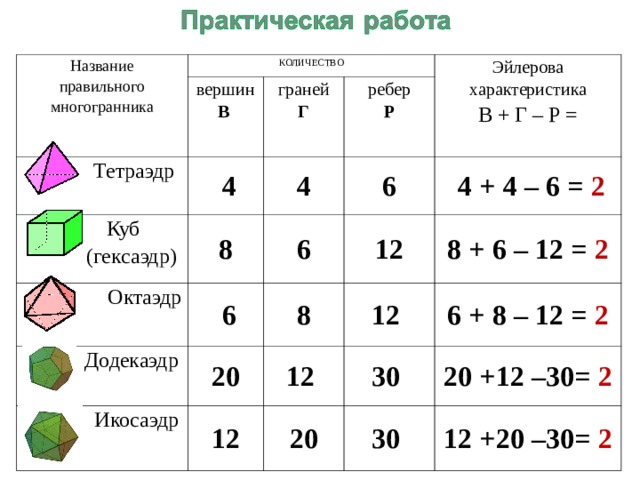
Сколько граней у куба?
Куб представляет собой правильный многогранник с шестью квадратными гранями. Таким образом, все ребра куба конгруэнтны.
Какие существуют виды геометрических фигур?
Кроме того, у каждого из них есть несколько сторон.
- Треугольник — 3 стороны.
- Четырехугольник – 4 стороны.
- Пентагон – 5 сторон.
- Шестиугольник — 6 сторон.
- Гептагон – 7 сторон.
- Октагон – 8 сторон.
- Эннеагон – 9 сторон.
- Декагон – 10 сторон.
Каковы элементы пространственной геометрии?
Пространственная геометрия возникает из примитивных элементов, которые называются так потому, что не имеют определения. Это: точка, линия, плоскость и пространство.
Сколько граней у параллелепипеда?
Параллелепипед — это геометрическое тело, имеющее 6 граней, 8 вершин и 12 ребер.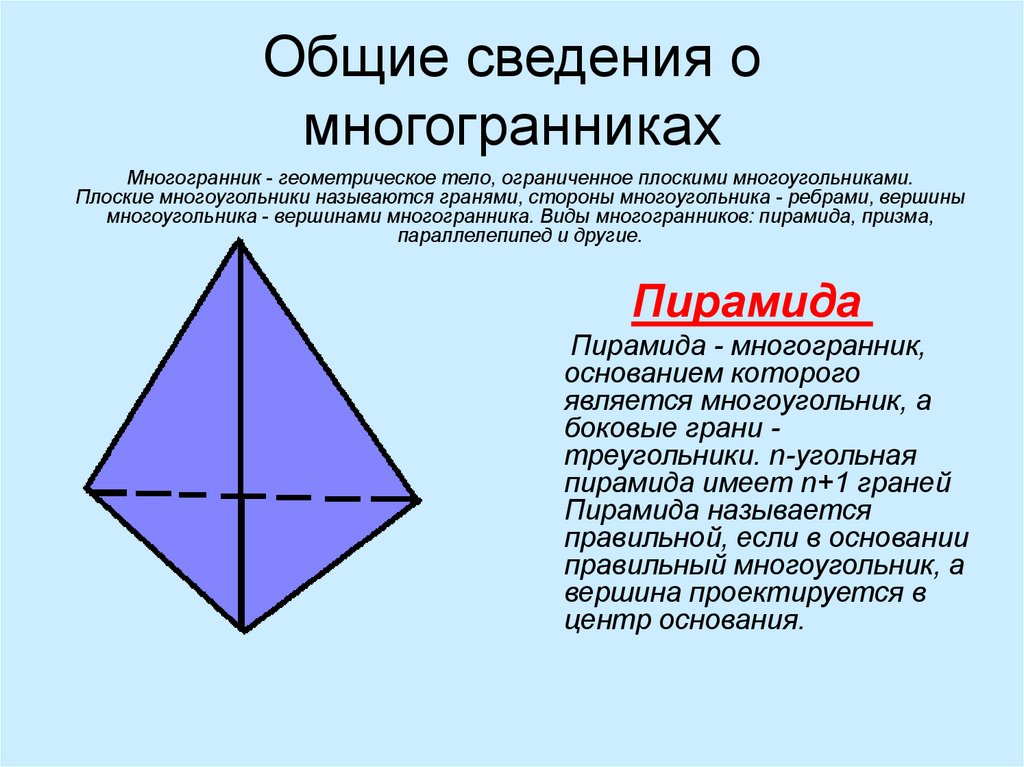 Грани параллелепипеда образованы параллелограммами. Параллелепипед может быть прямым или косым.
Грани параллелепипеда образованы параллелограммами. Параллелепипед может быть прямым или косым.
Это пространственная геометрическая фигура, имеющая 6 плоских граней в виде прямоугольников?
Параллелепипед имеет: 6 граней (параллелограммы)
Сколько граней у шара?
Это геометрическое тело очень круглое. У него нет плоских граней: на самом деле у него только одна изогнутая грань, и он катится, как футбольный мяч.
Является ли это пространственной геометрической фигурой, у которой все грани квадратные?
Также известный как шестигранник, куб представляет собой геометрическое тело, все грани которого образованы квадратами. У него 6 граней, 12 ребер и 8 вершин. Куб представляет собой шестигранный многогранник, все грани которого квадратные.
Что касается названия шестиугольной призмы и пространственной формы?
Шестиугольная призма: основание образовано шестиугольником.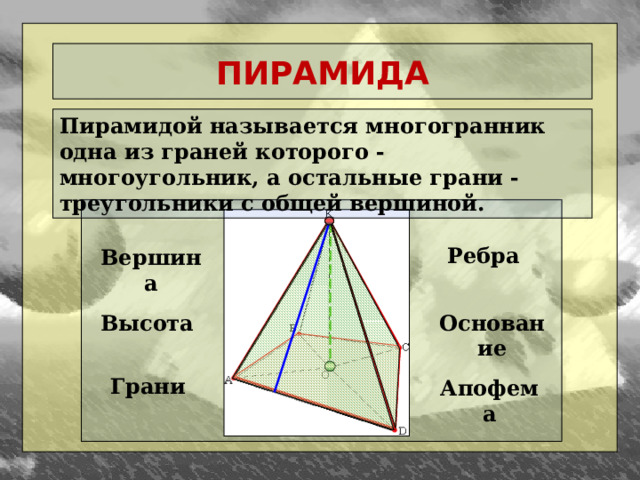 Семиугольная призма: основание образовано семиугольником.
Семиугольная призма: основание образовано семиугольником.
Как преподавать пространственную геометрию?
Начните занятие с представления некоторых объектов в виде многогранников, чтобы можно было изучить некоторые элементы, принадлежащие к твердым телам. каждая грань также является вершиной многогранника. Пример куба: куб имеет длину, ширину и высоту (3 измерения) и состоит из 6 квадратов (плоских фигур).
Что такое плоские фигуры?
Плоские фигуры: треугольник, квадрат, круг, ромб и прямоугольник. Плоская геометрия постоянно присутствует в нашей повседневной жизни. Когда мы наблюдаем за окружающим миром, можно заметить различные геометрические фигуры. Когда геометрические фигуры имеют два измерения, они являются объектом изучения плоской геометрии.
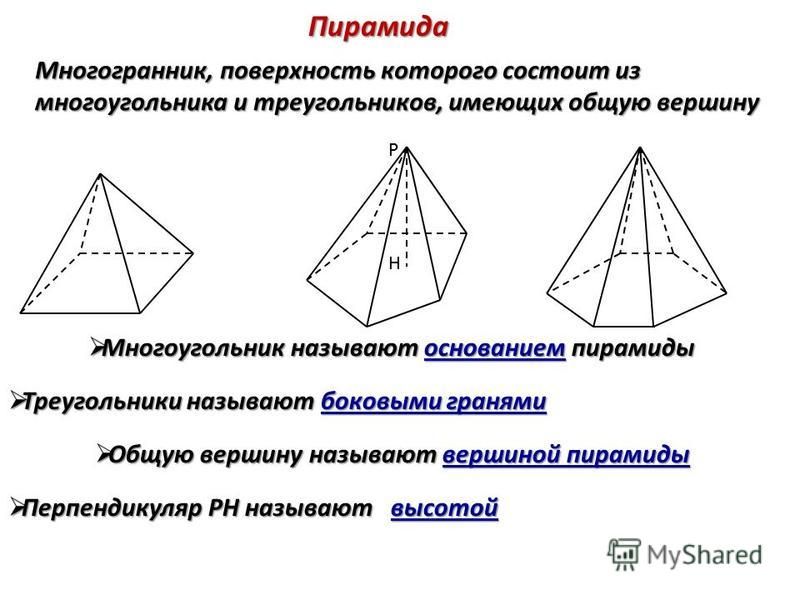
Сколько граней у пирамиды с квадратным основанием?
Четырехугольная пирамида: ее основание представляет собой квадрат, состоящий из пяти граней: четырех боковых граней и базовой грани. Пятиугольная пирамида: ее основание представляет собой пятиугольник, состоящий из шести граней: пяти боковых граней и базовой грани.
Пятиугольная пирамида: ее основание представляет собой пятиугольник, состоящий из шести граней: пяти боковых граней и базовой грани.
Как называется фигура, у которой 5 граней?
J. 2 полигона
| треугольник | 3 | 3 |
| четырехугольник | 4 | 4 |
| пятиугольник | 5 | 5 |
| Гексагоно | 6 | 6 |
| Семиугольник | 7 | 7 |
Как называется геометрическая фигура, имеющая 6 граней?
Шестигранник, также называемый кубом, образован 12 ребрами, 8 вершинами и 6 гранями. Согласно греческому философу Платону, шестигранник представляет собой элемент земли, фигуру, образованную 12 ребрами, 8 вершинами и 6 гранями в четырехугольном формате. Шестигранник также можно назвать кубом.
Как называется фигура, у которой 7 граней?
Семигранник – это многогранник с семью гранями. Семигранник может иметь удивительное количество различных основных форм или топологий.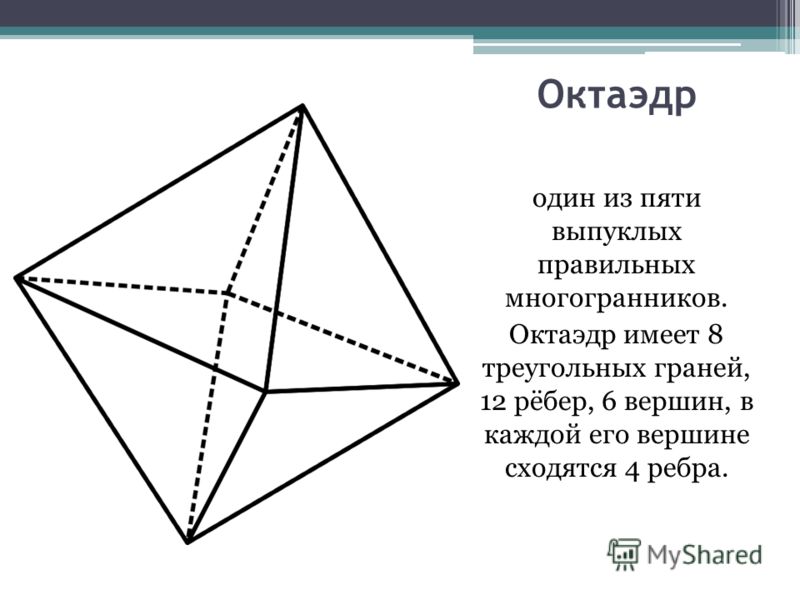 Вероятно, наиболее знакомыми являются шестиугольная пирамида и пятиугольная призма.
Вероятно, наиболее знакомыми являются шестиугольная пирамида и пятиугольная призма.
Какие 4 фазы?
Человек проходит 4 стадии жизни: детство, юность, взрослость и старость.
Какие типы фазы?
Фаза материи — это фаза или физическая форма, которую представляют тела. Они могут быть трех разных форм или фаз: твердой, жидкой и газообразной.
Как определяется фаза?
Значение фазы
существительное женского рода Каждый период, каждая из стадий чего-либо в развитии или того, что претерпевает последовательные изменения: фазы лечения. [Астрономия] Каждый из аспектов, которые планеты и Луна выражают в соответствии с их орбитами вокруг Земли: фазы Луны.
Как называются грани призмы?
Основания: параллельные и конгруэнтные грани призмы. Боковые грани: все параллелограммы. В случае прямой призмы боковые грани представляют собой прямоугольники. Высота (h): кратчайшее расстояние между вашими базами.
Как называются призмы?
четырехугольная призма: имеет каждое из оснований в форме четырехугольника; пятиугольная призма: имеет каждое из оснований в форме пятиугольника; шестиугольная призма: имеет каждое из оснований в форме шестиугольника; восьмиугольная призма: имеет каждое из оснований в форме восьмиугольника.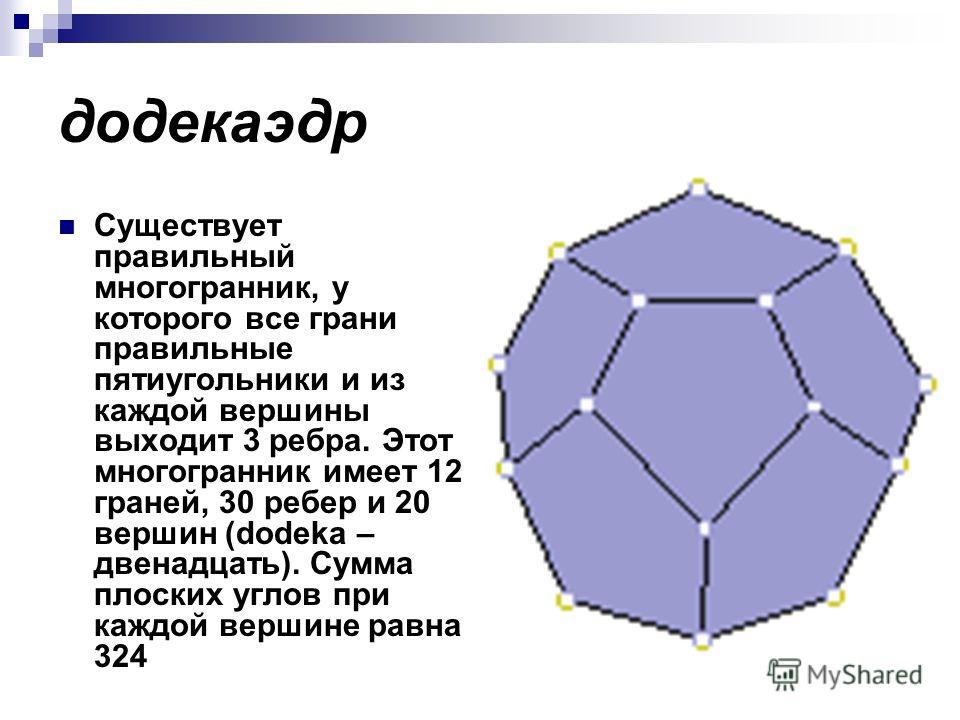
Сколько фаз имеет треугольная призма?
Треугольные призмы представляют собой объемные геометрические фигуры, имеющие два параллельных треугольных основания. Треугольные призмы имеют 5 граней, 9 ребер и 6 вершин. Эти призмы имеют две треугольные грани и три прямоугольные грани.
Сколько вершин у куба?
Из рисунка видно, что куб имеет 8 вершин.
Что такое круглое тело?
Круглые тела — это геометрические тела с закругленными гранями. Круглые тела – это геометрические тела, имеющие закругленные поверхности. Также известные как тела вращения, основными круглыми телами являются сфера, цилиндр и конус.
Чем куб отличается от параллелепипеда?
Самыми примитивными телами пространственной геометрии, а также имеющими множество применений и полезностей в нашей повседневной жизни, являются куб и параллелепипед. Куб — это тело с 6 гранями, все в форме квадрата, в то время как параллелепипед также имеет 6 граней, но они могут быть прямоугольными.
Какие грани у пирамиды?
Пирамида представляет собой геометрическое тело, имеющее многоугольное основание и треугольные боковые грани, которые встречаются в точке, известной как вершина. Боковые грани пирамиды всегда треугольные. Поскольку все грани пирамиды являются многоугольниками, ее можно классифицировать как многогранник.
Боковые грани пирамиды всегда треугольные. Поскольку все грани пирамиды являются многоугольниками, ее можно классифицировать как многогранник.
Сколько вершин у цилиндра?
Цилиндр: круглое тело с двумя основаниями, образованными кругами. Поскольку это круглое тело, у него нет ни вершин, ни ребер.
Какова форма цилиндра?
Цилиндр образован двумя круглыми основаниями и боковым участком. Поскольку он имеет круглое основание, он классифицируется как круглое тело.
Сколько в нем пространственных геометрических фигур?
Пространственные геометрические фигуры# Пространственная геометрия изучает различные геометрические тела, среди основных у нас есть: цилиндр, куб, конус, сфера, параллелепипед и пирамида.
Что такое геометрические и пространственные фигуры?
ПРОСТРАНСТВЕННЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ ИЛИ ГЕОМЕТРИЧЕСКИЕ ТЕЛА ЯВЛЯЮТСЯ ТЕ, КОТОРЫЕ ПРОИСХОДЯТ В ПРОСТРАНСТВЕ, В СВЯЗИ С ИХ ТРЕХМЕРНОСТЬЮ, Т.Е. ИМЕЮТ ТРИ ИЗМЕРЕНИЯ (ВЫСОТУ, ШИРИНУ И ДЛИНУ).
Какие плоские фигуры образуют пространственную фигуру?
Какие плоские фигуры образуют пространственную фигуру? Поэтому любая фигура, для построения и определения которой необходимы три измерения, называется пространственной геометрической фигурой.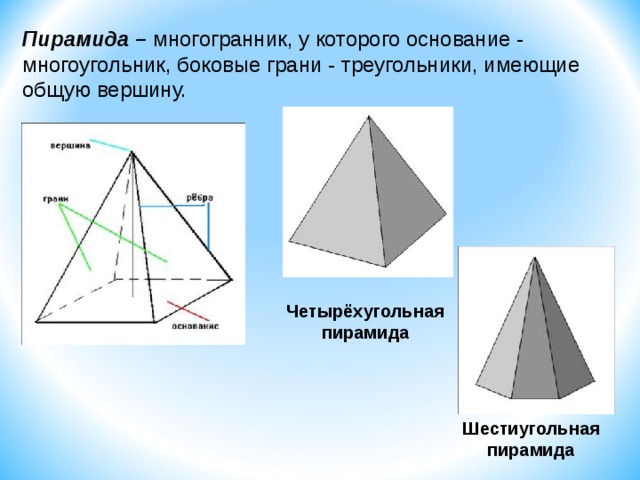 Примеры пространственных фигур: куб, призма, параллелепипед, пирамида, конус, цилиндр, сфера и др.
Примеры пространственных фигур: куб, призма, параллелепипед, пирамида, конус, цилиндр, сфера и др.
Гармония правильных многогранников / Этюды // Математические этюды
Гармония правильных многогранников / Этюды // Математические этюдыМатематические этюды
К списку
Правильные многогранники интересовали многих великих учёных. И этот интерес выходил далеко за пределы математики. Платон (427 до н.э. — 347 до н.э.) рассматривал их как основу строения Вселенной, Кеплер (1571—1630) пытался связать правильные многогранники с движением планет Солнечной системы (которых в его время было известно пять). Возможно, именно красота и гармония правильных многогранников заставляла великих учёных прошлого предполагать какое-то более глубокое их назначение, чем просто геометрических объектов.
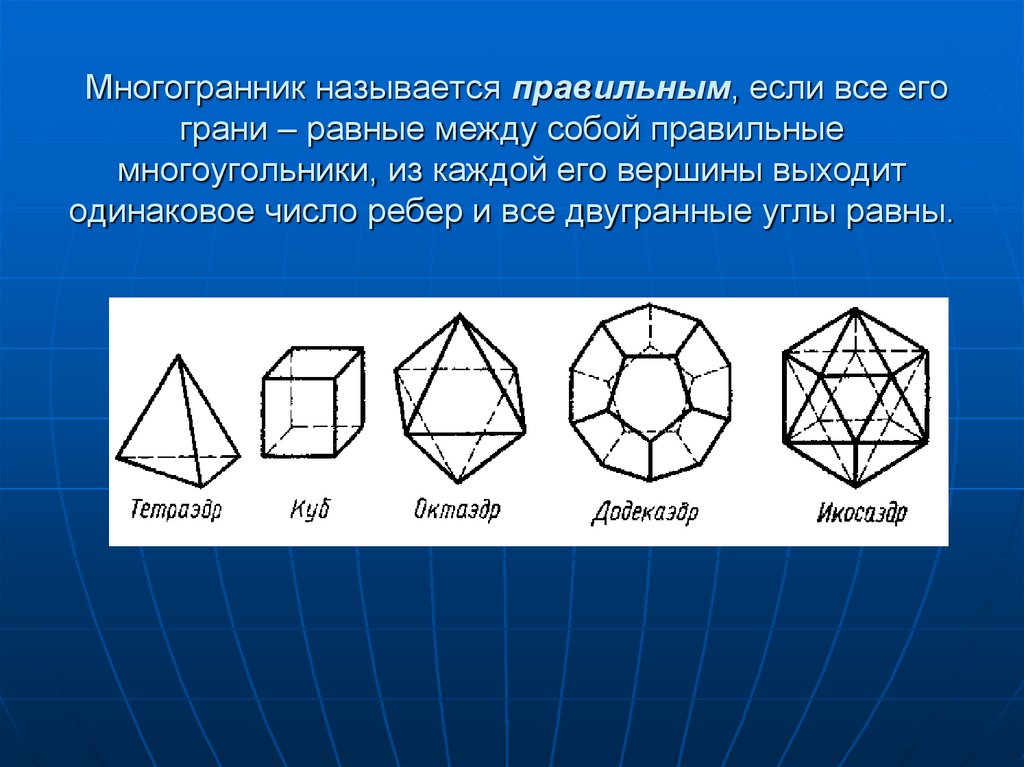
Правильным многогранником называется многогранник, все грани которого суть правильные многоугольники, все плоские углы которого равны между собой и двугранные углы которого равны между собой.
Возьмём в серединах граней тетраэдра по точке и соединим их между собой отрезками. Эти отрезки равны по длине и образуют равносторонние треугольники. Точки являются вершинами, отрезки — рёбрами, а треугольники — гранями ещё одного тетраэдра.
Аналогичное построение применимо и в более общем случае. Рассмотрим произвольный выпуклый многогранник и возьмём точки в серединах его граней. Соединим между собой точки соседних граней отрезками. Тогда точки являются вершинами, отрезки — рёбрами, а многоугольники, которые ограничивают эти отрезки, гранями ещё одного выпуклого многогранника. Этот многогранник называется двойственными к исходному.
Как было показано выше, двойственным к тетраэдру является тетраэдр.
Увеличим размер тетраэдра, вершинами которого являются середины граней исходного тетраэдра, до размеров последнего. Восемь вершин так расположенных тетраэдров являются вершинами куба. \circ$.
\circ$.
Отметим середины граней октаэдра и перейдём к двойственному к октаэдру многограннику. Это — куб или гексаэдр (от греч. εξά — шесть). У куба грани являются квадратами. Он имеет 6 граней, 8 вершин, 12 рёбер. Плоские углы куба равны $\pi/2$, двугранные углы также равны $\pi/2$.
Если взять точки на серединах граней куба и рассмотреть двойственный к нему многогранник, то можно убедиться, что им снова будет октаэдр. Верно и более общее утверждение: если для выпуклого многогранника построить двойственный, а затем двойственный к двойственному, то им будет исходный многогранник (с точностью до подобия).
Возьмём на рёбрах октаэдра по точке, с тем условием, чтобы каждая делила ребро в соотношении $1:(\sqrt5+1)/2$ (золотое сечение) и при этом точки,
принадлежащие одной грани, являлись вершинами правильного треугольника. Полученные 12 точек являются вершинами ещё одного правильного многогранника — икосаэдра (от греч.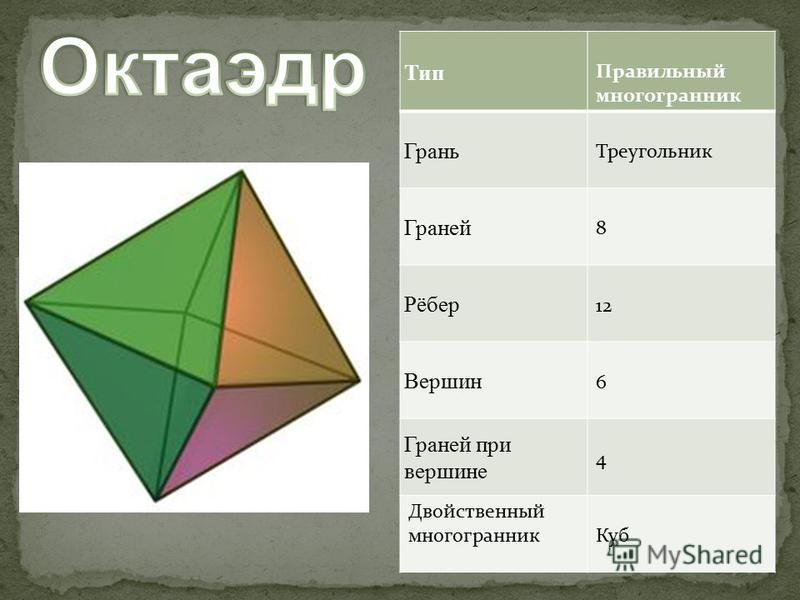
Взяв середины граней додекаэдра, и перейдя к двойственному ему многограннику, получим снова икосаэдр. Итак, икосаэдр и додекаэдр двойственны друг другу. Это ещё раз иллюстрирует тот факт, что двойственным к двойственному будет исходный многогранник.
Заметим, что при переходе к двойственному многограннику, вершины исходного многогранника соответствуют граням двойственного, рёбра — рёбрам двойственного, а грани — вершинам двойственного многогранника. Если у икосаэдра 20 граней, значит у двойственного ему додекаэдра 20 вершин и у них одинаковое число рёбер, если у куба 8 вершин, то у двойственного ему октаэдра 8 граней.
Существуют различные способы вписывания правильных многогранников друг в друга, приводящие ко многим замечательным конструкциям. Интересные и красивые многогранники получаются также при объединении и пересечении правильных многогранников.
В додекаэдр впишем куб так, чтобы все 8 вершин куба совпадали с вершинами додекаэдра.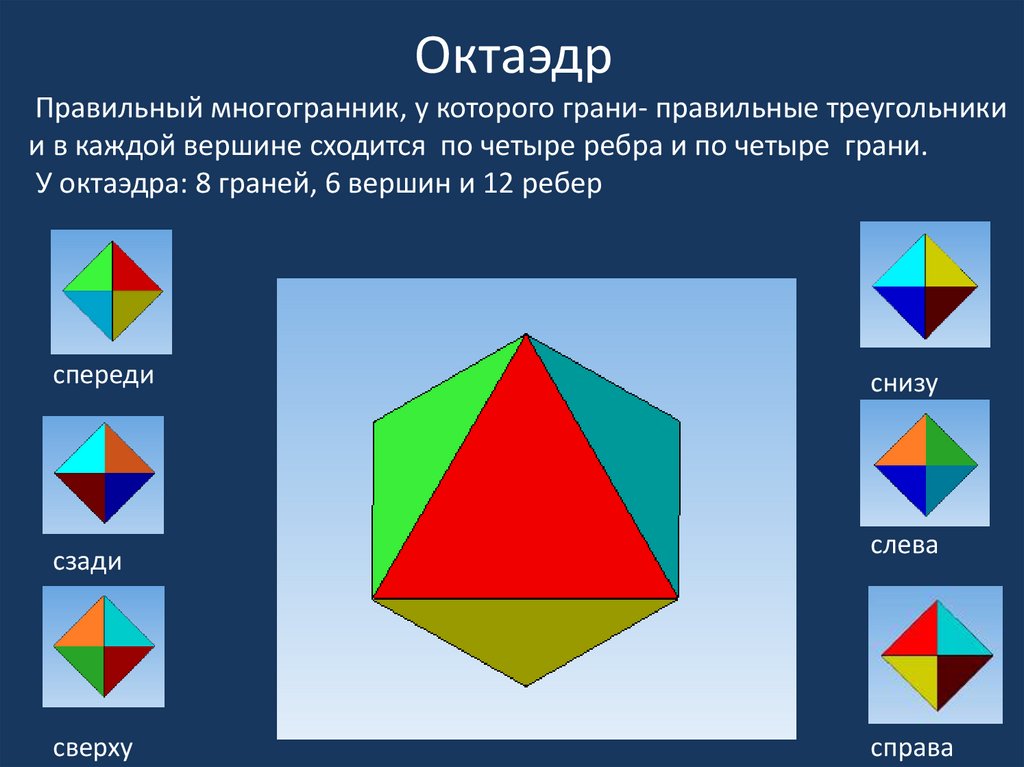 Вокруг додекаэдра опишем икосаэдр
так, чтобы его вершины оказались в серединах граней икосаэдра. Вокруг икосаэдра опишем октаэдр, так, чтобы вершины икосаэдра лежали на рёбрах октаэдра.
Наконец, вокруг октаэдра опишем тетраэдр так, чтобы вершины октаэдра попали на середины рёбер тетраэдра.
Вокруг додекаэдра опишем икосаэдр
так, чтобы его вершины оказались в серединах граней икосаэдра. Вокруг икосаэдра опишем октаэдр, так, чтобы вершины икосаэдра лежали на рёбрах октаэдра.
Наконец, вокруг октаэдра опишем тетраэдр так, чтобы вершины октаэдра попали на середины рёбер тетраэдра.
Такую конструкцию из кусочков сломанных деревянных лыжных палок сделал ещё ребёнком будущий великий математик XX века В. И. Арнольд. Владимир Игоревич хранил её долгие годы, а затем отдал в лабораторию популяризации и пропаганды математики Математического института им. В. А. Стеклова.
Литература
Кокстер Г. С. М. Введение в геометрию. — М. : Наука, 1966.
Адамар Ж. Элементарная геометрия. — Часть 2. Стереометрия. — М. : Просвещение, 1951.
Евклид. Начала Евклида. Книги XXI—XXV. — М.—Л.: ГИТТЛ, 1950.
Другие этюды раздела «Внешняя геометрия многогранников»
Тени Увеличение объёма выпуклых многогранников Удивительные объёмы многогранников Кусочно гладкое вложение многогранника Изгибаемые многогранникиМатематические этюды
Треугольная призма имеет 5 граней, 9 ребер и 6 вершин.
 Государство ИСТИНА ИЛИ ЛОЖЬ
Государство ИСТИНА ИЛИ ЛОЖЬВопрос
Вопрос
NCERT Пример-практическая геометрия Симметрия и визуализация сплошных форм
20 видеоРеклама
KHAREEDO DN Pro and Deh ки рукаават ке!
Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.
সংশ্লিষ্ট ভিডিও
Напишите количество вершин, ребер и граней пятиугольной призмы ?
40375124
Заполните пропуски:
(i) Объект, занимающий место, называется …………..
(ii) Прямоугольный параллелепипед имеет …….. Грани….. Ребра и ….. Вершины.
(iii) ………… грани прямоугольного параллелепипеда идентичны.
(iv) A ………….. не имеет ни вершины, ни ребра.
(v) Все грани …….. одинаковы.
(vi) Квадратная пирамида имеет …….. боковые треугольные грани и …….. ребра.
 треугольные боковые грани и …….. ребра.
треугольные боковые грани и …….. ребра. (viii) Треугольная призма имеет ………..вершины …………прямоугольные боковые грани …………треугольные основания и … ………. края.
283257300
Напишите (T) для True и (F) для False:
(ii) Куб имеет 6 граней, 12 ребер и 8 вершин.
283262074
Если у многогранника 5 граней и 9 ребер, то сколько у него будет вершин?
585435287
Если у многогранника 9 граней и 15 вершин, то сколько у него ребер?
589192999
Укажите, верно (T) или нет (F) :
Прямоугольный параллелепипед имеет больше ребер, чем вершин.
644033726
Состояние Верно или Ложно:
a. Треугольная призма имеет три боковые грани и одно треугольное основание.
б. Кубоид также называют прямоугольной призмой.
644040722
Треугольная призма часто имеет форму калейдоскопа. У него треугольные грани. Количество треугольных граней: ____________ Количество прямоугольных граней: ____________ Количество кромок: ____________ Количество вершин: ____________
644243111
Укажите, являются ли следующие утверждения верными/неверными: Треугольная призма имеет две прямоугольные грани.
644243138
एक त्रिभुजाक| इसका आधार और ऊपरी सिरा त्रिभुज के आकार के होते है
फलक : ………..……..
किनारे: …….……….
कोने : ………..…………
644939649
Все грани квадратной пирамиды, кроме основания, треугольные. скажи правда или ложь
6455
Прямоугольная пирамида имеет 5 прямоугольных граней. укажите истинное или ложное
6455
Сколько ребер в треугольной призме?
646308878
Сколько граней, ребер, вершин в треугольной призме? Нарисовать фигуру?
646308946
Какие из следующих цифр удовлетворяют заданным условиям?
Рисунок (i) Грани: 4, Ребра: 6, Вершины: 4
Рисунок (ii) Грани: 5, Ребра: 9, Вершины: 6
646308976
9.1: Многогранники — K12 LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2166
трехмерных фигуры, образованные многоугольниками, охватывающими области в пространстве.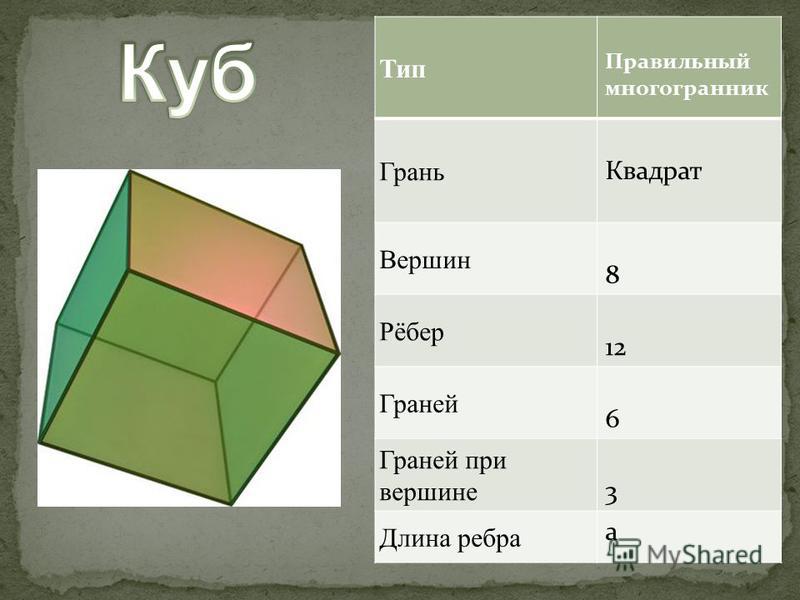
Многогранник — это трехмерная фигура, образованная многоугольниками, ограничивающими область в пространстве. Каждый многоугольник в многограннике является гранью . Отрезок, на котором пересекаются две грани, является ребром . Точка пересечения двух ребер является вершиной .
Рисунок \(\PageIndex{1}\)Примеры многогранников включают куб, призму или пирамиду. Конусы, сферы и цилиндры не являются многогранниками, потому что их поверхности не являются многоугольниками. Ниже приведены еще примеры многогранников:
Рисунок \(\PageIndex{2}\)Рисунок \(\PageIndex{3}\)Количество граней (\(F\)), вершин (\(V\)) и ребер (\(E\)) связаны одинаково для любого многогранника. Их взаимосвязь была открыта швейцарским математиком Леонардом Эйлером и называется теоремой Эйлера.
Теорема Эйлера: \(F+V=E+2\).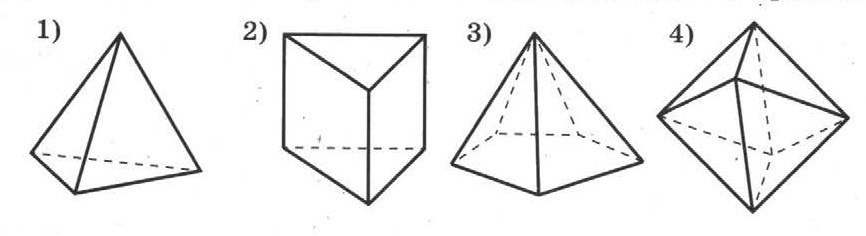
\(Границы+Вершины=Ребра+2\)
\(5+6=9+2\)
Правильный многогранник — это многогранник, все грани которого являются конгруэнтными правильными многоугольниками. Есть только пять правильных многогранников, называемых платоновыми телами.
- Правильный Тетраэдр : Четырехгранный многогранник, все грани которого являются равносторонними треугольниками.
- Куб: Шестигранный многогранник, все грани которого квадраты.
- Правильный октаэдр: Восьмигранный многогранник, все грани которого представляют собой равносторонние треугольники.
- Правильный додекаэдр: Многогранник с 12 гранями, все грани которого являются правильными пятиугольниками.
- Правильный икосаэдр: 20-гранный многогранник, все грани которого представляют собой равносторонние треугольники.

Что, если бы вам дали цельную трехмерную фигуру, например коробку мороженого? Как определить, как связаны грани, вершины и ребра этой фигуры?
Пример \(\PageIndex{1}\)
- Рисунок \(\PageIndex{6}\)
- Рисунок \(\PageIndex{7}\)
- Рисунок \(\PageIndex{8}\)
Решение
Основание представляет собой треугольник со всеми сторонами, поэтому это треугольная пирамида, также известная как тетраэдр . Имеются 4 грани, 6 ребер и 4 вершины.
Пример \(\PageIndex{2}\)
В шестигранном многограннике 10 ребер. Сколько вершин у многогранника?
Решение
Найдите \(V\) в теореме Эйлера.
\(\begin{aligned} F+V&=E+2 \\ 6+V&=10+2 \\ V&=6\end{aligned} \)
Таким образом, имеется 6 вершин.
Пример \(\PageIndex{3}\)
Маркус считает ребра, грани и вершины многогранника. У него 10 вершин, 5 граней и 12 ребер. Он сделал ошибку?
Решение
Подставьте все три числа в теорему Эйлера.
\(\begin{выровнено} F+V&=E+2 \\ 5+10&=12+2 \\ 15 &\neq 14 \end{выровнено}\)
Поскольку две стороны не равны, Маркус допустил ошибку.
Пример \(\PageIndex{4}\)
Найдите количество граней, вершин и ребер в восьмиугольной призме.
Рисунок \(\PageIndex{9}\)Решение
Имеется 10 граней и 16 вершин. Используйте теорему Эйлера, чтобы найти \(E\).
\(\begin{aligned} F+V&=E+2 \\ 10+16&=E+2 \\ 24&=E \end{aligned}\)
Таким образом, имеется 24 ребра.
Пример \(\PageIndex{5}\)
Усеченный икосаэдр представляет собой многогранник с 12 правильными пятиугольными гранями, 20 правильными шестиугольными гранями и 90 ребрами. Этот икосаэдр очень напоминает футбольный мяч.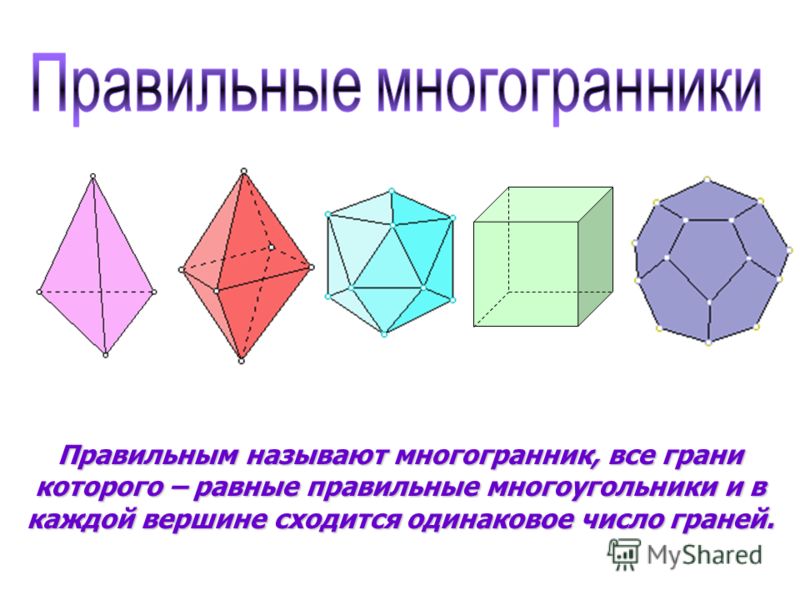 Сколько у него вершин? Объясните свои рассуждения.
Сколько у него вершин? Объясните свои рассуждения.
Решение
Мы можем использовать теорему Эйлера для определения количества вершин.
\(\begin{align} F+V&=E+2 \\ 32+V&=90+2 \\ V&=60\end{aligned}\)
Следовательно, у него 60 вершин.
Обзор
Заполните таблицу, используя теорему Эйлера.
| Имя | Лица | Края | Вершины | |
|---|---|---|---|---|
| 1. | Прямоугольная призма | 6 | 12 | |
| 2. | Восьмиугольная пирамида | 16 | 9 | |
3. | Правильный икосаэдр | 20 | 12 | |
| 4. | Куб | 12 | 8 | |
| 5. | Треугольная пирамида | 4 | 4 | |
| 6. | Октаэдр | 8 | 12 | |
| 7. | Семиугольная призма | 21 | 14 | |
8. | Треугольная призма | 5 | 9 |
Определите, являются ли следующие фигуры многогранниками. Если да, то назовите фигуру и найдите количество граней, ребер и вершин.
- Рисунок \(\PageIndex{11}\)
- Рисунок \(\PageIndex{12}\)
- Рисунок \(\PageIndex{13}\)
- Рисунок \(\PageIndex{14}\)
- Рисунок \(\PageIndex{15}\)
Обзор (ответы)
Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 11.1.
Дополнительные материалы
Видео: Принципы работы с многогранниками — основы
Упражнения: Многогранники Вопросы для обсуждения
Учебные пособия: Учебное пособие по многогранникам
Практика: Многогранники
Реальный мир: Роли-поли-многогранник!
Эта страница под названием 9.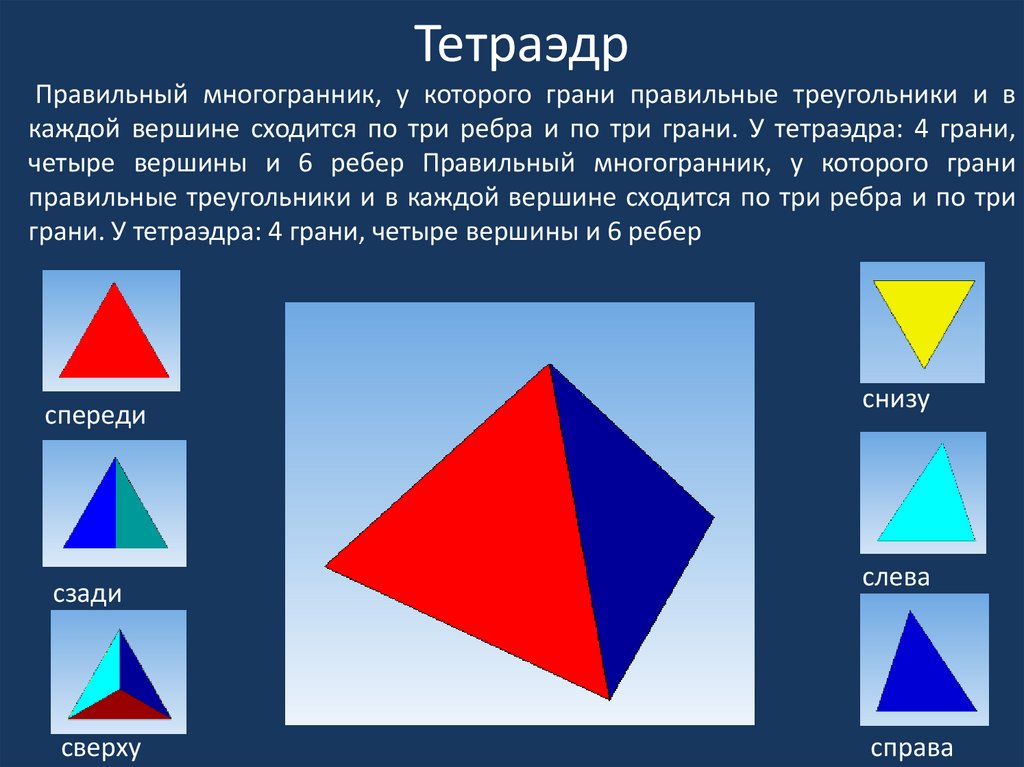

Leave A Comment