Тренажер по решению линейных уравнений. | Тест по алгебре (7 класс) по теме:

Опубликовано 02.10.2016 — 1:24 — Егорова Раушания Леонидовна

Тренажер «Решение линейных уравнений»

Скачать:


Предварительный просмотр:

Тренажер по теме «Решение линейных уравнений»

Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель

Образец:

2х=10

х=10:2

х=5

Решите уравнение по образцу:

  1. 5х=10
  2. 10х=90
  3. 13у=78
  4. 25m=375
  5. 2х=-12
  6. -3к=15
  7. -12у=-36
  8. 31в=-93
  9. -4х=1,2
  10. 6у=-0,36
  11. -12к=-1,44
  12. -0,2х=-1,2
  13. 1.7у=-0,34
  14. -7,4m=-1,48
  15. 3х=1
  16. 7r =-4
  17. 13у=-10
  18. -10v=-7
  19. х=4
  20. у=6
  21. к=-.
  22. х=-1
  23. а=-1

Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак на противоположный.

Образец:

х+5=10

х=10-5

х=5

Образец:

х-4=10

х=10+4

х=6

Решите уравнения:

  1. Х+6=10.
  2. У+14=19,
  3. а+41=60,
  4. 2х+3=13,
  5. 3у+14=77,
  6. 5х+13=73,
  7. Х-4,5=10,
  8. 5-у=4,
  9. 10-х=6,
  10. х -7,8=1,2,
  11. 2х-3=16,
  12. 100-5х=17,
  13. 0,2х+3=-1,5,
  14. -1,2у-4,7=-3,5,
  15. 4х+х=-15,
  16. 3у-5у=7,
  17. -4х-3у=-49,
  18. Х+4=3х,
  19. -3у+7=2у.
  20. 5а-1,5=2а.
  21. -0,2х+7=-1,6х,
  22. t+5=t-7,
  23. 2у=7у,
  24. -3к+8=-3к+9,
  25. 6,9-9n=-5n-33,1,

Образец:

3х+6=4х-1

3х-4х=-1-6

-х=-7

х=7

Решить уравнения:

  1. 2х+8=6х-2,
  2. 10у+3=2у-1,
  3. -4+3к=8к+5.
  4. 9+4а=8а-9,
  5. 3в+9=8в+2,
  6. 6-2с=3с-10,
  7. 5-2у=8у+9,
  8. -4х+3=4х-5,
  9. 4а+4=-6а-5.
  10. 3у+3=-2-7у.
  11. -10х+3=-1-8х,
  12. 9-4х=-4-9х,
  13. -8а+9=3-4а,
  14. с+3=с+5,
  15. t-t+2=t-3,
  16. x+x+5=x,
  17. 0,2f+2,3=0,7f-3,2,
  18. -0,4x-14=0,3x,
  19. -40·(-7x+5)=-1600,
  20. (-20t-50)·2=100,
  21. 2,1·(4-6e)=-42,
  22. -3·(2-15k)=-6,
  23. -20·(x-13)=-220,
  24. (30-7r)·8=352,
  25. (2,8-0,1h)·3,7=7,4,
  26. (3x-1,2)·7=10,5,
  27. x-=.

Образец:

2·(х-7)=3, 2х-14=3, 2х=3+14, 2х=17, х=17:2, х=8,5.

Решить уравнение.

  1. 5·(у-9)=-2.
  2. 3=4·(к+2),
  3. 5·(с+5)=-7,
  4. 7·(а-1)=3а.
  5. 7·(-3+2х)=-6х-1,
  6. 2·(7+9к)=-6к+2,
  7. 6·(5-3с)=-8с-7,
  8. 4·(2-3х)=-7х+10,
  9. -4·(-к+7)=к+17,
  10. -5·(0,8t-1,2)=-t+7,2,
  11. -5·(3а+1)-11=-16,
  12. -3,2n+4,8=-2·(1,2n+2,4),
  13. -5·(0,8f-1,4)=-f+7,
  14. 5·(r-7)=3·(r-4)-27,
  15. 8-7·(c-2)=2·(2c-3)+3c,
  16. 4·(x-3)-16=5·(x-5),
  17. 5·(y-3)+27=4y+3·(2y-5),
  18. -4·(3-5z)=18z-7,
  19. 1,2-2·(1,3y+1)=5,6y-27,04,
  20. 8·(2f-6)=2·(4f+3),
  21. -3·(2,1m-1)+4,8=-6,7m+9,4,
  22. 6·(2c-3)+2·(4-3c)=5,
  23. h+- =2-h+2h,
  24. 1-1x+3x=1x-2x+2,5,
  25. 2·(z+1)+3=4-·(z-1).

Образец:

=,  

9х=5·4

9х=20

х=,

х=2,

Решить уравнения.

  1. =,
  2.  = ,
  3. =,
  4.  = ,
  5.  = ,
  6.  = ,
  7.  = ,
  8.  =4,
  9.  =7,
  10.  = ,
  11.  =  ,
  12.  = ,
  13.  =  ,
  14.  =  ,

Образец:

Решите уравнения:

Предварительный просмотр:

Тренажер по теме «Решение линейных уравнений»

Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель

Образец:

2х=10

х=10:2

х=5

Решите уравнение по образцу:

  1. 5х=10
  2. 10х=90
  3. 13у=78
  4. 25m=375
  5. 2х=-12
  6. -3к=15
  7. -12у=-36
  8. 31в=-93
  9. -4х=1,2
  10. 6у=-0,36
  11. -12к=-1,44
  12. -0,2х=-1,2
  13. 1. 7у=-0,34
  14. -7,4m=-1,48
  15. 3х=1
  16. 7r =-4
  17. 13у=-10
  18. -10v=-7
  19. х=4
  20. у=6
  21. к=-.
  22. х=-1
  23. а=-1

Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак на противоположный.

Образец:

х+5=10

х=10-5

х=5

Образец:

х-4=10

х=10+4

х=6

Решите уравнения:

  1. Х+6=10.
  2. У+14=19,
  3. а+41=60,
  4. 2х+3=13,
  5. 3у+14=77,
  6. 5х+13=73,
  7. Х-4,5=10,
  8. 5-у=4,
  9. 10-х=6,
  10. х -7,8=1,2,
  11. 2х-3=16,
  12. 100-5х=17,
  13. 0,2х+3=-1,5,
  14. -1,2у-4,7=-3,5,
  15. 4х+х=-15,
  16. 3у-5у=7,
  17. -4х-3у=-49,
  18. Х+4=3х,
  19. -3у+7=2у.
  20. 5а-1,5=2а.
  21. -0,2х+7=-1,6х,
  22. t+5=t-7,
  23. 2у=7у,
  24. -3к+8=-3к+9,
  25. 6,9-9n=-5n-33,1,

Образец:

3х+6=4х-1

3х-4х=-1-6

-х=-7

х=7

Решить уравнения:

  1. 2х+8=6х-2,
  2. 10у+3=2у-1,
  3. -4+3к=8к+5.
  4. 9+4а=8а-9,
  5. 3в+9=8в+2,
  6. 6-2с=3с-10,
  7. 5-2у=8у+9,
  8. -4х+3=4х-5,
  9. 4а+4=-6а-5.
  10. 3у+3=-2-7у.
  11. -10х+3=-1-8х,
  12. 9-4х=-4-9х,
  13. -8а+9=3-4а,
  14. с+3=с+5,
  15. t-t+2=t-3,
  16. x+x+5=x,
  17. 0,2f+2,3=0,7f-3,2,
  18. -0,4x-14=0,3x,
  19. -40·(-7x+5)=-1600,
  20. (-20t-50)·2=100,
  21. 2,1·(4-6e)=-42,
  22. -3·(2-15k)=-6,
  23. -20·(x-13)=-220,
  24. (30-7r)·8=352,
  25. (2,8-0,1h)·3,7=7,4,
  26. (3x-1,2)·7=10,5,
  27. x-=.

Образец:

2·(х-7)=3, 2х-14=3, 2х=3+14, 2х=17, х=17:2, х=8,5.

Решить уравнение.

  1. 5·(у-9)=-2.
  2. 3=4·(к+2),
  3. 5·(с+5)=-7,
  4. 7·(а-1)=3а.
  5. 7·(-3+2х)=-6х-1,
  6. 2·(7+9к)=-6к+2,
  7. 6·(5-3с)=-8с-7,
  8. 4·(2-3х)=-7х+10,
  9. -4·(-к+7)=к+17,
  10. -5·(0,8t-1,2)=-t+7,2,
  11. -5·(3а+1)-11=-16,
  12. -3,2n+4,8=-2·(1,2n+2,4),
  13. -5·(0,8f-1,4)=-f+7,
  14. 5·(r-7)=3·(r-4)-27,
  15. 8-7·(c-2)=2·(2c-3)+3c,
  16. 4·(x-3)-16=5·(x-5),
  17. 5·(y-3)+27=4y+3·(2y-5),
  18. -4·(3-5z)=18z-7,
  19. 1,2-2·(1,3y+1)=5,6y-27,04,
  20. 8·(2f-6)=2·(4f+3),
  21. -3·(2,1m-1)+4,8=-6,7m+9,4,
  22. 6·(2c-3)+2·(4-3c)=5,
  23. h+- =2-h+2h,
  24. 1-1x+3x=1x-2x+2,5,
  25. 2·(z+1)+3=4-·(z-1).

Образец:

=,  

9х=5·4

9х=20

х=,

х=2,

Решить уравнения.

  1. =,
  2.  = ,
  3. =,
  4.  = ,
  5.  = ,
  6.  = ,
  7.  = ,
  8.  =4,
  9.  =7,
  10.  = ,
  11.  =  ,
  12.  = ,
  13.  =  ,
  14.  =  ,

Образец:

Решите уравнения:


По теме: методические разработки, презентации и конспекты

Открытый урок по математике в 6 классе «Решение линейных уравнений»

здесь представлен план — конспект урока по математике в 6 классе «Решение линейных уравнений» с применением ЭОР….

Проект по теме «Решение линейных уравнений с параметрами»

Проект по теме «Решение линейных уравнений с параметрами». ..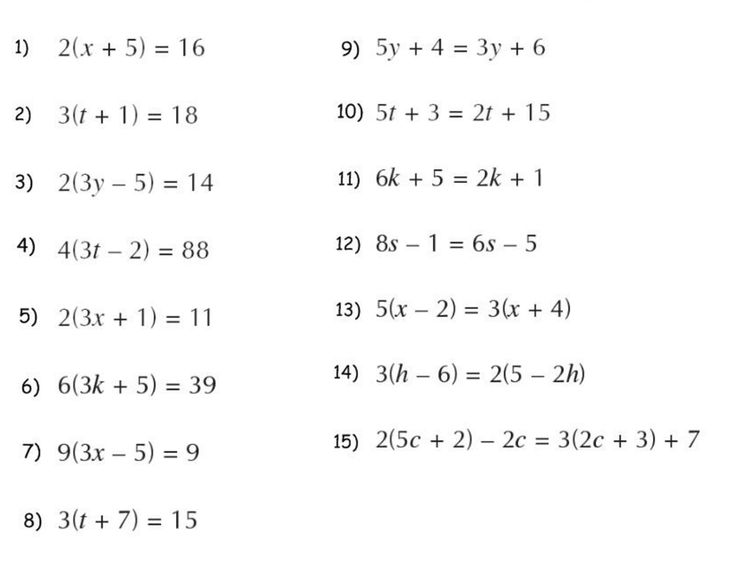

Разработка методических рекомендаций решения линейных уравнений с параметрами.

Разработка методических рекомендаций решения линейных уравнений с параметрами….

Функционально-графический подход к решению линейных уравнений с параметром и модулем

План-конспект урока с использованием ЦОР для обобщающих уроков по теме «Линейные уравнения с параметром и модулем» для учащихся 7-9 классов и для подготовки к ГИА (презентация к уроку)…

Презентация:»Решение линейных уравнений»

Презентация по алгебре «Решение линейных уравнений».Данная презентация может быть использована на уроке алгебры в 7 классе при изучении темы: «Линейное уравнение с одной переменной». Данная тема изуча…

Задание по теме «Решение линейных уравнений», составление фигуры «Танграм»

Задания по теме решение линейных уравнений для 6, 7 классов. Задания комбинированные. Вначале решить все уравнения, а затем составить фигуру танграм….

Тематический тренажер для подготовки к ГИА в 2014 г.
по математике 9 класс. Тематические тренировочные задания. Отработка заданий: модуль «Алгебра» Тема№2 «Решение линейных уравнений»

Представляю вашему вниманию очередной тематический тренажер для подготовки к ГИА в 2014г по алгебре по теме «Решение линейных уравнений». Подобраны упражнения, которые соответствуют типовым заданиям К…


Поделиться:

 

Системы линейных уравнений с двумя переменными – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД

Система уравнений – это два или несколько уравнений, для которых необходимо найти все их общие решения. Систему уравнений принято записывать с помощью фигурной скобки.

Например: \(\begin{cases} 2x+3y=1\\ x-5y=0 \\ \end{cases}\)

Пара значений переменных, обращающая в истинное равенство каждое уравнение системы, называется решением системы уравнений с двумя переменными. Решить систему уравнений – значит найти множество ее решений.

Графическое решение

Графическим решением линейного уравнения являются все точки некоторой прямой на плоскости. Для системы линейных уравнений будем иметь несколько прямых (по количеству уравнений). А решением системы уравнений, будет являться точка, в которой пересекаются все прямые. Если такой точки нет, то система не будет иметь решений. Точка, в которой пересекаются все прямые, принадлежит каждой из этих прямой, поэтому решение называют общим.

Способ подстановки

Алгоритм решения системы линейных уравнений способом подстановки:

1. Выбрать одно уравнение (лучше выбирать то, где числа меньше) и выразить из него одну переменную через другую, например, x через y.

2. Полученное выражение подставить вместо соответствующей переменной в другое уравнение. Таким образом, у нас получится линейное уравнение с одной неизвестной.

3. Решаем полученное линейное уравнение и получаем решение.

4. Подставляем полученное решение в выражение, полученное в первом пункте, получаем вторую неизвестную из решения.

5. Выполнить проверку полученного решения.

Например: \(\left\{ \begin{array}{l} 2x — 3y = 1 \\ x + 2y = 4 \\ \end{array} \right. \Rightarrow \left\{ \begin{array}{l} 2(4 — 2y) — 3y = 1 \\ x = 4 — 2y \\ \end{array} \right. \)\(\Rightarrow \left\{ \begin{array}{l} 8 — 4y — 3y = 1 \\ x = 4 — 2y \\ \end{array} \right. \Rightarrow \left\{ \begin{array}{l} y = 1 \\ x = 2 \\ \end{array} \right.\)

Ответ: (2; 1).

Способ сложения

Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.

1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.

2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным.

3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.

4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.

5. Сделать проверку решения.

Например:

\(\left\{ \begin{array}{l} 3x+2y=10 \\ 5x+3y=12 \\ \end{array} \right.\)

Так как одинаковых коэффициентов нет ни у одной из переменных, уравняем коэффициенты у переменной \(y\). Для этого умножим первое уравнение на три, а второе уравнение на два.

\(\left\{ \begin{array}{l} 3x+2y=10/ \cdot3 \\ 5x+3y=12 / \cdot2\\ \end{array} \right.\)

Получим следующую систему уравнений: из второго уравнения вычитаем первое. Приводим подобные слагаемые и решаем полученное линейное уравнение.

\(\left\{ \begin{array}{l} 39x+6y=30 \\ 10x+6y=24\\ \end{array} \right. \Rightarrow x+0=-6 \Rightarrow x=-6\)

Полученное значение подставляем в первое уравнение из нашей исходной системы и решаем получившееся уравнение.

\(\left\{ \begin{array}{l} 3\cdot(-6)+2y=10 \\ 2y=28 \ \Rightarrow y=14 \end{array} \right.\)

Ответ: (6; 14).

Linear Equations Пошаговое решение математических задач

6.2  Решение линейных уравнений

   Уравнения вида ax+b=0 называются линейными уравнениями относительно переменной x. В этом разделе мы будем заниматься проблемой решения линейных уравнений и уравнений, сводящихся к линейным уравнениям.

  Мы определяем два уравнения как эквивалентные, если они имеют одно и то же множество решений. Следующие две операции над уравнением всегда приводят к новому уравнению, эквивалентному исходному. Этими операциями, иногда называемыми элементарными преобразованиями, являются:

   T.1  Одно и то же выражение, представляющее действительное число, может быть добавлено к обеим частям уравнения.

   T.2 Одно и то же выражение, представляющее ненулевое действительное число, может быть умножено на обе части уравнения.

  Используя эти операции, мы можем преобразовать уравнение, множество решений которого неочевидно, через ряд эквивалентных уравнений в уравнение, имеющее очевидное множество решений.

Пример 1.   Решить уравнение

  (a) 2x-3=4+x

  Добавьте -x к обеим сторонам, чтобы получить

       -x+2x-3=-x+4+x  (T. 1)=-3 4 или   

  Добавьте 3 к обеим сторонам, чтобы получить что, в свою очередь, эквивалентно x=7, набор решений которого, очевидно, равен {7}, мы знаем, что набор решений (a) равен {7}.

Давайте посмотрим, как наш решатель линейных уравнений решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.

Решить похожую задачуВведите свою задачу

Пример 2.   Решить уравнение

  (b) 1/2x+2/3=5/2x-1 Получите

2/3 = 5/2x-1/2x-1 (T.1)

или 2/3 = 2x-1

Добавить 1 к обеим сторонам, чтобы получить

1+2/3 = 2x ( T.1)

  или  5/3=2x

  Умножьте обе части на 1/2, чтобы получить 6}.

  Каждое линейное уравнение можно решить так же, как и в приведенных выше примерах. В самом деле, давайте рассмотрим общее линейное уравнение

  ax+b=0

  Добавим -b к обеим частям, чтобы получить

  ax=-b

  Умножим обе части на 1/a, чтобы получить =

9000 б/а)

  если а а!=0. Таким образом, общее линейное уравнение имеет в качестве решения множество {b/a}, если a!=0. Таким образом, каждое линейное уравнение имеет не более одного решения.

  Следующие два примера представляют собой уравнения, которые сводятся к линейным уравнениям. 92 в обе стороны, чтобы получить

  23+16y=9+30y

   Теперь решим, как в предыдущих примерах.

  23+16y=9+30y

  23-9=30y-16y

  14=14y

  y=1

  решение есть {набор}.

Давайте посмотрим, как наш пошаговый математический решатель решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.

Решите похожую задачуВведите свою задачу

Пример 4.  Решите уравнение

  (c) (2x)/(x-1)=2/(x-1)+1

  Замещающий набор (c) состоит из всех действительных чисел, кроме 1. Предполагая, что x!=1, мы умножаем оба стороны (c) на x-1, чтобы получить

  (d) 2x=2+x-1,x!=1

  Решая уравнение 2x =2+x- 1, мы получаем 1 как единственное решение Поскольку 1 не находится в замене (d), (d) не имеет решения. Кроме того, (c) эквивалентно (d), поэтому (c) не имеет решения.

6.3  Решение буквенных уравнений

  Уравнение, содержащее более одной переменной или содержащее символы, представляющие константы, такие как a, b и c, может быть решено для одного из символов в терминах остальных символов с помощью применения операции T.1 и T.2 в предыдущем разделе. Студент столкнется с такими проблемами в других курсах.

Пример 1.   Решите cx-3a=b для x.

  Добавьте 3a с обеих сторон.

  cx=b+3a

  Умножьте обе части на 1/c.

  x=(b+3a)/c

  Последнее уравнение выражает x через другие символы.

Пример 2.   Решите 3ay-2b=2cy для y.

  Добавьте 2b с обеих сторон.

  3ay=2cy+2b

  Добавьте -2cy к обеим сторонам.

  3ay-2cy=2b

  Вычтите y.

  (3a-2c)y=2b

  Умножьте обе части на 1/((3a-2c))

  y=(2b)/(3a-2c)

Пример 3.    Решите a/x+b/(2x)=c относительно x.

  Умножьте обе стороны на 2x.

  2a+b=2cx

  2cx=2a+b

  Умножить на 1/(2c).

  x=(2a+b)/(2c)

   В заключение этого раздела мы включим еще два примера, подобных тем, с которыми учащийся может столкнуться в других областях.

Давайте посмотрим, как наш математический решатель решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.

Решите похожую задачуВведите свою задачу

Пример 4.   Решите A=P(1+rt) для r.

  Применить распределительный закон.

  A=P+Prt

  Добавить -P к обеим сторонам.

  A-P=Prt

  Умножьте обе части на 1/(Pt).

  (A-P)/(Pt)=r

Пример 5.   Решить 1/R=1/r_1+1/r_2 для r_1.

  Добавьте два члена справа.

  1/(R)=(r_2+r_1)/(r_1r_2)

  Умножить на Rr_1r_2.

  r_1r_2=R(r_2+r_1)

  r_1r_2=Rr_2+Rr_1

  Добавить -Rr_1 к обеим сторонам.

  r_1r_2-Rr_1=Rr_2

  Вычтите r_1.

  r_1(r_2-R)=Rr_2

  Умножить на 1/(r_2-R).

  r_1=(Rr_2)/(r_2-R)

6.4  Решение задач с формулировками

  Одним из фундаментальных приложений алгебры является решение задач, сформулированных словами. Задача-постановка — это словесное описание ситуации, в которой участвуют как известные, так и неизвестные величины. В этом разделе каждая задача будет решена с помощью одного уравнения с одним неизвестным.

  Наша задача состоит в том, чтобы выбрать неизвестное и определить уравнение, которому оно должно удовлетворять. Хотя единого подхода ко всем проблемам не существует, иногда могут оказаться полезными следующие рекомендации:

   1. Внимательно прочитайте задачу, пока не поймете ситуацию полностью.

   2. Определите, какие количества запрашиваются, затем выберите то, которое лучше всего использовать в качестве неизвестного.

   3. Установить связь между неизвестной и другими величинами в задаче.

   4. Найдите информацию, которая говорит, какие две величины равны.

   5. Используйте информацию в (4), чтобы написать уравнение.

   6. Решите уравнение и проверьте решение, чтобы убедиться, что оно удовлетворяет исходной задаче.

  На этом этапе основное внимание будет уделяться переводу задач-постановок в уравнения. Хотя некоторые задачи могут быть решены почти путем проверки, практика, которую мы приобретаем при составлении уравнений, окажется полезной при решении более сложных задач.

Пример 1.   Если 2 раза прибавить определенное целое число к следующему последовательному целому числу, получится 34. Найдите целые числа.
Шаг 1. Перечитайте!
Шаг 2. Пусть x будет первым целым числом.
Шаг 3. Тогда x+ 1 — следующее последовательное целое число.
Шаг 4.  2 раза определенное целое число плюс следующее последовательное целое число равно 34.
Шаг 5.  2x+(x+1)=34

Шаг 6.  Решить.

  2x+(x+1)=34

  3x+1=34

  3x=33

  x=11

  Проверить. 2*11+(11+1)=34

Пример 2.   Боб и Джо вместе заработали 60 долларов. Оба получали одинаковую ставку, но Боб работал в три раза дольше, чем Джо. Сколько получил каждый?

Шаг 1. Перечитайте!

Шаг 2. Пусть x будет количеством долларов, которые получил Джо.

Шаг 3. Тогда умножьте на 3 количество долларов, которое получил Боб

Шаг 4. Боб и Джо вместе заработали 60 долларов.
Шаг 5. 3x+x=60

Шаг 6.  Решить.

3x+x = 60

4x = 60

x = 15

3x = 45

Проверка 3*15+15 = 60

Пример 3. Сумма цифров двухзначного числа — это 12. Если переставить цифры местами, число уменьшится на 36. Что это за число?

Шаг 1. Перечитайте!

Шаг 2. Пусть x — цифра десятков.

Шаг 3. Тогда 12 — x — это цифра единиц.

Шаг 4. Если цифры поменять местами, то число уменьшается на 36. Решать.

  10(12-х)+х = 10х+ (12-х) -36

  =120-10х+х=10х+12-х-36

  =120-9х=4х-4=4 -24

18x

  =x=8

  =12-x=4

  Поэтому число равно 84.

  Проверьте. 84-36=48

Пример 4.   Сколько фунтов конфет стоимостью 48 центов за фунт нужно добавить к 50 фунтам конфет стоимостью 80 центов за фунт, чтобы владелец магазина мог продавать конфеты по 60 центов за фунт ?
Шаг 1. Перечитайте!
Шаг 2. Пусть x будет количеством фунтов конфет по 48 центов за фунт.
Шаг 3. Тогда 50+x будет фунтами конфет, которые он получит по 60 центов за фунт.
Шаг 4. Количество конфет по 48 центов за фунт, умноженное на 48 центов, плюс количество конфет по 80 центов за фунт, умноженное на 80 центов, должно быть равно количеству конфет по 60 центов за фунт, умноженному на 60 центов.
Шаг 5. (48 центов/фунт)(x фунтов) + (80 центов/фунт) (50 фунтов) = (60 центов/фунт) [(50+x)фунт]

Шаг 6.  Решить.

48x+80*50 = 60 (50+x)

48x+4000 = 3000+60x

1000 = 12x

x = (83 (1)/3) LBS

Проверка. (83+1/3)48+80*50=60(50+83+1/3)

  Задачи, связанные со скоростями (или скоростями), будут использовать формулу

  d=rt

  где d — пройденное расстояние, r — скорость, t — время. При использовании формулы d и r должны быть выражены в одних и тех же единицах расстояния, а r и t должны быть выражены в одних и тех же единицах времени.

Пример 5.   Группа студентов поехала на озеро в северном лесу ловить рыбу. Они преодолели 380 миль за 7 часов, из них 4 часа по асфальтированной дороге, а остальное время по грунтовой дороге. Если средняя скорость по грунтовой дороге была на 25 миль в час меньше средней скорости по шоссе, то найти для каждого участка пути среднюю скорость и пройденное расстояние.

Шаг 1 . Перечитай!

Шаг 2. Пусть x будет скоростью на грунтовой дороге.

Шаг 3. Тогда х+25 — это скорость на шоссе.

Шаг 4. Расстояние, пройденное по шоссе, плюс расстояние, пройденное по грунтовой дороге, равно 380 милям. Шаг 5

Шаг 6.  Решить.

  (x+25)4+3x=380

  4x+100+3x=380

  7x=280

  x=40 миль в час

  x+25=65 миль в час

  Проверить. (40+25)4+40*3=380

   Рабочие задачи, связанные со скоростью выполнения, часто можно решить, сначала найдя дробную часть задачи, выполняемой каждым человеком или машиной за единицу времени, а затем найдя уравнение, которое связывает эти различные дробные части.

Пример 6.    Мальчик может подстричь газон за 4 часа, а отец за 3 часа. Сколько времени им понадобится, чтобы подстричь один и тот же газон, работая вместе?

Шаг 1. Перечитайте!

Шаг 2. Пусть x будет количеством часов, которые им потребуется, чтобы подстричь газон Работая вместе.

Шаг 3 . Выберите один час в качестве нашей единицы времени. Теперь мальчик может скосить 1/4 газона за один час, отец может скосить 1/3 газона за один час, а вместе они могут скосить 1/x газона за один час.


Шаг 4. Сумма, срезанная мальчиком за один час, плюс сумма, срезанная отцом за один час, равна количеству, которое они могут срезать вместе за один час.

Шаг 5. 1/3+1/4=1/x

Шаг 6.  Решить.

  1/3+1/4=1/x

  7/12=1/x

  x=12/7 часов

Калькулятор системы уравнений кнопка для решения линейных уравнений с помощью калькулятора системы линейных уравнений

Калькулятор системы уравнений

Калькулятор системы уравнений — это инструмент, который используется для одновременного решения системы линейных уравнений. Для решения системы линейных уравнений этот калькулятор использует метод подстановки и метод исключения.

Что такое система уравнений?

Система уравнений – это набор линейных уравнений, которые необходимо решать одновременно. Значения переменных, которые удовлетворяют всем уравнениям в системе, будут оцениваться путем решения системы линейных уравнений.

Есть два известных метода решения системы линейных уравнений.

  • Метод исключения
  • Метод замены

Что такое метод замены?

Этот метод используется для решения системы линейных уравнений путем подстановки значения одной переменной. Найдите значение одной переменной (скажем, «х»), которая зависит от другой переменной (скажем, «у») по одному уравнению, и подставьте его в другое уравнение. Чтобы решить систему линейных уравнений подстановкой, выполните следующие шаги.

  • Возьмите одно уравнение из линейной системы и решите его для одной переменной через другую.
  • Подставьте вышеуказанное значение переменной в другие уравнения и исключите значение переменной, используя некоторые арифметические операции.
  • Решите уравнение, сформированное на первом этапе, используя любое из значений переменных, уже найденных на предыдущих этапах.

Пример метода подстановки

Решите следующую систему линейных уравнений методом подстановки.

x + 3y = -4

4x — y = 1

Решение:

Шаг 1: напишите приведенное выше уравнение и дайте имя eq (i) & eq (ii).

х + 3у = -4 ——> (i)

4x — y = 1———> (ii)

Шаг 2: Решите уравнение (i) для «x».

x + 3y = -4

x = -4 -3y

Шаг 3: Подставьте приведенное выше значение в уравнение (ii) и упростите вместо «y».

Поместите x = -4 -3y в (4x — y = 1)

4(-4 -3y) – y = 1

-16 – 12y — y = 1

-16 – 13y = 1

– 13y = 1 + 16

– 13y = 17

  y = 17/(-13)

y = — 17/13

Шаг 4: Поместите указанное выше значение «y» в шаге 2 и упростите.

y = — 17/13 дюйма (x = -4 -3y)

x = — 4 – 3 (-17/13)

x = — 4 + (51/13)

Решите, взяв ЛКМ правой стороны.

х = (-52 + 51)/13

х = -1 / 13

Отсюда

х = -1 / 13, у = — 17/13 является решением данной системы линейных уравнений.

Каков метод устранения?

В этом методе мы исключаем переменную, дающую один и тот же коэффициент, с помощью некоторой алгебраической операции (умножения или деления). Некоторые шаги по устранению значения переменной приведены ниже.

  • Возьмите переменные, которые вы хотите исключить из уравнения, и сделайте коэффициенты переменных одинаковыми.
  • Найдите НОК выбора переменной путем выбора коэффициентов из всех уравнений.
  • Умножьте обе части всех уравнений с помощью НОК, чтобы получить одинаковые коэффициенты.
  • В зависимости от ситуации добавьте или вычтите уравнение, чтобы отменить выбранную переменную.
  • На предыдущем этапе мы получаем значение одной переменной и используем это значение в любом уравнении, чтобы найти значение исключенной переменной.