Сколько диагоналей у треугольника, четырехугольника, пятиугольника, шестиугольника, восьмиугольника?
Главная > Нью бест > Сколько диагоналей у треугольника, четырехугольника, пятиугольника, шестиугольника, восьмиугольника?
Диагональ в многоугольнике (полиэдре) — отрезок, соединяющий любые две несмежные вершины, другими словами, вершины, не принадлежащие одной стороне многоугольника (одному ребру полиэдра).
У полиэдров различают диагонали граней (рассматриваемых как плоские многоугольники) и пространственные диагонали, выходящие за границы граней. У полиэдров, имеющих треугольные грани есть только пространственные диагонали.
Подсчет диагоналей
Диагоналей нет у треугольника на плоскости и у тетраэдра в пространстве, так как все вершины этих фигур попарно связаны сторонами (ребрами).
Количество диагоналей N у многоугольника просто вычислить по формуле:
N = n·(n — 3)/2,
где n — число вершин многоугольника. По этой формуле несложно отыскать, что
По этой формуле несложно отыскать, что
Количество диагоналей полиэдра с числом вершин n просто подсчитать только для варианта, когда в каждой верхушке полиэдра сходится однообразное число ребер k. Тогда есть возможность воспользоваться формулой:
N = n·(n — k — 1)/2,
которая даем сумманое число пространственных и граневых диагоналей. Отсюда есть возможность отыскать, что
В том случае в различных верхушках полиэдра сходится различное число ребер, подсчет приметно усложняется и должен проводится персонально для каждого варианта.
Фигуры с равными диагоналями
На плоскости существует два правильных многоугольника, у каких все диагонали равны меж собой. Это
Единственный верный полиэдр, у которого все диагонали равны меж собой — верный восьмигранник октаэдр. У него три диагонали, которые попарно перпендикулярно пересекаются в центре. Все диагонали октаэдра — пространственные (диагоналей граней у октаэдра нет, т.к. у него треугольные грани).
Кроме октаэдра еще есть один верный полиэдр, у которого все пространственные диагонали равны меж собой. Это куб (гексаэдр)
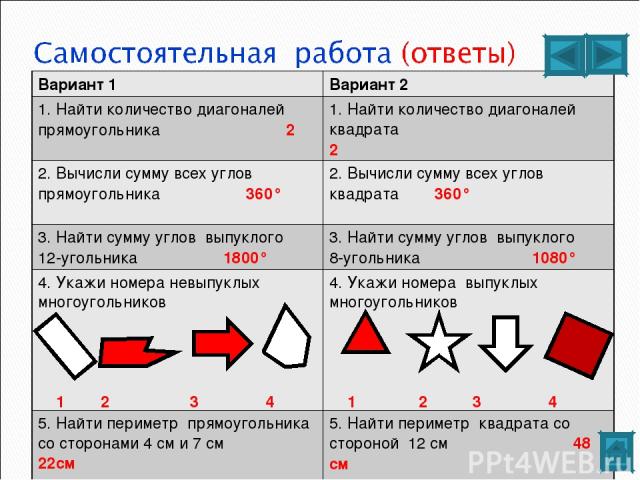
Полезные ссылки:
Дополнительно в базе данных New-Best.comа:
Как найти диагональ квадрата? – Обзоры Вики
Диагональ квадратной формулы равна д = а√2; где d — диагональ, а a — сторона квадрата. Формула диагонали квадрата выводится с помощью теоремы Пифагора. Диагональ делит квадрат на два равнобедренных прямоугольных треугольника.
Из этого следует, что такое диагональная формула прямоугольника? В формуле диагонали прямоугольника w относится к ширине прямоугольника. Формула дается как, d = √ (l2 + ш2), где l — длина прямоугольника, а w — ширина прямоугольника.
Чему равна диагональ квадрата 5×5? Как найти диагональ квадрата – формула.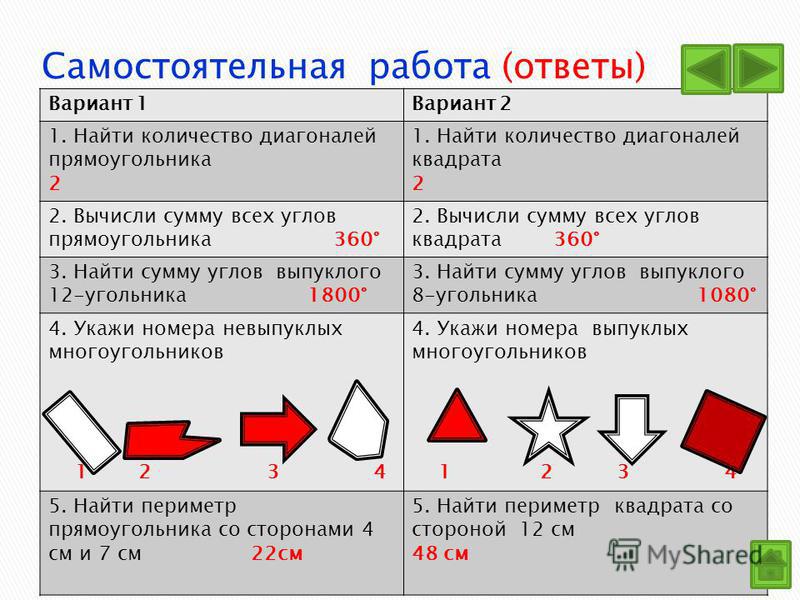 Так, например, если сторона квадрата равна 5 дм, то диагональ равна 5√2 дюйма ≈ 7.071 дюйма.
Так, например, если сторона квадрата равна 5 дм, то диагональ равна 5√2 дюйма ≈ 7.071 дюйма.
Дополнительно Как найти гипотенузу? Как найти гипотенузу равнобедренного прямоугольного треугольника?
- Найдите длину одной из сторон без гипотенузы.
- Возведите в квадрат длину стороны.
- Удвойте результат предыдущего шага.
- Корень квадратный из результата шага 3. Это длина гипотенузы.
Сколько диагоналей в квадрате? Квадрат имеет две диагонали равной длины, которые пересекаются в центре квадрата. Отношение диагонали к стороне. У правильного пятиугольника пять диагоналей одинаковой длины.
Какова длина диагонали прямоугольника размером 9 на 40 дюймов?
Вывод: для прямоугольника, имеющего ширину 9 единиц и длину 40 единиц, длина диагонали равна 41 единиц.
Сколько диагоналей в прямоугольнике? прямоугольники имеют две диагонали соединяющие две противоположные вершины. Они одинакового размера.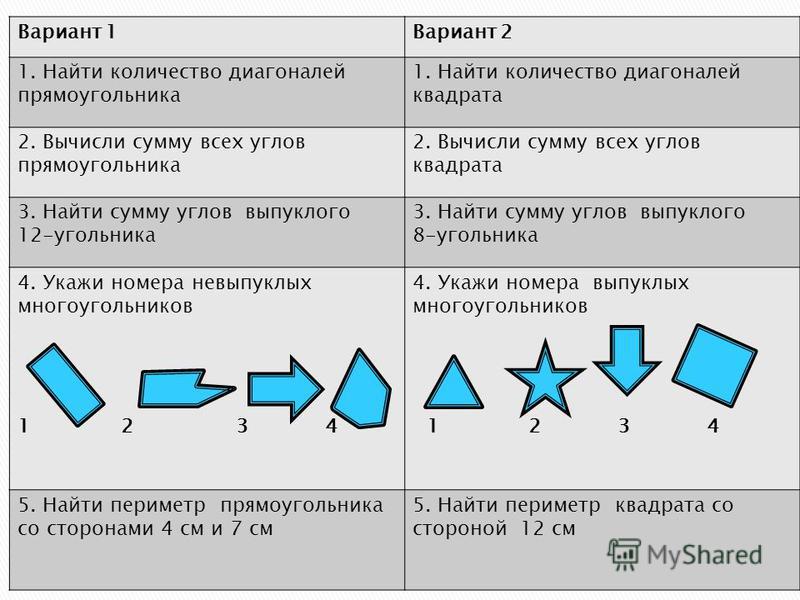
Сколько диагоналей у пятиугольника? Многоугольники: сколько диагоналей? (Для пар или групп учащихся) Диагональ правильного многоугольника – это прямая линия, соединяющая две несмежные вершины. Таким образом, у квадрата две диагонали, а у правильного пятиугольника 5, как показано ниже.
Диагонали квадрата равны?
Диагонали квадрата делят его углы пополам. Противоположные стороны квадрата параллельны и равны по длине. Все четыре угла квадрата равны (каждый равен 360°/4 = 90°, прямой угол). … Диагонали квадрата равны равный.
Также Какова диагональ квадратной тарелки, длина которой 28 см? сторона = 28 см. = 28√2. значит диагональ квадрата 28√2 см.
Как найти гипотенузу с помощью Sohcahtoa?
Что вы понимаете под гипотенузой? Определение гипотенузы
1: сторона прямоугольного треугольника, лежащая против прямого угла.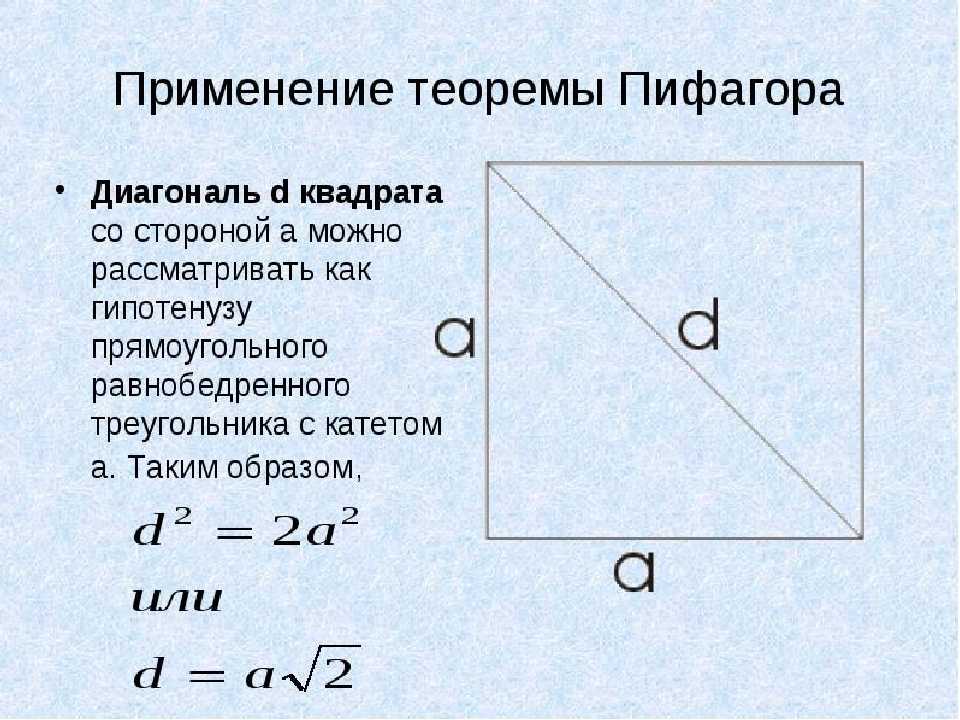 2: длина гипотенузы.
2: длина гипотенузы.
Для чего используется гипотенуза?
Гипотенуза самая длинная сторона прямоугольного треугольника. Это также сторона, противоположная прямому углу. Это полезно в различных ситуациях, связанных с необходимостью найти расстояние или величину угла.
Сколько диагоналей в пятиугольнике?
Многоугольники: сколько диагоналей? (Для пар или групп учащихся) Диагональ правильного многоугольника – это прямая линия, соединяющая две несмежные вершины. Таким образом, у квадрата две диагонали, а у правильного пятиугольника 5, как показано ниже.
Какой многоугольник имеет 35 диагоналей? Многоугольник с 10 сторонами называется декагон. ∴ Декагон имеет 35 диагоналей.
Какая фигура диагональ? Это (диагональ) отрезок линии . Многоугольники — это плоские фигуры, имеющие по крайней мере три стороны и углы, и обычно он используется для обозначения фигур, имеющих пять или более сторон и углов. Вершина — это угол фигуры.
…
Диагональ — Определение с примерами.
| Имена форм | Количество вершин | Количество диагоналей |
|---|---|---|
| декагон | 10 | 35 |
Как по диагонали прямоугольника найти площадь?
Зная диагонали, можно вычислить только площадь квадрата. А = d² / 2. Это максимальная площадь любого прямоугольника с диагональю d.
Сколько диагоналей у пятиугольника?
Многоугольники: сколько диагоналей? (Для пар или групп учащихся) Диагональ правильного многоугольника – это прямая линия, соединяющая две несмежные вершины. Таким образом, у квадрата две диагонали, а у правильного пятиугольника 5, как показано ниже.
Какая диагональ пятиугольника?
Итак, вычитание сторон даст общее количество диагоналей, содержащихся в многоугольнике. Таким образом, общее количество диагоналей внутри 11-стороннего многоугольника = 55 -11, что равно 44 .
Таким образом, общее количество диагоналей внутри 11-стороннего многоугольника = 55 -11, что равно 44 .
…
Решенные примеры.
| Имя многоугольника | Количество сторон | Количество диагоналей |
|---|---|---|
| пятиугольник | 5 | 5 |
| Hexagon | 6 | 9 |
| семиугольник | 7 | 14 |
Сколько диагоналей в правильном десятиугольнике? У правильного десятиугольника все стороны одинаковой длины, и каждый внутренний угол всегда будет равен 1440, как показано на рисунке. (n-3) умножьте на количество вершин и разделите на 2. Таким образом, количество диагоналей в десятиугольнике равно 35. Итак, это необходимый ответ.
Сколько диагоналей у 12-угольника?
Следовательно, есть 54 диагонали в двенадцатиугольнике.
…
Треугольники в додекагоне.
| Предложения | Ценности |
|---|---|
| Внутренний угол | 150° |
| Внешний угол | 30° |
| Количество диагоналей | 54 |
| Количество треугольников | 10 |
— формула, свойства, примеры
Диагональ квадрата — это отрезок, соединяющий любые две несмежные вершины. Квадрат имеет две диагонали, которые равны по длине и делят друг друга пополам под прямым углом. Формула диагонали квадрата используется для вычисления длины диагонали квадрата, когда известна длина его стороны.
| 1. | Что такое диагональ квадрата? |
| 2. | Что такое Диагональ формулы квадрата? |
| 3. | Вывод диагонали квадрата по формуле |
4. | Примеры использования диагональной формулы квадрата |
| 5. | Часто задаваемые вопросы о диагонали квадратной формулы |
Что такое диагональ квадрата?
Квадрат имеет две диагонали, каждая из которых образована соединением противоположных вершин квадрата. Обратите внимание на следующий квадрат, чтобы соотнести свойства диагоналей, приведенные ниже.
- Диагонали квадрата равны по длине.
- Они перпендикулярны друг другу.
- Они делят квадрат на два равных равнобедренных прямоугольных треугольника.
Что такое Диагональ формулы квадрата?
Диагональ формулы квадрата равна d = a√2; где «d» — диагональ, а «а» — сторона квадрата. Формула диагонали квадрата выводится по теореме Пифагора. Диагональ делит квадрат на два равнобедренных прямоугольных треугольника. Обе диагонали равны и делят друг друга пополам под прямым углом. Давайте разберемся, как вывести формулу для нахождения диагонали квадрата.
Вывод диагонали квадрата по формуле
В квадрате длина обеих диагоналей одинакова. Длина диагонали «d» квадрата со стороной «а» вычисляется по теореме Пифагора. Обратите внимание на следующий квадрат, чтобы увидеть, что длина диагонали обозначена буквой «d», а длина стороны обозначена буквой «a».
Диагональ квадрата Формула
Рассмотрим треугольник ADC в квадрате. Мы знаем, что все углы квадрата равны 9.0 °, поэтому, используя теорему Пифагора, мы можем найти гипотенузу, которая в данном случае равна «d».
D 2 = A 2 + A 2
D = √ (A 2 + A 2 )
D = √ (2A 2 )
D = √2 × × a = √ (2A 2 )
D = √a 2
= √2a
Следовательно, диагональ квадрата равна: d = a√2
☛ Похожие статьи
- Диагонали прямоугольника 9004
- Диагональ куба Формула
- Диагональ формулы параллелограмма
- Диагональ многоугольника Формула
- Диагональ ромба
Часто задаваемые вопросы о диагонали квадратной формулы
Что такое диагональ квадрата в математике?
Диагональ квадрата — это отрезок, соединяющий две несмежные вершины. Квадрат имеет две диагонали, которые равны по длине и делят друг друга пополам под прямым углом. Свойства диагоналей квадрата следующие:
Квадрат имеет две диагонали, которые равны по длине и делят друг друга пополам под прямым углом. Свойства диагоналей квадрата следующие:
- Они одинаковой длины.
- Они перпендикулярны друг другу.
- Они делят квадрат на два равных равнобедренных прямоугольных треугольника.
Какова формула диагонали квадрата?
Квадрат имеет две диагонали одинаковой длины, которые можно рассчитать по формуле d = a√2, где а — сторона квадрата.
Как рассчитать диагональ квадрата по формуле диагонали?
Чтобы вычислить длину диагонали квадрата, мы используем следующие шаги:
- Шаг 1: Проверьте длину стороны квадрата, a.
- Шаг 2: Подставьте значение «а» в формулу диагонали квадрата, d = a√2.
- Шаг 3: Запишите полученное значение в соответствующей единице измерения.
Как получить диагональ квадратной формулы?
Диагональ квадратной формулы можно вывести с помощью теоремы Пифагора.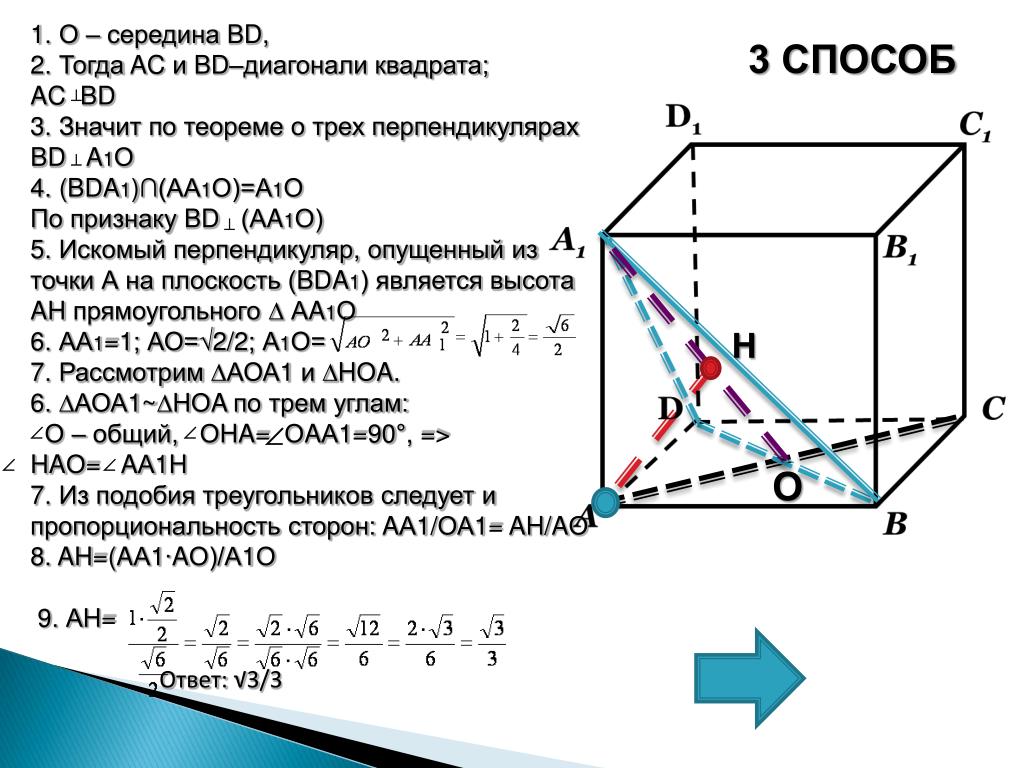
- Шаг 1: Проведите диагонали квадрата.
- Шаг 2: Образуются два прямоугольных треугольника. Рассмотрим один из треугольников.
- Шаг 3: Две стороны прямоугольного треугольника будут одинаковыми, так как все стороны квадрата равны.
- Шаг 4: Примените теорему Пифагора и вычислите длину гипотенузы треугольника, являющегося диагональю квадрата.
Таким образом, диагональ d = √(a 2 + a 2 ) = (√2)а = а√2; где «а» — сторона квадрата.
Что такое «а» в диагонали формулы квадрата?
Так как квадрат имеет четыре равные стороны, поэтому в формуле диагонали квадрата «а» представляет сторону квадрата. Таким образом, диагональ квадратной формулы задается как d = a√2.
Диагональ квадрата равна его стороне?
Нет, диагональ квадрата не равна его стороне. Поскольку все углы квадрата равны 90°, диагональ квадрата становится гипотенузой треугольников, образуемых в квадрате.
Как найти диагональ квадрата, зная площадь?
Если известна площадь квадрата, можно вычислить длину стороны квадрата.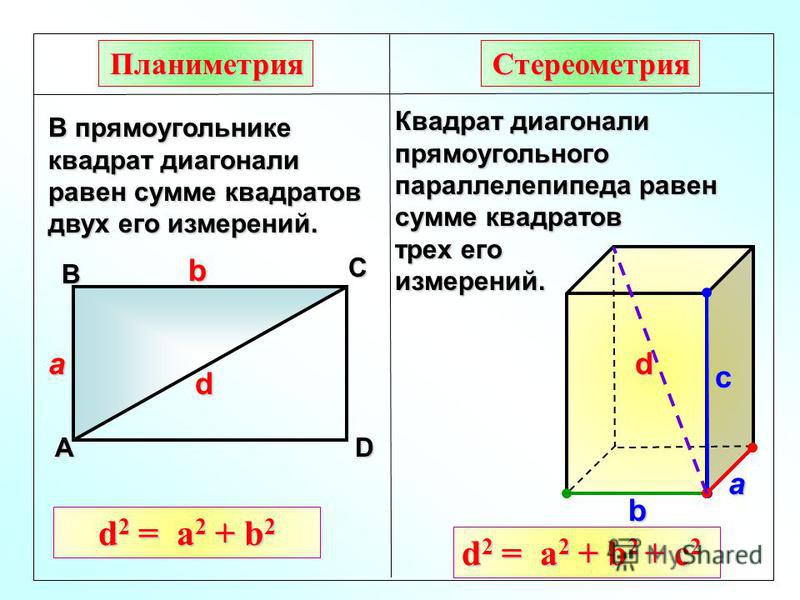 Затем значение длины стороны можно использовать для нахождения диагонали квадрата с помощью формулы d = a√2. Например, если площадь квадрата составляет 81 кв. Сначала найдем длину его стороны, так как мы знаем, что площадь квадрата = a 2 . Следовательно, сторона «а» = √81 = 9 единиц. Теперь мы будем использовать это значение в формуле d = a√2, d = 9√2 = 12,72 единицы.
Затем значение длины стороны можно использовать для нахождения диагонали квадрата с помощью формулы d = a√2. Например, если площадь квадрата составляет 81 кв. Сначала найдем длину его стороны, так как мы знаем, что площадь квадрата = a 2 . Следовательно, сторона «а» = √81 = 9 единиц. Теперь мы будем использовать это значение в формуле d = a√2, d = 9√2 = 12,72 единицы.
Как найти диагональ квадрата, если дана сторона?
Диагональ квадрата можно вычислить, если известна сторона. Диагональ квадратной формулы = a√2; где «а» — длина стороны. Данную длину стороны подставляют в эту формулу, чтобы получить длину диагонали. Например, если длина стороны квадрата равна 10 см, мы подставим в формулу значение d = a√2. Это означает, что длина диагонали (d) = a√2 = 10√2 = 14,14 см.
Как найти диагональ квадрата с периметром?
Диагональ квадрата можно вычислить, если известен периметр квадрата. Давайте разберемся в этом на примере. Например, если периметр квадрата равен 32 единицам, найдем диагональ, выполнив следующие шаги:
- Шаг 1: Мы знаем, что формула для нахождения периметра квадрата = 4 × длина стороны.

- Шаг 2: Зная длину стороны, можно вычислить диагональ квадрата по формуле Диагональ квадрата = a√2; где «а» — длина стороны. Теперь мы можем подставить это значение в формулу Диагональ квадрата = a√2 = 8 × √2 = 11,313 единиц.
Как вычислить длину диагонали квадрата
Квадрат — это двумерная плоская фигура, которую можно найти в геометрии. У него четыре стороны одинаковой длины, а каждый из четырех углов равен 9.0 градусов. Характеристики прямоугольника относительно сопоставимы с характеристиками квадрата; однако ключевое различие между ними заключается в том, что прямоугольник имеет равные стороны только на противоположных сторонах. Из-за этого прямоугольник можно назвать квадратом только в том случае, если все четыре его стороны имеют одинаковую длину.
Квадрат является примером правильного четырехугольника, который представляет собой фигуру, имеющую четыре стороны одинаковой длины и углы одинаковой степени. Все четыре угла квадрата имеют меру 90 градусов, что делает их прямыми углами. Кроме того, диагонали квадрата параллельны друг другу и пересекаются под прямым углом. Один из альтернативных способов определить квадрат — это прямоугольник с двумя сторонами одинаковой длины на противоположных сторонах.
На рисунке справа изображен квадрат, все четыре стороны которого имеют одинаковую длину, а каждый угол равен 90 градусам.
Ромб, который также является выпуклым четырехугольником и имеет все четыре равные стороны, может считаться квадратом так же, как прямоугольник, если его угол при вершине прямой, точно так же, как квадрат такой же, как прямоугольник.
Точно так же из параллелограмма можно составить квадрат, если у него две равные соседние стороны и правильный угол при вершине.
Квадрат — это многоугольник с четырьмя сторонами, который характеризуется параллельными сторонами одинаковой длины и углами, имеющими величину 90 градусов. Конфигурация квадрата такова, что если бы его разделить посередине плоскостью, то обе получившиеся половины были бы симметричны. Когда квадрат разрезается пополам, каждая половина принимает форму прямоугольника с параллельными сторонами, равными по длине.
Свойства квадрата:Ниже приведен список четырех наиболее важных характеристик квадрата:
- Каждый из четырех внутренних углов имеет угол 90 градусов.
- Каждая из четырех сторон квадрата равна или равна трем другим сторонам.
- Противоположные стороны квадрата параллельны друг другу.
- Диагонали квадрата пересекаются под углом 90 градусов.
- Обе диагонали квадрата параллельны друг другу и имеют одинаковую длину.
- Квадрат имеет четыре точки пересечения и четыре стороны.

- Диагональ квадрата делит его на два равнобедренных треугольника, идентичных друг другу.
- Длина диагоналей квадрата больше длины любой из его сторон.
Каждая из диагоналей квадрата получается путем соединения противоположных углов квадрата, поэтому у квадрата всего две диагонали. Обратите внимание на следующий квадрат, который поможет вам понять информацию о качествах диагоналей, представленную ниже.
- Длины диагоналей в квадрате одинаковы.
- Они пересекают друг друга перпендикулярно друг другу.
- Они создают два конгруэнтных и равнобедренных треугольника с прямыми углами вне квадрата. Формула диагонали квадрата: . Теорема Пифагора используется для получения формулы диагонали квадрата, которую затем можно использовать в расчетах квадратных футов. Квадрат можно разрезать на два равнобедренных треугольника с прямыми углами, если использовать диагональ. Обе диагонали одинаковы и пересекаются под прямым углом, образуя правильный квадрат.
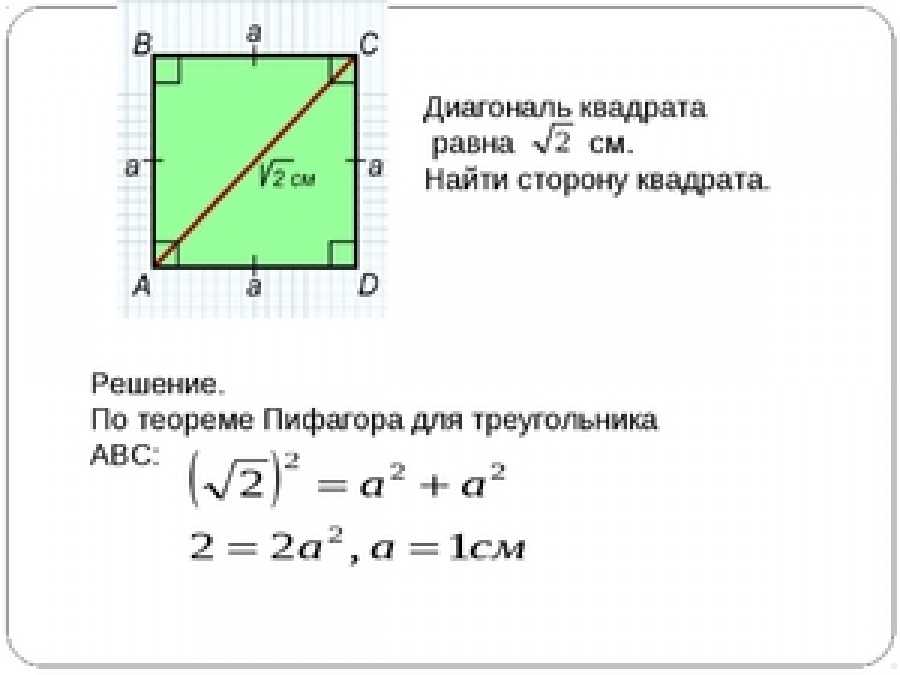
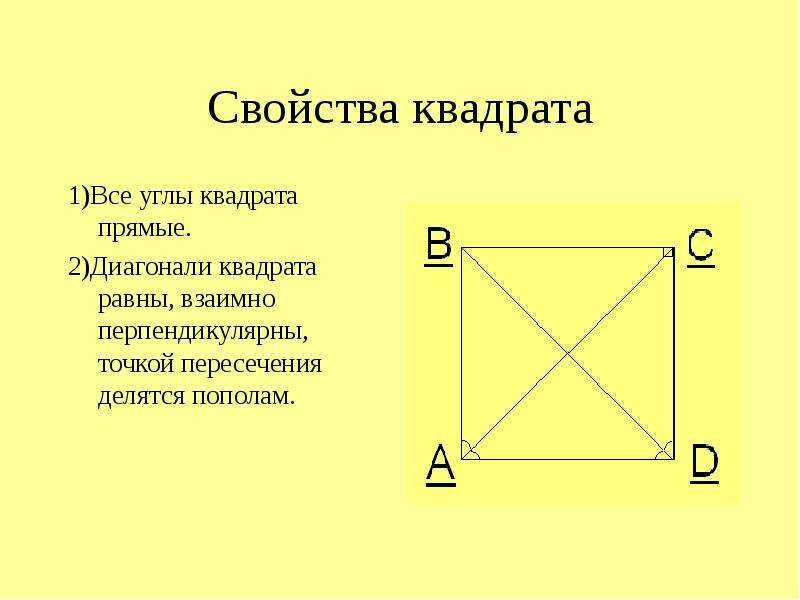
 Вывод формулы диагонали квадрата:
Вывод формулы диагонали квадрата: Обе диагонали квадрата имеют одинаковую длину, поскольку квадрат является квадратом. Теорему Пифагора можно использовать для определения длины диагонали квадрата, обозначаемой буквой d, по длине его стороны a. Изучив следующий квадрат, вы заметите, что длина диагонали представлена буквой «d», а длина стороны — буквой «a».
Диагональ квадрата формула:Рассмотрим треугольник ADC в квадрате. Мы знаем, что все углы квадрата равны 90°, поэтому, используя теорему Пифагора, мы можем найти гипотенузу, которая в данном случае равна «d».
d² = a² + a²
d = √(a² + a²)
d = √(2a²)
d = √2 × √a²
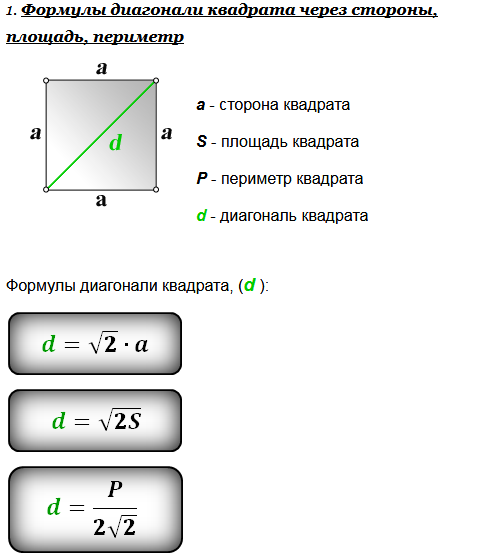
= √2a квадрат равен формуле
,900 : d = a√2
Значение диагонали квадрата:Каждая диагональ делит квадрат на два конгруэнтных равнобедренных прямоугольных треугольника, которые представляют собой особые прямоугольные треугольники с углами 45 и 90 градусов.


 Вывод формулы диагонали квадрата:
Вывод формулы диагонали квадрата: 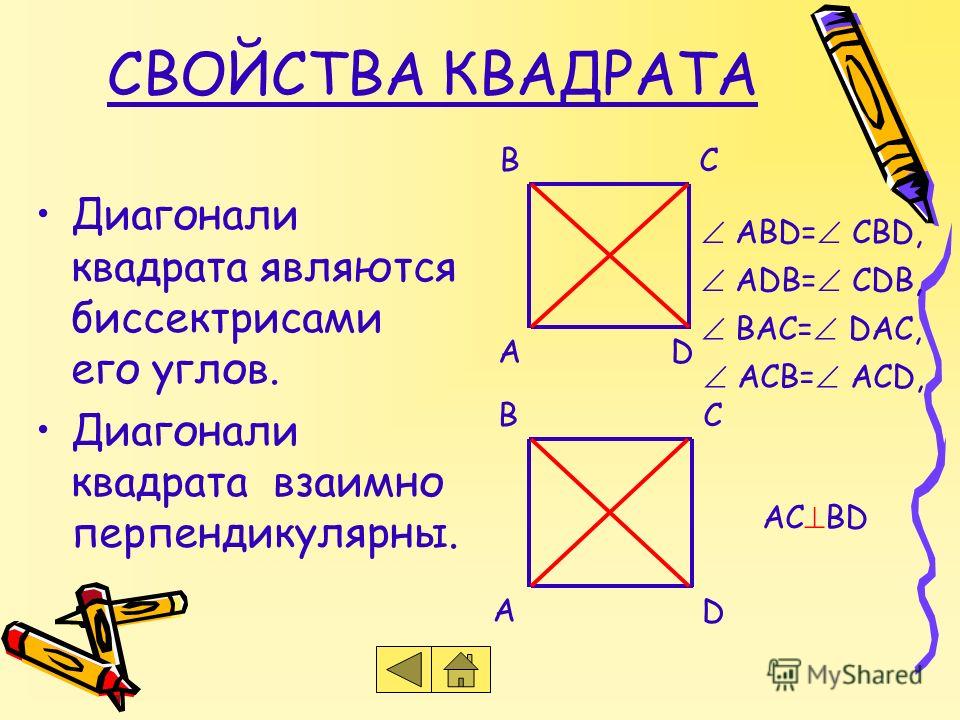
Leave A Comment