Формулы для первой производной функции
y есть функция y = y(x)
C = постоянная, производная (y’) постоянной есть 0
y = C => y’ = 0
пример: y = 5, y’ = 0
Если y есть функцией типа y = xn, формула для производной есть:
y = xn => y’ = nxn-1
пример: y = x3 y’ = 3x3-1 = 3x2
y = x-3 y’ = -3x-4
Из вышеприведенной формулы мы можем сказать, что для производной y’ функции y = x = x1 that:
если y = x тогда y’=1
y = f1(x) + f2(x) + f3(x) …=>
y’ = f’1(x) + f’2(x) + f’3(x) …
Эта формула представляет производную функции, являющейся суммой функций.
Пример: Если мы имеем две функции f(x) = x2 + x + 1 и
g(x) = x5 + 7 и y = f(x) + g(x) тогда y’ = f'(x) + g'(x) =>
y’ = (x2 + x + 1)’ + (x
Если функция есть произведением двух функций, формула производной выглядит так:
y = f(x). g(x) => y’ = f'(x)g(x) + f(x)g'(x)
g(x) => y’ = f'(x)g(x) + f(x)g'(x)
Если f(x) = C(C есть постоянной) и y = f(x)g(x)
y = Cg(x) y’=C’.g(x) + C.g'(x) = 0 + C.g'(x) = C.g'(x)
y = Cf(x) => y’ = C.f'(x)
Формулы вычисления производной
| y = |
| y’ = |
|
y = ln x => y’ =
y = ex => y’ = ex
y = sin x => y’ = cos x
y = cos x => y’ = -sin x
y = tg x => y’ = 1/cos2x
y = ctg x => y’ = —1/sin2x
| y = arcsin x | => | y’ = |
|
| y = arccos x | => | y’ = |
|
| y = arctg x | => | y’ = |
|
| y = arcctg x | => | y’ = |
|
если функция есть функцией функции: u = u(x)
y = f(u) => y’ = f'(u).u’
Пример. Пусть у нас есть функция y = sin(x2)
в этом случае u = x2, f(u) = sin(u), производные есть f'(u) = cos(u), u’ = 2x
y’ = (sin(u))’.u’ = cos(x2).2x = 2.x.cos(x2)
Задачи с производными
1) f(x) = 10x + 4y. Найдите первую производную f'(x)
 Поэтому f’2(x) = (4y)’ = 0. Отсюда производная функции f(x) есть: f'(x) = 10 + 0 = 10.
Поэтому f’2(x) = (4y)’ = 0. Отсюда производная функции f(x) есть: f'(x) = 10 + 0 = 10.| 2) Вычислите производную f(x) = |
|
ОТВЕТ:
функция f(x) есть h(x), разделенная на g(x). h'(x) = 10x9 g'(x) = 0 — sin x = -sin x
| f'(x) = |
|
| f'(x) = |
| = |
|
3) f(x) = ln(sinx). Какая производная функции f(x)?
ОТВЕТ:
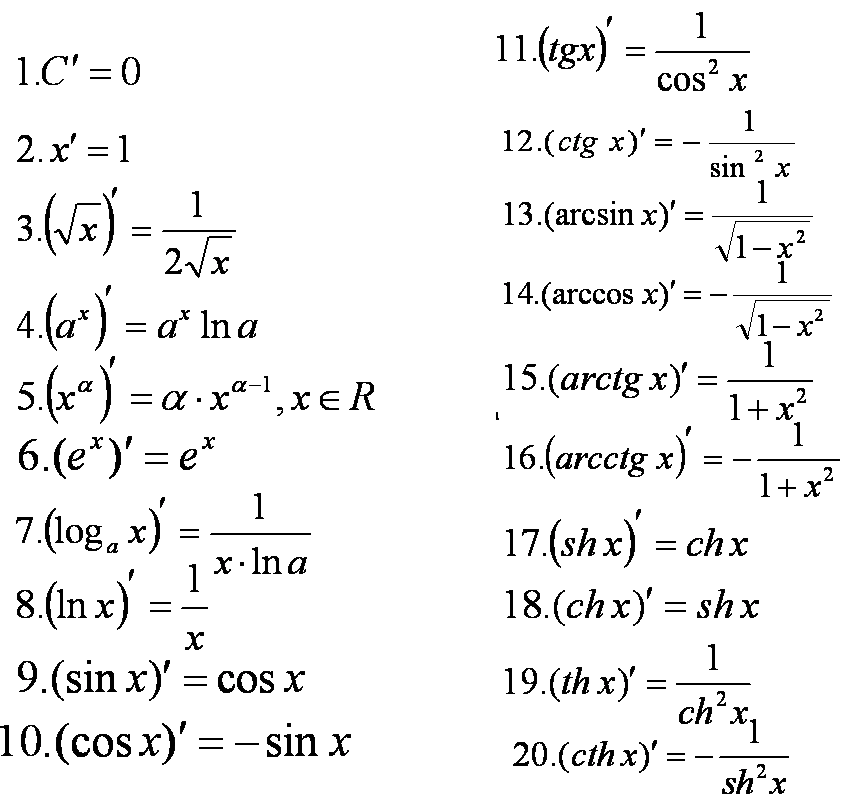

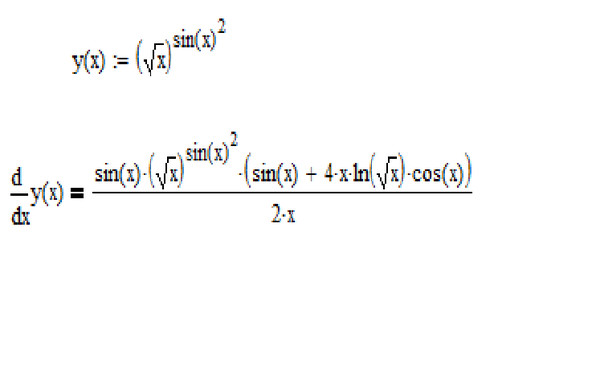 x
x
Leave A Comment