Траектория, длина пути, вектор перемещения

Определение 1

Траектория движения тела – это линия, которая была описана материальной точкой при перемещении из одной точки в другую с течением времени.

Виды движений тела

Существуют несколько видов движений и траекторий твердого тела:

  • поступательное;
  • вращательное, то есть движение по окружности;
  • плоское, то есть перемещение по плоскости;
  • сферическое, характеризующее движение по поверхности сферы;
  • свободное, иначе говоря, произвольное.

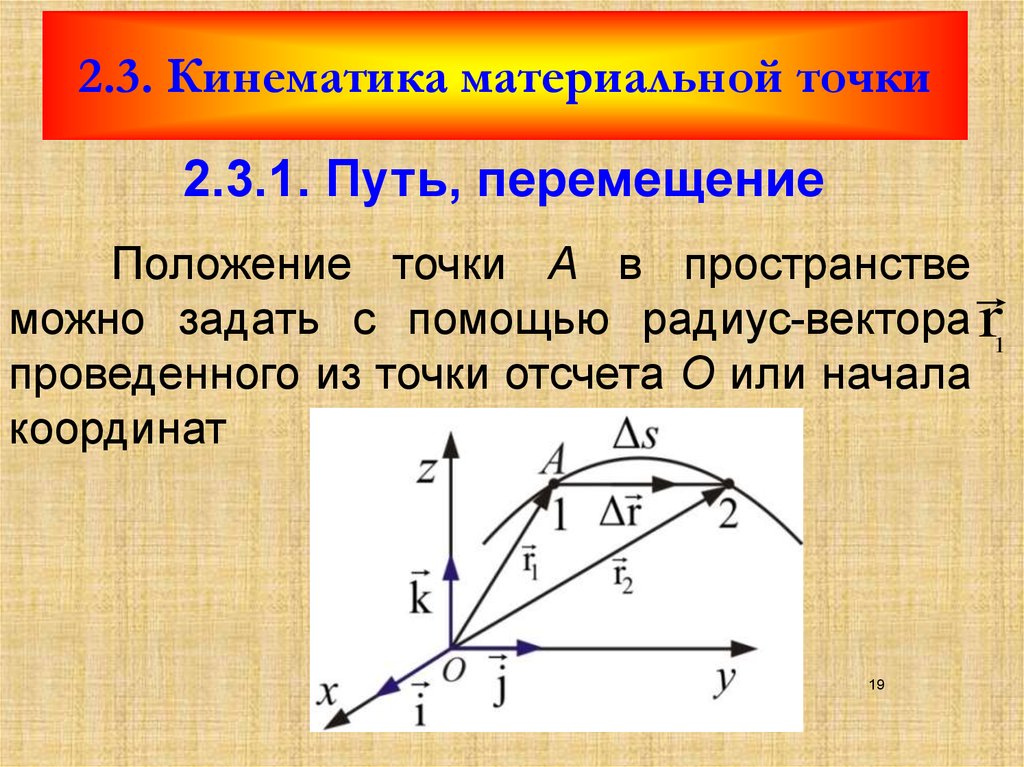
Рисунок 1. Определение точки при помощи координат x=x(t), y=y(t), z=z(t) и радиус-вектора r→(t), r0→ является радиус-вектором точки в начальный момент времени

Положение материальной точки в пространстве в любой момент времени может быть задано при помощи закона движения, определенный координатным способом, через зависимость координат от времени x=x(t), y=y(t), z=z(t)или от времени радиус-вектора r→=r→(t), проведенного из начала координат к заданной точке.

Это показано на рисунке 1.

Перемещение тела

Определение 2

Перемещение тела s→=∆r12→=r2→-r1→ – направленный отрезок прямой, соединяющий начальную с конечной точкой траектории тела. Значение пройденного пути l равняется длине траектории, пройденной телом за определенный промежуток времени t.

Рисунок 2. Пройденный путь l и вектор перемещения s→ при криволинейном движении тела, a и b – начальная и конечная точки пути, принятые в физике

Определение 3

По рисунку 2 видно, что при движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути.

Перемещение принято считать векторной величиной. Этот отрезок имеет направление.

Путь – скалярная величина. Считается числом.

Сумма двух последовательных перемещений из точки 1 в точку 2 и из токи 2 в точку 3 является перемещением из точки 1 в точку 3, как показано на рисунке 3.

Рисунок 3. Сумма двух последовательных перемещений ∆r→13=∆r→12+∆r→23=r→2-r→1+r→3-r→2=r→3-r→1

Когда радиус-вектор материальной точки в определенный момент времени t является r→(t), в момент t+∆t есть r→(t+∆t), тогда ее перемещение ∆r→ за время ∆t равняется ∆r→=r→(t+∆t)-r→(t).

Перемещение ∆r→ считается функцией времени t: ∆r→=∆r→(t).

Пример 1

По условию дан движущийся самолет, представленный на рисунке 4. Определить вид траектории точки М.

Рисунок 4

Решение

Необходимо рассмотреть систему отсчета I, называемую «Самолет» с траекторией движения точки М виде окружности.

Будет задана система отсчета II «Земля» с траекторией движения имеющейся точки М по спирали.

Пример 2

Дана материальная точка, которая совершает движение из А в В. Значение радиуса окружности R=1 м. Произвести нахождение S, ∆r→.

Решение

Во время движения из А в В точка проходит путь, который равен половине окружности, записываемой формулой:

S=πR.

Подставляем числовые значения и получаем:

S=3,14·1 м=3,14 м.

Перемещением ∆r→ в физике считается вектор, соединяющий начальное положение материальной точки с конечным, то есть А с В.

Подставив числовые значения, вычислим:

∆r→=2R=2·1=2 м.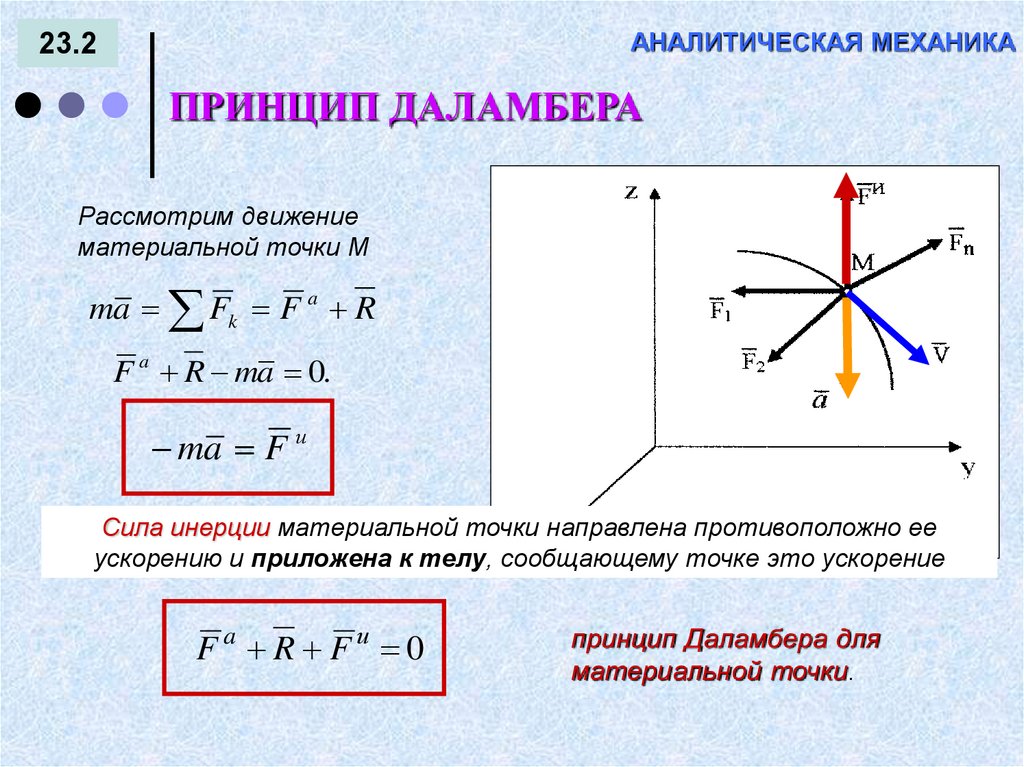

Ответ: S=3,14 м; ∆r→=2 м.

Автор: Роман Адамчук

Преподаватель физики

Помогите найти № 1392 ГДЗ Физика 7-9 класс Перышкин А.В. – Рамблер/класс

Помогите найти № 1392 ГДЗ Физика 7-9 класс Перышкин А.В. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

На рисунке 178 показаны перемещения трех ма­териальных точек: sl, s2, s3. Найдите:
а)   координаты начального положения каждой точки;
б)   координаты конечного положения каждой точки;
в)   проекции перемещения каждой точки на коорди­натную ось ОХ;
г)   проекции перемещения каждой точки на коорди­натную ось OY;
д)  модуль перемещения каждой точки.

ответы

Помогу:

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Досуг

Химия

похожие вопросы 5

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?

Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло.

В обоих (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Ребята нужны ответы на пересдачу по математике 9 класс 11 регион. Срочно!

ГИА9 класс

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 12. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

МЕТОД ДИНАМИЧЕСКОЙ АДАПТАЦИИ ДЛЯ МЕТОДА МАТЕРИАЛЬНОЙ ТОЧКИ. (Конференция)

ТЕХНИКА ДИНАМИЧЕСКОЙ АДАПТАЦИИ ДЛЯ МЕТОДА МАТЕРИАЛЬНОЙ ТОЧКИ. (Конференция) | ОСТИ.GOV

перейти к основному содержанию

  • Полная запись
  • Другое связанное исследование

Аннотация не предоставлена.

Авторов:
Руджерелло, Кевин П.; Шумахер, Шейн Кристиан
Дата публикации:
Исследовательская организация:
Национальная лаборатория Сандия. (SNL-NM), Альбукерке, Нью-Мексико (США)
Организация-спонсор:
Национальная администрация по ядерной безопасности Министерства сельского хозяйства США (NNSA)
Идентификатор ОСТИ:
1080392
Номер(а) отчета:
ПЕСОК2013-4361К
455926
Номер контракта с Министерством энергетики:  
АК04-94АЛ85000
Тип ресурса:
Конференция
Отношение ресурсов:
Конференция
: предложена для презентации на Particles 2013, проходившем 18-20 сентября 2013 г.
в Штутгарте, Германия.
Страна публикации:
США
Язык:
Английский

Форматы цитирования

  • ГНД
  • АПА
  • Чикаго
  • БибТекс

Руджерелло, Кевин П., и Шумахер, Шейн Кристиан. МЕТОД ДИНАМИЧЕСКОЙ АДАПТАЦИИ ДЛЯ МЕТОДА МАТЕРИАЛЬНОЙ ТОЧКИ. . США: Н. П., 2013. Веб.

Копировать в буфер обмена

Руджерелло, Кевин П., Шумахер, Шейн Кристиан. МЕТОД ДИНАМИЧЕСКОЙ АДАПТАЦИИ ДЛЯ МЕТОДА МАТЕРИАЛЬНОЙ ТОЧКИ. . Соединенные Штаты.

Копировать в буфер обмена

Руджерелло, Кевин П. , и Шумахер, Шейн Кристиан. 2013. «МЕТОД ДИНАМИЧЕСКОЙ АДАПТАЦИИ ДЛЯ МЕТОДА МАТЕРИАЛЬНОЙ ТОЧКИ». Соединенные Штаты. https://www.osti.gov/servlets/purl/1080392.

Копировать в буфер обмена

@статья{osti_1080392,
title = {МЕТОД ДИНАМИЧЕСКОЙ АДАПТАЦИИ ДЛЯ МЕТОДА МАТЕРИАЛЬНОЙ ТОЧКИ},
автор = {Руджирелло, Кевин П. и Шумахер, Шейн Кристиан},
abstractNote = {Аннотация не предоставлена.},
дои = {},
URL = {https://www.osti.gov/biblio/1080392}, журнал = {},
номер =,
объем = ,
место = {США},
год = {2013},
месяц = ​​{5}
}

Копировать в буфер обмена

Просмотр конференции (0,40 МБ)

Дополнительную информацию о получении полнотекстового документа см. в разделе «Доступность документа». Постоянные посетители библиотек могут искать в WorldCat библиотеки, в которых проводится эта конференция.

Экспорт метаданных

Сохранить в моей библиотеке

Вы должны войти в систему или создать учетную запись, чтобы сохранять документы в своей библиотеке.

Аналогичных записей в сборниках OSTI.GOV:

  • Аналогичные записи

12.4 Эластичность и пластичность | University Physics Volume 1

Цели обучения

К концу этого раздела вы сможете:

  • Объяснить предел, при котором деформация материала является упругой
  • Опишите диапазон, в котором материалы проявляют пластические свойства
  • Анализ упругости и пластичности на диаграмме напряжения-деформации

Константу пропорциональности между напряжением и деформацией мы назвали модулем упругости. Но почему мы называем это так? Что означает для объекта быть эластичным и как мы описываем его поведение?

Упругость – это тенденция твердых объектов и материалов возвращаться к своей первоначальной форме после устранения внешних сил (нагрузки), вызывающих деформацию. Объект является эластичным, когда он возвращается к своим первоначальным размерам и форме, когда нагрузка больше не присутствует. Физические причины упругого поведения различаются в зависимости от материала и зависят от микроскопической структуры материала. Например, эластичность полимеров и каучуков обусловлена ​​растяжением полимерных цепей под действием приложенной силы. Напротив, упругость металлов вызвана изменением размера и формы кристаллических ячеек решеток (которые являются материальными структурами металлов) под действием внешних сил.

Двумя параметрами, определяющими эластичность материала, являются его модуль упругости и его предел упругости . Высокий модуль упругости характерен для труднодеформируемых материалов; другими словами, материалы, которые требуют высокой нагрузки для достижения значительной деформации. Примером может служить стальная лента. Низкий модуль упругости характерен для материалов, легко деформируемых под нагрузкой; например, резинка. Если напряжение под нагрузкой становится слишком высоким, то при снятии нагрузки материал больше не возвращается к своей первоначальной форме и размеру, а принимает другую форму и размер: материал становится необратимо деформированным. предел упругости — это значение напряжения, выше которого материал перестает вести себя упруго, а становится необратимо деформированным.

Наше восприятие эластичного материала зависит как от его предела упругости, так и от его модуля упругости. Например, все каучуки характеризуются низким модулем упругости и высоким пределом упругости; следовательно, их легко растянуть, и растяжение заметно велико. Среди материалов с одинаковыми пределами упругости наиболее эластичным является материал с наименьшим модулем упругости.

Когда нагрузка увеличивается от нуля, результирующее напряжение прямо пропорционально деформации, как показано на (Рисунок), но только тогда, когда напряжение не превышает некоторого предельного значения. Для значений напряжения в пределах этого линейного предела мы можем описать упругое поведение по аналогии с законом Гука для пружины. Согласно закону Гука степень растяжения пружины под действием приложенной силы прямо пропорциональна величине этой силы. И наоборот, сила реакции пружины на приложенное растяжение прямо пропорционально растяжению. Точно так же деформация материала под нагрузкой прямо пропорциональна нагрузке, и, наоборот, возникающее напряжение прямо пропорционально деформации. Предел линейности (или предел пропорциональности ) — это максимальное значение напряжения, выше которого напряжение перестает быть пропорциональным деформации. За пределом линейности связь между напряжением и деформацией перестает быть линейной. Когда напряжение превышает предел линейности, но все еще находится в пределах предела эластичности, поведение остается упругим, но связь между напряжением и деформацией становится нелинейной.

При напряжениях, превышающих предел упругости, материал демонстрирует пластическое поведение . Это означает, что материал необратимо деформируется и не возвращается к своей первоначальной форме и размеру даже при снятии нагрузки. Когда напряжение постепенно превышает предел упругости, материал подвергается пластической деформации. Резиноподобные материалы показывают увеличение напряжения с увеличением деформации, что означает, что их становится труднее растянуть, и, в конце концов, они достигают точки излома, где они ломаются. Пластичные материалы, такие как металлы, демонстрируют постепенное снижение напряжения с увеличением деформации, что означает, что они легче деформируются, когда значения напряжения-деформации приближаются к пределу прочности. Микроскопические механизмы, ответственные за пластичность материалов, различны для разных материалов.

Мы можем изобразить взаимосвязь между напряжением и деформацией на диаграмме напряжения-деформации . Каждый материал имеет свою характеристическую кривую деформации. Типичная диаграмма деформации пластичного металла под нагрузкой представлена ​​на (рис. ). На этом рисунке деформация представляет собой частичное удлинение (не в масштабе). Когда нагрузка постепенно увеличивается, линейное поведение (красная линия), которое начинается в точке без нагрузки (начало координат), заканчивается на пределе линейности в точке H . Для дальнейшего увеличения нагрузки после точки H зависимость напряжение-деформация является нелинейной, но все же упругой. На рисунке эта нелинейная область видна между точками H и E . Все большие нагрузки доводят напряжение до предела упругости E , где упругое поведение заканчивается и начинается пластическая деформация. За пределом эластичности, когда нагрузка снимается, например, при P материал релаксирует, принимая новую форму и размер вдоль зеленой линии. Это означает, что материал постоянно деформируется и не возвращается к своей первоначальной форме и размеру, когда напряжение становится равным нулю.

Материал подвергается пластической деформации при нагрузках, достаточно больших, чтобы вызвать напряжение, превышающее предел эластичности в E . Материал продолжает пластически деформироваться до тех пор, пока напряжение не достигнет точки разрушения (точки разрыва). За пределами точки разрушения у нас больше нет ни одного образца материала, поэтому диаграмма заканчивается в точке разрушения. Для полноты этого качественного описания следует сказать, что пределы линейности, упругости и пластичности обозначают диапазон значений, а не одну острую точку.

Рисунок 12.25 Типичная диаграмма напряжения-деформации для металла под нагрузкой: График заканчивается в точке разрушения. Стрелки показывают направление изменений при постоянно возрастающей нагрузке. Точки Н и Е — пределы линейности и эластичности соответственно. Между точками H и E поведение нелинейно. Зеленая линия, начинающаяся в точке P, показывает реакцию металла при снятии нагрузки. Остаточная деформация имеет значение деформации в точке, где зеленая линия пересекает горизонтальную ось. 9{4}\,\text{lb}, [/latex], а разрывная нагрузка для стального стержня примерно в девять раз выше.

Резюме

  • Предмет или материал является упругим, если он возвращается к своей первоначальной форме и размеру, когда напряжение исчезает. При упругих деформациях со значениями напряжения ниже предела пропорциональности напряжение пропорционально деформации. Когда напряжение выходит за предел пропорциональности, деформация остается упругой, но нелинейной вплоть до предела упругости.
  • Объект или материал имеет пластическое поведение, когда напряжение превышает предел упругости. В пластической области объект или материал не возвращается к своим первоначальным размерам или форме после исчезновения напряжения, а приобретает постоянную деформацию. Пластическое поведение заканчивается в точке разрыва.

Ключевые уравнения

«>
Первое условие равновесия [латекс] \sum _{k}{\overset{\to }{F}}_{k}=\overset{\to }{0} [/latex]
Второе условие равновесия [латекс] \sum _{k}{\overset{\to }{\tau}}_{k}\,=\overset{\to}}{0} [/latex]
Линейная зависимость между

напряжение и деформация

 [латекс] \text{напряжение}=\text{(модуль упругости)}\,×\,\text{деформация} [/латекс]
Модуль Юнга [латекс] Y = \ frac {\ text {напряжение растяжения}} {\ text {деформация растяжения}} = \ frac {{F} _ {\ perp}} {A} \, \ frac {{L} _ { 0}}{\text{Δ}L} [/латекс]
Объемный модуль [латекс] B=\frac{\text{объемное напряжение}}{\text{объемное напряжение}}=\text{-}\text{Δ}p\frac{{V}_{0}}{\text {Δ}V} [/латекс]
Модуль сдвига [латекс] S = \ frac {\ text {напряжение сдвига}} {\ text {деформация сдвига}} = \ frac {{F} _ {\ parallel}} {A} \, \ frac {{L} _ { 0}}{\text{Δ}x} [/латекс]

Концептуальные вопросы

Примечание: Если не указано иное, вес проводов, стержней и других элементов считается незначительным. {2}\текст{?} [/латекс]

Один конец вертикальной металлической проволоки длиной 2,0 м и диаметром 1,0 мм прикрепляют к потолку, а другой конец прикрепляют к чаше с грузом 5,0 Н, как показано ниже. Положение указателя перед панорамой 4.000 см. Затем к области панорамирования добавляются различные веса, а положение указателя записывается в показанную таблицу. Постройте график зависимости напряжения от деформации для этой проволоки, затем используйте полученную кривую для определения модуля Юнга и предела пропорциональности металла. Какой металл это скорее всего?

9{2}\text{?} [/latex]

Дополнительные задачи

Коэффициент статического трения между резиновым ластиком карандаша и столешницей равен [латекс] {\mu }_{s}=0,80. [/latex] Если сила [латекс] \overset{\to }{F} [/латекс] приложена вдоль оси карандаша, как показано ниже, под каким минимальным углом может стоять карандаш, не скользя? Не обращайте внимания на вес карандаша.

Показать решение

Карандаш упирается в угол, как показано ниже. Заостренный конец карандаша касается гладкой вертикальной поверхности, а конец ластика касается шероховатого горизонтального пола. Коэффициент статического трения между ластиком и полом составляет [латекс] {\mu }_{s}=0,80. [/latex] Центр масс карандаша расположен 90,0 см от кончика ластика и 11,0 см от кончика грифеля карандаша. Найдите минимальный угол [латекс]\тета[/латекс], при котором карандаш не скользит.

Однородная доска длиной 4,0 м и весом 200,0 Н упирается в угол стены, как показано ниже. В месте соединения доски с углом трения нет. а) Найдите силы, с которыми угол и пол действуют на доску. б) Каков минимальный коэффициент трения покоя между полом и доской, чтобы доска не скользила? 9{2}. [/latex] Если к каждому концу комбинации приложено растягивающее усилие в 10 000 Н, найдите: (а) напряжение в каждом стержне; б) деформации в каждом стержне; и (c) удлинение каждого стержня.

Показать решение

Два стержня, один из меди, а другой из стали, имеют одинаковые размеры. Если при некотором напряжении медный стержень растянется на 0,15 мм, то на сколько растянется стальной стержень при таком же напряжении?

Задачи-задачи

Горизонтальная сила [латекс] \overset{\to }{F} [/латекс] приложена к однородной сфере в направлении точно к центру сферы, как показано ниже. Найдите модуль этой силы, чтобы шар оставался в статическом равновесии. Чему равна сила трения наклона о шар?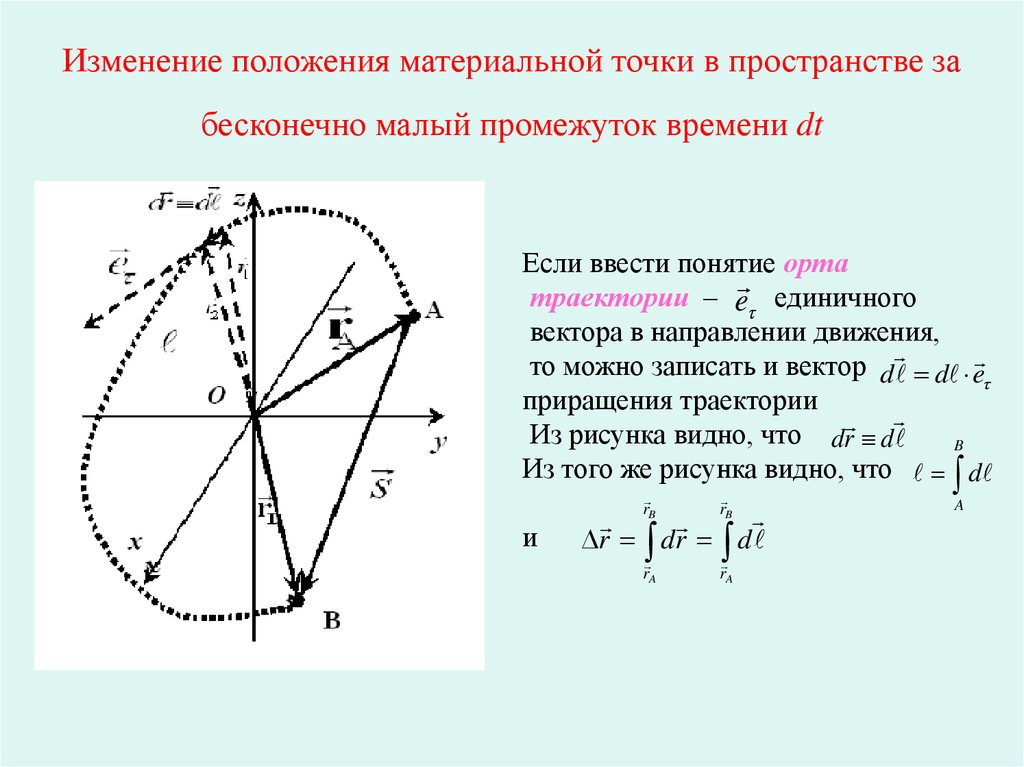

Показать решение

Когда двигатель установлен на поворотной опоре, показанной ниже, его вес можно использовать для сохранения натяжения приводного ремня. Когда двигатель не работает, натяжения [латекс] {T}_{1} [/латекс] и [латекс] {T}_{2} [/латекс] равны. Суммарная масса платформы и двигателя 100,0 кг, а диаметр шкива приводного ремня [латекс] 16,0\,\text{см.} [/латекс] при выключенном двигателе найти: а) натяжение ремня и (b) усилие на опоре шарнирной платформы в точке С . Предположим, что центр масс двигателя и платформы находится в центре двигателя.

Два колеса A и B с грузами w и 2 w соответственно соединены однородным стержнем с весом w /2, как показано ниже. Колеса могут свободно катиться по наклонным поверхностям. Определить угол, который образует стержень с горизонтом, когда система находится в равновесии. Подсказка: На стержень действуют пять сил, а именно два веса колес, две силы нормальной реакции в точках контакта колес с клином и вес стержня.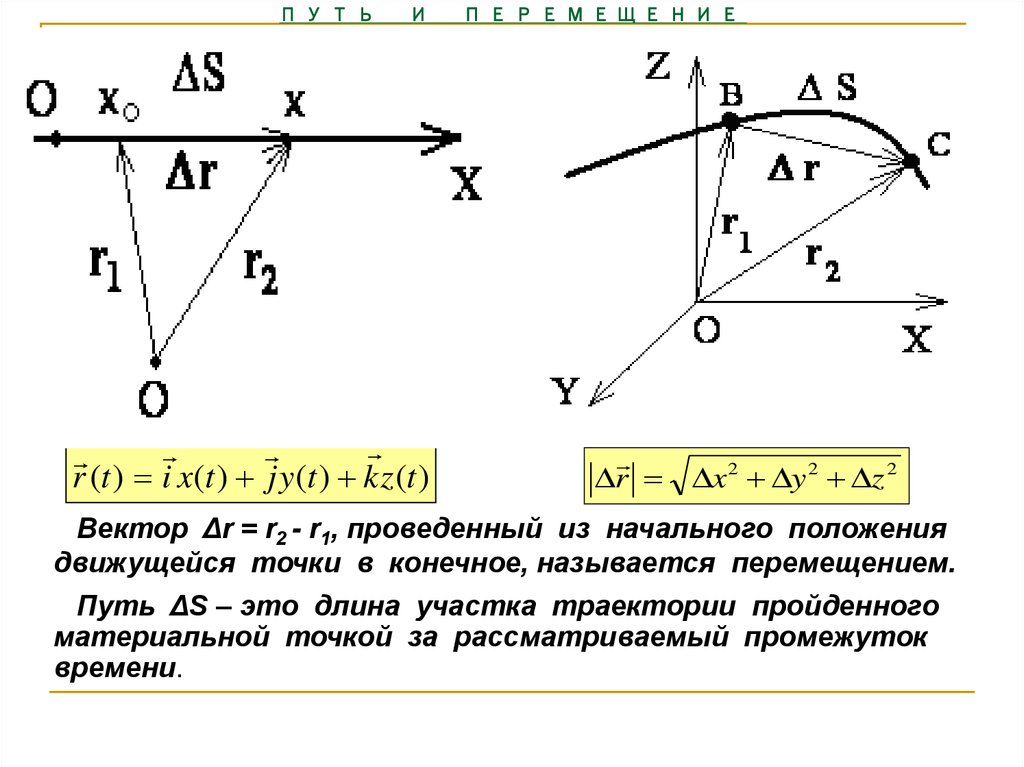

Показать решение

Грузы постепенно добавляются к чаше до тех пор, пока колесо массой M и радиусом R не проедет над препятствием высотой d , как показано ниже. Какова минимальная масса гирь плюс чаша, необходимая для этого?

Чтобы поднять лопату земли, садовник нажимает на конец лопаты вниз и тянет вверх на расстоянии [латекс] {l}_{2} [/латекс] от конца, как показано ниже. Вес лопаты составляет [латекс] m\overset{\to }{g} [/latex] и действует в точке приложения [латекс] {\overset{\to }{F}}_{2}. [/latex] Рассчитайте величины сил [латекс] {\ overset {\ to {F}}_ {1} [/latex] и [латекс] {\ overset {\ to {F}} _ {2 } [/latex] как функции [latex] {l}_{1}, [/latex] [latex] {l}_{2}, [/latex] мг , а вес Вт груза. Почему ваши ответы не зависят от угла [латекс]\тета[/латекс], который лопата образует с горизонтом?

Показать решение

Однородный стержень длиной 2R и массой M прикреплен к небольшой втулке C и опирается на цилиндрическую поверхность радиусом R , как показано ниже.

Related Posts

Leave A Comment

Добавленная загрузка (включая поддон)

(Н)

 Показание шкалы

(см)

0 4. 000
15 4.036
25 4.073
35 4.109
45 4.146
55 4.181
65 4.221