Задание 1. Брошены 2 игральные кости. Найти вероятность того, что сумма очков на выпавших гранях равна 7.
Ответ:
Задание 2. Брошены 2 игральные кости. Найти вероятности следующих событий: a) сумма выпавших очков равна 8, а разность –4; b) сумма выпавших очков равна 8, если известно, что их разность равна 4.
Ответ: a) b) .
Задание 3. Брошены две игральные кости. Найти вероятности следующих событий: а) сумма выпавших очков равна семи; б) сумма выпавших очков равна пяти, а произведение – четырем.
Ответ: a) b) .
Задание 4. Монета брошена два раза. Найти вероятность того, что хотя бы один раз появится «герб».
Ответ: .
Задание
5. В коробке
шесть одинаковых, занумерованных
кубиков. Наудачу по одному извлекают
все кубики. Найти вероятность того, что
номера извлеченных кубиков появится
в возрастающем порядке.
Ответ:
Задание 6. В урне 15 шаров: 5 белых, 10 черных. Какова вероятность вынуть из урны синий шар?
Ответ:0.
Задание 7. В урне 12 шаров: 3 белых, 4 черных, 5 красных. Какова вероятность вынуть из урны черный шар.
Ответ:
Пример 4. В ящике 10 одинаковых деталей, помеченных номерами
1, 2, …, 10. Наудачу извлечены шесть деталей. Найти вероятность того, что среди извлеченных деталей окажутся: а) деталь № 1; б) детали № 1 и № 2.
Решение. А) общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь шесть деталей из десяти, т.е.
Найдем
число исходов, благоприятствующих
интересующему нас событию: среди
отобранных шести деталей есть деталь
№ 1 и, следовательно, остальные пять
деталей имеют другие номера. Число таких
исходов, очевидно, равно числу способов,
которыми можно отобрать пять деталей
из оставшихся девяти, т.е. .
Число таких
исходов, очевидно, равно числу способов,
которыми можно отобрать пять деталей
из оставшихся девяти, т.е. .
Искомая вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу возможных элементарных исходов: .
Б) Число исходов, благоприятствующих интересующему нас событию (среди отобранных деталей есть детали № 1 и « 2, следовательно, четыре детали имеют другие номера), равно числу способов, которыми можно извлечь четыре детали из оставшихся восьми, т.е . Искомая вероятность Р= .
Пример 5. В урне 10 шаров: 6 белых и 4 черных. Вынули 2 шара. Какова вероятность, что оба шара белые..
Решение. Общее число случаев: .
Число благоприятных случаев: , .
Ответ: .
Задание 1.В
ящике имеется 15 деталей, среди которых
10 окрашенных. Сборщик наудачу извлекает
три детали.
Ответ: .
Задание 2. В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная.
Ответ: .
Задание 3. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены четыре детали. Найти вероятность того, что среди извлеченных деталей: а) нет бракованных; б) нет годных.
Ответ:а) 0.65; б)0.00005.
Задание 4.Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
Ответ: .
Алгебра Решение типичных задач по теории вероятности. Задача 6
Материалы к уроку
35-52. Задачи.doc
74 KBСкачать
Конспект урока
Задача 1
Вспомним, что вероятность события равна отношению числа благоприятных исходов к числу всевозможных исходов
Задача. Брошена игральная кость. Какова вероятность того, что выпадет четное число очков?
1,3,5 – нечетные числа, 2,4,6 – четные. Число возможных исходов при бросании игральной кости – 6, число благоприятных исходов – 3 (т.е. выпадение двойки, четверки или шестерки). Таким образом, вероятность выпадения четного числа очков равна 3:6 = 1/2 или 0,5.
Ответ: 0,5.
Задача 2
Задача. Брошена игральная кость. Какова вероятность того, что выпадет число меньше 4?
Другими словами – какова вероятность того, что выпадете либо 1, либо 2, либо 3.
Число возможных исходов – 6, число благоприятных исходов – 3 (т.е. выпадение 1,2 или 3). Таким образом, вероятность выпадения числа меньше 4 равна 3:6 = 0,5.
Ответ: 0,5.
Задача 3
Задача. В ящике 6 белых и 4 черных шара. Какова вероятность того, что первый наудачу выбранный шар окажется белым?
Всего 10 шаров, значит число возможных исходов – 10. Число благоприятных исходов – 6, потому что в ящике 6 белых шаров. Вероятность того, что первый выбранный шар окажется белым – 6:10 = 0,6.
Ответ: 0,6.
Задача 4
Задача: Набирая номер телефона, абонент забыл последнюю цифру. Какова вероятность того, что он правильно дозвонится, набрав последнюю цифру наугад?
Итак, абоненту нужно выбрать одну цифру из 10, т.е. число возможных исходов – 10. Число благоприятных исходов – 1, потому что верной может быть только одна цифра. Вероятность того, что абонент правильно дозвонится, равна 1:10=0,1.
Ответ: 0,1.
Задача 5
Задача: Ученика попросили назвать число от 1 до 100. Какова вероятность того, что он назовет число 56?
Число возможных исходов – 100, т.е. 100 чисел. Верно названное число – одно, это 56. Значит, благоприятный исход один. Вероятность того, что ученик назовет число 56, будет 1:100=0,01.
Ответ: 0,01.
Задача 6
Задача:
Число возможных исходов – 100. Чисел, кратных пяти – 20 (5,10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90,95,100), т.е. число благоприятных исходов – 20. Вероятность, что ученик назовет число, кратное пяти равна 20:100=0,2.
Ответ: 0,2.
Задача 7
Задача: Ученика попросили назвать число от 1 до 100. Какова вероятность того, что он назовет число, принадлежащее промежутку от 5 до 20 включительно?
Число возможных исходов – 100.
Ответ: 0,16.
Задача 8
Задача: В фирме такси в данный момент свободно 10 машин: 5 черных, 1 желтая и 4 зеленых. На вызов выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
Возможное число исходов – 10, потому что всего 10 машин. Число благоприятных исходов – 1, потому что желтая машина одна. Искомая вероятность 1:10=0,1.
Ответ: 0,1.
Задача 9
Задача: Валя выбирает трехзначное число. Найдите вероятность того, что оно делится на 51.
Число возможных исходов – это количество трехзначных чисел, их существует от 100 до 999. Быстрее всего их можно посчитать так: 1000 – 1 – 99 = 900, т.е. исключаем 1000 и числа от 1 до 99. Число всевозможных исходов – 900.
Быстрее всего их можно посчитать так: 1000 – 1 – 99 = 900, т.е. исключаем 1000 и числа от 1 до 99. Число всевозможных исходов – 900.
Найдем, сколько трехзначных чисел делится на 51. Если мы поделим 999 (самое большое трехзначное число) на 51, то получим приблизительно 19,58, т.е. в 999 вмещается 19 чисел, кратных 51. Но среди них есть и само число 51, которое не является трехзначным, а значит трехзначных чисел, делящихся на 51 – 18. Поэтому число благоприятных исходов – 18.
Вероятность того, что выбранное число делится на 51 — 18:900=0,02
Ответ: 0,02.
Задача 10
Задача: При двукратном бросании игрального кубика в сумме выпало 6 очков. Найдите вероятность того, что первый раз выпало меньше 3 очков.
Сумму в 6 очков можно получить следующими способами:
1+5, 2+4, 3+3, 4+2, 5+1,
т.е. всего их 5. Это и есть число возможных исходов. Из представленных вариантов видно, что менее 3 очков при первом броске может выпасть только в двух случаях: 1+5 и 2+4.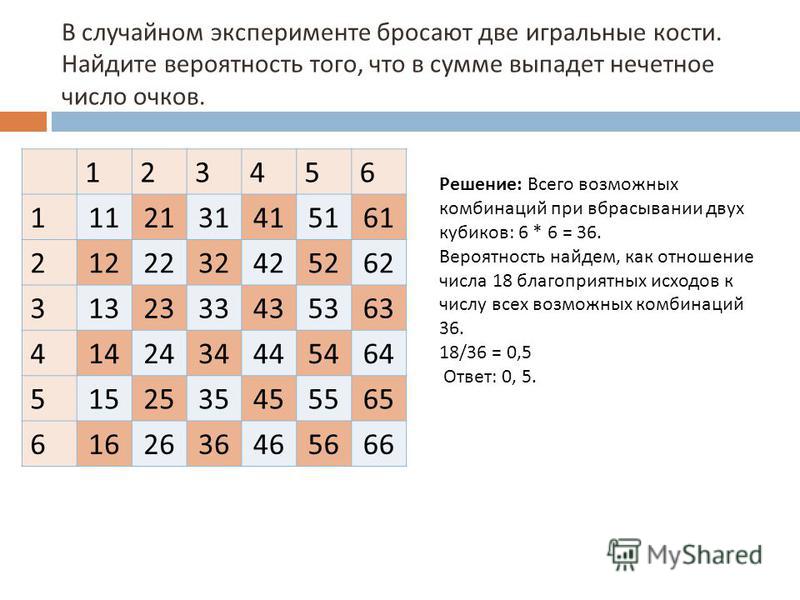
Ответ: 0,4.
Задача 11
Задача: Монету бросают трижды. Найдите вероятность того, что первые два броска окончатся одинаково.
Найдем число возможных исходов, для этого переберем все варианты бросков. В подобных задачах лучше всего составлять таблицу – так считать гораздо удобнее.
|
|
1-й бросок |
2-й бросок |
3-й бросок |
|
1 |
орел |
орел |
орел |
|
2 |
орел |
орел |
решка |
|
3 |
орел |
решка |
решка |
|
4 |
орел |
решка |
орел |
|
5 |
решка |
решка |
решка |
|
6 |
решка |
решка |
орел |
|
7 |
решка |
орел |
орел |
|
8 |
решка |
орел |
решка |
Итак, в данной таблице отражены все возможные варианты бросков. Всего их 8, поэтому возможных исходов 8. Первые два броска одинаково могут окончиться в 4 случаях: это случаи 1,2 и 5,6, т.е. благоприятных исходов 4. Поэтому искомая вероятность равна 4:8 = 0,5.
Всего их 8, поэтому возможных исходов 8. Первые два броска одинаково могут окончиться в 4 случаях: это случаи 1,2 и 5,6, т.е. благоприятных исходов 4. Поэтому искомая вероятность равна 4:8 = 0,5.
Ответ: 0,5.
Задача 12
Задача: В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
В данной задаче составляется таблица всех возможных вариантов бросков:
|
|
1-й бросок |
2-й бросок |
3-й бросок |
|
1 |
орел |
орел |
орел |
|
2 |
орел |
орел |
решка |
|
3 |
орел |
решка |
решка |
|
4 |
орел |
решка |
орел |
|
5 |
решка |
решка |
решка |
|
6 |
решка |
решка |
орел |
|
7 |
решка |
орел |
орел |
|
8 |
решка |
орел |
решка |
По данной таблице видно, что орел не выпадет ни разу только в одном варианте из восьми – это пятый вариант.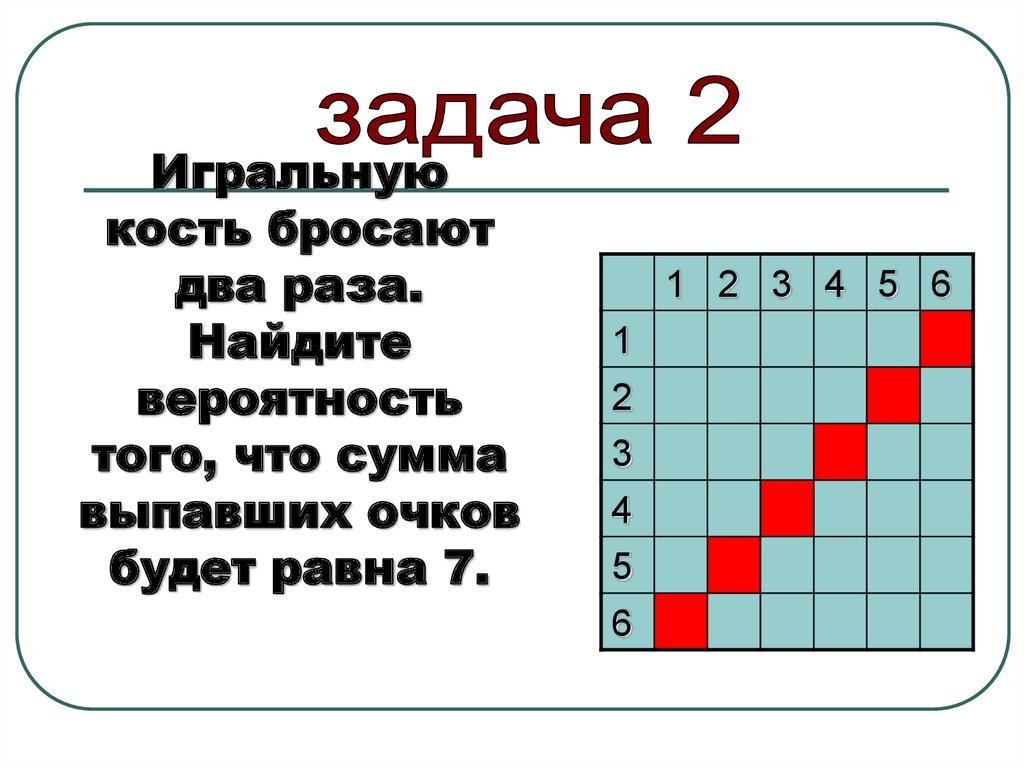 Поэтому возможных исходов 8, благоприятных исходов – 1. Искомая вероятность 1:8 = 0,125.
Поэтому возможных исходов 8, благоприятных исходов – 1. Искомая вероятность 1:8 = 0,125.
Ответ: 0,125.
Задача 13
Задача: В среднем на 150 карманных фонариков приходится три неисправных. Какова вероятность того, что Вы купите исправный фонарик?
Количество возможных исходов – 150. Количество благоприятных исходов: 150-3=147, т.е. на 150 приходится 147 исправных фонариков. Вероятность купить исправный фонарик – 147:150=0,98.
Ответ: 0,98.
Задача 14
Задача: В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
В подобных задачах для удобства следует составить таблицу сумм для двух костей, т.е. все варианты сумм, которые могут выпасть. Вот данная таблица:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
По ней мы видим, что при первом броске может выпасть 1 и при втором 1, в сумме – 2; при первом, например, 5, при втором – 4, в сумме – 9, и т. д. Таким образом, всего исходов 36 (6х6=36), благоприятных исходов – 5, вот они 5 восьмерок. Вероятность того, что в сумме выпадет 8 очков, равна 5:36 0,14.
д. Таким образом, всего исходов 36 (6х6=36), благоприятных исходов – 5, вот они 5 восьмерок. Вероятность того, что в сумме выпадет 8 очков, равна 5:36 0,14.
Ответ: 0,14.
Задача 15
Задача: В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные – из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Давайте представим, что все спортсменки одновременно подошли к шляпе, и вытянули из нее бумажки с номерами. Кому-то из них достанется первый номер. Вероятность того, что его вытянет китайская спортсменка, равна 5 к 20. Т.е. всего спортсменок 20, спортсменок из Китая 5, потому что 8 из России, 7 из США – в сумме 15, 20-15=5. Поэтому вероятность того, что первый номер вытянет китайская спортсменка, равна 5:20=0,25.
Ответ: 0,25.
Задача 16
Задача: Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений – по одному от каждой страны. В первый день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьевкой. Какова вероятность того, что представителя России состоится в третий день конкурса?
Всего заявлено 80 выступлений – по одному от каждой страны. В первый день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьевкой. Какова вероятность того, что представителя России состоится в третий день конкурса?
Выясним, как распределятся выступления по дням. Первый день – 8 выступлений, оставшиеся 4 дня – по 18 выступлений в день (потому что всего 80, в первый – 8, остается 72. 72 делим на оставшиеся 4 дня – получаем 18). Это значит, что возможных исходов 80, а благоприятных исходов – 18. Т.е. выступление представителя России состоится в третий день конкурса с вероятностью 18:80=0,225.
Ответ: 0,225.
Задача 17
Задача: На семинар приехали 3 ученых из Норвегии, 3 из России и 4 из Испании. Порядок докладов определяется жеребьевкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Восьмым может оказаться любой ученый, значит возможных исходов 10, потому что всего ученых 10. Из России приехало трое, значит благоприятных исходов 3. Вероятность того, что восьмым окажется доклад ученого из России 3:10=0,3.
Из России приехало трое, значит благоприятных исходов 3. Вероятность того, что восьмым окажется доклад ученого из России 3:10=0,3.
Ответ: 0,3.
Задача 18
Задача: Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России.
В данном случае нужно поставить себя на место Руслана Орлова. Он будет играть с кем-то из 25 спортсменов. На чемпионат приехал Руслан и еще 25 спортсменов, значит возможных исходов 25. Из них осталось 9 спортсменов из России, т.е. всего 10, за исключением Руслана – 9. Поэтому 9 – это и есть число благоприятных исходов. Вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России 9:25=0,36.
Ответ: 0,36.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
Какова вероятность того, что при бросании двух игральных костей в сумме выпадет 7?
Вероятность означает возможность. Он указывает, насколько вероятно событие, которое вот-вот произойдет. Вероятность события может существовать только между 0 и 1, где 0 указывает на то, что событие не произойдет, т.е. невозможность, а 1 указывает, что оно обязательно произойдет, т.е. определенность.
Чем выше или ниже вероятность события, тем больше вероятность того, что событие произойдет или не произойдет соответственно.
Например – Один раз подбрасывается беспристрастная монета. Таким образом, общее количество исходов может быть только 2, то есть либо «орел», либо «решка». Вероятность обоих исходов равна, т.е. 50% или 1/2.
Таким образом, общее количество исходов может быть только 2, то есть либо «орел», либо «решка». Вероятность обоих исходов равна, т.е. 50% или 1/2.
Значит, вероятность события равна Благоприятных исходов/Общее количество исходов . Он обозначается скобками, т. е. P (событие).
P(Событие) = N(Благоприятные исходы) / N (Всего исходы)
Примечание: Если вероятность наступления события A равна 1/3, то вероятность того, что событие не произойдет А равно 1-P(A) т. е. 1- (1/3) = 2/3
Что такое Sample Space?
Все возможные исходы события называются пространствами образцов.
Примеры-
Типы событий
- Шестигранная игральная кость бросается один раз. Таким образом, общее количество результатов может быть равно 6, и
Пространство выборки будет [1, 2, 3, 4, 5, 6]- Подбрасывается беспристрастная монета.
Таким образом, общее количество результатов может быть равно 2, и
Пространство выборки будет равно [Голова, Хвост]- Если два игральных кубика бросить вместе, то общее число результатов будет 36 и 1, 6)
(2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)
(3, 1) (3, 2) (3, 3 ) (3, 4) (3, 5) (3, 6)
(4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)
(5 , 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)
(6, 1) (6, 2) (6, 3) (6, 4) ( 6, 5) (6, 6) ]
Независимые события: Если два события (A и B) независимы, то их вероятность будет равна
P(A и B) = P (A ∩ B) = P(A).P(B), т. е. P(A) * P(B)
Пример: Если подбрасываются две монеты, то вероятность того, что обе выпадут решкой, равна 1/2 * 1/2 = 1/4
Взаимоисключающие события:
- Если событие A и событие B не могут произойти одновременно, тогда они называются взаимоисключающими событиями.

- Если два события являются взаимоисключающими, то вероятность того, что они произойдут, обозначается как P (A ∩ B) и
P (A и B) = P (A ∩ B) = 0 - Если два события являются взаимоисключающими, то вероятность каждого из них обозначается как P (A ∪ B)
P (A или B) = P ( A ∪ b)
= p (a) + p (b) — p (a ∩ b)
= p (a) + p (b) — 0
= p (a) + p (b)
Пример: Вероятность того, что на шестигранном кубике выпадет 2 или 3, равна P (2 или 3) = P (2) + P (3) = 1/6 + 1/6 = 1/3
Не взаимоисключающие события: Если события не исключают друг друга, то
P (A или B) = P (A ∪ B) = P (A) + P (B) − P (A и B)
Что такое условная вероятность ?
Для вероятности некоторого события A задано появление некоторого другого события B. Записывается как P (A ∣ B)
P (A ∣ B) = P (A ∩ B) / P (B)
Пример- В мешочке 3 черных шара и 2 желтых шаров (всего 5 шаров), вероятность взятия черного шара равна 3/5, а для взятия второго шара вероятность того, что это будет либо черный шар, либо желтый шар, зависит от ранее вынутого шара. Так как, если бы был взят черный шар, то вероятность снова взять черный шар была бы 1/4, так как осталось бы только 2 черных и 2 желтых шара, если бы ранее был взят желтый шар, вероятность взятия черный шар будет 3/4.
Так как, если бы был взят черный шар, то вероятность снова взять черный шар была бы 1/4, так как осталось бы только 2 черных и 2 желтых шара, если бы ранее был взят желтый шар, вероятность взятия черный шар будет 3/4.
Какова вероятность выпадения 7 при бросании двух игральных костей?
Решение:
Когда два игральных кубика бросают вместе, то общее количество результатов равно 36, а пространство выборки равно
[ (1, 1) (1, 2) (1, 3) (1, 4) (1, 5 ) (1, 6)
(2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)
(3, 1) (3, 2) (3 , 3) (3, 4) (3, 5) (3, 6)
(4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)
(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)
(6, 1) (6, 2) (6, 3) (6, 4) ) (6, 5) (6, 6) ]Итак, пары с суммой 7 равны (1, 6) (2, 5) (3, 4) (4, 3) (5, 2) (6, 1) т.е. всего 6 пар
Всего результатов = 36
Похожие вопросы
Вопрос 1: Какова вероятность того, что на обеих костях выпадет 1?
Решение:
Когда два игральных кубика бросают вместе, то общее количество результатов равно 36, а пространство выборки равно
[ (1,1) (1,2) (1,3) (1,4) (1, 5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) ( 3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6, 4) (6,5) (6,6) ]Таким образом, пары с обеими единицами равны (1,1), т.
е. только 1 пара
Общие результаты = 36
Полезные результаты = 6Вероятность получить пару из 1 = благоприятные результаты / общие результаты
= 1 /36Итак, p (1,1) = 1/36.
Вопрос 2: Какова вероятность получить сумму 4?
Решение:
Когда два игральных кубика бросают вместе, то общее количество результатов равно 36, а пространство выборки равно
[ (1,1) (1,2) (1,3) (1,4) (1 ,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3, 4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) ( 5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) ]Итак, пары с суммой 4 равны (1,3) (2,2) (3,1) то есть всего 3 пары
Всего исходов = 36
Благоприятных исходов = 3Вероятность получения сумма 4 = благоприятные исходы / общее число исходов0003
Итак, P(сумма 3) = 1/12.

Вопрос 3: Какова вероятность получить сумму 5?
Решение:
При бросании двух игральных костей общее количество результатов равно 36, а пространство выборки равно
[ (1,1) (1,2) (1,3) (1,4) (1, 5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) ( 3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) ]Итак, пары с суммой 5 равны (1,4) (2,3 ) (3,2) (4,1), т. Е. Всего 4 пары
Общее количество результатов = 36
Благоприятные результаты = 4Вероятность получения суммы 5 = благоприятных результатов / общие результаты
= 4 /36 = 1/9Итак, P(5) = 1/9.
Калькулятор вероятности игры в кости
Создано Wojciech Sas, PhD
Рецензировано Bogna Szyk и Jack Bowater
Последнее обновление: 13 февраля 2023 г.
- Многогранные кости
- Как рассчитать вероятность броска костей?
- Когда использовать калькулятор вероятности игры в кости?
- Играть или пасовать? — Давай сыграем в игру!
- Часто задаваемые вопросы
Калькулятор вероятности броска кости является отличным инструментом, если вы хотите оценить вероятность броска броска во множестве вариантов. В набор входит множество различных многогранных кубиков, так что вы можете исследовать вероятность выпадения 20-гранного кубика и обычного кубического кубика.
Итак, просто оценивайте шансы и играйте! Вы также найдете краткие описания каждой опции в тексте.
🔎 У тебя нет физических кубиков? Нет проблем — попробуйте наш калькулятор игры в кости!
Многогранные игральные кости
Все знают, что такое обычный шестигранный кубик, и, скорее всего, многие из вас уже сыграли тысячи игр, где использовалась одна (или более) t Но знаете ли вы, что существует различных типов штампа ? Из бесчисленных возможностей самые популярные кости включены в Набор игральных костей Dungeons & Dragons , который содержит семь различных многогранных игральных костей:
- Четырехгранные игральные кости , также известные как тетраэдр — каждая грань представляет собой равносторонний треугольник;
- 6-гранный кубик , классический куб — каждая грань квадратная;
- 8-гранная игральная кость , также известная как октаэдр — каждая грань представляет собой равносторонний треугольник;
- 10-гранный кубик , также известный как пятиугольный трапецоэдр — каждая грань — воздушный змей;
- 12-гранный кубик , также известный как додекаэдр — каждая грань представляет собой правильный пятиугольник; и
- 20-гранная игральная кость , также известная как икосаэдр — каждая грань представляет собой равносторонний треугольник.

💡 Вы можете отточить свою стратегию D&D, используя калькулятор покупки очков Omni 5e.
Не волнуйтесь, мы учитываем каждый из этих кубиков в нашем калькуляторе вероятности. Вы можете выбрать то, что вам нравится, и, например, притвориться, что бросаете сразу пять 20-гранных кубиков!
Как рассчитать вероятность броска костей?
Что ж, вопрос сложнее, чем кажется на первый взгляд, но вскоре вы убедитесь, что ответ не так уж и страшен! Все дело в математике и статистике.
Прежде всего, мы должны определить какую вероятность броска костей мы хотим найти . Мы можем выделить несколько, которые вы можете увидеть в этом калькуляторе вероятности игры в кости.
Прежде чем приступать к каким-либо вычислениям, давайте определим некоторые переменные, которые мы будем использовать в формулах. n – количество игральных костей, s – количество отдельных граней кости, p – вероятность выпадения любого значения с кости, а P – общая вероятность решения задачи. Существует простое соотношение – p = 1/s , поэтому вероятность выпадения 7 на 10-гранном кубике вдвое больше, чем на 20-гранном кубике.
Существует простое соотношение – p = 1/s , поэтому вероятность выпадения 7 на 10-гранном кубике вдвое больше, чем на 20-гранном кубике.
Вероятность выпадения одного и того же значения на каждом кубике – при этом шанс выпадения определенного значения на одном кубике равен p , нам нужно только умножить эту вероятность на саму себя столько раз, сколько игральных костей. Другими словами, вероятность P равна p в степени n , или P = pⁿ = (1/s)ⁿ . Если мы рассмотрим три 20-гранных игральных кубика, вероятность выпадения 15 на каждом из них составит: P = (1/20)³ = 0,000125 (или P = 1,25·10⁻⁴ в экспоненциальной записи). И если вы заинтересованы в броске набора из любых одинаковых значений, просто умножьте результат на общее количество граней кости: Р = 0,000125 · 20 = 0,0025 .

Вероятность выпадения всех значений, равных или превышающих y – задача аналогична предыдущей, но на этот раз p равна 1/с , умноженная на все возможности, удовлетворяющие начальному условию . Например, допустим, у нас есть обычный кубик и y = 3 . Мы хотим, чтобы прокатанное значение было либо 6 , 5 , 4 , либо 3 . Тогда переменная p равна 4 · 1/6 = 2/3 , а окончательная вероятность равна P = (2/3)ⁿ .
Вероятность выпадения всех значений, равных или меньших y — этот вариант почти такой же, как и предыдущий, но на этот раз нас интересуют только числа, равные или меньшие нашей цели. Если мы возьмем идентичные условия ( s=6 , y=3 ) и применим их в этом примере, мы увидим, что значения 1 , 2 , & 3 удовлетворяют правилам, и вероятность равна: P = (3 · 1/6)ⁿ = (1/2)ⁿ .

Вероятность выпадения ровно X одинаковых значений (равных y ) из набора — представьте, что у вас есть набор из семи 12-гранных игральных костей, и вы хотите узнать вероятность выпадения ровно двух 9 с . Это как-то отличается от того, что было раньше, потому что только часть всего набора должна соответствовать условиям . Здесь на помощь приходит биномиальная вероятность. Формула биномиальной вероятности:
P(X=r) = nCr · pʳ · (1-p)ⁿ⁻ʳ ,
, где r — количество успехов, а nCr — количество комбинаций (также известное как « n выбрать r »).
В нашем примере мы имеем n = 7 , p = 1/12 , r = 2 , nCr = 21 , поэтому окончательный результат: P(X=2) = 21 · (1 /12)² · (11/12)⁵ = 0,09439 или P(X=2) = 9,439% в процентах.

🙋 Более подробную информацию по этой теме вы можете найти в нашем калькуляторе биномиального распределения.
Вероятность выпадения как минимум X одинаковых значений (равных y ) из набора — задача очень похожа на предыдущую, но на этот раз результатом является сумма вероятностей для X =2,3,4,5,6,7 . Переходя к числам, мы имеем: P = P(X=2) + P(X=3) + P(X=4) + P(X=5) + P(X=6) + P(X=7) = 0,11006 = 11,006% . Как и следовало ожидать, результат немного выше. Иногда точная формулировка проблемы увеличивает ваши шансы на успех.
Вероятность выпадения точной суммы r из множества n s двугранных игральных костей — общая формула довольно сложная:
P(r,n,s)=1sn∑k=0⌊(r−n)/s⌋(−1)k(nk)(r−s⋅k−1n−1)\scriptsize \начать{разделить} P (r, n, s) = \ frac {1} {s ^ n} \ sum ^ {\ lfloor (rn) / s \ rfloor} _ {k = 0} (-1) ^ k & \ binom {n} {k}\\ &\binom{r\!-s\!\cdot\!k\!-\!1}{n\!-\!1} \end{split}P(r,n,s)=sn1k=0∑⌊(r−n)/s⌋(−1)k(kn)(n−1r−s⋅k−1 )
Однако мы также можем попробовать решить эту проблему вручную. Один из подходов состоит в том, чтобы найти общее количество возможных сумм. С парой обычных игральных костей мы можем получить 2,3,4,5,6,7,8,9,10,11,12 , но эти результаты не эквивалентны !
Один из подходов состоит в том, чтобы найти общее количество возможных сумм. С парой обычных игральных костей мы можем получить 2,3,4,5,6,7,8,9,10,11,12 , но эти результаты не эквивалентны !
Взгляните; есть только один способ получить 2 : 1+1 , но для 4 есть три разных возможности: 1+3 , 2+2 , 3+1 , и 12 есть, опять же, только один вариант: 6+6 . Оказывается, 7 является наиболее вероятным результатом с шестью вариантами: 1+6 , 2+5 , 3+4 , 4+3 , 5+2 и 6+ 1 . Количество перестановок с повторениями в этом наборе равно 36 . Наш калькулятор перестановок может быть полезен для поиска перестановок для других типов игральных костей. Мы можем оценить вероятности как отношение благоприятных исходов ко всем возможным исходам: P(2) = 1/36 , P(4) = 3/36 = 1/12 , P(12) = 1/36 , P(7) = 6/36 = 1/6 .
Чем больше игральных костей, тем ближе функция распределения сумм к нормальному распределению. Как и следовало ожидать, по мере увеличения количества игральных костей и граней все больше времени уходит на оценку результата на листе бумаги. К счастью, это не относится к нашему калькулятору вероятности игры в кости!
Вероятность выпадения суммы из множества, не ниже X — как и в предыдущей задаче, мы должны найти все результаты, которые соответствуют начальному условию, и разделить их на количество всех возможностей. Учитывая набор из трех десятигранных игральных костей, мы хотим получить сумму не менее 27 . Как мы видим, мы должны сложить все перестановки для 27 , 28 , 29 и 30 , то есть 10, 6, 3 и 1 соответственно. Всего из 1000 возможностей 20 хороших исходов, поэтому конечная вероятность: P(X ≥ 27) = 20/1000 = 0,02 .

Вероятность выпадения суммы из множества, не выше X — процедура точно такая же, как и для предыдущей задачи, но складывать нужно только суммы меньше или равные заданной. Имея тот же набор костей, что и выше, какова вероятность того, что выпадет не более 26 ? Если бы вы делали это шаг за шагом, потребовались бы годы, чтобы получить результат (суммировать все 26 сумм). Но, если подумать, мы только что вычислили дополнительное событие в предыдущей задаче. Суммарная вероятность дополнительных событий точно равна 1 , поэтому вероятность здесь равна: P(X ≤ 26) = 1 — 0,02 = 0,98 .
Когда использовать калькулятор вероятности игры в кости?
Существует множество настольных игр, в которых вы по очереди бросаете кубик (или игральные кости), и результаты могут использоваться в различных контекстах. Допустим, вы играете в Dungeons & Dragons и атакуете. Класс брони вашего противника 17 . Вы бросаете 20-гранный кубик, надеясь, что выпадет как минимум 15 с вашим модификатором +2. Этого должно быть достаточно. При этих условиях вероятность успешной атаки равна 0,30 . Если вы знаете шансы на успешную атаку, вы можете выбрать, хотите ли вы атаковать эту цель или выбрать другую с лучшими шансами.
Класс брони вашего противника 17 . Вы бросаете 20-гранный кубик, надеясь, что выпадет как минимум 15 с вашим модификатором +2. Этого должно быть достаточно. При этих условиях вероятность успешной атаки равна 0,30 . Если вы знаете шансы на успешную атаку, вы можете выбрать, хотите ли вы атаковать эту цель или выбрать другую с лучшими шансами.
Или, может быть, вы играете в Поселенцы Катана и надеетесь, что на двух шестигранных кубиках выпадет ровно 8 , так как этот результат принесет вам драгоценные ресурсы. Просто воспользуйтесь нашим калькулятором вероятности в костях, и вы увидите, что вероятность составляет около 0,14 – вам лучше повезти на этом ходу!
Играть или пасовать? — Давай сыграем в игру!
Существуют различные виды игр, например, лотереи, где ваша задача состоит в том, чтобы сделать ставку в зависимости от шансов. Бросание игральных костей является одним из них. Хотя некоторые риски неизбежны, вы можете выбрать наиболее выгодный вариант и максимизировать свои шансы на победу. Взгляните на этот пример.
Взгляните на этот пример.
Представьте, что вы играете в игру, в которой у вас есть один из трех вариантов на выбор , а именно:
- Сумма пяти десятигранных костей не менее 30 ;
- Сумма пяти 12-гранных костей не превышает 28 ;
- Сумма пяти 20-гранных костей не меньше 59 .
Вы выиграете, только если выпадет выбранный вами вариант. Вы также можете отказаться, если чувствуете, что ничего из этого не произойдет. Интуитивно трудно оценить наиболее вероятный успех, но с нашим калькулятором вероятности в костях для оценки всех вероятностей требуется всего лишь мгновение ока.
Полученные значения:
- P₁ = 0,38125 для 10-гранного игрального кубика;
- P₂ = 0,3072 для 12-гранной кости; и
- P₃ = 0,3256 для 20-гранной кости.
Вероятность успешного прохода равна произведению дополнительных событий остальных вариантов:
- P₄ = (1-P₁) · (1-P₂) · (1-P₃) = 0,61875 · 0,6928 · 0,6744 = 0,2891 .

Мы видим, что самый благоприятный вариант — первый, а прохождение — наименее вероятное событие. Мы не можем гарантировать, что вы всегда будете выигрывать, но мы настоятельно рекомендуем вам выбрать для игры 10-гранный набор костей.
Часто задаваемые вопросы
Что такое вероятность?
Вероятность определяет, насколько вероятны определенные события . Простая формула для вероятности: число желаемых исходов/количество возможных исходов . В настольных играх или азартных играх вероятность используется для определения вероятности выпадения определенного числа , например, какова вероятность получения определенного числа одним кубиком?
Сколько возможных исходов может быть при бросании двух игральных костей?
Есть 36 исходов при бросании двух игральных костей . Для одного игрального кубика есть шесть граней, и для любого броска есть шесть возможных исходов . Для две кости , вы должны перемножить количество возможных исходов вместе, чтобы получить 6 × 6 = 36 . При последующих бросаниях просто умножьте результат на 6 . Если вы используете игральные кости другой формы, вместо 6 введите число их граней .
Для две кости , вы должны перемножить количество возможных исходов вместе, чтобы получить 6 × 6 = 36 . При последующих бросаниях просто умножьте результат на 6 . Если вы используете игральные кости другой формы, вместо 6 введите число их граней .
Какова вероятность того, что при броске 2 игральных костей выпадет 7?
Это 1/6 или 0,1666667 . Предположим, что всего 7 встречается хотя бы один раз . На 2 игральные кости есть 6 способов бросить сумму 7 — (1,6), (2,5), (3,4), (4,3), (5,2), (6 ,1) . Общее количество комбинаций для пары кубиков равно 36 . Таким образом, вероятность суммирования до 7 равна 6/36 = 1/6 = 0,1666667 .
Сколько раз я выбрасываю 5 на паре игральных костей?
20 . Предположим, что пару игральных костей бросают 180 раз .

 Таким образом, общее количество результатов может быть равно 2, и
Таким образом, общее количество результатов может быть равно 2, и 
 е. только 1 пара
е. только 1 пара





Leave A Comment