ТОП-50 Важнейших формул по математике — Математика — Теория, тесты, формулы и задачи
- Главная —
- Формулы и прочее —
- Математика: ТОП-50 Формул
Знание формул по математике является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по математике, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении математических задач. На этой странице сайта представлены 50 важнейших формул по математике.
Изучать ТОП-50 Важнейших формул по математике онлайн:
- Назад
- Вперёд
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше.

- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Графики важнейших функций и их преобразования — Математика — Теория, тесты, формулы и задачи
- Главная —
- Формулы и прочее — org/ListItem»> Математика: Графики функций
На этой странице представлены графики важнейших функций, изучаемых в школьном курсе математики. Также представлены примеры преобразования этих графиков в различных типичных ситуациях (рассмотрены случаи когда графики смешаются вдоль осей, симметрично отражаются относительно различных осей). Представлен также вид некоторых графиков функций с модулями. Знание того, как выглядят графики основных математических функций, а также того, как они преобразовываются в различных ситуациях, может очень помочь при решении различных сложных задач на экзаменах.
Изучать графики основных функций и их преобразования онлайн:
- Назад
- Вперёд
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте.

- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике.
 Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка.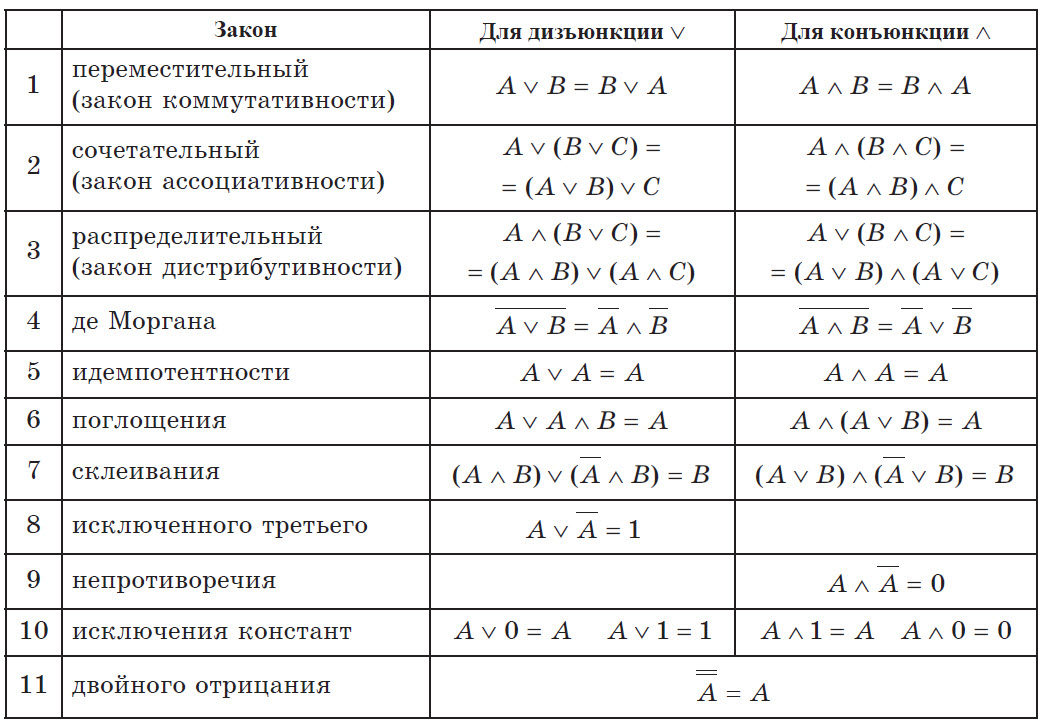
Алгебраические формулы — различные алгебраические формулы, используемые в математике
Алгебраические формулы — это основные формулы, используемые для упрощения алгебраических выражений. Алгебраические формулы составляют основу для решения различных сложных задач. Алгебраические формулы полезны при решении алгебраических уравнений, квадратных уравнений, многочленов, уравнений тригонометрии, вероятностных вопросов и других.
Алгебраические формулы – тождества
Тождество – это уравнение, истинное во всех смыслах для любых значений, присвоенных переменным. Алгебраические тождества используются для решения различных уравнений. Для алгебраических тождеств LHS всегда равно RHS.
Алгебраические идентичности
Некоторые важные алгебраические идентичности:
| (A + B) 2 | A 2 + B 2 + 2AB | + B 2 + 2AB | |||
| ( | ( | (7 ( | (7 (7 ( | (7 ( (2 (7 ( ( (2 . | a 2 + b 2 – 2ab |
| (a + b)(a – b) | a 2 – b 2 | ||||
| (x + a)(x + b ) | х 2 + 2(а + б) + аб |
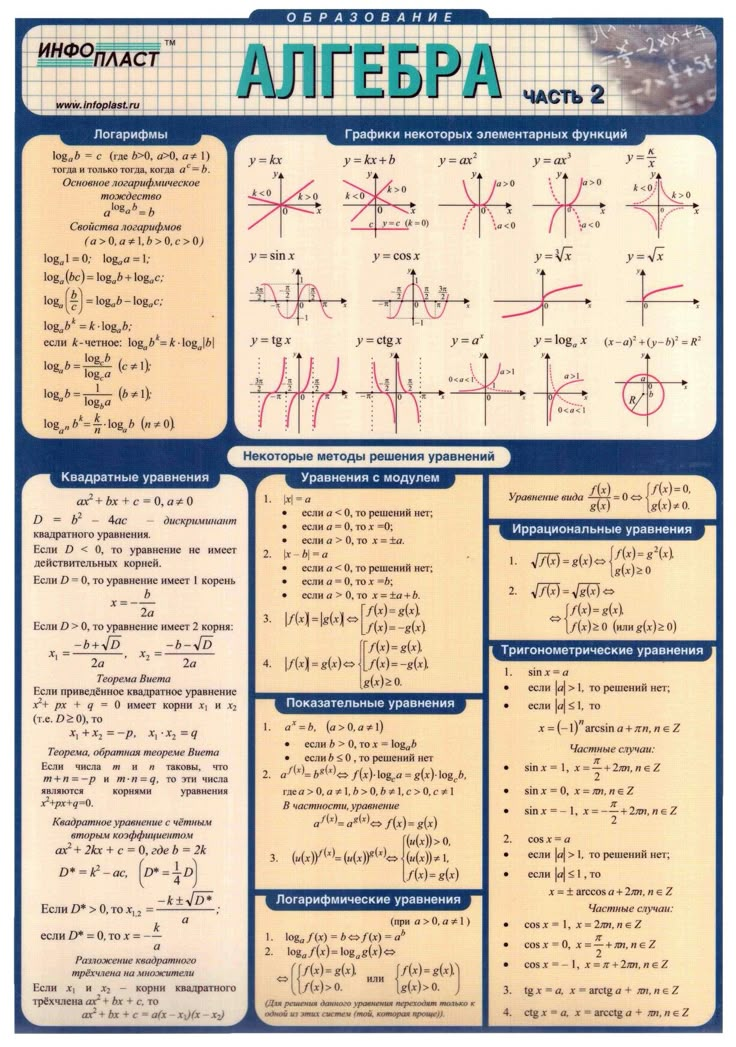
Что такое алгебраические формулы?
Алгебраические формулы — это уравнения, требующие алгебраического выражения по обе стороны от «равно», т. е. как по левой, так и по правой стороне. Алгебраические формулы, как правило, верны для всех значений. Алгебраическая формула упрощает алгебраические уравнения и требуется для решения различных математических задач. Алгебраические формулы для различных классов обсуждаются ниже в этой статье.
Алгебраические формулы для 8-го класса
Алгебраические формулы для 8-го класса обсуждаются ниже в этой статье. Для трех переменных a, b и c различные алгебраические формулы таковы:
- (A + B) 2 = A 2 + 2AB + B 2
- (A — B) 2 = A 2 — 2AB + B 2 9007 (A + + 9007 (A + + 9007 (A + 9007 (A + + 9007 (A + 9007 (A + 9007 (A + 9007 (A + (A + 9007 (A + 9007 (A + 9007 (A + 9007 (A + 9007 (A + 9007 (A + 9007 (A + 9007 (A + 9007 (A + 9007 (AST B) (A — B) = A 2 — B 2
- (A + B) 3 = A 3 + 3A 2 B + 3AB 2 + B 3
- 2 + B 3
- + B 3
- 7.
 (а – б) 3 = а 3 – 3а 2 б + 3аб 2 – б 3
(а – б) 3 = а 3 – 3а 2 б + 3аб 2 – б 3 - а 3 + б 3 = (a + b)(a 2 – ab + b 2 )
- a 3 – b 3 = (a – b)(a 2 + ab + b6 2 )
- (a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2bc + 2ca
Формулы алгебры для класса 9
полезный. Они полезны для вычисления очень сложных задач на умножение и деление. Экспоненциальная форма 3 2 = 9 можно легко преобразовать в логарифмическую форму, как log 3 9 = 2. Кроме того, сложное умножение и деление можно легко преобразовать в сложение и вычитание, следуя логарифмическим формулам.
Наиболее часто используемые важные логарифмические формулы обсуждаются ниже: а х – бревно а у
.
 Законы экспоненты используются для решения задач с большей степенью. Некоторые из общих законов показателей степени с одинаковыми основаниями, имеющими разные степени, и разными основаниями, имеющими одинаковую степень, полезны для решения сложных экспоненциальных членов. Более высокие экспоненциальные значения могут быть легко решены без какого-либо расширения экспоненциальных членов. Эти экспоненциальные законы также полезны для вывода некоторых логарифмических законов.
Законы экспоненты используются для решения задач с большей степенью. Некоторые из общих законов показателей степени с одинаковыми основаниями, имеющими разные степени, и разными основаниями, имеющими одинаковую степень, полезны для решения сложных экспоненциальных членов. Более высокие экспоненциальные значения могут быть легко решены без какого-либо расширения экспоненциальных членов. Эти экспоненциальные законы также полезны для вывода некоторых логарифмических законов.- A M × A N = A M + N
- A M /A N = A M — N
- (A M ) 9. 9. 9. 9. 9. . 9. 9. 9. 9. 9. 9. 9. 9. 9. 9. . 9. млн.
- (AB) M = A M × B M
- A 0 = 1
- A -M = 1/ M 9007 9007 4007 9007 4007 4007 4007 4007 4007 40074
- Решение с использованием алгебраического метода
- Использование квадратичной формулы
- n-й член, a n = a + (n – 1) d 9 2 ,…}
- N -й срок, A N = A R N — 1
- Сумма первых n терминов, S N = a (1 — R N 9007) / (1 — R N 9007) / (1 — R ) / (1 — R ) / (1 — R ) / (1 — R ) / (1 — R ). 1 – r)
- Сумма бесконечных членов при r<1, S = a / (1 – r)
Алгебраические формулы для 11-го класса
Алгебраические формулы для 11-го класса, которые в основном используются, представляют собой формулы перестановок и комбинаций.
 Если требуются разные расположения r вещей из n доступных вещей, то используются формулы перестановки, тогда как формулы комбинаций используются для нахождения различных групп r вещей из n доступных вещей.
Если требуются разные расположения r вещей из n доступных вещей, то используются формулы перестановки, тогда как формулы комбинаций используются для нахождения различных групп r вещей из n доступных вещей.Важные формулы перестановок и комбинаций:
Формула факториала:
n! = n × (n – 1) × (n – 2) × … × 3 × 2 × 1
Формулы перестановки:
n P r = n! / (н – р)!
Комбинированная формула:
n C r = n!/[r!(n−r)!]
Биномиальная теорема — еще одна формула, чрезвычайно важная для учащихся 11-го класса.
Формулы алгебры для 12-го класса
Важные формулы для учащихся 12-го класса включают формулы векторной алгебры. Эти формулы обсуждаются ниже,
Возьмите любые три вектора, a, b и c, затем
- Для вектора a = x i+y j+z k тогда величина |a| =√(x 2 +y 2 +z 2 ).

- Единичный вектор вдоль a равен a / |a|
- Скалярное произведение двух векторов a и b определяется как a ⋅ b = |a| |б| cos θ
, где θ — угол между векторами a и b. - Перекрестное произведение векторов a и b определяется как a × b = |a| |б| sin θ
, где θ — угол между векторами a и b. - Скалярное тройное произведение трех векторов a, b и c определяется как [a b c ] = a ⋅ (b × c) = (a × b) ⋅ c.
Also, Check
- Algebraic Identities of Polynomials
- Vector Algebra
- Percentage Formula
Solved Examples on Algebra Formulas
Example 1: Find out the value of the term, (2x + 3 ) 2 с помощью алгебраических формул.
Решение:
Использование алгебраической формулы,
(A + B) 2 = A 2 + B 2 + 2AB
(2x + 3) 2 = (2x) 2
+ 3 2 = (2x) 2 + 3 2 = (2x) 2 + 3 2 = (2x) 2 + 3) 2 + 2 × 2x × 3(2x + 3) 2 = 4x 2 + 9 + 12x
используя алгебраические формулы.

Решение:
Используя алгебраическую формулу,
(a – b) 2 = a 2 + b 2 – 2ab
(5x – 3y) 2 = (5x) 2 – 9×9 9017 + (3y) 2 90 × 3y
(5 – 3) 2 = 25x 2 + 9y 2 – 30xy
Пример 3. Найдите значение 105×95 с помощью алгебраических формул.
Решение:
Используя алгебраическую формулу,
(a + b)(a – b) = a 2 – b 2
105 × 95 = (100+5) (100-5)
= 100 2 -5 2
= 10000-25
= 9975Пример 4: Найдите коренные уравнения. x 2 +6x+8=0 с использованием алгебраических формул для квадратных уравнений.
Решение:
Данное квадратное уравнение равно x 2 + 6x + 8 = 0
Сравнивая вышеприведенное уравнение с ax 2 +bx+c=0, c=1, a=1, =8
Подставляя значения в квадратную формулу, получаем 8))] / 2(1)
= [−6 ± √(36 − 4(1)(8))] / 2
= [−6 ± √(36 − 32)] / 2
= [−6 ± √4] / 2
= (-6 + 2)/2 и (-6 – 2)/2
= -4/2 и -8/2
= -2 и -4Таким образом, значения x равны -2 и -4
Часто задаваемые вопросы по формулам алгебры
Вопрос 1: Какова формула числа 2 – б 2 по алгебре?Answer:
Вопрос 2: Что такое алгебраические выражения?The formula for a 2 – b 2 defined in algebra is
a 2 – b 2 = (a+b)(a-b)
Эту формулу также называют формулой разности квадратов.

Ответ:
Вопрос 3: Каковы три основные формулы алгебры?Алгебраические выражения представляют собой комбинации переменных и констант с использованием арифметических операций, таких как сложение, вычитание, умножение и деление.
Пример: 11 x 3 + 5x — алгебраическое выражение. Это выражение имеет два члена 11 х 3 и 5х.
Ответ:
Вопрос 4: Напишите упрощенную форму (a+b)².Три основных формула алгебры:
- (A + B) 2 = A 2 + B 2 + 2AB 4242424242424242424242424242424242424242424242424242424242424242424242424242424242424242424242424242424242424242424242424 2 . ) 2 = а 2 + б 2 – 2ab
- (a + b)(a – b) = a 2 – b 2

 10
10«Квадратная формула» — важная алгебраическая формула, с которой знакомятся учащиеся 10-го класса. Она используется для решения общих квадратных уравнений. Общая форма любого квадратного уравнения ax 2 + bx + c = 0 , где x — переменная a, b — коэффициент, а c — константа. Есть два способа решения этого квадратного уравнения.
Другими важными формулами, используемыми в классе 10, являются


 Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.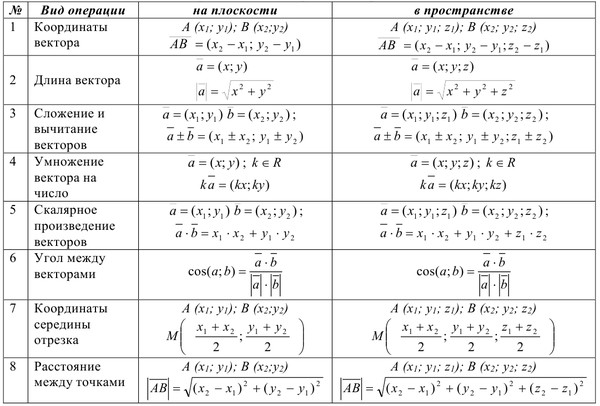 (а – б) 3 = а 3 – 3а 2 б + 3аб 2 – б 3
(а – б) 3 = а 3 – 3а 2 б + 3аб 2 – б 3  Если требуются разные расположения r вещей из n доступных вещей, то используются формулы перестановки, тогда как формулы комбинаций используются для нахождения различных групп r вещей из n доступных вещей.
Если требуются разные расположения r вещей из n доступных вещей, то используются формулы перестановки, тогда как формулы комбинаций используются для нахождения различных групп r вещей из n доступных вещей.



Leave A Comment